Testing Hungarian oak (Quercus frainetto Ten.) provenances in Romania
iForest - Biogeosciences and Forestry, Volume 13, Issue 1, Pages 9-15 (2020)
doi: https://doi.org/10.3832/ifor3108-012
Published: Jan 08, 2020 - Copyright © 2020 SISEF
Research Articles
Abstract
In this study ten Hungarian oak provenances from Southern Romania were tested in two comparative trials 10 years after planting. The diameter at breast height (dbh) and tree height (Th) were measured in family progenies and the survival rate was determined. In both trials, the local provenances (Bals and Seaca 2) revealed superior fitness in terms of growth and adaptability traits, confirming the recommendation of using local provenances with priority in afforestation activities. Based on the measured traits, families which ranked in the first ten positions at age 3 and age 10 years were identified in both trials. The analysis of variance revealed statistically significant differences in growth traits between provenances and families in both comparative trials. Duncan’s test for 5% transgression probability revealed different results for dbh and Th in terms of provenance homogeneity in the two test sites, with a superior homogeneity in the Aramadia trial for dbh and in the Bals trial for Th. Growth performances of the Hungarian oak provenances were significantly influenced by the experimental location and by the interactions between provenance, family and locality, suggesting that maximum precaution must be taken in the choice of forest reproductive materials to be planted in different environmental conditions. The family mean heritability (h2f) was significantly lower than the individual heritability (h2i), suggesting the possible adoption of an individual selection strategy in the next stage of the current breeding programme. The juvenile-adult correlations will be made at the age of 40 years and will take advantage of the results of this study to shorten the testing period for the selection of genetically improved material in Hungarian oak.
Keywords
Age-to-age Correlations, Breeding, Forest Steppe, Oaks’ Adaptability, Selection Strategy
Introduction
Hungarian oak (Quercus frainetto Ten.) is a tree species native to the Mediterranean and southeastern Europe (Albania, Bosnia and Herzegovina, Bulgaria, Croatia, Czech Republic, Greece, Italy, Macedonia, Romania, Serbia, Slovakia) and Asian Turkey. It has been formerly introduced in Slovenia and, despite the name, its native/non-native status in Hungary is still uncertain ([18], [17]). Previous research on the genetic diversity of oak species indicated that Q. frainetto belongs to the genus section Dascia, which is genetically close to Q. pubescens and clearly differentiated from Q. robur and Q. petraea ([14], [31], [2], [9], [15]).
The importance of Hungarian oak mainly comes from its ability to grow on highly compact soils in low productivity areas ([19]) and by its capacity of resprouting after fire ([24]). It is a meso-xerophilous species which grows well in the plain and forest-steppe areas ([10], [26], [1]). In some countries of the southeastern Europe (e.g., Greece, Bulgaria), Hungarian oak is the dominant deciduous oak species in terms of wood production ([28], [3], [21], [22], [25], [24]). Hungarian oak forests are listed under the EU Habitats Directive (code 9280 - [4]). Also, it is listed as a vulnerable species in Slovakia ([13]), while in Greece it is considered as the least tolerant to drought among oak species ([16]). In the United Kingdom, outside of its natural range, Q. frainetto showed the highest radial growth up to 10 years of age but the highest sensitivity to drought out of 5 oaks species at age of 45 years ([34]). In Bulgaria, during the seasonal drought period (August), its physiological activity is reduced, particularly in the oldest stands ([37]).
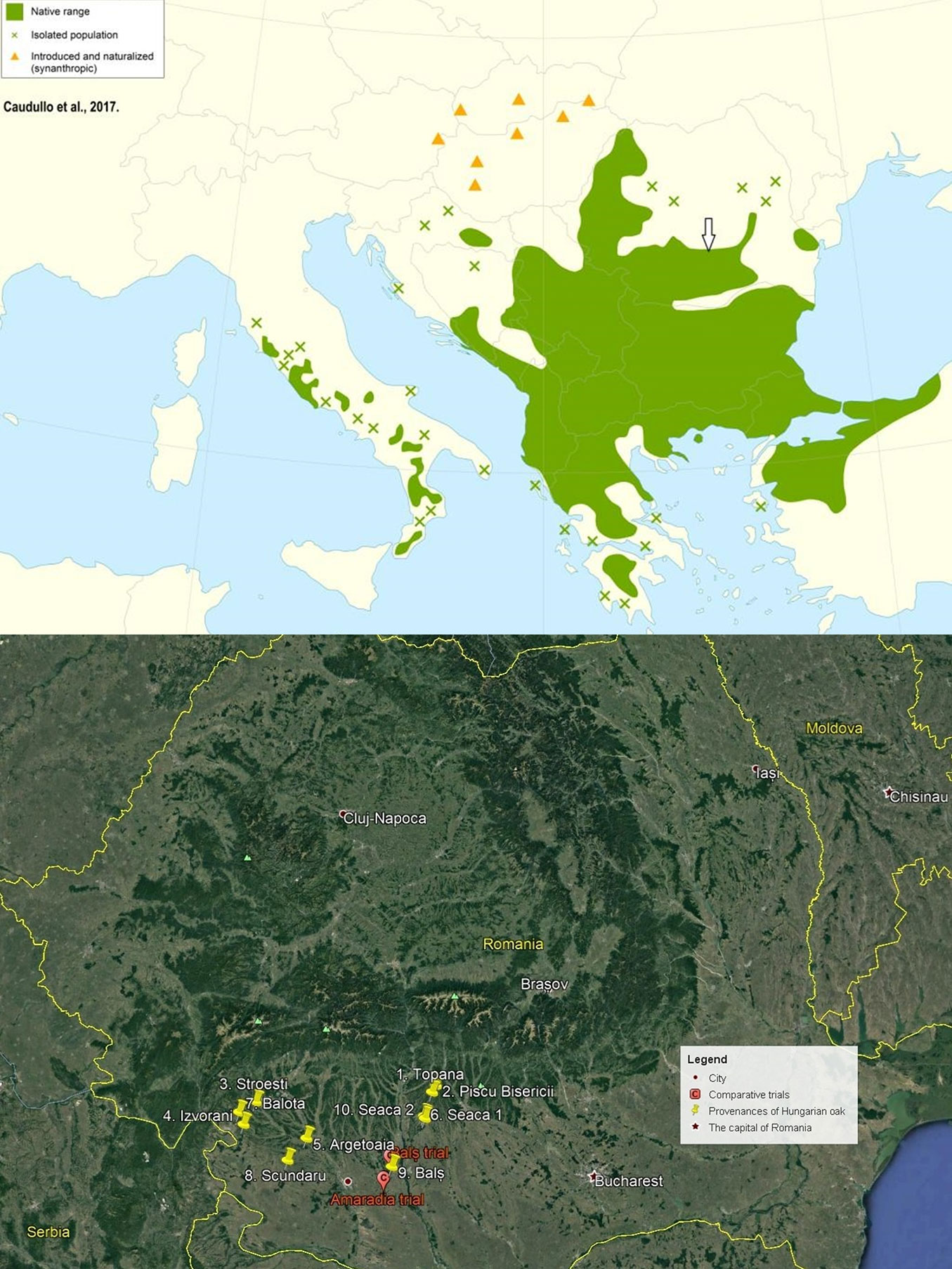
The Hungarian oak in Romania reaches the northern limit of its natural range (Fig. 1). Its current distribution in Romania comprises approximately 130.000 ha (which represents 2% of the total forest area), growing especially in the forest steppe of Oltenia and Muntenia regions. Here, the most extensive Hungarian oak forests of the whole natural range are found on the Cotmeana platform, where it can reach up to 80% of share in term of species composition (Seaca forest - [36]).
Fig. 1 - (top): Natural range of Hungarian oak (Quercus frainetto Ten.) in southeastern Europe (source: [6]); (bottom): locations of comparative trials (red pins) and sites of origin of the tested populations (yellow pins) in Romania.
Increasing the adaptability of the species by genetic improvement could greatly increase the ecological, economic and social values of Hungarian oak stands ([7]) as well as enhance the conservation of this species in its natural habitat. Genetic improvement programmes include the individual selection of plus-trees from the most valuable populations (including forest genetic resources and seed sources catalogues) and testing their progeny in multisite comparative trials ([39]). In general, Hungarian oak stands regenerate naturally in Romania, although there are many situations where gap filling, re-establishments or substitutions are required, in which forest reproductive materials originating from selected seed sources are needed ([5]). One of the most important challenges for Romanian forest geneticists is to identify, preserve, test and promote those tree species with high adaptability to the forest-steppe area of Southern Romania, and the Hungarian oak is undoubtedly one of these.
It has been reported that the adaptability of forest tree populations to climate change is, to some extent, determined by individual inbreeding levels ([20]). This study aims to analyse 10 Hungarian oak provenances from southern Romania, which have been tested in two comparative trials established in the same region. The main objectives were: (i) to identify the provenances showing the highest degree of adaptation and the best-performing families within them; (ii) to analyse the growth performances of local provenances; (iii) to determine the influence of the testing site and the interaction between locality, provenance, and family; (iv) to analyse the age-to-age correlations at the provenance and family levels as well as the correlations between traits and the ecological gradients of the site of origin of populations; (v) to determine the variance components and the narrow-sense heritability.
The obtained results will be used for determining the future juvenile-adult correlations in the current breeding programme.
Materials and methods
In this study, the term population will be used henceforth with the meaning of provenances’ origin.
Ten populations of Hungarian oak (Quercus frainetto Ten.) were selected across the natural distribution range of the species in Southern Romania (Fig. 1): two in the Oltenia plain (J2 provenance region) and eight in the Subcarpathian region of the Outer Southern Carpathians (C2 region - [30]). A preliminary field analysis was carried out aimed at the selection and description of populations known as seed sources and their most representative (plus-) trees, taking into account several relevant phenotypic traits (dbh, total height, pruning height, crown diameter).
The selected populations (i.e., sites of origin) had an elevation range from 220 to 420 m a.s.l., with average annual rainfall between 515 and 630 mm and annual average temperatures between 10.2 and 11.7 °C. All selected sites were characterized by predominantly pure Hungarian oak stands or mixed with 10% Turkey oak (Quercus cerris L.). The stand age was between 85 and 145 years.
To determine the genetic variation within the natural populations under different environmental conditions, two comparative trials were established with seedlings from seed harvested from the plus-trees of all 10 populations, taking advantage of the abundant fructification occurred in the autumn of 2003.
The experiment was carried out in two comparative trials with the following locations and environmental characteristics: (i) Bals trial (44° 24′ N‚ 24° 12′ E; altitude 320 m a.s.l.), Olt county, managed by the Bals forest district and located in V Bistrita production unit (plot 97E, area 0.81 ha) in an oak stand of medium productivity on luvosoil; (ii) Amaradia trial (44° 15′ N‚ 24° 08′ E; altitude 260 m a.s.l. - Fig. 2), Dolj county, managed by the Amaradia forest district and located in IV Viisoara production unit (plot 95A, area 1.0 ha) in a mixed oak stand (sessile oak, Turkey oak and Hungarian oak) of medium productivity on luvosoil.
Fig. 2 - The Amaradia comparative trials on Hungarian oaks provenances at age of 10 years (left) and the experimental design (right).
In both trials, the annual average temperature is 10.5 °C, with -2.8 °C in January (coldest month) and 20.8 °C in July (warmest month). Annual precipitation is 540 mm, 64% of that being registered in the bioactive vegetation season, from March to September ([29]).
The study material consisted of 10 Hungarian oak provenances, each composed of six families (maternal trees), tested in the two comparative trials described above. The experimental design is a split-plot type, with 10 populations and 6 families per population, established with 3 replications in the Bals trial and 4 replications in the Amaradia trial. In each unitary plot, the families were represented by 12 seedlings, planted with a scheme of 1.5 × 2 m (Fig. 2).
For the analysis of adaptive and growth performances, the following variables were measured: (i) survival rate (Sr, %) for each family; (ii) diameter at breast height (dbh, mm) and root collar diameter (Drc, mm), measured using an electronic calliper; (iii) total height (Th, m) measured at ages three and ten using a Vertex IV® instrument (Hanglöf AB, Långsele, Sweden).
The data obtained for all traits were processed using the software STATISTICA® ver. 10.0 (StatSoft Inc., Tulsa, OK, USA). The Kolmogorov-Smirnov test was applied to check the normal distribution of variables, and the assumptions of analysis of variance (ANOVA) were verified using Levene’s test. The total variance was split into the variance due to replications, provenances, families and the variance of error (residual) by applying the ANOVA test, corresponding to the adopted experimental design ([27], [38]) and the biological material type. The significance level of the differences was established using the Fisher’s (F) test for the transgression probabilities of 5%, 1% and 0.1%. The ranking of populations and their separation into homogeneous groups was achieved using the Duncan test for a 5% transgression possibility. The statistical analysis was based on individual tree measurements using the mathematical model developed by Nanson ([27] - eqn. 1)
where Yijk is the performance of the kth individual trees in the jth family in the ith replications, μ is the overall mean, αi is the effect of the ith replication, βj is the effect of the jth family, and εijk is the random error associated with the ijkth trees. This model allows for the analysis of the mean effect of the three factors. For the determination of the variance components needed to calculate the heritability a different statistical model was used, which also include the interaction among factors ([27]).
Provenances × localities interaction were investigated using factorial ANOVA, in which the total variance was calculated for locality, provenance, family and theirs interactions ([27]).
The narrow-sense individual heritability (h2i) and half-sib family mean heritability (h2f) were calculated as follows ([27] - eqn. 2, eqn. 3, eqn. 4):
where σ2Ph1 and σ2Ph2 are the phenotypic variances, σ2A is the additive genetic variance, σ2f is the family variance, σ2f×r is the family × replication interaction variance, σ2e is the variance within plot and r is the number of replications. In experiment with half-sib families σ2A = 4σ2f ([23]).
The genetic correlations were calculated as the ratio of the traits covariance and the square root of their additive genetic variances ([12]). Pearson’s correlations between the analysed traits and the ecological gradients of the provenances origin were also determined. Both type of correlations were calculated based on family means.
Results
Survival rate (Sr)
In assessing the genetic variability between provenances, the survival rate is an important indicator of adaptability for populations of different geographic origins when facing to new environmental conditions.
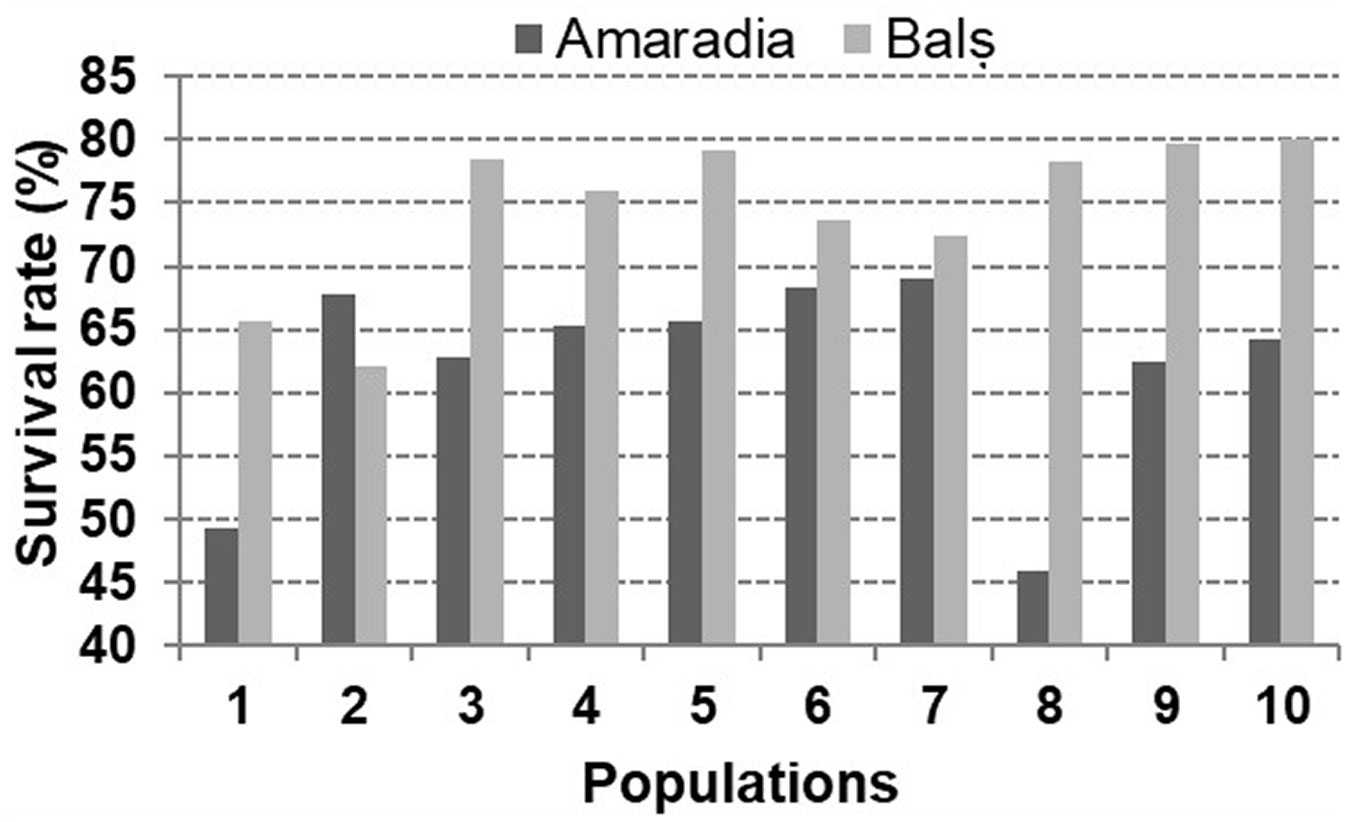
In the Amaradia trial, the survival rate had values ranging from 45.8% for the Scundaru population to 69.1% for the Balota population, with an average of 62.1% (Fig. 3). Among the families with the highest survival rate, families 1 and 2 from Piscul Bisericii reached 85% of survival, similar to family 5 from Balota. Of all the families tested in the Amaradia trial, at 10 years after plantation, 81% had survival rates over 50%.
Fig. 3 - Survival rate of the Hungarian oak provenances at age of 10 years in the two comparative trials (Amaradia and Bals). The population code is the same as in Fig. 1.
In the Bals trial, the survival rate had values ranging from 62% for the Piscul Bisericii population to 80% for Seaca 2 population, with an average of 74% (Fig. 3). The family with the highest survival rate (97%) belongs to the Izvorani population, followed by families from Seaca 2 (5 out of the 6 tested families had survival rate over 79%).
Analyses of the intrapopulational variability in the Amaradia trial showed variation coefficients ranging from 20% (Izvorani population) to 54% (Scundaru), while in the Bals trial values ranged between 19% (Bals) and 40% (Topana population). The homogeneity was higher in the Bals trial for 70% of the tested families, the local provenance (Bals) being the most homogeneous.
Diameter at breast height (dbh)
In the Amaradia trial, the average dbh value was 40.9 mm, with values between 37.0 mm (Balota) and 44.4 mm (Izvorani - Tab. 1). At age 10, 1.8% of the measured trees had values above the mean by two standard deviations (dbh > 79.3 mm). The highest average family value (52.8 mm) was found for family 6 of the Seaca 2 population, and the families 2, 3 and 5 from Izvorani had mean dbh values between 49.8 and 51.6 mm. The analysis of variance revealed a significant influence (p < 0.05) of provenance and an insignificant influence of family on dbh (Tab. 2).
Tab. 1 - Results of the Duncan test for diameter at breast height (dbh) in the Amaradia and Bals trials. (Hom5%): homogeneous groups for 5% transgression probability.
| Provenance | Amaradia trial | Provenance | Bals trial | |||||
|---|---|---|---|---|---|---|---|---|
| dbh (mm) |
Hom5% | dbh (mm) |
Hom5% | |||||
| Izvorani | 44.4 | *** | - | Bals | 24.6 | *** | - | - |
| Seaca 2 | 44.2 | *** | - | Seaca 2 | 22.7 | *** | *** | - |
| Piscul Bisericii | 41.4 | *** | *** | Scundaru | 22.7 | *** | *** | - |
| Bals | 41.2 | *** | *** | Stroiesti | 20.8 | - | *** | *** |
| Argetoaia | 41.2 | *** | *** | Seaca 1 | 20.1 | - | *** | *** |
| Stroiesti | 40.9 | *** | *** | Topana | 20.0 | - | *** | *** |
| Scundaru | 39.4 | *** | *** | Piscul Bisericii | 19.9 | - | *** | *** |
| Seaca 1 | 39.4 | *** | *** | Izvorani | 19.6 | - | *** | *** |
| Topana | 38.0 | - | *** | Balota | 19.3 | - | - | *** |
| Balota | 37.0 | - | *** | Argetoaia | 18.8 | - | - | *** |
Tab. 2 - Results of the ANOVA for dbh and total height in the Amaradia and Bals trials. (SS): sum of squares; (DF): degrees of freedom; (MS): mean square; (F): Fisher’s test; (*): p < 0.05; (**): p < 0.01; (***): p < 0.001.
| Variable | Source of variation |
Amaradia trial | Bals trial | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SS | DF | MS | F | SS | DF | MS | F | ||
| dbh | Replication | 61 | 3 | 20 | 0.055 | 4662.2 | 2 | 2331.1 | 24.3*** |
| Provenance | 7732 | 9 | 859 | 2.349* | 3660.7 | 9 | 406.7 | 4.24*** | |
| Family | 761 | 5 | 152 | 0.416 | 2922.8 | 5 | 584.6 | 6.093*** | |
| Error | 520124 | 1422 | 366 | - | 104855.0 | 1093 | 95.9 | - | |
| Total height | Replication | 8.43 | 3 | 2.81 | 4.49** | 10.64 | 2 | 5.319 | 27.0*** |
| Provenance | 18.30 | 9 | 2.03 | 3.25* | 7.54 | 9 | 0.838 | 4.25*** | |
| Family | 0.18 | 5 | 0.04 | 0.06 | 4.11 | 5 | 0.821 | 4.17*** | |
| Error | 890.28 | 1422 | 0.63 | - | 215.37 | 1093 | 0.197 | - | |
In the Bals comparative trial, the average dbh value was 20.8 mm, ranging from 18.8 mm (Argetoaia population) and 24.6 mm (Bals population - Tab. 1). Out of the 1110 trees in the trial, 46 (4.1%) showed dbh values exceeding the overall mean by more than two standard deviations (SD = 10.2). The highest dbh mean values were found for families 1, 2 and 6 belonging to the Bals population and for families 2 and 3 from Seaca 2. All the factors considered showed a highly significant effect (p < 0.001) on dbh after ANOVA (Tab. 2).
The Duncan test for the transgression probability of 5% showed a superior homogeneity in the Amaradia trial, separating the tested populations in two homogeneous groups including 8 and 2 provenances, respectively. In the Bals trial, three groups were detected, with the first one composed by only three provenances (Tab. 1).
Significant differences in mean dbh between trials are likely due the fact that in Bals cut-backs were performed after seedling establishment to prevent dieback caused by frequent droughts in that area.
Total height (Th)
In the Amaradia trial, the average value of Th was 3.06 m, ranging from 2.89 m for the Topana population to 3.27 m for the Izvorani population (Tab. 3). Out of the total number of tested trees, 1.5% exceed the average height value plus two standard deviations (SD = 0.8) showing Th > 4.66 m. The highest values were recorded for the progeny from Seaca 2 and Argetoaia populations. Analysis of performances of each family revealed that family 2 from the Izvorani population had the highest Th (3.66 m), while the smallest mean Th value was recorded by the fourth family of the Scundaru population (2.36 m). ANOVA revealed a highly significant influence (p < 0.001) of provenance and a significant influence (p < 0.01) of the replication on Th (Tab. 2).
Tab. 3 - Results of the Duncan test for tree height in the Amaradia and Bals trials. (Hom5%): Homogeneous groups for 5% transgression probability.
| Provenance | Amaradia trial | Provenance | Bals trial | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Height (m) | Hom5% | Height (m) | Hom5% | ||||||
| Izvorani | 3.27 | *** | - | - | - | Bals | 2.18 | *** | - |
| Seaca 2 | 3.21 | *** | *** | - | - | Seaca 2 | 2.14 | *** | - |
| Argetoaia | 3.11 | *** | *** | *** | - | Scundaru | 2.13 | *** | - |
| Stroiesti | 3.07 | *** | *** | *** | *** | Stroiesti | 2.10 | *** | *** |
| Bals | 3.04 | - | *** | *** | *** | Balota | 1.99 | - | *** |
| Scundaru | 3.00 | - | - | *** | *** | Izvorani | 1.99 | - | *** |
| Piscul Bisericii | 3.00 | - | - | *** | *** | Argetoaia | 1.98 | - | *** |
| Seaca 1 | 2.99 | - | - | *** | *** | Piscul Bisericii | 1.98 | - | *** |
| Balota | 2.96 | - | - | *** | *** | Seaca 1 | 1.97 | - | *** |
| Topana | 2.89 | - | - | - | *** | Topana | 1.97 | - | *** |
In the Bals trial, the average value of Th was 2.06 m, with a range between 1.97 m in Topana and Seaca 1 and 2.18 m in the Bals population (Tab. 3). The analysis of family performances revealed that family 2 from Bals and family 3 from Seaca 2 population had the highest average Th (2.43 m and 2.36 m, respectively). The smallest Th values in this trial was for family 4 from the Piscul Bisericii population, with an average of 1.63 m. All the factors considered showed a significant effect (p < 0.001) on Th after ANOVA (Tab. 2).
The Duncan test for the transgression probability of 5% showed a superior homogeneity in the Bals trial, separating the tested populations in two homogeneous groups including 4 and 6 provenances, respectively (Tab. 3). Contrastingly, four groups were detected in the Amaradia trial, the first being composed of four provenances.
Provenance and family ranking at 3 and 10 years
The analysis of the growth performance of trees (dbh and height) at ages 3 and 10 years allowed to track the evolution of the ranking of families and provenances in the comparative trials. In the Aramadia trial, Izvorani and Seaca 2 populations ranked first at both 3 and 10 years of age, while Balota was the last one (Tab. 4). Moreover, six out of the best 10 ranking families at age 3 were also present in the top ranking at the age of 10 years, and three of them were from the Izvorani provenance, which had the best performance for both growth traits at the age of 10 years.
Tab. 4 - Growth ranking evolution of the tested provenances.
| Trial | dbh ranking 10 years |
Provenance | Dcollar ranking 3 years |
Th ranking 10 years |
Provenance | Th ranking 3 years |
|---|---|---|---|---|---|---|
| Amaradia | 1 | Izvorani | 3 | 1 | Izvorani | 3 |
| 2 | Seaca 2 | 1 | 2 | Seaca 2 | 2 | |
| 3 | Piscul Bis. | 5 | 3 | Argetoaia | 6 | |
| 4 | Bals | 2 | 4 | Stroesti | 7 | |
| 5 | Argetoaia | 8 | 5 | Bals | 5 | |
| 6 | Stroesti | 9 | 6 | Scundaru | 9 | |
| 7 | Scundaru | 6 | 7 | Piscul Bis. | 1 | |
| 8 | Seaca 1 | 7 | 8 | Seaca 1 | 4 | |
| 9 | Topana | 4 | 9 | Balota | 8 | |
| 10 | Balota | 10 | 10 | Topana | 10 | |
| Bals | 1 | Bals | 2 | 1 | Bals | 5 |
| 2 | Seaca 2 | 1 | 2 | Seaca 2 | 1 | |
| 3 | Scundaru | 3 | 3 | Scundaru | 3 | |
| 4 | Stroesti | 4 | 4 | Stroesti | 6 | |
| 5 | Seaca 1 | 7 | 5 | Balota | 10 | |
| 6 | Topana | 8 | 6 | Izvorani | 4 | |
| 7 | Piscul Bis. | 5 | 7 | Argetoaia | 8 | |
| 8 | Izvorani | 6 | 8 | Piscul Bis. | 7 | |
| 9 | Balota | 10 | 9 | Seaca 1 | 9 | |
| 10 | Argetoaia | 9 | 10 | Topana | 2 |
In the Bals trial, the local provenance (Bals) registered the highest values for dbh and Th at both ages (Tab. 4). In addition, the Seaca 2 and Scundaru provenances remained at the top of ranking since age 3 to age 10. Conversely, the Argetoaia and Topana populations were at the bottom of the rank order for dbh and Th, respectively (Tab. 4). At the family level, out of the best 10 ranking families at age of 3 years, four for dbh and six for Th were also in the top 10 at the age of 10 years. For dbh, the best-performing families were from Bals and Seaca 2 (two from each), while for Th, besides the two provenances mentioned above (Bals with two families), Scundaru, Stroesti and Topana were in the top ten at both ages.
Correlations
In the Amaradia and Bals comparative trials, the age-to-age correlations were, in general, significant for both growth traits (Tab. 5), the r value ranging between 0.26 and 0.60.
Tab. 5 - Age-to-age genetic correlations and the effect of the ecological gradients (phenotypic correlations) of the provenance origin in Amaradia (above diagonal) and Bals (below diagonal) trials. (Drc3y): root collar diameter at age three; (Th3y, Th10y): trees height at age three and ten; (Dbh10y): breast height diameter at age ten; (Lat N): north latitude; (Lon E): east longitude; (Alt): altitude (a.s.l.); (MAT): mean annual temperature; (SAP): sum of the annual precipitation; (*): p < 0.05.
| Factors | Drc3y | Th3y | Dbh10y | Th10y | Sr10y | Lat N | Lon E | Alt | MAT | SAP |
|---|---|---|---|---|---|---|---|---|---|---|
| Drc3y | - | 0.49* | 0.40* | 0.30* | -0.04 | -0.10 | 0.26* | 0.11 | -0.05 | -0.09 |
| Th3y | 0.26* | - | 0.45* | 0.35* | 0.16 | 0.03 | 0.18 | 0.19 | -0.04 | 0.02 |
| Dbh10y | 0.38* | 0.43* | - | 0.59* | 0.13 | -0.09 | 0.01 | 0.08 | 0.01 | 0.00 |
| Th10y | 0.35* | 0.44* | 0.60* | - | 0.14 | -0.09 | -0.13 | -0.01 | 0.13 | 0.08 |
| Sr10y | 0.20 | 0.07 | 0.20 | 0.26* | - | 0.04 | -0.04 | 0.03 | 0.10 | 0.21 |
| Lat N | -0.20 | -0.20 | -0.29* | -0.30* | -0.40* | - | - | - | - | - |
| Lon E | 0.13 | 0.06 | 0.18 | 0.06 | -0.21 | - | - | - | - | - |
| Alt | -0.07 | -0.16 | -0.23 | -0.28* | -0.39* | - | - | - | - | - |
| MAT | -0.12 | -0.18 | -0.09 | -0.05 | 0.11 | - | - | - | - | - |
| SAP | -0.28* | -0.34* | -0.35* | -0.32* | -0.22 | - | - | - | - | - |
In both trials, more intensive genetic correlations were found between Th and dbh at the same age (Tab. 5), compared to age-to-age correlations. In Bals trial, at age 10 a significant and positive correlation was detected between Th and Sr, while dbh and Sr value were also positively correlated, though not significantly. Moreover, a significant correlation of the latitude and altitude of the site of origin (provenance) with dbh and Th at age 10 was detected, while in Amaradia such correlation was not significant at age 10 (Tab. 5). This finding seems to contradict the expectations, as the Amaradia trial is located further south and at lower altitude than the Bals trial.
Genotype × environment interaction
For both the analysed traits, a highly significant effect of locality (experimental site) was detected (p < 0.001). Also, the differences between provenances were highly significant (Tab. 6), while differences between families of the same provenance were not significant. Furthermore, the locality × provenances and locality × provenances × families interactions were statistically significant, indicating that provenances did react differently to the change of the environmental conditions (Tab. 6).
Tab. 6 - Variance partition and genotype × environment interaction in Hungarian oak progeny trials. (DF): degrees of Freedom; (MS): mean square; (F): Fisher’s test; (*): p < 0.05; (**): p < 0.01; (***): p < 0.001.
| Variable | Factors | DF | MS | F |
|---|---|---|---|---|
| DBH | Locality (L) | 1 | 225342 | 923*** |
| Provenance (P) | 9 | 800 | 3.28*** | |
| Family (f) | 5 | 399 | 1.64 | |
| L × P | 9 | 521 | 2.14* | |
| L × F | 5 | 501 | 2.05 | |
| P × F | 45 | 416 | 1.71** | |
| L × P × f | 45 | 358 | 1.47* | |
| Error | 2430 | 244 | - | |
| Height | Locality (L) | 1 | 581 | 1371*** |
| Provenance (P) | 9 | 1.44 | 3.40*** | |
| Family (f) | 5 | 0.55 | 1.29 | |
| L × P | 9 | 1.1 | 2.61* | |
| L × F | 5 | 0.68 | 1.60 | |
| P × F | 45 | 1.08 | 2.54*** | |
| L × P × f | 45 | 0.84 | 1.98*** | |
| Error | 2430 | 0.42 | - |
Heritability
The narrow-sense individual heritability showed a high genetic control for the growth traits analysed, especially for dbh (Tab. 7). In the Amaradia trial, h2i was 0.39 for dbh and 0.28 for Th, while in Bals the highest heritability for dbh (0.46) and the lowest for Th (0.1) were recorded. The family mean heritability (h2f) at age of 10 years was much lower, varying between 0.05 and 0.21, the best result being registered in Bals trial for dbh (Tab. 7).
Tab. 7 - Variance components, narrow-sense individual heritability (h2i) and family mean heritability (h2f) at age 10 years in Hungarian oak comparative trials.
| Trial | Trait | σ 2 f | σ 2 f × r | σ 2 e | σ 2 Ph1 | σ 2 Ph2 | h 2 f | h 2 i |
|---|---|---|---|---|---|---|---|---|
| Amaradia | dbh | 11.096 | 13.667 | 360 | 101.096 | 114.763 | 0.11 | 0.387 |
| Th | 0.022 | 0.161 | 0.55 | 0.160 | 0.321 | 0.138 | 0.275 | |
| Bals | dbh | 7.32 | 29.36 | 82.1 | 34.68 | 64.04 | 0.211 | 0.458 |
| Th | 0.003 | 0.065 | 0.17 | 0.060 | 0.125 | 0.05 | 0.096 |
Discussion
Ten years after plantation, ANOVA revealed significant differences between and within provenances of Hungarian oak for selected growth traits (Tab. 2). In the Amaradia comparative trial, the provenance factor contributed to the total variation by 61% for dbh and 37% for Th, while in the Bals trial, the provenance contribution was only 12% for both traits. The family factor had a smaller contribution (1-17%), as well as the individual variability within trees (3-26%). The replication factor had the major impact (except for dbh in the Amaradia trial), accounting for 51-74% of the total variance. This fact strengthens the need of establishing multiple replications in comparative trials to minimize the local microenvironmental variation at the experimental sites and its influence on provenance tests.
The Duncan test for 5% transgression probability presents different results for dbh and Th in terms of provenance homogeneity in the two testing sites. A superior homogeneity was observed in the Amaradia trial for dbh, while for Th the homogeneity was superior in the Bals trial. For the advanced generation of the current breeding programmes, more variability is required ([38]).
The comparative analysis of the survival rate showed that at the current age (10 years), in both trials, a sufficient number of trees survived for all the populations and families. Indeed, the survival rate was more than 62% at the population level, with the exceptions of Topana and Scundaru provenances which had lower survival rates (49.3% and 45.8%, respectively) in the Amaradia trial. The best-performing population in both trials (Seaca 2) in terms of growth traits, also showed survival rates superior to the average by 3.4% and 8.1% in the Amaradia and Bals trials, respectively. In the Bals trial, the local provenance (Bals) had the second performances in terms of survival rate (after Seaca 2) and the first for growth traits. In addition, it showed the highest homogeneity among families in terms of survival rate.
The Bals and Seaca 2 populations can be considered as local provenances, as their site of origin is situated close to both trials, particularly the Bals provenance which is the closest (Fig. 1). Moreover, both populations were the best performing in terms of growth and adaptability in both trials. Such finding reinforces the recommendation for the priority use of local provenances in afforestation projects, also known as “the golden law of local provenances” ([35]).
The age-to-age correlations were very significant for growth traits measured at 3 and 10 years in both trials. In addition, several populations and families were found at the top of the performance ranking at both ages. This type of correlation will be useful in the future to investigate the behaviour of provenances through time, providing support for genotype selection at the juvenile stage and thus reducing the length of breeding programmes ([33]). However, the optimal age for selection has been intensely debated in the past and it is currently thought that it can be achieved from 20-30 years to an age equivalent to half the production cycle of the stand ([40], [8], [11], [38], [32]).
The provenances originated from high altitudes and from the northern part of the species range showed lower growth in the Bals trial, while we did not observe any influence of the site of origin on growth performances in the Amaradia trial. This contrasts with our expectations, as the Bals trial is located further to north and at an altitude higher than Amaradia.
The highly significant effect of genotype × environment interaction suggests that maximum caution must be taken regarding the movement of forest reproductive materials across regions with different environmental conditions. The large and highly significant effect of the locality on growth performances of Hungarian oak provenances suggests the need of using the best performing provenances only in similar environmental conditions, preferably in the same region where the trials are performed.
The average values registered for family heritability (h2f), which was significantly lower than the individual heritability (h2i), denotes a high variability within families. This leads to the recommendation of adopting a strategy of individual selection for the next stage of the current breeding programme. However, in the case of the comparative trials analysed, the breeding strategy will be decided later (at 40 years), and will take advantage of the results of this study in order to shorten the testing period for genotype selection.
Conclusions
The best-performing provenances of Hungarian oak in Romania in term of growth traits were Izvorani and Seaca 2 at the Amaradia trial, while in the Bals trial the local provenance (Bals) is seconded by the Seaca 2 population, the latter being highlighted in both experiments. In both comparative trials, several families were identified which were among the ten best performing families both at 3 and 10 years.
ANOVA revealed significant differences between provenances and families for growth traits in both comparative trials. This genetic variation allows the breeder to choose those among the tested families which are best suited for the intended purpose. In the case of the analysed trials, the selection of the best-performing provenances will be made later, at the age of 40 years, when the juvenile-adult correlations (10 to 40 years) will be made based on the results of the present study.
Performances of the Hungarian oak provenances were highly significant influenced by trial site and the interactions between provenance, family and locality, which suggests maximum precaution when the movement of forest reproductive materials across regions with different climatic conditions is required. The family mean heritability (h2f) was significantly lower than the individual heritability (h2i), which recommend the adoption of individual selection strategy in the next generation of the current breeding programme.
To ensure a forest sustainable management in the context of climate change, with new pests and diseases, invasive alien species and wood products needs, breeding programmes should consider ex situ conservation as a critical strategy for the future. In addition, genetically improved forest tree species will be the main source of reproductive materials for future stable forests. Drought-resistant species (including Hungarian oak) will be highly appreciated in the future.
Acknowledgments
This paper was financed by the Romanian Ministry of Scientific Research and Innovation, in the frame of the RMSRI programme contracted with the National Institute for Research and Development in Forestry “Marin Dracea” (Project PN18040203 and PN19070 301).
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Online | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Elena Stuparu
Virgil Scarlatescu
Marius Budeanu 0000-0001-9849-0527
National Institute for Research and Development in Forestry “Marin Dracea”, Voluntari, 128 Eroilor Boulevard, 077190, Ilfov County (Romania)
Corresponding author
Paper Info
Citation
Apostol EN, Stuparu E, Scarlatescu V, Budeanu M (2020). Testing Hungarian oak (Quercus frainetto Ten.) provenances in Romania. iForest 13: 9-15. - doi: 10.3832/ifor3108-012
Academic Editor
Marco Borghetti
Paper history
Received: Mar 25, 2019
Accepted: Oct 23, 2019
First online: Jan 08, 2020
Publication Date: Feb 29, 2020
Publication Time: 2.57 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2020
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 45337
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 38598
Abstract Page Views: 3289
PDF Downloads: 2594
Citation/Reference Downloads: 10
XML Downloads: 846
Web Metrics
Days since publication: 2237
Overall contacts: 45337
Avg. contacts per week: 141.87
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2020): 2
Average cites per year: 0.33
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Review Papers
Prospects for evolution in European tree breeding
vol. 17, pp. 45-58 (online: 06 March 2024)
Research Articles
Age trends in genetic parameters for growth and quality traits in Abies alba
vol. 9, pp. 954-959 (online: 07 July 2016)
Research Articles
Preliminary study on genetic variation of growth traits and wood properties and superior clones selection of Populus ussuriensis Kom.
vol. 12, pp. 459-466 (online: 29 September 2019)
Research Articles
Patterns of genetic variation in bud flushing of Abies alba populations
vol. 11, pp. 284-290 (online: 13 April 2018)
Research Articles
Genetic variation and heritability estimates of Ulmus minor and Ulmus pumila hybrids for budburst, growth and tolerance to Ophiostoma novo-ulmi
vol. 8, pp. 422-430 (online: 15 December 2014)
Review Papers
Genetic diversity and forest reproductive material - from seed source selection to planting
vol. 9, pp. 801-812 (online: 13 June 2016)
Research Articles
Chloroplast microsatellites as a tool for phylogeographic studies: the case of white oaks in Poland
vol. 8, pp. 765-771 (online: 19 July 2015)
Research Articles
Genetic control of intra-annual height growth in 6-year-old Norway spruce progenies in Latvia
vol. 12, pp. 214-219 (online: 25 April 2019)
Research Articles
Adaptive response of Pinus monticola driven by positive selection upon resistance gene analogs (RGAs) of the TIR-NBS-LRR subfamily
vol. 10, pp. 237-241 (online: 02 February 2017)
Research Articles
Seedling emergence capacity and morphological traits are under strong genetic control in the resin tree Pinus oocarpa
vol. 17, pp. 245-251 (online: 16 August 2024)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword