Prediction of stem diameter and biomass at individual tree crown level with advanced machine learning techniques
iForest - Biogeosciences and Forestry, Volume 12, Issue 3, Pages 323-329 (2019)
doi: https://doi.org/10.3832/ifor2980-012
Published: Jun 14, 2019 - Copyright © 2019 SISEF
Research Articles
Abstract
Knowledge about the aboveground biomass (AGB) and the diameters at breast height (DBH) distribution can lead to a precise estimation of carbon density and forest structure which can be very important for ecology studies especially for those concerning climate change. In this study, we propose to predict DBH and AGB of individual trees using tree height (H) and crown diameter (CD), and other metrics extracted from airborne laser scanning (ALS) data as input. In the proposed approach, regression methods, such us support vector machine for regression (SVR) and random forests (RF), were used to find a transformation or a transfer function that links the input parameters (H, CD, and other ALS metrics) with the output (DBH and AGB). The developed approach was tested on two datasets collected in southern Norway comprising 3970 and 9467 recorded trees, respectively. The results demonstrate that the developed approach provides better results compared to a state-of-the-art work (based on a linear model with the standard least-squares method) with RMSE equal to 81.4 kg and 92.0 kg, respectively (compared to 94.2 kg and 110.0 kg) for the prediction of AGB, and 5.16 cm and 4.93 cm, respectively (compared to 5.49 cm and 5.30 cm) for DBH.
Keywords
Aboveground Biomass, Diameter at Breast Height, Airborne Laser Scanning (ALS), Remote Sensing (RS), Support Vector Machine for Regression (SVR), Random Forests (RF)
Introduction
Forests are considered a major component of the global carbon cycle. A precise characterization of forest ecosystems in terms of carbon stock density and forest structure is an important key in international efforts to mitigate climate change. Carbon density can be estimated directly from the aboveground biomass (AGB) of trees, while the knowledge about the distribution of diameter at breast height (DBH) can be useful in understanding the forest structure ([19]). Having precise information about the distribution of those two parameters can help to understand the structure and the dynamics of forests. In the past, assessing those characteristics was primarily done with field-based inventory data and sometimes combined with conventional remote sensing (RS) data such as aerial photography and optical satellite images ([4], [5]). ALS sensors, also referred to as airborne LiDAR (Light Detection And Ranging), are nowadays the most accurate remote sensing technology for monitoring forest carbon ([12], [1]), as they can produce highly detailed 3D point clouds pinpointing locations on branches and the forest floor ([4]) and they measure surface elevation within a precision of a few centimeters, which offers the potential for studying forests at tree level.
In forest inventories in general, DBH and height (H) are measured and registered in the field in order to predict the AGB using allometric models. AGB is then converted to carbon density for each field-reference tree ([3], [17], [23], [18]). With ALS, it became possible to measure the heights of trees in large forests in a short time, which makes it more practical compared to filed-measured methods. However, DBH cannot be measured directly with ALS sensors. Therefore, many studies have been carried out to try to predict DBH from airborne remote sensing data (ARS). The work of Gobakken & Naesset ([6]) is considered the first where the DBH (and also basal area) distribution was predicted by using ALS data at the plot level. Their approach was based on a Weibull density function ([22]) and regression analysis was used to estimate the corresponding parameters. Recent studies have extracted ARS variables from each individual tree crown (ITC) detected in ARS data ([8], [9], [10], [11], [15], [5]). Among this last group of studies, Jucker et al. ([10]) proposed new allometric models to predict DBH and AGB based on H and crown diameter (CD) extracted from ARS data. Dalponte et al. ([5]) in a recent study successfully linked field-reference DBH and AGB with H and CD extracted from ALS data using linear models.
The objective of the current study is to analyze the use of machine learning methods, such as Support Vector Machines for Regression (SVR) and Random Forest (RF) to predict DBH and AGB at the ITC level using metrics extracted from ALS data. In the first part of the experiment, only H and CD are used as input in order to compare with the work of Dalponte et al. ([5]). After that, additional ALS metrics are used as input in order to see their impact on the quality of the prediction.
Materials and methods
Datasets description
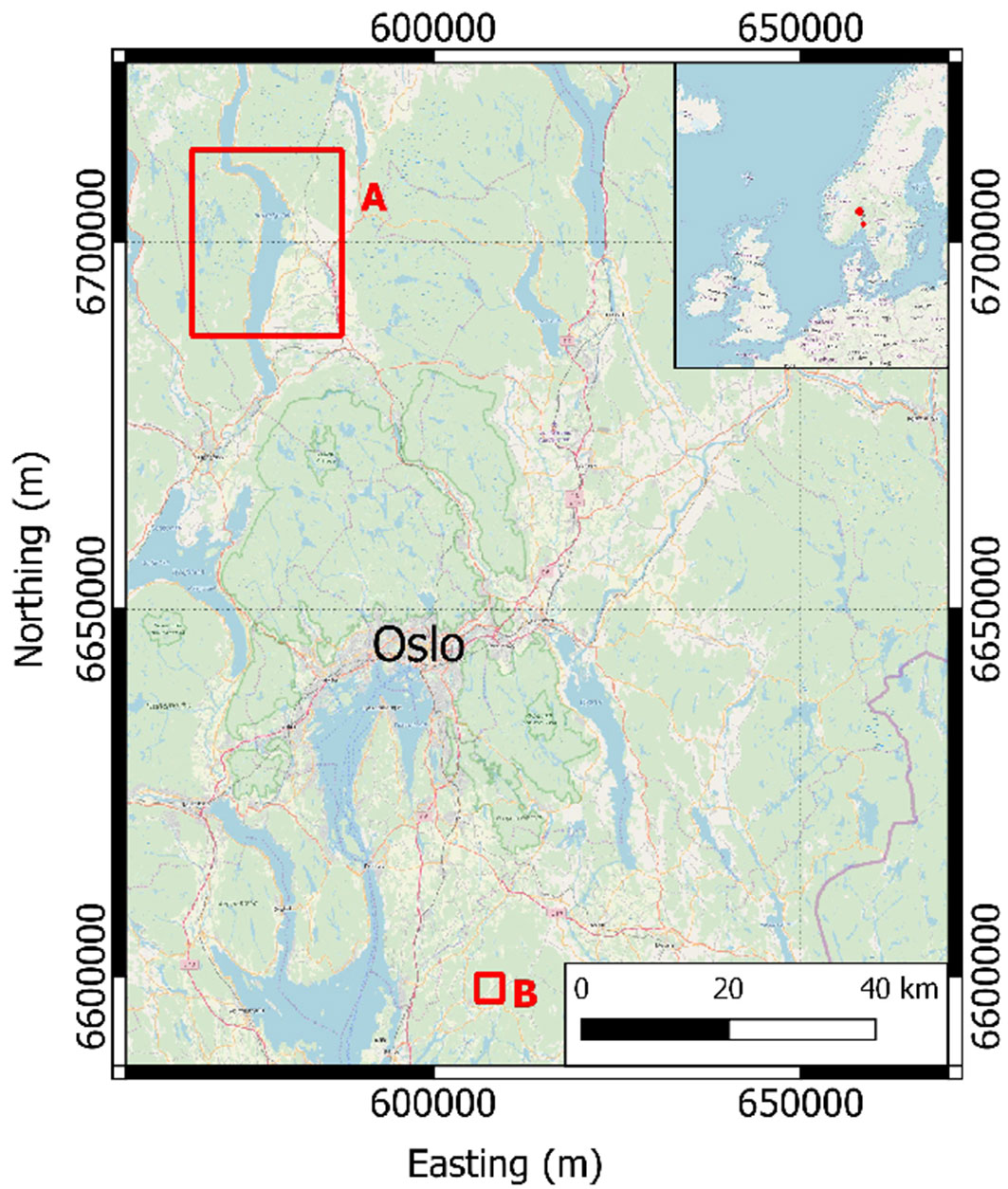
In this study, two datasets located in boreal forests of southeastern Norway were used: Hadeland and Våler (Fig. 1). The main tree species in the two areas are Norway spruce (Picea abies [L.] H. Karst), Scots pine (Pinus sylvestris L.), and deciduous tree species, such as birch (Betula spp. L.) and aspen (Populus tremula L.). A summary of the field data of the two datasets is presented in Tab. 1 where only the trees chosen for the experiments are showed and grouped according their species.
Tab. 1 - Summary statistics of the field data for all datasets. For the tree height, DBH and AGB the data range and the mean (in brackets) are provided. For the species the number of trees and the percentage (in brackets) are provided.
| Variable | Species | Hadeland | Våler |
|---|---|---|---|
| Tree height (m) | Spruce | 5.8 - 25.4 (15.8) | 3.5 - 33.3 (18.6) |
| Pine | 4.7 - 23.1 (16.0) | 4.4 - 26.0 (15.1) | |
| Broadleaves | 5.1 - 22.9 (13.8) | 5.8 - 26.3 (15.3) | |
| DBH (cm) |
Spruce | 5.1 - 44.1 (19.3) | 4.3 - 50.3 (21.1) |
| Pine | 4.7 - 51.1 (25.6) | 4.0 - 47.9 (20.2) | |
| Broadleaves | 4.0 - 49.5 (14.8) | 4.7 - 38.9 (16.2) | |
| Tree AGB (kg) | Spruce | 6.1 - 681.4 (155.1) | 4.2 - 1232.9 (216.3) |
| Pine | 3.1 - 691.0 (214.3) | 2.4 - 728.4 (146.3) | |
| Broadleaves | 2.4 - 738.2 (103.2) | 4.1 - 680.4 (125.5) | |
| Species | Spruce | 737 (59.7%) | 1326 (50.2%) |
| Pine | 315 (25.5%) | 956 (36.2%) | |
| Broadleaves | 182 (14.8%) | 361 (13.6%) |
Hadeland dataset
The field data acquired in the Hadeland district (Fig. 1) were collected on 13 circular sample plots of size 500 m2 and 21 circular sample plots of size 1000 m2 over a total area of about 1300 km2. Within each sample plot, tree species, DBH, and tree coordinates were recorded for all trees with DBH > 3 cm. A total of 3970 trees were recorded. AGB of each tree was calculated using the allometric models of Marklund ([16]).
ALS data were acquired on 21st and 22nd of August 2015 using a Leica ALS70 laser scanner operated at a pulse repetition frequency of 270 kHz. The flying altitude was of 1100 m above ground level. Up to four echoes per pulse were recorded and the resulting density of single and first echoes was 5 m-2.
Våler dataset
The data were acquired in the Våler municipality in the southern part of Norway (Fig. 1). The field data were collected on 152 circular sample plots of size 400 m2. Within each sample plot, tree species, DBH, and tree coordinates were recorded for all trees with DBH > 5 cm. A total of 9467 trees were recorded. AGB of each tree was calculated using the allometric models of Marklund ([16]).
The ALS data were acquired on 9th September 2011 using a Leica ALS70 system operating with a pulse repetition frequency of 180 kHz. The flying altitude was of 1500 m above ground level. Up to four echoes per pulse were recorded and the resulting density of single and first echoes was 2.4 m-2.
Methods
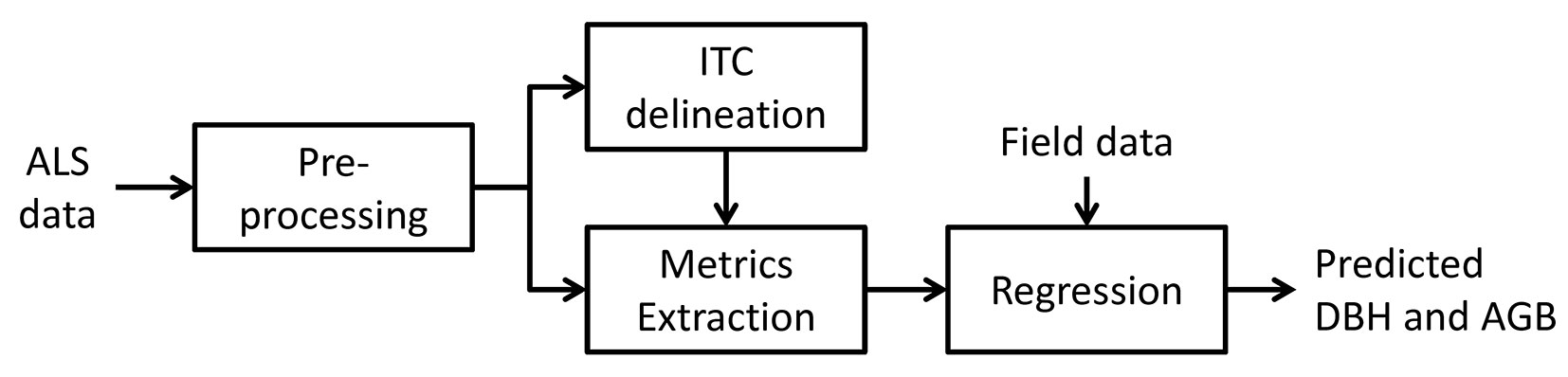
In Fig. 2 the architecture of the prediction system used is provided, and in the following paragraphs each step is detailed.
ITC delineation
ITCs were delineated using an approach based on the ALS data and the delineation algorithm of the R package “itcSegment”. The algorithm starts first by finding the local maxima within a rasterized Canopy Height Model (CHM) and designates them as tree tops, and then uses a decision tree method to grow individual crowns around the local maxima. The different steps for this adopted approach are as follows ([4]):
- apply a 3 × 3 low-pass filter to the rasterized CHM in order to smooth the surface and reduce the number of local maxima;
- localization of local maxima by using a circular moving window of variable size. The user provides a minimum and maximum size of the moving window; the window size is adapted according to the central pixel of the window: the size of the window is linearly related to the CHM height. A pixel of the CHM is considered as local maximum if its value is greater than all other values in the window, and if it is greater than some minimum height above ground. The window size is adapted according to the height of the central pixel of the window;
- labeling each local maximum as an “initial region” around which a tree crown can grow;
- extraction of the heights of the four neighboring pixels from the CHM and adding them (the pixels) to the region if their vertical distance from the local maximum is less than a predefined percentage of the local maximum height, and less than a predefined maximum difference;
- reiteration of the previous step for all the neighboring cells included in the region until no further pixels are added to the region;
- extraction of single and first echoes from the ALS data from each identified region (having first removed low elevation echoes, i.e., below 2 m);
- application of a 2D convex hull to these echoes. The resulting polygons become the final ITCs. For each ITC CD and H are provided. The CD is computed as 2 · √(ITCarea/π), while the height is computed as the 99th percentile of the elevation of the single and first return ALS echoes inside each ITC.
The delineated ITCs were automatically matched to the trees in the field data sets. If only one field-measured tree was included inside an ITC, then that tree was associated with that ITC. In the case that more than one field-measured tree was included in a segmented ITC, the field-measured tree with the height most similar to the ITC height was chosen.
ALS metrics extraction
From each delineated ITC, metrics were extracted in order to build the regression models. In particular, two sets of metrics were considered. The first set, called H+CD, contained two geometric metrics of the extracted ITCs, the height and crown diameter. The second set contains metrics extracted from the ALS points falling inside each ITC. This set of metrics comprised 50 statistics and they are summarized in Tab. 2. They were extracted from both elevation (Z) and intensity (I) of ALS points. We used the function “lasmetrics” of the library “lidR” of the software R to extract those ALS metrics.
Tab. 2 - Metrics extracted from the ALS points.
| Metric | Description |
|---|---|
| Zmax | Maximum Z |
| Zmean | Mean Z |
| Zsd | Standard deviation of Z distribution |
| Zskew | Skewness of Z distribution |
| Zkurt | Kurtosis of Z distribution |
| Zentropy | Entropy of Z distribution |
| ZqP | Ph percentile of height distribution, with P from 5 to 95 at steps of 5 |
| ZpcumP | Cumulative percentage of points in the Pth layer, with P from 5 to 95 at steps of 5 |
| Itot | Sum of intensities for each return |
| Imax | Maximum intensity |
| Imean | Mean intensity |
| Isd | Standard deviation of intensity |
| Iskew | Skewness of intensity distribution |
| Ikurt | Kurtosis of intensity distribution |
| IpcumzqP | Percentage of intensity returned below the Pth percentile of Z, with P from 5 to 95 |
| pRth | Percentage of Rth return, with R from 1 to 4 |
Support vector machine for regression
Let us consider a matrix of training observations X = [x1, x2, …, xN]′, where N is the number of observations and each vector xi is represented in the d-dimensional measurement space. In our case, N corresponds to the number of ITCs used for the training and the measurement space is their corresponding H, CD, and the ALS metrics. Let us also consider the output vector y = [y1, y2, …, yN]′ associated with X and corresponds to the measured DBH and the AGB. The aim of our proposed method is to estimate the relationship between the input vectors xi and their target values yi.
Support Vector machine for Regression (SVR - [21], [20]) performs linear regression in a feature space using an epsilon-insensitive loss (ε-SVM). This technique is based on the idea of deducing an estimate g′(xi) of the true but unknown relationship yi = g(xi) (i = 1, …, N) between the vector of observations xi and the target value yi such that: (i) g′(xi) has, at most, ε deviation from the desired targets yi; and (ii) it is as smooth as possible. This is performed by mapping the data from the original feature space of dimension d to a higher d′-dimensional transformed feature space (kernel space), i.e., Φ(xi) ∈ Rd’ (d′ > d), to increase the flatness of the function and, by consequence, to approximate it in a linear way as follows (eqn. 1):
Therefore, SVR is formulated as minimization of the following cost function (eqn. 2):
subject to (eqn. 3):
where ξi and ξi* are the slack variables that measure the deviation of the training sample xi outside the ε-insensitive zone. c is a parameter of regularization that allows tuning the tradeoff between the flatness of the function g′(x) and the tolerance of deviations larger than ε.
The aforementioned optimization problem can be transformed through a Lagrange function into a dual optimization problem expressed in the original dimensional feature space in order to lead to the following dual prediction model (eqn. 4):
where K is a kernel function, U is a subset of indices (i = 1, …, N) corresponding to the nonzero Lagrange multipliers αi’s or αi*’s. The training observations that are associated to nonzero weights are called SVs. The kernel K(·,·) should be chosen such that it satisfies the condition imposed by the Mercer’s theorem, such as the Gaussian kernel functions ([21], [20]). In this study, the SVM implemented in the “kernlab” library of the software R was used.
Random Forest (RF)
The Random Forest (RF) method, which was proposed by Breiman ([2]), is considered as one of the most effective machine learning method for predictive analytics. It consists of many decision trees trained on different parts (selected randomly) of the same training set at each node with the goal of reducing the variance. Each node is split using the best among a subset of its corresponding predictors. The strategy of randomness used in RF has been demonstrated to be robust against over-fitting problems ([2], [13]).
Given training set X = [x1, x2, …, xN]′, with response y = [y1, y2, …, yN]′ where N is the number of observations which is used in building a forest. Inside the forest a set of K trees Ti = 1, …, K is constructed. The output of each tree predicts the outputs for the actual value {y′1 = T1(x), …, y′m = Tm(x)}, where m = 1, …, K. The final result of the RF is the average of all tree predictions and is calculated as follows ([7], [14] - eqn. 5):
The evaluation of the Random Forest regression is done through the minimization of the mean square error (MSE) in order to select the optimum trees in the forest. In this study, the Random Forest classifier implemented in the “randomForest” library of the software R was used.
Parameter setting
In order to evaluate our methods, each dataset (i.e., Hadeland, and Våler) was divided in two subsets (same as in [5]). The first set was used for calibration and the second for the validation phase. The split in the two sets was carried out in order to have similar characteristics in both sets in terms of spatial distribution, and DBH and AGB variation. For the Hadeland dataset, 607 observations were used for calibration and 627 observations were used for validation, while for the Våler dataset, 1398 and 1245, respectively.
Regarding the SVR, the Radial Basis Function (RBF) was used as kernel functions. To compute the best parameter values, we use a cross-validation technique with a number of folds equal to 3. During the cross validation, the parameter of regularization of the SVR c and the width of its kernel function γ were varied in the range [1, 104] and [10-3, 5], respectively. The ε value of the insensitive tube was fixed to 10-3.
For the RF method, we fix the number of trees to grow to 100, while the number of variables which will be randomly sampled as candidates at each split is fixed to 1 when using only CD and H as features and to 25 when using all the features (CD+ H+ALS data).
Performance evaluation
In order to evaluate the developed method of prediction and perform a direct comparison with results of the state-of-the-art methods, we adopted the Root Mean Square Error (RMSE) which measures the differences between values predicted by our model and the ground-reference values (eqn. 6):
where Nt is the total number of test observations, yti is the ground-reference target value and y′ti is the predicted value of the developed regression method (ARS-predicted). Both yti and y′ti correspond to the ith test observation xti.
We also adopted the percentage improvement ratio measure (PIR) in order to evaluate the level of improvement of our method compared to those of the state-of-the-art (SOA). It is formulated as follows (eqn. 7):
Results and discussion
In the first part of the analysis, only H and CD were used as input in order to compare the obtained results with those reported in Dalponte et al. ([5]). Tab. 3 reports the results obtained with the set of metrics H+CD in terms of RMSE and PIR.
Tab. 3 - Accuracy statistics for DBH and AGB predictions using H+CD as input.
From Tab. 3, it can be seen that the proposed method using SVR and RF provide better results in terms of RMSE compared to the state-of-the-art method ([5]) for both DBH and AGB predictions. SVR shows substantial improvements while the RF results are located between those of SVR and the state-of-the-art method ([5]).
In greater detail, considering the AGB prediction, RMSE for the Hadeland dataset was 81.43 kg with SVR and 84.35 kg with RF, while it was 92.04 kg with SVR and 95.46 kg with RF in the Våler dataset. The improvement is significant compared to the results obtained by the state-of-the-art method (94.19 kg and 109.99 kg for Hadeland and Våler, respectively - [5]) with a maximum PIR equal to 13.55% for Våler dataset and 16.32% for Hadeland dataset. Regarding the DBH prediction, the RMSE by using SVR was 5.16 cm for Hadeland dataset and 4.93 cm for Våler dataset. Those results show also significant improvements compared to the state-of-the-art method ([5]) where RMSE was 5.49 cm for Hadeland and 5.30 cm for Våler. However, RF did not show considerable improvement and provided results close to those of the reference method (5.42 cm for Hadeland and 5.19 cm for Våler). In term of PIR, the maximum improvement was equal to 6.98% and 16.32% for Hadeland and Våler datasets, respectively.
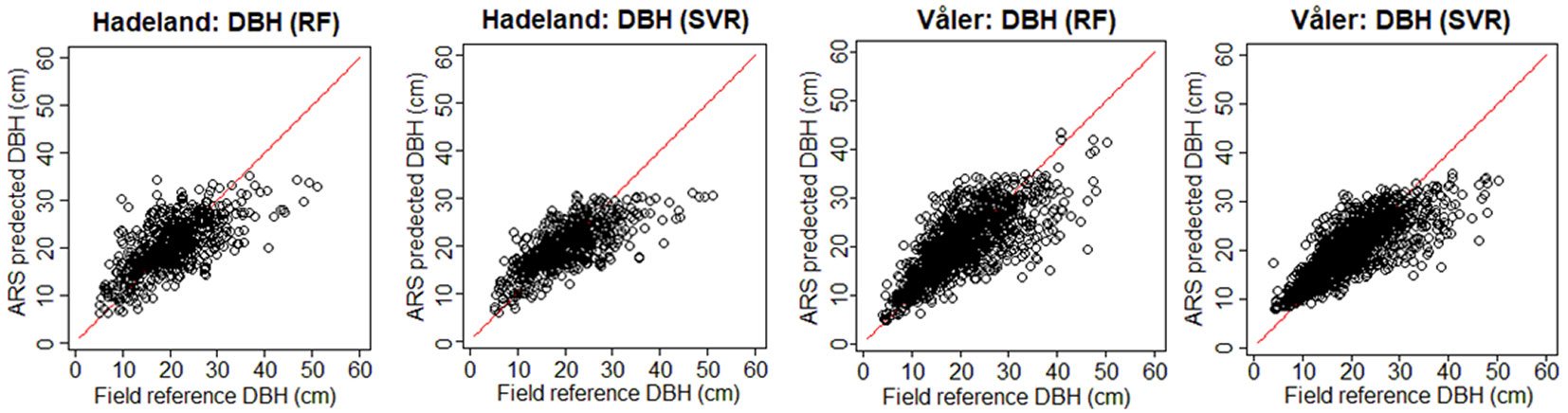
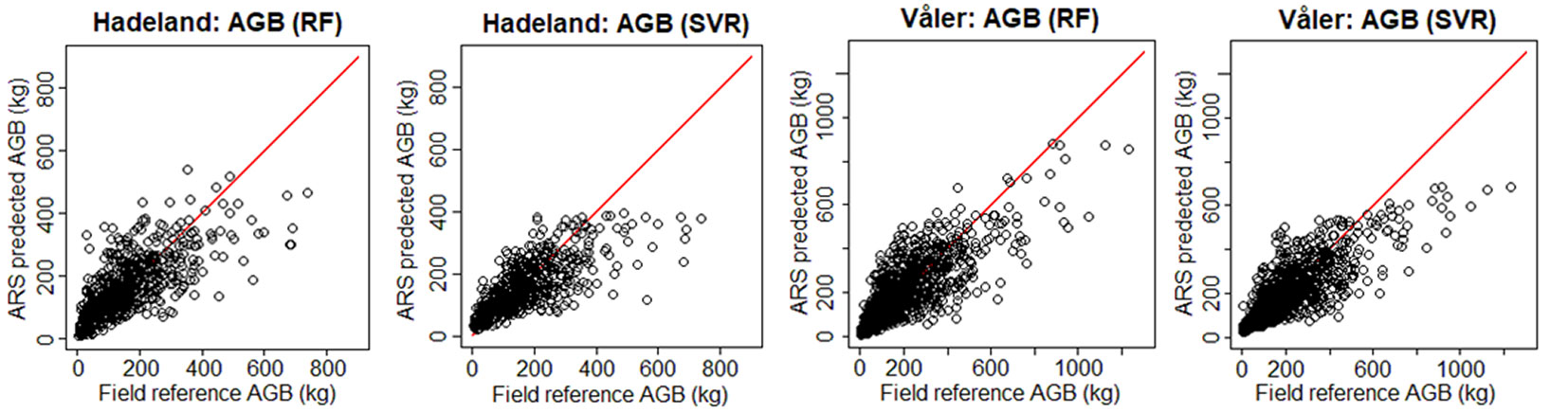
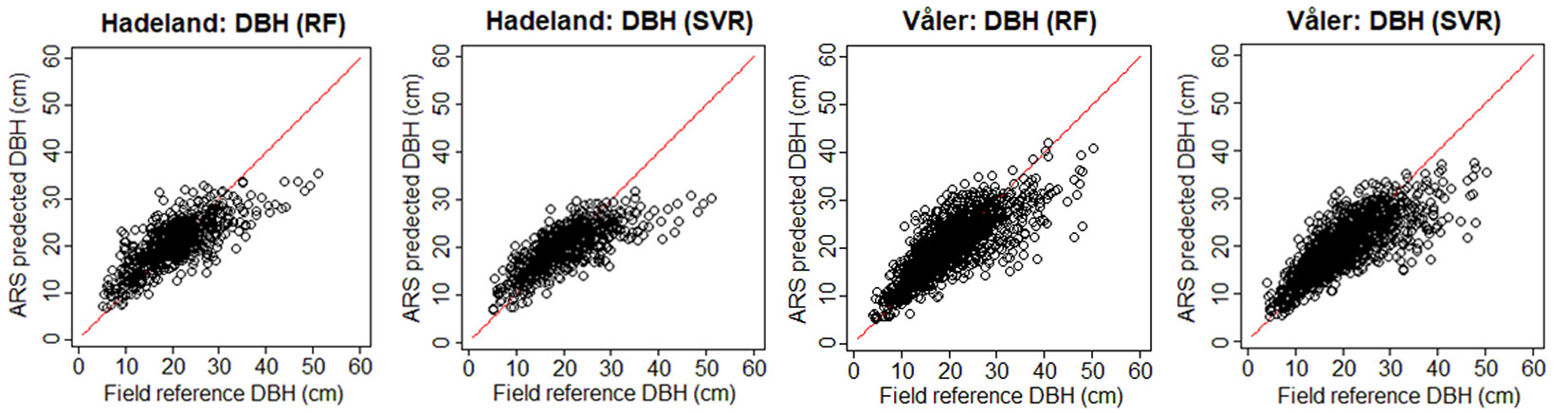
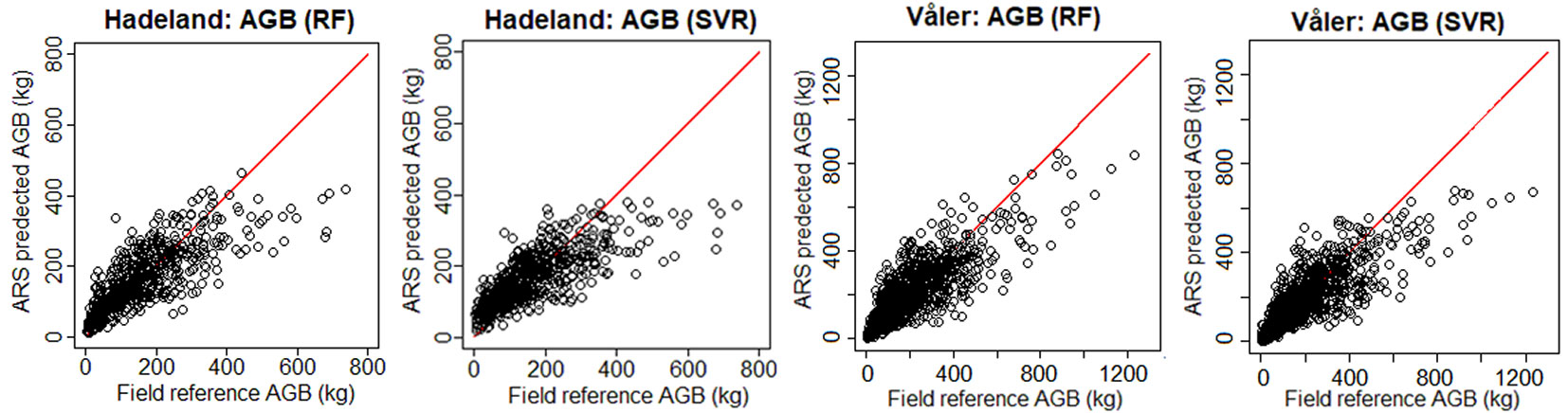
To see visually the quality of the results, we show in Fig. 3 the field-reference DBH vs. ARS predicted DBH, and in Fig. 4 the field predicted AGB vs. ARS predicted AGB. The ARS predicted values are close to the regression line only until a certain value, while afterwards the bias is increasing. For example, if we consider the worst case corresponding to the prediction of DBH for the Hadeland dataset, the prediction values were close to the regression line when the DBH was inferior to 35 cm, while above this value, the predictions were giving values around 30 cm. This can be explained by the fact that among the 607 observations presented in the training, there were only 23 observations which have value higher than 35 cm which represents only 3.8% of the total training data. Moreover, the relationship between the tree DBH (and AGB) and its height is not linear as, after a certain age, trees stop to growth in height and they grow mainly in DBH. Thus, models that are based on ALS data have problems in modelling the DBH and AGB of old trees. Additionally, the traditional ground-based inventories require a big effort in terms of time and they may not be the best choice to provide a balanced dataset regarding the tree height, stem diameter and other features. It can be more efficient to select remotely the best samples (trees) to be later annotated in the field by experts. In terms of RMSE, our method showed good results since most of the predicted values fall close to the regression line except a few observations, but those few ones occupy a large range (between 35 and 50 cm which represents 30% of the total occupied range).
Fig. 3 - Field-reference DBH vs. ARS-predicted DBH for the two datasets using H+CD as input. In red the 1:1 line.
Fig. 4 - Field-reference AGB vs. ARS-predicted AGB for the two datasets using H+CD as input. In red the 1:1 line.
In order to improve the results, a set of ALS metrics were used together with the previous metrics (H and CD). The obtained results (Tab. 4) show that the ALS metrics help to improve the results, especially when using the RF method. For example, regarding the prediction of AGB, the RMSE reached a value less than 80 for the Hadeland dataset (78.5 with SVR and 76.0 by RF) which represents an improvement of 16.62% by using SVR and 19.34% by using RF. For the Våler dataset RMSE was lower than 90 (88.9 with RF) with a PIR equals to 19.15. The same remarks can be given for the DBH prediction part where the improvement was significant and the PIR was 12.75% and 8.11% for Hadeland and Våler datasets, respectively.
Tab. 4 - Accuracy statistics for DBH and AGB predictions using H+CD+ALS metrics.
| Dataset | Method | DBH | AGB | ||
|---|---|---|---|---|---|
| RMSE (cm) | PIR (%) | RMSE (kg) | PIR (%) | ||
| Hadeland | RF | 4.79 | 12.75 | 75.97 | 19.34 |
| SVR | 4.93 | 10.20 | 78.54 | 16.62 | |
| Våler | RF | 4.88 | 7.92 | 88.93 | 19.15 |
| SVR | 4.87 | 8.11 | 91.15 | 17.13 | |
In Fig. 5 and Fig. 6, we present the field-reference DBH vs. ARS-predicted DBH and the field-predicted AGB vs. ARS-predicted AGB, respectively, by using ALS metrics along with H and CD. From the different graphs, a slight improvement can be noticed compared to the previous ones (using only H and CD metrics in Fig. 3 and Fig. 4). However, the problem of inaccurate prediction of high values of AGB and DBH appeared also in this part of the experiments. We think that such problem can be investigated in a separate work in order to explore better the possible challenges that it may present.
Conclusion
In this work, we proposed an approach to predict DBH and AGB of trees from remote sensing data by using SVR and RF regression methods. The developed approach was tested on two datasets. On the first part of the experiments, the metrics H and CD were used in order to predict DBH and AGB. The obtained results were promising and the improvements were noticeable, especially in terms of RMSE. In order to improve the results, we proposed to introduce ALS metrics and use them together with H and CD. The obtained results were encouraging, especially with RF where the improvement was large. However, our method was not able to predict the isolated samples with highest values of AGB and DBH. This was probably due to the fact that the relationship among the height of a tree (and thus of the majority of the ALS metrics) and the DBH and AGB was saturating, and also to the fact that there was a limited number of training observations for the larger trees.
Finally, in order to improve the quality of the results and to get better predictions for old trees with large values of DBH and AGB, we think it can be more advantageous to use techniques that preprocess the data in order to yield a balance for their distribution over all the scale of the different metrics.
Acknowledgements
This work was supported by the HyperBio project (project 244599) financed by the BIONR program of the Research Council of Norway and TerraTec AS, Norway.
References
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Franco Miglietta 0000-0003-1474-8143
Institute of Biometeorology, CNR, 50145 Firenze (Italy)
Erik Næsset 0000-0002-2460-5843
Faculty of Environmental Sciences and Natural Resource Management, Norwegian University of Life Sciences, P.O. Box 5003, NO-1432 s (Norway)
Damiano Gianelle 0000-0001-7697-5793
Michele Dalponte 0000-0001-9850-8985
Dept. of Sustainable Agro-ecosystems and Bioresources, Research and Innovation Centre, Fondazione E. Mach, v. E. Mach 1, 38010 San Michele all’Adige, TN (Italy)
Corresponding author
Paper Info
Citation
Malek S, Miglietta F, Gobakken T, Næsset E, Gianelle D, Dalponte M (2019). Prediction of stem diameter and biomass at individual tree crown level with advanced machine learning techniques. iForest 12: 323-329. - doi: 10.3832/ifor2980-012
Academic Editor
Carlotta Ferrara
Paper history
Received: Oct 22, 2018
Accepted: Apr 06, 2019
First online: Jun 14, 2019
Publication Date: Jun 30, 2019
Publication Time: 2.30 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2019
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 46141
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 37218
Abstract Page Views: 4347
PDF Downloads: 3769
Citation/Reference Downloads: 5
XML Downloads: 802
Web Metrics
Days since publication: 2432
Overall contacts: 46141
Avg. contacts per week: 132.81
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2019): 14
Average cites per year: 2.00
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Three-dimensional forest stand height map production utilizing airborne laser scanning dense point clouds and precise quality evaluation
vol. 10, pp. 491-497 (online: 12 April 2017)
Research Articles
Integrating area-based and individual tree detection approaches for estimating tree volume in plantation inventory using aerial image and airborne laser scanning data
vol. 10, pp. 296-302 (online: 15 December 2016)
Research Articles
Determining basic forest stand characteristics using airborne laser scanning in mixed forest stands of Central Europe
vol. 11, pp. 181-188 (online: 19 February 2018)
Technical Advances
Forest stand height determination from low point density airborne laser scanning data in Roznava Forest enterprise zone (Slovakia)
vol. 6, pp. 48-54 (online: 21 January 2013)
Review Papers
Accuracy of determining specific parameters of the urban forest using remote sensing
vol. 12, pp. 498-510 (online: 02 December 2019)
Research Articles
Exploring machine learning modeling approaches for biomass and carbon dioxide weight estimation in Lebanon cedar trees
vol. 17, pp. 19-28 (online: 12 February 2024)
Research Articles
Are we ready for a National Forest Information System? State of the art of forest maps and airborne laser scanning data availability in Italy
vol. 14, pp. 144-154 (online: 23 March 2021)
Technical Reports
Remote sensing of american maple in alluvial forests: a case study in an island complex of the Loire valley (France)
vol. 13, pp. 409-416 (online: 16 September 2020)
Research Articles
Estimation of aboveground forest biomass in Galicia (NW Spain) by the combined use of LiDAR, LANDSAT ETM+ and National Forest Inventory data
vol. 10, pp. 590-596 (online: 15 May 2017)
Research Articles
Estimation of forest biomass components using airborne LiDAR and multispectral sensors
vol. 12, pp. 207-213 (online: 25 April 2019)
iForest Database Search
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords