Exploring machine learning modeling approaches for biomass and carbon dioxide weight estimation in Lebanon cedar trees
iForest - Biogeosciences and Forestry, Volume 17, Issue 1, Pages 19-28 (2024)
doi: https://doi.org/10.3832/ifor4328-016
Published: Feb 12, 2024 - Copyright © 2024 SISEF
Research Articles
Abstract
Accurate estimates of total tree biomass are of critical importance to obtain reliable estimation of the carbon dioxide weight sequestered from the atmosphere by trees and forest stands. This information has the potential to guide appropriate forest management decisions which allow for both the improvement of forest sustainability and the implementation of multi-task reforestation designs aimed to mitigate the detrimental effects of climate change. The current laborious and tree-destructive procedures needed to attain such information has led to the development of machine learning (ML) models aimed at providing accurate estimations of the tree biomass sequestering the atmospheric carbon dioxide. We tested the Levenberg-Marquardt artificial neural network and the support vector machine for regression techniques as an alternative to non-linear allometric regression (NLR) modelling approaches commonly used for tree biomass estimation. We tested the developed ML models using primary ground-truth data from the Lebanon cedar forests in the Western Inner Anatolian regions of Turkey, and their predictions were compared to those of NLR models developed using the same dataset. The results showed that the ML approaches outperformed the NLR models in accurately estimating tree biomass and its components (above- and belowground dry biomass, dry branches biomass, etc.), and the support vector regression (SVR) models gave the highest accuracy of estimates. Therefore, the carbon dioxide weight sequestered in Lebanon cedar trees were reliably estimated, with the aim of supporting the best forest management practices to be applied in Lebanon cedar tree stands in Turkey.
Keywords
Tree Biomass, Carbon Dioxide Weight, Levenberg-Marquardt Artificial Neural Network, Support Vector Machine For Regression, Lebanon Cedar Trees
Introduction
The carbon cycle represents the earth’s natural way of reusing the atoms of carbon. In recent years the planet is experiencing global changes due to the human intervention that can deeply impact the balance of the carbon cycle. Living organisms along with water, atmosphere, and soil, play a vital role in maintaining the carbon cycle equilibrium. Carbon dioxide removal from the atmosphere is made by two processes. First, carbon is converted into a solid form that is stored in leaves, stems, trunks, branches, and roots of the trees, helping them to grow. The second process includes the oxygen that is released back into the atmosphere. In this way, trees and forests can provide food and oxygen which living organisms depend upon for their survival. Moreover, biomass energy, forest health and ecosystem productivity can be predicted through the estimation of total tree biomass and its components. Therefore, accurate biomass equations are key components of carbon measurements and estimation ([15], [27]).
To produce reliable and accurate models of tree biomass, this is usually separated into above-ground and below-ground biomass. Further, the tree stem, bark, branches, and foliage are modeled as different parts of the above-ground biomass, due to their significant variation which is difficult to describe using a single, comprehensive model. Similarly, different models are developed to estimate the different uses of tree components (industrial wood, chip-board wood, bioenergy wood). Finally, all components of above- and below-ground tree biomass can absorb and store remarkable quantities of the atmospheric carbon dioxide, with up to half of the annually cycled carbon in forests stored in the root system ([23], [15]).
Because of its valuable wood properties, Lebanon cedar (Cedrus libani A. Rich.) is one of the most important tree species from an economic and ecological perspective for Turkish forestry ([5]). Natural Lebanon cedar forests in Turkey cover an area of about 482,391 ha, with a current standing volume of approximately 27.4 million m3 ([13]). Moreover, afforestation efforts using Lebanon cedar are also carried out beyond its natural range of distribution in many countries, owing to its adaptability and high survival rate. For this reason, cedar is one of the most widely used species in reforestation worldwide, and represents approximately 15% of plantation forests in Turkey ([22]). Messinger et al. ([32]) stated that the economic potential of cedar in forestry is high, deserving further investigations to be used in silvicultural plantations. Also, Lebanon cedar has the potential to be used in reforestation activities across Central Europe, due of its resistance to heat and cold. To this end, the study of the carbon sequestration potential of this species is fundamental.
Previous studies aimed at developing accurate and reliable models for estimating cedar trees biomass are very rare. Durkaya et al. ([11]), and Aydin ([1]) developed biomass equations for natural cedar stands from the Mediterranean region of Turkey, using the least-squares regression modeling procedure. However, this approach resulted in inconsistent biomass estimates, which frequently violate the additivity of a system of tree component regression equations and failed to match the compatibility of the aboveground biomass estimates with total tree biomass. Moreover, the same set of equations might ignore the inherent correlation among the biomass components ([38]).
Multiple linear and non-linear regression approaches have been used for tree biomass estimation, being log transformed data used to overcome the heteroscedasticity of datasets ([38]). Later, due to their flexibility to deal with heteroscedasticity of the tree biomass components, linear and non-linear regressions seemingly unrelated each other, along with generalized linear models, were used ([38], [52], [40]). Lately, there has been an increasing interest in the use of machine learning (ML) models as a powerful mean with suitable characteristics in forest research ([46], [43], [24], [18], [33], [27]). The ML technique is characterized by its outstanding generalization ability and the potential of learning from noisy or incomplete data, by detecting inherent complex nonlinear relationships between output and input variables. Successful effort to produce reliable and accurate models for tree biomass estimation using ML techniques have been previously reported ([16], [37], [29], [15]). In addition, Artificial Neural Networks (ANNs) and Support Vector Machines for regression (SVR), have recently gained scientific interest in forestry research ([51], [36], [3], [44], [4]), thanks to their independence of a priori specifications of the (i) form of an equation describing the ground truth data, (ii) data distribution, and (iii) potential transformations of the variables, which are all to be matched in the case of regression modeling. In particular, ANN modeling is considered as a valid alternative to non-linear modeling, especially for complex biological ecosystems such as the forests ([49], [37], [29], [15]). Similarly, the interest in using SVR in forestry has been increasing since their introduction in the late 1990s ([7], [47]), due to their ability in learning from noisy data and minimizing the generalization errors. Chen & Hay ([6]) adopted an SRV modeling approach to assess forest biophysical parameters. Malek et al. ([29]) used SRV to predict the stem diameter and biomass at individual level, while Hamidi et al. ([17]) modeled the volume increment at the plot level using different machine learning techniques. Other studies proved the potential of the nonparametric, supervised SVR technique in successfully modeling forest attributes ([51], [3]).
To our best knowledge, biomass estimation modelling of cedar trees has been focused so far on allometric models. For example, the least-squares regression modeling used for biomass estimation for cedar trees in Turkey ([11]) resulted in acceptable, though high, standard errors of biomass estimation. In this study, advanced machine learning algorithms such as the Levenberg-Marquardt optimization algorithm of the multi perceptron ANNs and the non-linear ε-Support Vector Regression (ε-SVR), were applied with the aim to achieve reliable estimation of both the whole tree biomass and tree components biomass (branches, barks, needles, stems, above-ground and below-ground) at the same time. Allometric regression models were also developed to compare variable estimates obtained by ML techniques with those resulting from non-linear regression modeling. Furthermore, the additive capacity of the ML models was examined as an indicator of their proper construction. The most reliable and accurate biomass estimation model was used to predict the carbon dioxide weight sequestered in Lebanon cedar trees. The perfomances of both machine learning models (LMANN and SVR) were evaluated for the accuracy and reliability of biomass estimates.
Materials and methods
Study area
The study was conducted in an area located between 37° 46′ - 40° 10′ N and 29° 40′ - 32° 01′ E in the Western Inner Anatolian regions of Turkey, with elevation ranging from 900 to 1500 m a.s.l. The most common soil types are Cambisols and Luvisols ([20]) with pH ranging between 4.3 and 7.9, and total CaCO3 content between 0.0% and 54.6%. The mean annual temperature varies from 10.8 to 11.1 °C, annual precipitation ranges from 374 to 436 mm, and climate ranges from semi-arid to humid ([14]).
Cedar plantations were established in the period 1977-2011 in the Western Inner Anatolian regions of Turkey for erosion control of dry lands. Seedlings were planted at 3 × 2 m spacing. Thinning was not applied to these plantations until today. The age of the study plots varies between 12 and 46 years.
Field work
To fully reflect the variability of stand conditions in the study area, 40 sample trees were selected from 40 sample plots representing different aspects, slope degrees and positions, and tree development stages. Sample plots where randomly distributed over an area of 7500 ha. Plots were circular in shape, 25 to 400 m2 in size and included 11-19 individuals with different stand structures. According to the method reported by Njana et al. ([34]), in each sample plot one sample tree was cut from ground level in such a way to reflect different diameter and height classes. The age of sampled trees ranged from 12 to 46 years. Total height (tht) and diameter at breast height (dbh) of each sample tree were measured after felling. First, the main stem was divided into 2-m long sections which were weighted after branch removal. Then, 3-5 cm thick subsamples were taken from the middle of each section. Needles were separated from branches by hand. Stumps and roots of sampled trees were excavated from the ground by using a shovel and hand chain hoist. All tree components and subsamples, including dead and live branches, stems, needles, bark, and roots, were weighed in the field and subsamples were taken to the laboratory to determine the moisture content.
Laboratory work
Samples were oven-dried in the lab until constant weight at 65 °C to calculate the dry weight (DW) to fresh weight (FW) ratio of each component. Oven-dried biomass of each tree was calculated multiplying the DW/FW ratio by the whole tree fresh biomass. The bark biomass of trees was calculated by weighing the oven-dried disks befor and after bark removal. The bark coefficient was calculated using the ratio of bark weight to the weight of disc with bark. The stem bark weight was calculated multiplying the bark coefficient by the fresh weight of the whole stem. The summary statistics of diameter at breast height (dbh), total tree height (tht), age, total dry weight, and dry weight of the different components (branches, barks, needles, stems, above-ground and below-ground), as well as the carbon ratio of each component, are reported in Tab. 1.
Tab. 1 - Summary statistics of the sampled trees used for biomass estimation.
| Variables | N | Min | Max | Mean | STD | |
|---|---|---|---|---|---|---|
| Diameter at breast height (dbh, cm) | 40 | 4.10 | 35.50 | 17.69 | 9.48 | |
| Total height (tht, m) | 40 | 1.92 | 20.16 | 9.82 | 5.07 | |
| Age (years) | 40 | 12.0 | 46.0 | 31.0 | 10.62 | |
| Dry total biomass for whole tree (dwt, kg) | 40 | 4.09 | 558.15 | 170.76 | 178.08 | |
| Dry above-ground biomass (dwag, kg) | 40 | 3.35 | 462.43 | 142.32 | 149.55 | |
| Dry below-ground biomass (dwbg, kg) | 40 | 0.74 | 95.72 | 28.44 | 29.60 | |
| Dry stem biomass without bark (dws, kg) | 40 | 0.53 | 290.71 | 80.53 | 91.09 | |
| Dry branch biomass (dwb, kg) | 40 | 1.41 | 126.68 | 34.73 | 37.52 | |
| Dry needle biomass (dwn, kg) | 40 | 1.09 | 67.68 | 12.96 | 13.35 | |
| Dry bark biomass (dwbark, kg) | 40 | 0.32 | 49.84 | 14.11 | 14.47 | |
| Carbon content ratio (%) of the tree components | Stem | 40 | 0.50 | 0.53 | 0.52 | 0.01 |
| Branch | 40 | 0.25 | 0.53 | 0.48 | 0.01 | |
| Bark | 40 | 0.50 | 0.53 | 0.52 | 0.01 | |
| Needle | 40 | 0.50 | 0.53 | 0.51 | 0.01 | |
| root | 40 | 0.48 | 0.50 | 0.49 | 0.01 | |
Modeling approaches
The basic scope of any modeling approach is the construction of a reliable and accurate model that can effectively describe the relationships between the variables of interest. To this purpose, the second order Levenberg-Marquardt (LMANN) optimization algorithm ([25], [30]) has shown its potential by effectively dealing with non-linearity ([42]), while its efficiency for small and medium size datasets has been discussed in the literature ([48], [2]). Both the above conditions are met in forest ground-truth data. Further, due to its cumulative advantages of the gradient descent methods and the Gauss-Newton algorithm, the LMANN methodology has proven to produce stable systems which avoid to be captured in local minima and reach rapid convengence at the same time ([48], [49], [50]). The combination of the update rule of weights from the Gauss-Newton algorithm can be described by the eqn. 1:
and the update rule of weights by the gradient descent algorithm by eqn. 2:
The update rule for the Levenberg-Marquardt (LM) algorithm is of the following form (eqn. 3):
where H = JtT J + μI is the LM algorithm approximation to Hessian matrix of second order derivatives, μ is the combination coefficient that allows the LM algorithm to take advantage of the desired properties of each one of the Gauss-Newton and the gradient descent algorithms, namely stability and convergence speed, I is the identity matrix, J is the Jacobian matrix that contains first derivatives of the network errors with respect to the weights and biases, et is the training error at output t, wt is the weight at output t, gt = JtT et is the first-order derivative of the total error function (sum square error) and α is the step size of the gradient descent algorithm.
The LMANN models were developed by The Math Works TM Inc. ([31]) at Aristotle University of Thessaloniki, Greece. LMANN models is built in a three layer back-propagation neural network architecture, including: (i) an input layer with the variables showing the most significant impact to the configuration of the output variable, as inferred from sensitivity analysis; (ii) an input layer with the optimum number of hidden nodes resulting from the trial and error procedure concerning overfitting, undertraining and training efficiency; and (iii) an output layer with the estimation variable.
Due to its effectiveness, the continuous and bounded nonlinear transfer function transmitting the information from the input to the hidden layer was the hyperbolic tangent function ([12] - eqn. 4):
where s = Σ (wi xi), s ∈ [-∞, +∞] and tanh(s) ∈ [-1, +1].
Finally, a linear activation function was used to transfer the incoming weighted values from the hidden to the output layer, as the combination of the hyperbolic tangent and the linear transfer functions between the two layers proved more effective.
The basic concept of the SVR methodology is to find an optimal surface lying within the limits determined by the Support Vectors, using a loss function and minimizing the regression error of all training samples (xi’s). In the case of tree biomass modeling, the ε-insensitive loss function supported by the radial basis kernel functions (RBF) in non-linear ε-SVR algorithm ([46], [47]) was used. The methodology behind the non-linear RBF kernel ε-SVR algorithm has been thoroughly described ([43]). In summary, into the ε-insensitive tube that was set by the Support Vectors, the desired learning error has been determined, and its dimension mapped onto a higher dimensional space. For this purpose, a fixed non-linear mapping function φ(x)∈Rn (n-dimensional space) is applied, until at the end a linear combination is constructed of the form f(x)=[w,φ(x)]+b, f(x)∈R. The configuration of the weights (w) is determined by the minimization of the loss function ([43]) containing the cost parameter C, which represents the smoothness of the model, the variables called “slack” variables, which reflect the deviation of points laying outside the ε-insensitive zone, and the weight parameters. The minimization of the loss function is the solution of the quadratic programming problem under the determination of the Lagrange multipliers ([21]). In this procedure SVR makes use of the RBF kernels. To map the input vector x onto a higher dimensional feature space, the Gaussian radial basis function (RBF) kernels was used ([8] - eqn. 5):
where γSVR = (1/2σ2) is the free parameter of the RBF kernels, called “gamma” parameter, and ||xi - xj|| is the Euclidean distance between the support vectors.
For the construction of the ε-SVR models, libraries of scikit-learn ([39]) in Python programming language ([45], [41]) were used.
Allometric models for the total tree biomass and its components were also developed to compare the performances of ML models described above with those from the traditional non-linear regression modeling techniques (NLR). Also, much effort was spent to handle the heteroscedasticity of the dependent variable on one hand, and to select the proper form of equation on the other hand. Each regression model form (i.e., linear, logarithmic, inverse, quadratic, cubic, power, compound, S-curve, growth, and exponential models) was evaluated based on the mean square error and coefficient of determination ([19]), and the best performing model was the allometric one (eqn. 6):
where hat{y} is the dependent variable and xi are the independent variables used for the ML models construction, in order to compare the different modeling approaches under the same basis of the available information.
Concepts of the machine learning modeling
To avoid over/under-fitting of both the machine learning modeling approaches (LMANN and SVR), the three-way data splits method ([35]) was used. The available dataset was randomly split into two distinctive parts for calibrating/training (including 90% of the whole dataset) and validating/testing (10%) the above models. The calibration dataset was further split using the k-fold (k=10) cross-validation resampling technique to minimize the effect of a possible poor separation of the calibration sample into the fitting and validation datasets (for further details, see Fig. S1 in Supplementary material).
According to the LMANN modeling construction (see eqn. 1 to eqn. 3), the effective convergence of the LM algorithm depends on the value of the combination coefficient (μ). For large values of μ, the update of weights resulted in the gradient descent update, meaning fast convergence and stability, while small values of μ resulted in the Gauss-Newton update, meaning accuracy in prediction. The initial value of μ was set to 0.01, and then it was iteratively multiplied/divided by an adjustment factor (v = 0.001) leading to an increment/ decrement in the weight’s values until the lowest sum of squared error was obtained by the whole node network.
As for the SVR modeling approach, its effective convergence depends on the best combination of three meta-parameters that controls the estimation error, the Kernel’s spread and the simplicity of the constructed model. Specifically, the ε parameter represents the length of the ε-insensitive tube (i.e., the estimation error); the gamma parameter γSVR (eqn. 5) sets the kernel spread and the cost parameter C reflects the model smoothness ([8]). When the selected γSVR values are too small, the model has a high probability not to capture the complexity of data, while the model could probably suffer from overfitting when γSVR values are too large. Further, unsuccessful selection of the cost parameter C values can lead to unnecessary support vectors, resulting in unnecessary complexity of the model. In this study, the best combination of the three meta-parameters described above was obtained by the grid-search method ([41]), which can be considered as a complete brute-force algorithm ([26]) making an exhaustive search over the combination of predefined ranges of the three meta-parameters. We simultaneously tested ε over the range from 0.001 to 0.120 by steps of 0.001, γSVR over the range 0.01-1.00 by 0.01, and the C parameter from 4 to 800 by 2i where i ∈[2.10] for i∈N. This algorithm can be time-consuming, especially for big data sets, though crucial to construct the most accurate and reliable SVR model, as expressed by its prediction errors for the calibration and test data sets.
Models performance
The criteria used to assess the performances of the constructed models are listed below. In all subsequent equations, yi are the observed values, hat{y}i are the values estimated by the models, bar{y} is the mean of the observed values, bar{hat{y}} is the estimated mean values, and n is the total number of data used for fitting. The correlation coefficient (r) was calculated as a measure of linear correlation between the observed values and ML model predictions (eqn. 7):
The mean square error (mse) was calculated as the average of the square of the difference between actual and estimated values (eqn. 8, eqn. 9):
The mean bias (bias) was calculated as an indicator the models’ precision (eqn. 10):
and the mean absolute deviation (mad) used as an overall indication of the models’ error variance (eqn. 11):
Carbon dioxide weight estimation
According to the above model’s performance criteria, the best model was selected for estimating each of the tree components. The results were then used to derive the estimates of the carbon content (kg) of both each component and the whole tree. For this purpose, the carbon ratio (CR) previously measured in the laboratory for each biomass component was used (eqn. 12):
where CC is the carbon content, DB is the dry biomass and i is the i-th biomass component of the tree. The carbon dioxide weight (in kg) per tree can be calculated as follows (eqn. 13):
where k is the k-th tree and 3.66 is the constant ratio of the CO2 to C in a CO2 molecule, which is composed of two oxygens (atomic weight = 15.999u) and one carbon (12.011u), therefore the ratio is 44.009/ 12.011 = 3.66.
As the age of each tree sampled in this study is known, the mean carbon dioxide weight sequestered by Lebanon cedar tree plantations per year and per tree wascalculated. This information can be used to estimate the carbon dioxide weight in cedar stands of the same area, as long as stand density and the distribution of diameters are known.
Results
As expected, the relationships between the dependent variables (total and component biomass) and the independent variables (dbh and tht) showed nonlinear trend. Details on the relationship between dry components / diameter / height are reported in Fig. S2 (Supplementary material). For a given tree height, there is a larger variation in the component and total biomass values than for a tree of a given diameter. The variance in estimation of crown (foliage and branch) biomass was greater (in relative terms) than that obtained in the estimation of wood biomass. This is due to the variability of the crown structure, the number of branches, and the variation in wood density along branches. In this study we attempted to capture the non-linear nature of the biomass by applying ML techniques (LMANN and SVR).
Ground-truth measurements based on variables selected in advance due to a priori knowledge related to a specific problem is usually carried out in forest research ([28]). In this study, the above approach was used to get measurements for a wide range of variables that could affect the biomass estimation. Sensitivity analysis for the variables measured in the field was conducted. The complete ML model (i.e., including all variables as model inputs) was fitted on the data, and the estimation error was recorded (rmseall) along with the level of significance of each variable. Then, a new model was constructed excluding one variable, and the estimation error was recorded (rmseall-1). If (rmseall-1 / rmseall) < 1, the excluded variable was considered as non-significant in the model construction and therefore discarded. The latter procedure was repeated for each input variable in the construction of the LMANN model. The significant variables obtained as described above were then used as inputs in the construction of the SVR model.
Levenberg-Marquardt ANN models
Sensitivity analysis was applied to all the variables and their compound, and the most significant input variables for the LMANN model were detected. The analysis revealed the strong effect of the variables (i) diameter at breast height, (ii) total height of trees and stands, and (iii) age of the stand, on the dependent variables (total tree biomass and biomass of tree components). The exclusion of anyone of the above variables and/or their combinations from the models led to inaccurate predictions of the tree biomass components.
An example of the above procedure is reported in Fig. S3 (Supplementary material) where the dry branch biomass (dwb) and its combinations showed a ratio (rmseall-1 / rmseall) > 1, meaning that this variable was significant in the model construction. Similar distribution errors can be derived from all different outputs of the models.
Using the same trial and error procedure, all the building elements of the models (epochs, combination coefficient, hidden nodes, etc.) were determined, and the three-way data splits method implemented. Fig. 1shows the results of the repetitions under the different handle of the building elements of each network, in respect to the possible minimum values of both network estimation and prediction errors, in order to maximize the generalization ability of the model.
Fig. 1 - Construction of the best LMANN fitted models for all dry biomass components (dwn, dwb, dws, dwbark, dwbg, dwag) along with the total dry biomass (dwt).
The best performing LMANN model (Fig. 1) for each biomass elements and the total biomass (both above- and below-ground) satisfied simultaneously the following conditions: (i) minimum deviation (in terms of mean square error) from the validation datasets; (ii) minimum overall mean square error value of the fitting data set.
The proper values of the combination coefficient (μ), the numbers of the hidden nodes of each model in the hidden layer, and the proper number of the repetitions (epochs) in the model construction, were tested in the interval between 1.0e-6 and 1.0, 2-12 nodes, and 1-500 epochs, respectively. The lowest rmse% values were obtained using the best fitting LMANN model for dry stem biomass, while the model that estimates the dry biomass of branches had the largest rmse% values, due to the large variance observed in the data (Tab. 2).
Tab. 2 - Values of the construction elements for the best LMANN models and evaluation statistics according to the adaptation of the best models to the whole data set, for all biomass components and for the total tree biomass of the cedar trees. (a): Input nodes (5): stand age, stand dbh, stand tht, dbh, tht.
| Output node | aInput nodes | Hidden nodes | Best epoch | Comb. coef. (μ) | mse | rmse (%) | bias | mad | r |
|---|---|---|---|---|---|---|---|---|---|
| dwn | 5 | 6 | 19 | 1.0e-3 | 1.76 | 10.24 | -0.075 | 0.918 | 0.9949 |
| dwb | 5 | 8 | 35 | 1.0e-2 | 35.30 | 17.11 | -0.204 | 2.089 | 0.9871 |
| dws | 5 | 8 | 42 | 1.0e-2 | 0.34 | 0.72 | -0.013 | 0.295 | 0.9999 |
| dwbark | 5 | 4 | 34 | 1.0e-4 | 0.45 | 4.78 | 0.049 | 0.346 | 0.9989 |
| dwbg | 5 | 5 | 18 | 1.0e-3 | 9.81 | 11.01 | -0.098 | 1.921 | 0.9943 |
| dwag | 5 | 5 | 22 | 1.0 e-1 | 64.37 | 5.64 | -0.261 | 5.341 | 0.9985 |
| dwt | 5 | 7 | 13 | 1.0e-2 | 54.78 | 4.322 | 0.633 | 4.441 | 0.9991 |
Support vector regression models
The same variables selected via sensitivity analysis for the construction of the LMANN models were also used for developing SRV models for each biomass component and the total tree biomass. The k-fold (k=10) cross-validation method was applied to the calibration data set, and the best combination of the model parameters has been selected (Fig. 2) using the grid-search meth-od, namely the GridSearchCV function ([41]). The optimal values for the ε, γ, and C parameters selected for the best SVR models, along with the values of the evaluation statistics, are given in Tab. 3. The best selected SVR models gave acceptable modeling errors ranging from 0.26% for the dry stem weight of trees to 10.4% of the dry needle mean weight. According to the results of Tab. 2and Tab. 3, both the ML models developed in this study can produce reliable and accurate biomass estimation results.
Fig. 2 - Mean square values of the SVR fitted models, for different parameters’ combination, for all dry biomass components (dwn, dwb, dws, dwbark, dwbg, dwag) along with the total dry biomass (dwt).
Tab. 3 - Values of the construction elements for the best SVR models and evaluation statistics according to the adaptation of the best models to the whole data set, for all biomass components and for the total tree biomass of the cedar trees. (a): Input variables 5: stand age, stand dbh, stand tht, dbh, tht
| Output variable |
aInput variables |
Cost parameter (C) |
Parameter (ε) |
“gamma” parameter γSVR |
mse | rmse (%) |
bias | mad | r |
|---|---|---|---|---|---|---|---|---|---|
| dwn | 5 | 30 | 0.001 | 0.06 | 1.81 | 10.40 | -0.265 | 0.395 | 0.9950 |
| dwb | 5 | 66 | 0.011 | 0.06 | 4.69 | 6.24 | 0.395 | 0.795 | 0.9988 |
| dws | 5 | 250 | 0.001 | 0.02 | 0.04 | 0.261 | 0.008 | 0.071 | 0.9999 |
| dwbark | 5 | 250 | 0.001 | 0.01 | 0.34 | 4.16 | -0.106 | 0.144 | 0.9992 |
| dwbg | 5 | 435 | 0.001 | 0.01 | 0.19 | 1.54 | -0.064 | 0.107 | 0.9999 |
| dwag | 5 | 347 | 0.001 | 0.02 | 35.41 | 1.56 | -0.998 | 1.565 | 0.9992 |
| dwt | 5 | 684 | 0.1 | 0.03 | 40.96 | 3.75 | -0.956 | 1.709 | 0.9999 |
Allometric models were also developed for biomass estimation of cedar trees (components and total). The Levenberg-Marquardt algorithm was used for the optimization of non-linear regression models. To avoid local minima during the convergence of the models, the initial values of their parameters were obtained following the approaches described in Draper & Smith ([10]). The parameters estimate obtained for the NLR biomass models are given in Tab. 4.
Tab. 4 - Parameters estimates of the NLR allometric models developed, for the whole data set, for all biomass components and for the total tree biomass of the cedar trees. (a): Independent variables associated with the bi parameters, for i=1,…,5: stand age, stand dbh, stand tht, dbh, tht, respectively.
| NLR model parametersa | Dependent variable | ||||||
|---|---|---|---|---|---|---|---|
| dwn | dwb | dws | dwbark | dwbg | dwag | dwt | |
| b0 | 0.003 | 0.012 | 0.017 | 0.008 | 0.020 | 0.050 | 0.057 |
| b1 | 1.146 | 0.050 | 0.086 | 0.268 | -0.030 | 0.163 | 0.122 |
| b2 | 2.221 | 0.499 | -0.084 | 0.476 | 0.789 | 0.235 | 0.305 |
| b3 | -1.955 | -0.367 | 0.072 | -0.509 | -.820 | -0.190 | -0.279 |
| b4 | 2.110 | 2.133 | 1.788 | 0.687 | 1.700 | 1.778 | 1.826 |
| b5 | -1.646 | 0.285 | 1.107 | 1.736 | 0.743 | 0.697 | 0.714 |
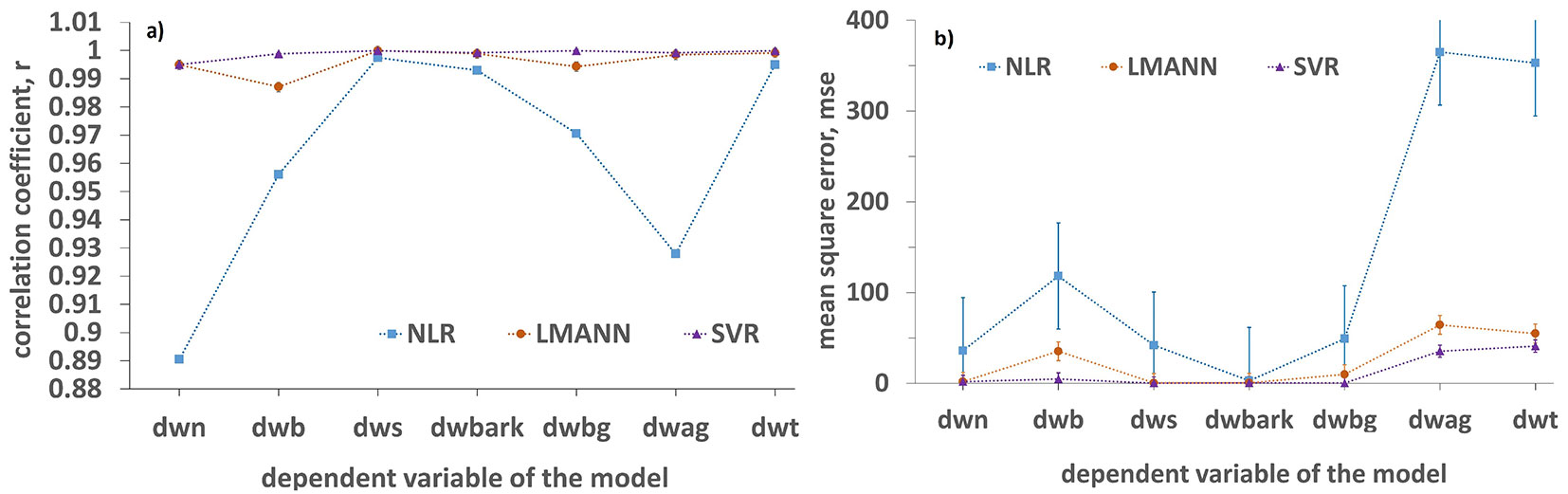
For the comparison of the performance of allometric models in predicting cedar tree biomass (components and total) versus LMANN and SVR models developed for the same variables, the correlation coefficient and the mean square error values derived by all models were used (Fig. 3). Both ML models outperformed NLR models with high differences both in terms of correlation (Fig. 3a) and mean square error estimations (Fig. 3b). NLR models showed rmse values ranging between 1.7 kg in the case of the bark biomass to 19.1 kg in the case of the above ground biomass. Error estimations were higher by 1.02-11.39 kg using the NLR models as compared to LMANN models, while error estimation using NLR models are 1.11-13.15 kg higher than those obtained using SVR models. Therefore, the precision of NLR estimates could not be considered sufficient for biomass estimation of cedar tree plantations.
Fig. 3 - (a) Correlation coefficient and (b) mean square error values derived by NLR, LMANN and SVR models, for biomass components and for the total biomass of the trees.
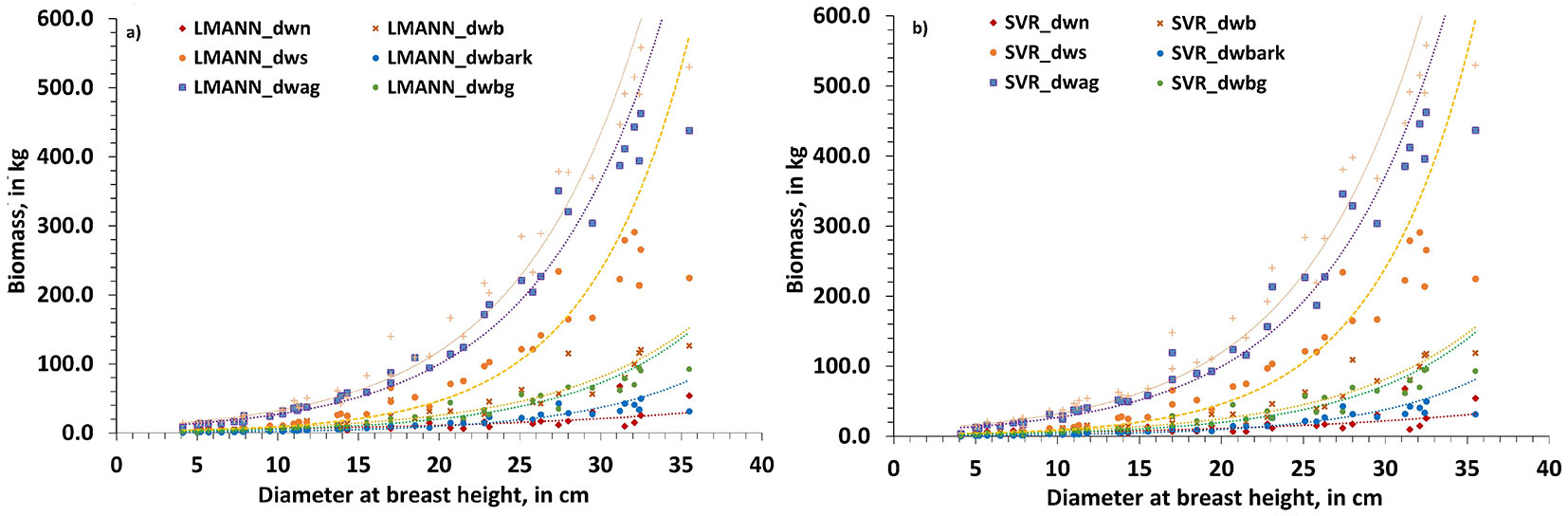
Another significant advantage of ML models used for biomass estimation is their additive property. Both machine learning modeling approaches used in this study have shown that the additive property of variable predictions was not violated, and this holds for multiple layers. That is, the estimations of the sectional biomass (dwn, dwb, dws, dwbark, dwbg, dwag) gave values smaller than those obtained for the total biomass (dwt) using both LMANN (Fig. 4a) and SVR (Fig. 4b) models. To test for the equality of the total biomass estimates with the sum of the sectional biomass estimates obtained using the ML models, the Wilcoxon’s non-parametric signed rank test for related samples was used. The results showed p-values of 0.638 and 0.882 for the LMANN and the SVR models, respectively, meaning that the equality cannot be rejected at α=0.05. In addition, the distribution of residuals of the difference between the sum of the component biomass estimates and the observed total biomass was fairly close to zero using both ML modelling approaches (see Fig. 4 in Supplementary material).
Fig. 4 - Additivity of the constructed (a) LMANN and the (b) SVR models’ estimates of the component biomass (dwn, dwb, dws, dwbark, dwag and dwbg) to the estimate of the total tree biomass (dwt).
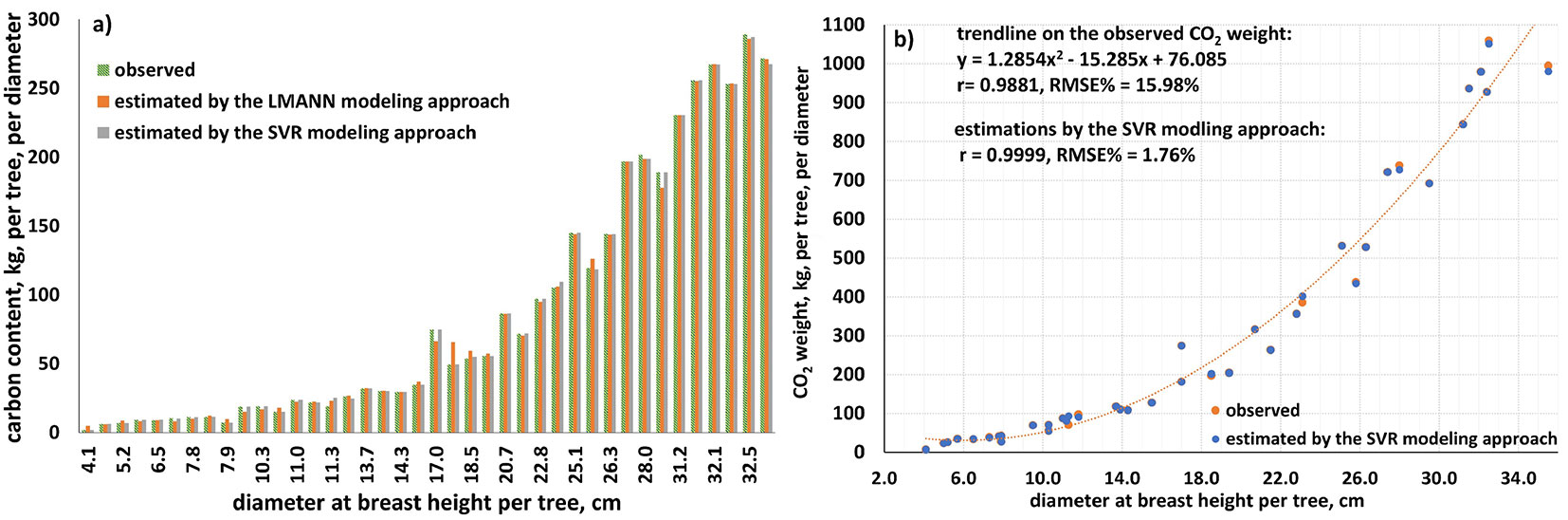
Regarding the performances of ML models in the estimation of different component of cedar trees, both approaches gave similar results for the dry needle weight, while the support vector regression approach gave significantly more accurate results in estimating the other tree components (Tab. 2, Tab. 3). The same results have been obtained for the estimated carbon content in kg per tree and per diameter at breast height (Fig. 5a). Using the best fitting LMANN model the estimation bias (eqn. 10) was equal to -0.167 kg, while it was -0.015 kg using the best fitting SVR model. For this reason, we estimated the carbon content (eqn. 12, Fig. 5a) and the carbon dioxide weight (eqn. 13, Fig. 5b) for the sampled cedar trees and stands based on the results derived from the SVR models (Tab. 3).
Fig. 5 - Estimated (a) carbon content by both ML modeling approaches and (b) CO2 sequestration per tree and per diameter at breast height, by the SVR modeling approach.
Discussion
Carbon storage by trees can represent a useful parameter for decision-making in multipurpose forest management of Lebanon cedar plantations. Due to its valuable properties, this species is widely used for afforestation in Turkey and its potential in carbon gas sequestration from atmosphere is worth to be investigated.
Taking advantage of powerful machine learning techniques currently available, neural network (LMANN) and support vector regression (SVR) models were developed in this study with the aim of obtaining accurate and reliable estimations of tree biomass and its components, and assessing the carbon stored in Lebanon cedar tree plantations in Western Turkey.
Sensitivity analysis was used for selecting the best combination of input variables for the models. The results of showed that the biomass estimates of all the tree components examined depends mainly on the breast height diameter and the height of the representative tree of each plot, but also on some characteristics of the plot, such as the average diameter, height, and stand age.
The results of biomass modeling using ML approaches in this study are in agreement with those reported in the literature in the last decade. For example, Guo et al. ([16]) compared machine learning methodologies for above-ground biomass estimation using multisource remote sensing data and found that support vector machine algorithm can provide more accurate results compared with different neural network architectures. Malek et al. ([29]) investigated the use of machine learning techniques (support vector regression and random forest) using airborne laser scanning data and field measurements, finding significant improvements in biomass and stem diameters estimations. In this study, the models developed using support vector regression provided significant improvement in biomass (total and components) estimation as compared to the Levenberg-Marquardt artificial neural network models. Specifically, the rmse values for the LMANN models were in the range of 0.58 kg for dws to 8.02 kg in the case of dwag, while the range of rmse for the SVR model were found between 0.2 kg (dws) to 5.95 kg (dwag). In both models, the lowest rmse value was obtained for the dry stem biomass without bark, while the highest were obtained for the dry above ground biomass estimated by LMANN models and the total biomass (above- and belowground) by SVR models. As reported in Tab. 2and Tab. 3, the results differ somehow when the rmse% of the mean of each input (dependent) variable was considered. The maximum rmse% was recorded for the dry branch biomass and the dry needle biomass estimates by the LMANN and the SVR models, respectively.
The performances of the machine learning models was further evaluated through their comparison to the allometric non-linear regression models which were developed for the same sample of cedar trees. According to biomass (components and total), the developed NLR allometric models provided more than two times higher error values than both the ML models, while the mean error difference in above-ground biomass estimates was 13.15 kg lower using the best fitting SVR model as compared to the related NLR model. Taking into account the effort required to build a regression model and its higher estimation errors, the use of the nonlinear regression approach takes a back seat when advanced modeling methods such as those based on machine learning are available. However, the latter modeling approach requires hyperparameters to be determined through programming efforts and suitable skills.
Our modeling strategy produced a single model for each biomass component and for the whole tree biomass separately. This led to the best optimization of the modeling parameters according to the different variability of each target variable, for both ML modeling approaches used. According to our results, the support regression modeling procedure yielded the most accurate and reliable biomass predictions as compared to the Levenberg-Marquardt neural network modeling approach, except for the needle dry weight estimation which showed no significant differences were found at α = 0.05. As reported in Tab. 3, the SVR models gave rmse values 2.74, 2.91, 1.15, 7.18, 1.34 and 1.15 times smaller than the LMANN models’ corresponding values for the dry weight of the branches (live and dead - dwb), stem wood (dws), stem-bark (dwbark), below-ground biomass (dwbg), total above-ground biomass (dwag), and total biomass (dwt) of sampled trees, respectively.
Similar results were obtained for the estimation of the CO2 sequestration. The SVR models developed in this study led to the most accurate estimations per tree and per diameter at breast height both for carbon content and CO2 sequestration (see Fig. S4 in Supplementary material). The available biomass of a forest ecosystem is a measure of its capability to absorb carbon dioxide and store carbon, as well as to reduce the relative harmful effects by releasing oxygen to the atmosphere. When carbon storage and CO2 sequestration by cedar plantations can be obtained by accurate models, adequate forest management decisions can be taken allowing for both the improvement of forest sustainability and the implementation of multi-task reforestation designs aimed to mitigate the detrimental effects of climate change. Moreover, the development of new models and methods to improve the prediction of tree attributes related to forest productivity was deemed essential ([15], [9]). As displayed in Fig. 5b, the carbon dioxide weight sequestered by cedar trees can be estimated with remarkable accuracy by the constructed SVR models. The error calculated using eqn. 9 was about 1.8% of the observed CO2 mean. The usual procedures to obtain CO2 quantities are laborious and tree destructive, whereas using reliable models the carbon weight sequestered in trees can be accurately estimated.
Conclusions
In this study, modern machine learning (ML) techniques have been applied to accurately predict carbon dioxide sequestration by plantations of Lebanon cedar trees in Western Turkey. Levenberg-Marquardt artificial neural network models and Support vector regression models were constructed for the accurate estimation of the tree biomass components and the whole tree biomass. According to the results, both the above models showed significantly better performances than the non-linear regression allometric models developed for the same dataset, providing higher accuracy in predicting cedar trees biomass (both the components and total) and consequently more accurate prediction of the standing cedar trees carbon content and the CO2 sequestration per tree and per diameter at breast height.
Our study also indicates the superiority of the support vector regression models in producing the most accurate results. These findings provide an effective basis for further exploration of machine learning techniques as a powerful tools for solving significant problems that are considered difficult to be approached in forestry research.
List of abbreviations
ML: machine learning; tht: total height; dbh: diameter at breast height; DW: dry weight; FW: fresh weight; ANN: artificial neural network; LMANN: Levenberg-Marquardt artificial neural network; LM: Levenberg-Marquardt; SVR: support vector machines for regression; RBF: radial basis function.
Acknowledgements
This study is part of the project titled “Determining the carbon stocks of Cedrus libani plantations in Regional Directorate of Eskisehir” [ESK-13(6310)] funded by the Turkish General Directorate of Forestry.
References
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Faculty of Agriculture, Forestry and Natural Environment, School of Forestry and Natural Environment, Aristotle University of Thessaloniki, GR-54124 Thessaloniki (Greece)
Aegean Forestry Research Institute, 35515 Urla, Izmir (Turkey)
Faculty of Forestry, Isparta University of Applied Sciences, 32260 Isparta (Turkey)
Department of Forestry, Ulus Vocational School, Bartin University, 74600 Ulus, Bartin (Turkey)
Corresponding author
Paper Info
Citation
Diamantopoulou MJ, Çömez A, Özçelik R, Güner ST (2024). Exploring machine learning modeling approaches for biomass and carbon dioxide weight estimation in Lebanon cedar trees. iForest 17: 19-28. - doi: 10.3832/ifor4328-016
Academic Editor
Giorgio Alberti
Paper history
Received: Feb 15, 2023
Accepted: Nov 15, 2023
First online: Feb 12, 2024
Publication Date: Feb 29, 2024
Publication Time: 2.97 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2024
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 17134
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 11212
Abstract Page Views: 2748
PDF Downloads: 2899
Citation/Reference Downloads: 0
XML Downloads: 275
Web Metrics
Days since publication: 671
Overall contacts: 17134
Avg. contacts per week: 178.75
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
(No citations were found up to date. Please come back later)
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
The use of tree crown variables in over-bark diameter and volume prediction models
vol. 7, pp. 132-139 (online: 13 January 2014)
Research Articles
Total tree height predictions via parametric and artificial neural network modeling approaches
vol. 15, pp. 95-105 (online: 21 March 2022)
Research Articles
Analyzing regression models and multi-layer artificial neural network models for estimating taper and tree volume in Crimean pine forests
vol. 17, pp. 36-44 (online: 28 February 2024)
Research Articles
Prediction of stem diameter and biomass at individual tree crown level with advanced machine learning techniques
vol. 12, pp. 323-329 (online: 14 June 2019)
Research Articles
Estimation of above-ground biomass and sequestered carbon of Taurus Cedar (Cedrus libani L.) in Antalya, Turkey
vol. 6, pp. 278-284 (online: 01 July 2013)
Research Articles
A geographically weighted deep neural network model for research on the spatial distribution of the down dead wood volume in Liangshui National Nature Reserve (China)
vol. 14, pp. 353-361 (online: 27 July 2021)
Research Articles
Yield of forests in Ankara Regional Directory of Forestry in Turkey: comparison of regression and artificial neural network models based on statistical and biological behaviors
vol. 16, pp. 30-37 (online: 22 January 2023)
Research Articles
Stand structure and regeneration of Cedrus libani (A. Rich) in Tannourine Cedar Forest Reserve (Lebanon) affected by cedar web-spinning sawfly (Cephalcia tannourinensis, Hymenoptera: Pamphiliidae).
vol. 11, pp. 300-307 (online: 13 April 2018)
Research Articles
Estimation of above-ground biomass using machine learning approaches with InSAR and LiDAR data in tropical peat swamp forest of Brunei Darussalam
vol. 17, pp. 172-179 (online: 17 June 2024)
Research Articles
Artificial intelligence associated with satellite data in predicting energy potential in the Brazilian savanna woodland area
vol. 13, pp. 48-55 (online: 05 February 2020)
iForest Database Search
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords