Do different indices of forest structural heterogeneity yield consistent results?
iForest - Biogeosciences and Forestry, Volume 15, Issue 5, Pages 424-432 (2022)
doi: https://doi.org/10.3832/ifor4096-015
Published: Oct 20, 2022 - Copyright © 2022 SISEF
Research Articles
Abstract
Forest management with a focus on high structural heterogeneity is a major goal in modern forestry to increase multifunctionality. The assessment and quantification of forest structures has, therefore, gained much attention in recent years. However, there is no standardized approach to surveying forest heterogeneity; instead, a variety of structural indices, which have been developed over past decades, are used. This makes it difficult to interpret the results of different studies and to base management decisions on such data. In this study, we compared six structural indices that differ in terms of their complexity and the method of data acquisition. These included the Gini coefficient of the diameter at breast height and of tree height, the Shannon index of tree species diversity, two complex indices of structural heterogeneity, one based on conventional inventory data and one on terrestrial laser scanning (TLS) data, and a simple-holistic TLS-based stand structural complexity index. For the comparison of these six indices, we used data from 84 plots in 12 different forest stand types in two study areas in Germany. The stand types consisted of different dominant tree species and included different age classes. The degree of correlations among the different indices was highly variable. In addition, we did not find a clear age-dependency of the indices. We conclude that the choice of a specific index plays an important role in the evaluation and interpretation of forest structural heterogeneity. Because TLS data offer multiple benefits in terms of precision, reproducibility and comprehensiveness, we recommend to use TLS-based indices of structural heterogeneity.
Keywords
Forest Structure, Shannon Index, Gini Coefficient, Stand Structural Complexity Index, Structural Heterogeneity Index
Introduction
During the last centuries, timber production has been the primary aim of forest management in central European forests. In recent decades, however, multifunctional forestry came into focus, with which the conservation of biological diversity and other ecosystem services such as groundwater protection or recreation increasingly gained in importance. In these forest management systems the structural complexity of stands is enhanced by using natural regeneration approaches, mixing different tree species and increasing the number of structural elements such as deadwood objects or habitat trees ([16], [3], [6]). There is strong evidence that structurally complex forests have a higher resilience to disturbances, show a better adaptability to environmental stressors and have a higher biodiversity, while often being at least as productive or even more productive than more homogeneously structured forests ([13], [45], [48]). Therefore, “management for complexity” ([38]) is a common goal in modern forestry. Furthermore, there are currently intensive discussions about payments for forest ecosystem services ([43], [37]). For these purposes it is mandatory to establish an evaluation system with reliable indicators for the comparison of the outcomes of different management options and for the monitoring of their performance. An index of structural heterogeneity ([29], [42]) is such an indicator.
However, various definitions of structural complexity and heterogeneity exist in forest science today. The differences between these definitions are vague and boundaries are often not precisely definable. Both terms, complexity and heterogeneity, describe, according to the current literature ([2], [4], [41]), the entirety of all horizontal and vertical non-uniformities in the structural and distributional composition of the stand structure of a forest. In this study, these two terms are considered as synonyms, and in the following the term “structural heterogeneity” is preferred.
Reich et al. ([41]) classified existing indices of structural heterogeneity based on their degree of complexity and the method of data acquisition (see Tab. S1 in Supplementary material). For the former aspect a division was made into simple, basic indices and complex, comprehensive indices. The method of data acquisition was classified either as conventional inventories or as modern non-destructive recordings using terrestrial laser scanning (TLS). In the resulting four-field matrix the Gini coefficient ([15]) and the Shannon index ([50]) represent simple indices by which the input data are recorded by conventional inventories. The Gini coefficient, originally developed by economists, can be considered as a classic statistical measurement of the inequality of a distribution. The Gini coefficient is well suited for the use of classical forest inventory data ([25]), such as tree height or diameter at breast height (DBH). The Shannon index has in particular received much attention due to its popularity for quantifying species diversity. The Shannon index combines the two components of diversity ([24]): the number of different conditions and the extent of their equal distribution, and describes the diversity of observed data, taking into account both the number of different data categories (e.g., the number of species) and their abundance (number of individuals per species - [7], [26]). At the maximum value, all species are represented with equal proportions ([34]).
The Gini coefficient and the Shannon index have been used in many studies on structural heterogeneity of forests. However, recent studies conclude that the structural heterogeneity is inadequately determined by using single structural attributes ([49], [46]). On the basis of the methodology presented by McElhinny et al. ([29]), Sabatini et al. ([42]) developed a structural heterogeneity index (SHI). In the following, this index will be referred to as the conventional structural heterogeneity index (SHICONV). Here we classify the SHICONV as a complex index that is based on the conventional inventory data (Tab. S1 in Supplementary material).
Typically, the data sets of conventional inventories only contain one- or two-dimensional attributes (e.g., DBH, volume, tree position). However, these tree attributes do not adequately represent the three-dimensional (3D) structure of forests. Accurate 3D recordings are difficult to make with traditional measuring instruments (e.g., measuring tape, calliper, tree height gauges or crown mirror) and usually involve a great effort including destructive methods. New technical approaches and methods surpass these problems and provide new opportunities to analyse the structural heterogeneity of forests in great detail. This applies in particular to modern surveying technology such as terrestrial laser scanning (TLS - [27], [8]). The point clouds obtained from TLS allow the analysis of standard tree and stand dendrometrics as well as 3D tree structure properties ([40], [5], [21], [14]). TLS approaches are complex, non-destructive, and highly reproducible due to their data storage and modeling. Based on TLS data, Reich et al. ([41]) presented a new complex though easy-to-use structural heterogeneity index (SHITLS). This index uses 3D point clouds of individual trees that were derived from multiple TLS scans. The main focus of the SHITLS calculations was laid on tree crown attributes, because this is of special significance for the 3D structure of forests ([22], [36]). In the four-field matrix of existing structural heterogeneity indices (Tab. S1) the SHITLS is classified accordingly as complex and TLS-derived.
Furthermore, a fourth class of structural indices exists, being simple-holistic and TLS-based. An example for this is the stand structural complexity index (SSCI) by Ehbrecht et al. ([12]). The SSCI makes use of single scans and is composed of two elements, the mean fractal dimension index (MeanFrac) and the effective number of layers (ENL). It has been found that the SSCI increases with stand height and stand age ([32]).
The focus of this study was to analyse the relationships between different indices which are supposed to characterise the structural heterogeneity at the plot level, but differ with regard to their degree of complexity and the technology used for data acquisition. In this study we investigate six indices from the above-mentioned four classes: Gini coefficient of DBH, Gini coefficient of tree height, Shannon index of tree species diversity, SHICONV, SHITLS and SSCI. Specifically, four hypotheses were tested: (1) the indices consisting of a single attribute and the SHICONV correlate closely with each other; (2) the two complex indices, SHICONV and SHITLS, correlate closely with each other; (3) the SSCI correlates closely with the Gini coefficient of tree height; (4) all indices except for the SHITLS are age-dependent. The hypotheses are selected and formulated based on preliminary considerations and research. Hypotheses (1) and (2) are based on the data collection and data basis used in this study. Since SSCI is strongly based on quantifying vertical stand structure, hypothesis (3) relates SSCI and the Gini coefficient of tree height. The fourth hypothesis is related to the use of the mean of different structural attributes. The assumption was: as age increases, the mean value changes (i.e., it increases or decreases). Therefore, it may be better to use alternative parameters (e.g., range, variance) for descriptive statistic and evaluation.
Materials and methods
Study areas
The study was conducted in two areas in Germany, one is located in north-eastern Hesse (51° 02′ N, 10° 04′ E - henceforth: “NE Hesse”), the other in the north-western part of the Lusatian hill country, Saxony (51° 28′ N, 14° 04′ E - “Lusatia”). Both forests sites are privately owned and managed. Further information on the study areas is presented in Tab. 1.
Tab. 1 - Brief description of the two study areas. (MAP): mean annual precipitation; (MAT): mean annual temperature. Climate data from DWD ([10]).
| Variable | Study area | |
|---|---|---|
| NE Hesse | Lusatia | |
| Elevation (m a.s.l.) | 172-515 | 120-320 |
| Climate | suboceanic-subcontinental | subcontinental |
| MAP (mm) | 600-1000 | 670-720 |
| MAT (°C) | 6.5-8.0 | 7.8-8.5 |
| Soil type | terra fusca, brown earth | sandy brown earth |
| Natural vegetation | Hordelymo-Fagetum Luzulo-Fagetum | Vaccinio vitis-idaeae-Quercetum Galio sylvatici-Carpinetum |
| Tree species composition | Fagus sylvatica (44%), Picea abies (24%), Fraxinus excelsior (8%), Acer spec. (5%), Quercus sp. (4%), other (15%) |
Pinus sylvestris (65%), Picea abies (13%), Betula pendula (6%), Quercus spec. (4%), other (12%) |
Sampling design
The data collection was conducted on an existing grid of forest inventory plots. Based on forest management plans and available inventory data, eight and four forest stand types were defined in NE Hesse and Lusatia, respectively. Here, a stand type represents a uniformly managed area with similar stocking in terms of tree species, tree age and growth rates. In NE Hesse, stand types included dominating European beech (Fagus sylvatica, hereafter “Fs”) with further admixed tree species and dominating Norway spruce (Picea abies, “Pa”) with further admixed tree species, each represented with the three age classes pole wood (pw), immature forest stands (ifs) and mature forest stands (mfs). In addition, there are two stand types with other coniferous tree species (in the following “OCTS”), one ifs and one mfs. In Lusatia three stand types with strongly dominating Scots pine (Pinus sylvestris, “Ps”) with the three age classes pw, ifs, and mfs were selected, and additionally pine with admixed deciduous tree species (henceforth “PADTS”) with the age class ifs. The following DBH thresholds were applied when classifying pw, ifs and mfs: (i) pw: DBH < 20 cm; (ii) ifs: 20 cm ≤ DBH < 30 cm; (iii) mfs: DBH ≥ 30 cm. Each of these 12 stand types were represented by 6 to 8 sample plots. A table with characteristics of these stand types is provided in Tab. S2 (Supplementary material). The test of the age dependence of the indices (see hypothesis 4) was performed for the four groups of forest stand types Fs, Pa, OCTS, and Ps.
Data sampling
Both the conventional inventory data and the TLS data were recorded on circular plots with a diameter of 12 m. The conventional inventory was carried out in both study areas in February and March 2018. The TLS sampling in NE Hesse were done in February 2018. In Lusatia, these measurements were conducted in April 2019.
For all living trees with a DBH ≥ 7 cm, species identity, spatial position, DBH (stem diameter at 1.30 m) and tree height were recorded. The DBH was measured with a caliper, tree height was determined using a laser hypsometer. Tree height was measured on a subsample of two trees per unit in each circular plot, with unit defined as a group with the same tree species, vertical structure, and age class in each stand type. Among all other trees, tree height was estimated and transferred based on measured values using conventional H = f(DBH) models. Deadwood recordings were carried out similar to the criteria of the living stock: minimum diameter > 7 cm, for lying deadwood the thick end must be in the plot. The diameter of lying deadwood, as equivalent to “DBH”, was measured horizontally 1 m away from the thicker end. The length of lying deadwood was measured using a tape measure. The diameter of standing deadwood was measured with a caliper at a height of 1.3 m.
The TLS data were obtained with a Riegl VZ®400i (RIEGL, Horn, Austria) terrestrial laser scanner with full-waveform capabilities. To take full advantage of the TLS and to achieve a high point density, each plot was scanned from five positions using a multi-scan approach ([27]). In our scan design, the plot centre represented the first scanning position. Four more positions were established in all four cardinal directions about 18 m from the centre. Two scans were taken at each scan position. Given the 100° × 360° field-of-view, the scanner was tilted by 90° horizontally after the first scan and a second scan was performed to cover the whole canopy above the scanner. The following scan settings were chosen for all scans: angular resolution of 0.04 deg (corresponding to a resolution of 7 mm at 10 m distance), laser frequency of 600 kHz. All scans were carried out under a clear and calm skies.
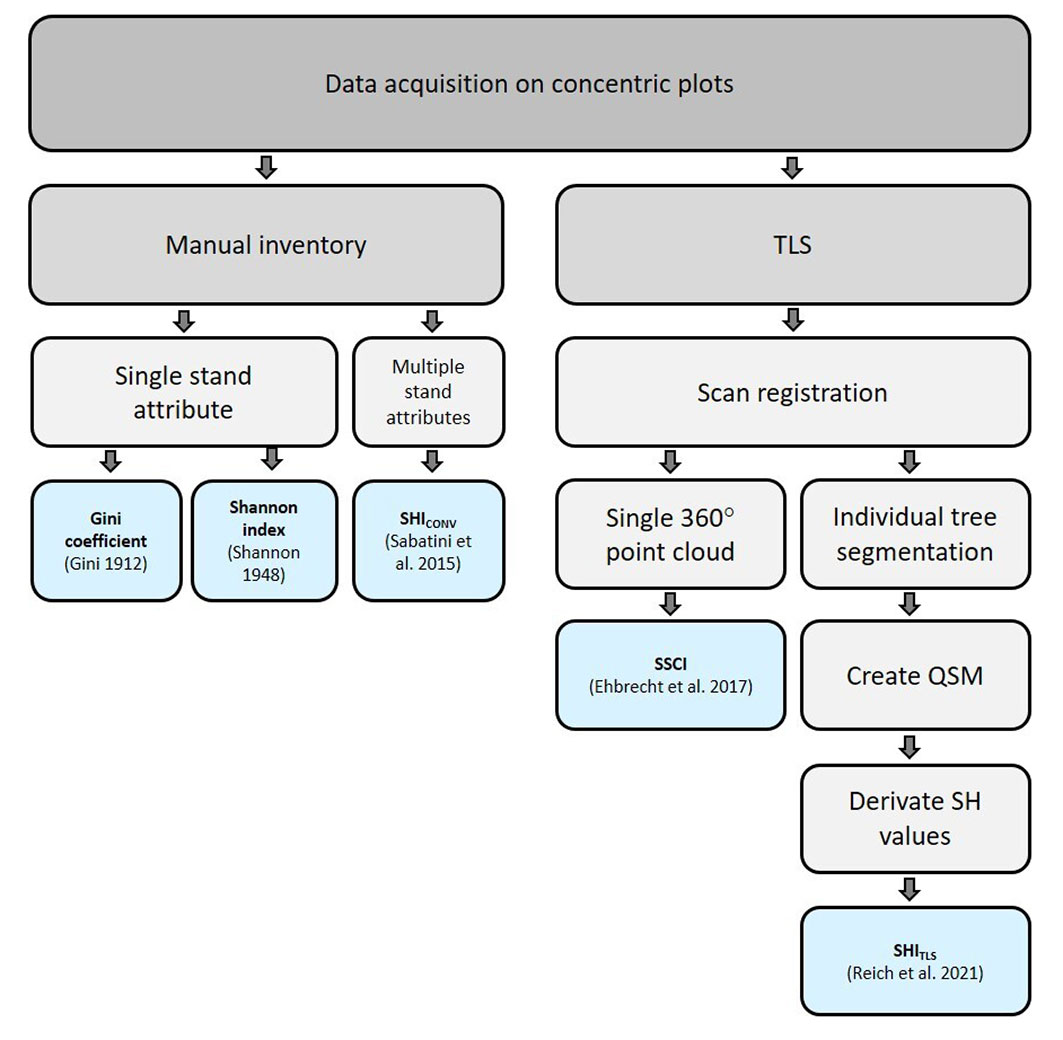
In order to fully utilise the TLS data and to calculate the SHITLS, the raw data were processed according to the workflow presented in Fig. 1. All scans of a plot were registered with each other once all point clouds were filtered to remove stray points and noise with a reflectance less than -15 dB or a pulse shape deviation greater than 15 ([33]). During registration, the coordinate origin was placed at the first scanning position (i.e., in the centre of the plot).
Fig. 1 - Workflow of data acquisition and processing. (TLS): terrestrial laser scanning; (QSM): quantitative structure model; (SH): structural heterogeneity; (SHICONV): structural heterogeneity index based on conventional inventory data; (SSCI): stand structural complexity index (based on single TLS scans); (SHITLS): structural heterogeneity index (based on multiple TLS scans and individual tree segmentation and QSM modelling).
To automatically segment individual trees, we used the open-source tool SimpleTree v. 4.33.06, a plugin of the CompuTree v. 5.0.054 platform ([17]). For further analyses and calculations, only trees with a DBH ≥ 7 cm were considered. Segmented single trees were modelled using quantitative structure models (QSMs - [40]). QSMs are based on cylinders fitted to the segmented individual-tree point cloud by the principle of least squares. With the software TreeQSM v. 2.30 ([1]), running under MATLAB v. R2018a, we computed QSMs using the average values of five model runs for each tree. The following parameter values were used to obtain the QSMs: minimum patch size = 20 mm; maximum patch size = 40 mm; relative cylinder length 3, 4, 6; relative radius for outlier removal 3, 4.5; minimum cylinder radius = 0.5 mm. All needed tree structural attributes were either derived from the point clouds or the QSMs.
Indices based on single attributes
The Gini coefficient (GC) is used to describe the inequality of a distribution, and is based on the Lorenz curve. GC is bounded between 0 and 1, allowing a simple interpretation. For a perfectly equal distribution the GC is 0. The more unequal the distribution, the closer the value is to 1. The following formula was used to calculate GC at the plot level (eqn. 1):
where x is the observed value, n is the number of trees measured in the plot and i is the rank of the observed value in ascending order. The GC was applied to the DBH (hereafter: GCDBH) and to tree height (hereafter: GCH).
The Shannon index (HS) indicates the diversity of biotic communities and is based on the dominance of each species (S), measured from 0 to ln(S). If the species distribution is uneven, HS approaches 0. For the calculation the following formula is used (eqn. 2, eqn. 3, eqn. 4):
with S being the total number of tree species per plot; pi the probability of occurrence of tree species i, which is the relative abundance of the i-th tree species from the total number of tree individuals per plot, measured from 0.0 to 1.0; N being the total number of tree individuals; and ni the number of tree individuals of the tree species i.
Calculation of SHICONV
The SHICONV was calculated using the eight structural attributes following the method introduced by Sabatini et al. ([42]). These attributes were: (i) living volume; (ii) number of trees with DBH > 40 cm; (iii) DBH diversity Gini-Simpson index; (iv) tree height (standard deviation); (v) coarse woody debris (CWD) index; (vi) tree species richness; (vii) basal area of standing deadwood and (viii) volume total deadwood. The exact calculation of the eight attributes can be found in Tab. S3 (Supplementary material). Sabatini et al. ([42]) showed that the SHICONV was higher in multi-layered forests than in single and double layer forests. Furthermore, a linear increase with increasing age of the forest stands was observed. Each structural attribute was given a score between 0 and 1. This score is based on a linear regression assigned to each structural attribute variable. Here, the eight attributes were each used as independent variables. To avoid outliers, the minimum attribute score of 0 was allocated to the 12.5-percentile, and the maximum attribute score of 10 was allocated to the 87.5-percentile. Values above and below this limit have been removed. Using the remaining values, a linear regression through quartile values could be determined to ensure a uniform distribution. Subsequently, the score of each structural attribute could be determined, all eight individual scores were summed and put into perspective. No weighting of individual attributes took place. To implement the SHICONV in our study, a few adjustments had to be made in advance. The entirety of sample plots was randomly subdivided into a training (30 %) and test (70 %) data set. The training data set was used to generate a regression to evaluate each structural attribute. The regression equation could then be applied in the test data set to calculate the SHICONV. Successively, the total data set was randomly divided again into a training and test data set and the calculations were repeated fifty times. The mean of each plot was used in further analyses.
Calculation of SHITLS and SSCI
The data of the SHITLS and SSCI were taken from Reich et al. ([41]). The methods of how to calculate these two TLS-based indices are described in detail for the SHITLS in Reich et al. ([41]) and for the SSCI in Ehbrecht et al. ([12]). In short, the following eight TLS-based structural attributes were used to calculate the SHITLS: (i) crown density (range); (ii) ratio crown width to crown length (coefficient of variation - CV); (iii) CBH (GC); (iv) volume of branches of 1st, 2nd, and 3rd order (range); (v) ratio crown displacement to height (range); (vi) crown surface area (GC); (vii) ratio crown area to crown volume (CV); and (viii) crown sinuosity (GC). In order to eliminate possible age effects, the mean or median of the examined attributes was not taken into account, instead the respective range, the GC or the CV of the examined attribute was used. The methodological approach to the calculations is similar to that of the SHICONV. Again, the dataset was subdivided into a training and a testing set, regressions have been derived, and scores were assigned. As with the SHICONV, the eight structural attributes were each used as independent variables.
The SSCI was calculated on all plots according to the approach introduced in Ehbrecht et al. ([12]). The calculations require a 360° scan generated from the superimposition of scan 1 and 2 on the first scan position (plot centre point). The SSCI exists of two components: the mean fractal dimension index (MeanFRAC) and the effective number of layers (ENL). The MeanFRAC is calculated from the average of all 2560 FRACs. A single FRAC is calculated by connecting the points of a vertical planar scan line to a polygon and taking the ratio of the area (A) to the respective perimeter (P). The following formula was used for this purpose (eqn. 5):
The resulting MeanFRAC is a dimensionless ratio with no absolute scale. The ENL is an index of layer complexity based on the ratio of occupied voxels (p) in a layer (i). Our calculations are based using a voxel grid with a size of 20 cm and a layer thickness of 1 m. The following formula is used for the ENL and the overall SSCI (eqn. 6, eqn. 7):
MeanFRAC and ENL were calculated using R v. 3.6.1 ([39]) with the “VoxR” ([23]) and “sp” ([31]) packages, respectively.
Since the calculations for the SSCI, more precisely for the ENL, are based on the assumption that the layers run parallel to the ground ([11]), an adjustment to the typical mountain ranges on the study sites in Hesse and Lusatia had to be performed beforehand.
Following the approach of Perles-Garcia et al. ([32]) the point clouds were rotated on the x- and y-axis around the scanner position to eliminate a possible influence of slope effects. First, ground points within a 3 m radius of the scanner were extracted by fitting a 3D plane using singular value decomposition with the scan centre at (0.0.0). All points were then rotated about the derived surface normal vector. Thus, the recomputed point cloud always contains a horizontally oriented terrain surface.
Statistical analysis
The statistical analysis and all calculations with structural attributes were performed using R v. 3.6.1 ([39]). The GC was calculated with R using the package “ineq” ([53]). Correlation analyses between the different indices were performed using Spearman’s rank correlation coefficient using the R package “pspearman” ([44]). Furthermore, a principal component analysis (PCA) and a concordance analysis were performed. PCA is used to structure, reduce and visualize the amount of data. Based on linear combinations and correlations, it aims to bundle a large proportion of the information of the variables in the principal components. The PCA was calculated with the package “factoextra” ([19]) in R. Finally, the concordance of the respective indices to each other was determined. This was done using the concordance correlation coefficient (CCC) according to Lin ([28]) using the R-package “DescTool” ([51]). The CCC includes a Lin-correction term about the precision of the correlation to the ideal angle bisector. It thus evaluates the degree to which the pairs of observation fall on the 45° line through the origin of the coordinate system. For the calculation and the comparability of the CCC, all indices were standardized between 0 and 1 in advance. Differences between age classes within the four groups of forest stand types (i.e., Fs, Pa, OCTS, Ps) were tested using analysis of variance (ANOVA) followed by post-hoc analysis (Tukey’s test).
Results
Most significant correlations were found between the three simple indices GCDBH, GCH, HS, and the SHICONV (Tab. 2). The two GCs were highly positively correlated with each other, both for the total of all 12 stand types as well as for the two study areas separately (always r > 0.53). Interestingly, the HS was much closer correlated with the GCH than with the GCDBH (e.g., over all the 12 stand types: r = 0.61 and r = 0.38, respectively). Among the correlations of the three simple indices with the SHICONV, the HS had the highest values and the GCDBH the lowest (e.g., total: r = 0.76 and r = 0.42, respectively). The GCH was more similar to the HS than to the GCDBH (e.g., total: r = 0.64). The correlations of these four indices with the SSCI were all not significant, with a range from r = -0.04 to r = 0.18. Compared to the SSCI, the second TLS-based index (SHITLS) showed a different pattern. A large variation in correlation coefficients emerged, though only in the range between r = 0 to r = 0.49. Over all 12 stand types, the GCDBH was not correlated at all with the SHITLS, while very weak correlations were found with GCH, HS, and SHICONV (r = 0.27, r = 0.23, r = 0.21, respectively), and a weak correlation was observed between the SSCI and SHITLS (r = 0.33). In a separate analysis of the two study areas, NE Hesse showed lower correlations coefficients between SHITLS and the other indices than Lusatia, with the exception of SSCI (r = 0.36 in NE Hesse, r = 0.03 in Lusatia).
Tab. 2 - Spearman’s rank correlation coefficient between all structural heterogeneity indices, both in total and separately for the two study areas NE Hesse and Lusatia. (SHITLS): structural heterogeneity index (terrestrial laser scanning); (SHICONV): conventional structural heterogeneity index; (SSCI): stand structural complexity index; (GCDBH): Gini coefficient (diameter at breast height); (GCH): Gini coefficient (tree height); (HS): Shannon index; (*): p < 0.05; (**): p < 0.01; (***): p < 0.001; (ns): not significant.
| Study Area |
Index | SHITLS | SSCI | SHICONV | GCDBH | GCH |
|---|---|---|---|---|---|---|
| Total | SSCI | 0.329** | - | - | - | - |
| SHICONV | 0.208 ns | -0.036 ns | - | - | - | |
| GCDBH | 0.004 ns | 0.014 ns | 0.421*** | - | - | |
| GCH | 0.267* | 0.123 ns | 0.635*** | 0.641*** | - | |
| HS | 0.228* | 0.030 ns | 0.758*** | 0.384*** | 0.607*** | |
| NE Hesse | SSCI | 0.362** | - | - | - | - |
| SHICONV | 0.157 ns | 0.014 ns | - | - | - | |
| GCDBH | -0.066 ns | 0.009 ns | 0.396** | - | - | |
| GCH | 0.192 ns | 0.116 ns | 0.533*** | 0.718*** | - | |
| HS | 0.306* | 0.113 ns | 0.692*** | 0.261ns | 0.521*** | |
| Lusatia | SSCI | 0.027 ns | - | - | - | - |
| SHICONV | 0.464** | 0.091 ns | - | - | - | |
| GCDBH | 0.221 ns | 0.134 ns | 0.454* | - | - | |
| GCH | 0.488** | 0.183 ns | 0.767*** | 0.532** | - | |
| HS | 0.327* | 0.060 ns | 0.855*** | 0.585*** | 0.76*** |
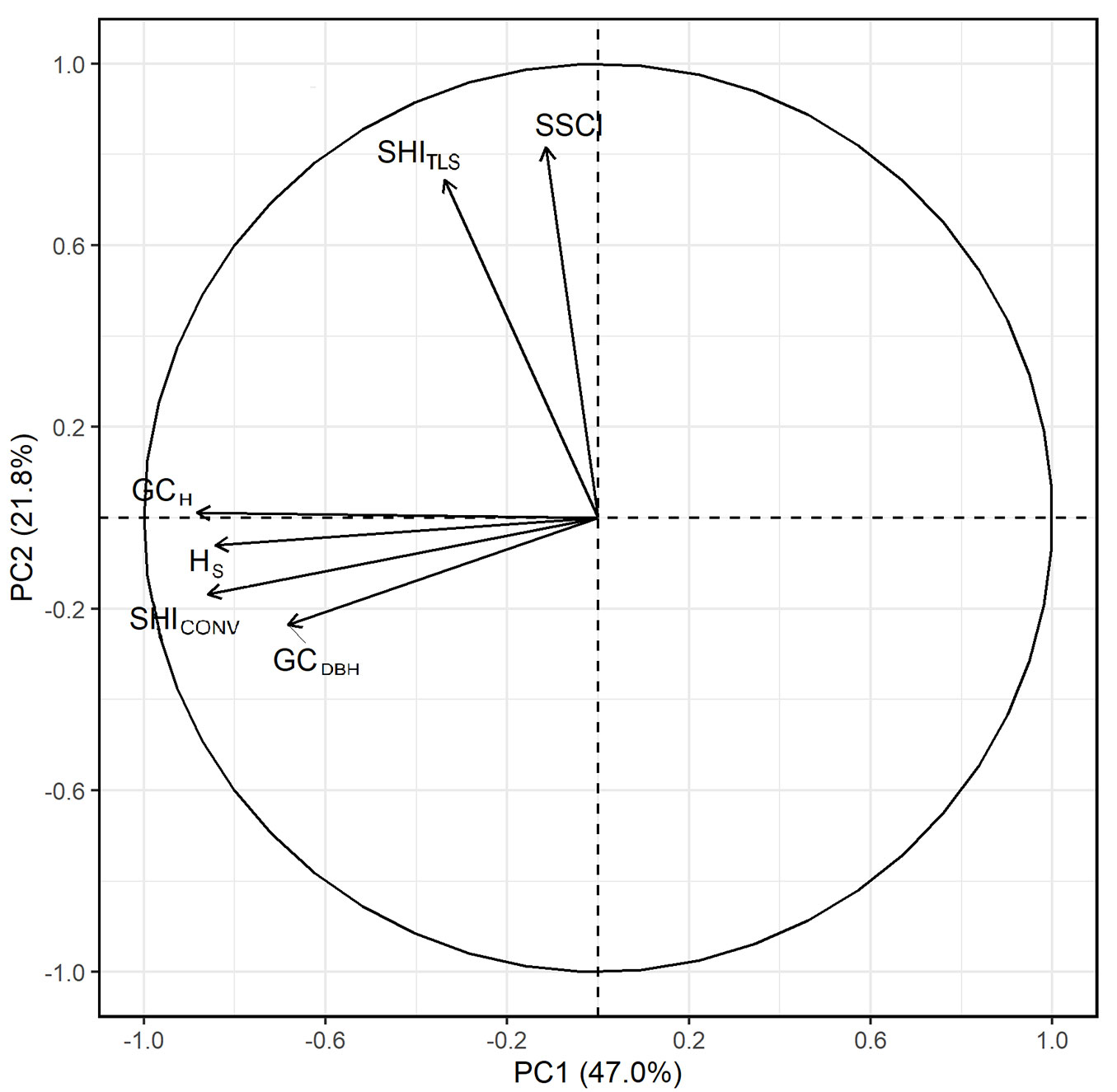
The PCA confirms the pattern that emerges from the Spearman’s rank correlations (Fig. 2). Two groups can be identified: on the one hand, GCDBH, GCH, HS and SHICONV, on the other hand, SSCI and SHITLS.
Fig. 2 - Principal component analysis of the calculated indices. (SHITLS): Structural heterogeneity index (terrestrial laser scanning); (SHICONV): conventional structural heterogeneity index; (SSCI): stand structural complexity index; (GCDBH): Gini coefficient (diameter at breast height); (GCH): Gini coefficient (tree height); (HS): Shannon index.
The concordance analysis showed CCCs between 0.000 and 0.596 (Tab. 3). Here, similar to the Spearman’s rank correlations, the highest CCCs were found for the GC. The CCC between GCDBH and GCH was 0.578. Solely the concordance between GCH and the HS was higher (0.596). Further moderate concordance values were observed between the SHITLS and the simple indices GCDBH (0.366), GCH (0.401), and HS (0.424). The SSCI and SHICONV displayed weak and very weak concordances to all other calculated indices. The lowest values were found for SSCI and GCDBH (0.000), SHICONV and GCDBH (0.013), and SHICONV and HS (0.016), respectively.
Tab. 3 - Concordance correlation coefficient (CCC) according to Lin ([28]) between all structural heterogeneity indices in total for the two study areas NE Hesse and Lusatia. (SHITLS): structural heterogeneity index (terrestrial laser scanning); (SHICONV): conventional structural heterogeneity index; (SSCI): stand structural complexity index; (GCDBH): Gini coefficient (diameter at breast height); (GCH): Gini coefficient (tree height); (HS): Shannon index.
| CCC total | SHITLS | SSCI | SHICONV | GCDBH | GCH |
|---|---|---|---|---|---|
| SSCI | 0.185 | - | - | - | - |
| SHICONV | -0.063 | 0.314 | - | - | - |
| GCDBH | 0.336 | 0.000 | 0.013 | - | - |
| GCH | 0.401 | 0.151 | 0.069 | 0.578 | - |
| HS | 0.424 | 0.113 | 0.016 | 0.313 | 0.596 |
From Fig. 3 it appears that there is no clear age trend within the four groups of stand types ( for further information on descriptive statistics, see also Tab. S4 in Supplementary material). This is confirmed by the ANOVA (Tab. S5). An important reason is the generally high variability within the individual stand types. No significant differences could be detected for the three groups of stand types in NE Hesse (i.e., Fs, Pa, OCTS - Tab. S5 in Supplementary material). In Lusatia the only significant differences were found for GCDBH (significantly higher in ifs than in mfs), GCH and in SHICONV (in both indices: significantly higher in ifs than in pw and in mfs).
Fig. 3 - Boxplots of six indices of structural heterogeneity for 12 forest stand types in the two study areas NE Hesse (eight stand types) and Lusatia (four stand types). (A) Gini coefficient of diameter at breast height (DBH); (B) Gini coefficient of tree height; (C) Shannon index (based on tree species); (D) structural heterogeneity index based on data from conventional inventory (SHICONV); (E) stand structural complexity index based on single-scan TLS data (SSCI); (F) structural heterogeneity index based on multiple-scan TLS data (SHITLS). (Fs): European beech (Fagus sylvatica); (Pa): Norway spruce (Picea abies); (OCTS): other coniferous tree species; (Ps): Scots pine (Pinus sylvestris); (PADTS): pine with admixed deciduous tree species. Stand age classes: (pw) pole wood; (ifs) immature forest stands; (mfs) mature forest stands. Data for SHITLS and SSCI from Reich et al. ([41]).
Discussion
Although the general goal of “management for complexity” ([38]) is very often pursued, we lack a comprehensive evaluation system of the performance of management measures implemented by foresters. The results of our study show that the outcomes of the different approaches to quantify forest structural heterogeneity are highly variable. Thus, the choice of a specific index plays an important role in the evaluation and interpretation of forest structural heterogeneity.
Our results provide evidence congruent with our first hypothesis that the three indices consisting of a single attribute and the SHICONV correlate closely with each other. GCDBH, GCH, HS and SHICONV had rank correlation coefficients, that were almost consistently considerably higher than those of the other indices studied and were strongly clustered in the PCA loading plot. The CCCs were particularly high among GCDBH, GCH and HS. DBH and tree height are those silvicultural parameters most commonly used to characterize tree dimension. Given the close relationship between these two parameters ([35]), a positive correlation and a high concordance between GCDBH and GCH was expected, which was confirmed by our results. Interestingly the rank correlations and concordance correlations between GCH and HS were much closer than those between GCDBH and HS. This means that a higher diversity in tree species is mainly reflected in a higher inequality of the tree height distribution. We assume that this finding can be attributed primarily to the effects of interspecific niche complementarity between trees at the plot level, which rises with increasing tree species diversity ([14]). A higher tree species diversity enhances the likelihood that trees differ with respect to growth-related functional traits, in this case height growth and light requirements. Other studies with a similar approach to analyse the correlation between GC and HS found mixed results. Whereas Keren et al. ([20]) observed only very weak correlations in GC (examining the basal area, i.e., DBH) in old-growth forests dominated by beech and fir in south-eastern Europe, Lexerod & Eid ([25]) demonstrated strong positive correlations in Norway spruce and pine forests. The tightness of the rank correlations to SHICONV increased very sharply in the order GCDBH, GCH and HS. Two of the structural attributes used to compute SHICONV were DBH diversity and standard deviation of tree height. DBH diversity was calculated using the Gini-Simpson index, which is an extension of the Simpson index and describes the probability that two individuals exhibit a different characteristic (e.g., DBH). However, the use of a measure of DBH variability and the standard deviation of tree height as one of the eight structural attributes of the SHICONV alone cannot explain the close rank correlation to GCDBH and GCH, respectively. Obviously, at least some of the other attributes also have a close relation to the DBH and tree height inequality, e.g., living volume and tree species richness (see above). HS and SHICONV were particularly closely correlated. In addition to the aspects mentioned above it would be interesting to analyse how HS is related to the three deadwood attributes included in the SHICONV (i.e., CWD index, basal area of standing deadwood, total volume of deadwood). Del Río et al. ([9]) and Park et al. ([30]) also observed that species diversity effects strongly impact structural diversity of forest stands. Due to the close rank correlations between the SHICONV and the indices consisting of a single structural attribute, it can be concluded that the SHICONV, despite its complex calculation and extensive data input, may not comprehensively reflect the stand structural heterogeneity.
Both correlation analyses (i.e., rank and concordance correlation) showed that SHICONV and SHITLS were only weakly correlated, and this was confirmed by the PCA. Thus, we have to reject our second hypothesis, which was based on the fact that both indices are complex and were supposed to be comprehensive. As stated above, this might not be the case with the SHICONV. For the elaboration of the SHITLS Reich et al. ([41]) used the same principal approach, but very different types of structural attributes which were selected to calculate this index. The tree crown represents an elementary fundamental component for the determination of 3D structural diversity ([22], [36]). In addition, the inner crown structure may differ from the outer shape ([18]). The SHITLS integrates stand attributes such as crown sinuosity, crown width to crown length ratio or crown compactness and has therefore the potential to fully represent the 3D nature of forests.
As a general pattern, it emerged that the four indices based on conventional inventory data (GCDBH, GCH, HS and SHICONV) were only very weakly or not at all correlated with the two TLS-based indices (SHITLS and SSCI). This is particularly pronounced for the SSCI, for which all rank correlation coefficients and CCCs with the other four indices were < 0.2 and < 0.31, respectively. Since the SSCI contains with the ENL a parameter that is very sensitive to tree height, the assumption in the third hypothesis was that GCH correlates closely with the SSCI. However, with correlation coefficients of < 0.2 this cannot be confirmed. ENL is age-dependent, initially increasing and then decreasing as stand age progresses ([11]). In addition, the variability of ENL decreases slightly in older and thus higher stands ([11]). Given the range of ages classes we included in our study this dependency of ENL, and by this of SSCI, on tree height variation was obviously not large. This might be different when also very young and considerably older stands would be included. Ehbrecht et al. ([12]) tested the relation between SSCI and GCDBH and found a considerably closer relation (r2 = 0.36 over all plots of their study) than that in our study (r = 0.014). This is surprising because in both studies very similar approaches were used, including the range of age classes and dominant tree species (beech, spruce and pine). We can only speculate about the reasons, one might be a shorter gradient in GCDBH in our study. From Fig. 4 in Ehbrecht et al. ([12]) it appears that GCDBH ranged from < 0.1 to > 0.4 in their study, whereas a large number of plots had index values between 0.1 and 0.25 in our study (see Fig. 2A). Anyhow, our findings support the conclusion of Ehbrecht et al. ([12]) that the SSCI quantifies stand structural complexity holistically and with a high spatial resolution by taking into account the entire 3D arrangement of structural elements without focusing on individual objects.
We found very little evidence to support our fourth hypothesis that most indices are age-dependent. We based our expectation for example on the assumption that the variance around the median of DBH and tree height increases with increasing age of forest stands. However, this usually requires planting or seeding for establishment of forest stands which results in stands with uniform age structure. Therefore, for an accurate evaluation of the age-dependence of the indices, the mode of establishment of the studied stands must be considered. The beech stands in NE Hesse were mostly established by natural regeneration through shelterwood cuttings and so-called “standards”. Therefore, still-standing mature trees of the previous generation were present in the pole wood, having a strong potential to influence the results of the index calculations. Accordingly, the index values of GCH, HS, SHICONV, and SHITLS showed a higher median in pole wood than in immature forest stands. In the mature forest stands, an increase in these indices can be observed again. Similar results have been found in other studies for beech forests ([47], [42], [52]). The conifer stands were mainly established either with small clear cuts, the so-called “femel” selection cutting or patch cuts. Remnants of mature trees were rare exceptions. Whereas pole wood and immature forest stands of spruce in NE Hesse mostly had similar index values, higher index values were often observed in mature forest stands (the SSCI being the only exception). Remarkably, this pattern was not found in the pine stands in Lusatia. The reasons for this can be found in the mixture of tree species, since the areas in NE Hesse have higher degrees of mixtures than those in Lusatia, where especially young stands are characterized by an almost pure stand.
Conclusion
The choice of a specific index plays an important role in substantively evaluating and interpreting forest structural heterogeneity. In view of future sustainable forest management strategies as well as ongoing climate change, a standardization and harmonization would be highly desirable. Several studies indicate that indices based on multiple structural attributes should be preferred over those including only one attribute. Since the SHICONV has close correlations to simple indices, the recommendation goes for using the SHITLS, which places a particular focus on tree crown attributes because of their great contribution to overall stand structural heterogeneity. The use of TLS data offers multiple benefits in terms of precision, reproducibility and comprehensiveness. This approach, however, requires more intensive work than the other TLS-based approach, the SSCI, both in the field and at the computer. Future studies should therefore be profoundly devoted to the in-depth comparison of SHITLS and SSCI.
Acknowledgements
The research was funded by the Agency for Renewable Resources (FNR 22024714) through the project “User-oriented inventory and planning procedures for adaptive multifunctional forest management” (NOWA_IP). We would like to thank the two private forestry offices for their help and cooperation. We would also like to thank the student assistants who helped with data collection. Furthermore, we wish to thank all colleagues involved in the NOWA_IP project.
References
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Online | Gscholar
CrossRef | Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
CrossRef | Gscholar
Authors’ Info
Authors’ Affiliation
Matthias Kunz 0000-0002-0541-3424
Goddert Von Oheimb 0000-0001-7408-425X
Institute of General Ecology and Environmental Protection, Technische Universität Dresden, Pienner Straße 7, 01737 Tharandt (Germany)
Institute of Forest Economics and Forest Management Planning, Technische Universität Dresden, Pienner Strasse 23, 01737 Tharandt (Germany)
Corresponding author
Paper Info
Citation
Reich KF, Kunz M, Bitter AW, Von Oheimb G (2022). Do different indices of forest structural heterogeneity yield consistent results?. iForest 15: 424-432. - doi: 10.3832/ifor4096-015
Academic Editor
Claudia Cocozza
Paper history
Received: Mar 07, 2022
Accepted: Aug 09, 2022
First online: Oct 20, 2022
Publication Date: Oct 31, 2022
Publication Time: 2.40 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2022
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 31260
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 25582
Abstract Page Views: 3072
PDF Downloads: 2160
Citation/Reference Downloads: 8
XML Downloads: 438
Web Metrics
Days since publication: 1169
Overall contacts: 31260
Avg. contacts per week: 187.19
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2022): 6
Average cites per year: 1.50
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Consistency among forest structure and biodiversity potential index (IBP): an assessment of stand structural complexity for floodplain poplar woodlands
vol. 18, pp. 335-343 (online: 04 November 2025)
Research Articles
An index of structural complexity for Apennine beech forests
vol. 8, pp. 314-323 (online: 03 September 2014)
Research Articles
How biomass and other tree architectural characteristics relate to the structural complexity of a beech-pine forest
vol. 16, pp. 368-376 (online: 19 December 2023)
Research Articles
Selection priority for harvested trees according to stand structural indices
vol. 10, pp. 561-566 (online: 05 May 2017)
Research Articles
Assessment of age bias in site index equations
vol. 9, pp. 402-408 (online: 11 January 2016)
Research Articles
Endangered and endemic species increase forest conservation values of species diversity based on the Shannon-Wiener index
vol. 9, pp. 469-474 (online: 02 January 2016)
Research Articles
Oak often needs to be promoted in mixed beech-oak stands - the structural processes behind competition and silvicultural management in mixed stands of European beech and sessile oak
vol. 13, pp. 80-88 (online: 01 March 2020)
Research Articles
Comparison of drought stress indices in beech forests: a modelling study
vol. 9, pp. 635-642 (online: 06 May 2016)
Technical Advances
A simplified methodology for the correction of Leaf Area Index (LAI) measurements obtained by ceptometer with reference to Pinus Portuguese forests
vol. 7, pp. 186-192 (online: 17 February 2014)
Research Articles
Remote sensing of Japanese beech forest decline using an improved Temperature Vegetation Dryness Index (iTVDI)
vol. 4, pp. 195-199 (online: 03 November 2011)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword