Multi-aged micro-neighborhood patches challenge the forest cycle model in primeval European beech
iForest - Biogeosciences and Forestry, Volume 13, Issue 3, Pages 209-214 (2020)
doi: https://doi.org/10.3832/ifor3309-013
Published: Jun 06, 2020 - Copyright © 2020 SISEF
Short Communications
Abstract
As currently framed, the forest cycle model that underlies close-to-nature management in temperate beech forests throughout the globe specifies an orderly sequence of temporal development within even-aged patches comprising the forest mosaic. Although this model has been widely applied to European beech (Fagus sylvatica L.) forests, the underlying assumptions of disturbance-induced even-agedness (i.e., within-patch age homogeneity) and competition-induced size differentiation (i.e., within-patch size heterogeneity) have not been tested in natural beech forests due to prohibitions on tree coring in primeval forest reserves. In a rare and unprecedented test dataset of spatially explicit tree ages in an old-growth European beech forest, we employed triangulated irregular networks of Delaunay triangles to objectively identify natural tree neighborhoods to determine if neighboring (i.e., within-patch) trees were even- or, at most, two-aged. Age differences among neighboring trees (summarized in 25-yr age classes) were rarely <25 yrs and mostly >50 yrs, while the few "even-aged" patches were very small (100 m2) and relatively young (<150 yrs). In this first assessment of the assumptions underlying the forest cycle model in European beech, we observed neither the even-aged cohorts expected for disturbance-induced patches in different phases of development, nor the size differentiation among similarly aged trees that should arise from the neighborhood dynamics of competition, self-thinning, and growth. The lack of patches indicating demographic turnover is fundamentally inconsistent with the forest cycle model as it is currently framed. We call for further exploration of spatially-explicit tree age datasets to determine the generality of these observations.
Keywords
Age Reconstruction, Carpathians, Dendrochronology, Development Stage, Forest Cycle, Stand Development, Structure, Triangulated Irregular Network (TIN)
Introduction
Widespread throughout the temperate Northern Hemisphere, dominant in much of Europe, and economically important on at least three continents, beech (Fagus) forests have been a persistent topic of applied research for over two centuries. For the last seven decades, the management of beech forests has drawn upon our understanding of structure and dynamics as framed by the pattern-process hypothesis embedded in the conceptual patch mosaic model ([31]). Central to this model is the recognition of the patch as the fundamental spatial unit embodying forest development, such that forest dynamics are reflected in a complex space-time-structure mosaic formed by the assemblage of patches ([1], [26], [33]). Patches are more-or-less discrete spatial and temporal entities differentiated by floristic composition, age, size distribution, or structure ([16], [10], [12]). Rather than merely reflecting the life history (e.g., birth, growth, and death) of individual trees, patches are thought to capture the demographic turnover of tree generations (i.e., the forest life cycle - [31]). In temperate European beech (Fagus sylvatica L.) old-growth forests, patches arise through disturbances that typically range between several hundred to a few/several thousand square meters ([5], [11], [12]), exceeding the scale of individual canopy gaps following the death of a single or a small group of trees ([25]) to encompass greater extents of synchronized, spatially and temporally confined canopy break-up ([21]).
The forest cycle model stipulates that these newly initiated patches pass as a cohort through an orderly temporal sequence of development phases in which the initial upgrade phases associated with birth, growth, and biomass accumulation (i.e., renewal / regeneration / early growth phases) peak in the mature phase following the death of dominant trees, and end in a downgrade series of phases (i.e., ageing / breakdown / decay phases) associated with dead, dying, and rotting stems, declining biomass, and ultimately the initiation of a new tree generation ([31], [1], [26]). Patch cohorts are thus conceptualized as roughly even-aged, cycling in age and structure over time but more-or-less homogeneous in age structure within the patch at any given point in time ([16], [26]). At the same time, natural beech forests are known to be structurally diverse and multi-sized ([32]). This within-patch size heterogeneity is generally attributed to neighborhood dynamics (i.e., inter-tree competition, self-thinning, and growth and size differentiation) that structurally diversifies the roughly even-aged patches over time ([20], [7]) and drives progression through the series of development phases in the forest cycle.
However, despite the wide application of the patch mosaic model in temperate old-growth forests ([11]) and a long history of patch dynamics modeling ([33]), the central assumption of the forest cycle model (i.e., the existence of even-aged patches that become structurally diversified over time) has rarely been challenged ([13]) and never, to our knowledge, empirically verified. Historically, the dynamics underlying the forest life cycle model have been inferred from descriptions of forest structure (e.g., diameter distributions, canopy stratification, mortality rates, amount of deadwood, regeneration - [16], [11], [12], [13], [36]). More recently, dendrochronological methods have become available to facilitate verification, but prohibitions of tree coring in the few remaining remnants of natural beech forest ([29]) have permitted only sparse and spatially dispersed sampling to sketch overall stand age structure, identify establishment and release periods, and characterize past disturbances ([28], [37]). Moving beyond descriptive classifications to quantitatively assess the assumptions of the forest cycle model requires the innovative approach of reconstructing ages within actual tree neighborhoods to determine if trees within a patch are indeed even- or, at most, two-aged.
The current reconstruction was made possible by unprecedented permission to destructively sample in the Uholka-Shyrokyi Luh reserve within the primeval beech forest of the Carpathian Biosphere Reserve. We take advantage of a rare complete inventory of individual tree ages in portions of this old-growth forest ([29]) for a novel, spatially explicit analysis seeking demographic evidence of the implicit assumptions of the forest cycle model. In this first quantitative validation of the model, we test whether or not objectively defined neighborhoods of adjacent trees demonstrate within-patch age homogeneity (i.e., are even-aged) and if comparably aged trees demonstrate size heterogeneity. Although limited in scope, we hope this work will spur additional exploration into the assumptions and framework of the model that forms the theoretical basis for applied forest restoration and sustainable management in temperate forest ecosystems.
Materials and methods
The data collection methods for the raw data were reported in detail in Trotsiuk et al. ([29]). Sampling took place in a primeval European beech (Fagus sylvatica L.) forest at 660-730 m a.s.l. on south-east facing slopes of 30-45% within the core (48° 25′ N, 23° 61′ E) of the Uholka-Shyrokyi Luh reserve in the temperate Ukrainian Carpathians, which averages 7.7 °C with annual precipitation of 1134 mm ([8]). Four 0.1 ha circular plots (Tab. 1) ~200 m apart were selected in 2010 to be collectively representative of the range of size structures found in a nearby permanent monitoring area in which tree coring was not permitted, which is now known to be dominated by structural conditions indicative of downgrade phases ([23], [36]). Within each plot, the diameter at breast height (1.3 m) and spatial location were recorded for all live trees with diameters ≥ 6 cm (all European beech). All sampled trees (N=164) were cored parallel to the slope at either 100 cm above the ground (143 trees) or, when not possible, at 80 cm (21 trees). One to two saplings per plot were randomly selected and cross sectioned in 20 cm intervals upwards from the root collar to estimate the years required to reach coring height. Although Acer was common in the regeneration layer of the nearby permanent monitoring area, trees of breast height were nearly pure (95%) European beech ([2]).
Tab. 1 - Mean (± standard deviation) values for each plot. Mean ageA was calculated across all trees, while Max ageR was calculated only across trees with reliable ages. Max age† was calculated across all trees, but capped at 500 yrs for analysis. Note that averages for the Min and Max age† are based on individual trees rather than the plot level.
| Parameter | Plots | Average | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| Mean age A [yr] | 206 ± 141 | 132 ± 86 | 245 ± 121 | 244 ± 101 | 207 ± 112 |
| Min age [yr] | 57 | 43 | 84 | 91 | 112 |
| Max age † [yr] | 647 | 506 | 545 | 464 | 541 |
| Max age R [yr] | 166 | 295 | 460 | 417 | 335 |
| Basal area [m 2 ha -1] | 63.5 | 30.9 | 62.7 | 40.8 | 49.5 |
| Tree density [stems ha -1] | 370 | 590 | 410 | 270 | 410 |
| Mean Diameter [cm] | 31 | 17.3 | 31.6 | 35.3 | 28.8 |
| Quadratic Mean Diameter [cm] | 46.7 | 25.8 | 44.1 | 43.9 | 39.2 |
| Max Diameter [cm] | 108 | 98 | 90 | 95 | 98 |
Measurement of tree ring widths and detailed cross-dating methods are described in Trotsiuk et al. ([29]). Annual ring widths were measured using a stereomicroscope and a LintabTM sliding-stage measuring station, in tandem with the TSAP-WinTM software (Rinntech, Heidelberg, Germany). The best synchronized ring-width series was used to construct a master-chronology, in which negative pointer years made precise dating of all 164 cores over the past 200 years possible. Cross-dated ring series were used to directly determine the ages of 32% of trees, while 46% were estimated after fitting concentric circles to the curvature of the inner rings and predicting the number of rings in early life given a constant growth rate ([6]). For the 22% of trees with a rotten core, the length of the radius was taken as the difference between the geometrical radius and total core length ([27]) and then the missing age was computed from an age-radius equation based on the cumulative growth of complete tree cores, capped at 500 years (4 trees). Finally, based on the sapling data, 11 years were added to trees cored at 100 cm and 9 years to those cored at 80 cm. Trees for which the core reached the pith or no more than 20 years of missing age had to be added (n=116) are considered to have “reliable” age estimates.
In the current study, trees were assigned to 25-year age classes (starting at 50) and the relative abundance of trees in each age class was computed, by plot and averaged across plots. To asses within-patch even-agedness (i.e., if adjacent trees belonged to the same cohort, reflecting age homogeneity), we first used spatial tessellation to objectively identify neighboring trees by creating a triangulated irregular network of maximally equilateral Delaunay triangles (i.e., Delaunay TINs), which optimally connects horizontally adjacent trees to one another in three-tree micro-neighborhood patches (e.g., Fig. 1i in [35]). Age differences at the micro-neighborhood level were then computed as the maximum difference in absolute ages among the three constituent trees, which were then assigned to 25-yr difference classes for which the relative abundance was computed by plot and averaged across plots. To quantify within-patch even-agedness, three categories of age differences were recognized: (i) even-aged, when only one age difference class was observed (i.e., all three trees were within 25 yrs in age); (ii) two-aged, when two age classes were observed; or (iii) multi-aged, if all three trees belonged to different age difference classes. The cumulative area within each plot of all micro-neighborhoods belonging to each age-difference class was also summed. Size differences at the micro-neighborhood level were computed as the maximum difference in diameter among the three constituent trees of each micro-neighborhood patch, which were then assigned to 10-cm difference classes. To assess within-patch uneven-sizedness (i.e., if adjacent trees differed in size, reflecting size heterogeneity), three categories of size differences were recognized: (i) even-sized, if only one size difference class was observed (i.e., all three trees were within 10 cm in diameter); (ii) two-sized, if two size classes were observed; or (iii) multi-sized, if all three trees belonged to different size difference classes. Computations were performed in Matlab™ v. 8.2.0 (Mathworks Inc., Natick, MA, USA). Average differences in tree diameter within even-aged micro-neighborhoods were compared to those across all micro-neighborhoods using a paired t-test (N=4) in SAS® v. 9.3 (SAS Institute, Cary, NC, USA).
Results
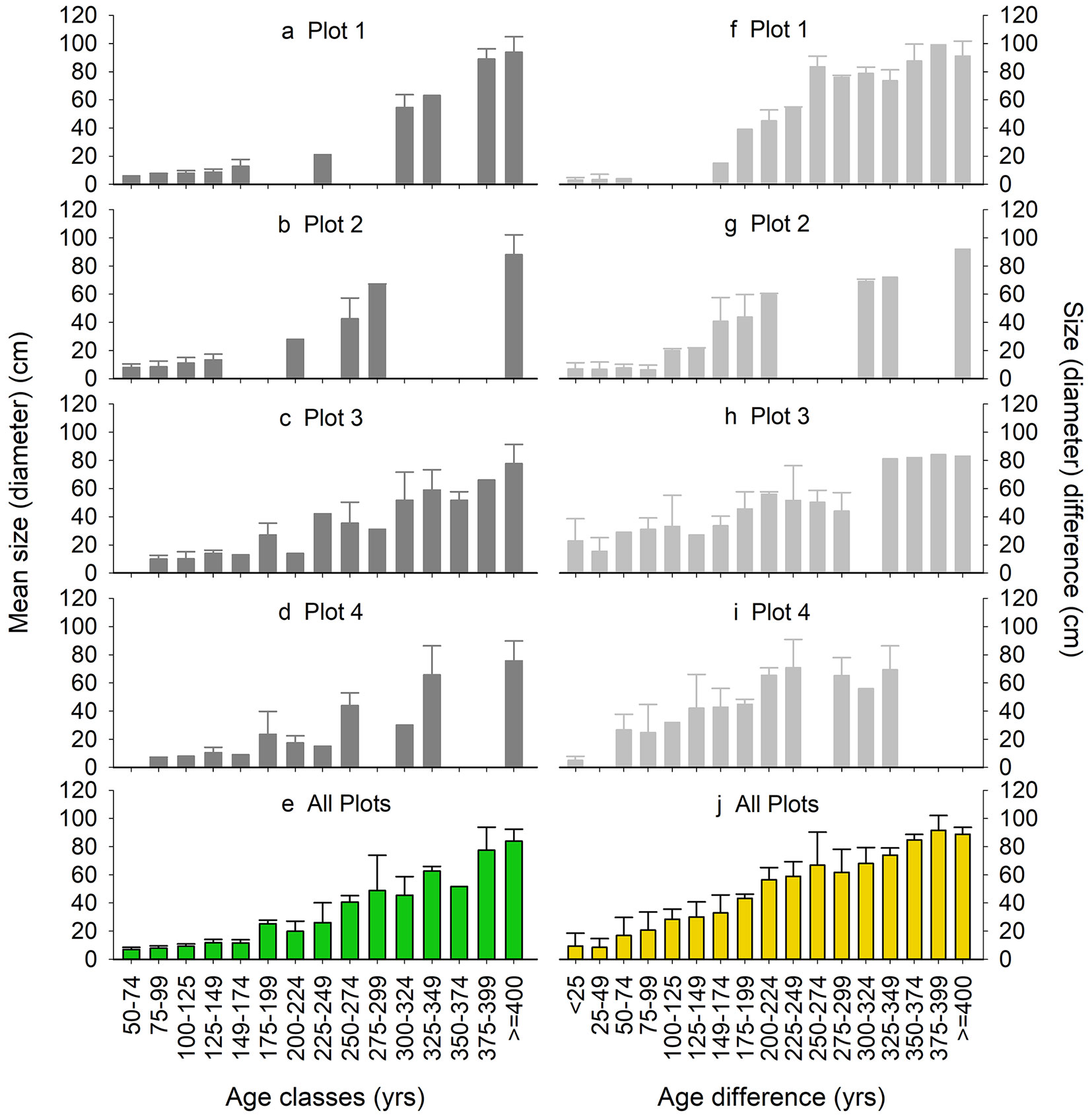
Reliable ages of these ≥6 cm trees ranged from 43 to 470 years (Tab. 1). The 25-year age class distributions (Fig. 1) varied among plots from multi-modal with missing age classes to more evenly distributed and relatively continuous. At least some trees became established in the majority of 25-year periods in each plot over the entire ca. 450-year period, and when averaged across all plots tree establishment was detected in every 25-year period (Fig. 1e). In plot 1, only 24% of micro-neighborhood patches had within-patch maximum age differences of less than 50 years and almost as many (22%) differed by over 400 years; the majority of micro-neighborhoods had age differences among trees between 175-400 years (Fig. 1f). In plot 2, 52% of all micro-neighborhoods differed in age by less than 50 years and only 7% by over 225 years (Fig. 1g). While plot 3 had a peak (35%) in age differences less than 50 years (Fig. 1h), in plot 4 the micro-neighborhoods exhibited age differences up to 350 years in very similar proportions (all classes < 14%) and no micro-neighborhood differed in age by more than 350 years (Fig. 1i).
Fig. 1 - Age homogeneity. Distribution of individual tree ages by 25-yr age classes in each plot (A-D, dark grey) and across all plots (E, blue), and of micro-neighborhoods (i.e., patches) by 25-yr age difference classes in each plot (F-I, light grey) and across all plots (J, red).
Few micro-neighborhood patches were even-aged: when averaged across plots, only 14% ± 13% (standard deviation, std) of micro-neighborhoods differed in age by less than 25 years and only 28% ± 19% by less than 50 or even 100 years. In contrast, a cumulatively equal number had age differences of 150-275 years (Fig. 1j). The proportion of micro-neighborhoods was surprisingly comparable among age differences ranging from 50 to over 400 years (each class averaging <10%). Two-aged micro-neighborhoods comprised 31% ± 9%, 34% ± 9%, and 51% ± 13% of neighborhoods when age difference cutoffs of <25, <50, and <100 years were used, respectively. Using those same cutoffs, multi-aged micro-neighborhoods made up 55% ± 20%, 38% ± 17%, and 21% ± 9% of all neighborhoods, respectively.
Using a 10 cm size difference cutoff, roughly one quarter (24% ± 16%, std) of all micro-neighborhood patches were even-sized, 34% ± 6% two-sized, and 42% ± 19% multi-sized. On average within micro-neighborhoods, mean tree diameter increased with increasing tree age, although diameters remained fairly consistently low (<20 cm) up to 175 yrs in age (Fig. 2e). Despite considerable differences in age among comparably sized trees (see Fig. S1 and Fig. S2 in Supplementary material), even-aged micro-neighborhoods (up to 50-yr differences) were largely composed of similarly sized trees (Fig. 2j). On average, diameter differences among adjacent trees were smaller in neighborhoods composed of even-aged trees, based on both a 25 yr age difference (by 32 ± 9 cm, std) and even a 100 yr age difference (by 29 ± 8 cm - both p = 0.04), ranging from 9.4 ± 9.1 cm for even-aged micro-neighborhoods that spanned a 25 yr age difference to 12.8 ± 9.0 cm for those that spanned 100 yr age differences.
Fig. 2 - Size heterogeneity. Mean (with standard deviation bars) micro-neighborhood (i.e., patch-level) tree diameters by 25-yr tree age classes in each plot (A-D, dark grey) and across all plots (E, green), and mean diameter differences by 25-yr age difference classes for each plot (F-I, dark grey) and across all plots (J, yellow).
The high proportion of micro-neighborhood patches with large age differences reflects the close proximity of trees belonging to differing age classes. All plots demonstrated substantial intermingling of differently aged trees, such that micro-neighborhoods contained trees belonging to most age class combinations. Not only were none of these small plots composed primarily of even-aged trees (and only one with barely >50% of even-aged + two-aged), but within plots there were few contiguous patches of similarly-aged trees (see Fig. S3 in Supplementary material). The sum of micro-neighborhoods in which tree ages differed by less than 25 years averaged only 100 ± 95 m2 (range: 28-240 m2). Even the cumulative spatial extents of micro-neighborhoods in which tree ages differed by less than 100 years averaged only 287 m2 (38% of the sum of micro-neighborhood convex hull areas) and ranged from 152-499 m2 (27-62%).
Discussion
Although this study represents a necessarily retrospective case-study of limited statistical inference, it provides rare and unprecedented empirical data addressing the demographic predictions of the forest cycle model. In this first attempt to validate the model, we failed to observe either the even-aged patches reflective of disturbance-driven within-patch age homogeneity ([16], [26]) or the uneven-sizedness of comparably aged trees reflective of neighborhood dynamics-driven size heterogeneity ([20], [7]). First, neighboring trees were not mostly similarly aged, even when adopting the relaxed definition of even-agedness as a single age class with a range of tree ages <20% of the “rotation” age (100 years assuming a 500-year beech life span/rotation - [9]). Second, similarly aged trees (even when they were adjacent) were similar in size up to 175 years of age, such that the range of tree sizes observed cannot be predominantly attributed to competitive stratification in even-aged patches.
Rather, we observed an irregular mosaic of structurally variable patches composed of uneven-aged trees (spanning >376 yrs within a mere 0.1 ha) that was a function of intensive intermixing of young and old trees. Every plot had trees belonging to 9-14 different 25-year age classes and tree establishment spanning the majority of the 400+ year history, indicating essentially continuous recruitment rather than temporally discrete cohorts. Trees of the same size reflected regeneration events up to a century apart (one fifth of the lifespan of European beech - [4]), a majority of micro-neighborhoods had age differences >150 yrs, and more than a third were multi-aged. The few even-aged neighborhoods that were observed encompassed cumulative extents averaging only 100 m2 at age differences <25 yrs (i.e., less than the ca. 156 m2 spatial extent of a single canopy beech tree - [18]), only 287 m2 at <100 yr differences, and were not spatially contiguous.
Given the structural representativeness of these plots to the intensively-studied nearby 10 ha monitoring plot ([2]) and of that plot to the 10.000 ha reserve in which it is situated ([23]), these observations may not be atypical. Although further dendrological work in a wider array of field sites will be required to definitively assess the validity of the forest cycle model in natural beech forest, the patterns of the current study are consistent with the age span (hundreds of years - [24]) and complex age structure ([3]) of other beech forests, the silvics of European beech (which has the capacity for continuous initiation and establishment - [30]), and the small scale of the predominant disturbance regime (tens to hundreds of m2 - [5], [34]). In fact, the key to the observed pattern of intimate intermingling of tree generations may be the successful release (either continuously or in disturbance pulses - [19]) of understory regeneration at extremely fine scales. The main exogenous disturbance agent in these forests is wind ([32]) and stem breakage the prevailing mode of mortality ([34]). If beech regeneration is able to respond to release in mini-gaps on the scale of individual branch breakage, the result of such frequent and spatially and temporally asynchronous small-scale disturbance would be to create and maintain the multilayered stand structures ([2], [32], [14]) associated with multi-/all-agedness ([21]). Subsequently, the intermingling of tree generations could reflect the successful release of continuously establishing understory regeneration ([24]) at the extremely fine scales of the prevailing mode of mortality, as suggested by a stop-and-go growth release pattern ([29], [19]). Our results thus support the structure-based findings by Paluch ([21]) that patches are rarely homogeneous at scales exceeding the crown size of one or a few canopy trees, which would explain the inadequacy of development phases to explain the cross-scale multi-/all-agedness of old-growth European beech forests ([21]).
Multi-/all-agedness implies that demographic turnover is continuous in time and space, undermining the delineation of demographic turnover from “one tree generation to another” ([16]) that is fundamental to the forest cycle model. Although it is possible that some of the plots in the current study could be classified to the Plenter (sensu [10]) phase (as was the case for the nearby monitoring plot - [36]) on the basis of structural conditions reflecting an accumulation of biomass in a young cohort beneath residuals from the previous cohort (as per [10]), it could not be argued that stands spanning eight age classes are two-aged, as Korpel further implies, or in an early temporal “up-growing” phase. This may explain why the “Plenter” steady-state phase has been persistently placed outside of the development cycle ([16], [11]), is purportedly not very common in old-growth forests ([10]), has never received a satisfactory ecological explanation under the patch mosaic model ([11]), and is underestimated in importance ([12]), even though the age and size structure of this phase most closely portrays the fine-scale heterogeneity consistently documented in temperate old-growth forests characterized by small-scale gap dynamics ([21], [22]). Thus any model of the dynamics of pattern and process in beech forests must be considered within the context of a disturbance regime that maintains the multi-age as well as multi-size structures observed here and in other old-growth beech forests ([3]).
Our results are not, however, inconsistent with Watt’s ([31]) central idea of an upgrade and downgrade series of structurally distinct patches ([16]), likely reflecting processes linked to the persistence of large/old overstory trees ([21]), repeated release of midstory trees ([29]), and continuous presence of understory trees ([2]). Multi-agedness results in different allocations of growing stock to various age (and size) classes and canopy layers ([17]), and it is the variability in age hierarchy across space that gives the impression of patchiness. In this context, discrete phases based upon structural criteria (“structure” phases) may still be useful for describing the hierarchical, nested, cyclic space-time dynamics of spatially shifting patches in old-growth forests ([31], [33]).
Conclusions
Although limited in scope, this first use of spatially explicit age reconstructions to validate the forest cycle model failed to detect either even-aged patches or uneven-sizedness in comparably aged trees. Instead, we exclusively observed structurally variable, uneven-aged patches of intensively intermixed young and old trees. If these observations were to prove typical, and multi-aged structural phases were found in other primeval European beech forests to frequently predominate over even-aged developmental stages, the conceptual model of the forest cycle may prove unrealistic and thus impede efforts at conservation, restoration, and sustainable forest management ([15]). At the same time, the prevalence of multilayered stand structures with multi-/ all-agedness does not preclude the use of structure phases to describe the patch mosaic.
Acknowledgements
We are grateful to the Carpathian Biosphere Reserve for permitting tree coring in the Uholka virgin beech forest (Ukraine). EZ conceived the approach; all authors developed the methodology; VT acquired data; EZ performed statistical analyses; JP and EZ wrote the first draft of the manuscript and all authors contributed to the final version. This work was supported by the USDA National Institute of Food and Agriculture Hatch Appropriations under Project #PEN04639 and Accession #1015105.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Jerilynn E Peck
Department of Ecosystem Science and Management, The Pennsylvania State University, University Park, PA, 16802 (USA)
Faculty of Forestry and Wood Sciences, Czech University of Life Sciences Prague, Kamycka 129, Prague (Czech Republic)
Corresponding author
Paper Info
Citation
Zenner EK, Peck JE, Trotsiuk V (2020). Multi-aged micro-neighborhood patches challenge the forest cycle model in primeval European beech. iForest 13: 209-214. - doi: 10.3832/ifor3309-013
Academic Editor
Jesus Julio Camarero
Paper history
Received: Dec 03, 2019
Accepted: Apr 10, 2020
First online: Jun 06, 2020
Publication Date: Jun 30, 2020
Publication Time: 1.90 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2020
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 39494
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 32970
Abstract Page Views: 3970
PDF Downloads: 1898
Citation/Reference Downloads: 6
XML Downloads: 650
Web Metrics
Days since publication: 2018
Overall contacts: 39494
Avg. contacts per week: 137.00
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2020): 4
Average cites per year: 0.67
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Development phases and structural characteristics of the Penteleu-Viforta virgin forest in the Curvature Carpathians
vol. 13, pp. 389-395 (online: 01 September 2020)
Research Articles
Long-term dynamics of stand structure and regeneration in high-stocked selection fir-beech forest stand: Croatian Dinarides case study
vol. 14, pp. 383-392 (online: 24 August 2021)
Research Articles
Wind contribution to yearly silver fir (Abies alba Mill.) compression wood development in the Romanian Carpathians
vol. 9, pp. 927-936 (online: 02 October 2016)
Research Articles
Application of indicators network analysis to support local forest management plan development: a case study in Molise, Italy
vol. 5, pp. 31-37 (online: 27 February 2012)
Research Articles
Use of LIDAR-based digital terrain model and single tree segmentation data for optimal forest skid trail network
vol. 8, pp. 661-667 (online: 22 December 2014)
Research Articles
Impact of inbreeding on growth and development of young open-pollinated progeny of Eucalyptus globulus
vol. 15, pp. 356-362 (online: 20 September 2022)
Research Articles
Consistency among forest structure and biodiversity potential index (IBP): an assessment of stand structural complexity for floodplain poplar woodlands
vol. 18, pp. 335-343 (online: 04 November 2025)
Research Articles
Runoff reconstruction and climatic influence with tree rings, in the Mayo river basin, Sonora, Mexico
vol. 13, pp. 98-106 (online: 11 March 2020)
Research Articles
Response to climate and influence of ocean-atmosphere phenomena on annual radial increments of Pinus oocarpa Schiede ex Schltdl. & Cham in the Lagunas de Montebello National Park, Chiapas, Mexico
vol. 16, pp. 174-181 (online: 30 June 2023)
Research Articles
Green oriented urban development for urban ecosystem services provision in a medium sized city in southern Italy
vol. 7, pp. 385-395 (online: 19 May 2014)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword