Use of LIDAR-based digital terrain model and single tree segmentation data for optimal forest skid trail network
iForest - Biogeosciences and Forestry, Volume 8, Issue 5, Pages 661-667 (2014)
doi: https://doi.org/10.3832/ifor1355-007
Published: Dec 22, 2014 - Copyright © 2014 SISEF
Research Articles
Abstract
The implementation of rational forest management that takes into consideration the requirements of sustainable forest development requires many decisions to be made, ranging from simple rules to extremely complex procedures. This is also true of logging operations, where the applied techniques and technologies should relate not only to economic aspects, but also be maximally adapted to the specific forest environment. One of the most important determinants of environmentally safe and effective logging work is forest accessibility through an appropriately planned road and skid trail network. This paper presents the possibilities of using the Airborne Laser Scanner (ALS) and Geographic Information System (GIS) to determine the optimal or near-optimal locations of forest skid trails. Choosing skid trails depends on the adopted logging method, existing road network, forest stand development phase, and terrain conditions. The process of optimization takes into account existing stand gaps to reduce the number of trees that must be removed for the network. Segments representing single trees and the Digital Terrain Model (DTM) served as inputs for the GIS analysis. The research was carried out in Scots pine stands. The obtained results show that the total length of skid trails, with 40 m distance between them, after optimization for traditional harvesting method decreased by 2%. For fully mechanized harvesting method, the skid trail network was decidedly denser (20 m) and an original length was reduced only by 0.06%. The results obtained confirmed the practical usefulness of the adopted procedures.
Keywords
Logging, Airborne Laser Scanner, Single Tree Detection, Digital Terrain Model, Optimal Forest Skid Trail Network
Introduction
The efficiency of logging operations in forest stands are largely dependent on the availability of an adequate access through a transportation network, in terms of roads adjacent to wood storage areas and operational trails allowing machines to easily move inside the stand.
Secondary forest roads, known as strip roads or skid trails, are constructed infrastructure occasionally used to execute the tasks of a management plan. They are primarily intended for skidding or forwarding operations ([22]). The density of skid trails and their arrangement depend on many factors ([19]): timber harvesting method and system, configuration, terrain rockiness, tree density and dimensions, and the position of the main forest truck road, to which the timber is extracted.
Optimizing the system of roads and trails is a complex process. Optimal trail spacing can be influenced by many factors, such as logging method, price of products, taxation policies, landing costs, overhead costs, equipment opportunity costs, road width and size of landing, skidding pattern, profit of logging contractor, slope, topography and soil disturbance ([4]).
The first forest road-spacing scheme, along with the theoretical mean skidding distance, was presented by Matthews ([13]). Models of optimal road networks for forest areas have been published many-fold in the literature. Some papers proposed an evaluation of alternative trail routes based on economic considerations only ([7], [20], [6]), while others were based on specific information obtained by interpreting aerial photographs, field surveys and integrated DTM data ([26], [2], [3], [8]).
The problem of accessing a forest through a network of secondary forest traffic infrastructure is particularly important for thinning, and for those mature stands where selective harvesting is performed. Even though machinery can move freely over the entire area in a uniform clear-cut, it is always recommended fixed trails to be used.
Almost all the negative effects of the use of machines in the forest reflect on trails ([16]), mainly soil compaction and damages to residual trees after forest operations. Skidders, tractors, and other heavy machinery used in forest practices may compact soils remarkably, depending on the type of equipment used, soil characteristics, etc. Compaction can take many years to recover, depending on the level of damage and many other environmental conditions. Limiting the area where compaction occurs by reducing machine drives to appropriately designed skid trails is one of best way to alleviate such problem ([24]). Skid trail planning before felling operations can also reduce skidding damages. Machines moving only on trails cause damages which are located mostly near their working route ([18], [30]).
In recent years, new opportunities have been developed to optimize roads and skid trails. This is mainly due to the use of information from the Airborne Laser Scanner (ALS) and Geographic Information System (GIS). Laser scanning provides precise data layers representing terrain surfaces in the form of Digital Terrain Models (DTM). DTM layers have attracted great interest to support forestry operations since they provide thorough and detailed information about terrain topography, which in turn is used to choose the best skidding system in complex forest areas ([15], [12], [32]). Krč & Košir ([10]) have also used Digital Elevation Models (DEM) to develop a model for terrain classification based on the best predicted skidding direction on a steep terrain. High resolution DTMs are also used to define various soil moisture indexes, providing information about the path to be taken by machines on a given terrain ([17]).
Apart from DTM, ALS provides very precise and complex information about vegetation. Many different stand and tree characteristics can be determined with the use of ALS point cloud or Canopy Height Model (CHM), such as height, structure, biomass volume, growth and density ([21], [23], [28], [29]). Once acquired ALS data can be utilized not just in forest inventory or monitoring, but also in many other management activities, such as optimization of the forest skid trail network.
The purpose of this paper is to present an analytical procedure that allows the optimal determination of skid trails by using data from the Airborne Laser Scanner and digital forest maps. Single tree segmentation results in such decision support designing system are involved for the first time. Specific aims of the paper can be defined as follows:
- creation of a procedure for forest skid trail network optimization, fully based on GIS and ALS data;
- evaluation of pre- and post-procedure results on network length and the biomass volume planned to be cut;
- analysis of the results with respect to the implementation of the method.
Material and Methods
Study site
The study site was a 1000 ha forest area owned by the Warsaw University of Life Sciences - SGGW, located at the experimental station in Gluchów, central Poland (51° 45′ 19″ N, 20° 06′ 30″ E). Different forest types exist in the area, ranging from single-layer stands of Scots pine (Pinus silvestris L.) and Common oak (Quercus robur L.) to multilayer, mixed stands of Birch (Betula pendula Roth), Alder (Alnus glutinosa L.), European beech (Fagus sylvatica L.) and Hornbeam (Carpinus betulus L.). Stand age varied between 30 and 120 years. The study area has a generally flat relief, with a mean elevation of about 185 m a.s.l. In order to verify the theoretical model presented hereinafter, Scots pine stands with different tree stocking and dimensions were studied, and skid trail network was optimized for each stand selected.
The model presented below was tested over 170 stands, where Scots pine was the dominant species (cover > 70%). The main characteristics of the studied stands are reported in Tab. 1.
Tab. 1 - General characteristics of selected Scots pine stands (no. stands = 170).
| Parameter | Minimum | Maximum | Sum | Mean | Standard deviation |
|---|---|---|---|---|---|
| Area (ha) | 0.38 | 24.91 | 481.33 | 2.38 | 3.11 |
| Height (m) | 5 | 28 | - | 21 | 4 |
| Age (years) | 21 | 80 | - | 52 | 17 |
| Stocking | 0.3 | 1 | - | 0.73 | 0.72 |
| Dbh (cm) | 5 | 38 | - | 23 | 6 |
| Volume (m3/ha) | 0 | 526 | - | 231 | 93 |
Airborne Laser Scanning - data and processing
The Falcon II airborne laser scanner system from Topographische Systemdaten GmbH (TopoSys, Biberach, Germany) was used for LIDAR small footprint data acquisition. The TopoSys System is based on two separate glass fiber arrays of 127 fibers each. Its specific design produces a push-broom measurement pattern of the ground. Details about the flight mission were described by Sterenczak & Kozak ([27]).
Based on data obtained, a 1-m digital terrain model was generated by the TSFFCVJC® software (FELIS, Germany). For more details about software description and the algorithms implemented therein, see Weinacker et al. ([31]).
Optimization procedure
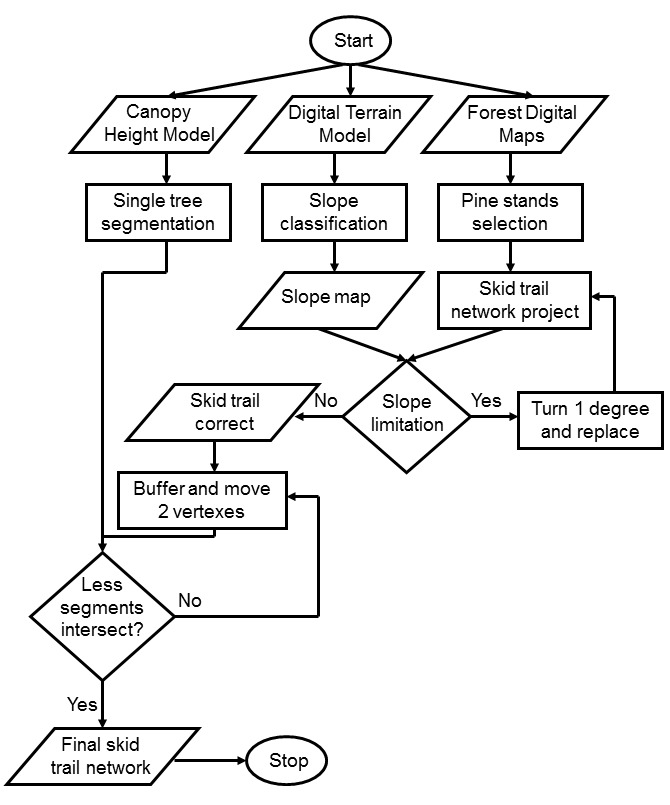
The model represented in Fig. 1 simulates the most common harvesting methods used nowadays in Poland: (i) the traditional method, based on timber felling by chainsaws and extraction by skidders (TR); (ii) the fully mechanized method, using harvesters and forwarders (FM). The selected algorithm takes into consideration three types of inputs: Canopy Height Model (CHM), Digital Terrain Model (DTM) and layers from Forest Digital Maps (road network and forest compartments). The main steps for the implementation of the optimization algorithm are described in following paragraphs.
(1) A single-tree segmentation was carried out based on the CHM from Airborne Laser Scanning (ALS) data ([14]). Segments representing single trees (polygon layer) were used in the next step as a point layer (Fig. 2). Each tree is represented by the centroid of a polygon.
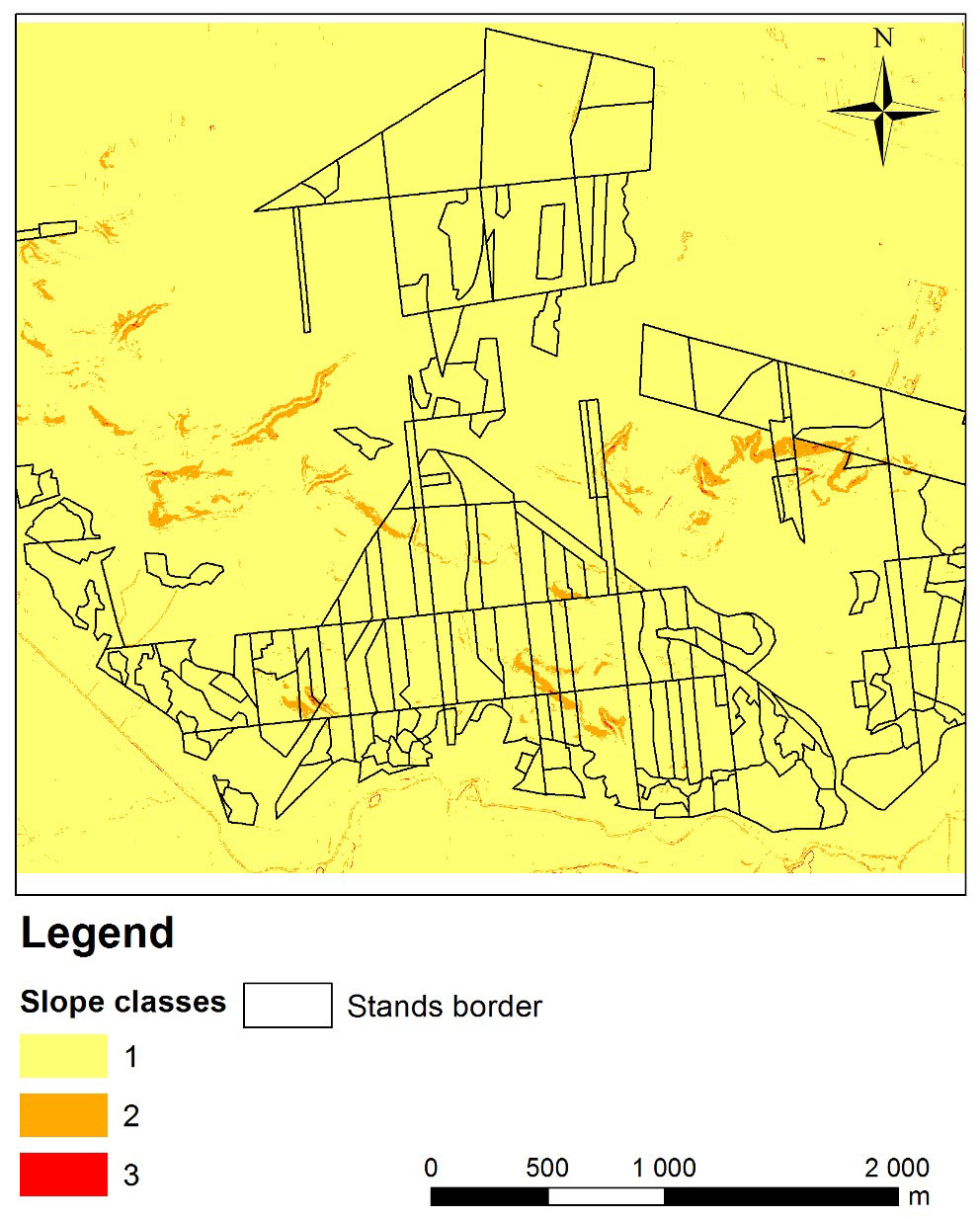
(2) The Digital Terrain Model was first processed. The slope layer was generated using the SPATIAL ANALYSIS® extension of the ARC GIS® 10.1 package (ESRI, Redwoods, CA, USA). To take into account the limits of traditional skidding by using skidders or agricultural tractors (maximum slope < 18%) and forwarders (maximum slope < 40%), slope was reclassified using the following classes: (class 1) 0-18%; (class 2) 18-40%; (class 3) slope > 40%. According to Antonczyk ([1]), the maximal slope limits for skidders are 33% uphill and 50% downhill, while is 18% (uphill and downhill) for agricultural tractors not equipped with Front Wheel Drive (FWD). In Poland, agricultural tractors without FWD are mostly used for thinning operations. For that reason, in the case of the traditional timber harvesting method, we assumed the maximum slope limit as 18%. In other cases or countries, when tractors are equipped with FWD, the maximum limit is higher, especially in downhill direction. Areas smaller than 10 m2 with steep slopes were omitted from the analysis, being either local errors in the DTM or not important from a technological point of view. These data were used later for skid trail optimization.
(3) Forest Digital Maps were used to select the stands to be harvested and the roads to be used for timber transportation. Selected stands were 21 to 80 years old (Fig. 3). Based on the selected roads and compartments (forest units), a skid trail network was then created. If a forest road was already present, the longest side of the compartment was always used as the basis for planning skid trails. In cases of irregular-shaped forest units, trails were plotted in such a way to optimize the access (for example, along the longest axis of the unit), thus minimizing the sum of their lengths. Theoretical skid trails were designed with orthogonal direction to the base road and spacing of 40 m (traditional logging) or 20 m (fully mechanized logging).
(4) Optimization involved two main steps: the first was concerning the DTM slope limitation and the second was related to the minimal number of trees to be cut for the establishment of skid trails. The accessible area was determined for each harvesting system using the slope limits listed above. If the planned route of the skidding track crossed a pixel of the DTM too steep for the system considered (traditional or fully mechanized), a vertex was added to the modeled trail and a curve was created. The angle of the curve increased at each iteration by 1 degree until it was limited by the length of the logged tree. The iteration was terminated and the trail outlining was stopped when the radius of the curve falls below the following threshold (eqn. 1):
where R is the minimum radius of the curve (m), L is the length of felled timber (m), D is the width of the skid trail (m). However, to reach inaccessible areas, such trail was extended to connect to the nearest adjacent trail leading to the road. The result of this step is the design of trails optimized in terms of the accessible slopes present in the area.
(5) The next step was aimed at minimizing the number of trees to be felled by taking advantage of the existing gaps in the forest stand. The input layer consists of the network of trails previously optimized by slope. One by one, each trail was optimized by shifting two vertices along its length in the range of ± 2 times the width of the trail from its original axis. The largest gaps among all the available gaps allowing for a shift of a vertex (1 vertex per iteration) was identified within a buffer area (of size equal to four times the trail width) surrounding the skid trail considered. Using the above procedure, the best trail that minimize the number of trees to be felled was delineated. In the case of multiple trails with a tied number of trees to be felled, the shortest route was selected.
Such optimization process results in a new network of modeled skid trails that takes into account the type of the terrain and the distribution of trees in the forest stand.
Comparisons of the trail lengths and number of trees to be felled located on the routes of modeled trails were carried out before and after model optimization. Differences between network variants were tested by Student’s t-test using the statistical package STATISTICA® 10.0 (StatSoft, Tulsa, OK, USA).
Based on the number of trees to be removed to construct the trails, estimates of the total tree stem volume and the volume of the aboveground tree biomass were obtained. To this purpose, simple equations were used ([5]) based only on tree height as obtained from individual tree measurements by the ALS data (eqn. 2, eqn. 3):
where H is the tree height (based on ALS single tree measurements, m), V is the single tree volume (m3), BA is the aboveground biomass (kg) of a single tree, a1 is 0.000074, a2 is 0.0023, b1 is 3.1, b2 is 4.1398.
Results
Based on the procedure described above, skid trails were traced and the trail network expanded to its maximum possible extent by taking advantage of the existing gaps in the study site.
Total length of skid trails for the traditional harvesting method was 109.17 km before optimization (TRBO_L), whereas it decreased by 2.14 km (2%) to 107.03 km after optimization (TRAO_L). For fully mechanized harvesting, the skid trail network was remarkably denser and longer, with an original length of 227.27 km (FMBO_L) that was reduced by 142 m (0.06%) to 227.13 km after optimization (FMAO_L).
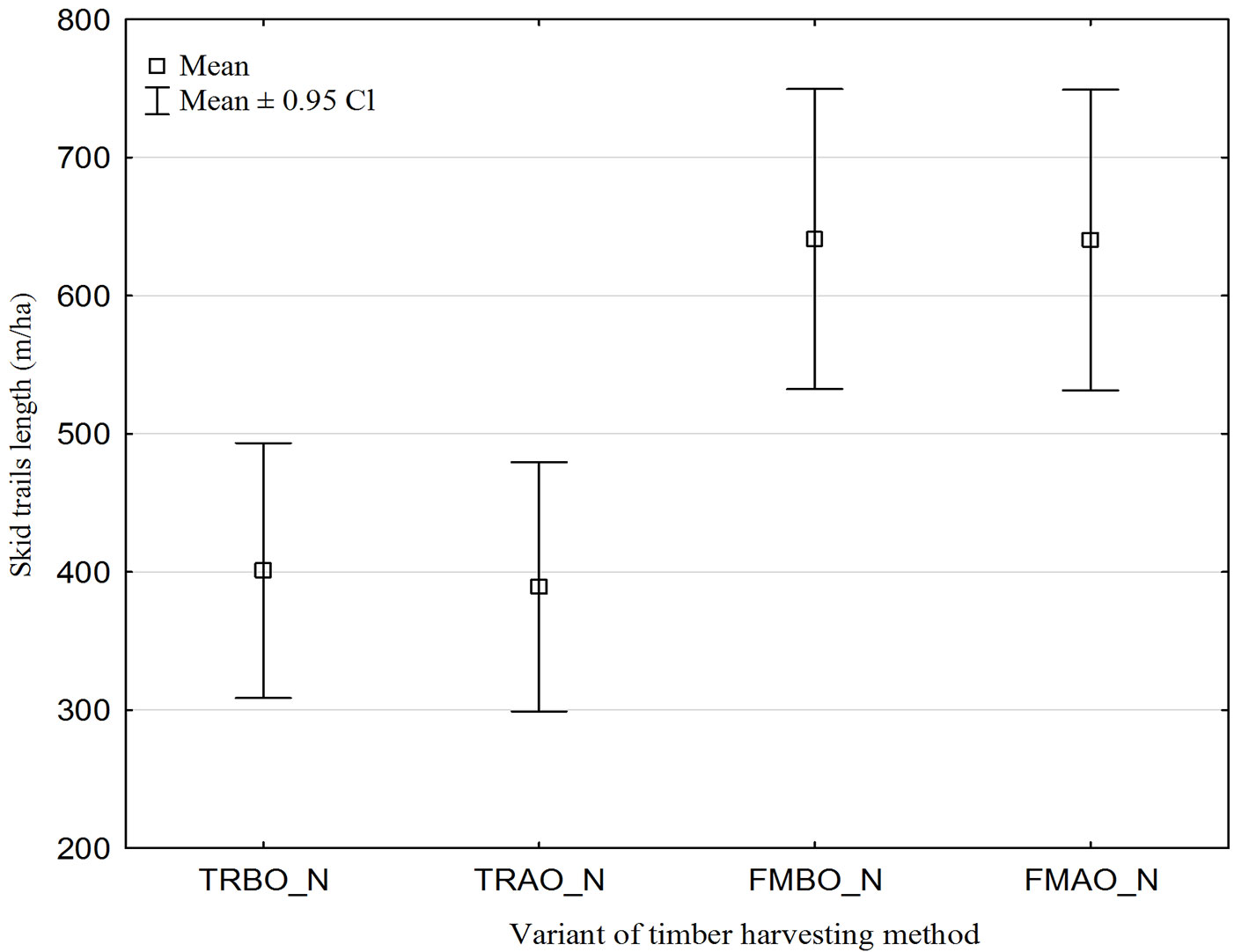
A comparison of the average length of skid trails per ha before and after the optimization step is reported in Fig. 4 for the different harvesting methods considered. The large difference between trail lengths obtained for traditional and mechanized logging methods (over 60%) was mainly due to the different distances between adjacent trails, which was initially set to 20 and 40 m, respectively. Optimization by taking into account stand gaps did not significantly change the overall trail length. The observed difference in the average length of skid trails per ha using traditional methods was 2.01%, while with fully mechanized methods was only 0.12%. As shown in Tab. 2, such differences were not statistically significant.
Fig. 4 - Average skid trail length (m ha-1) in the study area before and after optimization.(TRBO_L): Traditional logging method before optimization; (TRAO_L): traditional logging method after optimization; (FMBO_L): fully-mechanized logging method before optimization; (FMAO_L): fully-mechanized logging method after optimization.
Tab. 2 - Results of the Student’s t-test for the comparison of the trail length per ha and the number of trees to be felled before and after the optimization process. Labels are the same reported in Fig. 4 and Fig. 5.
| Variable | Comparison | Mean 1 | Mean 2 | t | df | p | N 1 and N 2 | SD 1 | SD 2 | F ratio | p |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Av. length of skid trails ha-1 | TRBO_L vs. TRAO_L | 399.11 | 391.09 | 0.1239 | 338 | 0.9013 | 170 | 60.76 | 53.58 | 1.0275 | 0.8601 |
| FMBO_L vs. FMAO_L | 641.02 | 640.28 | 0.0092 | 338 | 0.9926 | 170 | 59.92 | 71.21 | 1.0064 | 0.9669 | |
| N. trees to be felled |
TRBO_N vs. TRAO_N | 59.59 | 58.06 | 0.1687 | 338 | 0.8660 | 170 | 24.11 | 21.29 | 1.0371 | 0.8127 |
| FMBO_N vs. FMAO_N | 113.22 | 112.35 | 0.2259 | 338 | 0.8213 | 170 | 31.88 | 35.23 | 1.0374 | 0.8115 |
Also, the single tree segmentation carried out allowed to determine the total number of trees to be felled for the construction of the skid trails in the study site. Before optimization, such figure was 16 785 using the traditional harvesting method (TRBO_N), whereas after optimization (TRAO_N) it decreased by 465 (2.8%) to 16 320. Using the fully mechanized harvesting method, the number of trees was originally 55 995 (FMBO_N), while after optimization (FMAO_L) this number was reduced by 308 (0.55%) to 55 687.
Fig. 5 shows the number of trees (per ha) standing on the surface of the designed skid trails in the study area. The trends obtained were similar to those observed for the trail length. However, differences between traditional and mechanized logging methods were higher, increasing to about 90%. Also in this case, the optimization process adopted did not significantly reduce the number of trees to be felled. Differences in the numbers of trees before and after optimization were not statistically significant (Tab. 2), amounting to 2.57% and 0.77% for the traditional and the mechanized methods, respectively.
Fig. 5 - Number of trees to be removed before and after the optimization process. (TRBO_N): Traditional logging method before optimization; (TRAO_N): traditional logging method after optimization; (FMBO_N): fully-mechanized logging method before optimization; (FMAO_N): fully-mechanized logging method after optimization.
The volume of trees to be felled on the modeled skid trails decreased after optimization by 368 m3 (from 12 363 to 11 995 m3, 2.9%) using the traditional harvesting method. For fully mechanized harvesting, this reduction was 214 m3 (from 41 160 to 40 945 m3, 0.5%). Similarly, the amount of aboveground biomass using the traditional harvesting method decreased after optimization from 9 053 to 8 782 tons (2.9%), and from 30 123 to 29 971 tons (0.5%) using the fully mechanized method.
Discussion
Accessing forest stands using an appropriately planned skid trail network allows not only logging and skidding operations to be carried out, but also other works related to silviculture and forest protection.
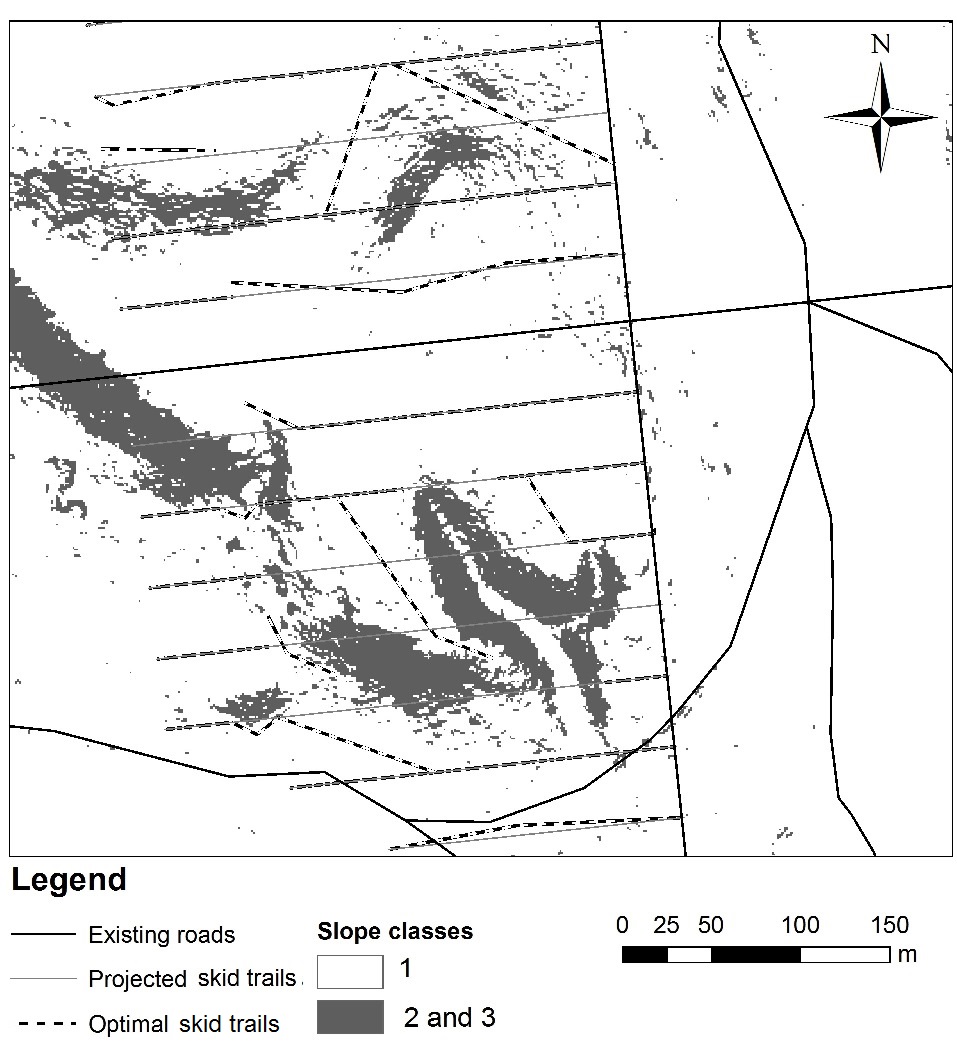
It is recommended to establish trails during the first thinning associated with logging operations. Trails should be designated along the shortest routes to extraction roads; however, schematic, rectilinear routes should be avoided, as well as the less accessible portions of the stand, such as wetlands, ponds, areas with steep slopes etc. Existing gaps, trails, etc., should be taken into account. An example of the skid trail network obtained after optimization on part of the study area is displayed in Fig. 6.
As reported by previous studies, harvest volume is an important factor to be considered in planning the forest transportation network, since a larger number of roads and higher skid trail densities are needed to reach those parts of the forest with higher annual growth and harvesting rates ([9], [25]). In this paper, we estimated the harvest volume to be removed during thinning operation is about 35 m3 ha-1. According to Zarzycki ([33]), the area needed for skid trails covers about 10% of the total forest area using the traditional harvesting method, and 20% using fully-mechanized methods. This means that the wood volume which could be harvested during thinning operation reaches about 3.5 and 7 m3 ha-1, respectively.
The optimization algorithm used in this study allowed the verification of a theoretical network of skid trails prior to their actual construction. Such procedure is time-saving and allows an early identification of areas inaccessible using different harvesting methods. The spatial analysis carried out using advanced GIS tools allowed alternative trail routes to be assessed, taking into account the type of terrain and the harvested wood to be extracted ([10]). An additional advantage of the proposed method stems from the use of segmentation aimed at distinguishing single trees in the crown layer, thus obtaining their spatial distribution on the ground. Such approach allowed to identify existing gaps or partial cutting plots to be included as preferential routes in developing the trail network.
The decrease in the overall trail length after optimization results from the avoidance of inaccessible steep areas that need to be circumvented by the modeled trails. However, as elevation increases, trail lengths also increase, mainly if inaccessible sites are small and linear-shaped, thus requiring the construction of longer routes.
Out results showed large differences between the traditional and machine-harvesting methods in the length of planned trails, and therefore in the number of trees to be felled for trail construction. Such differences are primarily due to the different distance between trails chosen as starting parameters for the two methods. In mountainous conditions, with greater restrictions due to steeper slopes, where trails are laid unevenly, somewhat different dependencies should be expected.
The trail optimization process using the existing stand gaps in the stand allowed to achieve better results, though the observed differences with the non-optimized network were relatively small. This could be interpreted as due to the high stocking rate (average of 0.73) and the fairly high stand densities in the study area. Indeed, starting plant density in Polish pine stands are often higher than in any other country (about 8000 ha-1). As the stands develop, a reduction in density takes place by natural thinning or silvicultural practices; however, the gap size still remains quite small.
The algorithm used in our model was designed based on the criteria of minimizing the number of trees to be felled in the construction of the trail network. Of course, different criteria can be adopted, such as the avoidance of natural renewal areas, wetlands, particularly valuable plots in the stand, etc. In general, it is expected that the inclusion of more criteria in the model might enhance its utility, in terms of optimization of the skid trail network at the planning step.
The present paper aimed at demonstrating an alternative use of remote sensing data already available. Although collecting ALS data is quite expensive, their use for planning purposes may be prolonged for several years in sites where no management activities have been carried out.
Conclusions
The application of laser scanning technology and the use forest digital maps, along with the development of adequate algorithms, may allow the optimization of skid trail networks, as well as the reduction of number of trees to be felled in the network construction. Both the length of skid trails and the number of trees to be felled are mainly affected by the distance required between trails. This in turn depends on the logging and wood extraction technology to be used.
The use of existing stand gaps for trail delineation may contribute to the reduction of the number of trees to be felled in the construction of the skid trail network. However, our results did not show significant differences between the modeled network variants before and after the optimization procedure applied.
Acknowledgements
We are grateful to Krzysztof Bedkowski (Warsaw Universities of Life Sciences, Poland) for the permission of using ALS data obtained within the project of the Polish Ministry of Science and Higher Education: “Using airborne and terrestrial LIDAR scanning for analyzing forest spatial structure and forest function in landscape” (project no. 2 P06L 02229).
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Online | Gscholar
Online | Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Forest Research Institute, Department of Information Technology and Modelling, Braci Lesnej 3, 05-090 Raszyn (Poland)
Warsaw University of Life Sciences - SGGW, Department of Forest Utilization, Faculty of Forestry, Nowoursynowska 159, 02-776 Warszawa (Poland)
Corresponding author
Paper Info
Citation
Sterenczak K, Moskalik T (2014). Use of LIDAR-based digital terrain model and single tree segmentation data for optimal forest skid trail network. iForest 8: 661-667. - doi: 10.3832/ifor1355-007
Academic Editor
Enrico Marchi
Paper history
Received: May 20, 2014
Accepted: Aug 22, 2014
First online: Dec 22, 2014
Publication Date: Oct 01, 2015
Publication Time: 4.07 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2014
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 59062
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 49483
Abstract Page Views: 3668
PDF Downloads: 4429
Citation/Reference Downloads: 28
XML Downloads: 1454
Web Metrics
Days since publication: 4034
Overall contacts: 59062
Avg. contacts per week: 102.49
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2015): 25
Average cites per year: 2.27
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Integrating area-based and individual tree detection approaches for estimating tree volume in plantation inventory using aerial image and airborne laser scanning data
vol. 10, pp. 296-302 (online: 15 December 2016)
Research Articles
Assessment of timber extraction distance and skid road network in steep karst terrain
vol. 10, pp. 886-894 (online: 06 November 2017)
Research Articles
Use of terrestrial laser scanning to evaluate the spatial distribution of soil disturbance by skidding operations
vol. 8, pp. 386-393 (online: 08 October 2014)
Research Articles
Integration of tree allometry rules to treetops detection and tree crowns delineation using airborne lidar data
vol. 10, pp. 459-467 (online: 04 April 2017)
Research Articles
Optimizing line-plot size for personal laser scanning: modeling distance-dependent tree detection probability along transects
vol. 17, pp. 269-276 (online: 07 September 2024)
Technical Advances
Forest stand height determination from low point density airborne laser scanning data in Roznava Forest enterprise zone (Slovakia)
vol. 6, pp. 48-54 (online: 21 January 2013)
Research Articles
Three-dimensional forest stand height map production utilizing airborne laser scanning dense point clouds and precise quality evaluation
vol. 10, pp. 491-497 (online: 12 April 2017)
Research Articles
Are we ready for a National Forest Information System? State of the art of forest maps and airborne laser scanning data availability in Italy
vol. 14, pp. 144-154 (online: 23 March 2021)
Research Articles
Comparing image-based point clouds and airborne laser scanning data for estimating forest heights
vol. 10, pp. 273-280 (online: 23 February 2017)
Research Articles
Short-term recovery of fine root carbon stock is inhibited by skid trails in a humid tropical forest
vol. 18, pp. 344-349 (online: 30 November 2025)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword