Development phases and structural characteristics of the Penteleu-Viforâta virgin forest in the Curvature Carpathians
iForest - Biogeosciences and Forestry, Volume 13, Issue 5, Pages 389-395 (2020)
doi: https://doi.org/10.3832/ifor3094-013
Published: Sep 01, 2020 - Copyright © 2020 SISEF
Research Articles
Abstract
The stand structure of a virgin forest situated at an average altitude of 1130 m a.s.l. in the Milea Viforâta Nature Reserve (Southern Carpathians, Romania) was investigated to determine the specific development phases of the forest and understand how they influence the stand structure, with the aim of providing optimal solutions and structural models for sustainable forest management. All trees with breast height diameter (dbh) ≥ 8 cm were inventoried in the study plot (1 ha), and the main dendrometrical variables were measured. Radial increment cores were taken from all the trees and were subsequently processed. A total of 317 trees from three species - European beech (Fagus sylvatica), silver fir (Abies alba) and Norway spruce (Picea abies) - were sampled at different development phases (optimum, ageing, breakdown and dieback, rejuvenation). Testing stand structural diversity with the Gini index, a minimal stability was found in the rejuvenation development phase and a maximum stability in the ageing phase. No significant match was found between standard theoretical functions (Normal, Weibull, Gamma and Exponential) and the observed distribution of tree diameter. Also, it was confirmed that dominance of beech in all development phases is a consequence of its high competitive ability and its capacity to endure difficult environmental and biologically stressful conditions. The results revealed a series of structural models specific to these forest ecosystems, which can help managing forests under the selection system.
Keywords
Primary Forest, Development Phases, Uneven Aged Forests, Carpathians Forest
Introduction
The Food and Agriculture Organization ([42]) defines virgin forests as “forests developed under natural conditions and undisturbed by human activities”. In Europe, in managed forests, sustainable management and silvicultural practices at the beginning of the 21st century aim to reproduce virgin forest complex structures and their multi-functional outcomes ([44]). The complexity of uneven-aged forest structures ensures economic value through superior timber quality, as well as high biodiversity at all levels ([34], [14]). The dynamics of virgin forests, their response to stress factors, natural competition, species exclusion, species complementarity and niche development have been the subject of research and a reference model, as well as an inspiration for theories and principles of silviculture ([34], [43]). Furthermore, due to the impact of climate change on managed forests and the new upcoming challenges, a different approach in the way forests are managed is needed. New practices and management strategies are required, and virgin forests can provide a model for future silvicultural practices ([22]) and forest management planning to address the challenge of climate change. New approaches should include silvicultural practices aimed at improving the forest stability otherwise reached by unmanaged forests ([31]). However, silvicultural treatments are indispensable, under certain circumstances, to achieve a higher diversity and stability then that attainable following the forest natural dynamics ([6]).
Virgin forests are a natural heritage of extraordinary value and timeless interest. Most of the world’s remaining virgin forests survive thanks to limits on logging and restrictions to human access. However, these limitations are now being removed because of new harvesting techniques and the high value of timber, thus virgin ecosystems are becoming increasingly rare ([34], [14]). Considering the negative impacts that have been recorded on forest succession ([21]), the growing research interest and concern on the survival of virgin forests are justified.
In this study, the term “virgin forest” is used according to the reference literature ([20], [23]), as synonymous of primaveral forest, primary forest and pristine forest ([39]). This study focuses on understanding and modelling virgin forest development phases, defined as theoretical concepts which help characterise the structural dynamics of natural forests ([38]) under the influence of internal and external factors ([47], [11]).
The development phases offer information on virgin forests’ growth dynamics, about how natural processes run without being disturbed by human activities and also how we can reproduce these structures through future management practices ([47], [44]). The aim of this study is to determine the characteristics of each development phase in order to develop solutions for structural models applied in forest management. The main objectives of the study are: (i) to characterise the structure of a virgin stand and its development phases; (ii) to describe the stand structure in relation with diameter (for the entire stand and for each development phase) by theoretical functions; (iii) to determine the relationships among tree species and their respective development phase, age and growth.
Materials and methods
The study area is situated in the Curvature Carpathians - more specifically, in the Penteleu Massif, which is a part of the Buzau Mountains - in a temperate continental zone at an altitude of 1128 m a.s.l., on a southern slope (Fig. 1). The lithological substrate is composed of sandstone and dune sand with variable granulation. The dominant winds come from NNE and the average annual temperature is 6.1 °C. The inventoried plot is part of the Milea Viforâta Nature Reserve. It is circular in shape, with a radius of 56 m, and has an area of 1 ha. A tape was used to measure trees with a circumference > 25 cm at breast height, corresponding to a diameter of at least 8 cm. The height of each tree in the plot was measured using an ultrasound instrument system (Vertex IV®, Haglof, Sweden). The measured variables were: tree position, circumference, height, species, and storey position. Also, wood core samples were obtained with a Pressler’s increment borer, as radial growth, together with the structure of stand in relation with tree diameter, represent the most important element in describing the stand evolution and its development phases ([15]).
Tree radial growth was measured on cores using the software CooRecorder® v. 7.4 (Cybis Elektronik & Data AB, Saltsjöbaden, Sweden) based on image analysis, and the validation of measurements was done by COFECHA software ([18]). A mean radial growth of the last ten years was computed for each tree (ir10). Nonlinear regression analysis using the “nls” function in R ([4]) was conducted for each species to determine a radial growth (ir) model using the following mathematical expression (eqn. 1):
where ir10 is the mean ir of the last ten years for each tree and a0, a1 and a2 are the species-specific parameters to be estimated. The radial increment derived from wood core samples allows us to distinguish different growth rates among groups of trees, and thus to determine the stand’s development phases.
Theoretical distributions (normal - [35]; gamma - [16]; weibull - [28]; exponential - [25]) were fitted using the “fitdristr” function of the R “fitdistrplus” package ([9]). Kolmogorov-Smirnov (KS - [41]), Anderson-Darling (AD -[2]) and chi-square (CHI) tests were used to assess the fit of theoretical distribution to the experimental diameter distribution. Also, to compute the diameter limit of the stand, an exponential distribution of the following form was used ([27] - eqn. 2):
where y is the number of trees in a narrow diameter interval yx, x is the diameter at breast height, e is the base of the natural logarithm, and k and α are constants characterising a certain structure.
Volume growth was established using a method based on single-inventory information and on wood cores taken from standing trees ([13]). The following equation was used to calculate the volume of each individual tree ([13] - eqn. 3):
where h is the tree height (m), dbh is the diameter at breast height (cm) and a0, …, a4 are the regression coefficients (spruce: a0 = -4.18161, a1 = 2.08131, a2 = -0.11819, a3 = 0.70119, a4 = 0.148181; beech: a0 = -4.11122, a1 = 1.30216, a2 = 0.23636, a3 = 1.26562, a4 = -0.079661; fir: a0= -4.46414, a1 = 2.19479, a2 = -0.12498, a3 = 1.04645, a4 = -0.016848) established for the most important species in Romania’s forests ([13]).
To analyse structural diversity, the Gini index ([12]) was calculated for each development phase ([19]). Each tree was assigned to one of four virgin forest’s development phases ([11]): (i) optimum; (ii) ageing; (iii) breakdown and dieback; (iv) rejuvenantion. The classical method ([26]) was applied for delimitating the development phases on the ground, using the following stand characteristics: number of trees, basal area, volume growth, stand class, vitality, mortality, age structure, stability of the stand and regeneration (see also Tab. S1 in Supplementary material). GPS technology was used for spatial delimitation of the development phases.
All statistical analyses were conducted using the R software ([37]).
Results
All development phases (optimum, ageing, breakdown and dieback, rejuvenation) were found in the study plot, but with a high variability in the size of the area covered by each phase (Tab. 1). The small area covered by early development phases is the consequence of the lower limit (8 cm) adopted for trees to be inventoried. The number of trees in each development phase was highly positively correlated with the basal area (r= 0.896; p<0.01562). The smallest number of trees was recorded for the optimum phase, followed by the rejuvenation phase, with 90 trees. The breakdown and dieback and ageing phases were well represented within the plot, with 178 and 112 trees, respectively. The optimum phase covered 14 per cent of the total surface area of the plot, with basal areas of 1.05 m2. With the exception of the optimum phase, mean radial growth showed a weak correlation with the average age of trees (r = 0.25, p<0.001), as well as with tree volume (r = 0.35, p<0.001). The volume per tree (overall aboveground tree volume for broadleaves and trunk volume for coniferous) ranged between 0.11 m3 and 3.28 m3.
Tab. 1 - Main structural characteristics of the four development phases recorded at the studied virgin forest.
| Characteristics | Development phase | Total | |||
|---|---|---|---|---|---|
| Optimum | Ageing | Breakdown and dieback |
Rejuvenation | ||
| Number of trees | 17 | 112 | 178 | 90 | 397 |
| Covered area (%) | 31 | 21 | 41 | 7 | 100 |
| Basal area (m2) | 1.08 | 7.01 | 20.06 | 15.58 | 43.73 |
| Gini Index | 0.57 | 0.78 | 0.69 | 0.52 | - |
| Min radial growth (ir, mm) | 0.42 | 0.15 | 0.14 | 0.15 | 0.14 |
| Max radial growth (ir, mm) | 2.04 | 3.56 | 4.36 | 4.33 | 4.36 |
| Mean radial growth (ir, mm) | 0.97 | 1.06 | 1.08 | 1.42 | 1.15 |
| Min age (yrs) | 32 | 11 | 24 | 27 | 11 |
| Max age (yrs) | 329 | 365 | 328 | 334 | 365 |
| Average age (yrs) | 115.88 | 89.17 | 112.46 | 145.72 | 113.57 |
| Mean unitary volume (m3) | 0.70 | 0.86 | 1.74 | 2.83 | 1.69 |
Characterisation of the stand using dbh theoretical distributions
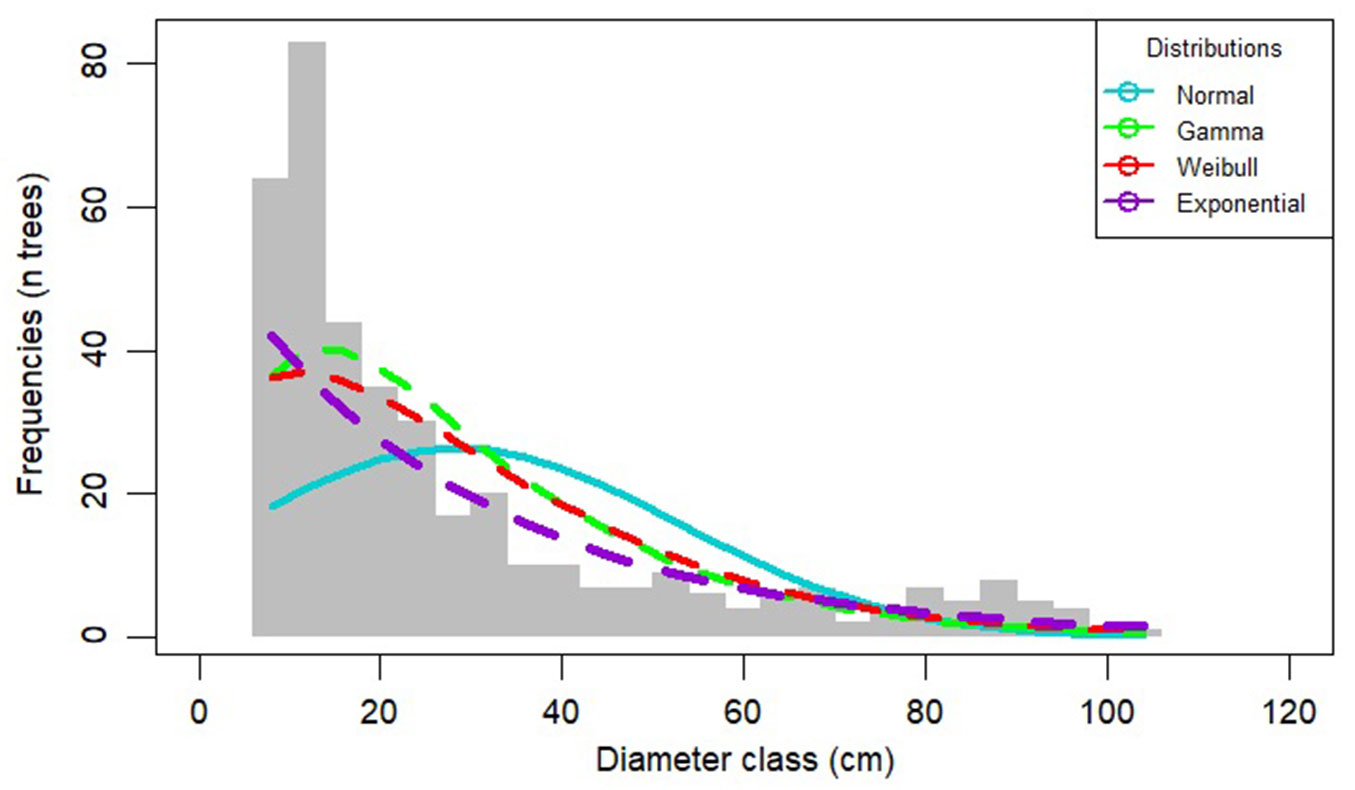
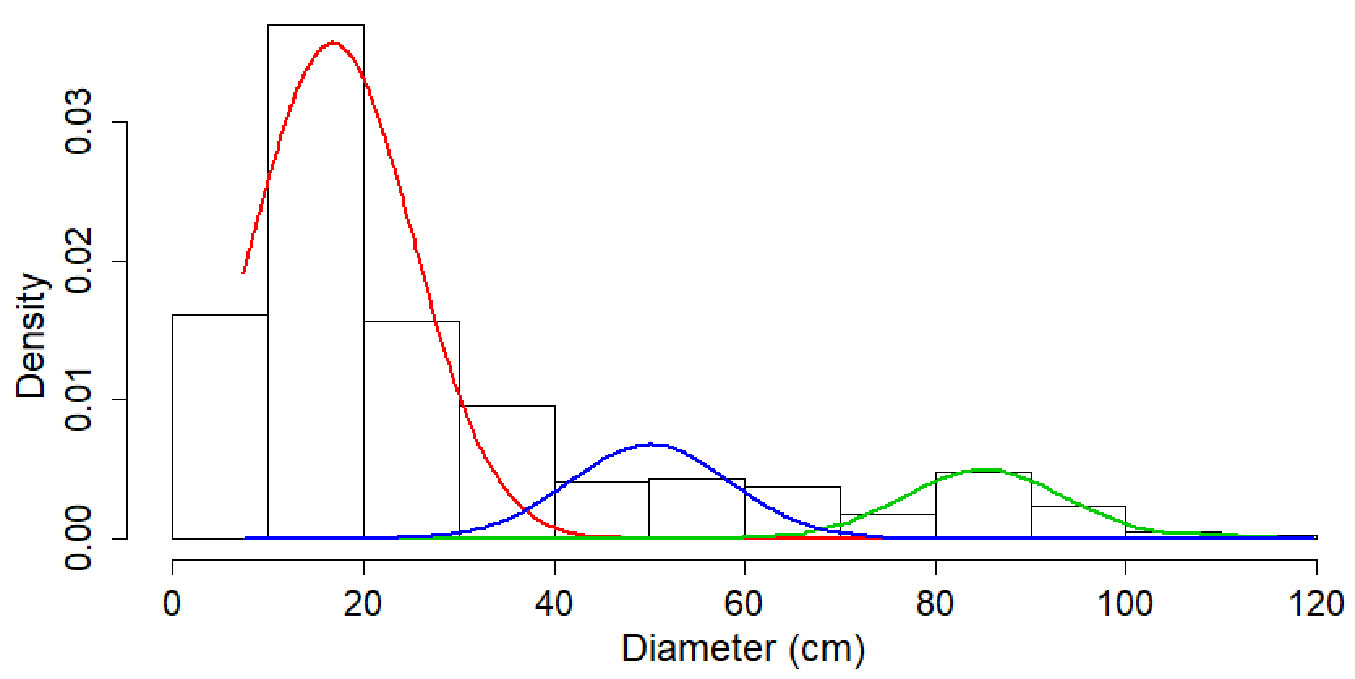
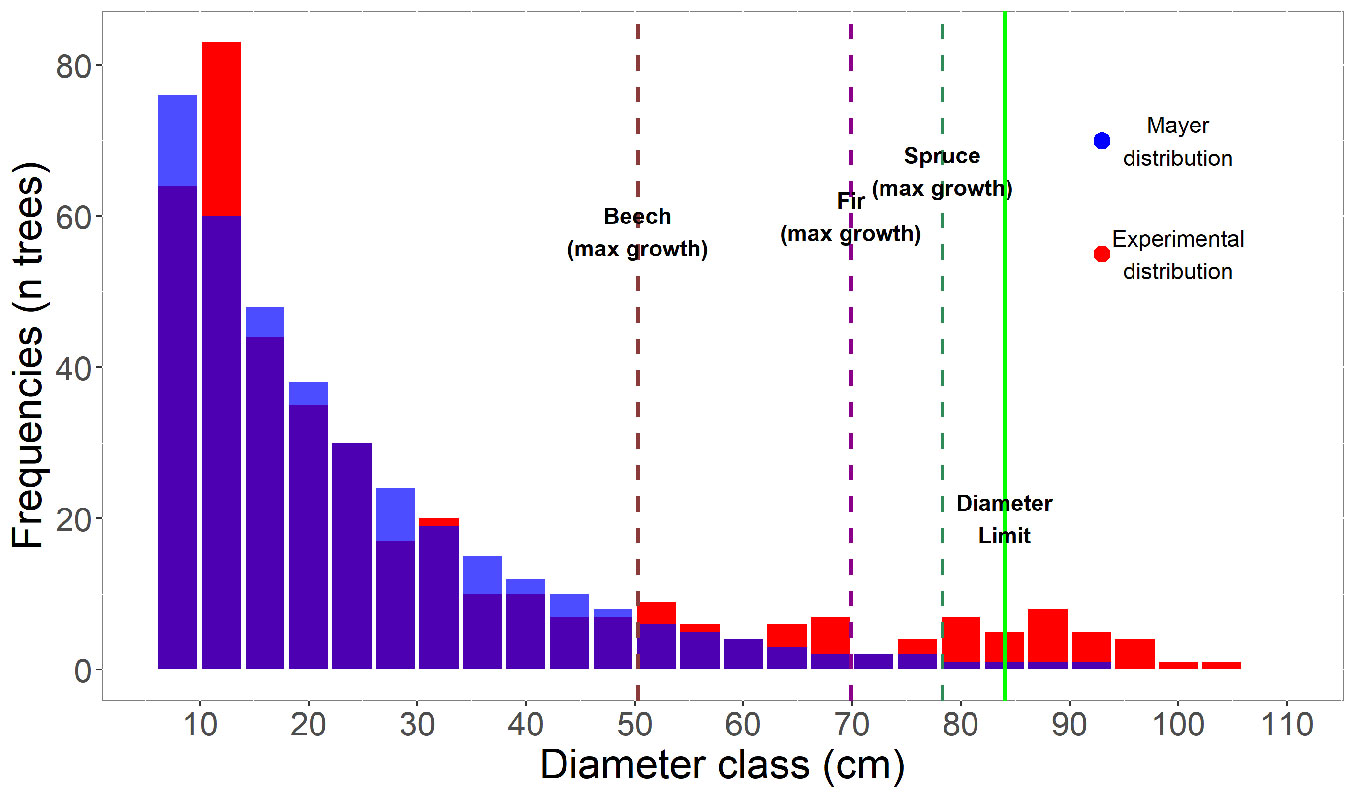
Theoretical functions (normal, gamma, weibull, exponential) were fitted to the experimental distribution of diameters (Fig. 2). All the statistical tests applied (Kolmogorov-Smirnov, Anderson-Darling and chi-square - Tab. 2) confirmed that none of these distributions corresponds to that observed in the virgin forest stand at Penteleu-Viforâta. Therefore, a mixture of three normal distributions was used to describe the stand structure (Fig. 3). The significant (p<0.001) fitting confirmed the existence of a three-modal distribution of tree diameters, where each peak corresponds to a storey position in the canopy (see also Tab. S2 in Supplementary material).
Fig. 2 - Theoretical (colored lines) vs. experimental (bars) distributions of tree dbh at the Penteleu-Viforâta virgin forest.
Tab. 2 - Goodness-of-fit of theoretical functions to the experimental distribution of diameters at the Penteleu-Viforâta virgin forest.
| Theoretical Function |
Statistical tests | |||
|---|---|---|---|---|
| CHI | Kolmogorov-Smirnov NO/YES |
Kolmogorov- Smironov |
Anderson-Darling | |
| Normal | 595.53 | rejected | 0.20 | 31.07 |
| Weibull | 212.92 | rejected | 0.15 | 14.09 |
| Gamma | 193.78 | rejected | 0.12 | 13.78 |
| Exponential | 217.63 | rejected | 0.24 | 19.78 |
Fig. 3 - The mixture of three normal distributions used to describe the distribution of diameters at the Penteleu-Viforâta virgin forest. The significant (p<0.001) fitting confirmed the existence of a three-modal distribution, where each peak corresponds to a storey position in the canopy.
Similar results were obtained when theoretical functions were fitted on observed diameter distribution of each development phase (whenever sufficient samples were available), except for the rejuvenation phase (Tab. 3) where significant (p<0.001) fitting was found for normal, gamma and weibull functions. In the case of all other phases and functions, fitting was rejected.
Tab. 3 - Goodness-of-fit of theoretical functions to the experimental distribution of diameters for each development phase at the Penteleu-Viforâta virgin forest. Results for the optimum phase are not reported due to the limited sample size.
| Theoretical function | Statistical test |
Phase | ||
|---|---|---|---|---|
| Ageing | Rejuvenation | Breakdown and dieback |
||
| Normal | KS | 0.24 | 0.12 | 0.21 |
| AD | 13.67 | 1.37 | 14.32 | |
| CHI | 215.94 | 27.79 | 198.81 | |
| TEST | Reject | Fitted | Reject | |
| Weibull | KS | 0.21 | 0.07 | 0.15 |
| AD | 7.47 | 0.40 | 6.87 | |
| CHI | 94.99 | 15.57 | 74.25 | |
| TEST | Reject | Fitted | Reject | |
| Gamma | KS | 0.16 | 0.06 | 0.16 |
| AD | 6.75 | 0.37 | 6.73 | |
| CHI | 75.68 | 14.21 | 65.28 | |
| TEST | Reject | Fitted | Reject | |
| Exponential | KS | 0.31 | 0.19 | 0.23 |
| AD | 10.17 | 3.63 | 9.60 | |
| CHI | 115.37 | 24.52 | 80.02 | |
| TEST | Reject | Reject | Reject | |
Relation between development phase and species
Beech was the dominant species in all layers and phases, being present in large numbers in every development phase. Ageing, breakdown dieback and rejuvenation were the three phases which mainly cover the study plot, and they were well covered by all three species (beech, fir and spruce). As mentioned above, the limited number of trees falling in the optimum development phase is the consequence of the adoption of a lower limit (8 cm) for trees to be inventoried (Tab. 4).
Tab. 4 - Species distribution in relation with development phase.
| Development phase | Number of trees | |||
|---|---|---|---|---|
| Fir | Beech | Spruce | Total | |
| Ageing | 21 | 82 | 9 | 112 |
| Breakdown and dieback | 52 | 108 | 18 | 178 |
| Optimum | 5 | 11 | 1 | 17 |
| Rejuvenation | 18 | 58 | 14 | 90 |
| Total | 96 | 259 | 42 | 397 |
Relation between age and species
The predominance of trees belonging to lower age class (80-100 years old) was observed in the studied plot. However, a significant number of trees belonging to upper age class were also found, but with a lower frequency. Beech reach an age of 380 years in the Penteleu-Viforâta virgin forest, while fir and spruce are no longer present after 340 years (Tab. S3 in Supplementary material). Most of beech trees, however, are in the lower age classes, with the highest abundance recorded in the age class 80-120 years. Both beech and fir have an uneven-aged distribution characterised by a large number of trees in the younger classes, whereas for spruce, the distribution is platykurtic, with a similar number of trees in every age class.
Relation between diameter and growth by species
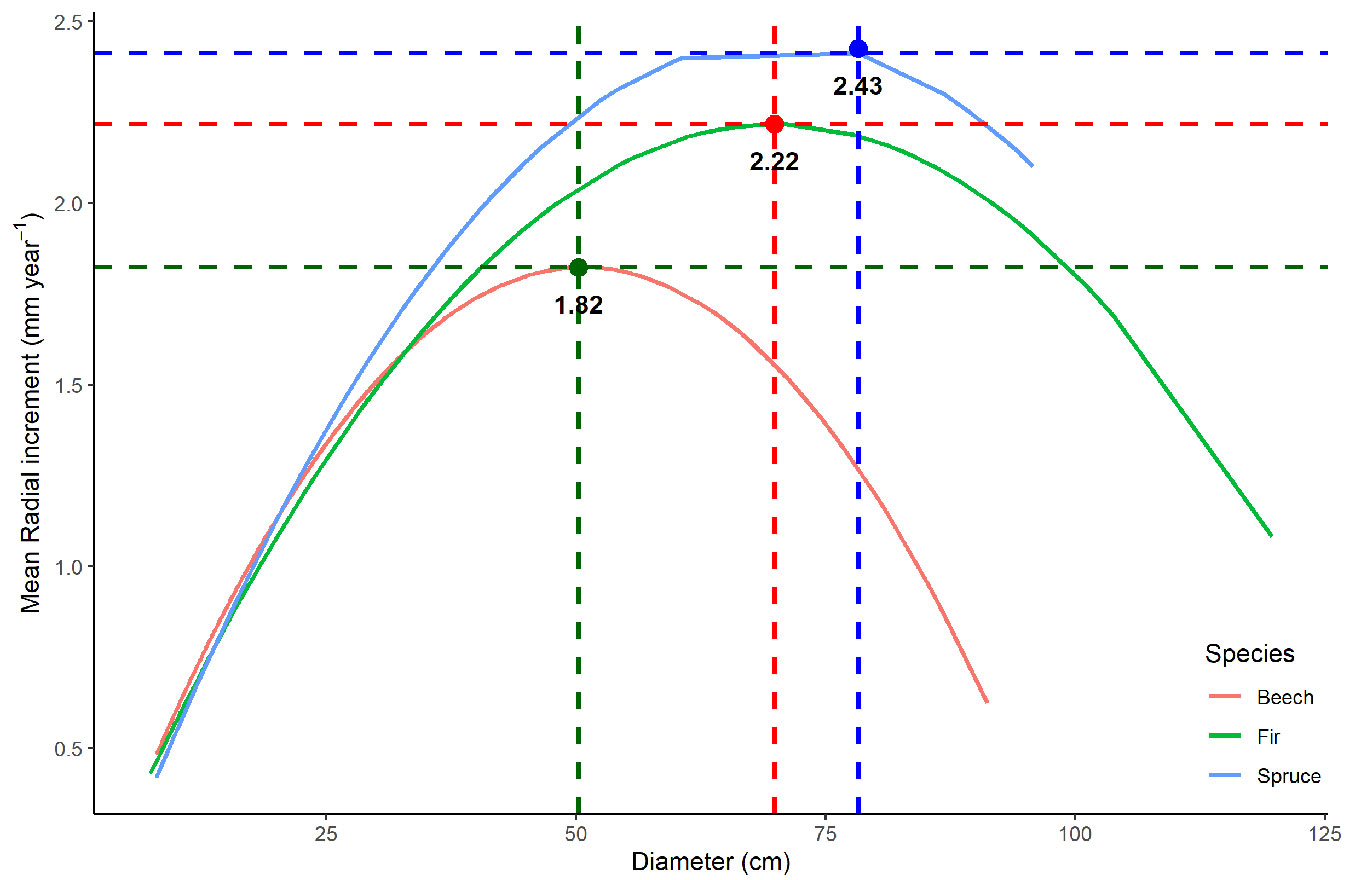
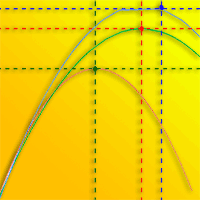
The analysis of mean radial growth based on wood core samples allowed to build species-specific growth models (Fig. 4), which revealed high increment values for all the species. For beech, the highest radial increment (1.82 mm year-1) was recorded for trees with a diameter of 50 cm, while for fir and spruce higher increment values were observed at larger diameters (2.22 mm year-1 at 70 cm diameter and 2.43 mm year-1 at 75 cm diameter, respectively - Fig. 4). However, after reaching these maximum increment levels, radial growth rate decreases and trees enter a senescent overstory stage. This is characterised by high mortality with the stand density curve sloping downward, reaching the diameter limit. In our study, the diameter limit corresponds to the category of 84 cm (Fig. 5).
Fig. 5 - Stand diameter limit and maximum point of growth for beech, spruce and fir at Penteleu-Viforâta virgin forest.
Discussion
Compared with even-aged stands, virgin forests are thought to better withstand natural disasters, such as insect outbreaks, windthrows and severe drought, thanks to the co-occurrence of different development phases which ensure long-term sustainability and continuity of the forest ecosystem ([29]). The typical process of identification of development phases in virgin forests can suffer from subjectivity ([11]), whereas the adoption of quantitative methods to investigate stand dynamics based on repetitive measurements combined with GIS data and stand structural characteristics is required to obtain more precise and reliable results.
In the studied forest, the number of trees per ha was 225-400 and the basal area was 32-47 m2. Such values are at the upper limit of the ranges reported in the literature for other old-growth European forests ([17], [47]). Also, the dominance of the ageing and breakdown and dieback phases at Penteleu-Viforâta is likely the result of the protection from wind provided by the surrounding reliefs. Indeed, the analysed plot is situated on a south-facing slope with dominant winds blowing from NNE, and this is similar to other virgin forests reported in the literature ([3]).
The values of the Gini coefficient observed at Penteleu-Viforâta reflect the structural characteristics of each development phase and support the hypothesis of a high stability of the stand ([7]). The lower values of Gini coefficient recorded in the rejuvenation phase indicate a reduced structural diversity. Contrastingly, high values were found in the ageing phase, thus indicating a higher structural diversity and stability. Moreover, the values of Gini coefficient recorded for each development phase were fairly similar to those reported in the literature for virgin forests ([47]), i.e., 0.69-0.76 for the optimum phase, 0.51-0.64 for the ageing phase and 0.51-0.60 for the rejuvenation phase. We believe that such values can be used as reference for further studies focused on virgin beech-fir-spruce forests in Europe. This information, along with the species growth models, could be relevant for the development of a model to manage cultivated forests based on evidences obtained from virgin forests ([32]), thereby increasing long-term functionality and stability of stands ([14]).
The diameter distribution of trees in our study area did not fit any of the most common distributions suited to managed forests, due to the structural complexity of each development phase in virgin forest ecosystems ([14]). It is known that diameters in uneven-aged forests do not follow a general theoretical distribution, although in some cases experimental data showed a fairly good fit to Weibull, Beta and Meyer distributions ([1]). In fact, the structure of a virgin forest stand keeps changing as a result of the balance of inputs and outputs. Inputs are provided by new areas covered by regeneration, and the outputs are the result of the high tree mortality rate due to the strong competition that exists in a virgin forest.
Regarding the relation between development phases and species, the dominance of beech in all development phases, especially in lower-diameter categories, confirms previous findings on this species ([10], [44]). In virgin beech-fir-spruce forests, disturbances are frequent, though balanced by rapid stand growth ([33]). Since virgin ecosystems are not directly influenced by any anthropic disturbances, this growth pattern may occur as a response to climate change ([44]). Furthermore, our results confirm the capacity of beech for regeneration and survival in the understory, showing an increase in growth even under the canopy ([46], [30]).
Leuschner & Meier ([24]) in a study on 42 European forest tree species, reported a maximum longevity of 450, 450 and 300 years for beech, fir and spruce, respectively. In this study, we found several individuals of beech reaching up to 380 years of age, confirming that the Penteleu-Viforâta forest is an optimum site for beech. Although the general climatic conditions suggest a good vegetation site also for the other two species (fir and spruce), their capacity to grow in the understory is lower than that of beech, and this affects their growth dynamics and longevity. Indeed, beech shows a superior capacity of surviving under stress conditions, making it more competitive than fir and spruce. This is reflected by the high-intensity growth of beech in the optimum phase, compared with the two conifers.
Uneven-aged stands are more productive than even-aged stands ([8]); this also holds for mixed forests compared to pure stands ([36]). The most common natural mixed composition in uneven-aged forests of Central Europe consists of beech, spruce and fir, due to their ecological complementarity. Nonetheless, these species show different growth dynamics and competitive ability, particularly in an uneven-aged forest. As mentioned above, beech has a higher capacity to survive in the understory ([5]) due to a well-developed root system reaching deeper soil layers. Moreover, beech growth has a low variability compared to the conifer species ([45]), as a consequence of its capacity to endure a wider range of environmental conditions (including drought). In general, beech shows high growth rates up to approximately 100-120 years of age, while spruce and fir outstrip beech productivity and maintain growth longer than beech and at a higher level, as indicated from the different peaks of mean radial growth for each species observed in this study.
The identification of the maximum growth increment by wood core analysis and the ascertainment of the diameter limit for each species could help define silvicultural practices aimed at optimizing selective cutting in uneven-aged and/or mixed stands. For virgin forests, the diameter limit is taken, from the physiological point of view, as the last category of the diameter distribution a living tree can reach ([40]). In uneven-aged forest management, the maximum point of species growth can be used for predicting the diameter limit of the stand. The diameter limit is dynamic, depending on the site species and the stand history. According to Meyer’s negative exponential distribution, the diameter limit is the diameter category with a frequency of one tree.
Conclusions
Virgin forests are a natural heritage of great value, offering solutions and structural models for sustainable forest management. The analysis of development phases of virgin forests may provide important information to be included in silvicultural practices aimed at enhance the stability and functionality of these ecosystems.
The structural diversity of the Penteleu-Viforâta virgin forest was analyzed by the Gini index. We observed the dominance of the breakdown and dieback as well as ageing development phases, while maximum and minimum stability were recorded for ageing and rejuvenation phases.
Tree diameter distribution did not match any of the tested theoretical functions, due to the complexity of the stand structure and its dynamics continuously changing in time and space. The study of the relation between development phases and species confirmed the dominance of beech in all phases as a consequence of its competitive ability and capacity to endure a wider range of stressful conditions. Moreover, the wood core analysis revealed a different mean radial increment and maximum radial growth for the three species analyzed, which should be taken into account by forest management planners when establishing the diameter limit.
Virgin forests can be considered as in situ laboratories for forest research, particularly for better understanding the principles underlying the stability and functionality of these ecosystems. These types of forests provide a vast array of resources, offering at the same time a higher level of protection, conservation and biodiversity. In this context, further research on development phases in virgin forests are needed in order to devise sustainable forest management strategies.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Authors’ Info
Authors’ Affiliation
Albert Ciceu 0000-0002-4090-8705
Stefan Leca 0000-0002-6110-8379
Bogdan Apostol 0000-0002-5935-4407
Ovidiu Badea
National Institute for Research and Development in Forestry ”Marin Dracea” (Romania)
Molecular Biology Center, Institute of Interdisciplinary Research in Bio-Nano-Sciences, Babes-Bolyai University, Cluj-Napoca (Romania)
Corresponding author
Paper Info
Citation
Chivulescu S, Ciceu A, Leca S, Apostol B, Popescu O, Badea O (2020). Development phases and structural characteristics of the Penteleu-Viforâta virgin forest in the Curvature Carpathians. iForest 13: 389-395. - doi: 10.3832/ifor3094-013
Academic Editor
Paola Mairota
Paper history
Received: Mar 11, 2019
Accepted: Jun 17, 2020
First online: Sep 01, 2020
Publication Date: Oct 31, 2020
Publication Time: 2.53 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2020
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 38159
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 32361
Abstract Page Views: 2866
PDF Downloads: 2274
Citation/Reference Downloads: 3
XML Downloads: 655
Web Metrics
Days since publication: 2000
Overall contacts: 38159
Avg. contacts per week: 133.56
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2020): 9
Average cites per year: 1.50
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Soil CO2 efflux in uneven-aged and even-aged Norway spruce stands in southern Finland
vol. 11, pp. 705-712 (online: 06 November 2018)
Short Communications
Multi-aged micro-neighborhood patches challenge the forest cycle model in primeval European beech
vol. 13, pp. 209-214 (online: 06 June 2020)
Research Articles
Twenty years of conversion: from Scots pine plantations to oak dominated multifunctional forests
vol. 10, pp. 75-82 (online: 19 October 2016)
Research Articles
Modelling dasometric attributes of mixed and uneven-aged forests using Landsat-8 OLI spectral data in the Sierra Madre Occidental, Mexico
vol. 10, pp. 288-295 (online: 11 February 2017)
Research Articles
Dimensionless numbers for the net present value and the perpetual value of sustainable timber harvests from a monospecific uneven-aged forest
vol. 12, pp. 35-42 (online: 10 January 2019)
Research Articles
Selection priority for harvested trees according to stand structural indices
vol. 10, pp. 561-566 (online: 05 May 2017)
Research Articles
Changes in aboveground biomass following alternative harvesting in oak-hickory forests in the eastern USA
vol. 8, pp. 652-660 (online: 13 January 2015)
Research Articles
Estimating biomass of mixed and uneven-aged forests using spectral data and a hybrid model combining regression trees and linear models
vol. 9, pp. 226-234 (online: 21 September 2015)
Research Articles
Optimizing the management of uneven-aged Pinus nigra stands between two stable positions
vol. 9, pp. 599-607 (online: 01 March 2016)
Research Articles
Historical and contemporary forest ecosystem changes in the Beskid Mountains (southern Poland) between 1848 and 2014
vol. 10, pp. 939-947 (online: 19 December 2017)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword