Leaf transpiration of drought tolerant plant can be captured by hyperspectral reflectance using PLSR analysis
iForest - Biogeosciences and Forestry, Volume 9, Issue 1, Pages 30-37 (2015)
doi: https://doi.org/10.3832/ifor1634-008
Published: Oct 05, 2015 - Copyright © 2015 SISEF
Research Articles
Abstract
A clear understanding of plant transpiration is a crucial step for water cycle and climate modeling, especially for arid ecosystems in which water is one of the major constraints. Traditional field measurements of leaf scale transpiration are always time-consuming and often unfeasible in the context of large spatial and temporal scales. This study focused on a dominant native plant in the arid land of central Asia, Haloxylon ammondendron, with the aim of deriving the leaf-scale transpiration through hyperspectral reflectance using Partial Least Squares Regression (PLSR) analysis. The results revealed that the PLSR model based on the first-order derivative spectra at wavelengths selected through stepwise regression analysis can closely trace leaf transpiration with a high accuracy (R2 = 0.78, RMSE = 1.62 µmol g-1 s-1). The accuracy is also relatively stable even at a spectral resolution of 10 nm, which is very close to the bandwidths of several running satellite-borne hyperspectral sensors such as Hyperion. The results also proved that the first-order derivative spectra within the shortwave infrared (SWIR) domain, especially at 2435, 2440, 2445, and 2470 nm, were critical for PLSR models to predict leaf transpiration. These findings highlight a promising strategy for developing remote sensing methods to potentially characterize transpiration at broad scales.
Keywords
Arid Land, Leaf Transpiration, PLSR, Derivative Spectra, Drought-tolerant, Haloxylon ammondendron
Introduction
Plant transpiration, defined as the process of water movement through a plant and its evaporation from aerial parts, is a basic process regulated over short time periods by stomatal conductance (gs - [32]) and is a key parameter in climate models for quantifying the biosphere-atmosphere interactions ([35]). So far, this process has not been fully understood yet, especially in arid areas, where water resources are one of the major constraints. In this context, a more accurate understanding of plant transpiration is very important for water cycle and climate modeling ([21]), especially for arid environments where water plays a determinant role in the ecosystem functions.
Field measurements of leaf scale transpiration are always based on the measurement of vapor added by transpiration into the air inside a chamber enclosing the leaf or a leaf surface ([24], [39]). Such methods are time-consuming and often unfeasible for tracing the dynamics of transpiration. To tackle this problem, various models considering the energy balance have been developed for simulating the multi-scale transpiration, e.g., the model at the level of individual leaves ([13], [49]), the multilayer model for estimating daily transpiration of the whole plant ([4], [43]), and the Penman-Monteith’s model for canopy transpiration or regional level evaporation ([19], [33], [57]). However, modelling the transpiration of a plant or a stand in a given environment is challenging due to the interaction of complex physical and physiological phenomena ([13]), which led to argue about the performances of these models.
Such challenge calls for the development of new approaches to determine absolute transpiration rates of plant leaves. Recently, the transpiration rate sensor with a multi-channel hygrometer using near infrared (NIR) tunable diode laser absorption spectroscopy (TDLAS) at 1.37 µm was developed ([21]). This new tool can be used in the measure of the absolute, high-resolution water transpiration. However, a straightforward relationship between leaf transpiration and reflected information has still to be verified, while it has already been done for other parameters related to the biological status of plants ([15]).
With the development of hyperspectral remote sensing and imaging spectrometry, many empirical approaches have been proposed for spectroscopic analysis, such as vegetation indexes, single regression, stepwise multiple linear regression, partial least squares regression (PLSR), artificial neural networks, and others ([15]). PLSR, a multivariate extension of the multiple regression model, is the most widely used approach in chemometrics, owing to its ability to analyze data with many noisy, collinear, and even incomplete variables in both input (X) and output (Y) measurements ([52]). It has been claimed that PLSR analysis can provide a more useful and accurate estimation tool for plant spectroscopic analysis compared with other empirical approaches; for example, PLSR can improve the prediction of green biomass and leaf nitrogen concentration compared to hyperspectral indices ([10], [18]), and carotenoid estimation results based on PLSR were significantly better than those based on stepwise multiple linear regression and vegetation indexes ([54]). In addition, the PLSR model is more suitable than the multiple linear regression model for predicting the nitrogen content at the heading stage using the hyperspectral reflectance ([46]).
Reflected data collected by spectrometers hold thousands of generally collated bands within the visible to near-infrared domains. PLSR deals efficiently with such data sets including many highly correlated bands by avoiding the potential overfitting typically associated with multiple linear regression ([20]). Many studies have applied PLSR to estimate various biochemical and nutritional parameters of leaves and canopies through hyperspectral reflectance data, for example biomass estimation ([10], [17], [18]), nitrogen concentration/content prediction ([18], [20], [23], [36], [45], [46]), phosphorous concentration and potassium content determination ([42], [55]), glucose, sucrose, specific gravity, and soluble solids prediction ([41]) and carotenoids estimation ([54]). In comparison, far fewer attempts have targeted the determination of physiological functional attributes from reflectance using PLSR analysis. Among the few attempts carried out, Serbin et al. ([47]) reported that the key determinants of photosynthetic capacity, namely the maximum rates of RuBP carboxylation (Vcmax) and regeneration (Jmax), can be effectively captured by reflectance using PLSR models even across species ([47]). However, to the best of our knowledge, yet there is no such study on transpiration.
On the other hand, former studies exploring plant traits from reflectance suggested that a number of other modes or transformed formats of spectra, such as transmittance and derivative spectra, were helpful for data mining ([41]). Among those, derivative techniques are commonly used and, in particular, the first-order derivative transformation is widely employed in hyperspectral data analysis ([2]). Previous studies on the relationship between canopy transpiration and hyperspectral indexes also proved that the first-order derivative transformation is superior to the original reflectance for tracing the dynamics of canopy transpiration (Jia & Wang, unpublished). Hence, the combination of derivative techniques and the PLSR model for tracing leaf-scale transpiration is also worthy to be explored.
The main objective of the present study is to examine data taken simultaneously on both leaf transpiration and reflected spectra, from which the PLSR model was built up, to estimate leaf transpiration based on hyperspectral reflectance. The final target was the development of a methodology that can trace leaf transpiration promptly and accurately. This study focused on a dominant native plant in deserts, Haloxylon ammondendron, a well-distributed species in the arid land of northwestern China as well as in central Asia. Detailed goals were: (1) to verify the statistical relationships between transpiration and spectra; (2) to select corresponding feature bands that can be used for building up a PLSR model to estimate transpiration; and (3) to build a PLSR model based on selected feature bands that can be used in tracing leaf-scale transpiration.
Materials and methods
Study site
Field measurement was carried out in 2013 at the Integrated Remote Sensing Experimental Site, 20 km north of the Fukang Station of Desert Ecology, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, located at 44° 17′ N, 87° 56′ E, with an elevation of 475 m a.s.l.
This region has a continental arid temperate climate and drought is quite prevalent. The extreme minimum temperature can reach -40 °C in winter, while the maximum temperature can be 40 °C in summer in the growing season. It is so far from the sea that the annual mean precipitation is as low as 80-160 mm, while pan evaporation can reach about 2000 mm in summer due to the high temperature ([29]). As a result, the drought-resistant plant H. ammodendron, a stem-succulent shrub and typical desert plant, is the dominant species in this area and the focus of this research. H. ammodendron possesses distinct structural features of xeromorphism, in which the leaves are reduced in size and degenerated or exist as basal leaves ([30]).
Field measurements
Leaf-scale transpiration
The leaf-scale transpiration rate (Tr) was measured using a portable gas exchange system (HCM-1000, Walz, Germany). Diurnal variation measurements were made once per month at the key growth stages in the growing season from June to August. In each diurnal course measurement, two groups of leaves from the upper and lower layers of the sampling canopy were selected and inserted into the leaf chamber of the HCM-1000 for leaf transpiration measurement once per hour from 8:00 to 18:00 local time. As the system measures the change of H2O pressure, and the transpiration rate (Tr, µmol g-1 s-1) is calculated from the pre-set weight, the leaves placed in the chamber were clipped for fresh weight measurement. The real transpiration rate values were then converted from the values recorded by the HCM-1000.
Leaf reflectance and derivative spectra
Leaf hyperspectral spectra data (350 to 2500 nm, 1 nm step) were recorded with a field spectroradiometer (ASD FR Inc., Boulder, CO, USA) equipped with a leaf clip which can illuminate the leaves with a constant inner light source. To obtain spectra, five measurements were taken each time and the average value was used for further analysis. As the transpiration measurements took about 10 minutes each, the leaf spectra measurement was conducted on the leaves next to those whose transpiration was being measured in the meantime.
Based on the original reflectance data, the first-order derivative spectra of leaf reflectance were calculated using the following formula (eqn. 1):
where dλ is the first-order derivative of reflectance at the wavelength of band λ, Rλ+1 and Rλ are the reflectance at the wavelengths λ and λ+1 respectively, and Δλ is the wavelength increment of the spectrometer.
Modeling approaches
Band selection
Selection of wavelengths is critical for the predictive ability of the PLSR model ([37]). Using the original 1 nm step, the spectrum had massively redundant information. To decrease the computation time required for variable and component selection ([47]), the entire spectrum from 350 to 2500 nm was sub-sampled by retaining every fifth band of the total wavelengths (almost equal to a 5 nm resolution). Relevant spectral wavelengths for PLSR models were then selected based on a stepwise approach. Stepwise regression is a systematic method of adding and removing terms from a multi-linear model based on their statistical significance in the regression. At each step, the p value of an F-statistic is computed to test the model with and without a potential term/variable ([25]). When the term is not included in the model, the null hypothesis is that the term would have a zero coefficient when it is added to the model. If there is sufficient evidence to reject the null hypothesis, the term is included in the model. Conversely, if a term is currently included in the model, the null hypothesis is that the term has a zero coefficient. If there is insufficient evidence to reject the null hypothesis, the term is removed from the model.
Cross-validation
With numerous X-variables, there is a substantial risk of “over-fitting” in any empirical modeling procedure. To this purpose, it is necessary to test the predictive significance of each PLSR uncorrelated principal components (PCs) generated from selected spectral wavelengths, and to stop when components start to be non-significant ([52]).
Cross-validation is a model validation technique for assessing how the results of a statistical analysis will generalize to an independent data set. Cross-validation was used to determine the number of principal components of the PLSR models by minimizing the predicted residual sums of squares (PRESS - [9]). The “leave-p-out cross-validation” (LpO CV) approach, which implies the use of p observations for the validation set and the rest as the training set ([48]), was applied in this study. Seven (15%) out of 45 samples were used for validation, while the remaining 38 samples were included in the training set.
Partial least squares analysis
To calculate the spectral loadings (or regression coefficients) of bands, a standard PLSR approach was applied, using the relevant spectral wavelengths selected by the stepwise regression, and the number of components determined by cross-validation. PLSR is a basically linear way to estimate relevant parameters in a model by reducing the large number of measured collinear spectral variables to a few uncorrelated principal components (PCs), which represent the relevant structural information contained in the measures of reflectance ([18]). More details about the PLSR technique can be found in Wold et al. ([52]).
The coefficient of determination (R2) and the root mean square error (RMSE) between measured and estimated transpiration values were then calculated and used to quantify the performance of the PLSR model. Of course, an effective model for assessing the transpiration should have a high R2 and small RMSE.
Results
Transpiration, reflectance, and their correlations
Diurnal variation in leaf transpiration was evident throughout the daytime, with a double-peak trend. Leaf transpiration rate rises in the morning, reaches the first peak around 11:00 local time, and then drops to low levels until about 17:00, due to the high temperature and the intensive light. Later, the transpiration rate rises again reaching a second peak, and then drops to the trough as the temperature falls, at the end of the daytime. Based on our field measurements taken from June to August, seasonal changes in leaf transpiration rate were not fully evident, but transpiration rates appeared to be higher in June than in July/August.
To generate the PLSR model for the estimation of leaf transpiration, both original reflectance and the first-order derivative spectra were examined. Generally, the leaves have the highest reflectance in August, though this trend was partially confounded by the diurnal variation in reflectance. Although monotonic variations in the reflectance and in the first-order derivative spectra cannot be identified over the whole range (350-2500 nm), consistent changes at some particular wavelengths were detected based on their high correlation coefficients with the transpiration rate.
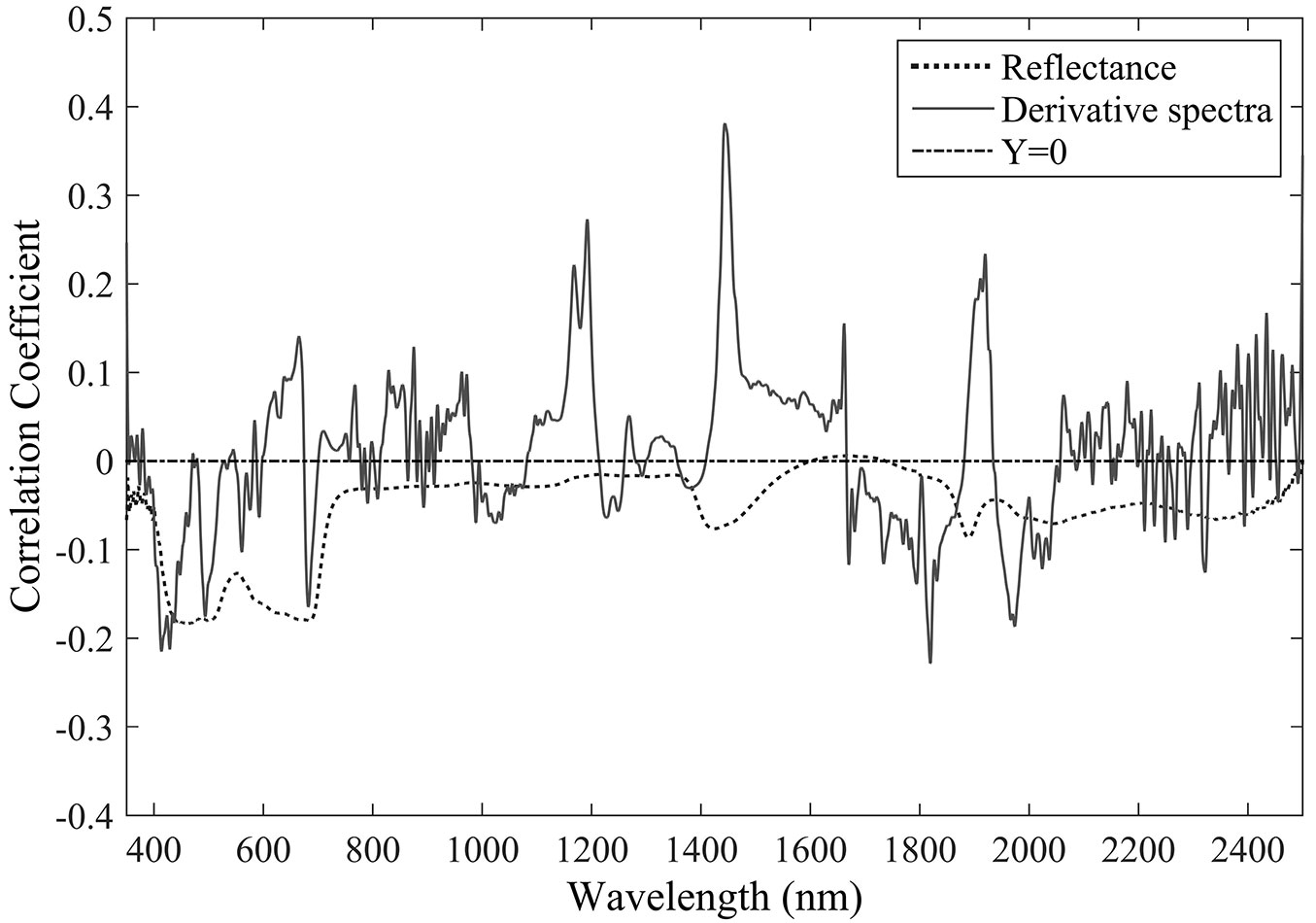
The first-order derivative spectra clearly captured leaf transpiration more effectively, with higher correlation coefficients at many featured wavelengths (Fig. 1). In general, negative (though non-significant) correlations between the original reflectance wavelengths and leaf transpiration were identified throughout the range 350-2500 nm, with the highest correlation coefficient at the wavelength of 463 nm. Contrastingly, using the first-order derivative spectra several significant correlations with leaf transpiration were identified around the wavelengths 1190, 1470, and 1910 nm, across the NIR (near-infrared) and SWIR (short-wave infrared) regions.
PLSR model based on original reflectance
Stepwise regression analysis based on the original reflectance data and transpiration rate was carried out first. Ten different wavelengths (465, 1545, 375, 1860, 440, 1400, 1800, 1795, 370, and 1885 nm) were finally selected for the PLSR analysis based on the results of the stepwise regression analysis.
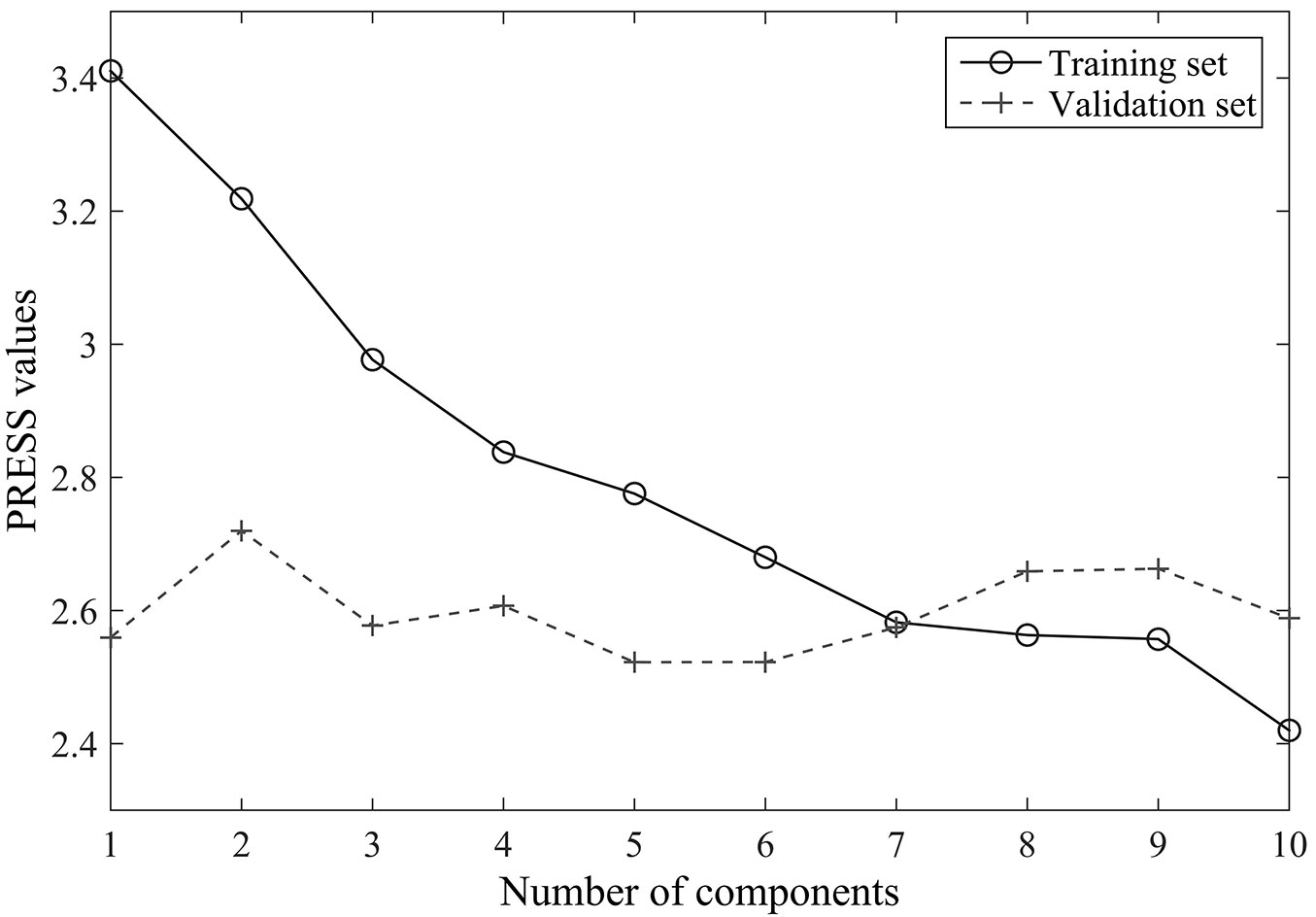
The results of the cross-validation carried out to determine the number of components for PLSR analysis are reported in Fig. 2. The predicted residual sums of squares (PRESS) of the training set decreases monotonically with the number of components, while the values of the validation set initially decrease and then increase later. The predictive ability of the PLSR components started to be non-significant after the 8th PLSR component was added to the model, thus seven components were selected to develop the PLSR model in the following analysis.
Fig. 2 - Cross-validation results for the original reflectance data set: relationships between the numbers of components and the predicted residual sums of squares (PRESS).
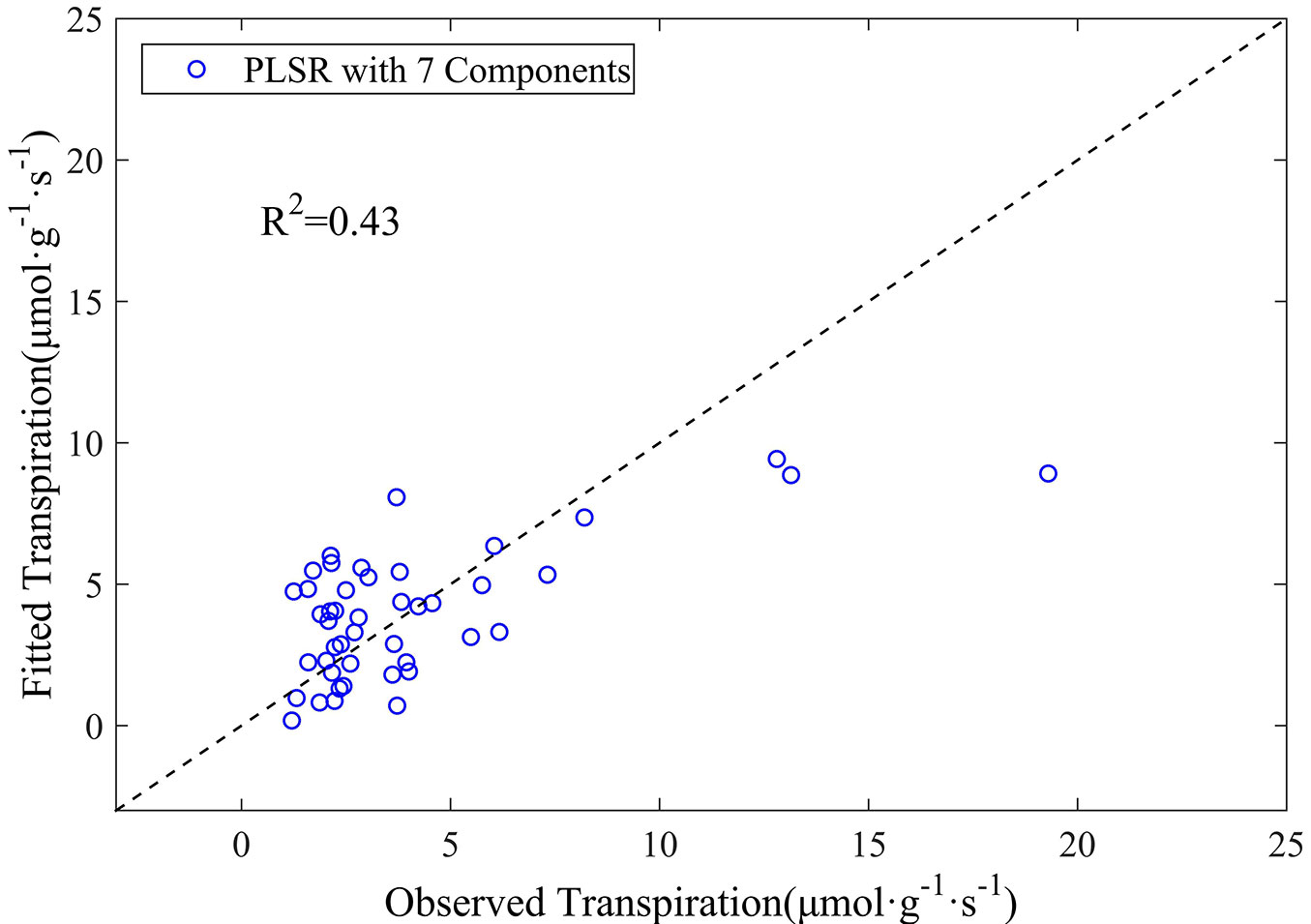
Tab. 1 lists the coefficients of the 10 wavelengths finally included in the PLSR model using the original reflectance data. The relationship between the observed leaf transpiration and its estimate obtained by the PLSR model is shown in Fig. 3. The results reveal that the PLSR model based on original reflectance measures does not perform very well in estimating leaf transpiration, although the above relationship was statistically significant. The coefficient of determination (R2) for transpiration estimation was 0.43, with an RMSE of 2.6 µmol g-1 s-1 (p<0.001). Despite leaf transpiration could be captured by reflectance measures to some extent, the PLSR model based on the original reflectance data yielded only fairly good results.
Tab. 1 - The coefficients of the ten wavelengths from the original reflectance data set that were included in the PLSR model. (Int): intercept.
| Int | Wavelength (nm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 370 | 375 | 440 | 465 | 1400 | 1545 | 1795 | 1800 | 1860 | 1885 | |
| 2.96 | -488.15 | 900.42 | -716.20 | 216.04 | -750.42 | 1672.63 | -395.58 | -623.18 | 465.25 | -297.06 |
Fig. 3 - The observed versus estimated leaf transpiration values from the PLSR model based on the original reflectance data.
PLSR model based on derivative spectra
Stepwise regression analysis, cross-validation, and PLSR analysis were carried out as described above on the first-order derivative spectra of leaf reflectance, obtaining much better performances in model predictions (Fig. 4).
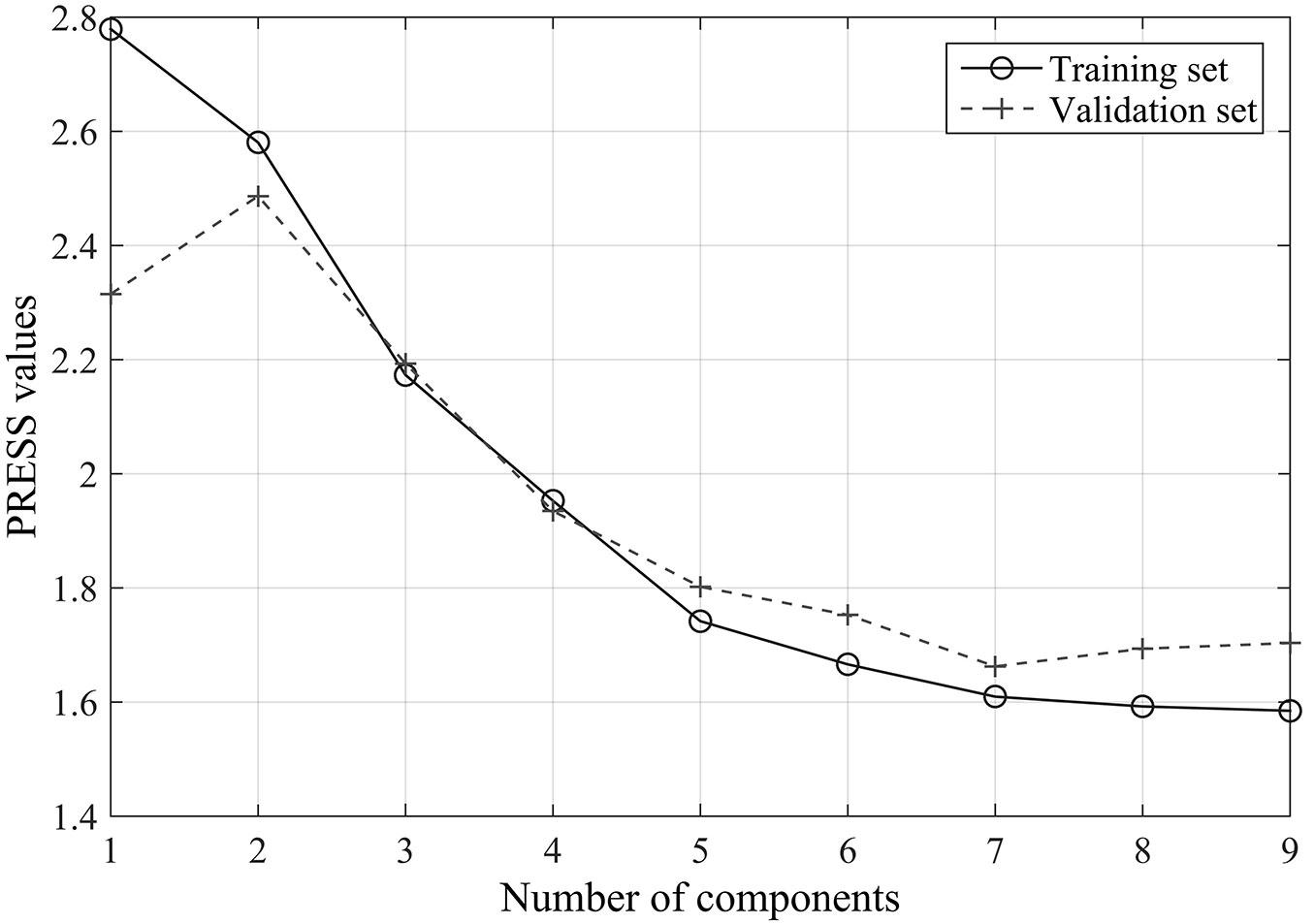
Fig. 4 - Cross-validation results for first-order derivative spectra mode: the relationships between the numbers of components and the predicted residual sums of squares (PRESS).
Unlike the original spectra data, wavelengths of the first-order derivative spectra selected by stepwise regression analysis (9) were mainly distributed within the SWIR domain, and were namely 2435, 2355, 1190, 2180, 2445, 2470, 2275, 2440, and 675 nm. Cross-validation results showed that the optimal number of components for the PLSR analysis was seven. The PRESS values obtained for the training set and the validation set were 1.61 and 1.66, respectively.
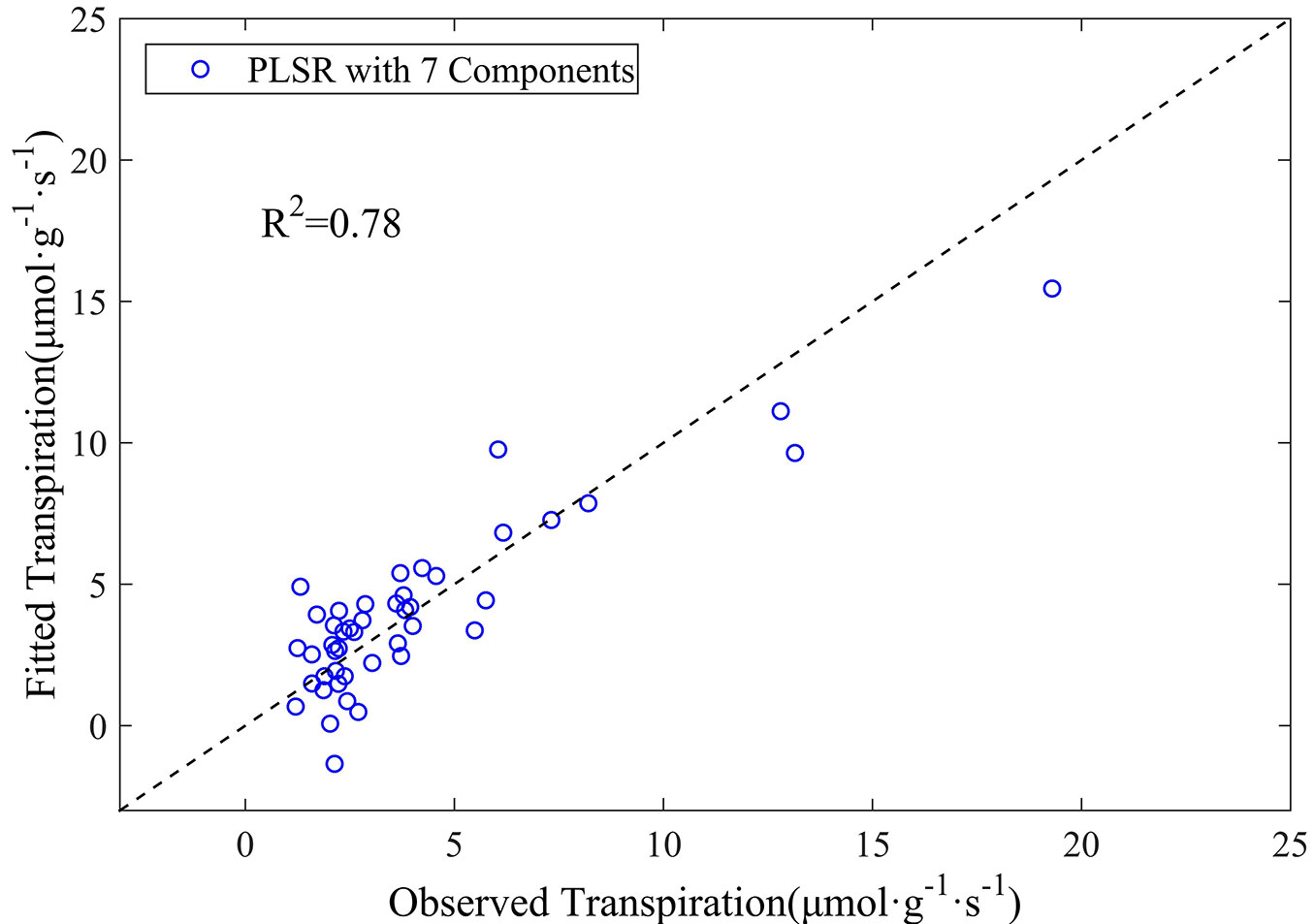
The PLSR model was finally run based on the above nine wavelengths of the first-order derivative spectra of leaf reflectance. Their coefficients obtained from the model are listed in Tab. 2. The coefficient of determination (R2) for the transpiration estimate reached 0.78, and the RMSE between the observed and predicted values was 1.62 µmol g-1 s-1 (Fig. 5), clearly indicating the superiority of the use of first-order derivative spectra for the prediction of leaf transpiration rate. We concluded that the PLSR model could predict leaf transpiration with higher accuracy when first-order derivative spectra were used, as compared with the original reflectance data.
Tab. 2 - The coefficients of the nine selected wavelengths of the first-order derivative spectra included in the PLSR model.
| Intercept | Wavelength (nm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 675 | 1190 | 2180 | 2275 | 2355 | 2435 | 2440 | 2445 | 2470 | |
| 3.06 | 23001.37 | 87810.41 | 23790.46 | -50988.63 | -51988.05 | 20650.22 | 18325.10 | 16480.77 | 7987.47 |
Fig. 5 - The observed versus estimated leaf transpiration values from the PLSR model based on the first-order derivative spectra.
Discussion
Important wavebands identified for leaf transpiration estimation
In the scientific literature, reflectance has rarely been related to plant ecophysiological variables as compared with plant biochemical parameters, whose relationships with reflected wavelengths have been widely analyzed ([8], [40]). Indeed, only a few studies have attempted to relate plant physiological parameters with hyperspectral reflected properties so far. Recent reports suggested that full-spectrum optical properties can potentially be used for assessing photosynthetic parameters such as Jmax and Vcmax ([16], [47]). The only study in the literature focusing on the assessment of the whole tree transpiration using canopy spectral reflectance indexes also showed that the water index (WI - R900/R970) is well correlated with the whole plant transpiration (R2 = 0.668 - [31]).
In this study, the observed high collinearity throughout the full spectrum and poor knowledge of the feature wavelengths for transpiration led to the difficult task of selecting the relevant information to be included in the PLSR model. Stepwise regression analysis was performed to select the wavelengths to be considered in themodel, instead of using the entire spectrum (350-2500 nm). Tab. 3 shows the number of wavebands of the first-order derivative spectra as well as the original reflectance selected within the visible (VIS), NIR, shortwave infrared 1 (SWIR1), and shortwave infrared 2 (SWIR2) spectral regions.
Tab. 3 - The number of wavebands selected for transpiration estimation PLSR modeling within the visible (VIS), near-infrared (NIR), short-wave 1 (SWIR1), and short-wave 2 (SWIR2) spectral regions.
| Origin | PLSR components |
Number of wavebands | ||||
|---|---|---|---|---|---|---|
| 350-2500 nm | VIS (350-700nm) |
NIR (700-1300nm) |
SWIR1 (1300-1900nm) |
SWIR2 (1900-2500nm) |
||
| Original reflectance | 7 | 10 | 4 | 0 | 6 | 0 |
| Derivative spectra | 7 | 9 | 1 | 1 | 0 | 7 |
To assess the reliability of the band-selection approach described above, we checked the performance of PLSR analysis using the entire spectrum (350-2500 nm) of first-order derivative data rather than the selected bands only. The generated PLSR model showed poor predictive performances in the estimation of leaf transpiration (R2 = 0.21, RMSE = 3.07 µmol g-1 s-1). The low effectiveness of this model is reasonably due to large noise derived from the inclusion in the model of a large amount of irrelevant information from the full spectrum.
High linear correlations between leaf transpiration and the original reflectance were frequently noted within the wavelengths of 400-800 nm and around 1400 or 1900 nm (Fig. 1). The wavebands selected by stepwise regression analysis for PLSR modeling were also distributed in the VIS (350-700 nm) and SWIR1 (1300-1900 nm) regions, with four and six wavebands, respectively (Tab. 3). The lower performance of the PLSR model based on the original reflectance is likely due to the fact that the selected wavelengths are mainly related with other leaf parameters rather than transpiration or gs. Indeed, wavebands such as 430-445 nm are known to be related to carotenoids, bands 531-570 nm to xanthophylls, and 550-680 nm and the “red-edge” position to chlorophyll ([40]), which are not directly related to the water cycle.
More accurate predictions of leaf transpiration were obtained when first-order derivative spectra of the leaf reflectance were included in the PLSR model. Tab. 3 shows that most of the wavebands selected (seven out nine) were within the domain of SWIR2 (1900-2500 nm), which is negatively related to leaf water content. However, the only waveband within the NIR domain (700-1300 nm) was almost independent of the variation in water content ([26], [51], [44], [7], [38]).
The importance of the different wavebands selected can be identified from the loading weights on principal components extracted by the PLSR model. High numerical values indicate high importance of the reflected wavelength in the PLSR analysis ([18] - Tab. 4). Wavebands at 2435, 2445, and 2470 nm had much higher loading weights on the first PC, with values of 3.68 × 10-4, 3.60 × 10-4, and 3.28 × 10-4, respectively. In addition, the wavelength of 2440 nm showed high loading weights on the fourth and fifth PCs. Therefore, we concluded that the first-order derivative spectra at 2435, 2440, 2445, and 2470 nm were critical to predict leaf transpiration using PLSR models.
Tab. 4 - Loading weights (LW, × 10-4) of each waveband for the PLSR model based on the first-order derivative spectra of reflectance for the estimation of leaf transpiration. (a): high absolute numerical values indicate a high loading weight of the waveband to the given principal component (PC).
| Axis | Wavelength (nm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 675 | 1190 | 2180 | 2275 | 2355 | 2435 | 2440 | 2445 | 2470 | |
| PC1 | -0.28 | 0.51 | -0.41 | 0.59 | 0.38 | 3.68 a | -0.20 | 3.60 a | 3.28 a |
| PC2 | -0.25 | -0.08 | 0.41 | -0.93 | -0.71 | 2.42 a | -0.72 | 0.18 | -6.72 a |
| PC3 | -0.20 | -0.83 | 1.06 | -1.45 | -1.55 | -0.78 | 0.29 | -1.21 | 2.91 a |
| PC4 | 0.64 | 0.79 | -0.66 | 1.24 | -0.05 | -0.49 | 2.99 a | 0.99 | -0.71 |
| PC5 | 0.73 | 0.65 | -0.44 | -0.25 | -0.68 | -0.53 | -2.56 a | 0.29 | 0.14 |
| PC6 | 0.10 | 0.84 | -0.07 | -0.02 | 1.12 | 1.66 | 0.84 | -2.17 a | 0.32 |
| PC7 | -0.78 | 0.09 | 0.49 | -1.06 | 0.51 | -1.03 | 0.04 | 1.34 | -0.19 |
Superiority of derivative spectra over original spectra
PLSR analysis based on first-order derivative spectra yielded much more accurate estimations of leaf transpiration. Similarly, more accurate indexes of canopy transpiration could be identified based on derivative spectra in a former study (Jin & Wang, unpublished). This confirms that the derived spectra can improve the efficiency of transpiration predictions using PLSR models.
As already mentioned, the high accuracy of transpiration estimation based on derivative spectra may be primarily due to a better signal-to-noise ratio, according to Demetriades-Shah et al. ([14]) and Yao et al. ([53]). It has been reported that chlorophyll-induced changes can be captured in the primary derivatives of the reflectance spectra ([27]). Furthermore, increased reflectance of SWIR wavelengths is the most consistent response of leaf reflectance to plant stress, including water stress ([6], [38]). As the SWIR band is known to provide information on the water content of plants, it has been widely used to assess the water stress of plants ([51], [3], [44], [5], [11]).
To further illustrate such relationship, we carried out a correlation analysis of leaf transpiration with each wavelength selected for the PLSR models based on both original reflectance and derivative spectra (Tab. 5 and Tab. 6, respectively). Selected wavebands from original reflectance data showed much lower correlation coefficients with leaf transpiration than the bands selected from derivative spectra. The highest negative correlation coefficients between transpiration and reflectance only reached -0.18 (wavelengths 440 and 465 nm). On the contrary, the correlation coefficients for derivative spectra bands exceeded 0.4 at two wavelengths of 2435 nm (0.49) and 2445 nm (0.40). Furthermore, the pairwise correlations between the selected bands were much higher for the original reflectance data (all above 0.48, most > 0.8 - Tab. 5). Contrarily, the pairwise correlation coefficients between the selected wavelengths of the PLSR model based on the derivative spectra had much lower correlations (generally below 0.4 - Tab. 6). This confirms that the use of derivative spectra may potentially provide more information when a limited number of wavelengths are included in the PLSR analysis.
Tab. 5 - Correlation matrix between leaf transpiration (Tr) and the original reflectance of wavelengths involved in the PLSR model.
| - | Tr | Wavelength (nm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 370 | 375 | 440 | 465 | 1400 | 1545 | 1795 | 1800 | 1860 | 1885 | ||
| Tr | 1.00 | - | - | - | - | - | - | - | - | - | - |
| 370 | -0.05 | 1.00 | - | - | - | - | - | - | - | - | - |
| 375 | -0.04 | 0.99 | 1.00 | - | - | - | - | - | - | - | - |
| 440 | -0.18 | 0.77 | 0.80 | 1.00 | - | - | - | - | - | - | - |
| 465 | -0.18 | 0.71 | 0.75 | 0.99 | 1.00 | - | - | - | - | - | - |
| 1400 | -0.06 | 0.53 | 0.57 | 0.90 | 0.92 | 1.00 | - | - | - | - | - |
| 1545 | -0.02 | 0.51 | 0.55 | 0.88 | 0.90 | 0.99 | 1.00 | - | - | - | - |
| 1795 | -0.01 | 0.48 | 0.53 | 0.86 | 0.88 | 0.99 | 1.00 | 1.00 | - | - | - |
| 1800 | -0.01 | 0.48 | 0.53 | 0.86 | 0.88 | 0.99 | 1.00 | 1.00 | 1.00 | - | - |
| 1860 | -0.04 | 0.50 | 0.54 | 0.87 | 0.90 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | - |
| 1885 | -0.08 | 0.58 | 0.63 | 0.91 | 0.92 | 0.98 | 0.97 | 0.96 | 0.96 | 0.97 | 1.00 |
Tab. 6 - Correlation matrix between leaf transpiration (Tr) and the first derivative spectra of reflectance of wavelengths involved in the PLSR model.
| - | Tr | Wavelength (nm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 675 | 1190 | 2180 | 2275 | 2355 | 2435 | 2440 | 2445 | 2470 | ||
| Tr | 1.00 | - | - | - | - | - | - | - | - | - |
| 675 | -0.03 | 1.00 | - | - | - | - | - | - | - | - |
| 1190 | 0.27 | 0.08 | 1.00 | - | - | - | - | - | - | - |
| 2180 | 0.07 | -0.19 | -0.70 | 1.00 | - | - | - | - | - | - |
| 2275 | -0.12 | 0.14 | 0.59 | -0.71 | 1.00 | - | - | - | - | - |
| 2355 | -0.25 | 0.16 | 0.39 | -0.33 | 0.32 | 1.00 | - | - | - | - |
| 2435 | 0.49 | -0.12 | 0.34 | -0.16 | 0.13 | 0.22 | 1.00 | - | - | - |
| 2440 | 0.01 | 0.05 | 0.15 | -0.12 | 0.39 | 0.27 | -0.07 | 1.00 | - | - |
| 2445 | 0.40 | -0.08 | 0.24 | -0.32 | 0.26 | 0.12 | 0.39 | -0.04 | 1.00 | - |
| 2470 | 0.13 | 0.00 | -0.03 | -0.05 | 0.15 | 0.09 | -0.14 | 0.08 | 0.14 | 1.00 |
Potential large-scale applications with satellite-borne hyperspectral data
Two important criteria should be taken into account for extending in situ results (such as those obtained in this study) to monitoring transpiration at large scale in the field using satellite-born hyperspectral data. The first is the width of the bands considered, that should be as close as possible to the resolutions of the available hyperspectral sensors; the second is that noise bands should be excluded from the analysis through a suitable selection process. Bandwidths taken at 10 nm intervals are close to those of some popular hyperspectral sensors currently available, such as Hyperion and AVIRIS ([22]), and the spectral regions 350-399, 1355-1420, 1810-1940, and 2470-2500 nm are known as noise regions ([12], [50], [28], [34], [56], [1]) and should therefore be removed from any further analysis.
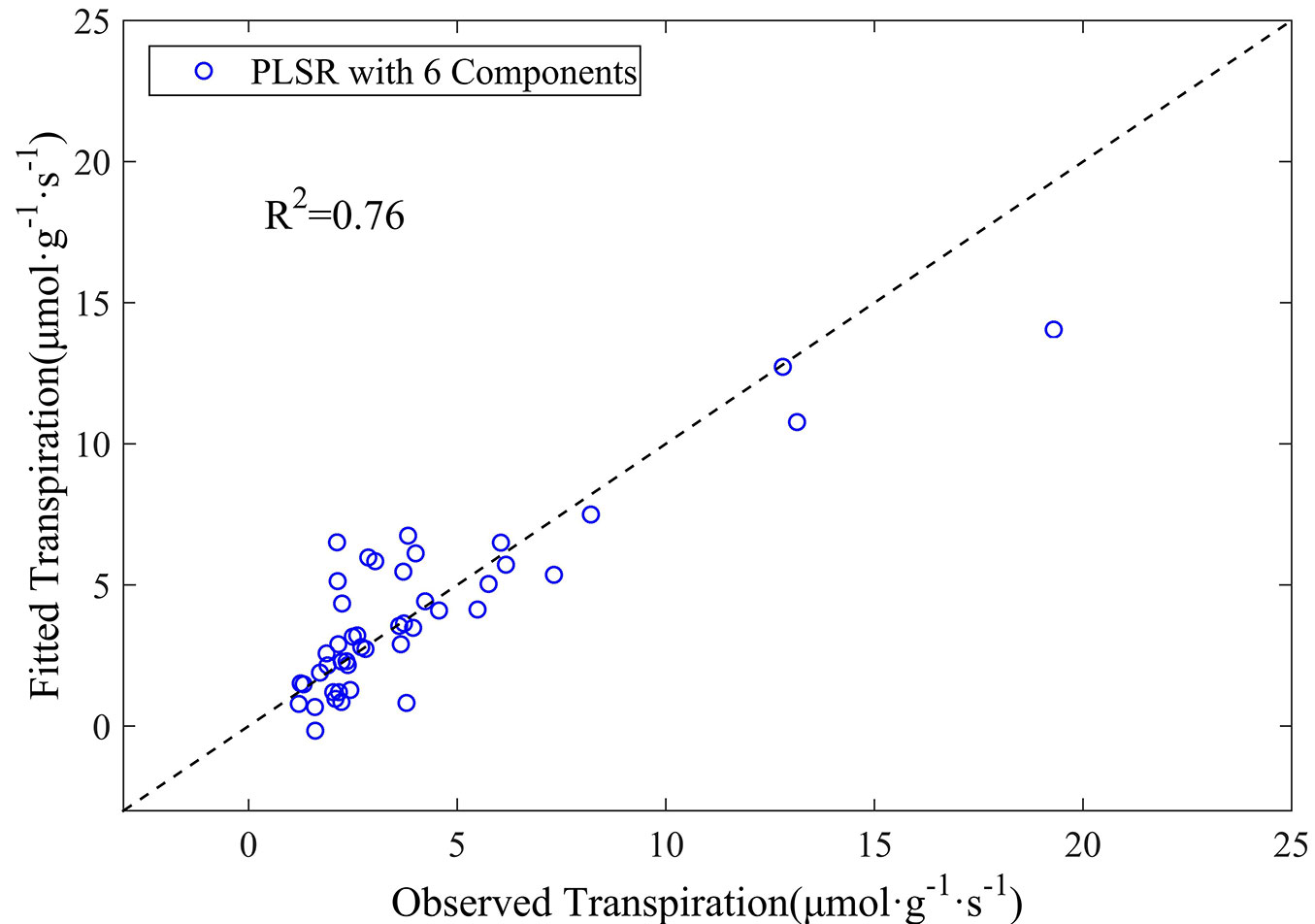
In this context, an additional PLSR analysis based on the first-order derivative spectra was carried out excluding all the above-mentioned noise bands by retaining every tenth wavelength in the spectrum 350-2500 nm. Such procedure finally resulted in 191 out of 2150 wavelengths being involved in the analysis. Eight wavelengths of 1450, 1960, 2000, 1070, 1980, 970, 920, and 2060 nm were then selected by stepwise regression analysis and included in the PLSR model. Six components were determined through cross-validation analysis (Fig. 6). The coefficient of determination (R2) was 0.76, with an RMSE of 1.69 μmol g-1 s-1 (Fig. 7), which is comparable to the results obtained using 5 nm intervals presented above. These findings highlight a promising strategy for developing remote sensing methods to characterize leaf transpiration at a broad scales.
Fig. 6 - Cross-validation results for the first-order derivative spectra with removal of known noise regions for canopy data: the relationships between the numbers of components and the predicted residual sums of squares (PRESS).
Fig. 7 - The observed versus estimated leaf transpiration values from the PLSR model based on the first-order derivative spectra with removal of known noise regions for canopy data.
Conclusions
To verify straightforward statistical relationships between leaf transpiration and reflectance and its derivative spectra, we applied PLSR analysis based on transpiration measures and canopy reflectance spectra (as well as its first derivatives) taken simultaneously. This was carried out on a dominant native plant Haloxylon ammondendron, which is well distributed in the deserts of central Asia. The results demonstrated that the PLSR model based on the first-order derivative spectra of leaf reflectance can trace leaf transpiration with high accuracy, while lower performances were obtained when the original reflectance data were considered. Furthermore, the accuracy was also relatively stable for a spectral resolution of 10 nm, which is close to the specification of several hyperspectral sensors such as Hyperion and AVIRIS. This supports the feasibility of directly applying satellite-borne data to trace the dynamics of leaf-scale transpiration. Our results also suggested that first-order derivative spectra at 2435, 2440, 2445, and 2470 nm were critical for the prediction of leaf transpiration by PLSR models. The results obtained in this study should help to lay the basis for developing remote sensing methods aimed at characterizing leaf transpiration at broad scales.
Acknowledgements
This study was partly supported by the JSPS Grants-in-Aid for Scientific Research (Grant No. 25302001) to Q. Wang. The members of Quantitative Remote Sensing Group of XIEG, CAS are highly acknowledged for their support in field measurements.
References
CrossRef | Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Authors’ Info
Paper Info
Citation
Wang Q, Jin J (2015). Leaf transpiration of drought tolerant plant can be captured by hyperspectral reflectance using PLSR analysis. iForest 9: 30-37. - doi: 10.3832/ifor1634-008
Academic Editor
Davide Travaglini
Paper history
Received: Mar 05, 2015
Accepted: Aug 06, 2015
First online: Oct 05, 2015
Publication Date: Feb 21, 2016
Publication Time: 2.00 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2015
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 54533
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 40612
Abstract Page Views: 3564
PDF Downloads: 9102
Citation/Reference Downloads: 28
XML Downloads: 1227
Web Metrics
Days since publication: 3742
Overall contacts: 54533
Avg. contacts per week: 102.01
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2016): 11
Average cites per year: 1.10
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Chemometric technique performances in predicting forest soil chemical and biological properties from UV-Vis-NIR reflectance spectra with small, high dimensional datasets
vol. 9, pp. 101-108 (online: 15 July 2015)
Research Articles
Oak sprouts grow better than seedlings under drought stress
vol. 9, pp. 529-535 (online: 17 March 2016)
Research Articles
Links between phenology and ecophysiology in a European beech forest
vol. 8, pp. 438-447 (online: 15 December 2014)
Research Articles
Diurnal dynamics of water transport, storage and hydraulic conductivity in pine trees under seasonal drought
vol. 9, pp. 710-719 (online: 21 August 2016)
Research Articles
Sap flow, leaf-level gas exchange and spectral responses to drought in Pinus sylvestris, Pinus pinea and Pinus halepensis
vol. 10, pp. 204-214 (online: 01 November 2016)
Research Articles
Developing stand transpiration model relating canopy conductance to stand sapwood area in a Korean pine plantation
vol. 14, pp. 186-194 (online: 14 April 2021)
Research Articles
Effects of mild drought on the morphology of sun and shade needles in 20-year-old Norway spruce trees
vol. 12, pp. 27-34 (online: 10 January 2019)
Research Articles
Sodium and potassium allocation under drought stress in Atlas mastic tree (Pistacia atlantica subsp. mutica)
vol. 6, pp. 90-94 (online: 07 February 2013)
Research Articles
Drought tolerance in cork oak is associated with low leaf stomatal and hydraulic conductances
vol. 11, pp. 728-733 (online: 06 November 2018)
Research Articles
Magnolia grandiflora L. shows better responses to drought than Magnolia × soulangeana in urban environment
vol. 13, pp. 575-583 (online: 07 December 2020)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword