Chemometric technique performances in predicting forest soil chemical and biological properties from UV-Vis-NIR reflectance spectra with small, high dimensional datasets
iForest - Biogeosciences and Forestry, Volume 9, Issue 1, Pages 101-108 (2015)
doi: https://doi.org/10.3832/ifor1495-008
Published: Jul 15, 2015 - Copyright © 2015 SISEF
Research Articles
Abstract
Chemometric analysis applied to diffuse reflectance spectroscopy is increasingly proposed as an effective and accurate methodology to predict soil physical, chemical and biological properties. Its effectiveness, however, largely varies in relation to the calibration techniques and the specific soil properties. In addition, the calibration of UV-Vis-NIR spectra usually requires large datasets, and the identification of techniques suitable to deal with small sample sizes and high dimensionality problems is a primary challenge. In order to investigate the predictability of many soil chemical and biological properties from a small dataset and to identify the most suitable techniques to deal with this type of problems, we analysed 20 top soil samples of three different forests (Fagus sylvatica, Quercus cerris and Quercus ilex) in southern Apennines (Italy). Diffuse reflectance spectra were recorded in the UV-Vis-NIR range (200-2500 nm) and 22 chemical and biological properties were analysed. Three different calibration techniques were tested, namely the Partial Least Square Regression (PLSR), the combinations wavelet transformation/Elastic net and wavelet transformation/Supervised Principal Component (SPC) regression/ Least Absolute Shrinkage and Selection Operator (LASSO), a kind of preconditioned LASSO. Calibration techniques were applied to both raw spectra and spectra subjected to wavelet shrinkage filtering, in order to evaluate the influence on predictions of spectra denoising. Overall, SPC/LASSO outperformed the other techniques with both raw and denoised spectra. Elastic net produced heterogeneous results, but outperformed SPC/LASSO for total organic carbon, whereas PLSR produced the worst results. Spectra denoising improved the prediction accuracy of many parameters, but worsen the predictions in some cases. Our approach highlighted that: (i) SPC/LASSO (and Elastic net in the case of total organic carbon) is especially suitable to calibrate spectra in the case of small, high dimensional datasets; and (ii) spectra denoising could be an effective technique to improve calibration results.
Keywords
Elastic Net, PLSR, SPC/LASSO, Wavelets, Diffuse Reflectance Spectroscopy, Sample Size
Introduction
Monitoring of soil property dynamics needs quick and efficient systems avoiding long procedures involved in traditional methods. Diffuse Reflectance Spectroscopy (DRS) could address these needs by predicting soil properties using their spectroscopic signatures in the ultraviolet-visible-infrared (UV-Vis-IR) domain. Various approaches have been tested to relate UV-Vis-IR spectra to many soil parameters, such as soil organic matter (SOM), total organic carbon (TOC), total carbon, total nitrogen, texture, as well as biological properties ([8], [22], [10], [39], [46], [43], [21], [14]).
Two problems faced in analysing spectral data are their functional nature and their dimensionality. Indeed, spectra can be represented as functions of the wavelength xi(λ), with possibly thousands of values, especially for UV-Vis-IR spectra. A way to deal with functional variables in the case of high dimensional data, is to employ some regression penalties that take into account the ordering of the data, as in fused LASSO or trend filtering. These techniques, however, led to quadratic programming problems, that are computationally expensive and difficult to solve when dealing with a huge number of variables ([37]). Other methods, such as Partial Least Squares Regression (PLSR) and Principal Component Regression (PCR) overcome these problems by deriving a small number of linear combinations of the predictors and using these instead of the original variables to predict the outcome.
These techniques gained broad popularity to analyse spectral data and have widely been used to predict many soil properties from reflectance spectra ([40], [45], [14]). As usual in the case of high dimensional data, such methods generally need a great number of observations, splitted into a training set to calibrate the models, a validation set to estimate the prediction error for model selection, and a test set to assess the generalization error of the chosen model ([20]).
A high number of observations is generally difficult to obtain in ecological studies, and techniques like cross-validation (CV) can be used to overcome the problem of small sample sizes in assessing prediction error. CV randomly splits the dataset into a n number of folds and uses n - 1 folds as the training set and the last one as a validation set, repeating the operations until every fold is considered once as the validation set ([20]).
An alternative way to analyse spectra is to represent them by coefficients in a basis function in λ, such as wavelets, splines or Fourier bases ([20]). Coefficients can be then used as predictors in various forms of regression, such as Generalized Linear Models (GLM), Least Absolute Shrinkage and Selection Operator (LASSO) or even PCR and PLSR. This approach solves the problem by two steps: (i) addressing the functional nature of the spectra; and (ii) finding a function to relate the coefficients to the outcome. Regarding the first step, wavelets seem to be especially suitable to be used in spectra decomposition due to their multiresolution property which allow to model at the same time both the local and the global features of the spectra. In addition, wavelet decomposition usually produces coefficients with reduced correlations ([28]) in respect to the original wavelengths, which aid in reducing the multicollinearity problems in high-dimensional regressions. Lark & Webster ([23]) provided a detailed description of the use of wavelets in soil science, and Viscarra Rossel & Lark ([41]) employed wavelet decomposition of visible-near and mid infrared spectra, followed by various regression techniques, to predict TOC and clay content. The second step has the following goals: (i) to predict the dependent variable; and (ii) to find a sufficient and possibly small subset of predictors. The latter goal has particular importance for high dimensional regressions, where few variables which correctly predict the true response have to be identified among thousands of possible predictors. In this context, techniques such as the Bayesian variable selection approaches ([11]) or the Minimum Average Variance Estimation (MAVE - [1]), as well as methods that produce sparse solutions like the LASSO ([44]), could be used to reduce the dimensionality of the data. Most regression techniques try to address both goals at the same time, although this is not prerequisite: Paul et al. ([31]) recently proposed a new approach - called “pre-conditioning” - that uses two different methods to address the relative goals. Basically, a computational technique - usually the Supervised Principal Component (SPC) regression - is employed to predict the true response and then the predicted values are used in a L1-regularized regression, like the LASSO, to produce a sparse solution ([31]). In this way, the advantages of the SPC with its low prediction errors and the sparsity of the LASSO solutions are combined ([20], [31]).
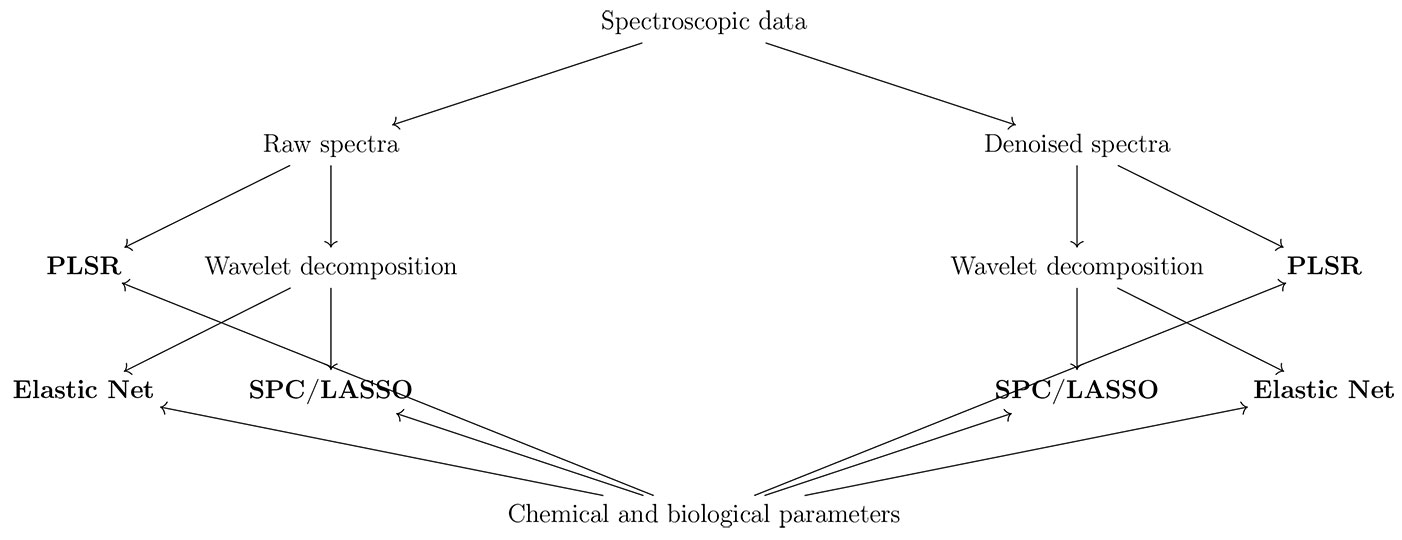
In this paper, an attempt to predict various chemical and biological properties from diffuse reflectance spectra with a small dataset was made using three techniques in order to test their relative powerfulness. The first two are based on wavelet decomposition of the spectra, followed by either an Elastic net (a generalization of the LASSO - [47]) or the combination SPC/LASSO, while the last technique (PLSR) directly used the spectra. The same techniques were tested starting from both raw spectra and spectra denoised with wavelet shrinkage, in order to test the effects of noise reduction on the solutions (Fig. 1). The data came from three soils (Andosols, Luvisols and Leptosols) of three different stands, representative of the Apennines forest types (Fagus sylvatica L., Quercus cerris L. and Quercus ilex L.) in southern Italy.
Materials and methods
Soil profiles and sampling
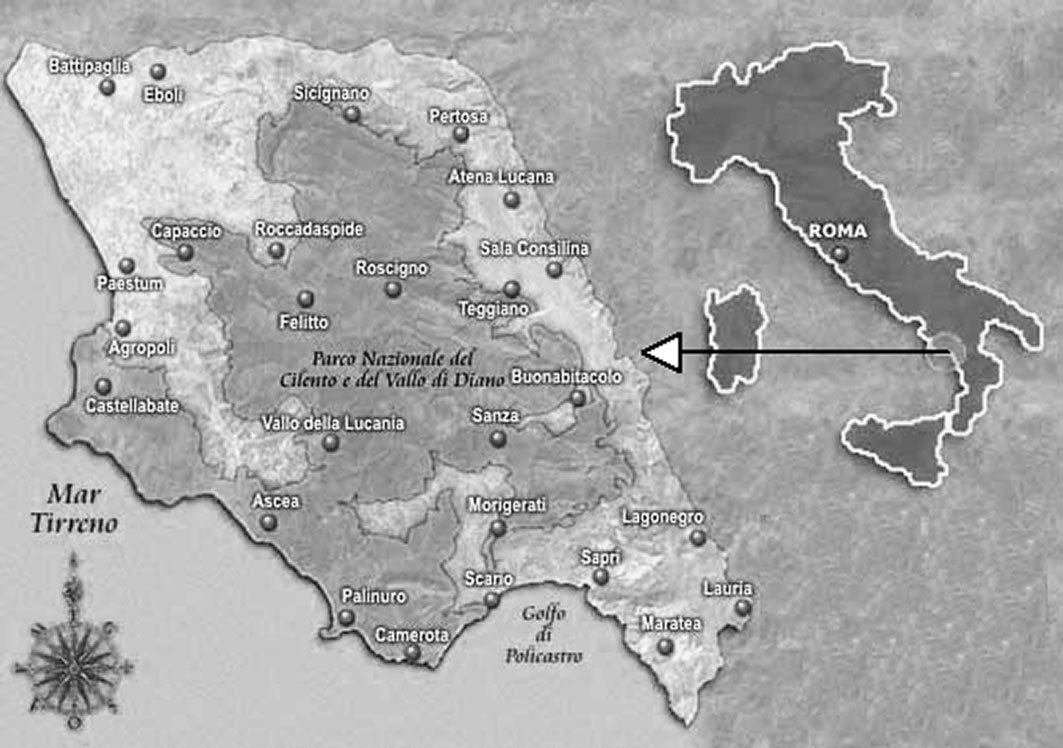
Three soil profiles were studied in three different forest ecosystems in southern Apennines (Fig. 2), in the Cilento and Vallo di Diano National Park (Salerno, Italy). The profiles were located along a climosequence starting from the beech (Fagus sylvatica L.) belt, at an altitude of 1200-2000 m a.s.l., through the Turkey oak (Quercus cerris L.) belt, at an altitude of 800-1200 m a.s.l., to the holm oak (Quercus ilex L.) belt, at an altitude of 500-800 m a.s.l. (Tab. 1). Soils developed on different parent rocks: soils under F. sylvatica and Q. ilex on hard carbonate, whereas soil under Q. cerris on argillite ([25]). All horizons of the three profiles, described using the FAO guidelines ([42]), were characterized for their skeleton (soil particles greater than 2 mm in diameter) content and texture (Tab. 2). Soil samples for chemical, biological and spectral analyses were collected in the layer 0-10 cm at the same sites (8 samples under F. sylvatica stands 8 samples under Q. cerris stands and 4 samples under Q. ilex stand) and were separately analyzed.
Fig. 2 - Localization of the Cilento and Vallo di Diano National Park, in southern Apennines (Italy).
Tab. 1 - Site and soil characteristics of the studied areas in southern Apennines (modified from [25]).
| Canopy | Latitude Longitude |
Elevation (m a.s.l.) |
Exposure (°) |
Soil profile depth(cm) |
WRB-FAO Soil Classification (2014) |
|---|---|---|---|---|---|
| F. sylvatica | 40°28’ N 15°24’ E |
1280 | 340 | 130 | Andic Umbrisols (Endoeutric, Eplarenic) |
| Q. cerris | 40°13’ N 15°29’ E |
915 | 240 | 85 | Gleyc Luvisols (Epidystric, Skeletic) |
| Q. ilex | 40°27’ N 15°19’ E |
575 | 150 | 30 | Mollic Leptosols (Eutric, Skeletic) |
Tab. 2 - Skeleton and texture (g/kg d.w.) of the horizons of the studied soil profiles.
| Component | F. sylvatica | Q. cerris | Q. ilex | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Profile horizons | A1 | A2 | Bw | Bb | A1 | A2 | Bt | Bg | Cg | O | A | AC |
| skeleton | 10 | 30 | 20 | 200 | 380 | 300 | 190 | 450 | 510 | 310 | 560 | 600 |
| coarse sand | 140 | 130 | 170 | 200 | 230 | 240 | 220 | 50 | 80 | 200 | 160 | 160 |
| fine sand | 610 | 620 | 300 | 310 | 410 | 400 | 420 | 390 | 360 | 400 | 400 | 390 |
| silt | 160 | 150 | 170 | 180 | 180 | 160 | 110 | 240 | 240 | 300 | 300 | 310 |
| clay | 90 | 100 | 360 | 310 | 180 | 200 | 250 | 320 | 320 | 100 | 140 | 140 |
Soil physico-chemical and biological analyses
All the analyses were performed in the soil granulometric fraction < 2 mm. For physico-chemical analyses samples were dried as described in Violante ([38]), while for biological analyses samples were kept at 4 °C.
Texture was obtained using the hydrometer method, after pre-treatment with H2O2, to oxidize organic matter, and dispersion by sodium hexa-metaphosphate. Soil pH was measured using a potentiometer (HI 4212®, Hanna, Woonsocket, RI, USA) in 1:2.5 H2O soil:solution suspensions. Total carbon (C) and nitrogen (N), as well as TOC after carbonates dissolution with HCl 10%, were measured using a CHNS-O Analyzer (Flash EA 1112®, Thermo Scientific, Waltham, MA, USA). Total C concentrations were used exclusively to calculate the C/N ratios and were not considered in the chemometric analyses. Total calcium (Ca), potassium (K), magnesium (Mg), manganese (Mn), sodium (Na), iron (Fe) and aluminium (Al) concentrations were measured on acid mineralized samples, as described by Baldantoni et al. ([6]). Fe and Al were extracted by ammonium oxalate (Ox-Fe, Ox-Al) and also by sodium pyrophosphate (Py-Fe, Py-Al), and then quantified with ICP-OES (Optima 7000DV®, PerkinElmer Inc, Waltham, MA, USA).
Soil respiration was measured as CO2 evolution after 48 h of incubation at 25 °C in the dark, with moisture content adjusted at 55% of the water holding capacity ([2]). The CO2 concentration in the headspace of incubation vials was measured by a gas chromatograph equipped with a thermo conductivity detector (6850 Network GC System®, Agilent Technologies, Santa Clara, CA, USA). The glucose-responsive fraction of microbial biomass was assessed by the substrate induced respiration (SIR), according to Anderson & Domsch ([3]). Fluorescein diacetate hydrolysis rate (hydrolase activity) was determined following the method of Schnürer & Rosswall ([35]) using 3.6-diacetyl fluorescein as substrate and measuring the absorbance of the released fluorescein at 490 nm. β-glucosidase (EC 3.2.1.21) activity was assayed by the hydrolysis rate of p-nitrophenyl-β-D-glucopyranoside as substrate, detecting the absorbance of the released p-nitrophenol at 398 nm ([34]) with spectrophotometry (Lambda EZ201®, PerkinElmer Inc). Phospholipid fatty acids (PLFAs) were extracted according to Frostegård et al. ([18]) and analyzed using a gas-chromatograph (Focus GC®, Thermo Scientific) equipped with a flame ionization detector. The sum of all the microbial PLFAs analyzed was considered as a proxy of microbial biomass ([4]). The fungal biomass was estimated by measuring soil ergosterol content through HPLC (Finningan Surveyor®, Thermo Scientific), as described in Bååth & Anderson ([4]).
UV-Vis-NIR soil spectroscopy
Soil air dried granulometric fractions were used for the spectroscopic analyses. Diffuse reflectance spectra in the ultraviolet-visible-near infrared (UV-Vis-NIR) region were recorded from 200 to 2500 nm in 2.0 nm steps at a scan speed rate of 30 nm min-1, using a spectrophotometer (V-570®, JASCO, Easton, MD, USA) equipped with a BaSO4-coated integrating sphere (ISV-469®, JASCO), 73 mm in diameter. Samples were gently pressed by hand to avoid undesired particles orientation in the 8×17 mm rectangular holes of glass holders.
Data analysis and statistical learning
Differences in the chemical and biological top soil properties among the three sampling sites were evaluated by non-metric multidimensional scaling (NMDS) with the superimposition of confidence ellipses (for α = 0.05) and through one-way analysis of variance (ANOVA) followed by the Tukey’s HSD post-hoc test (α = 0.05).
Diffuse reflectance spectra were transformed as log(1/R) (analogous to absorbance) and once-differenced to correct for baseline shifts across the wavelength range. The spectra, represented by vectors r = {r1, …, r1150}, were linearly interpolated at 210 equally spaced points to approximate the original spectra with vectors (xi with i = [1, 20]) of 210 elements, needed for the Discrete Wavelet Transformation (DWT). The vectors xi were either directly used in the regression analyses, or firstly denoised through wavelet shrinkage (Fig. 1).
In order to denoise the xi vectors, we employed the complex Daubechies wavelets ([24]) with 3 vanishing moments, followed by the complex multiwavelets style shrinkage ([7]). The spectra were then reconstructed (di vectors, with i = [1, 20]) by inverse transformation. The choice of the wavelet family and the shrinkage algorithm was based on the extensive simulations of Barber & Nason ([7]).
The xi and di vectors were used as predictors for each soil parameter in PLSR models using the “SIMPLS” algorithm ([16]). The number of latent variables (LVs) was chosen, for each model, through tenfold cross validation on ten possible models ranging from 1 to 10 LVs. For both the elastic net and the SPC/LASSO regressions, the xi and di vectors were decomposed through DWT with Daubechies least asymmetric wavelets, with 4 vanishing moments, and the resulting vectors of coefficients at each scale were used in the subsequent analyses.
In the Elastic net modeling, the estimation of the quadratic penalty parameter λ, the mixing penalty parameter α, the number of wavelet coefficients to retain and the lowest level of decomposition were all chosen basing on tenfold cross-validations. For the quadratic penalty parameter, 100 λ candidate values, ranging from 0 (equivalent to an ordinary least square regression) to 1 (maximum shrinkage) were tested, whereas five α candidate values for the mixing penalty parameter were tested, ranging from 0 (ridge regression behavior) to 1 (LASSO behavior). The candidate values for the number of coefficients and the lowest level of decomposition encompassed all the l-1 possible values, where 2l (with l = 10) is the length of the xi and di vectors.
The SPC/LASSO modeling consisted of four steps: (1) estimating the correlation of each predictor with the outcome; (2) selecting a threshold for the above correlation coefficients to be retained for the PCR; (3) predicting the outcome by a PCR; (4) using the predicted values as the dependent variable in a LASSO regression. All the mother wavelet coefficients, from all the decomposition levels (combined in a single vector), were used as predictors in the first step. The threshold in the second step was selected basing on tenfold cross-validations, with j = 100 (j [0.1]) candidate values, and the number of components for the PCR was fixed to three. The tuning parameter λ for the LASSO regressions was similarly selected basing on tenfold cross-validations along the entire LASSO path calculated through the LAR algorithm ([17]). The predictors in the LASSO regressions were either the mother wavelet coefficients at each single decomposition level or their combination as in the first step of SPC, and their choice was based on the Mean Squared Error of Prediction (MSEP) of the resulting LASSO models. MSEP was calculated, according to Mevik & Cederkvist ([26]), basing on leave-one-out cross-validation, in order to obtain a nearly unbiased estimator of the prediction error.
To compare the predictive power of the employed techniques four indexes were used: (i) the Standard Error of Prediction (SEP), calculated as the square root of the difference between the MSEP and the squared bias (the mean difference between the predicted and the actual values); (ii) the Bias; (iii) the Residual Prediction Deviation (RPD), calculated as the ratio of the standard deviation and the SEP; and (iv) the Coefficient of Variation of RMSEP (CV-RMSEP), calculated as the ratio between the square root of MSEP (RMSEP) and the mean.
All the analyses were performed using the software R 3.0.2 ([32]) using the packages “wavethresh” ([29]), “refund” ([15]), “superpc” ([5]) “pls” ([27]), “lars” ([19]), “vegan” ([30]) and “stats” ([32]).
Results
The characteristics of the soil profiles are reported in Tab. 2 and discussed in Marchetti et al. ([25]), while the results of the chemical and biological analyses carried out on the top-soil samples collected under F. sylvatica, Q. cerris and Q. ilex are reported in Tab. 3. The studied soils did not differ for pH, total Mn and respiration (Tab. 3). Soil samples under Q. ilex canopy showed the highest values of SOM, C/N, TOC and total N, followed by soil under F. sylvatica and then by soil under Q. cerris canopy (Tab. 3). In addition, soil samples under Q. ilex canopy showed the highest concentrations of total Ca and Mg, and the highest values of β-glucosidase, fungal biomass and total PLFA, whereas, the highest concentrations for all the other parameters were found in soils under F. sylvatica canopy (Tab. 3). NMDS highlighted a perfect separation of the soils from the three provenances on the base of the measured parameters (Fig. SM1 in Appendix 1).
Tab. 3 - Chemical and biological properties of the studied soils under the three canopies considered. Mean values ± standard deviations are reported for 8 samples from F. sylvatica, 8 samples from Q. cerris and 4 samples from Q. ilex. Different letters indicate significant differences among the three canopies, according to the post-hoc Tukey HSD test with α = 0.05.
| Parameter | F. sylvatica | Q. cerris | Q. ilex |
|---|---|---|---|
| pH | 6.07 ± 0.24 a | 6.57 ± 0.23 a | 6.87 ± 0.29 a |
| SOM (% d.w.) | 37.03 ± 3.95 a | 17.66 ± 2.57 b | 46.50 ± 11.55 c |
| TOC (mg/g d.w.) | 171.30 ± 26.80 a | 80.10 ± 9.70 b | 328.80 ± 50.30 c |
| Total N (mg/g d.w.) | 10.32 ± 1.85 a | 6.12 ± 0.71 b | 17.65 ± 3.47 c |
| C/N | 16.72 ± 1.59 a | 13.10 ± 0.55 b | 18.77 ± 1.07 c |
| Total Ca (mg/g d.w.) | 46.81 ± 11.68 a | 20.89 ± 12.93 a | 140.06 ± 49.95 b |
| Total K (mg/g d.w.) | 11.18 ± 4.08 a | 3.84 ± 1.70 b | 6.25 ± 3.04 b |
| Total Mg (mg/g d.w.) | 7.10 ± 2.82 a | 9.33 ± 4.62 ab | 15.12 ± 7.51 b |
| Total Mn (mg/g d.w.) | 1.35 ± 0.56 a | 1.98 ± 1.34 a | 0.96 ± 0.37 a |
| Total Na (mg/g d.w.) | 2.76 ± 1.17 a | 0.14 ± 0.06 b | 1.12 ± 0.69 b |
| Total Fe (mg/g d.w.) | 24.49 ± 6.70 a | 22.59 ± 4.72 a | 11.14 ± 2.47 b |
| Total Al (mg/g d.w.) | 42.46 ± 15.72 a | 22.23 ± 12.20 b | 25.13 ± 19.75 ab |
| Py-Fe (mg/g d.w.) | 6.18 ± 1.75 a | 1.95 ± 0.42 b | 1.64 ± 0.56 b |
| Py-Al (mg/g d.w.) | 18.02 ± 3.97 a | 2.23 ± 0.69 b | 4.86 ± 2.24 b |
| Ox-Fe (mg/g d.w.) | 12.65 ± 2.88 a | 8.33 ± 2.31 b | 5.22 ± 3.24 b |
| Ox-Al (mg/g d.w.) | 23.93 ± 7.79 a | 6.45 ± 2.37 b | 13.62 ± 10.35 ab |
| Respiration (µg CO2/g/h) | 11.58 ± 3.18 a | 9.83 ± 2.35 a | 13.48 ± 1.50 a |
| SIR (mg Cmic/g) | 2.50 ± 0.29 a | 2.46 ± 0.42 a | 1.46 ± 0.25 b |
| Fungal biomass (µg/g) | 35.84 ± 7.66 a | 25.88 ± 4.67 a | 66.28 ± 18.31 b |
| Hydrolase (µg FDA/g/h) | 0.82 ± 0.21 a | 0.33 ± 0.16 b | 0.54 ± 0.37 ab |
| β-glucosidase (µg PNP/g/h) | 1.06 ± 0.17 a | 0.94 ± 0.18 a | 1.46 ± 0.24 b |
| Total PLFA (µmol/g) | 466.73 ± 31.18 a | 440.33 ± 81.33 a | 724.54 ± 180.47 b |
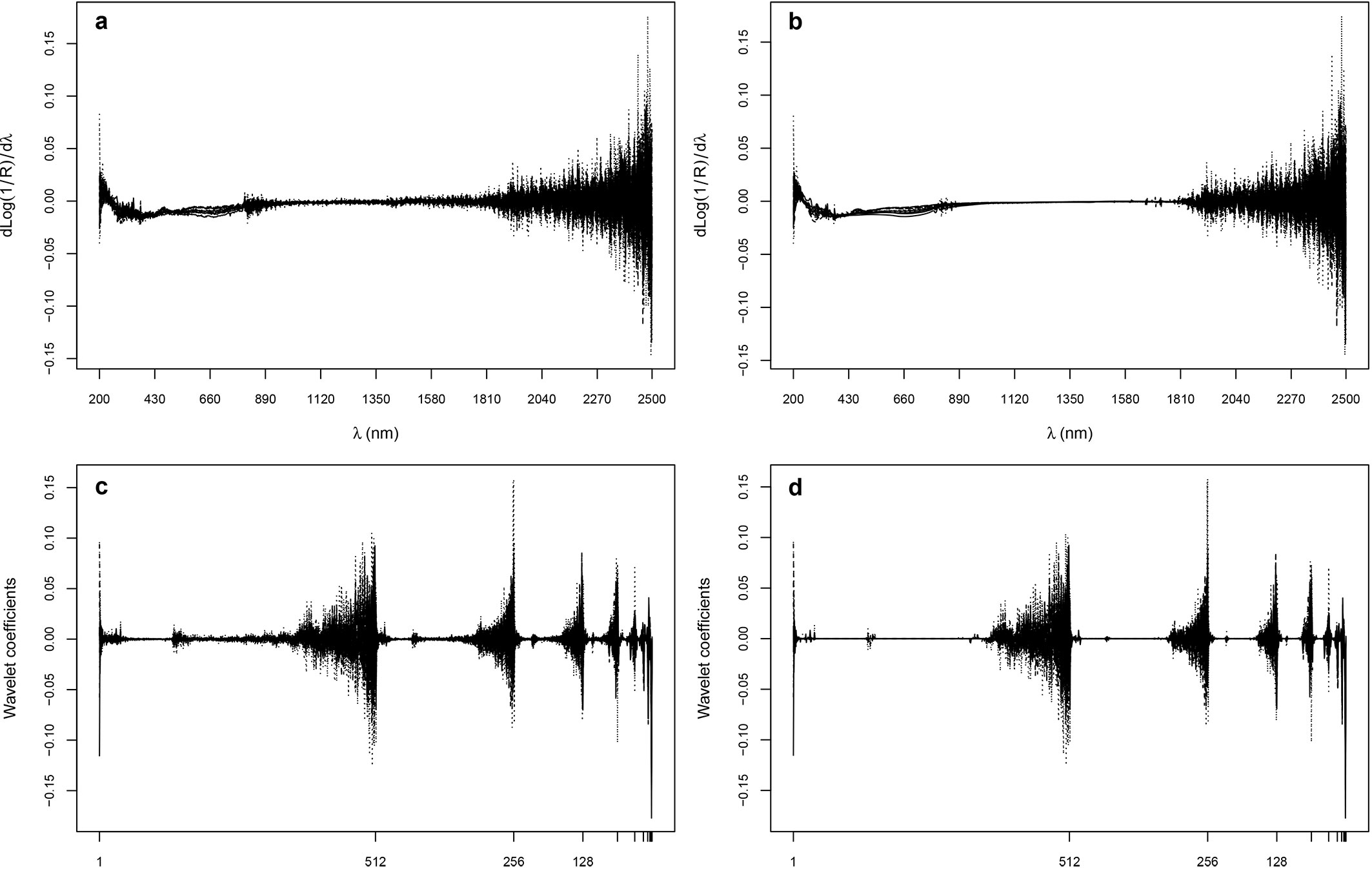
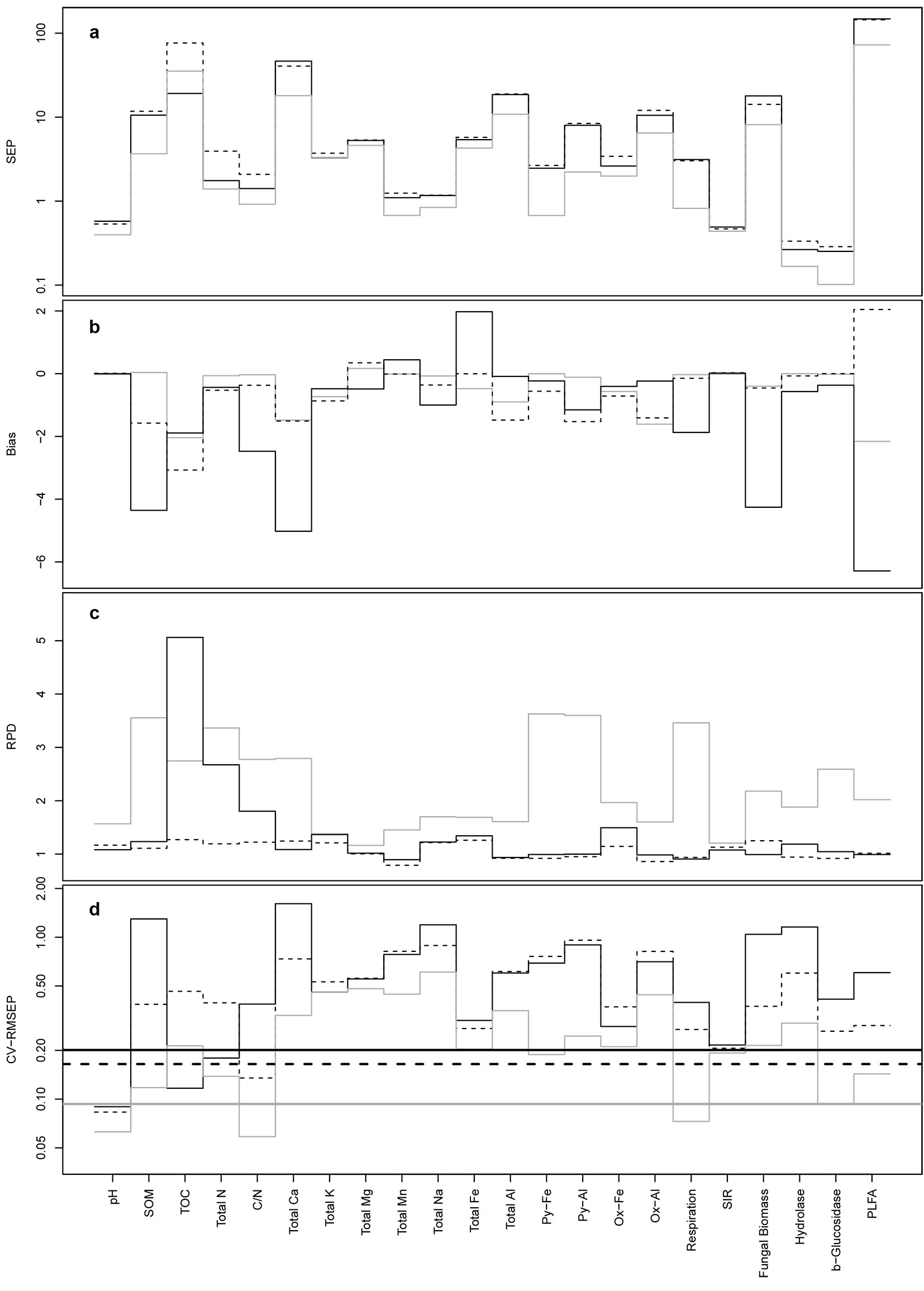
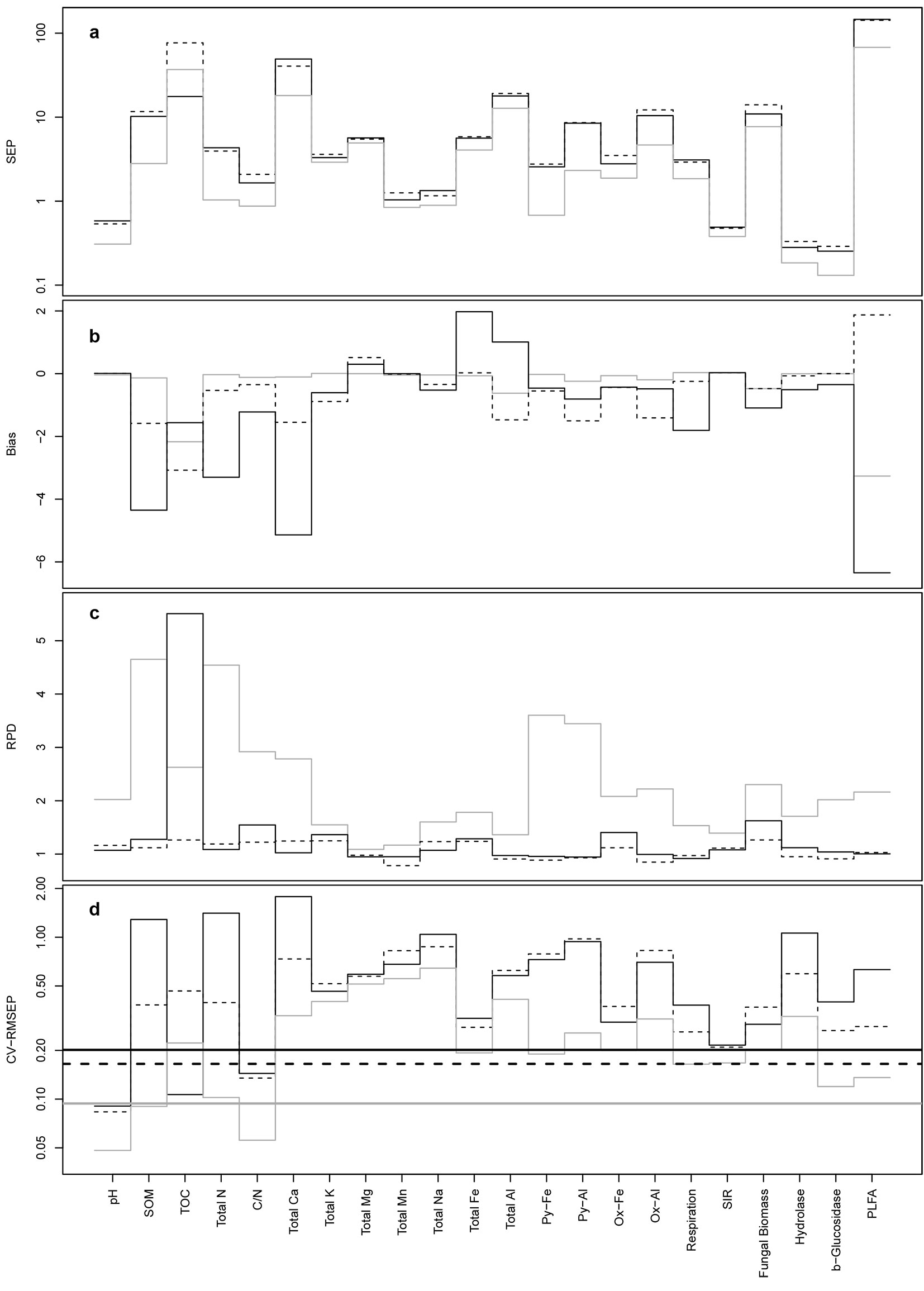
Processed reflectance spectra (xi and di) and their combined mother wavelet coefficients are shown in Fig. 3. The denoising step shrank to zero most of the coefficients associated to wavelengths in the range 900-1500 nm, but preserved the general features of the non-denoised spectra. The prediction accuracy of the three techniques, based on SEP, Bias, RPD and CV-RMSEP, varied in relation to the modeled parameter and the processing of the spectra (Fig. 4, Fig. 5). Overall, the SPC/LASSO gave by far the best results in terms of prediction accuracy, being the absolute values of Bias, SEP and CV-RMSEP almost constantly lower than those obtained with the two other techniques. In just one case (TOC), the Elastic net based on the wavelet coefficients achieved a significantly better prediction accuracy, reaching the highest value of RPD with both the xi and di predictors. The mixing penalty of the Elastic nets was equal to 1.00 for most parameters, the only exceptions were 0.75 for total Fe and K with both xi and di predictors, 0.75 for total Mn and Na with xi and 0.00, 0.25 and 0.75 for total Mn, pH and total Mg with di. PLSR gave the worst results, both with the xi and the di vectors, reaching values of the three criteria similar to those obtained with the Elastic nets, while overfitting many parameters (Fig. SM2 in Appendix 1). On the contrary, the SPC/LASSO (Fig. SM3 in Appendix 1) and the Elastic nets (Fig. SM4 in Appendix 1) did not show any evident overfit, particularly in the case of the SPC/LASSO that also provided better predictions for more parameters as compared with the Elastic nets.
Fig. 3 - Processed reflectance spectra (xi, a and di, b) and their combined mother wavelet coefficients (c and d, respectively).
Fig. 4 - SEP (a), Bias (b), RPD (c) and CV-RMSEP (d) of the Elastic net (solid black lines), PLSR (dashed lines) and SPC/LASSO (solid gray lines) models for xi vectors. Thicker lines in (d) indicate the means of CV-RMSEP for the three techniques. Bias values were transformed as hyperbolic arcsine due to their wide range.
Fig. 5 - SEP (a), Bias (b), RPD (c) and CV-RMSEP (d) of the Elastic net (solid black lines), PLSR (dashed lines) and SPC/LASSO (solid gray lines) models for di vectors. Thicker lines in (d) indicate the means of CV-RMSEP for the three techniques. Bias values were transformed as hyperbolic arcsine due to their wide range.
The denoising step produced heterogeneous results, with improvements in the prediction accuracy for about half of the parameters in the case of SPC/LASSO. In two cases (total N and SOM), there was a marked improvement in the RPD owed to the denoising of the spectra for the SPC/ LASSO, with values approximately 230% and 190% higher than those obtained with the non-denoised spectra. Moreover, the denoising step generally lowered the absolute values of Bias, particularly in the case of SPC/LASSO, for which the mean value and the standard deviation of bias were halved. The number of coefficients selected by the Elastic nets and the SPC/LASSO, both with the xi and di predictors, was on average similar (about 14 coefficients) for the two techniques. In few cases, particularly for total Fe, K and Na, the Elastic net selected far more coefficients than the SPC/LASSO, exceeding the number of observations in the data set.
Discussion
The Elastic net, the PLSR and the SPC/ LASSO were able to properly calibrate the spectra for many of the considered parameters, despite the high dimensionality of the data set analyzed. However, the three techniques provided heterogeneous results, each suffering from different limitations. Overall, the SPC/LASSO made most of the few available observations, producing homogeneous results for the various parameters considered, and reaching an acceptable level of predictability for a larger number of parameters as compared with other techniques. No evidence of overfit nor unacceptable relationships between the predicted and the measured values were observed among the results of the SPC/LASSO. The absence of overfit, quite pronounced instead in the PLSR and partly in the Elastic net, was due to the use of the SPC predicted values in the training of the LASSO, whereas the measured values were used in the evaluation of the models. The robustness toward the overfitting is of particular interest in high dimensionality problems ([20]), and makes the SPC/LASSO a promising alternative to more popular techniques. To our knowledge, this is the first time that this technique - and more generally preconditioned LASSO - was applied to predict soil properties using diffuse reflectance spectra. Further testing with possibly larger datasets are awaited.
Surprisingly, the worst results were obtained using the PLSR, that is the most employed technique to calibrate spectra for soil analysis ([39]). The small size of the dataset analyzed may partially explain such result. Indeed, the dependent variable in PLSR is used for the construction of the components, thus seeking directions that have both high variance and high correlation with the outcome. Likely, using few observations not sufficient information was available to efficiently estimate a high-dimensional covariance matrix, and this could explain the superior performance of other techniques. Although SPC has close affinities with PLS and could be considered its “denoised” version ([20]), it behaved completely different when applied to our dataset. Indeed, by filtering the coefficients in the first step, the SPC discards most noisy features and reduces the dimensionality of the model frame, whereas noisy features are downweighed (though not removed) by PLS, and this could affect the predictions obtained.
The Elastic net performance greatly varied in relation to the parameter considered. Despite its good prediction of TOC (highest value of RPD among all the developed models), it failed to properly calibrate the spectra for most parameters. The main differences between the Elastic net and the SPC/LASSO are the presence of a L2-regularization (with variable weight depending on the dependent variable) in the former, and the use of predicted (instead of raw) values as the dependent variable in the latter. Taken together, the above considerations should explain the differences in the results obtained with the two techniques. Since the mixing penalty was equal to 1.00 for most of the parameters and slightly lower (0.75) for few other ones, the Elastic nets behaved in most cases as the LASSO regressions. Therefore, the superior performance of the SPC/LASSO is due to the use of denoised outcomes instead of the raw ones.
Spectra denoising differently affected the performance of the three techniques in terms of prediction error, producing heterogeneous results. On the one hand, the denoising step reduces the dimensionality of the dataset (by shrinking to zero many predictors) and removes noise-related features that could otherwise be selected by the regression algorithms, affecting the predictions. On the other hand, this step could remove important features from the analysis and worsen the predictions. Unfortunately, the results of these processes could not be predicted, being dependent on the parameters considered and the technique applied, as demonstrated by our results. However, in some cases the improvement of prediction performances due to spectra denoising is remarkable, as in the case of pH, SOM and total N for the SPC/LASSO and fungal biomass for the Elastic net. In addition, the denoising step generally improved the prediction accuracy in terms of Bias, particularly in the case of SPC/LASSO. Therefore, it is advisable to test the relative performance of the calibration techniques using both raw and denoised spectra.
Our results indicate that SOM, TOC, C/N ratio, total N, total Ca, Py-Fe, Py-Al, respiration and, to a lesser extent, pH, Ox-Fe, Ox-Al, fungal biomass, hydrolase, β-glucosidase and PLFA, can be properly predicted using SPC/LASSO (or an Elastic net for TOC) on UV-Vis-NIR spectra in the range 200-2500 nm and few observations. Predictability of TOC, SOM and total N using Vis-IR spectra was repeatedly assessed in many researches relying on different calibration techniques (see [39] for an overview and [9]). A growing number of studies was also devoted to the prediction of soil biological properties ([36], [46], [21]), and many evidences of effective predictions were provided. However, most researches carried out so far addressed the issue of Vis-IR spectra calibration using large data sets, with comparatively low dimensionality. Despite the limitations of the small data set, we were able to predict many soil parameters with an accuracy comparable to those of many other researches. This is not only the case of major soil properties, like SOM, TOC and total N, but also of biological properties, such as respiration, which has no theoretical response in the UV-Vis-NIR spectral range. As repeatedly reported ([12], [13], [33]), this could be due to the high correlation of biological properties with other variables showing clear spectral features like TOC or SOM, although it was also suggested that some biological properties could be modeled independently ([46]). The possibility to predict soil properties using small data sets has important applicative implications. Although it is possible to use published models based on extensive libraries, it is advisable to develop specific models tailored ad-hoc to predict soil properties at a local scale. Indeed, models covering broad geographic areas and wide ranges of values can provide lesser accuracy at local scale than models developed for the specific areas of interest. However, it is usually difficult to obtain large data sets of measured parameters and UV-Vis-IR spectra needed to develop appropriate models, and it is usually beyond the scope of many investigations. In this context, the identification of calibration techniques suitable to the analysis of data sets with high dimensionality and few observations is a primary challenge. Our comparative approach revealed that wavelet decomposition followed by a combination of SPC and LASSO (or Elastic net for some parameters) is especially suitable to deal with the above problems, whereas PLSR should be reserved to large dataset analysis.
Conclusions
SPC/LASSO efficiently calibrates UV-Vis-NIR spectra to predict many soil chemical and biological properties. It generally outperforms Elastic net and PLSR in the case of small, high dimensional data sets, and is especially robust toward overfitting. Spectra filtering through wavelet shrinkage can improve prediction accuracy in terms of both prediction error and especially bias for various soil properties. Our findings highlight the possibility to build useful predictive models with small data sets using SPC/LASSO, allowing the development of laboratory-scale models tailored to specific applications.
Abbreviations
The following abbreviations are used throughout the text:
- ANOVA: Analysis of variance
- CV: Cross-validation
- CV-RMSEP: Coefficient of Variation of RMSEP
- DRS: Diffuse Reflectance Spectroscopy
- DWT: Discrete Wavelet Transformation
- GLM: Generalized Linear Models
- LASSO: Least Absolute Shrinkage and Selection Operator
- LV: latent variable
- MAVE: Minimum Average Variance Estimation
- MSEP: Mean Squared Error of Prediction
- NMDS: Nonmetric multidimensional scaling
- Ox-Al: Al extracted by ammonium oxalate
- Ox-Fe: Fe extracted by ammonium oxalate
- PCR: Principal Component Regression
- PLFA: Phospholipid fatty acid
- PLSR: Partial Least Square Regression
- Py-Al: Al extracted by sodium pyrophosphate
- Py-Fe: Fe extracted by sodium pyrophosphate
- RMSEP: Square root of MSEP
- RPD: Residual Prediction Deviation
- SEP: Standard Error of Prediction
- SIR: Substrate Induced Respiration
- SOM: Soil Organic Matter
- SPC: Supervised Principal Component
- TOC: Total Organic Carbon
- UV-Vis-IR: Ultraviolet-visible-infrared
- UV-Vis-NIR: Ultraviolet-visible-near infrared
- Vis-IR: Visible-infrared
- Vis-NIR: Visible-near infrared
Acknowledgements
This research was supported by funds from the Cilento and Vallo di Diano National Park and from FARB project (2009) of the University of Salerno. The authors wish to thank Dr. Roberto Senatore (Università di Salerno, Italy), Dr. Felicia Grosso (Università del Sannio, Italy) and Dr. Erika Di Iorio (Università del Molise, Italy), who performed part of the laboratory analyses. AB and DB performed the chemometric analyses and wrote the manuscript. DB and PI performed the soil chemical and biological analyses, respectively. CC and GP performed the UV-Vis-NIR reflectance analyses. AA and CC supervised works.
References
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Anna Alfani
Daniela Baldantoni
Dipartimento di Chimica e Biologia, Università degli Studi di Salerno, v. Giovanni Paolo II 132, I-84084 Fisciano, Salerno (Italy)
Giuseppe Palumbo
Dipartimento di Agricoltura Ambiente Alimenti, Università degli Studi del Molise, v. De Sanctis, I-86100 ampobasso (Italy)
Consiglio per la Ricerca e la Sperimentazione in Agricoltura (CRA), Centro di ricerca per l’Orticoltura, v. Cavalleggeri 25, I-84098 Pontecagnano, Salerno (Italy)
Corresponding author
Paper Info
Citation
Bellino A, Colombo C, Iovieno P, Alfani A, Palumbo G, Baldantoni D (2015). Chemometric technique performances in predicting forest soil chemical and biological properties from UV-Vis-NIR reflectance spectra with small, high dimensional datasets. iForest 9: 101-108. - doi: 10.3832/ifor1495-008
Academic Editor
Arthur Gessler
Paper history
Received: Nov 06, 2014
Accepted: Mar 10, 2015
First online: Jul 15, 2015
Publication Date: Feb 21, 2016
Publication Time: 4.23 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2015
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 50370
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 41873
Abstract Page Views: 2959
PDF Downloads: 4114
Citation/Reference Downloads: 22
XML Downloads: 1402
Web Metrics
Days since publication: 3821
Overall contacts: 50370
Avg. contacts per week: 92.28
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2016): 9
Average cites per year: 0.90
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Leaf transpiration of drought tolerant plant can be captured by hyperspectral reflectance using PLSR analysis
vol. 9, pp. 30-37 (online: 05 October 2015)
Research Articles
Visible and near infrared spectroscopy for predicting texture in forest soil: an application in southern Italy
vol. 8, pp. 339-347 (online: 09 September 2014)
Research Articles
Spectral reflectance properties of healthy and stressed coniferous trees
vol. 6, pp. 30-36 (online: 14 January 2013)
Research Articles
Selection of optimal conversion path for willow biomass assisted by near infrared spectroscopy
vol. 10, pp. 506-514 (online: 20 April 2017)
Research Articles
Calibration of a multi-species model for chlorophyll estimation in seedlings of Neotropical tree species using hand-held leaf absorbance meters and spectral reflectance
vol. 9, pp. 829-834 (online: 17 May 2016)
Research Articles
Feasibility study of near infrared spectroscopy to detect yellow stain on cork granulate
vol. 11, pp. 111-117 (online: 31 January 2018)
Research Articles
Characterization of technological properties of matá-matá wood (Eschweilera coriacea [DC.] S.A. Mori, E. odora Poepp. [Miers] and E. truncata A.C. Sm.) by Near Infrared Spectroscopy
vol. 14, pp. 400-407 (online: 01 September 2021)
Research Articles
Impact of climate change on tree-ring growth of Scots pine, common beech and pedunculate oak in northeastern Germany
vol. 9, pp. 1-11 (online: 13 October 2015)
Research Articles
Growth dynamics of the Norway spruce and silver fir understory in continuous cover forestry
vol. 13, pp. 56-64 (online: 05 February 2020)
Research Articles
Local ecological niche modelling to provide suitability maps for 27 forest tree species in edge conditions
vol. 13, pp. 230-237 (online: 19 June 2020)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword