Assessment of timber extraction distance and skid road network in steep karst terrain
iForest - Biogeosciences and Forestry, Volume 10, Issue 6, Pages 886-894 (2017)
doi: https://doi.org/10.3832/ifor2471-010
Published: Nov 06, 2017 - Copyright © 2017 SISEF
Research Articles
Abstract
This study aims to define a simple and effective method to calculate skidding distances on steep karst terrain, rich in ground obstacles (stoniness and rockiness) to support decision planning of secondary and primary forest infrastructure network for timber extraction in productive selective cut forests. Variations between geometrical extraction distances and actual distances were highlighted on the operational planning level (i.e., compartment level) through GIS-related calculation models, focusing on cable skidder timber extraction. Automation in defining geometrical and real extraction distances, as well as relative forest openness were achieved by geo-processing workflows in GIS environment. Due to variation of extraction correction factors at the compartment level from a minimum of 1.19 to a maximum of 5.05 in the same management unit, it can be concluded that planning harvesting operations (timber extraction) at operational level should not include the use of correction factors previously obtained for entire terrain (topographical) categories, sub-categories or even management units.
Keywords
Real Extraction Distance, Steep Terrain, Skid Road Network, GIS Environment, Karst Terrain
Introduction
When forest transportation network layout is not well developed, it can indirectly lead to productivity loss and cost increase during timber harvesting operations ([48], [11], [7]) together with an uncontrolled expansion of forest machine traffic in the forest stand, thus increasing the disturbance of forest soil ([31], [32], [9], [10], [46]).
Forest road network investigations provide a primary method for the evaluation of forest accessibility in terms of on-road transportation and forest operations efficiency ([21]). The fundamental of forest transportation goes back to Matthews ([33]) and his geometrical road spacing layout, two-dimensional (flat terrain) model and equally distributed amount of cut timber. Later, Segebaden ([43]) highlighted terrain irregularity and its uneven conditions that affect road network asymmetry together with non-linear and non-vertical timber movement to forest road which occur during timber extraction. Optimal forest openness (i.e., forest accessibility) represents the final goal of opening forests with roads and starts from the least cumulative costs of timber extraction together with building and maintenance costs of forest roads ([14], [45], [44]). Road density values do not give information about quality of road network layout in the forest stand ([40]), but simply of their quantity and therefore cannot be used for evaluating the current or future state of forest openness. On the other hand, relative openness as a quality parameter introduced by Backmund ([6]) is still used in grading forest openness but with variations in buffer width ([24]). Timber extraction distance (or skidding distance) as a parameter has a great influence in machine productivity and costs ([49]) thus affecting the whole timber supply chain.
Literature review shows that factors regarding timber extraction distance have been changing through time, firstly introduced by Segebaden ([43]) as: (i) V-corr or network correction factor; and (ii) T-corr or off-road correction factor. Folegatti ([19]) and Ackerman et al. ([1]) for “off-road correction factor” refer to as “wander factor”, while Silversides & Sundberg ([45]) call it “winding factor”. Various authors give different values for off-road correction factor, depending on terrain (topographical characteristics), from 1.2 to 2.5 ([14], [43], [6]), road network layout ([44]), organizational level of timber extraction activities ([28]) and machine type, along with working methods ([19], [29]). Most authors consider landing site position and road network layout to be the most significant factors affecting average extraction distance ([20], [12]).
Fundamental approaches in defining average extraction distances are still widely in use nowadays supported in GIS technologies ([23], [22]) which allow more detailed planning ([27]) and optimisation of both primary (extraction) and secondary (long-distance) timber transportation alternatives ([13], [24]).
From all stated above, one can conclude that differences in estimating average extraction distances can therefore be found in: (i) theoretical model vs. actual state, (ii) level of planning, i.e., management unit vs. compartment/sub-compartment level; and (iii) forest road layout in forest stand (geometry) vs. real timber extraction distance with defined vehicle/system.
In terms of forest management, choosing a vehicle for timber extraction will depend on many conditions ([3]), but terrain slope ([25]), ground obstacles ([50]) and soil bearing capacity ([4]), as well as primary and secondary forest infrastructure network, take an important part in overall vehicle choice. Steep terrain slope and/or ground obstacles affect longitudinal and lateral vehicle stability, with that their mobility, productivity and work safety ([50], [51], [2]). On the other hand, some authors highlight the importance of shape, position and density of secondary forest infrastructure network, i.e., skid roads and skid trails ([38]) as being critical parameters for basic vehicle-to-timber access during timber extraction (length of winch rope or boom reach). Also, timber harvesting is highly influenced by road network structure ([11]) and therefore cost-effective transport is a must.
High surface heterogeneities such as steep slopes, changes in aspect directions and high amount of ground obstacles are common in area of high karst ([30]), while various complexities of ground conditions such as caves, sinkholes and rockhead relief result as very difficult ground for civil engineers to overcome ([52]). Zhang et al. ([54]) highlight that karst landscape is distributed all over the world, but is mainly found in Eastern Europe and European Mediterranean, North America, and China with the largest and widest karst area. In Croatia, 46% of land (2.578.000 ha) is karst terrain ([26]), where the most common tree species - common beech (Fagus sylvatica L.) and silver fir (Abies alba Mill.) - comprise selective forests of great management and ecological value.
This study aims to define a simple and effective method to calculate skidding distances in steep karst terrain to support decision on planning secondary (skid roads) and primary (truck roads) forest infrastructure network for timber extraction.
Main hypothesis of this research is that there are clear differences between geometrical and actual skidding distances, and those will be highlighted at the operational planning level (i.e., compartment level) with accompanying GIS-related calculation models in a case study of timber extraction by a cable skidder in steep karst terrain and built secondary forest infrastructure network.
Automation in defining geometrical and real extraction distances, as well as relative forest openness will be achieved by using geo-processing workflows in GIS environment which will allow future use of models in varying conditions.
Materials and methods
Study area
The study was conducted in beech and fir selective forests of pre-mountainous area of Croatia, in the Management Unit (MU) Kupjački vrh, located at 45° 26′ N latitude and 14° 53′ E longitude. The Kupjački vrh MU consists of about 279 hectares of forests, of which 275 ha is productive forest area. The MU is divided into 16 compartments and average growing stock is 446 m3 ha-1, with an annual increment of 6.25 m3 ha-1. The 53% of growing stock is above 50 cm DBH and 35% is between 31 and 50 cm DBH. Over a period of 10 years (2015-2024) total allowable cut is 24.850 m3.
The Kupjački vrh MU is representative of high karst with many karst phenomenon and a centrally located peak from which terrain descends in all exposition directions. Mechanical soil composition in the area is highly skeletoid without a developed hydrological network ([15]).
In the study area, harvesting is traditionally performed by chainsaws and timber extraction is done by cable skidders with tree length or half-tree length system.
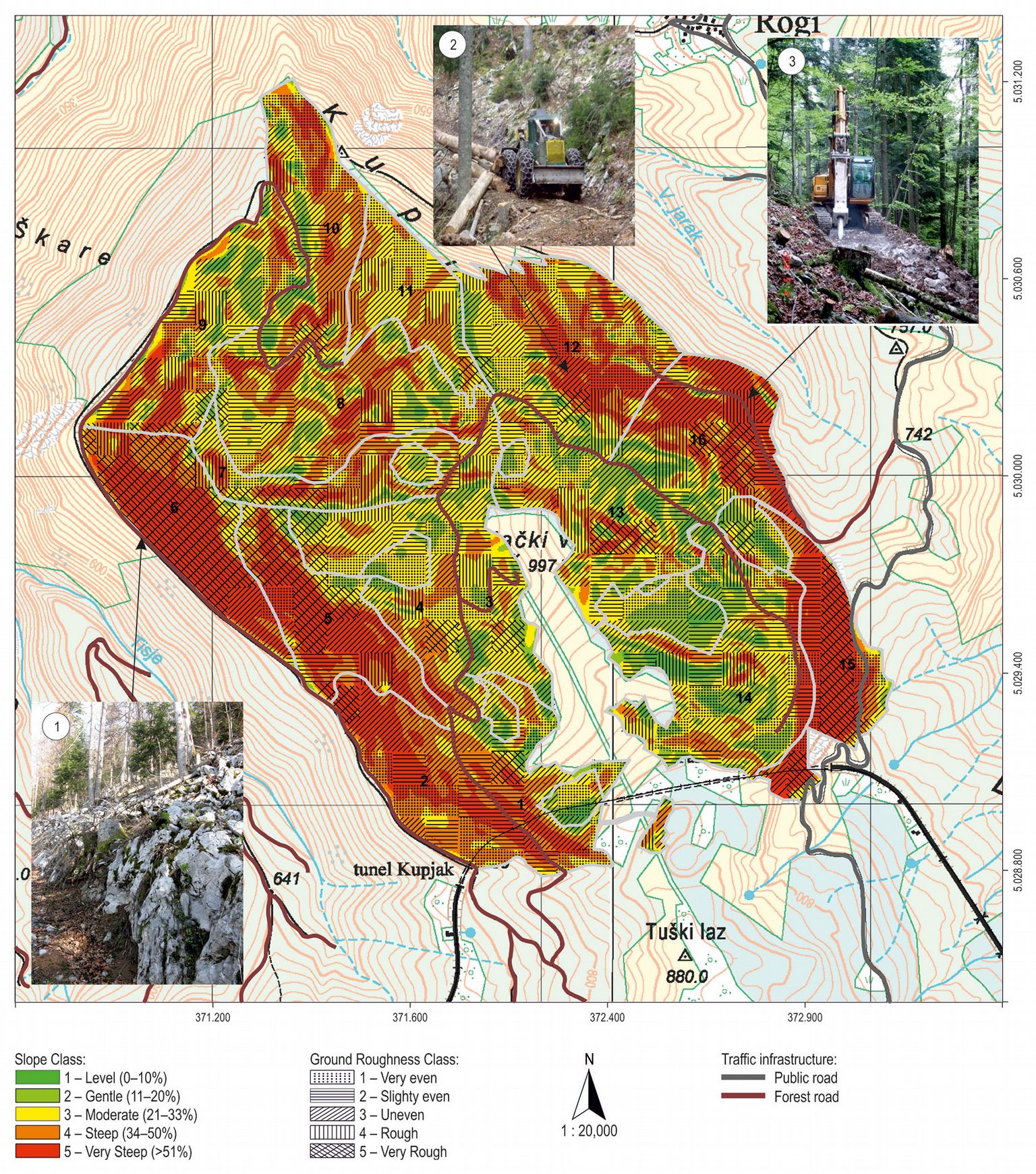
Without skid roads vehicle mobility would not be possible in this MU (Fig. 1) due to difficult terrain conditions in terms of terrain slope and ground obstacles ([15]).
Fig. 1 - Terrain trafficability and primary forest road network in study area (photo 1: terrain conditions, author: A. Duka; photo 2: timber extraction, author: T. Poršinsky; photo 3: building of a skid road, author: T. Poršinsky).
Data collection of terrain characteristics
GIS data of MU and its 16 compartments was taken from the official Management plan ([5]). Digital Elevation Model (DEM) was created based on two sets of elevation data obtained by aerial-photogrammetric survey and stereo-restitution processing and digitalization. The DEM was used to extract information regarding terrain gradient (slope) based on Horn’s method ([8]). Terrain roughness in terms of ground obstacles was described independently of slope by measurements on 319 sample plots regularly distributed in MU, each of 10 × 10 m in size and with 100 m distance ([15]). On each sample plot, the parameters describing obstacles (height, width and frequency) were recorded according to the methodology of Rowan ([42]) for the purpose of defining terrain roughness categories. Data was collected with hand-held GPS with <10 m accuracy and a laser rangefinder with <5 cm accuracy. Supporting data base was created where roughness classes were determined based on 4 height/depth classes of ground obstacles: (1) H20 (10-30 cm); (2) H40 (31-50 cm); (3) H60 (51-70 cm); (4) H80 (> 70 cm); and four frequency classes: (1) isolated (4-40 n ha-1); (2) infrequent (41-400 n ha-1); (3) moderately frequent (401-4000 n ha-1); and (4) frequent (> 4000 n ha-1). Since there is no available data on ground obstacles in study area, field survey data were then used for raster image creation.
As a consequence, the terrain of the study area was described by two fundamental spatial information: morphology (and derived information) and roughness.
Data collection of primary and secondary forest infrastructure network and analysis
The existing public and forest roads together with built skid roads were surveyed by a hand-held GPS with accuracy <10 m. A registry of primary and secondary forest infrastructure network was established according to Pentek et al. ([38]) in order to analyse share and lengths of skid roads in each compartment of researched area.
Primary traffic infrastructure consisted of all categories of forest roads as well as local public roads that can be used in forest management ([36]), while secondary forest infrastructure network consisted only of skid roads, i.e., built infrastructural objects with always present earthworks, but without upper road layer (Fig. 1).
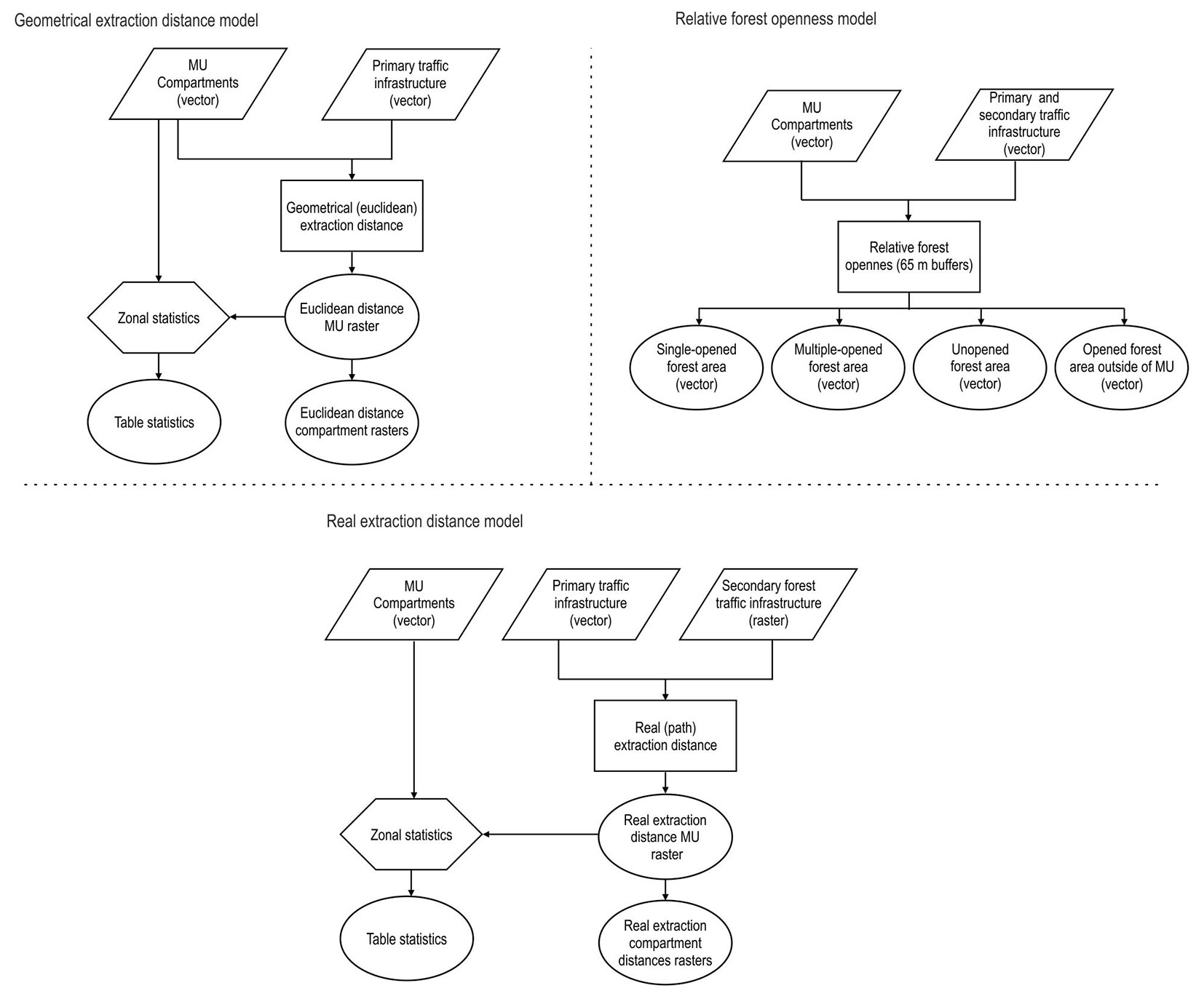
Defining extraction distances (use of “Euclidean distance” tool for geometrical extraction distances and “Path distance” tool for real extraction distances) together with relative forest openness, was done by using the ModelBuilder tool incorporated in the programme package ArcGIS® ver. 10.1. ModelBuilder is a visual programming language for building geo-processing workflows and automating spatial analysis and data management processes. Each model is represented with a diagram that connects sequences of process and geo-processing tools, using the output of one process as the input to another process ([17]).
All models used in this specific site can be reused and simply modified for use in different conditions regarding terrain, stand and traffic infrastructure network. Input data for each of forest openness parameters is shown in Fig. 2 and generally consists of: (1) polygon data of MU area and its compartments; (2) polyline data of primary traffic infrastructure; (3) polyline data of secondary forest infrastructure network; and (4) DEM, i.e., Digital Terrain Model (DTM) of the researched area.
Fig. 2 - Flowchart diagrams of the modeled computational steps for the estimation of extraction distance and forest openness parameters.
Geometrical values of timber extraction distances are based on Euclidean distances (the shortest distance to a determined source) and primary traffic infrastructure network (point to point distances), which correlates to already mentioned Segebaden ([43]) foundations of determining timber extraction distance. Model for geometrical extraction distances is solely based on two data inputs: (1) polygon shape file of MU and its compartments; and (2) polyline shape file of primary traffic infrastructure network. By using iteration and extraction functions, distinction at the compartment level is possible and statistical data for each compartment can be obtained (pixel count, pixel area, minimum value, maximum value, values range, mean value, standard deviation and sum value).
Relative forest openness calculation was based on both primary and secondary forest infrastructure network and buffer width equal to length of skidder’s winch rope (70 m), reduced for value of mean terrain gradient for the entire management unit. Even though 65 m winch rope length is the maximal length, it should be noted that terrain conditions regarding steep slope and ground obstacles, as well as the position of rejuvenation areas, will additionally shorten the winch rope length on certain surfaces and compartments, also because of the fact that main operator’s stressor when working on a steep slope is moving up and down the slope ([47], [35]). The model calculates values for: (1) single-opened forest area (no overlap in buffer area); (2) multiple-opened forest area (overlap in buffer area); (3) unopened forest area (areas beyond 65 m buffer width); and (4) opened areas outside of the management unit. Multiple opened forest areas can be categorized as poorly planned road network where the same forest area is multiply opened, even though single-openness should be an imperative. Nevertheless, multiple-opened forest areas are common in every road junction of both primary and secondary forest infrastructure network. Opened areas outside of management unit can be the result of an inadequate setting of the forest traffic infrastructure layout, but with the main focus on ownership or management structure of adjacent forest areas. If a boundary road is used between different forest owners and all benefit from it, maintenance agreement should be in order, otherwise boundary roads should be avoided.
Defining real extraction distances was based on the Path distance tool in ArcGIS, which gives each cell of skid road network least accumulative cost relationship to a source or a set of sources (i.e., forest road network), accounting for surface distance and vertical (slope) cost factors. In this way, actual distances that vehicle (here cable skidder) travels in each compartment while transporting timber to the nearest forest road are based on skid road length, terrain slope and irregularity of both secondary and primary forest infrastructure network, as well as irregularity of compartment’s shape and size. The Path distance tool can also consider horizontal constraints (in this case ground obstacles) and therefore it can be used in road planning where both horizontal and vertical terrain factors are used for computing the least accumulative path distance for each future truck or skid road raster cell to the nearest forest road.
While Euclidean distance is the straight line distance between locations, the Path distance tools explore the movement of a traveller over a landscape. The Path Distance tool is the primary tool for cost distance analysis, accounting for both horizontal and vertical cost factors as well as true surface distance. It creates an output raster in which each cell is assigned the accumulative cost from the cheapest source cell. The algorithm utilizes the node/link cell representation, where the center of a cell is considered a node, and each node is connected by links to the nodes adjacent to it. Every link has an impedance associated with it. The impedance is derived from the costs associated with the cells at each end of the link (from the cost surface) and from the direction of movement ([17]).
This model assumes that cut timber is in reach of skidder winch rope i.e. timber is already collected and vehicle does not descend/ascend from forest infrastructure network to forest stand. Path distance tool also requires precision regarding infrastructure network and MU/compartment positioning. Boundary roads must strictly be in contact of boundary compartments and there should be no gaps between polygons, otherwise tool will not give correct values.
Used software
For the creation of DEM, SAGA GIS, Global Mapper and ESRI ArcGIS® ver. 10.1 were used, while most spatial analysis and creation of model builders was conducted with ArcGIS® ver. 10.1 and QGIS ver. 2.14.3. Transferring data from GPS to computer was provided using the MapSource® software (Garmin, Switzerland). All statistical analysis was done by the computer package STATISTICA® ver. 7 (StatSoft inc., Tulsa, OK, USA). Figures and maps were modified using the CorelDRAW® X7 package (Corel Corp., Ottawa, Canada).
Results
Site characteristics
Based on DEM with 4 × 4 m resolution, all five slope classes are evident in the Kupjački vrh MU; terrain gradient above 34% is the most common and takes 50.4% of the area (Fig. 1 and Tab. 1). Depending on presence and frequency of ground obstacles, five ground roughness classes were defined from 1 - slightly even terrain to 5 - very rough terrain (Tab. 1 and Fig. 1).
Tab. 1 - Terrain slope and ground roughness classes in the study area.
| Terrain slope classes |
Area | Ground roughness classes |
Area | ||
|---|---|---|---|---|---|
| ha | % | ha | % | ||
| Level | 10.68 | 3.9 | Very even | 45.87 | 16.7 |
| Gentle | 37.78 | 13.7 | Slightly even | 45.94 | 16.7 |
| Moderate | 87.82 | 32.0 | Uneven | 111.88 | 40.7 |
| Steep | 81.34 | 29.6 | Rough | 27.12 | 9.9 |
| Very steep | 57.25 | 20.8 | Very rough | 44.06 | 16 |
Total length of the surveyed forest (truck) roads in this management unit is 8.895 m, while there is one segment of public road (coloured grey in maps) of 967 m in length.
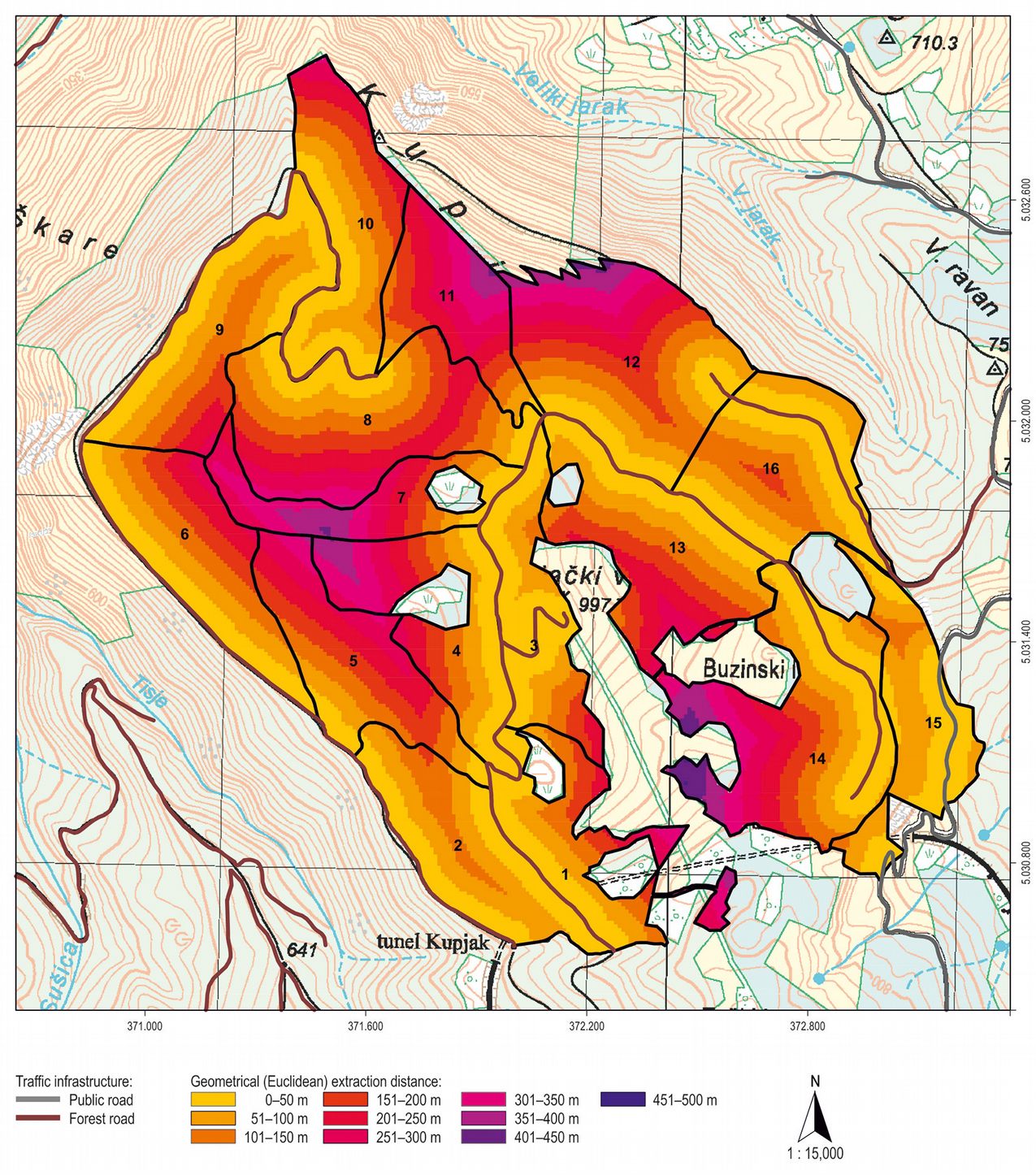
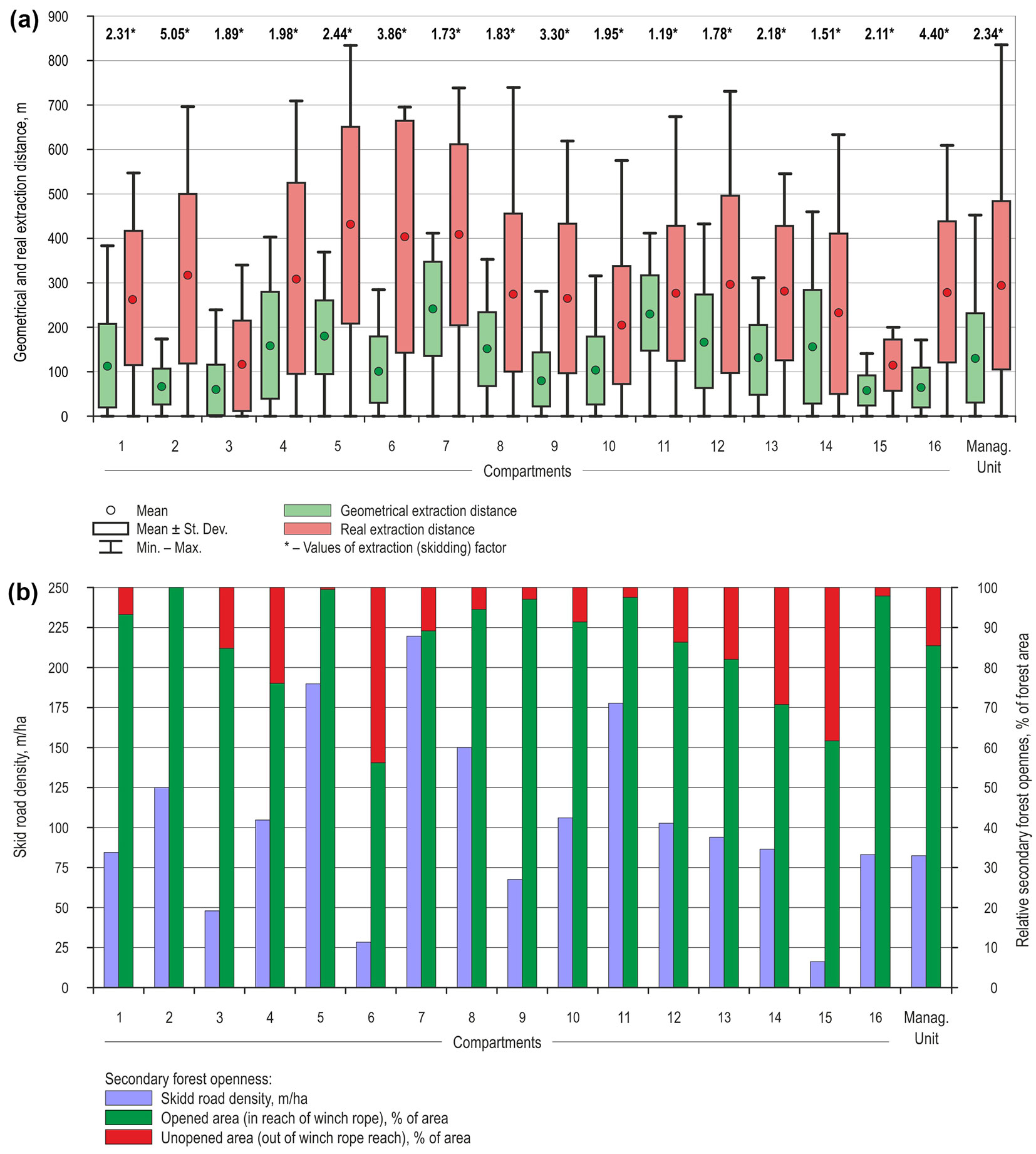
Maximal timber extraction distance in the whole MU and its 28.347 regularly placed network points (generated during raster creation) in the productive forest area is 451 m, while its mean is 126 m with 99 m of standard deviation. Highest geometrical extraction distances are in compartments 1, 2, 7, 11, 12, and 14, with a distance range from 400 to 500 m, while the lowest values with distance below 200 m are in compartments 2, 15 and 16 (Fig. 3). Still, this is only a two dimensional perspective without accounting the actual terrain morphology.
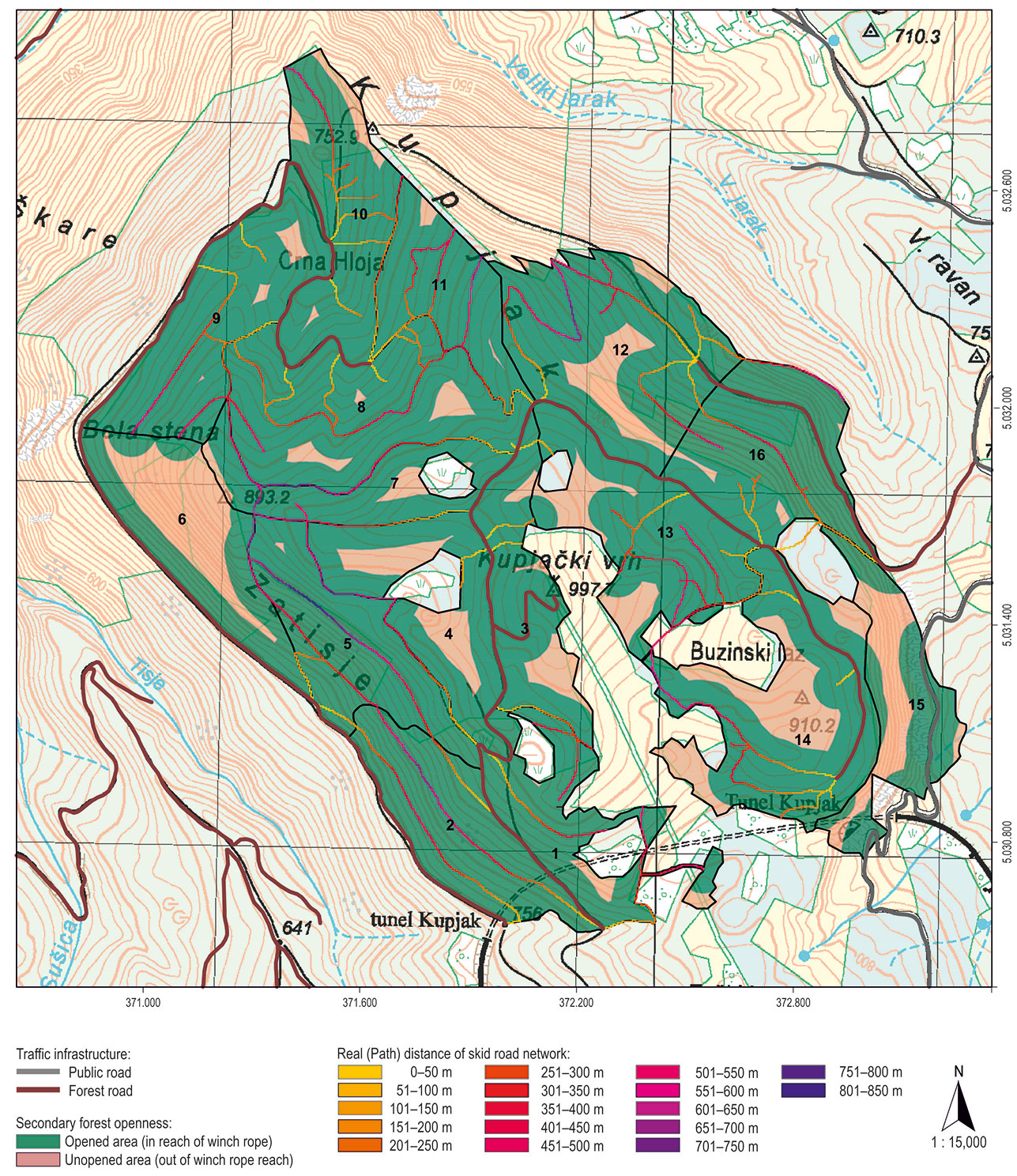
Relative openness model provided four different area classes in study area depending on buffer placement (inside/outside researched management unit) and overlap occurrence: (1) single opened forest areas - 113.03 ha; (2) multiple opened forest areas -126.61 ha; (3) unopened forest areas - 39.23 ha; and (4) opened area outside of this MU - 61.64 ha. Fig. 4 summarizes single and multiple opened areas (i.e., areas in reach of skidder’s winch rope), together with unopened areas of management unit (i.e., areas out of winch rope reach).
Maximal real extraction distance in the whole management unit is 833 m, with its mean value of 296 m and 189 m of standard deviation. By using an elevation raster with 4 × 4 m grid resolution, skid road network, polyline primary traffic infrastructure network and MU/compartments polygons shape files, real extraction distances were obtained, together with descriptive statistics at the compartment level (pixel count, pixel area, minimum and maximum values, value range, mean value, standard deviation and sum value).
Skid road lengths for each compartment and private areas are given in Tab. 2. Overall, 82 skid roads were measured and analysed. Total length of skid roads in this MU is 22.70 km, which means that skid road density is 82.6 m ha-1.
Tab. 2 - Skid roads in the investigated area. (*): boundary skid roads between compartments and/or private enclaves.
| Compartment | Length (m) |
Compartment | Length (m) |
Compartment | Length (m) |
Compartment | Length (m) |
Compartment | Length (m) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 453 | 5 | 725 | 8 - 11* | 769 | 12 | 1371 | 14 | 133 |
| 132 | 200 | 9 | 182 | 81 | 71 | ||||
| 192 | 303 | 644 | 86 | 219 | |||||
| 182 | 5 - 6* | 406 | 72 | 159 | 374 | ||||
| 517 | 5 - 7* | 152 | 149 | 367 | 690 | ||||
| 1 - 3* | 256 | 7 | 62 | 10 | 153 | 149 | 53 | ||
| 52 | 95 | 164 | 136 | 15 | 195 | ||||
| 2 | 857 | 7 - 8* | 1061 | 187 | 13 | 69 | 16 | 192 | |
| 893 | 8 | 21 | 112 | 122 | 16 | 131 | |||
| 267 | 184 | 77 | 327 | 16 | 21 | ||||
| 40 | 910 | 30 | 87 | 16 | 313 | ||||
| 3 | 66 | 178 | 52 | 347 | 16 | 490 | |||
| 97 | 245 | 541 | 258 | 16 | 116 | ||||
| 162 | 67 | 10 - 11* | 536 | 55 | Private | 173 | |||
| 4 | 163 | 146 | 11 | 322 | 13 - 14* | 233 | - | ||
| 4 - 5* | 912 | 69 | 257 | 13 - private* | 307 | ||||
| 4 - 7* | 461 | 8 - 9* | 325 | 249 | 14 | 25 | |||
Our analysis showed that values of real extraction distances are greater than geometrical extraction distances throughout the entire MU (Fig. 5a), since geometrical approach is based on the shortest linear distance from stand to forest road while “reality” could be very different. This resulted in variation of extraction (skidding) correction factors at the compartment level from a minumum of 1.19 (compartment 11) to a maximum of 5.05 (compartment 2) in the same management unit (Fig. 5a).
Fig. 5 - (a) Comparison of geometrical and real extraction distances in the study area; (b) Analysis of relative forest openness in the study area.
Analysis of skid road density vs. opened forest area (in reach of winch rope) is given in Fig. 5b. Most compartments of the researched management unit have relative openness above 80%.
Descriptive statistics of different extraction distances, relative openness, skid road density and skidding factor is given in Tab. 3. The highest correlation is between mean geometrical extraction distance and skid road density (r = 0.791, p<0.05). Since the geometrical approach is based solely on primary forest infrastructure network without considering skid roads, one can conclude that this strong correlation is coincidental. On the other hand, strong correlation between skid road density and opened forest area (r = 0.710, p<0.05) is expected, since all parameters are based on the secondary forest infrastructure network. Also, the aforementioned discrepancies between real and geometrical extraction distance have been statistically confirmed with a low correlation (r = 0.569).
Tab. 3 - Tab. 3 - Pearson’s correlation coefficients of secondary forest openness indicators in the study area. (*): p < 0.05.
| Parameter | Mean geometrical extraction distance |
Mean real extraction distance |
Skid road density |
Opened area |
Skidding factor |
|---|---|---|---|---|---|
| Mean geometrical extraction distance | 1.000 | 0.569* | 0.791* | 0.295 | -0.595* |
| Mean real extraction distance | 0.569* | 1.000 | 0.557* | 0.157 | 0.235 |
| Skid road density | 0.791* | 0.557* | 1.000 | 0.710* | -0.280 |
| Opened area | 0.295 | 0.157 | 0.710* | 1.000 | -0.030 |
| Skidding factor | -0.595* | 0.235 | -0.280 | -0.030 | 1.000 |
Discussion
According to Pentek et al. ([39]), primary road density in Croatia, depending on terrain category, ranges from 9.05 m ha-1 for lowland areas, 11.26 m ha-1 for hilly areas and 15.43 m ha-1 for pre-mountainous area. Primary road density for the analyzed MU is 35.87 m ha-1, which is much higher than mean national values and higher than the 26 m ha-1 of the karst area of northern-eastern Italy ([37]) or than the 18.5 m ha-1 of the European mountain region ([16]) or even than the 33.7 m ha-1 road density of the Austrian federal forests ([34]). However, much higher values (70.90 m ha-1) have been reported for some Austrian areas (district Hermagor in Carinthia - [18]).
In this study, the irregularity of management unit and its compartments shape, as well as the irregularity of primary traffic infrastructure network itself, which are the consequence of varying terrain conditions, resulted in the discrepancy between geometrical and real extraction distances (Fig. 5a). Such discrepancy is due to terrain characteristics (terrain slope and presence of ground obstacles). Ground obstacles and terrain roughness, even not directly included in presented models for calculating real extraction distances, are common in karst terrain and actually had affected the layout of skid road network during its planning and design and thus indirectly have affected skid road lengths.
According to Rebula ([41]), secondary road density in young stands should be 250-300 m ha-1 while in older stands with lower density it should be 100-180 m ha-1. Zdjelar ([53]) concludes that for this area of Croatia (pre-mountainous terrain of Gorski kotar) and selective forests, optimal secondary road openness should be 150 m ha-1, though it should be noticed that data on national level regarding secondary road density still does not exist.
Regarding the relative openness (Fig. 5b), 12 compartments have excellent (>80%) relative openness, according to Dietz et al. ([14]), while only two compartments (No. 6 and 15) are insufficiently relatively opened. These last two values did not affect the overall MU relative openness (85.92%). The reason of such low values for compartments 6 and 15 can be found in the fact that these are actually protective forests, where more than 60% of the area has terrain slope higher than 51% and very rough (class 5) ground conditions prevail.
Mean real extraction distance in the analyzed MU is 296 m and an excellent relative forest openness is present in 12 of totally 16 compartments with “only” 82.6 m ha-1 skid road density. This result highlights a good forest traffic infrastructure layout, especially considering that this is the area of high karst, sloped terrain, clear presence of ground obstacles and existence of private enclaves (Fig. 1). Real extraction distances at operational level of planning timber extraction should be considered in the context of secondary road density and in the context of (un)opened compartments’ areas (Fig. 5a, Fig. 5b).
Conclusions
The proposed method for determining extraction distances at compartment level is based on primary and secondary forest infrastructure network registry, digital terrain model and limited vehicle movement solely on forest infrastructure network without leaving it and descending/ascending into the forest stand. The observed differences in extraction distance obtained using the proposed and the geometrical methods make unjustified the use of correction factors, which is frequently reported in the literature, as variations ranging from 1.19 to 5.05 within the same management unit were present. Therefore, planning harvesting operations (timber extraction) at the operational level should not include the use of correction factors previously obtained for entire terrain categories, sub-categories or even management units.
Despite our study area was relatively small (278.80 ha), consisting of only 16 compartments, the proposed model can be freely applied with minor modifications in different harvesting systems, forest stands and management regimes, in order to obtain geometrical extraction distance, relative forest openness and real extraction distance. Moreover, model quality can be further improved with the use of high-definition Digital Elevation Model based on LiDAR data. Indeed, a high-definition terrain description based on LiDAR data could allow a better accuracy of the results, and a more precise measurement of ground obstacles, which is a time-consuming activity in the field.
In this study, the cumulative path distance for each cell of the skid road raster to the nearest forest road was modeled, taking into consideration both horizontal and vertical constraints. The use of digital terrain models and advanced spatial techniques has proved to effectively support decision planning of secondary and primary forest infrastructure network for timber extraction in productive selective cut forests.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Online | Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Ivica Papa
Tibor Pentek
Tomislav Poršinsky
Department of Forest Engineering, Faculty of Forestry, University of Zagreb, Svetošimunska 25, Zagreb (Croatia)
Department of Land, Environment, Agriculture and Forestry, University of Padova, v.le Dell’Università 16, Legnaro, PD (Italy)
Corresponding author
Paper Info
Citation
Duka A, Grigolato S, Papa I, Pentek T, Poršinsky T (2017). Assessment of timber extraction distance and skid road network in steep karst terrain. iForest 10: 886-894. - doi: 10.3832/ifor2471-010
Academic Editor
Rodolfo Picchio
Paper history
Received: Apr 24, 2017
Accepted: Aug 13, 2017
First online: Nov 06, 2017
Publication Date: Dec 31, 2017
Publication Time: 2.83 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2017
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 51444
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 41935
Abstract Page Views: 3945
PDF Downloads: 4335
Citation/Reference Downloads: 16
XML Downloads: 1213
Web Metrics
Days since publication: 3035
Overall contacts: 51444
Avg. contacts per week: 118.65
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2017): 21
Average cites per year: 2.33
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Use of LIDAR-based digital terrain model and single tree segmentation data for optimal forest skid trail network
vol. 8, pp. 661-667 (online: 22 December 2014)
Technical Reports
Qualitative evaluation and optimization of forest road network to minimize total costs and environmental impacts
vol. 5, pp. 121-125 (online: 05 June 2012)
Technical Reports
Decision making in forest road planning considering both skidding and road costs: a case study in the Hyrcanian Forest in Iran
vol. 6, pp. 59-64 (online: 21 January 2013)
Research Articles
Exploring the reliability of CAN-bus data in assessing forwarder rolling resistance under real working conditions
vol. 17, pp. 360-369 (online: 13 November 2024)
Research Articles
Use of terrestrial laser scanning to evaluate the spatial distribution of soil disturbance by skidding operations
vol. 8, pp. 386-393 (online: 08 October 2014)
Research Articles
Temporal analysis of the traffic loads on forest road networks
vol. 6, pp. 255-261 (online: 13 June 2013)
Research Articles
Large scale semi-automatic detection of forest roads from low density LiDAR data on steep terrain in Northern Spain
vol. 12, pp. 366-374 (online: 05 July 2019)
Research Articles
Deploying an early-stage Cyber-Physical System for the implementation of Forestry 4.0 in a New Zealand timber harvesting context
vol. 17, pp. 353-359 (online: 13 November 2024)
Research Articles
Fuel consumption comparison of two forwarders in lowland forests of pedunculate oak
vol. 12, pp. 125-131 (online: 11 February 2019)
Research Articles
Logging residue chipping options for short rotation poplar plantations
vol. 16, pp. 23-29 (online: 15 January 2023)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword