Trends and driving forces of spring phenology of oak and beech stands in the Western Carpathians from MODIS times series 2000-2021
iForest - Biogeosciences and Forestry, Volume 16, Issue 6, Pages 334-344 (2023)
doi: https://doi.org/10.3832/ifor4121-016
Published: Nov 19, 2023 - Copyright © 2023 SISEF
Research Articles
Abstract
This study focused on trends and driving forces of the leaf unfolding (LU) onset of oak and beech forests in the Slovak Carpathians along elevational gradients in the period 2000-2021. Particular attention was paid to improving the modelling of the LU onset using the MOD/MYD09 Moderate Resolution Imaging Spectroradiometer (MODIS) products. The LU onset was derived from the annual Normalized Difference Vegetation Index (NDVI) trajectories fitted with a double logistic function. An improved estimate of the onset was obtained by calculating 6 parameters of the logistic function and by comparing with the LU onset from phenological field observations. Between 2000 and 2021, we found a trend towards an earlier LU onset at the national level by ~0.39 day year-1 for oak stands (p = 0.13) and ~0.08 day year-1 for beech stands (p = 0.48). The analysis of trends in three elevation zones showed a difference in the LU onset of oak and beech stands as a function of elevation. For oak in 100-350 and 350-500 m zones was found a shift towards an earlier onset by ~0.41 day year-1 (p = 0.12). This corresponds to a shift of 8.6 days for the entire observation period 2000-2021. In the elevational zone above 500 m, the trend was milder, ~0.27 day year-1 (p = 0.21), i.e., 5.6 days for the entire analysed period. The shift towards an earlier onset at lower elevations and a later onset at higher elevations for beech was not statistically significant, with p-values between 0.44 and 0.51. The atypical year 2021, with the latest onset of LU during the entire observation period, fundamentally affected the significance of all trends. Nevertheless, the pixel-level analysis revealed a significant trend towards an earlier LU onset (p < 0.05) in 20.3% of oak stands. The same result was found only in 0.8% of beech stands. Strong negative correlations with R2 = 0.72 for oak and R2 = 0.81 for beech (p < 0.001) were found between the LU onset and March and April temperature deviations from the long-term normal. Temperature changes are the main driving force affecting the LU onset in the studied region.
Keywords
MODIS, NDVI, Oak, Beech, Leaf Unfolding, Double Logistic Function, Phenometric Trends, Air Temperature
Introduction
It is generally known from scientific studies that various factors influence the time of onset of spring phenophases. Spring development of many plants (mainly from warm regions) is primarily controlled by temperature, whereas early successional species native to temperate latitudes (e.g., Carpinus sp.) only become temperature-sensitive once their chilling demand has been fulfilled. Late successional taxa, such as beech (Fagus sp.), are photoperiod controlled, with temperature only exerting a limited modulating effect once the critical day length has passed. This mechanism prevents such taxa from sprouting at the “wrong” time ([24]). The potential disruption of this mechanism was pointed out by Zohner et al. ([54]), who showed that global warming leads to a reduction in the synchronous onset of spring phases (budding and flowering) by up to 55% in individual trees. Vitasse et al. ([49]) suggested that tree phenology has changed at different rates in recent decades due to different temperature changes at different elevations and different tree responses to these changes. This leads to more uniform phenology at different elevations. Nevertheless, many climate-related mechanisms, especially those related to different rates of warming at different elevations, are not well understood in forest tree phenology ([16], [30]).
The earlier onset of spring phenophases and the prolongation of vegetation seasons due to anthropogenic climate change is well documented in the literature ([13], [31], [30]). Keenan et al. ([20]) showed that carbon uptake by photosynthesis increased significantly more than carbon release by respiration in both earlier spring and later fall. They conclude that higher carbon uptakes contribute to slow down the rate of warming. However, results published by Chen et al. ([17]) suggest that the growing season length has not increased since 2000 for four temperate species in Europe, including oak and beech, due to the reduced temperature sensitivity of leaf development. A comprehensive model for green-up duration (GUD) was derived by Kern et al. ([21]) for deciduous forests in the broader Carpathian Basin region. An earlier start of the growing season (SOS) implies a longer GUD, whereas a delayed SOS is associated with a short GUD. It indicates smaller potential benefits of climate change in terms of a longer growing season than expected. Nonetheless, studies using multiple data sources and methods agree that earlier leaf unfolding is due to climate change, but these trends appear to have slowed or even reversed in recent years (Piao et al. ([36]). The diversity of results points to the need to refine, deepen, and synthesize the knowledge from regional phenological studies for later use in, for example, carbon sink modelling or forest adaptation measures.
Ground-based phenology (GP) and satellite-based phenology observations, commonly referred to as land surface phenology (LSP), are two basic approaches used in studies of vegetation phenology. LSP opened the possibility to analyse the course of phenological events in forest stands continuously (at daily intervals) and at low cost, providing an integrative view at a landscape level ([18]). Uncertainties and issues should be considered when using GP records to validate satellite sensor estimates of LSP ([28], [50], [13]). The main problems are: (i) insufficient field observations or spatial coverage; (ii) ground-based versus pixel-based observations; (iii) unknown measurement precisions and data entry errors; (iv) different measured phenological phenomena; (v) different temporal resolutions and a non-linear relationship between GP and LSP. Norris & Walker ([34]) and Younes et al. ([51]) pointed out at methodological risks in deriving and interpreting phenological models based on satellite data from different sensors. Berra & Gaulton ([3]) summarised that ground-based data do not represent the ground truth, which is a source of validation for LSP, but rather serve as a comparison, and both observational methods should be used in a complementary manner. GP records are used to confirm (or interpret) satellite estimates. LSP data are necessary to extrapolate/predict GP, which means that one can find similar temporal patterns in LSP and GP.
The satellite-based Normalized Difference Vegetation Index, NDVI ([44]) is widely used to study vegetation phenology in spite of its limitations, such as its tendency to saturate over dense canopies ([15], [12]). The most common alternative is the Enhanced Vegetation Index, EVI ([1], [42]). In Slovakia, the use of satellite imagery to determine phenological events of forest began in 2009 based on NDVI derived from MODIS data ([6], [26], [2]).
Modelling approaches are used to derive satellite-based phenological metrics. LSP modelling entails a mathematical expression of the vegetation index development (such as NDVI or EVI) during the year and determining the onset of major phenological events. Berra & Gaulton ([3]) state that the logistic function ([52]) and its double-sigmoid modification ([11]) are the most frequently used functions in deriving vegetation phenology at local and regional levels. Pavlendova et al. ([35]) and Lukasová et al. ([27]) used the mentioned Fisher’s modification and compared the satellite and ground-based phenology observations in beech stands in the Slovak Carpathians. The comparability of satellite and ground-based spring phenology of oak stands was confirmed by Bucha et al. ([9]). The proven close relation between GP and LSP leaf unfolding onset allows us to focus on two goals in our study.
The first goal is to study the spatial and temporal variability of leaf unfolding (LU) of beech and oak stands. The satellite metric of Growth Speed Day (GSD), represented by the first derivative of the Fisher sigmoid function in the spring phase, is tied to the LU onset and was selected as the commonly used SOS. The anticipation is that a longer time series of MODIS imagery from 2000 to 2021, climatological data, and a more precise determination of the GSD will provide a statistically relevant and a more objective derivation of LU trends compared to previous works. New insights into the relationship between the LU onset, air temperature deviations, and elevation gradients are also expected. The inadequate explanation of these relationships and their changing trend have been pointed out by Chen et al. ([16]) and Meier et al. ([30]).
The second objective of the study is to verify the 6-parameter Fisher’s function for modelling the onset of spring phenophases in beech and oak stands. A higher accuracy in estimating the parameters of Fisher’s sigmoidal function and thus objectifying the onset of spring phenophases is expected compared to our previous studies ([7], [8]), where we used the Fisher function with 4 parameters and set the minimum value and the amplitude of NDVI as constants.
Material and methods
Study area
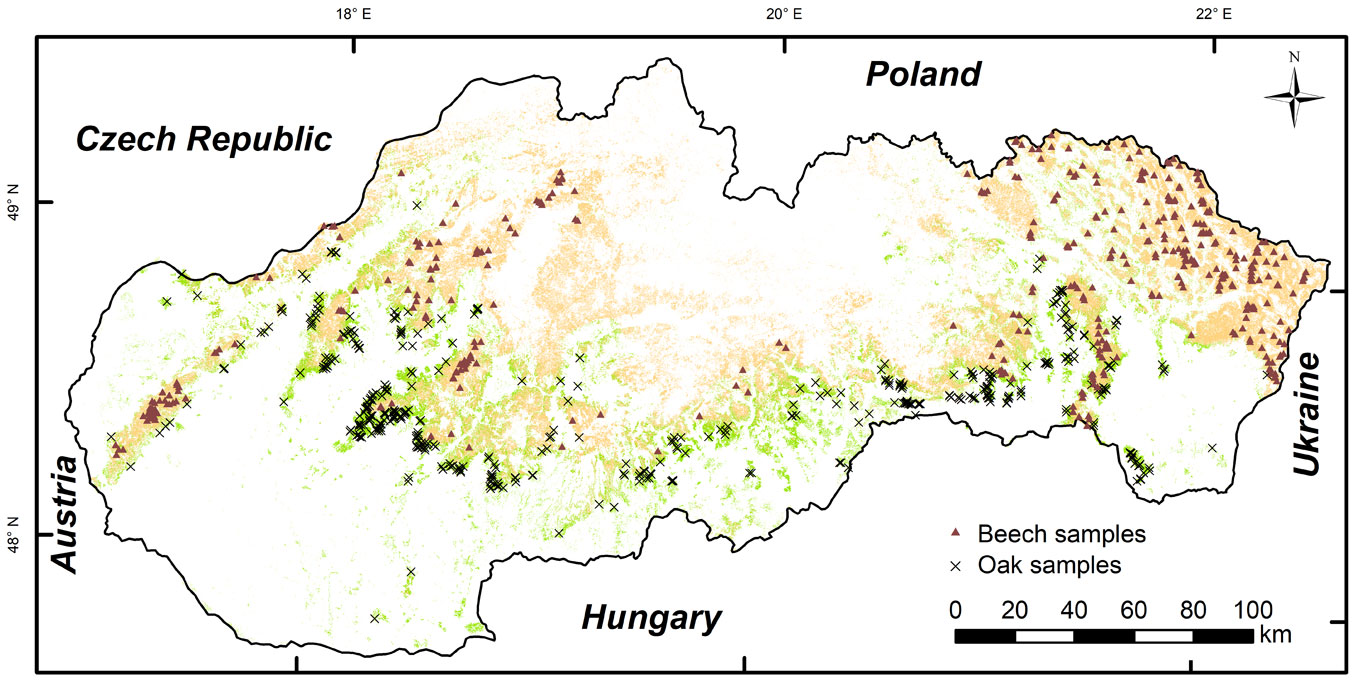
The study was conducted in forest stands in Slovakia dominated by European beech (Fagus sylvatica L.), Pedunculate oak (Quercus robur L.) and Sessile oak (Quercus petraea Liebl. - Fig. 1). These are the economically most important and most represented deciduous trees in Slovakia, as the occurrence of beech is 34.6% and oak 10.4% ([33]).
Fig. 1 - Forests in Slovakia with predominant occurrence of beech (orange colour) and oak (green colour), and spatial distribution of the analysed pixels with an occurrence of beech ≥ 90% (brown triangle) and oak ≥ 70% (black crosses).
Geographically, most of the territory belongs to the province of the Western Carpathians, and a part of Eastern Slovakia of about 21° 15′ longitude belongs to the province of the Eastern Carpathians ([22]). Slovakia is located in the northern temperate zone with a transitional climate, i.e., with the typical alternation of humid oceanic and dry continental air. The occurrence of oak stands is concentrated in the 1st to 3rd forest vegetation zones from the 8-point scale. This area has an average annual temperature of above 5.5 °C, annual precipitation up to 800 mm, and a growing season of 150 to 180 days. Most beech stands are in the 2nd to 5th forest vegetation zones with an average annual temperature of 4.5 to 8.5 °C, annual precipitation of 600 to 1050 mm, and a growing season of 110 to 180 days ([53]).
Cambisols are the predominant soil type on which oak and beech stands occur, followed by leptosols, luvisols and planosols, according to the Landscape Atlas of the Slovak Republic - Map of Soil Types ([32]). A large part of the studied beech stands, especially in the northeast of Slovakia, occurs in the flysch zone.
Workflow and selection of oak and beech stands
The study was based on MODIS satellite imagery, namely the products MOD09GQ, MYD09GQ, MOD09GA and MYD09GA. The products represent the spectral reflectance at the Earth’s surface, i.e., the effect of absorption and scattering of radiation in the atmosphere was eliminated (⇒ https://modis.gsfc.nasa.gov/data/dataprod/mod09.php).
The steps of the workflow are shown in the flowchart (see Fig. S1 in Supplementary material). The workflow consists of four main parts: (1) the selection of a homogenous sample for oak and beech stands; (2) the creation of the MODIS database and a derivation of the NDVI; (3) the modelling of the onset of spring phenophases for a set of oak and beech stands; and (4) the statistical data analysis.
For selecting oak and beech homogenous stands, we used the Landsat based tree species map of Slovakia ([5]), with a resolution resampled to 250 m corresponding to MOD09 pixel, combined with the Forest Management Information System database from the National Forest Centre. The database contains current compartment-level data and was used to calculate the proportion of beech and oak in 250 m pixels. Marginal pixels were excluded from the tree species map, since such pixels may be spectrally contaminated with other land cover categories in the MOD09 products ([43]), which could thus bias the derived NDVI values. Pixels where the proportion of beech was less than 90% were also left out. For oak, we excluded pixels with its proportion below 70% in order to keep a sufficient number of pixels for the analysis. The resulting masks of beech and oak stands contained 4539 and 981 pixels, respectively. Of these, we selected 376 pixels (beech) and 413 pixels (oak) by stratified random sampling, which were used for the LU onset analysis (Fig. 1). The number of pixels ensured that the samples fully represented the entire population of homogenous oak and beech stands.
The elevation distribution of the analysed oak and beech pixels is shown in Fig. S2a and Fig. S2b (Supplementary material). Elevations for individual pixels with oak and beech stands were estimated from Slovakia’s DMR3.5 digital relief model with a resolution of 10 m from the Geodetic and Cartographic Institute, resampled to the MOD09 resolution of 250 m.
Modelling of NDVI development and software solution
The MOD/MYD09GQ and MOD/MYD09GA products (collection 5 a 6) were downloaded from the United States Geological Survey Earth Resources Observation and Science Center ([45]) from 2000-2021. The products MOD/MYD09GA contain the quality assessment layer that was used to exclude pixels affected by clouds, cloud shadows, and high aerosol content from the analyses. From the MOD/MYD09GQ products, we derived the NDVI using red and infrared bands with a pixel resolution of 250 × 250 m according to the relationship (eqn. 1):
Layers for phenology modelling were created by overlapping the NDVI with oak and beech samples. The selection and pre-processing of MODIS images and the derivation of NDVI were described in detail in previuos studies studies ([7], [8]). Currently, a consistent database includes MOD/MYD09GQ and MOD/MYD09GA products and derived NDVI with a resolution of 250 × 250 m from 2000 to 2021.
The subject of the analysis was the NDVI time series from March to July over the years 2000-2021. The annual development of NDVI was modelled by the sigmoidal logistic function ([11] - eqn. 2):
where v(t) is the NDVI observed on a day of year t,vmin and vamp are parameters corresponding to the minimum value of the vegetation index (NDVI) and its amplitude, parameters m1 and n1 control the shape and the slope of the curve in the ascending (spring) phase, and parameters m2 and n2 control the descending (autumn) phase.
The annual NDVI profile was modelled by a double sigmoidal logistic function implemented in our proprietary and free software PhenoProfile (⇒ https://gis.tuzvo.sk/phenoprofile/). The main advantage of using proprietary software is the complete control of the modelling parameters, the setting of their initial values and possible ranges. Based on the input data (Julian day and NDVI), the application allows us to estimate the parameters of the Fisher’s sigmoidal function (eqn. 2) and calculate the first to third order derivatives and the corresponding day of the year (DOY - Fig. S3 in Supplementary material). The fitting of the phenological curves runs in parallel on the designated number of PC processor cores. The local extrema of the derivatives represent satellite metrics to which the onset of individual phenophases was assigned (Tab. 1).
Tab. 1 - Satellite-based phenological metrics and corresponding vegetative phenophases (GAD): Growth Acceleration Day (GSD): Growth Speed Day (GDD): Growth Deceleration Day (DOY): Day of Year.
| Satellite-based metrics | Mathematical representation of the satellite phenological metric ~ corresponding vegetation phenophase |
|---|---|
| GAD | Maximum (maximum acceleration) of the second derivative of eqn. 2 in the spring phase ~ beginning of bud burst |
| GSD | Extreme value of the first derivative of eqn. 2 in the spring phase ~ beginning of leaf unfolding (LU onset) |
| GDD | Minimum (maximum deceleration) of the second derivative of eqn. 2 in the spring phase ~ end of leaf unfolding |
In modelling the NDVI profiles for extensive (nationwide) pixel files, our previous studies ([6], [8]) used the Fisher’s function with the derivation of 4 parameters. The problems with using the 6-parameter model included the enormously increasing demands of computer power in the iterative derivation of model coefficients and the sensitivity of the model to the lack of data before and at the beginning of spring phases (budburst). Therefore, two parameters of eqn. 2 representing the minimum value and the amplitude of NDVI were set as constants. Their values were estimated from the NDVI at the end of winter dormancy and the period of maximum foliage ([6]). Tholt ([42]) obtained other values in a comprehensive analysis of the NDVI index for oak and beech forests from 2000 to 2020. The analysis also showed the differences between the minimum NDVI values for spring and autumn periods.
The subject of the refinement was the derivation of all six parameters of the Fisher’s function. To make the computation time acceptable, we defined the ranges of each parameter and divided the ranges into subspaces within which the iteration process proceeds. A higher number of subspaces allows for a more accurate estimation of the parameters but multiplies the duration of the iterative calculation. One solution is to perform the modelling in two steps for spring and fall phenophases separately. This approach is justified because the minimum value of NDVI vmin is different in spring and autumn ([42]). The ranges of parameters for modelling spring phenology for oak and beech are shown in Tab. 2. We achieved a computation time of 6-8 hours using a computer with a 6-core processor with samples containing around 400 pixels and ranges defined in Tab. 2.
Tab. 2 - Ranges of individual Fisher’s function parameters used for spring phenology modelling and partitioning of ranges into subspaces defined via the PhenoProfile configuration file. The NDVI layers used for modelling spring phenology covered a period from about the 70th to the 200th day of the year. The m2, n2 ranges and the subdivisional parameters Subdiv-m2 and Subdiv-n2 are crucial for autumn phenophases. We do not mention them because they have no influence on the calculation of the parameters for spring phenophases.
| Parameter | Oak | Beech |
|---|---|---|
| v min | 0.39 - 0.50 | 0.42 - 0.53 |
| v amp | 0.35 - 0.50 | 0.40 - 0.50 |
| m 1 | 10 - 40 | 10 - 35 |
| n 1 | 0.1 - 0.35 | 0.1 - 0.30 |
| Subdiv- vmin | 35 | 35 |
| Subdiv- vamp | 35 | 35 |
| Subdiv- m1 | 45 | 45 |
| Subdiv- n1 | 45 | 45 |
Satellite phenometrics and comparison with ground-based observations
A curve fitted according to eqn. 2 represented the basis for deriving the satellite metrics and determining the DOY of the phenophase onset. The vegetative phenophases corresponding to the satellite metrics are listed in Tab. 1.
The relationship between ground-based phenophase observations and satellite-based metrics was demonstrated by Pavlendova et al. ([35]) and Lukasová et al. ([27]) for beech stands. In this study, only the onset of leaf unfolding is analysed, i.e., the GSD metric. The LU onset is the phenological phase defined by DOY when the first light green leaves appeared on at least a half of individuals of the given observed group ([4]).
Ground-based phenological observations from the Slovak Hydrometeorological Institute (SHMI) stations, where more than 95% of LU onset data were available for each year from 2000 to 2021, were used to compare GSD modelling. The criteria were met by 22 oak and 36 beech phenology stations. The SHMI stations are evenly distributed across Slovakia and are located at sites where a higher number of woody plants can be observed at one plot. Therefore, the SHMI plots and the selected MODIS pixels do not spatially overlap. Using a two-sample Kolmogorov-Smirnov test, we tested the agreement between the SHMI plots and the MODIS pixels in terms of their elevation distribution. The test showed that the samples were identical and therefore suitable for the comparison of the ground and satellite-based LU onset (see Fig. S4 in Supplementary material for oak and beech samples).
Climatological data for analysis of leaf unfolding onset
Data from the Meteomanz web site (⇒ http://www.meteomanz.com/) were used to analyse relationships between climatological features and the DOY of leaf unfolding onset expressed by the GSD metric. Tab. S2, Tab. S3 and Tab. S4 (Supplementary material) contains the original downloaded data from the period 2000-2021, namely the monthly mean air temperature (T, in °C) in Slovakia and the calculated deviations of the monthly mean air temperatures (ΔT, in °C) from the long-term normal values (1961-1990) for February, March, and April in Slovakia.
Statistical evaluation of data
The basic data used for the statistical evaluation include the derived GSD values for each pixel of oak and beech samples and each year in the period 2000-2021. For the nationwide assessment of the LU onset, the GSD median for each year from 2000 to 2021 was calculated. The GSD intra-annual variability was expressed using 5th and 95th percentiles.
The nonparametric Mann-Kendall test (MKT) described in detail by Karmeshu ([19]) was used to evaluate GSD trends at the pixel level. The significance of the trend was expressed using the Z statistic. A positive Z-score indicates an upward trend (late onset of phenophases); conversely, a negative Z-score indicates a downward trend (earlier onset of phenophases). The pixels were grouped into six categories based on the Z statistics score, according to the nature of the trend (downward or upward) and its significance (non-significant, weakly significant and significant). The nationwide features of the trend (Z statistics, absolute and regression coefficients, and Tau coefficient) were calculated as an arithmetic mean of all pixels.
To check the changes in the GSD as a function of elevation, we derived trend characteristics for three elevation zones of oak (≤350 m, 350-500 m, and >500 m a.s.l.) and three of beech (≤500 m, 500-750 m, >750 m a.s.l.) in the same way as described above (Mann-Kendall test). The pixels that were located in the corresponding elevation zone were included in the respective calculation. In this study, the trend is significant (α = 0.05) when z > 1.96 (an upward trend) or z < -1.96 (a downward trend). If 1 ≤ z < 1.96 or -1.96 ≤ z < -1, the trend is considered weakly increasing or decreasing, respectively. If -1 ≤ z < 1, the trend is non-significant.
A nonlinear regression analysis was performed to analyse the relationships between the GSD and elevation using the arithmetic mean of GSD calculated for each pixel in the years 2000-2021.
Linear correlation and regression analyses were used to assess the dependence between the GSD and the nationwide deviation of monthly mean air temperature (ΔT in °C) from 1961-1990 long-term normal. The dependencies for February, March, and April and the arithmetic averages of February-April and March-April were examined separately. The GSD of oak and beech stands during 2000-2021 was calculated as the median of all analysed pixels, i.e., from 376 beech pixels and 413 oak pixels.
Results
Leaf unfolding: intercomparison of the satellite and ground-based observations
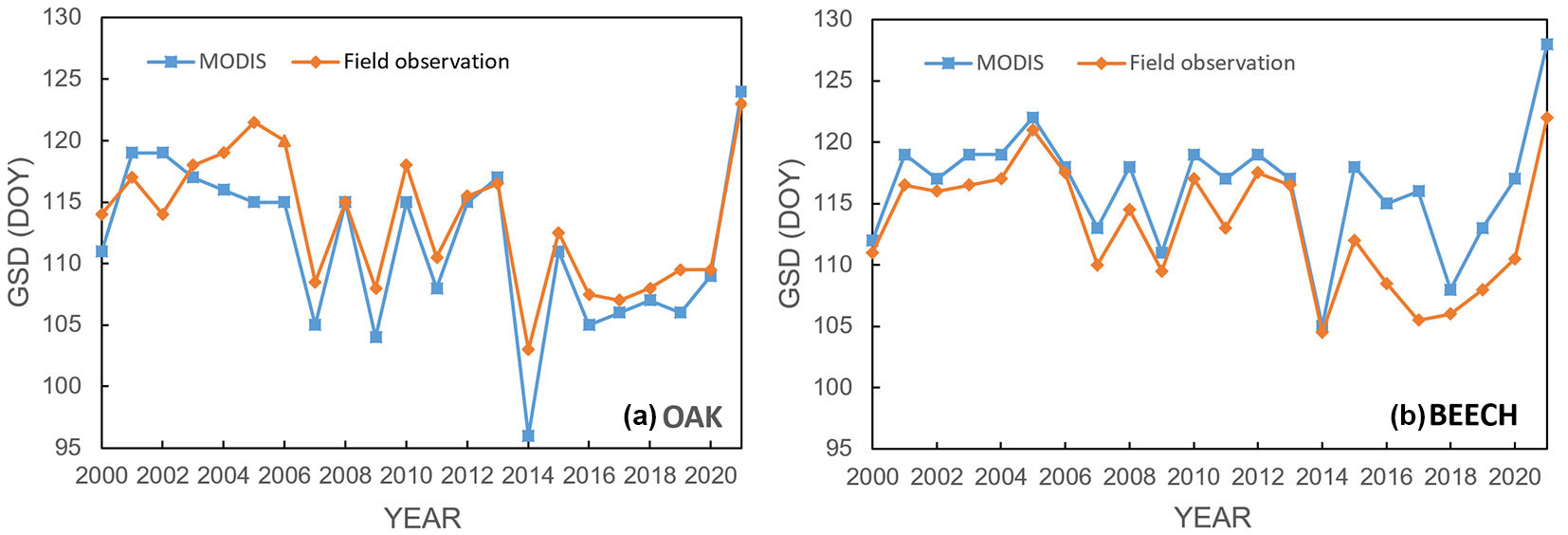
A comparison of the LU onset from ground-based phenological observations and MODIS observations expressed by the GSD metric is shown in Fig. 2a for oak and Fig. 2b for beech. The DOY of LU onsets represents the median calculated for each year 2000-2021 (see Tab. S1 in Supplementary material for the original data used to perform this analysis). The comparison of DOY over the entire period shows a close relationship between the ground-based and satellite determination of LU onset. This allowed identifying the years in which the differences between the satellite and ground-based DOY determination indicate possible errors that need to be checked. In the case of the oak stands, these are mainly the years 2002, 2005, 2006, and 2014. In the case of the beech stands, it is 2017. For the mentioned years, the GSD metric was re-derived by changing the original modelling parameters defined in Tab. 2. The aim was to extend the range of parameters of eqn. 2 and to double the subspaces within which the iteration process takes place. The calculation was extended to more than three days and confirmed the validity of the original GSD metrics. In no case the GSD difference exceeded 0.2 days compared to the calculation with the parameters given in Tab. 2. This confirmed our assumption that the setting of the parameter ranges is appropriate and does not bias the estimation of parameters.
Fig. 2 - Comparison of leaf unfolding onset (median) from MODIS and terrestrial phenological observations in oak (a) and beech (b) stands for 2000-2021. (X-axis): year; (Y-axis): day of the year (DOY).
Leaf unfolding development in 2000-2021
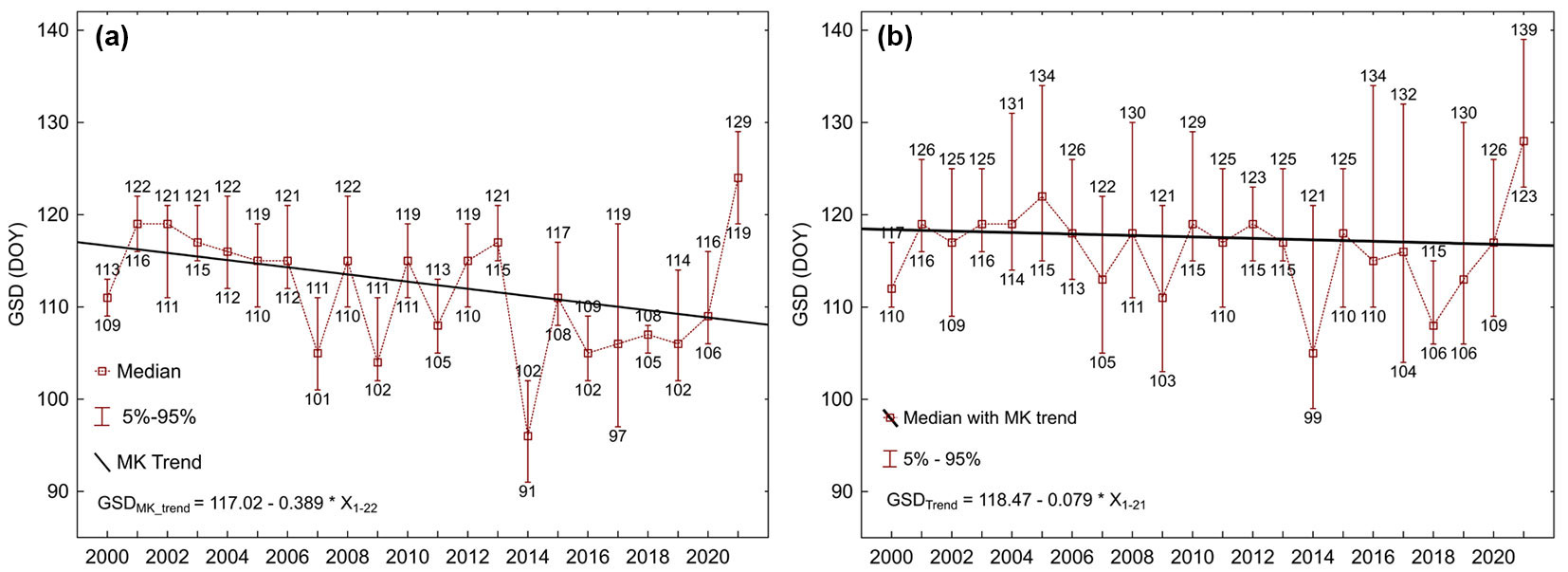
The LU onset expressed by the GSD metric and its intra-annual variability expressed by 5th and 95th percentiles from 2000 to 2021, and Mann-Kendall trend of GSD for oak and beech stands from the whole territory of Slovakia are shown in Fig. 3.
Fig. 3 - Onset of leaf unfolding (median of GSD), its duration (5th and 95th percentiles) and Mann-Kendall trend of GSD for (a) oak and (b) beech stands on the whole territory of Slovakia. (X-axis): year; (Y-axis): day of the year (DOY).
Fig. 3a (oak) and Fig. 3b (beech) show the significant intra- and inter-annual variability of the GSD. Under Carpathian conditions, the intra-annual variability was conditioned by elevation and the associated air temperature. The inter-annual variability of the GSD is determined and naturally varies according to the character of spring weather.
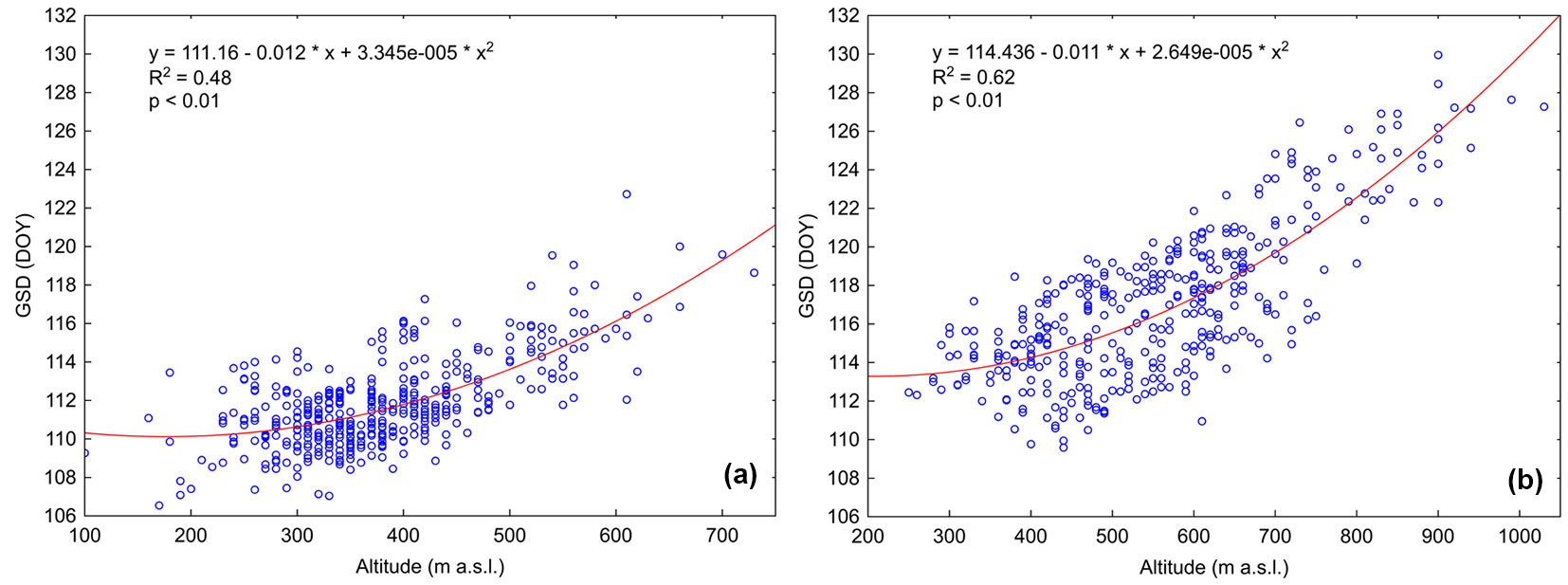
Fig. 4 shows the relationships between the GSD and elevation for oak and beech stands. The GSD was calculated for each pixel as the arithmetic mean for the period 2000-2021. The relation is nonlinear and is expressed in both cases (oak and beech) by the second-degree polynomial function. The later GSD with the increasing elevation is evident.
Fig. 4 - Correlation between elevation and onset of leaf unfolding (GSD average 2000-2021) for (a) oak and (b) beech.
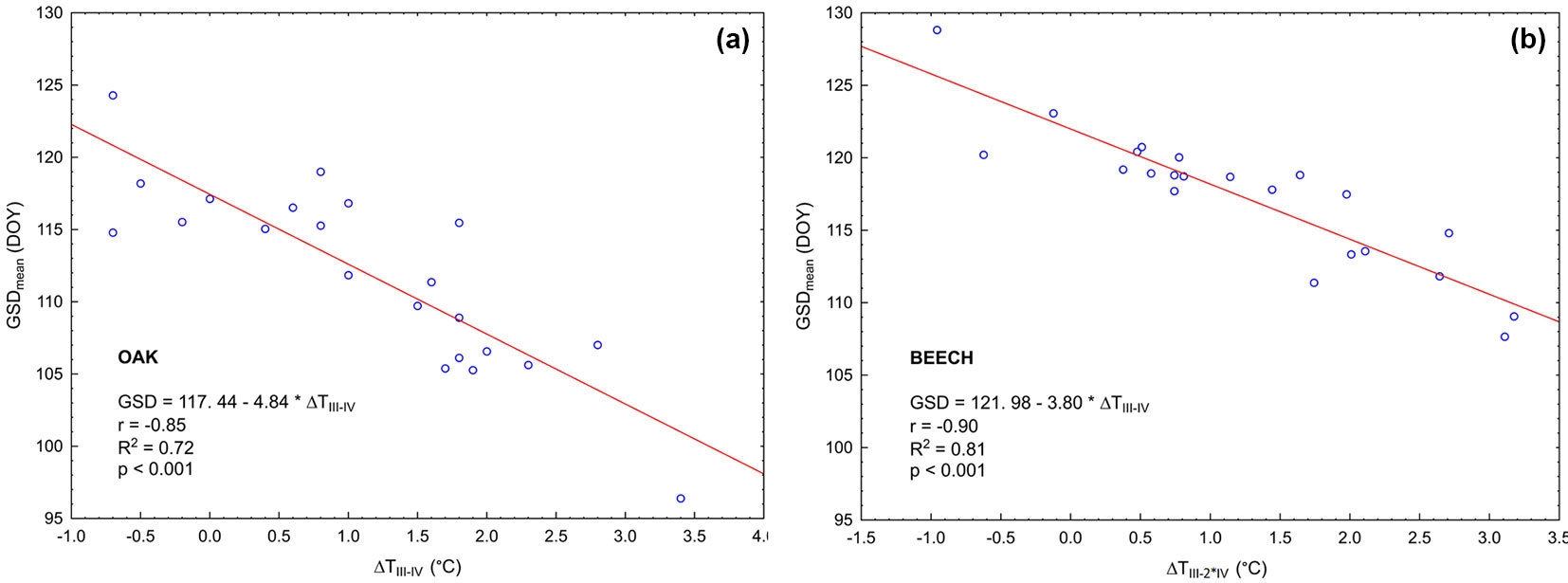
To quantitatively express the character of spring weather and to explain the year-to-year variability of GSD, we used the mean air temperature deviations of February, March, and April from 1961-1990 long-term normal. Fig. 5a for oak stands and Fig. 5b for beech stands show the highest dependences found between the arithmetic mean of temperature deviations in March and April ΔTIII-IV (°C) and GSD during 2000-2021. All correlations are listed in the supplementary material (Tab. S5). A weight of 2 was used for April to calculate the mean deviation ïΔTIII-IV (°C) for beech. We noted that the correlation coefficient would be the same if we used the mean temperature from TIII-IV (°C). The advantage of using a deviation is that its values directly quantify the magnitude of the temperature change. The prevailing positive deviations confirm the increase of temperature in the observed period (2000-2021) compared to the long-term normal 1961-1990. At the same time, it is thus possible to compare real deviations with different scenarios of temperature increase. For example, Kuster et al. ([25]) report that spring temperature in Central Europe is expected to increase by +2.2 to 4.2 °C in the 21st century.
Fig. 5 - Relationship between air temperature deviation and the GSD for (a) oak and (b) beech. X-axis: ΔTIII-IV (°C) - arithmetic mean of air temperature deviations of March and April in 2000-2021 from the long-term normal 1961-1990; Y-axis: GSDmean(DOY) - day of year of LU onset calculated as arithmetic mean of all pixels for each year from 2000-2021.
The statistical evaluation of the significance of the GSD trends (i.e., the slopes of regression equations in Fig. 5) using the Mann-Kendall test for the time series 2000-2021 is given in Tab. 3. The trends derived for each pixel of the oak and beech samples were grouped into six categories based on the Z-score, depending on the trend type (downward, upward) and its significance. The summary data for the whole samples of oak and beech are also given.
Tab. 3 - The distribution of oak and beech stands according to the statistical significance of the GSD trend for the period 2000-2021 based on the non-parametric Mann-Kendall test. (α): significance level; (Z-score): standardized Z-value; (P): confidence level in % (probability of the significance of the trend).
| Species | 2000-2021 | Significance level α |
Z-score | Confidence level P = (1 - α) |
Trend description | Number of pixels |
% of pixels |
|---|---|---|---|---|---|---|---|
| Oak | 1 | α < 0.05 | z < -1.96 | > 95 % | Significant downward | 84 | 20.3 |
| 2 | 0.05 ≤ α < 0.32 | -1.96 ≤ z < -1 | 68 - 95 % | Weak downward | 299 | 72.4 | |
| 3 | 0.32 ≤ α < 1 | -1 ≤ z < 0 | 0 - 68 % | Non-significant | 29 | 7 | |
| 4 | 0.32 < α ≤ 1 | 0 ≤ z < 1 | 0 - 68 % | Non-significant | 1 | 0.3 | |
| 5 | 0.05 < α ≤ 0.32 | 1 ≤ z < 1.96 | 68 - 95 % | Weak upward | 0 | 0 | |
| 6 | α ≤ 0.05 | z ≥ 1.96 | > 95 % | Significant upward | 0 | 0 | |
| - | Region-wide mean: | z = -1.61 | - | Weak downward | 413 | - | |
| Beech | 1 | α < 0.05 | z < -1.96 | > 95 % | Significant downward | 3 | 0.8 |
| 2 | 0.05 ≤ α < 0.32 | -1.96 ≤ z < -1 | 68 - 95 % | Weak downward | 139 | 37 | |
| 3 | 0.32 ≤ α < 1 | -1 ≤ z < 0 | 0 - 68 % | Non-significant | 174 | 46.3 | |
| 4 | 0.32 < α ≤ 1 | 0 ≤ z < 1 | 0 - 68 % | Non-significant | 46 | 12.2 | |
| 5 | 0.05 < α ≤ 0.32 | 1 ≤ z < 1.96 | 68 - 95 % | Weak upward | 13 | 3.4 | |
| 6 | α ≤ 0.05 | z ≥ 1.96 | > 95 % | Significant upward | 1 | 0.3 | |
| - | Region-wide mean: | z = - 0.48 | - | Non-significant | 376 | - |
The dependencies between the Kendall Theil-Sen slope (trend) of GSD and the elevation for oak and beech are depicted in Fig. S5 (Supplementary material). The trend over the period 2000-2021, calculated for each pixel, expresses the shift in the GSD in days per year. The relationship is nonlinear and is represented by a third-degree power function for both species. In oak stands, the trend towards an earlier GSD is more significant at lower elevations than at higher elevations. For beech the nature of the GSD trend changes at an elevation of about 700 m a.s.l. from an earlier to a later onset. The distribution of points in Fig. S5 (Supplementary material) served as the basis for a more detailed statistical evaluation of the significance of the trends in the GSD in 3 elevation zones using the Mann-Kendall test (Tab. 4). The derived statistics (Tau coefficient and p-value) determine the nature and the significance of the GSD trend for individual elevation zones and for the whole area of Slovakia with the occurrence of oak and beech stands.
Tab. 4 - GSD trends and their statistical significance determined by the nonparametric Mann-Kendall test. (T): Tau correlation coefficient; (p): p-value of significance of the regression coefficient; (n): number of pixels. The year (yr) as an independent variable is expressed from 1-22 (2000-2021) to directly convey the regression slope (trend) in days.
| Species | Elevational zone (m a.s.l) | n | Theil-Sen trend GSD = |
T | p | Trend type |
|---|---|---|---|---|---|---|
| Oak | 100-350 | 170 | 116.02 - 0.408 · yr | -0.26 | 0.12 | Weak downward |
| 350-500 | 186 | 117.16 - 0.409 · yr | -0.25 | 0.13 | Weak downward | |
| >500 | 57 | 119.58 - 0.269 · yr | -0.21 | 0.21 | Weak downward | |
| Whole country | 413 | 117.02 - 0.389 · yr | -0.25 | 0.13 | Weak downward | |
| Beech | 250-500 | 149 | 116.76 - 0.127 · yr | -0.12 | 0.44 | Non-significant downward |
| 500-750 | 189 | 119.04 - 0.090 · yr | -0.08 | 0.51 | Non-significant downward | |
| >750 | 38 | 122.54 + 0.162 · yr | 0.11 | 0.47 | Non-significant upward | |
| Whole country | 376 | 118.47 - 0.079 · yr | -0.07 | 0.48 | Non-significant downward |
Discussion
Notes on phenological modelling and intercomparison of results
Fig. 2 shows that the DOY of leaf unfolding onset from MODIS (expressed by GSD metric) and ground-based observations from SHMI phenological stations had the same patterns for both oak and beech stands during the 2000-2021 observation period. Four substantial differences found in 2002, 2005, 2006 and 2014 for oak and one in 2017 for beech were checked by recalculating the GSD from MODIS. The refined GSDs were not significantly different from the original ones. The observed differences remain unexplained, because no substantial differences occurred in other years. Moreover, the differences in 2002, 2005, 2006, and 2014 appeared only for oak, and the difference in 2017 appeared only for beech. Ground-based phenological observation errors cannot be excluded either. Therefore, we consider the MODIS-derived DOY validated and reliable for further analyses.
The assumption of a more accurate estimation of the parameters of the phenological curve using the 6-parameter Fisher function (eqn. 2) was confirmed in beech stands. This is most evident in the detection of gross errors in GSD in 2002 and 2003, published in Bucha & Koren ([8]). A more accurate result of the 6-parameter model was confirmed by the comparison of its output with ground-based observations in 2002 and 2003. In addition to the above differences, we found that the GSD identified with the 6-parameter model occurred on average 3 days later than the one from the 4-parameter model. This systematic shift was mainly caused by the low constant NDVI value vmin = 0.4295 used in the 4-parameter model of Bucha & Koren ([8]). Tholt ([42]) calculated vmin = 0.4671 in the comprehensive NDVI analysis from the spring period 2000-2020. In our study, an even higher average value vmin = 0.4805 was calculated when using the 6-parameter model (Tab. S1 in Supplementary material).
There were no substantial differences in the GSD of oak between the 6- and 4-parameter models, except for 2002 when we determined DOY 119 compared to DOY 112 in Bucha & Koren ([7]). DOY 115 from ground-based observations lies between the reported values and does not allow us to identify which value is incorrect. The mean difference between the 4- and 6-parameter models was -0.9 days, i.e., the later GSD was identified with the 6-parameter model, similar to beech.
It is worth noting the pitfalls of applying the 6-parameter model. In addition to the computational complexity that requires a more powerful computer, it is mainly the sensitivity of the 6-parameter model to missing data in the pre-vegetation period. This is the period in March and early April when snow cover can occur. Snow-contaminated pixels are usually excluded from the analysis by applying a quality layer because they distort the NDVI value. However, this causes a lack of data for modelling. In our case, this lack of data further exacerbates the exclusion of off-nadir images, even in the case of cloud-free images. One possible solution is to combine MODIS with MERIS (ESA) or Fengyun (China) images, which are in a nadir position to Slovakia on a given day.
The lack of data is reflected in inadequate estimates of the individual parameters of the Fisher’s function. This leads to unrealistic estimates of the days of onset of individual spring phenomena, including the GSD analysed in the study. In addition to the afore-mentioned combining with other satellite data, the solution is to define the ranges within which the individual parameters of the function can actually lie (Tab. 2).
Note that only NDVI data from DOY 70 to 200 were used to model the spring phenophases using Fisher’s sigmoidal function (eqn. 2). The m2, n2 parameters of the function are critical for autumn phenophases and do not affect the estimation of m1, n1 parameters.
Oak spring phenology
Oak GSD and its inter and intra-annual variability
The day of leaf unfolding onset (expressed as the median of GSD) varied naturally with the character of spring weather during 2000-2021, ranging from 96 to 124 DOY (Fig. 3a). The average of the medians for the 2000-2021 period was 111.6 DOY. The earliest dates of GSD were recorded in 2014 and 2009, when the median for Slovakia was 96 and 104 DOY, respectively. The most delayed to atypical GSD was observed in 2021 (124 DOY). According to SHMI meteorological reports, the temperature in March 2021 was normal. Nevertheless, April was below normal throughout Slovakia, with prevailingly unsettled and cold weather. This weather pattern contrasted with the above-average air temperatures in April over the past decade. It was related to atypical circulation conditions in the northern hemisphere due to the global climate change ([38]).
Intra-annual GSD variations are mainly caused by climatic conditions resulting from the elevation of oak stands and weather patterns. There is a strong nonlinear dependence between the GSD, expressed as the arithmetic mean of the years 2000-2021, and the elevation with the coefficient of determination R2 = 0.48 (Fig. 4a). The dependence shows that there is a shift in the GSD of ~0.14 days per 100 m in the 100-300 m elevation range, ~1.5 days per 100 m in the 300-500 m elevation range, and ~2.8 days per 100 m in the 500-700 m elevation range.
The time span of leaf unfolding onset of oak stands was expressed using 5th and 95th percentiles (Fig. 3a). The LU lasted shortest in 2018 and 2001, only 4 and 5 days, respectively. The short duration of the LU in 2018 was probably caused by a steep increase in air temperatures and an overall above-average to extremely warm April. The longest duration of LU equal to 23 days was recorded in 2017. According to SHMI climatological analyses, the LU onset in 2017 was accompanied by anomalies in weather patterns. The snowfall in the winter of 2016/ 2017 was extremely small, especially in the southern regions, resulting in a shortage of winter water supplies. The March 2017 with above-average temperatures, which could have ushered spring phenophases earlier, was followed by the cold and extremely wet April. This may have slowed and prolonged spring phenophases. In other years, the LU duration varied from 7 to 13 days. The average length of the LU for the entire study period was 10.1 days, substantially shorter than the 23.2 days derived from ground-based SHMI observations ([9]).
Relationship between oak GSD, climatic characteristics and trends
Several phenological observations of oak in the Carpathian region have shown that air temperature is crucial for the onset of spring phenophases. Skvareninová ([41]) found that the phenological phase of general bud burst depended on occurrence of average daily air temperatures exceeding 5 °C, and on the sum of mean temperatures exceeding 5 °C (TS5 = 124.1 °C). For the leaf unfolding onset, the temperature sum TS5 = 222.4 °C. The effect of temperature on GSD was also demonstrated in our results. The analysis of the whole period 2000-2021 at the national level showed the strongest dependence of the GSD on the mean air temperature deviation for March-April with the coefficient of determination R2 = 0.72 (Fig. 5a). The larger the positive/negative deviation from the normal (1961-1990), the earlier/later the LU onset (expressed by GSD). The relationship is linearly decreasing, i.e., a higher positive air temperature deviation leads to an earlier GSD. The regression coefficient in Fig. 5a shows that the March-April mean air temperature deviation from the normal by +1 °C causes an earlier GSD by 4.84 days. The effect of February temperature proved to be insignificant.
The length of the observed period (2000-2021) is sufficient for the statistically relevant derivation of GSD trends. Statistical results using the Mann-Kendal test at the national level showed a slight trend towards an earlier GSD in oak stands (Tab. 3). The rate of change at the national level is -0.39 days per year (see the regression coefficient for the whole country in Tab. 4). After dividing the entire set of 413 pixels into 6 categories according to the type of trend (downward, upward) and its significance (significant, weak, and insignificant), we found a significant or a weak trend towards an earlier GSD in 92.7% of oak stands (categories 1 and 2 in Tab. 3).
One of the manifestations of climate change in Slovakia is the increase in average annual air temperature by 1.1 °C over the last 100 years ([39]). The temperature growth also took place in the spring months of 2000-2021, as evidenced by the prevailing positive deviations of monthly average temperatures from the long-term normal 1961-1990 shown in Fig. 5a. Based on the strong relationships between GSD and elevation (Fig. 4a) and between GSD and deviation from reference temperatures (Fig. 5a), we conclude that the observed trend of earlier GSD (Fig. 3a, Tab. 3) can be explained by the increasing temperatures in the spring months and that warming leads to shifts in the onset of spring phenophases of oak stands.
Oak GSD in relation to elevation zones
From a practical perspective, when adapting a tree species composition to climate change, it is critical to know whether changes in GSD are uniform across the amplitude of the tree species occurrence. The answer for oak was provided by analysing the relationship between elevation and the shift in GSD (Fig. S5 in Supplementary material). The relationship shows that the trend in the onset of leaf unfolding is not uniform. Oak stands growing at different elevations respond differently to changes in climatic conditions. The Theil-Sen slope shows a more pronounced shift towards an earlier GSD at lower elevations from 100 to 500 m a.s.l. Most values range from -0.2 to -0.65 days per year. At elevations from 500 to 750 m, the shift towards an earlier GSD is less severe. The regression coefficients vary from -0.1 to -0.45 days per year. The 413 data points were widely spread out in the scatterplot between Elevation and TS Slope variables (Fig. S5 in Supplementary material).
Based on this finding, we divided the set of 413 pixels into 3 elevation zones and analysed the response of the oak stands in more detail using the MK test parameters: Theil-Sen slope, tau coefficient and p-value (Tab. 4). The analysis of the time series in 3 elevation zones showed a weak declining trend, i.e., a shift to an earlier GSD in all zones (see the negative regression coefficient for the regression equations in Tab. 4). This trend was more evident in the 100-350 m (p = 0.12) and 350-500 m (p = 0.13) zones than in the 500-750 m (p = 0.21) elevation zone. The shift to an earlier GSD was ~0.41 days per year in the first two zones. This corresponds to a shift of 8.6 days for the entire period 2000-2021. In the elevation zone of 500-750 m, the trend towards an earlier onset was milder, ~0.27 days per year, i.e., 5.6 days for the entire analysed period.
The findings show that the phenological response of oak stands to climate change is not linear along the elevation gradient. Therefore, adaptation measures in Slovak forestry practices are recommended to focus on elevations up to 500 m, where more significant changes were observed.
Beech spring phenology
Beech GSD and its inter and intra-annual variability
The GSD (median) of beech stands varied between 105 and 128 DOY from 2000 to 2021 (Fig. 3b). The earliest dates of GSD were recorded in 2014 (105 DOY) and 2018 (109 DOY). The latest leaf unfolding onset was observed in 2021 (128 DOY). The average of median values from 2000-2021 was 117.3 DOY, similar to the value of 116.6 DOY obtained by Vitasse & Basler ([48]) for the European beech at 107 sites in Germany during 1980-2009.
The intra-annual variability of the GSD is conditioned by the character of the weather in a given spring season and by the climatic conditions resulting from the elevation range of 250-1030 m a.s.l., where the studied beech stands are located. The time span of the onset of leaf unfolding was expressed by 5-95th percentiles of GSD values (Fig. 3b). The shortest time span lasted only 8 days in 2001. The longest one lasted 29 days in 2017, varying from 10 to 25 days in other years. The average duration of the LU onset for the whole observed period was 16.8 days (cf. for oak 10.1 days). The reason for the prolongation of the LU onset duration in 2017 might have been the interplay of several climatic anomalies described above for the oak stands (the cold but dry winter, warmer March than the long-term average and the cold and extremely rainy April).
There is a strong nonlinear dependence between the GSD, expressed as the arithmetic mean of years 2000-2021, and elevation with a coefficient of determination (R2 = 0.62 - Fig. 4b). The dependence shows that there is a shift in GSD of ~0.9 days per 100 m in the 250-500 m elevation range, ~2.2 days per 100 m in 500-750 m, and ~3.5 days per 100 m in 750-1000 m. These results refine previous findings of phenological observations of beech stands along the elevation gradient in Slovakia. Schieber et al. ([40]) found that in 2007-2011 the phenological gradient of spring phenological phases ranged from +2.83 to +3.00 days per 100 m. The cited authors used a linear relationship between elevation and the onset of leaf unfolding. However, a nonlinear relationship similar to ours (Fig. 4b) would better explain their data. Popescu & Sofletea ([37]) also revealed the nonlinear relationship between the LU onset and elevation under specific sub-mesothermal conditions of beech stands in the Romanian Carpathians. The shift of LU onset by 1.6 days in the elevation range 200-700 m and by 4.4 days in the range 700-1200 m is very close to our results in Slovak Carpathians.
A comparison of GSD of beech and oak stands at elevations of 200-500 m shows that the GSD of beech stands occurs 2 to 4 days later than in oak stands (Fig. 4a, Fig. 4b). This may indicate that leaf unfolding of beech is more strongly controlled by the day length (photoperiod) than that of oak. However, at an elevation of 700 m a.s.l., the GSDs of both species were almost identical. Vitasse et al. ([47]) demonstrated even more significant differences in the French Pyrenees. The authors reported that the bud burst of beech at low elevations (below 500 m) started 20 days later than in sessile oak, while at high elevations (above 1500 m) it started one week earlier. In summary, our results are consistent with those of Vitasse & Basler ([48]), according to whom beech can be considered a late-sprouting species under warm or mild climatic conditions, but not necessarily under colder climatic conditions in its range.
Relationship between beech GSD, climatic characteristics and trends
The analysis of the entire 2000-2021 period at the national level showed the strongest dependence of GSD on the air temperature deviation in March and April from the normal 1961-1990, with a coefficient of determination R2 = 0.81 (Fig. 5b). The influence of February temperature proved to be insignificant. The relation of March and April air temperatures with the LU onset was also found in studies of beech phenology in the Czech Republic ([23]) and Slovenia ([10], [46]). The deviations of March-April mean air temperatures from the long-term normal 1961-1990 shown in Fig. 5b are mostly positive, except for one more significant negative deviation, which corresponds to the atypical year 2021. The relationship is linearly decreasing, meaning that a higher positive air temperature deviation leads to an earlier GSD. The regression coefficient in Fig. 5b shows that the +1 °C deviation of the air temperature for March-April from the long-term normal (1961-1990) leads to an earlier GSD by 3.8 days. Marchand et al. ([29]) indicated that the onset of LU is also influenced by the onset of leaf senescence in the previous year. For a deeper understanding of the earlier LU onset, recent findings ([14]) that warmer temperatures during the previous growing season between May and September trigger earlier following spring phenology in the Northern Hemisphere need to be reviewed.
Based on the relationship between GSD and temperature, a change towards an earlier GSD in beech stands would have been expected during 2000-2021. However, only an insignificant trend was found (Tab. 3) towards an earlier GSD of ~0.08 days per year at the national level (see the regression coefficient for the entire country in Tab. 4). This is a significantly different result than for oak stands, which suggests that beech stands are not as sensitive to climate change as oak stands. After dividing the entire set of 376 analysed pixels into six categories based on the trend type (upward, downward) and its significance (significant, weak, and insignificant), the downward trend towards an earlier GSD was found in 37.8% of pixels representing beech stands (categories 1 and 2 in Tab. 3). In most pixels, 58.5% (categories 3 and 4 in Tab. 3), the trend was not significant, i.e., the analysis did not show a temporal shift in the onset of leaf unfolding phenophases. The analysis revealed an upward trend towards a later GSD in 3.7% of the pixels. These results do not contradict the latest studies; Piao et al. ([36]) reviewed that studies using multiple data sources and methods generally agree on the trend of advanced leaf unfolding due to climate change, but these trends appear to have slowed or even reversed in recent years.
Beech GSD in relation to elevation zones
The relationship between the elevation and the shift in GSD, expressed by the Kendall Theil-Sen slope, shows that the trend is not uniform (Fig. S5 in Supplementary material). Beech stands growing at different elevations responded differently to changes in climatic conditions. Theil-Sen slope shows a more pronounced shift towards an earlier GSD at lower elevations, from ~250 to ~700 m a.s.l. Most values range from 0.0 to -0.4 days per year. At elevations above 700 m, the nature of the trend changes towards a later GSD and the TS slopes vary from 0.0 to +0.4 days per year. As with oak, the data points were widely spread out in the scatterplot between Elevation and TS Slope variables. However, the dependence on elevation is stronger R2 = 0.29 (cf. R2 = 0.10 for oak). The set of 376 pixels was divided into 3 elevation zones to perform more detailed analyses using the MK test parameters: Theil-Sen slope, tau coefficient, and p-value (Tab. 4). The time series analysis revealed a shift towards an earlier GSD in the first and second elevation zones (250-500 and 500-750 m). However, the trend is statistically insignificant (p = 0.44 and p = 0.51, respectively). The opposite trend, a shift towards a later GSD, was observed in the third altitudinal zone (above 750 m). This trend was also statistically insignificant (p = 0.47).
In contrast to our results, Cufar et al. ([10]) found that the LU onset in beech stands in Slovenia occurred earlier at 1000 m a.s.l. (by 1.52 days per decade). Insignificant shifts were observed at lower elevations. This suggests that differences in the onset of spring phenophases are diminishing along elevational gradients. Similarly, an extensive climatological phenological study from Switzerland ([49]) on the spring phenophase of 4 tree species, including beech, has shown that global warming leads to a unification (loss of differences) of shifts in spring phenophases along elevation zones. The elevation phenological shift (EPS) in beech significantly decreased over time by 30% from ~28 days · 1000 m-1 in 1960 to ~17 days · 1000 m-1 in 2016.
In line with the mentioned results, Chen et al. ([16]) hypothesize that high elevation regions have been warming faster than low elevation regions under the current global warming. However, due to the lack of studies based on long-term and large-scale data, the relationship between tree spring phenology and elevation-dependent warming is unclear. Our results did not show a statistically significant trend in any altitudinal zone for oak or beech. For beech, the character of the trend suggests an earlier GSD at lower elevations and a later LU onset at higher elevations. In the oak case, a shift towards an earlier GSD can be observed, more pronounced at lower altitudes than at higher altitudes. Thus, there is a tendency to increase the difference in the GSD along the altitude for both species. This is in stark contrast to the reported findings of Cufar et al. ([10]), Vitasse et al. ([49]) and Chen et al. ([16]). Barka et al. ([2]), in one of the few macroregional studies of beech stands in Hungary and Slovakia, showed that the shift in the onset of spring phenophases is significantly influenced not only by elevation but also by latitude.
The different responses of oak and beech forests to climate change demonstrated in our work, together with discussed studies, confirm the need for more comprehensive macroregional and species-specific analyses to better understand the effects of climate change on forests and to use the new knowledge for forest management.
Conclusion
We analysed species-specific spring phenology in Slovakia using the land surface phenology approach. Based on the derived Mann-Kendall trend of the leaf unfolding onset from MODIS NDVI time series 2000-2021, we found the shift to an earlier onset by ~8.2 days for oak and statistically insignificant ~1.7 days for beech stands in Slovakia. The extended analyses of the GSD in relation to the altitude (3 zones) confirmed an earlier GSD in both beech and oak stands in all altitudinal zones, except for the beech in the zone above 750 m a.s.l. However, the intensity of the change was different; a stronger shift to an earlier onset was observed at lower altitudes and a milder shift was found at the highest zone. This implies that forestry decisions about changes in the restoration and target tree species composition in management models should first focus on altitudes up to 500 m, where more significant changes have been observed.
The revealed trends of earlier GSD were explained by rising temperatures in spring months. It was proved by mainly positive air temperature deviations in March and April from the long-term normal of 1961-1990 and, at the same time, by strong negative correlations between the LU onset and the mentioned temperature deviations. The results showed that oak stands reacted to climate change more sensitively than beech stands. It implies the need to analyse the species-specific response of forests to climate change.
In order to improve the quality of spatio-temporal analyses, several innovative approaches were applied in modelling the spring phenology development: (i) the 6-parameter model of Fisher’s sigmoidal function allowed to refine the estimation of phenological curve parameters. Compared to the 4-parameter model with constant values of vmin and vamp used in our previously published studies ([6], [7], [8]), the difference lies in calculating these parameters for each pixel. This refinement subsequently led to a more accurate derivation of the day of LU onset of the spring phenophases; (ii) to speed up the iterative process of the six parameters estimation of Fisher’s function (eqn. 2), we defined the allowed ranges of values of individual parameters. These ranges are written into the configuration file of the PhenoProfile application. The benefit is broader, as these values can be used as initial values when modelling Fisher’s function in other software applications, and thus can improve the modelling of the onset of phenophases.
The acquired knowledge about the non-linear response of tree species to climate change determines the direction of further research. There is a need to focus research on more detailed evaluations of relationships between climatic characteristics, and spatial (elevational and geographical) variability of changes in the onset of spring and autumn phenophases according to tree species. In future phenological-climatic analyses, it would be interesting to involve more detailed climatic characteristics on a daily or weekly basis, including precipitation, water balance and the observed increase of drought stress. A challenge is also using regional climate datasets based on a network of meteorological stations throughout Europe.
Author contributions
Conceptualization, T.B.; methodology, T.B.; software, M.K.; investigation, T.B. and Z.Si.; data curation, H.P. and Z.Si.; writing-original draft preparation, T.B.; writing-review and editing, T.B., M.K., Z.Si., H.P., and Z.Sn.; funding acquisition, T.B. and M.K. All authors have read and agreed to the published version of the manuscript.
Acknowledgements
This publication is the result of the implementation of the project “Research and Development for the Sustainable Development of the Forestry Sector in changing conditions” (TreeAdapt and DIGIWOOD subprojects) supported by the Ministry of Agriculture and Rural Development of the Slovak Republic and the project FOMON (ITMS 313011V465), supported by the Operational Programme Integrated Infrastructure (OPII) funded by the ERDF. We thank NASA for producing and distributing the MOD09 products.
References
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Online | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Zuzana Sitková 0000-0001-6354-6105
Hana Pavlendová 0000-0003-1336-9512
National Forest Centre - Forest Research Institute, T. G. Masaryka 22, 960 01 Zvolen (Slovak Republic)
Technical University in Zvolen, Faculty of Forestry, T.G. Masaryka 24, 960 01 Zvolen (Slovak Republic)
Slovak Hydrometeorological Institute, Zelená 5, 947 04 Banská Bystrica (Slovak Republic)
Corresponding author
Paper Info
Citation
Bucha T, Koren M, Sitková Z, Pavlendová H, Snopková Z (2023). Trends and driving forces of spring phenology of oak and beech stands in the Western Carpathians from MODIS times series 2000-2021. iForest 16: 334-344. - doi: 10.3832/ifor4121-016
Academic Editor
Angelo Nolè
Paper history
Received: Apr 25, 2022
Accepted: Sep 17, 2023
First online: Nov 19, 2023
Publication Date: Dec 31, 2023
Publication Time: 2.10 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2023
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 16544
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 12937
Abstract Page Views: 1904
PDF Downloads: 1345
Citation/Reference Downloads: 1
XML Downloads: 357
Web Metrics
Days since publication: 810
Overall contacts: 16544
Avg. contacts per week: 142.97
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2023): 1
Average cites per year: 0.33
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Remote sensing of Japanese beech forest decline using an improved Temperature Vegetation Dryness Index (iTVDI)
vol. 4, pp. 195-199 (online: 03 November 2011)
Research Articles
Phenology of the beech forests in the Western Carpathians from MODIS for 2000-2015
vol. 10, pp. 537-546 (online: 05 May 2017)
Research Articles
Assessing the performance of MODIS and VIIRS active fire products in the monitoring of wildfires: a case study in Turkey
vol. 15, pp. 85-94 (online: 19 March 2022)
Review Papers
Remote sensing-supported vegetation parameters for regional climate models: a brief review
vol. 3, pp. 98-101 (online: 15 July 2010)
Technical Reports
Detecting tree water deficit by very low altitude remote sensing
vol. 10, pp. 215-219 (online: 11 February 2017)
Review Papers
Accuracy of determining specific parameters of the urban forest using remote sensing
vol. 12, pp. 498-510 (online: 02 December 2019)
Research Articles
Fuel type characterization based on coarse resolution MODIS satellite data
vol. 1, pp. 60-64 (online: 28 February 2008)
Research Articles
Modelling the moisture status of habitats by using NDVI on the example of the Cerrado and Atlantic Forest biomes borderland (Brazil)
vol. 18, pp. 375-381 (online: 16 December 2025)
Review Papers
Remote sensing of selective logging in tropical forests: current state and future directions
vol. 13, pp. 286-300 (online: 10 July 2020)
Research Articles
Predicting phenology of European beech in forest habitats
vol. 11, pp. 41-47 (online: 09 January 2018)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword