Phenology of the beech forests in the Western Carpathians from MODIS for 2000-2015
iForest - Biogeosciences and Forestry, Volume 10, Issue 3, Pages 537-546 (2017)
doi: https://doi.org/10.3832/ifor2062-010
Published: May 05, 2017 - Copyright © 2017 SISEF
Research Articles
Abstract
The present paper introduces a satellite-based approach to the detection of phenology events in beech forests across Slovakia (the Western Carpathians) using the MOD/MYD09 products. Normalized vegetation index (NDVI) was used for determining the onset of the phenophases in spring and autumn. Double logistic sigmoid function was applied in order to fit the NDVI profile during the year. The satellite-derived phenological metrics was based on calculating the extreme values of the sigmoid function and its derivatives. Between 2000 and 2015, a time-series analysis using the linear regressions models revealed that the onset of leaf unfolding shifted at a rate of 0.8 day per decade, the onset of leaf fall was delayed at a rate of 1.9 day per decade, and the growing season (GS) extended at a rate of 1.1 day per decade. However, at a regional level, the trends were not found to be statistically significant in either case. Leaf unfolding/fall was significantly non-linearly delayed/advanced with the increase of altitude (p<0.01). GS duration varied extensively within the region. Theil-Sen estimation of GS trend revealed the median shift of 1.8 days, the range of shift being from -7.0 to +12.1 days at the 5-95 % quantile for 2000-2015. A significant inverse correlation between GS shift and GS length (p<0.01) was observed. The GS shift was positive in the sites with shorter GS and negative in the sites with longer GS.
Keywords
Introduction
Plant phenology studies the periodical recurrence of plant life cycle events. The importance of this traditional science has recently increased, especially in relation to climate change. The variations in the onset of the phenological phases of tree species are considered reliable indicators of environmental change ([22]). Several studies have verified the exploitability of AVHRR satellite data for the analysis of plant phenology at both trans-regional and global levels ([37], [29], [12]). The conditions for studying forest phenology noticeably improved after launching the Terra and Aqua satellites (NASA Earth Observation System Satellites) equipped with the MODIS spectroradiometer (Moderate Resolution Imaging Spectroradiometer). The instruments collect data in 36 spectral bands ranging in wavelength from 400 to 1450 nm at spatial resolutions from 250 m to 1000 m. The instruments capture an image of the entire Earth within 1-2 days ([17]). This allows the derivation of spectral indices for phenological observations. The most frequently used indices are the normalized difference vegetation index (NDVI) and the enhanced vegetation index (EVI), especially in broadleaf forests ([18], [25], [1], [14], [28], [15]). The latest research revealed that the combination of multiple indices may improve the prediction of phenological events ([35]).
Several approaches are available for modelling the seasonal variability of vegetation indices (VI), e.g., piecewise logistic functions ([36], [11]), an inverted parabola equation ([25]), an adaptive Savitzky-Golay filter, asymmetric Gaussians function ([8]), double logistic sigmoidal function ([7], [28]) and its modification ([15]).
During the last decade, phenology dynamics was analysed at pan-European level or at the level of European climatic zones ([29], [6], [13], [10], [12]). The research studies confirmed a general trend of extending season duration due to its earlier onset and its later end. However, extensive variations in this trend were observed within and between climatic zones and landscape types.
Phenological studies of forest tree species in Slovakia have been based on utilizing long-term ground-based observations obtained from a network of the phenological stations maintained by the Slovak Hydrometeorological Institute. Nevertheless, the observer’s possible bias and the sampling intensity applied are limiting factors in obtaining reliable data at a lower than the national level. Therefore, a combination of MODIS satellite data and phenological observations by monitoring sites is desirable and effective for understanding the processes through which forests respond to changing environmental condition. Consequently, the aim of this paper was: (i) to describe a satellite-based approach to creating a database for continuous regional phenological monitoring in deciduous forests including the quality check of selected images; (ii) to propose satellite phenological metrics and to derive the onset of spring and autumn phenophases in beech stands from the MODIS satellite images for the period of 2000-2015.
Materials and methods
Study area and data source
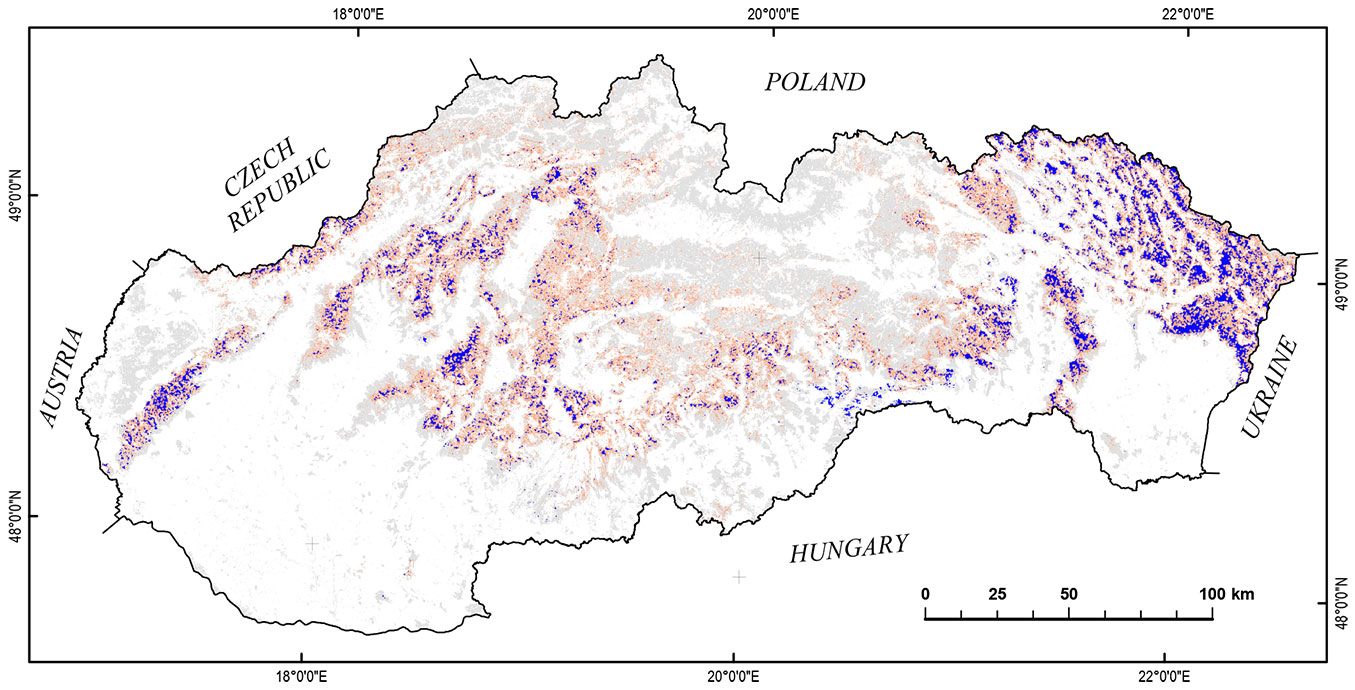
The research was conducted in the Slovak forests with the most important deciduous species of beech (Fagus sylvatica L.). The minimum proportion of beech was 40 % within 250 × 250 m pixels. The proportion was obtained from the official database of the Forestry Information System which contains data at compartment level (NFC Zvolen - ⇒ http://gis.nlcsk.org/lgis/). The total number of analysed pixels of beech stands was 24.969 covering an area of 156.056 ha (Fig. 1).
Fig. 1 - Beech stands representation ≥ 40 % in 250 × 250 m pixel (dark blue); beech occurrence in stands (orange); forest cover (grey - [4]).
Most of the beech stands extend between 250 and 1100 m with average in 565 m a.s.l. The altitudinal distribution is illustrated in Fig. S1 (Supplementary material). With regard to climatic conditions, the average annual temperature ranges from 4.5 to 8.5 °C, the annual precipitation is from 600 to 1050 mm, and the vegetation period lasts for 110-180 days.
MODIS product selection
The study was based on the MOD09 and MYD09 products (collection 5). The products represent the spectral surface reflectance with a spatial resolution of 250 m (MOD09GQ, MYD09GQ) and 500 m (MOD09GA, MYD09GA). The MOD/MYD09GA also provides 1-kilometer observation and geolocation statistics including a quality assessment (QA) layer.
The products in question had the radiometric and atmospheric corrections applied which eliminated the influence of absorption and scattering of radiation in the atmosphere. MOD09 images were obtained from the archives of USGS (United State Geological Survey - ⇒ http://e4ftl01.cr.usgs.gov). Despite the potentially adverse effect of anisotropic reflectance of the vegetation on the use of MODIS daily products ([16]), we used the MOD/ MYD09 because of spatial resolution and the necessity to capture immediate vegetation dynamics. Undoubtedly, Franch et al. ([9]) claim that the effect of surface anisotropy in the red and infrared band of MODIS data barely influence NDVI estimation, obtaining RMS around 1 %.
The MOD/MYD09GQ spectral bands 1 and 2 (centered at 648 nm and 848 nm) were used to derive the vegetation index NDVI at 250 m resolution. The “1km Reflectance Data State QA” layer from MOD/MYD09GA products was used for describing the quality of the product, particularly for cloud cover masking.
The extracted layers were decompressed and converted into ArcGIS format, subsequently transformed into the S-JTSK national coordinate system and clipped in order to cover the whole area of Slovakia. Using the Python programming language, we automated the retrieval of files from USGS servers and also partially automated their pre-processing in ArcGIS.
MODIS quality analysis
Image-level quality assurance
The quality of the assessment of phenological events is affected by image registration accuracy. Geolocation accuracy for MOD09 is approximately 50 m (1σ) at nadir ([34]). Moreover, the value of the spectral reflectance of each pixel is partly influenced by the spectral properties of adjacent pixels ([31]). This may increase the variability of the reflectance values. The pixels on the boundary between forest stands and other land cover classes were excluded from the analyses in order to minimize the variability of reflectance values.
Furthermore, we focused on the elimination of the pixels affected by clouds and cloud shadows as well as the impact of image distortions. All MODIS images covering the territory of Slovakia were reviewed at the NASA archive from 2000 to 2015, and their quality was visually assessed. Cloudless or partly cloudy imagery was utilized for the analyses.
Another criterion for the selection of appropriate images was the satellite position in relation to Slovakia during data collection. Since the MODIS tracks are stable with 16-day repetitions, we could identify that there were: 6 images in-nadir position related to Slovakia; 4 images in close-to-nadir position and 6 images in off-nadir position. Off-nadir images were completely excluded from downloading. Thus, we reduced the effect of anisotropic reflectance and achieved the spatial resolution close to 250 m. As the viewing angle increases, the actual ground pixel size increase continuously off-nadir both in along-track and along-scan directions ([20]).
Pixel-level quality assurance
In addition to the visual inspection of image quality, we analysed the “1km Reflectance Data State QA” layer present in the MOD09GA/MYD09GA products. The dataset enabled us to check the quality of recorded reflectance at the pixel level. The quality data of individual pixels are encoded as the values of individual bits in a 16-bit integer. MOD/MYD09 product quality description and an optimal combination of bit values applied in deciding on the inclusion or exclusion of a pixel in the analysis is given in Tab. 1.
Tab. 1 - MOD09 product - surface reflectance band quality description. Bold value = Accepted parameter state. The order at bit combinations starts with the highest bit.
| Bit No. | Value | Parameter name | Bit combination - parameter state |
|---|---|---|---|
| 0-1 | 1 2 | Cloud state | 00 - Clear; 01 - Cloudy; 10 - Mixed; 11 - Not set, assumed clear |
| 2 | 4 | Cloud shadow | 1 - Yes; 0 - No |
| 3-5 | 8 16 32 | Characteristics of land cover: land/water | 000 - shallow ocean; 001 - land; 010 - ocean coast or lake shore; 011 - Shallow inland water; 100 - ephemeral water; 101 - Deep inland water; 110 - continental/moderate ocean; 111 - Deep Ocean |
| 6-7 | 64 128 | Aerosol quantity | 00 - Climatology; 01 - Low; 10 - Average; 11 - High |
| 8-9 | 256 512 | Cirrus detection | 00- None; 01 - Small; 10 - Average; 11 - High |
| 10 | 1024 | Internal cloud algorithm | 1 - Cloud; 0 - No cloud |
| 11 | 2048 | Internal fire algorithm | 1 - fire; 0 - No fire |
| 12 | 4096 | Snow/ice | 1 - Yes; 0 - No |
| 13 | 8192 | Pixel is adjacent to cloud | 1 - Yes; 0 - No |
| 14 | 16384 | BRDF Correction performed | 1 - Yes; 0 - No |
| 15 | 32768 | Internal snow mask | 1 - snow; 0 - No snow |
Based on the data from the quality dataset, we selected pixels with the following bit values: 8, 72, 76, 136, 140, 200 and 8200. Other pixel values were replaced by 0. Reflectance values (DN values) of the selected pixels underwent a final quality analysis. The arithmetic mean of DN values and standard deviation (SD) were calculated for each day of an image selected from the database. A pixel was included in the analysis if its value ranged within x ± 2 SD. The pixels outside this range were assigned a bit value of 0.
After applying the rules for image and pixel selection, the total of 803 images of the MODIS images were used for the analyses of the period 2000-2015.
Constructing a phenological model
Modelling phenology entails predicting the onset of the main phenological events through the analysis of NDVI during the year. NDVI values were calculated from the MOD09 and MYD09. The annual development of NDVI was modelled on a sigmoidal logistic curve ([7] - eqn. 1):
where v(t) is NDVI observed at day of year t; vmin and vamp are parameters corresponding to the minimum value of the vegetation index (NDVI) and its amplitude; m1 and m2 parameters control the shape and slope of the curve of the ascending (spring) phase, and m3 and m4 parameters control the descending (autumn) phase.
In this study, vmin and vamp parameters were not subject to calculation using eqn. 1, but they were used as constants. For their determination, we first calculated the average value of NDVI (NDVIAVG) and its standard deviation (NDVISTD) for all deciduous stands with a dominant proportion of beech. The calculation of minimum NDVI values included 17 satellite images obtained before the spring vegetation period, primarily in late March and early April in order to avoid the contamination of reflectance by snow cover. The minimum value vmin was calculated as a difference NDVIAVG - NDVISTD. The calculation of the maximum NDVI values utilized 26 images acquired from late May to late August and the maximum value vmax was derived as NDVIAVG + NDVISTD. The amplitude vamp was calculated as a difference of vmax and vmin. In this manner, we calculated the values for beech: vmin = 0.429 and vamp = 0.497. Calculation of m1 - m4 parameters was done separately for each pixel with the beech occurrence. The extremes of the first and second derivatives of the eqn. 1 were used to determine the phenological events onset. The first derivative of the eqn. 1 had the following formula (eqn. 2):
The second derivative of the phenological function in eqn. 1 is as follows (eqn. 3):
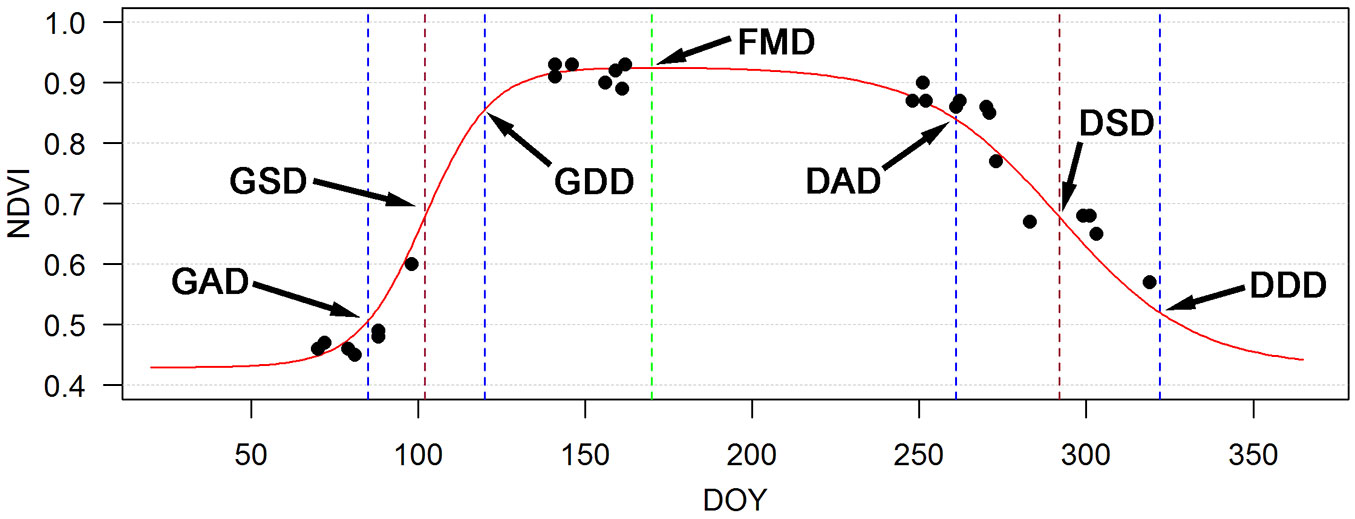
Days of the year (DOY) were assigned to the extremes (minimum or maximum) of the first and second derivatives, which were calculated for each pixel in spring and autumn. These days form the basis for satellite-derived phenological metrics (Fig. 2). The relation between ground-based phenological metrics and the proposed satellite-derived metrics were evaluated in a previous study ([24]). DOYs of onset of particular phenophases at 21 regional phenological stations of the Slovak Hydrometeorological Institute were compared with DOYs derived from MODIS. Linear regression was used in order to explain the relations between ground and satellite phenological observations.
The day of full foliage corresponds to the maximum value of the phenological function. The period of the maximal speed corresponds with the inflection point (IP) in spring or autumn phenological phases (Fig. 2). Other significant points of the function represent the days of maximal acceleration and maximal deceleration in spring and autumn phases, and these correspond to the local extremes of the second derivative of the sigmoid function.
Statistical evaluation of data
The onset of main phenophases (Tab. 2) in beech stands was expressed by median values of the day of the onset for each year from the period of 2000-2015. Intra-annual variation was expressed by the 5-95 % quantile.
Tab. 2 - Satellite-derived phenological metrics and corresponding vegetative phenophase.
| Metrics | Phenophase |
|---|---|
| GAD | Maximum (maximum acceleration) of the second derivative of the function in the spring phase ~ bud break onset |
| GSD | Extreme of the first derivative of the function in the spring phase (spring inflection point) ~ leaf unfolding onset |
| GDD | Minimum (maximum deceleration) of the second derivative of the function in a spring phase ~ end of leaf unfolding |
| FMD | Maximum of a phenological curve ~ Full foliage |
| DAD | Maximum (maximum acceleration) of the second derivative of the function in an autumn phase ~ leaf yellowing onset |
| DSD | Extreme of the first derivative of the function in an autumn phase (autumn inflection point) ~ leaf fall onset |
| DDD | Minimum (maximum deceleration) of the second derivative of the function in the autumn phase ~ the end of leaf fall |
The trends in the onset of spring and autumn phenophases were detected using the linear regression model during 2000-2015. The linear trend with the corresponding equation and the coefficient of determination was included in the graphs. The statistical significance of the regression model was tested by the Student’s t-test.
The linear correlation analysis was used in deriving the relationships between the onsets of individual phenophases.
Regression analyses were applied in analysing spatial variation of GSD (DSD) as the function of altitude, latitude and longitude. In the spatial analyses, we used the mean values of the onset of the phenophases pixel (GSDavg, DSDavg) calculated from the period of 2000-2015 for each pixel.
In order to evaluate GSD and DSD trends at the pixel level, we utilized the nonparametric Mann-Kendall test (MKT). The test is based on calculating the Mann-Kendall test Z statistics, which is a measure of the significance of the trend. A positive Z-score indicates an upward trend (late onset of phenophases); conversely, a negative Z-score indicates a downward trend (earlier onset of phenophases). A more detailed explanation of MKT is given in Karmeshu ([19]).
The statistical evaluation of the significance of the time series trends during 2000-2015 based on MKT was carried out at two levels: for each pixel and for the whole region. The results for individual pixels were put into a table within which the pixels, based on the Z statistics score, were grouped into six categories according to the nature of the trend (decreasing or increasing) and its significance (non-significant, weakly or moderately significant). The region-wide features of the trend (Z statistics) were evaluated as a mean value of all pixels. In this study, the trend is of moderate significance (P = 0.90, α = 0.10, z0.05 = 1.64) if z > 1.64 (upward trend) or z < -1.64 (downward trend). If 1 ≤ z < 1.64, we consider the trend as slightly increasing, or decreasing if -1.64 ≤ z < -1. If -1 ≤ z < 1, the trend is deemed insignificant.
The duration of the growing season (GS) at the region-wide level was calculated for each year of the period of 2000-2015 as the difference between the median day of the onset of leaf fall and the onset of leaf unfolding, i.e., GS = DSDmed - GSDmed . Simple linear regression was used for an estimation of GS trend between 2000 and 2015 at the region-wide level.
At the pixel level, an average duration of GS (GSavg) for 2000-2015 was calculated as the arithmetic mean of the differences between the day of onset of leaf fall and the onset of leaf unfolding. These differences were calculated for each pixel and each year during the period of 2000-2015.
For the evaluation of GS length trend at pixel level we used the nonparametric Mann-Kendall test (MKT) in the same way as for the phenophases. The Theil-Sen slope and intercept was used in order to estimate the change in the observations during the period of 2000-2015.
The growing season shift was calculated as: Theil-Sen slope × period length (15 years in this study). GS shift represents a change of the length of vegetation season in days during the period of 2000-2015.
Results
The dataset description
In total, 803 of the MOD09 and MYD09 images from the period of 2000-2015 passed the quality control. Due to cloudiness, not all years and seasons of the year were evenly covered. The numbers of images used for the analyses range from 31 in 2013 to 81 in 2010, which is considered as a sufficient number for phenology modelling. The description of the dataset included into analyses is given in Tab. S1 (Supplemetary material).
A leaf unfolding and leaf fall phenophase
The overview of the onsets of spring and autumn phenophases of beech stands during the period of 2000-2015 is given in Tab. 3.
Tab. 3 - Onset of spring and autumn phenophases.
| Phenophase | Statistics | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | AVG |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GAD | Median | 107 | 105 | 95 | 101 | 108 | 107 | 109 | 98 | 98 | 100 | 110 | 107 | 110 | 112 | 88 | 107 | 103.9 |
| 5 % quantile | 103 | 93 | 84 | 88 | 99 | 99 | 98 | 82 | 88 | 95 | 101 | 97 | 100 | 108 | 84 | 97 | 94.8 | |
| 95 % quantile | 111 | 116 | 116 | 116 | 115 | 119 | 116 | 106 | 115 | 107 | 117 | 113 | 116 | 118 | 99 | 115 | 113.4 | |
| Length | 8 | 23 | 32 | 28 | 16 | 20 | 18 | 24 | 27 | 12 | 16 | 16 | 16 | 10 | 15 | 18 | 18.7 | |
| GSD | Median | 111 | 117 | 110 | 113 | 117 | 119 | 118 | 110 | 114 | 110 | 119 | 116 | 118 | 118 | 106 | 117 | 114.6 |
| 5 % quantile | 109 | 108 | 99 | 104 | 112 | 112 | 111 | 104 | 106 | 104 | 114 | 108 | 111 | 115 | 98 | 110 | 107.8 | |
| 95 % quantile | 118 | 124 | 122 | 123 | 129 | 130 | 129 | 119 | 126 | 119 | 130 | 123 | 124 | 126 | 119 | 124 | 124.1 | |
| Length | 9 | 16 | 23 | 19 | 17 | 18 | 18 | 15 | 20 | 15 | 16 | 15 | 13 | 11 | 21 | 14 | 16.3 | |
| GDD | Median | 116 | 128 | 122 | 123 | 126 | 132 | 126 | 123 | 128 | 118 | 128 | 125 | 124 | 124 | 120 | 126 | 124.3 |
| 5 % quantile | 114 | 120 | 112 | 116 | 119 | 123 | 119 | 112 | 120 | 110 | 120 | 116 | 120 | 120 | 110 | 118 | 116.8 | |
| 95 % quantile | 126 | 137 | 132 | 133 | 144 | 144 | 144 | 133 | 141 | 133 | 150 | 137 | 137 | 137 | 139 | 136 | 137.7 | |
| Length | 12 | 17 | 20 | 17 | 25 | 21 | 25 | 21 | 21 | 23 | 30 | 21 | 17 | 17 | 29 | 18 | 21.1 | |
| DAD | Median | 265 | 277 | 277 | 272 | 273 | 281 | 279 | 273 | 265 | 278 | 273 | 283 | 273 | 273 | 273 | 281 | 274.8 |
| 5 % quantile | 253 | 260 | 265 | 253 | 263 | 273 | 265 | 253 | 253 | 267 | 257 | 266 | 259 | 257 | 263 | 272 | 261.2 | |
| 95 % quantile | 278 | 284 | 286 | 283 | 281 | 286 | 285 | 281 | 277 | 283 | 278 | 289 | 283 | 282 | 283 | 285 | 282.8 | |
| Length | 25 | 24 | 21 | 30 | 18 | 13 | 20 | 28 | 24 | 16 | 21 | 23 | 24 | 25 | 20 | 13 | 22.1 | |
| DSD | Median | 289 | 293 | 299 | 295 | 293 | 296 | 295 | 291 | 289 | 295 | 291 | 301 | 294 | 292 | 299 | 296 | 294.3 |
| 5 % quantile | 281 | 282 | 286 | 285 | 287 | 291 | 289 | 283 | 280 | 289 | 283 | 294 | 287 | 283 | 290 | 291 | 286.3 | |
| 95 % quantile | 299 | 301 | 314 | 303 | 299 | 300 | 301 | 297 | 295 | 302 | 299 | 306 | 306 | 299 | 311 | 301 | 302.1 | |
| Length | 18 | 19 | 28 | 18 | 12 | 9 | 12 | 14 | 15 | 13 | 16 | 12 | 19 | 16 | 21 | 10 | 15.8 | |
| DDD | Median | 311 | 311 | 319 | 318 | 313 | 311 | 309 | 310 | 311 | 313 | 311 | 319 | 314 | 311 | 324 | 312 | 313.6 |
| 5 % quantile | 298 | 298 | 300 | 310 | 305 | 305 | 304 | 304 | 298 | 305 | 302 | 312 | 303 | 300 | 311 | 306 | 303.8 | |
| 95 % quantile | 326 | 325 | 350 | 335 | 326 | 318 | 326 | 326 | 326 | 324 | 326 | 335 | 339 | 326 | 350 | 319 | 329.8 | |
| Length | 28 | 27 | 50 | 25 | 21 | 13 | 22 | 22 | 28 | 19 | 24 | 23 | 36 | 26 | 39 | 13 | 26.9 |
During the period of 2000-2015, the onset of leaf unfolding (GSD metrics) changed; the change chiefly depending on the temperature in late winter and spring. The earliest onset of the phenophase of GSD was recorded in 2014 the median value being DOY 106. The latest onset was observed in 2005 and 2010 (DOY 119). The average of the onset of leaf-unfolding for 2000-2015 was 114.6 days. The range within which the leaf unfolding of beech stands starts is expressed by the 5-95 % quantile. The shortest duration of the GSD phenophase occurred in 2000, namely 9 days from DOY 109 to 118. The longest duration was observed in 2002, namely 23 days from DOY 99 to 122. The average length of the phenophase for the whole studied period was 16.3 days.
The earliest onset of the phenophase of leaf fall (DSD metrics) of beech was recorded in 2000 and 2008, the median values in Slovakia being DOY 289. The latest onset was observed in 2011, namely DOY 301. The average onset of leaf-fall for the period of 2000-2015 was 294.3 DOY. The average duration of the leaf fall phenophase was 15.8 days, with the minimum of 9 days in 2005 and the maximum of 28 days in 2002 expressed by the 5-95 % quantile.
There was a significantly earlier onset of spring phenophases (GAD = 88, GSD = 106 DOY) in 2014 and a later onset of autumn phenophases (DSD = 319 DOY) in 2011. These onsets were caused by exceptionally warm spring in 2014 and autumn in 2011. Close relationships between the deviations of spring (autumn) temperature from long-term normal and GSD (DSD) onsets are illustrated in Fig. S2 and Fig. S3 in the Supplementary material.
Time-series analysis
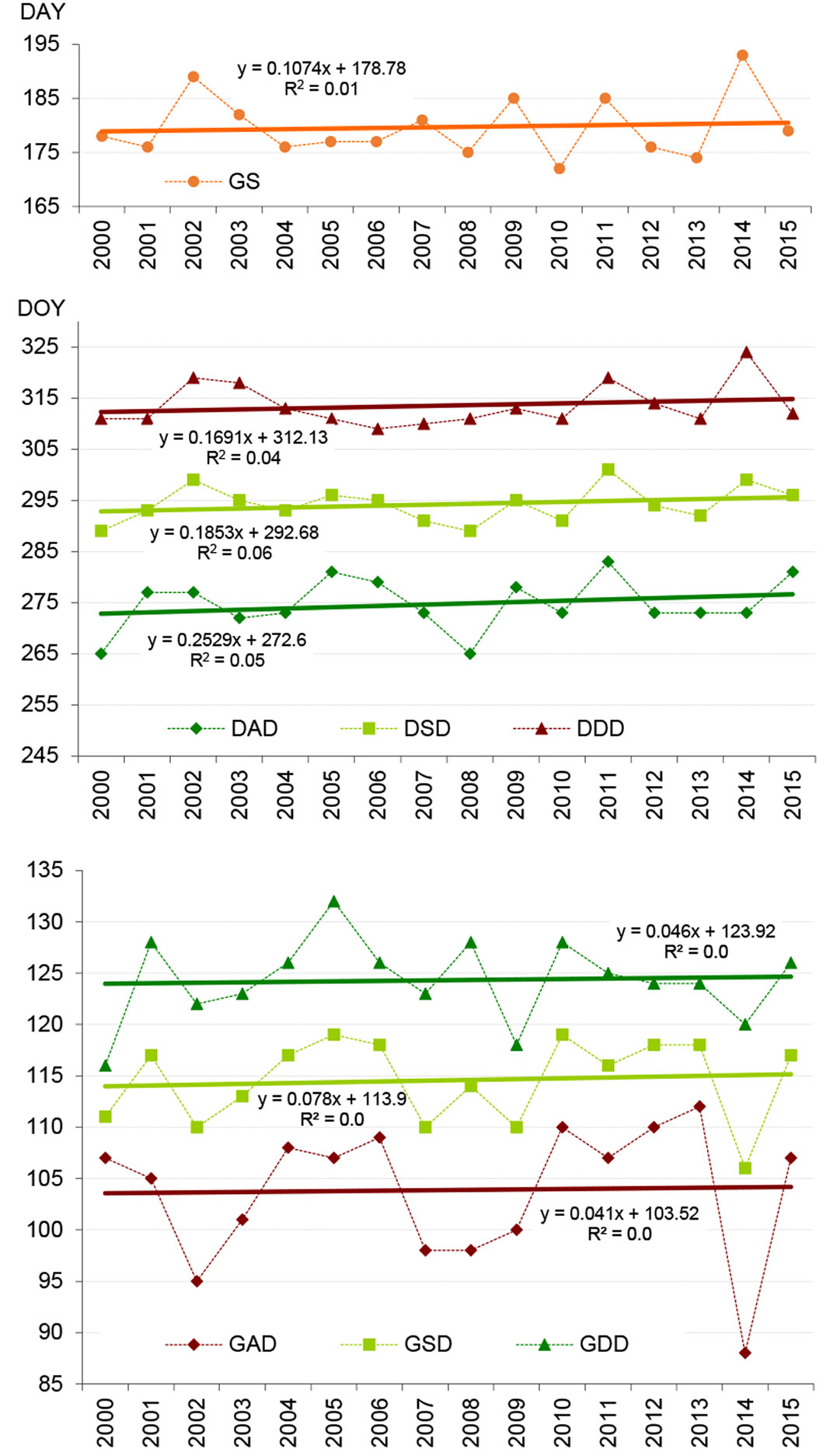
Our analysis based on the linear regressions model at a region-wide level demonstrated a very slight shift towards a later onset of the spring and autumn phenophases (see the positive regression coefficient in the regression equations in Fig. 3). The trends were not found to be statistically significant in either case (p > 0.34).
Fig. 3 - The onsets and trends of spring and autumn phenophases and growing season length in the period 2000-2015. (GAD): bud break onset; (GSD): leaf unfolding onset; (GDD): end of leaf unfolding; (GS): growing season; (DAD): leaf yellowing onset; (DSD): leaf fall onset; (DDD): end of leaf fall.
The correlation matrix of the onsets of individual phenophases (Tab. 4) showed strong interdependence between spring phenophases (GAD-GSD and GSD-GDD), as well as between autumn phenophases (DAD-DSD and DSD-DDD). Unexpected negative coefficients between the onset of spring and autumn events (GAD-DDD and GSD-DDD) were indicated: later GAD (GSD) are related to earlier DDD or vice versa earlier GAD (GSD) are related to later DDD.
Tab. 4 - Correlation matrix between the onsets of the phenophases of the period 2000-2015. (*): p<0.05; (**): p<0.01; (***): p<0.001.
| Correlations | GAD | GSD | GDD | DAD | DSD | DDD |
|---|---|---|---|---|---|---|
| GAD | 1 | 0.88 *** | 0.37 | 0.17 | -0.29 | -0.62 * |
| GSD | - | 1 | 0.75 *** | 0.30 | -0.17 | -0.55 * |
| GDD | - | - | 1 | 0.33 | -0.02 | -0.35 |
| DAD | - | - | - | 1 | 0.74 ** | 0.12 |
| DSD | - | - | - | - | 1 | 0.73 ** |
| DDD | - | - | - | - | - | 1 |
The results of the statistical evaluation yielded by the Mann-Kendall trend test at a regional level have not demonstrated any trend changes in the onset of phenophases GSD, DSD and growing season (GS) lengths (Tab. 5 - the region-wide average).
Tab. 5 - Non-parametric Mann-Kendall Test. Statistical significance and trends in the onset of spring and autumn phenophases and growing season length for the period 2000-2015. (P): Confidence level in %.
| Phenophase | GSD | Significance level α |
Z-value | P (1-α) |
Trend description |
Number of pixels |
% Pixels |
|---|---|---|---|---|---|---|---|
| GSD | 1 | α < 0.10 | z < -1.64 | >90 | Moderate downward trend | 139 | 0.6 |
| 2 | 0.10 ≤ α < 0.32 | -1.64 ≤ z < -1 | 68-90 | Weak downward trend | 918 | 3.7 | |
| 3 | 0.32 ≤ α < 1 | -1 ≤ z < 0 | 0-68 | Non-significant trend | 6807 | 27.3 | |
| 4 | 0.32 < α ≤ 1 | 0 ≤ z < 1 | 0-68 | Non-significant trend | 13055 | 52.3 | |
| 5 | 0.10 < α ≤ 0.32 | 1 ≤ z < 1.64 | 68-90 | Weak upward trend | 3287 | 13.2 | |
| 6 | α ≤ 0.10 | z ≥ 1.64 | >90 | Moderate upward trend | 763 | 3.1 | |
| Region-wide average: z = 0.288 | |z| < z0.05 = 1.64 | Non-significant trend | 24969 | - | |||
| DSD | 1 | α < 0.10 | z < -1.64 | >90 | Moderate downward trend | 85 | 0.3 |
| 2 | 0.10 ≤ α < 0.32 | -1.64 ≤ z < -1 | 68-90 | Weak downward trend | 390 | 1.6 | |
| 3 | 0.32 ≤ α < 1 | -1 ≤ z < 0 | 0-68 | Non-significant trend | 4285 | 17.2 | |
| 4 | 0.32 < α ≤ 1 | 0 ≤ z < 1 | 0-68 | Non-significant trend | 12156 | 48.7 | |
| 5 | 0.10 < α ≤ 0.32 | 1 ≤ z < 1.64 | 68-90 | Weak upward trend | 5145 | 20.6 | |
| 6 | α ≤ 0.10 | z ≥ 1.64 | >90 | Moderate upward trend | 2908 | 11.6 | |
| Region-wide average: z = 0.643 | |z| < z0.05 = 1.64 | Non-significant trend | 24969 | - | |||
| GS (DSD-GSD) |
1 | α < 0.10 | z < -1.64 | >90 | Moderate downward trend | 240 | 1 |
| 2 | 0.10 ≤ α < 0.32 | -1.64 ≤ z < -1 | 68-90 | Weak downward trend | 866 | 3.5 | |
| 3 | 0.32 ≤ α < 1 | -1 ≤ z < 0 | 0-68 | Non-significant trend | 6690 | 26.8 | |
| 4 | 0.32 < α ≤ 1 | 0 ≤ z < 1 | 0-68 | Non-significant trend | 12081 | 48.3 | |
| 5 | 0.10 < α ≤ 0.32 | 1 ≤ z < 1.64 | 68-90 | Weak upward trend | 3321 | 13.3 | |
| 6 | α ≤ 0.10 | z ≥ 1.64 | >90 | Moderate upward trend | 1771 | 7.1 | |
| Region-wide average: z = 0.352 | |z| < z0.05 = 1.64 | Non-significant trend | 24969 | - | |||
However, after organizing the whole set of analysed pixels into six categories based on the trend pattern (decreasing or increasing) and its significance (insignificant, slightly and moderately significant), we found that 16.3 % of the beech stands (Tab. 5 - GSD metrics: category 5 and 6) exhibited a later onset of the spring phenophase of leaf unfolding. The majority of stands (79.6 % category 3 and 4) showed no change in trend. A portion of stands (4.3 %) manifested a tendency to an earlier onset.
With regard to the autumn phenophase of leaf fall (Tab. 5 - DSD metric), 32.2 % of beech stands exhibited a tendency towards a later onset of the phenophase (upward trend), whereas a downward trend was observed in 1.9 % of the stands. For 65.9 % of stands no significant trend was observed.
Regarding the growing season, 20.4 % of stands exhibited a tendency towards an increased length (Tab. 5 - GS category 5 and 6), whereas the downward trend (shorter GS) was observed in 4.5 % of the stands. At 75.1 % stands, we did not observe any particular trend.
Spatial and altitudinal aspects of the onset of phenophases
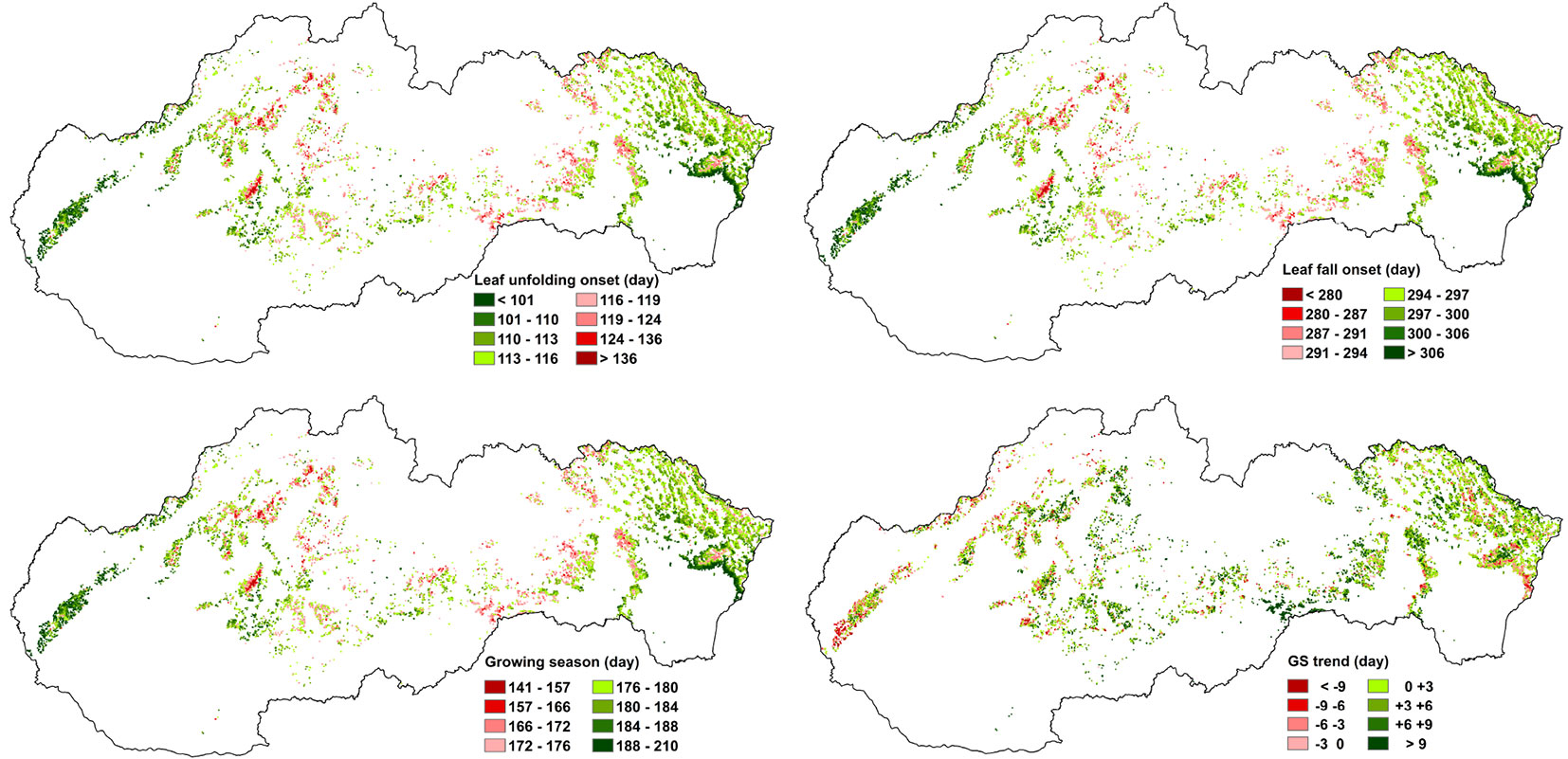
The maps graphically depicting the spatial variation of the beginning of leaf unfolding and leaf fall of beech stands in Slovakia, expressed as an average value for the period of 2000-2015, are presented in Fig. 4 (top). The average duration of the growing season and the growing season shift are illustrated in Fig. 4 (bottom). In order to enhance the visual perception, the number of pixels in all figures was magnified by a median filter with the dimensions of 3 × 3 pixels.
Fig. 4 - GSDavg (top-left) and DSDavg (top-right) - average values of the onset of leaf-unfolding and leaf-fall for the period of 2000-2015; GSavg (bottom-left) - average duration of the growing season for the period 2000-2015; GSshift (bottom-right) - growing season shift in days between 2000 and 2015: negative (red) values imply a shift to shorter GS, positive (green) value imply a shift to longer GS.
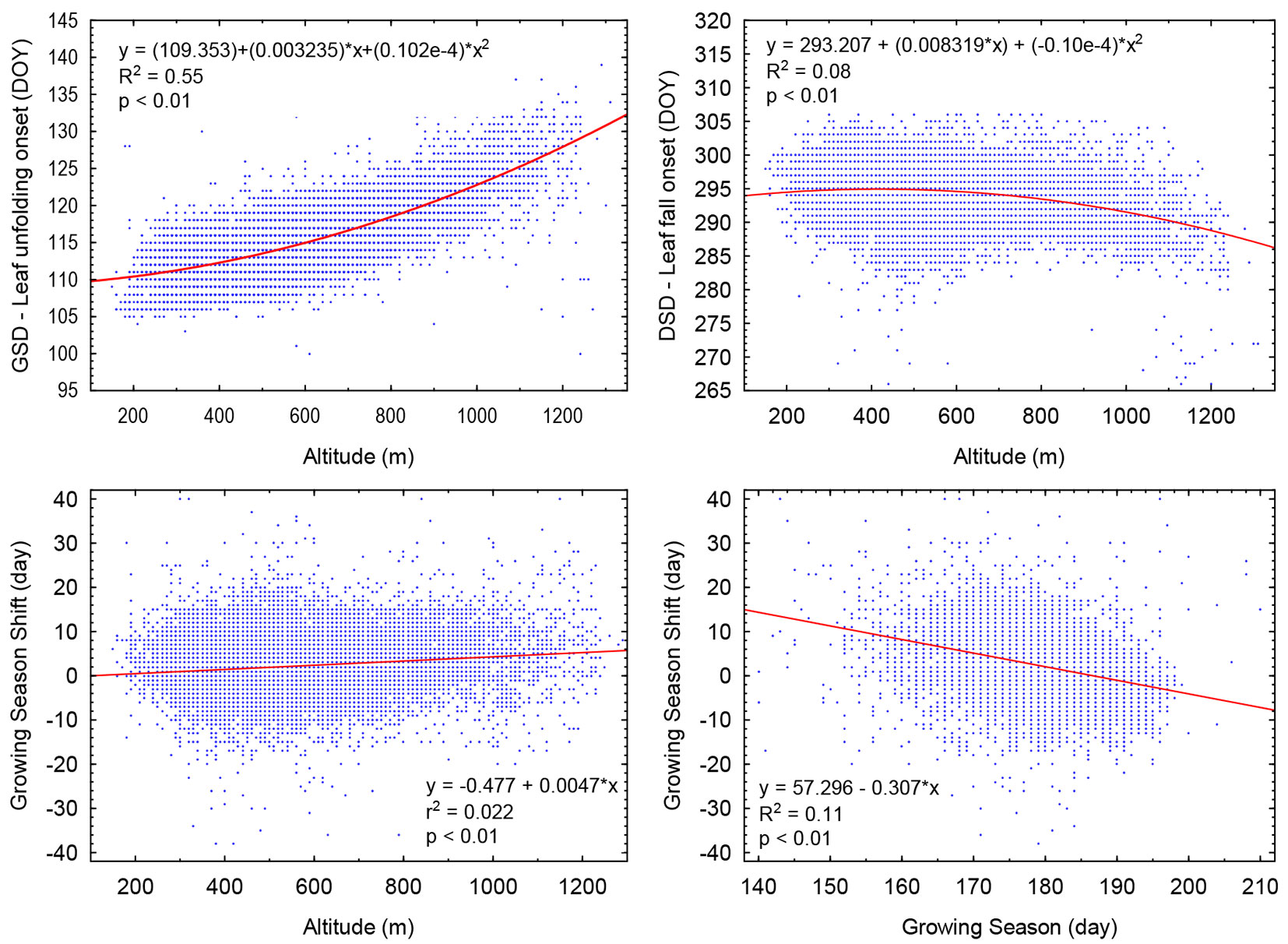
A strong non-linear correlation was revealed between altitude (x) and leaf unfolding onset (y = the average from the period of 2000-2015) with the correlation index of I = 0.74 (Fig. 5, top-left). The derived dependence was used for calculating the altitudinal delay of the onset of leaf-unfolding (PG, phenological gradient). There was a PG of 1.9 day between the altitudes of 200 and 400 m a.s.l. The delay of the onset gradually increased to 2.7 days between 400 and 600 m, to 3.7 days between 600 and 800 m, to 4.3 days between 800 and 1000 m, to 5.1 days between 1000 and 1200 m, and to 6 days above 1200 m a.s.l.
Fig. 5 - (Top-left): Relation between altitude and onset of leaf unfolding (GSDavg2000-2015). (Top-Right): Relation between altitude and onset of leaf fall (DSD avg2000-2015). (Bottom-left): A relation between altitude and growing season (GS) shift from 2000-2015. (Bottom-right): A relation between growing GS length and GS shift detected from 2000-2015: GS shift plus (+) value indicate prolongation of GS; minus (-) value implies shortening of GS.
Non-linear dependence with the correlation index of I = 0.29 (Fig. 5, top-right) was detected between the altitude (x) and the onset of leaf-fall (y = the average from the period of 2000-2015). There was no change in the onset between 200 and 600 m a. s. l. At the altitudes of 600 and 800 m, a shift to an earlier onset of leaf-fall of about 1.1 day was observed, between 800 and 1000 m it was 1.7 day, between 1000 and 1200 m 2.7 day, and above 1200 m a.s.l. the shift was of 3.5 days.
Theil-Sen estimation of the growing season (GS) trend revealed the average shift of 1.8 days (median) and a range from -7.0 to +12.1 days at 5-95 % quantile for the period of 2000-2015. The correlation analysis showed that GS shift depends partly on altitude (Fig. 5, bottom-left) but largely on the growing season length with r = -0.33 (Fig. 5, bottom-right). This figure illustrates that GS shift is +9.7 days in the sites with 155 days of GS length, and merely -2.6 day in the sites with 195 days of GS length.
The multiple regression analyses of spatial variation of GSD and DSD across the country revealed a statistically significant correlation (p < 0.01) between the onset of GSD (DSD) and the altitude, latitude, and longitude. The estimated latitudinal shifts (delay in onset) were 3.7 (0.83) day per 100 km to the North, the longitudinal shifts were approximately 0.24 (-0.23) day per 100 km to the East for GSD (DSD) at a steady altitudinal shift of 1.6 (-0.6) day per 100 m.
Discussion
Comparison with regional phenological studies
Numerous studies have reported advanced Northern Hemisphere spring phenology since the 1980s; e.g., the findings reported by German ([26]) and French research studies ([6]) predicted a trend for an earlier spring and delayed autumn phenophase onsets in beech and oak forests in the respective countries. Hamunyela et al. ([13]) observed similar trends in the deciduous forests in Western Europe based on the analysis of the period 2001-2011. Approximately 62.8 % of pixels have recorded a negative slope coefficient suggestive of the shift to an early start of growing season (SOS) during the period of 2001-2011, whereas 37.9 % recorded a positive slope coefficient indicative of the shift to a later SOS. However, a significance test of the slope coefficients at 5 % threshold revealed a negative trend in only 6.3 % of pixels, and a positive trend in 1.7 %. Fu et al. ([10]) summarized that the results in situ and NDVI observations both indicated that spring phenology significantly advanced during the period of 1982-2011 at an average rate of -0.45 days yr-1 in Central Europe. However, this trend considerably weakened over the period of 2000-2011; furthermore, opposite trends were observed between the in situ and NDVI observations. Based on NDVI AVHRR data in Continental and Alpine climatic zone in Europe, Garonna et al. ([12]) revealed the trends to an earlier start of a season and a later end of a season. They observed an earlier start of -1.6 (-0.8) days per decade and a later end of +2.2 (+0.8) days of a season for a Continental (Alpine) zone. Similarly, Menzel et al. ([23]) and Studer et al. ([30]) discovered that European beech has exhibited only slight spring phenological shift during the past 3-4 decades, whereas Vitasse et al. ([32]) observed no significant shift for beech and hornbeam.
Our results (Fig. 3) showed a later start of +0.8 days per decade (GSD) and a later end of +1.9 of the season (DSD); however, the trends in the onset of leaf-unfolding and leaf fall were not significant at the region-wide level. The Mann-Kendall test at pixel level revealed that 16.3 % of the beech stands exhibited a later onset of the spring phenological phase of leaf unfolding. These outcomes support the latest findings ([10]) of reversal or deceleration of the advanced spring trend in Central Europe. This recent reverse trend in the advancement of spring phenology in Western and Central Europe is probably related to the response of early spring species to the cooling trend in late winter. Regarding the onset of leaf fall, in our study (Tab. 5 - DSD metrics), approximately 32.2 % of beech stands exhibited a tendency towards a later onset of the phenophase. This finding supports the hypothesis of prolongation of the vegetation period due to climate change in beech forest observed in a number of European studies ([23], [30], [26], [6], [12]).
Regarding the altitudinal gradient, our results are consistent with other regional studies, e.g., Schieber et al. ([27]) during the period of 2007-2011 discovered that the phenological gradient for spring phenophases ranged from +2.83 to +3.00 days per 100 m and from -1.00 to -1.78 days per 100 m for autumn phenological phases. The duration of the growing season was about 128 days in the highest sites (1400 m a.s.l.), and increased to 181 days in the lowest sites (200 m a.s.l.). The above-mentioned researchers used linear relationship between altitude and the onset of leaf unfolding and leaf-fall, although non-linear relationship, similar to ours (Fig. 5, top-left), would provide a better explanation of the analysed data.
In addition to the altitudinal gradient, a significant spatial variability was observed between spring unfolding and latitude (delay 3.7 days per 100 km to the North), which might be explained by the impact of the warm climate of the Pannonian plate in the Southern part of the Carpathian Mountains. Towards the North, the influence of the Pannonian climate weakens and the climate changes to temperate and cold, which causes a later GSD onset. An explanation of the latitudinal gradient in autumn and longitudinal gradients would require a more detailed analysis with a comprehensive database of bio-climatological data.
With regard to the growing season, in our study, we discovered slight increases of GS length mainly as a result of later end of the season. The region-wide trend was not significant (Tab. 5). However, this trend, expressed at pixel level by GS shift, varied extensively across the country (Fig. 5 bottom-right). The regression analyses revealed that the GS shift depends on altitude (r = 0.15, p < 0.01). The prolongation of GS was more significant in higher altitude, namely it was 4.2 day in 1000 m a.s.l. (on average) compared to 1.4 day in 400 m a.s.l. (Fig. 5, bottom-left). We observed even more significant relationship between GS shift and GS length with r = -0.33 (p < 0.01). The negative regression coefficient indicates shortening of GS for beech stands growing in the sites with longer GS and prolongation of GS for the stands growing in the sites with shorter GS (Fig. 5, bottom-right). This may result from changes of chilling and forcing temperatures ([33]). Beech needs an adequate period of chilling for the release of winter dormancy and, and following this, an exposure to warm temperatures (forcing temperatures) is needed for triggering budburst. The number of years with insufficient chilling temperatures needed for fully breaking dormancy is likely to increase as a result to climate change, especially at a lower latitude or elevation and it will result in delayed budburst and foliation and, consequently, in decreasing GS. In contrast, in cooler winters at a high altitude, buds tend to be fully chilled and the onset dates might thus mostly depend on forcing temperatures, which have increased, and, consequently, this results in the prolongation of GS. Several studies supported this theory, e.g., Cufar et al. ([5]) reported an earlier leaf unfolding date at high altitudes over the past decades but no significant trend at low altitudes in a beech forests in Slovenia. In Switzerland ([32]), the observations of beech phenology along an altitudinal range of 200-1440 m a.s.l. manifest the same consistent pattern: beech populations inhabiting colder climates (high altitude) have exhibited a greater advance than populations inhabiting warmer climates (lower altitude) for the past three decades.
Phenological modelling approaches
Several approaches were used in order to determine the onset of phenological phases and the growing season (GS). Our study is based on Fisher & Mustard ([7]) definition of the date of leaf unfolding (leaf fall) as the date on which the sigmoid function reaches its half-maximum value. The half-maximum is identified as the steepest point on the sigmoid, or the maximum of the first derivative. Hmimina et al. ([15]) show that the inflection points of a model fitted to a MODIS NDVI time series allow accurate estimates of the onset of greenness in spring and the onset of yellowing in autumn in deciduous forests (RMSE ≤ one week). Brandysová & Bucha ([3]) confirmed the appropriateness of this approach in Slovak conditions through comparing satellite and terrestrial observation in five beech stands in the Kremnica Mountains. The onset of leaf unfolding is determined as the peak of the first derivative of the phenological function, i.e., the point of GSD.
Other approaches ([36], [11], [21]) identify the beginnings of phenological phases with regard to the change of curvature of the phenological function. The beginning and end of the growing season are derived from the extreme values of curvature. Heumann et al. ([14]) define the beginning and the end of the growing season as 20 % of the value on the increasing or decreasing section of a phenological curve. Similarly, Beck et al. ([2]) determine the onset of spring leaf unfolding and autumn leaf fall by a threshold value (25 and 75 %, respectively) on the NDVI amplitude.
All these approaches result in the prolongation of growing season compared to our GS defined as the difference between DSD and GSD. Brandysová & Bucha ([3]) pointed to the shortcomings of these approaches in the sense of estimation of beech GS. NDVI increasing value is related to the grass and shrub layers emerging before the beech leaf unfolding. Therefore, we consider Fisher & Mustard ([7]) approach as optimal for the purpose of our analyses focused on tree component of beech ecosystems.
Conclusions
The phenological development of the beech forests was successfully modelled by means of double logistic sigmoid function. As also indicated in other studies, the timing of phenological phases can be efficiently estimated by the analysis of the extreme values of the sigmoid function and its derivatives.
Our investigation revealed that the onset of leaf unfolding shifted by 0.8 days per decade, the onset of leaf fall shifted by 1.9 days per decade towards a later date. However, the trends were not found to be statistically significant (p > 0.34) in either case at region-wide level. The intra-annual variabilities of both phenophase onsets (leaf unfolding, leaf fall) were statistically significantly related to the altitude (p < 0.01).
At the pixel level, the Mann-Kendall test proved that 16.3 % of the beech stands exhibited a later onset of the spring phenological phase of leaf unfolding, but only in 3.1 % with p < 0.10. With regard to the onset of leaf fall, 32.2 % of beech stands exhibited a tendency towards a later onset of the phenophase; however, merely 11.6 % with p < 0.10.
Regarding the growing season, our study showed slight increases of GS length (~1.1 days per decade) in the region, mainly due to later end of the growing season. This finding supports the hypothesis of prolongation of vegetation period.
The GS length trend varied extensively within the region. The estimation of the trend revealed the GS shift 1.8 days (median) and a range from -7.0 to +12.1 days at 5-95 % quantile for the period of 2000-2015. We observed a significant inverse correlation between GS shift and GS length (p < 0.01). The shift is positive in the sites with shorter GS and negative in the sites with longer GS. This is a new finding which necessitates further investigation, especially with regard to the hypothesis claiming that forcing temperatures predominately drive phenological variations in beech growing in the climates with cold winters, whereas photoperiod and chilling temperatures reduce phenological variation in the sites with mild winters.
The statistically significant relationship between the onset of spring and autumn phenophases (GSD and GAD vs. DSD) has remained unexplained so far.
Finally, our study based on a relatively small area of Slovakia (49.035 km2) proved that the changes in beech leaf phenology are not uniform, and that they greatly differ along altitudinal and latitudinal gradients.
Further modelling of regional phenology development is needed in order to provide a better explanation of spatial variations of phenological events, especially if the results are to be transferred into species selection practice in forest restoration (after planned logging or disturbances) in relation to forest adaptation to climate change.
Acknowledgements
The collaborative research reported by the present study was conducted within the VEGA project 1/0953/13 entitled Geographic Information about the Forest and Landscape - Specifics of Development and Utilization, funded by the Slovak Scientific Grant Agency and the Centre of Excellence for Decision Support Systems in Forest and Landscape (ITMS 26220120069) co-funded by the Research Agency.
References
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Online | Gscholar
CrossRef | Gscholar
Authors’ Info
Authors’ Affiliation
National Forest Centre - Forest Research Institute, Department of Forest and Landscape Ecology, T.G. Masaryka 22, 960 92 Zvolen (Slovak republic)
Technical University in Zvolen, Faculty of Forestry, Department of Forest Management and Geodesy, T.G. Masaryka 2117/24 , 960 53 Zvolen (Slovak republic)
Corresponding author
Paper Info
Citation
Bucha T, Koren M (2017). Phenology of the beech forests in the Western Carpathians from MODIS for 2000-2015. iForest 10: 537-546. - doi: 10.3832/ifor2062-010
Academic Editor
Matteo Garbarino
Paper history
Received: Mar 15, 2016
Accepted: Feb 22, 2017
First online: May 05, 2017
Publication Date: Jun 30, 2017
Publication Time: 2.40 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2017
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 49747
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 40826
Abstract Page Views: 2922
PDF Downloads: 4293
Citation/Reference Downloads: 78
XML Downloads: 1628
Web Metrics
Days since publication: 3170
Overall contacts: 49747
Avg. contacts per week: 109.85
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2017): 21
Average cites per year: 2.33
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Trends and driving forces of spring phenology of oak and beech stands in the Western Carpathians from MODIS times series 2000-2021
vol. 16, pp. 334-344 (online: 19 November 2023)
Research Articles
A comparative study of four approaches to assess phenology of Populus in a short-rotation coppice culture
vol. 9, pp. 682-689 (online: 12 May 2016)
Research Articles
Predicting phenology of European beech in forest habitats
vol. 11, pp. 41-47 (online: 09 January 2018)
Research Articles
Remote sensing of Japanese beech forest decline using an improved Temperature Vegetation Dryness Index (iTVDI)
vol. 4, pp. 195-199 (online: 03 November 2011)
Research Articles
Modelling the moisture status of habitats by using NDVI on the example of the Cerrado and Atlantic Forest biomes borderland (Brazil)
vol. 18, pp. 375-381 (online: 16 December 2025)
Research Articles
Fuel type characterization based on coarse resolution MODIS satellite data
vol. 1, pp. 60-64 (online: 28 February 2008)
Research Articles
Assessing the performance of MODIS and VIIRS active fire products in the monitoring of wildfires: a case study in Turkey
vol. 15, pp. 85-94 (online: 19 March 2022)
Research Articles
Links between phenology and ecophysiology in a European beech forest
vol. 8, pp. 438-447 (online: 15 December 2014)
Research Articles
Landsat TM imagery and NDVI differencing to detect vegetation change: assessing natural forest expansion in Basilicata, southern Italy
vol. 7, pp. 75-84 (online: 18 December 2013)
Research Articles
Growing season water balance of an inner alpine Scots pine (Pinus sylvestris L.) forest
vol. 11, pp. 469-475 (online: 02 July 2018)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords