Soil water deficit as a tool to measure water stress and inform silvicultural management in the Cape Forest Regions, South Africa
iForest - Biogeosciences and Forestry, Volume 13, Issue 6, Pages 473-481 (2020)
doi: https://doi.org/10.3832/ifor3059-013
Published: Nov 01, 2020 - Copyright © 2020 SISEF
Research Articles
Abstract
An understanding of variations in water availability to plantation forests on a spatial and temporal scale is essential when designing risk averse and site-specific silvicultural management regimes. Various indices of site water availability were compared to each other and to an independent, unbiased estimate of stand productivity potential, namely site index, across the Tsitsikamma, Knysna and Boland forestry regions of South Africa. This was done to find the balance between water availability indices requiring intensive data inputs (that may be very accurate) and indices with lower input data requirements (but may sacrifice some accuracy). The following indices of water availability (in order from low to higher input data requirements) were tested: Mean Annual Precipitation (MAP); Aridity Index (AI), i.e., MAP as a fraction of mean annual potential evapotranspiration (Ep); Moisture Growing Season (MGS), i.e., the Julian days where long-term MAP exceeds 0.3 times Ep; Water Deficit (WD), an estimate based on a rudimentary water balance with relatively low data inputs. The first three estimates use only climatic variables while the WD incorporates soil water storage capacity to run a water balance calculation. Results showed that both regional climatic variability and soil properties significantly affected the level of water availability, and hence also the potential productivity of pine stands. The shallow and sandy soils from the Knysna and Boland regions exhibited rapid water depletion during periods of decreased precipitation and seasonal shifts, however, the large WD’s (up to 345 mm year-1) observed in several of these sites rapidly changed to surplus values following only one month of high precipitation. Sites from the Tsitsikamma region had significantly larger water retention capabilities and this was attributed to the regional soil properties and climatic conditions. Temporal variations in the WD were also quantified. The WD estimates correlated significantly (r = -0.80, p<0.001) to the respective site indices from sites across all regions. These results underscore the importance of soil water availability on plantation productivity, especially in moderately dry regions or in areas with either shallow soils or a seasonal rainfall pattern. We conclude that the WD is a fairly accurate estimate of site-specific water availability with relatively low data requirements. The WD estimates are far superior to currently used indices of water availability in Southern Africa and has data input requirements that are currently readily available for most plantation forest sites.
Keywords
Soil Water Availability, Climatic Gradient, Slash Pine, Monterey Pine, Edaphic Properties
Introduction
The silvicultural regime in plantation forestry can be viewed as consisting of a series of strategic decisions (e.g., which taxon to plant, which market to target) and site or stand management interventions (soil preparation, fertilisation, vegetation management, pruning, thinning, etc. - [12]). Over the last three decades, attempts have been made to ensure that silvicultural decision making becomes increasingly site specific in many plantation forest enterprises in Southern Africa ([10], [11], [27], [7], [22], [23], [13]). This is because researchers and managers have realised that forest productivity can be optimised (and risk profiles minimised) by site-specific management regimes (also referred to as precision forestry in some circles). However, attempts at site-specific silvicultural management in Southern Africa has been constrained by using fairly coarse input data and the fact that forestry is often an extensive form of land use in remote locations, where edaphic and climatic data may be somewhat sparse. Such examples are (a) the use of mean annual temperature (MAT), together with mean annual precipitation (MAP), with limited soil data, to make decisions on site-species matching ([11], [22], [13]) and (b) the use of very broad regions or soil groups to recommend fertiliser supplements ([9], [23]). One of the older site classification schemes used to inform tree planting in Southern Africa was that of Poynton ([32]). This system used Thornthwaite’s ([40]) estimates of evaporation (albeit on a broad scale due to limited data availability). However, the most recent site and climatic classification system that has been widely adopted by the South African forest industry ([37]) has reverted to MAP as the main driver of water availability, with no consideration of rainfall distribution and little consideration of evaporation and soil storage potential. The reason for using these low-precision inputs in the system was apparently driven by data constraints, as most of the forestry weather stations collected only rainfall data. This has subsequently changed with the expansion of the privately managed weather networks to supplement the national weather network in some areas. In the future, it may thus be possible to gauge the water availability of some sites using more complex estimates and data (Tab. 1). However, there are still many plantation forestry estates in Southern Africa where monthly mean rainfall and temperature data are the only reliable variables measured on site. A more accurate knowledge of soil water availability may help target increasingly site-specific silvicultural management.
Tab. 1 - Commonly used estimates of plant available water in agriculture and forestry, arranged from single estimates with low data requirements to increasingly complex inputs that require more data inputs.
| Estimate | Data inputs | Comments |
|---|---|---|
| Mean annual precipitation (MAP) and effective precipitation class (MAP per mean annual temperature [MAT] bracket, see [37]). | Monthly rainfall: An annual sum is used, in practice, monthly data is commonly added up. The estimate is sometimes considered alongside an estimate of soil depth and texture ([22]). | Very coarse approximation of water availability as it does not integrate seasonality, distribution and storage of rainfall. This estimate also does not effectively account for the atmospheric demand for moisture, which has negative implications when extrapolating results to different regions. |
| Aridity index (AI - [8], [13]). Moisture Growing Season (MGS - [21], [35]). | AI: Annual rainfall and potential evapotranspiration (ETp) estimates. MGS: Monthly rainfall and ETp estimates as well as a predefined threshold value to define water stress (e.g. where Precipitation< A·Etp; where A is the threshold value, commonly substituted with values from 0.3 to 0.5). | AI is a moderately crude index, but a substantial improvement on MAP estimates alone. It provides some balance between water supply as rainfall and atmospheric demand, but this is usually an annual time step and water storage is not factored in. MGS: Like the AI, however, slightly more sophisticated as a monthly time step is used. |
| Soil water deficit, initially by Thornthwaite ([41]), as used by Poynton ([32]). Additional application: Soil water holding capacity. The methodology described by Pereira et al. ([31]), used by Gonçalves et al. ([18]) and Hakamada et al. ([19]). | Monthly precipitation. Average monthly temperature (heat index and day length derived from temperature, time-of-year and location data). Soil water holding capacity. | Moderately sophisticated index of plant water availability derived from basic monthly rainfall and temperature data. If used with soil water storage capacity, it provides a moderately accurate picture of water deficits over a time step that is meaningful to the growth of deep-rooted crops (e.g. trees and forests). |
| Actual evapotranspiration (Eta)/ETp, where Eta is based on the Penman-Monteith equation. South African and international uses: Campion et al. ([5]), Sumner & Jacobs ([39]), Fricke ([17]) Bie et al. ([1]) as well as Fischer & Du Toit ([16]). | Air temperature, humidity, wind speed, atmospheric pressure and solar radiation for daily, weekly or monthly calculations. Soil water holding capacity and several crop factors. | Highly sophisticated model usually run on a daily time step. High input requirements make it a useful research tool, but less often used in management applications, due to the intensive input data requirements (that does not exist on a detailed enough spatial scale for many forest estates). |
The Southern coastal strip spanning the Western and Eastern Cape provinces in South Africa (hereafter referred to as the Cape Forest Regions) constitutes an important forestry region in the country: it harbours more than 100,000 ha of indigenous high forest as well as more than 70,000 ha of exotic pine plantations. A clear understanding of how soil water availability is affected by the individual physical properties of several soils in the Cape Forest Regions, across a spatial and temporal gradient, would help identify sites that are more likely to respond positively to silvicultural interventions (e.g., soil preparation, fertilisation and thinning), given varying and sometimes unfavourable climatic conditions. For example, stands seldom respond to improved nutrient status when experiencing water limitations ([9], [10]). Site-specific implementation of silvicultural operations would simultaneously reduce the overall cost and improve the productivity of responsive sites to what is achievable given the limitations and conditions of the growing environment.
Materials and methods
Site descriptions
Sixteen sites were carefully selected across the Cape Forest Regions, South Africa, to conduct the field study. These sites were geographically distributed in clusters from East (Tsitsikamma, Eastern Cape) to West (Jonkershoek, Western Cape) and ranged from 156-408 m above sea-level. Clustering was necessitated by the presence of a reliable weather station near each site, but individual sites within a cluster were chosen to have different soil depths and textures, so that water availability representative of various site types could be calculated. Sites from the Tsitsikamma (Eastern Cape) were located on the Lottering and Witelsbos plantations and harbour stands of Pinus elliottii. These plantations have a mean annual temperature and rainfall of approximately 17.5 °C and 1050 mm. Precipitation is uniformly distributed throughout the year, with a slight increase from August to November. The second cluster of sites were located on the Kruisfontein plantation near Knysna, Western Cape. This region has a mean annual temperature and rainfall of approximately 16.9 °C and 898 mm, respectively. The third cluster of sites were in the Boland region, Western Cape. These sites were extensively distributed throughout Grabouw, La Motte and Jonkershoek plantations where mean annual temperatures and rainfall values range from 15.1-18.3 °C and 773-1188 mm, respectively. The Knysna and Boland sites were afforested with P. radiata and these abovementioned regions are regarded as suitable sites for plantation forestry and are currently utilised for sawtimber production. Soils from the Tsitsikamma and Knysna regions are dominated by plinthic, cumulic, duplex and podzolic soil groups ([15]). Soils form the Boland region, i.e., Grabouw, La Motte and Jonkershoek, were located on plinthic, lithic and duplex soils ([15]). The soils from the Tsitsikamma had significantly larger porosities relative to the Knysna and Boland regions. The largest porosities were observed in Lottering plantation at site G and the smallest at A, with respective porosities of 63% and 46%. The Knysna and Boland regions had similar porosities of 43% - 44%. The smaller porosities observed in these regions were largely due to the greater sand contents of each site (Tab. 2).
Tab. 2 - Site locations and climatic conditions. (*): Site indices were adjusted to that of P. elliottii after applying eqn. 3.
| Site ID |
Region | Plantation | Coordinates | Altitude (m) |
MAT (°C) |
MAP (mm) |
MGS (days yr-1) |
AI | ETp (mm yr-1) |
Adjusted* SI20 |
Soil group ([15]) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | Tsitsikamma | Witelsbos | 34°01′ 32″ S 24°24′ 35″ E |
261 | 17.5 | 1094 | 354 | 0.95 | 1156 | 24.0 | Plinthic |
| B | Tsitsikamma | Witelsbos | 34°02′ 48″ S 24°08′ 06″ E |
162 | 17.5 | 1094 | 354 | 1.13 | 972 | 24.0 | Plinthic |
| C | Tsitsikamma | Lottering | 33°58′ 48″ S 23°44′ 58″ E |
233 | 17.5 | 1025 | 351 | 0.82 | 1250 | 29.0 | Cumulic |
| D | Tsitsikamma | Lottering | 34°00′ 30″ S 23°58′ 23″ E |
231 | 17.5 | 1025 | 351 | 0.81 | 1258 | 31.4 | Plinthic |
| E | Tsitsikamma | Lottering | 34°00′ 01″ S 23°50′ 22″ E |
219 | 17.5 | 1025 | 351 | 0.85 | 1205 | 28.3 | Podzolic |
| F | Tsitsikamma | Lottering | 34°00′ 23″ S 23°55′ 29″ E |
213 | 17.5 | 1025 | 351 | 0.96 | 1073 | 27.7 | Podzolic |
| G | Tsitsikamma | Lottering | 33°59′ 16″ S 23°46′ 29″ E |
227 | 17.5 | 1025 | 351 | 0.83 | 1242 | 26.7 | Plinthic |
| H | Tsitsikamma | Lottering | 33°59′ 39″ S 23°57′ 24″ E |
218 | 17.5 | 1025 | 351 | 0.80 | 1288 | 29.4 | Plinthic |
| I | Knysna | Kruisfontein | 34°01′ 26″ S 23°06′ 40″ E |
270 | 16.9 | 898 | 329 | 0.91 | 972 | 21.8 | Podzolic |
| J | Knysna | Kruisfontein | 34°02′ 02″ S 23°07′ 44″ E |
247 | 16.9 | 898 | 329 | 0.92 | 984 | 20.8 | Plinthic |
| K | Knysna | Kruisfontein | 34°02′ 60″ S 23°06′ 32″ E |
156 | 16.9 | 898 | 329 | 0.94 | 951 | 22.2 | Cumulic |
| L | Boland | Grabouw | 34°07′ 44″ S 19°00′ 54″ E |
350 | 15.1 | 1188 | 263 | 1.09 | 1093 | 20.1 | Lithic |
| M | Boland | Grabouw | 34°04′ 26″ S 19°04′ 26″ E |
394 | 17.1 | 954 | 263 | 0.85 | 1120 | 21.2 | Plinthic |
| N | Boland | Grabouw | 34°10′ 51″ S 19°07′ 30″ E |
368 | 16.9 | 773 | 263 | 0.70 | 1103 | 20.1 | Cumulic |
| O | Boland | Jonkershoek | 33°58′ 16″ S 18°56′ 06″ E |
246 | 17.0 | 1073 | 277 | 0.89 | 1208 | 21.2 | Lithic |
| P | Boland | La Motte | 33°54′ 14″ S 19°05′ 13″ E |
241 | 18.3 | 880 | 238 | 0.70 | 1261 | 21.2 | Cumulic (duplex) |
Sites from the Tsitsikamma are dominated by sandy loam texture classes. The remaining sites had significantly greater sand and smaller clay and silt contents. These soils were classified as having sandy textures. Soil depths ranged from maximum sampling depths of 4 m in the Tsitsikamma and the shallower depths were limited to the Boland region (commonly from 0.5 to 0.8 m) and this was representative of the lithic soils in the region (Tab. 3).
Tab. 3 - Soil classification and physical properties of 0-15 cm (Lottering and Witelsbos) and 0-20 cm (Kruisfontein, La Motte, Jonkershoek and Grabouw) topsoil layer for each site. (TXC): textural classification; (SC): plant-available storage capacity of the entire soil profile (field capacity minus wilting point, mm).
| Site | Plantation | Clay (%) |
Silt (%) |
Sand (%) |
Fine sand (%) |
Medium sand (%) |
Coarse sand (%) |
TXC | Max soil depth (m) |
SC (mm) |
|---|---|---|---|---|---|---|---|---|---|---|
| A | Witelsbos | 14.0 | 21.0 | 65.0 | 36.0 | 23.9 | 5.3 | SaLm | 4.00 | 386 |
| B | Witelsbos | 12.0 | 13.0 | 75.0 | 50.3 | 24.8 | 0.2 | SaLm | 1.20 | 130 |
| C | Lottering | 20.0 | 39.0 | 41.0 | 36.0 | 2.9 | 2.4 | SaLm | 2.20 | 309 |
| D | Lottering | 18.0 | 39.0 | 43.0 | 35.2 | 4.7 | 3.3 | SaLm | 2.55 | 356 |
| E | Lottering | 18.0 | 35.0 | 47.0 | 40.0 | 3.6 | 3.7 | SaLm | 2.00 | 287 |
| F | Lottering | 18.0 | 40.0 | 42.0 | 36.9 | 4.0 | 1.3 | SaLm | 1.20 | 134 |
| G | Lottering | 16.0 | 44.0 | 40.0 | 34.2 | 2.5 | 3.5 | SaLm | 1.60 | 230 |
| H | Lottering | 19.0 | 40.0 | 41.0 | 35.8 | 3.3 | 2.0 | SaLm | 3.20 | 343 |
| I | Kruisfontein | 2.8 | 2.4 | 94.8 | 57.9 | 36.5 | 0.4 | Sa | 2.00 | 153 |
| J | Kruisfontein | 3.0 | 11.5 | 85.5 | 76.6 | 8.9 | 0.2 | LmSa | 1.80 | 252 |
| K | Kruisfontein | 6.0 | 11.5 | 82.5 | 68.2 | 11.2 | 6.2 | LmSa | 1.90 | 241 |
| L | Grabouw | 2.3 | 1.3 | 96.4 | 45.7 | 26.9 | 23.9 | Sa | 2.00 | 115 |
| M | Grabouw | 13.0 | 26.0 | 61.0 | 54.8 | 3.0 | 3.5 | LmSa | 0.50 | 78 |
| N | Grabouw | 8.4 | 14.8 | 76.8 | 67.7 | 2.8 | 6.4 | SaLm | 0.60 | 93 |
| O | Jonkershoek | 3.3 | 0.8 | 96.1 | 38.3 | 49.2 | 8.6 | Sa | 0.80 | 63 |
| P | La motte | 2.8 | 2.0 | 95.2 | 65.2 | 24.7 | 5.3 | Sa | 2.00 | 139 |
Data collection and analyses
Soil sampling and analysis
An extendable soil auger was used to collect soil sample sets up to the regolith or up to a maximum depth of 4 m. Samples were taken with 20 cm intervals. Coarse textural fractions were determined by sieving after air drying soils. Sub-samples of soils were then dispersed a sodium-hexametaphosphate (calgon) solution, after which silt and clay contents were determined by using the sedimentation rates at 20 °C and an ASTM E100 (152H-TP) hydrometer. The soil water holding capacity was then mathematically calculated from the soil texture model by Saxton et al. ([34]). Two bulk density samples were collected per site. This was done by knocking metal cylinders with a 10-cm diameter into the soil, excavating it and drying the soil in an oven at 105 °C, until constant mass was obtained. Bulk density was then determined by dividing the dry weight of each sample by the fixed volume of soil from the ring and expressed as g cm-3.
Porosity
The soil porosity (P) was determined by means of the undisturbed bulk density and incorporated particle density of each soil (eqn. 1). Particle density varies according to the mineral content of the soil. Quartz is one of the dominant minerals and has a particle density of 2.65 g cm-3 ([2], [4]). Particle density ranges from 2.4 to 2.9 g cm-3 within the group of mineral soils ([33]). The soils from the Tsitsikamma region have sandy loam textures and the particle density was assumed to be 2.65 g cm-3 in this study (eqn. 1):
where P is the porosity, i.e., amount of pore space in the soil (%), BD is the bulk density (g cm-3), and PD is the particle density (2.65 g cm-3).
Calculated site index
Site index refers to the dominant height at 20 years of age ([24]). The dominant height of younger stands was projected to the selected age index of 20 years using the original Chapman Richards function and parameters of Pienaar & Turnbull ([30]), parameterised (β1, t0 and β3) for P. elliottii in South Africa (eqn. 2). This model is constrained to: if Age2 ≤ (-β2), then HD2 = 0.
where HD2 is the projected height (m), HD1 is the current height (m), Age2 is the projected age (years), Age1 is the Current age (years), β1 = -0.0423, t0 = β2 = -0.6, β3 = 1.179.
Sites in the Knysna and Boland regions were afforested with P. radiata and those in the Stormsriver region with P. elliottii. The site index development of P. elliottii and P. radiata differs by a fair margin on similar site qualities. To account for these differences, the site indices for P. radiata were scaled down to those of P. elliottii, with a correction factor derived from the site indices of both species at the age of 20 years, for the respective site quality in the regions of South Africa afforested with pine. Site indices at reference age (20 years) for P. radiata could be downscaled to that of P. elliottii using the following formula (eqn. 3):
where SI20R is the site index for P. radiata at base age 20, and SI20A is the P. radiata site index adjusted to that of P. elliottii
Soil water deficit
Monthly precipitation and temperature data from 2000-2010 was acquired for each region and the monthly soil WD for all sixteen sites were calculated using an adaptation of the original work by Thornthwaite & Mather ([42]), outlined in Pereira et al. ([31]). This 11-year period was chosen as comprehensive data sets were available on all sites and several weather stations were abandoned post 2010.
Potential evapotranspiration
The latitude of each trial area had to be known to calculate the potential evapotranspiration (ETp). The heat index (I) was computed from a table compiled by Thornthwaite ([41]), the table provided monthly heat-index values with corresponding mean monthly temperatures. The summation of the monthly values for one year provided the heat index required for eqn. 4. The unadjusted monthly ETp values were calculated based on the nomograph first published by Thornthwaite ([41]). The final step required the conversion of unadjusted ETp to adjusted ETp values. The adjusted ETp incorporates the number of hours of sunlight into units of 30 days of 12 hours each. The full methodology for WD calculation was recently described by Pereira et al. ([31]) and is summarised here (eqn. 4 to 16).
where ETp is the potential evapotranspiration expressed as millimetres (mean) for a 30-day month period (mm month-1), Tn is the mean monthly air temperatures (units in degrees centigrade), I is the heat index, and a is the cubic function of I.
Heat index
The heat index was calculated using eqn. 5. The value depends on the historical mean temperature of each month and included the monthly thermic effects for a year (eqn. 5):
where I is the heat index and Tn is the mean monthly air temperatures (°C).
Cubic function of I (a)
A polynomial function was used to calculate the exponent a (eqn. 6):
where a is the cubic function of I, and I the heat index.
Solar azimuth and time of sunrise
The solar azimuth (δ) refers to the projected angle of the sun relative to its position in the plane of the local horizon. The Thornthwaite ([41]) method requires the daily solar azimuth for each month of the year to determine the average monthly photoperiod. The first step requires calculating the daily solar azimuth angle for each site and required the day-number of the year as an input variable (eqn. 7):
where δ is the solar azimuth (degrees), NDA is the day number of the year.
The second step determined the angle at time of sunrise (hn). This function incorporated the solar azimuth value, determined in the preceding step, and the latitude of the selected region (eqn. 8):
where hn is the angle at time of sunrise (degrees), Φ is the latitude (degrees) and δ is the solar azimuth (degrees).
Average photoperiod
The photoperiod was defined as the time between sunrise and sunset for a given day, or more specifically the duration of the day. To calculate the photoperiod, the angle at time of sunrise was required (eqn. 9):
where N is the photoperiod (hours) and hn is the angle at time of sunrise (degrees).
Corrected ETp
The ETp calculated in eqn. 2, was for a one-month interval of 30 days and a photoperiod of 12 hours per day. To determine the ETp for the respective month, the ETp value needed to be corrected for the number of days in a month (eqn. 10):
where ETpcor is the corrected ETp (mm month-1), ND is the number of days for respective month (days), N is the average photoperiod for the respective month (hours).
Available soil water
Precipitation and ETp difference
The next step required calculating the difference between the actual monthly precipitation and calculated evapotranspiration for each site (eqn. 11).
where P is the actual precipitation (mm month-1), and ETp is the potential evapotranspiration (mm month-1).
Negative accumulation and soil-water storage capacity
Negative soil water accumulation and available soil water were calculated concurrently. If the difference in precipitation and potential evapotranspiration for the succeeding month was negative, the negative difference was cumulatively added to the difference of the preceding month. This was maintained for negative differences. A different approach was used for positive differences following a sequence of negative differences: the positive value was added to the available soil water of the preceding month, and this value should not have exceeded the soil water storage capacity of the soil. This available soil water value was then substituted into eqn. 12, derived from eqn. 13, to calculate the negative accumulation.
Available soil water was calculated as a function of the preceding and present months’ difference in precipitation and potential evapotranspiration. If the difference was negative, it was substituted in eqn. 13 to determine the available soil water. If the differences were positive, the values were cumulatively added to the following month’s difference (eqn. 12):
where NEG ACUM is the negative accumulation (mm month-1), CAD is the soil-water storage capacity (mm), and ASW is the available soil-water (mm) which is calculated as follows (eqn. 13):
Real evapotranspiration
The real evapotranspiration (ETr) was calculated as a function of the positive or negative difference between the real and potential evapotranspiration. A difference greater or equal to zero resulted in the potential evapotranspiration being recorded as the real evapotranspiration. If the difference was negative, the sum of the precipitation and change in available soil water for the current and preceding month was calculated as the ETr (eqn. 14):
where ETr is the real evapotranspiration (mm month-1), P is the precipitation (mm month-1), ASWcur is the available soil-water of current month (mm), and ASWprec is the available soil water of preceding month (mm).
Water surplus and deficit
If the available soil water was equal to the maximum soil-water storage capacity for the site, the water surplus (Sw) was calculated as the difference between the real and potential evapotranspiration and the change in available soil-water (eqn. 15):
where ETp is the potential evapotranspiration (mm month-1), P is the precipitation (mm month-1), ASWcur is the available soil-water of current month (mm), and ASWprec is the available soil water of preceding month (mm).
The monthly WD was calculated as the difference in potential (ETp, mm month-1) and real evapotranspiration (ETr, mm month-1 - eqn. 16).
The monthly WD values were summed per year to obtain an annual WD estimate from 2000-2010. Pearson correlations were done to examine the relationship between adjusted site index and four indices of water availability (MAP, AI, MGS and WD). Graphical illustrations were created by Sigma Plot® v. 11 (Systat Software Inc., San Jose, CA, USA) and statistical analyses were done in Statistica® v. 13 (StatsSoft Inc., Tulsa, OK, USA).
Results
Plant-available soil water storage capacity
The Tsitsikamma region had the largest regional variability in soil water storage capacity, with ranges of 130 to 386 mm. Soil depth in this region ranged from 1.20 to a maximum depth of 4.0 m. Water storage capacity in the Knysna and Boland regions ranged from 153 to 252 mm and 63 to 139 mm, respectively. Soils in these regions were shallower and ranged from 0.50 to 2.0 m. Water storage capacity was largest for sites J, K and P, with values of 252, 241 and 139 mm respectively. The smallest water storage capacities were observed in the Boland region, on sites N, M and O, with values of 93, 78 and 63 mm, respectively (Tab. 3).
Average annual soil water deficits
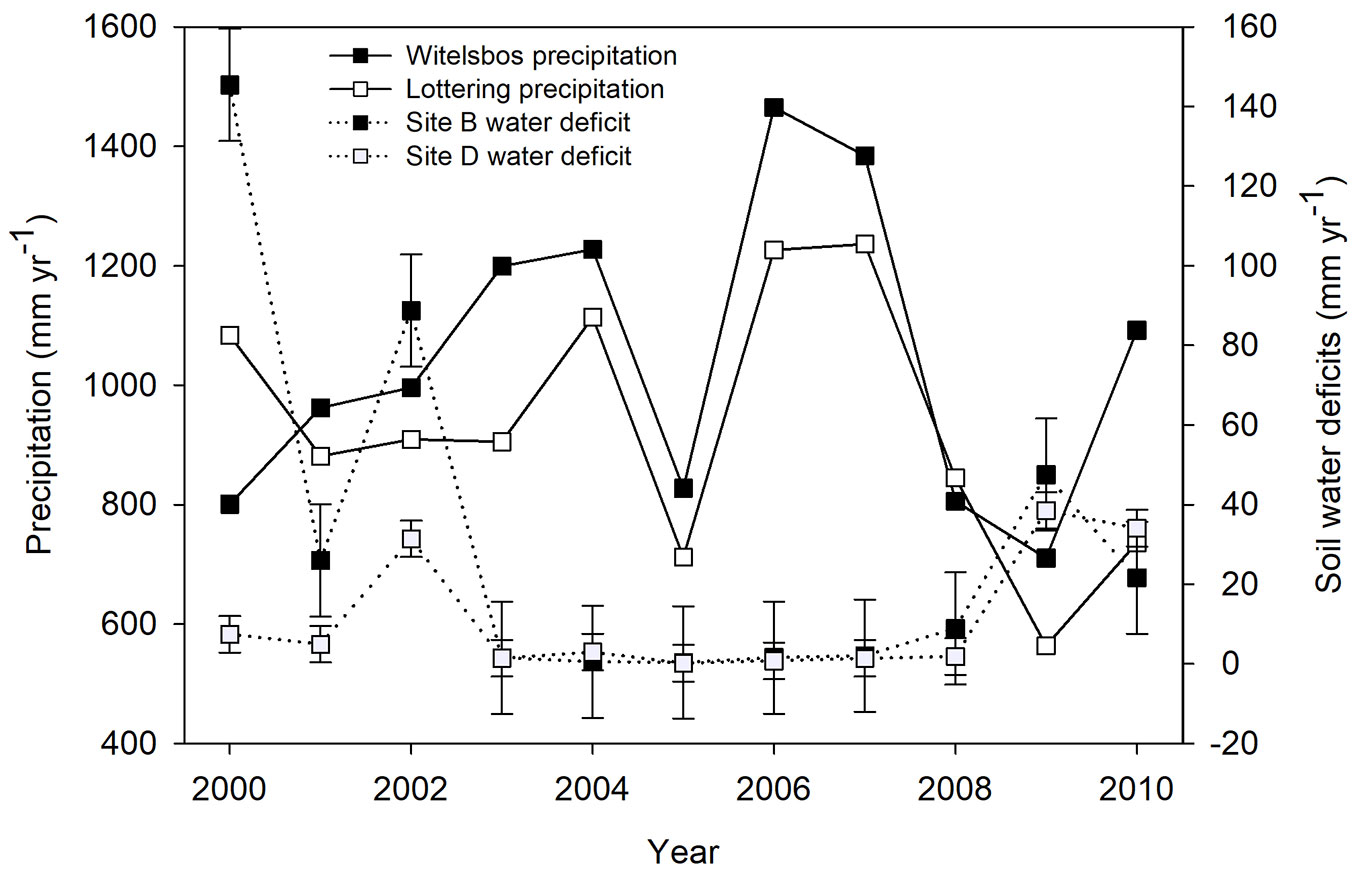
The average soil water deficits for the Tsitsikamma region were considerably smaller relative to the other regions, and this reflected in the cumulative, average annual water deficits and the variation observed over the experimental period (Tab. 4). Sites A to H had average annual deficits in the range of 11 to 31 mm. Sites B (Witelsbos) and D (Lottering plantation) had average annual deficits of 31 and 11 mm, respectively, with site D being in the lower range observed across most sites (Fig. 1).
Tab. 4 - Annual soil water deficit and standard error for 2000-2010. SE: Standard error.
| Site | Year | Soil water deficit 2000-2010 |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | Cumulative (mm) |
Annual average (mm yr-1) |
SE (mm) |
|
| A | 107 | 10 | 40 | 1 | 0 | 0 | 1 | 1 | 3 | 20 | 9 | 190 | 17 | 10 |
| B | 145 | 26 | 89 | 2 | 0 | 0 | 2 | 2 | 9 | 48 | 22 | 344 | 31 | 14 |
| C | 8 | 6 | 35 | 2 | 3 | 0 | 1 | 2 | 2 | 43 | 38 | 141 | 13 | 5 |
| D | 7 | 5 | 31 | 1 | 3 | 0 | 1 | 1 | 2 | 39 | 34 | 125 | 11 | 5 |
| E | 9 | 6 | 38 | 2 | 4 | 0 | 1 | 2 | 2 | 46 | 41 | 150 | 14 | 6 |
| F | 18 | 12 | 66 | 4 | 7 | 0 | 2 | 4 | 5 | 82 | 69 | 268 | 24 | 9 |
| G | 11 | 7 | 45 | 2 | 4 | 0 | 1 | 2 | 3 | 55 | 48 | 179 | 16 | 7 |
| H | 8 | 5 | 32 | 1 | 3 | 0 | 1 | 1 | 2 | 40 | 35 | 129 | 12 | 5 |
| I | 104 | 119 | 132 | 81 | 100 | 45 | 93 | 29 | 79 | 339 | 537 | 1657 | 151 | 46 |
| J | 74 | 103 | 102 | 55 | 73 | 29 | 63 | 21 | 55 | 275 | 449 | 1299 | 118 | 39 |
| K | 77 | 104 | 103 | 57 | 75 | 31 | 65 | 21 | 57 | 281 | 452 | 1324 | 120 | 39 |
| L | 194 | 254 | 317 | 263 | 230 | 114 | 136 | 70 | 141 | 242 | 227 | 2188 | 199 | 23 |
| M | 232 | 283 | 357 | 286 | 257 | 128 | 162 | 89 | 168 | 279 | 251 | 2493 | 227 | 24 |
| N | 215 | 271 | 340 | 276 | 246 | 123 | 151 | 80 | 156 | 263 | 256 | 2379 | 216 | 24 |
| O | 323 | 338 | 115 | 176 | 298 | 228 | 273 | 166 | 126 | 364 | 397 | 2803 | 255 | 30 |
| P | 297 | 330 | 322 | 363 | 418 | 342 | 372 | 233 | 348 | 381 | 394 | 3800 | 345 | 15 |
Fig. 1 - Annual soil WD and regional precipitation rates for the Witelsbos and Lottering plantations in the Tsitsikamma region. Error bars show the standard error of the evapotranspiration estimates.
Sites from the Kruisfontein plantation, Knysna region, had significantly greater water deficits relative to the Tsitsikamma region. Sites I to K (the Knysna cluster) had annual average deficits in the range of 118 to 151 mm, respectively. The largest deficits in this group were observed for site I, with an average annual deficit of 151 mm (Fig. 2, Tab. 4).
Fig. 2 - Annual soil WD and the regional precipitation rates for the sites in the Kruisfontein plantation, Knysna region. Error bars show the standard error of the evapotranspiration estimates.
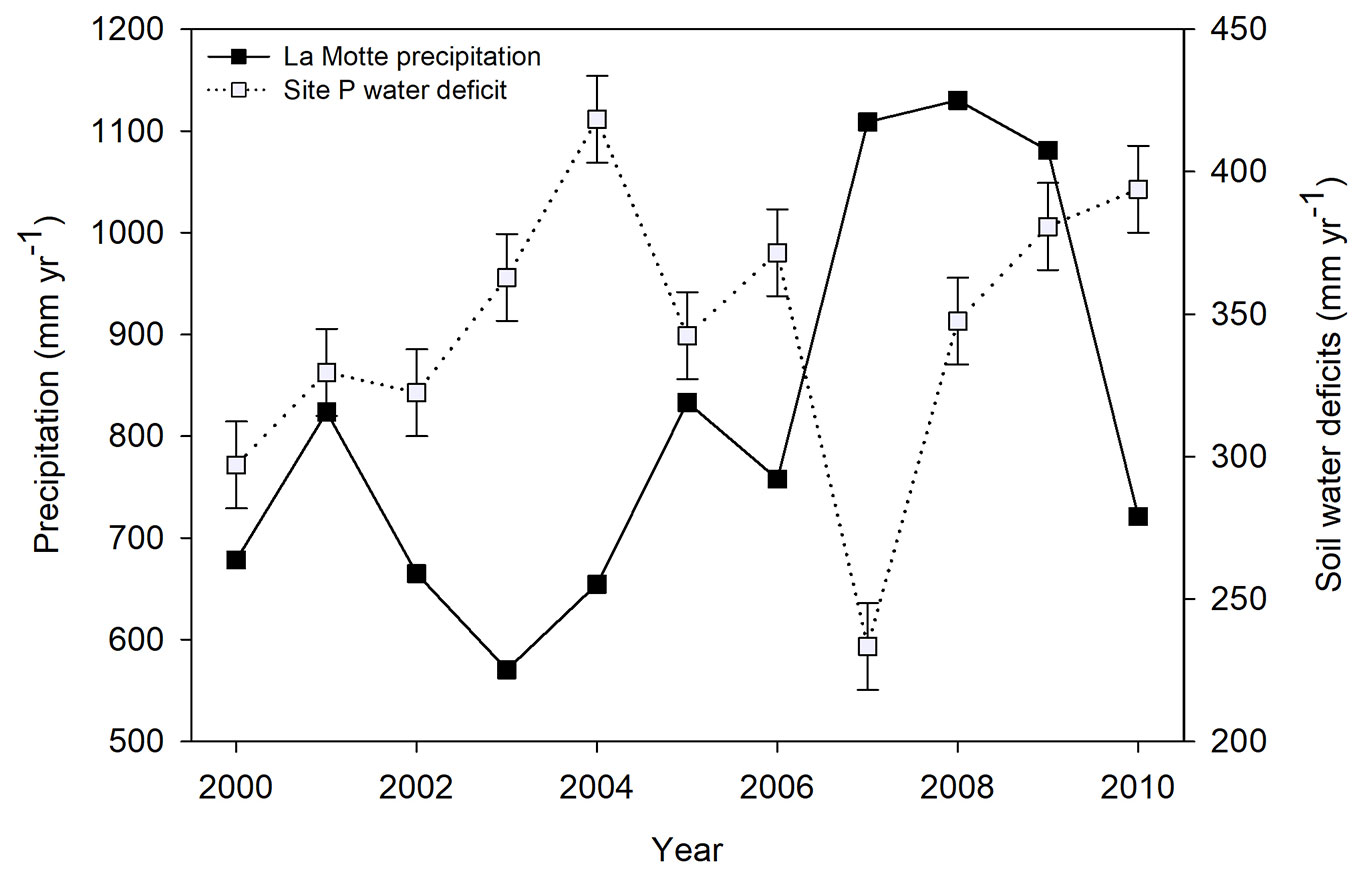
The largest variations were observed in the Boland region. Sites L to P had average annual soil water deficits of in the range of 199 to 345 mm respectively. The largest deficits were observed at site P, La Motte plantation, with a mean value of 345 mm (Fig. 3). Site N (Grabouw plantation) had better water storage capabilities and had an average deficit of 216 mm (Fig. 4, Tab. 4). The large decrease in annual rainfall from 2008 to 2010, as illustrated in Fig. 1to Fig. 4, resulted in increased water deficits across most regions. This relationship accentuates the dependence of soil- and plant-water availability on precipitation and soil storage capacity.
Fig. 3 - Annual soil WD and the regional precipitation rates for site P in the La Motte plantation, Boland region. Error bars show the standard error of the evapotranspiration estimates.
Fig. 4 - Annual soil WD and regional precipitation rates for site N in the Grabouw plantation, Boland region. Error bars show the standard error of the evapotranspiration estimates.
Correlations
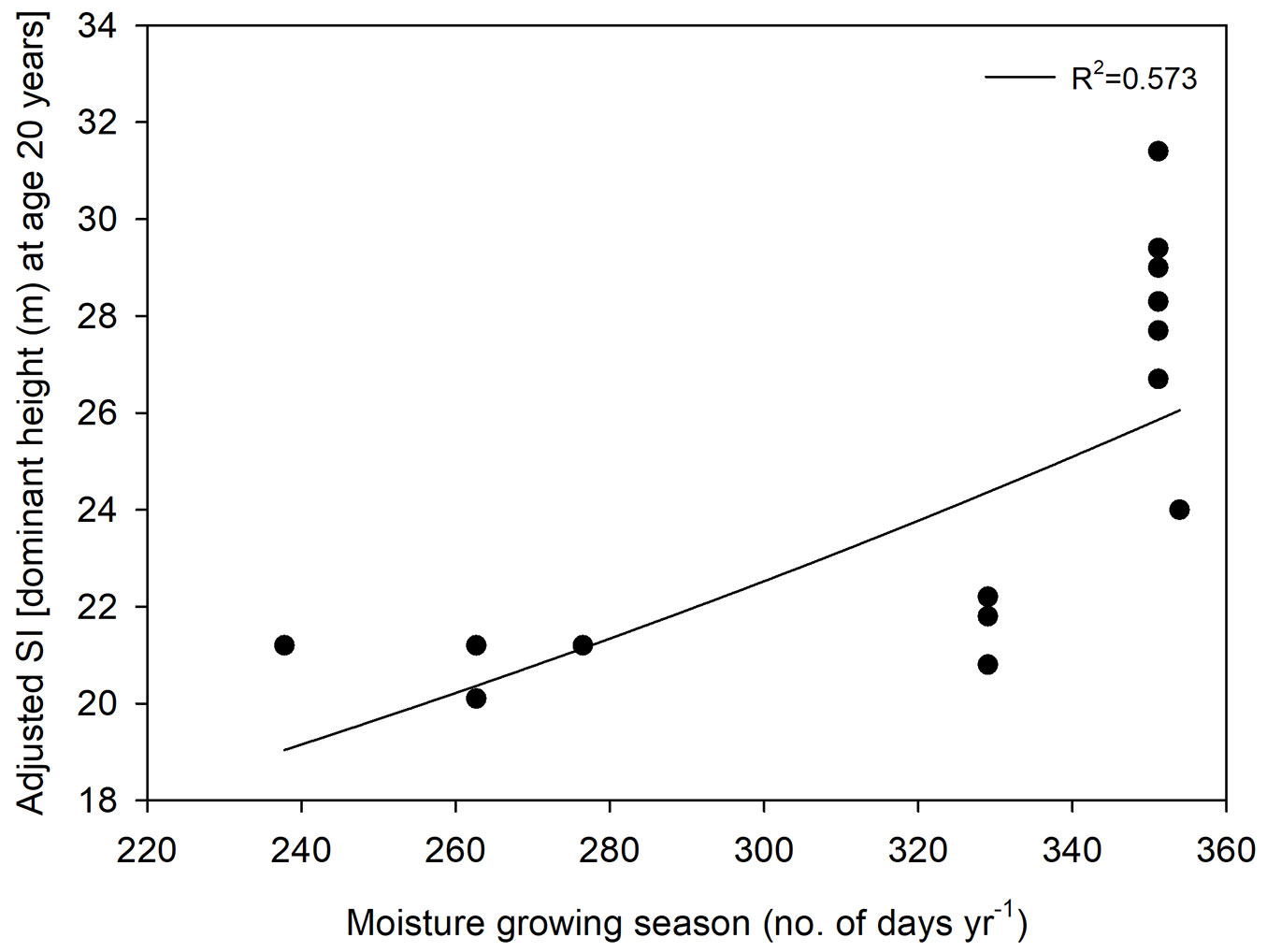
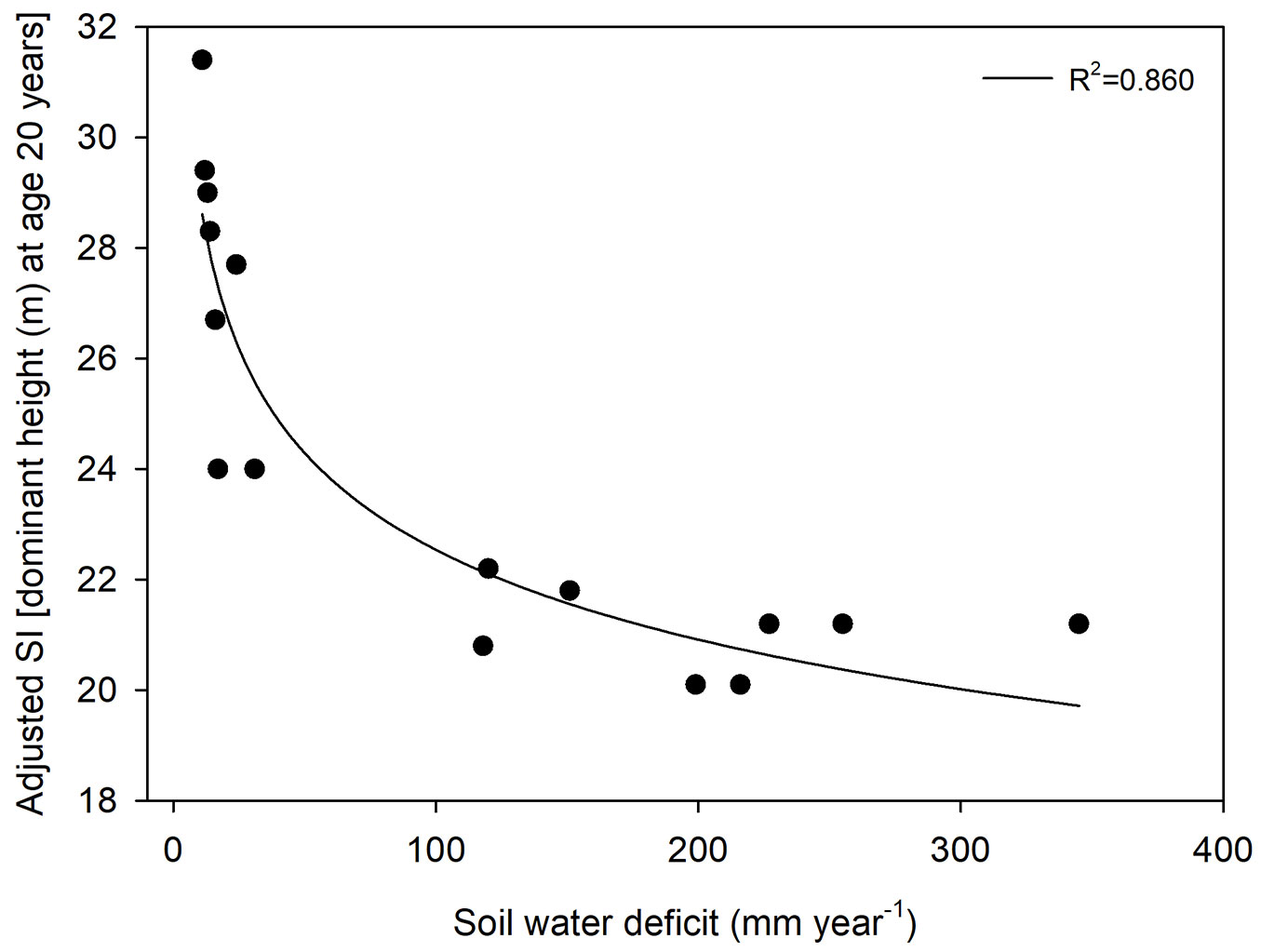
The Pearson’s correlation, a measure of the correlation between two variables, revealed a significant, strongly positive correlation between the moisture growing season (MGS) estimate and site index (r = 0.74, p < 0.001 - Tab. 5). The fitted relationships between MGS with site index showed an R2 value of 0.57 (Fig. 5). An even stronger, significant negative correlation between the soil water deficit (WD) and the site index of each site was found (r = -0.80, p < 0.001 - Tab. 5). The fitted relationship between WD and adjusted Site index (SI) can be described by the power function: SI = 37.063 · WD-0.108 (R2 = 0.86 - Fig. 6).
Tab. 5 - Pearson’s correlation coefficients (listed as the top entry in each cell) and the p-value (bottom entry in brackets). P-values < 0.05 denote a significant relationship between variables. (SI): dominant height (m) at 20 years of age.
| Variables | MAP (mm) |
ETp (mm yr-1) |
MGS (no. of days per year) |
AI | SI |
|---|---|---|---|---|---|
| Soil WD (mm yr-1) |
-0.39 (0.113) |
-0.09 (0.741) |
-0.96 (<0.001) |
-0.25 (0.369) |
-0.80 (<0.001) |
| MAP (mm) |
- | 0.22 (0.410) |
0.30 (0.258) |
0.64 (0.010) |
0.32 (0.229) |
| ETp (mm yr-1) |
- | - | -0.03 (0.923) |
-0.61 (0.010) |
0.54 (0.031) |
| MGS (days yr-1) |
- | - | - | 0.27 (0.320) |
0.74 (<0.001) |
| AI | - | - | - | - | -0.16 (0.539) |
Significant correlations were observed between the soil WD and the MGS estimate, with a Pearson’s correlation coefficient of -0.96 (p < 0.001 - Tab. 5).
Discussion
Climatic and edaphic effects
The average rainfall in the Tsitsikamma region varies from approximately 1.000 to 1.100 mm year-1 in the plantation forestry regions and is distributed evenly throughout the year, with slight peaks from August to November. The rainfall in the Knysna region is approximately 900 mm year-1 and is more seasonal: the monthly rainfall increases from November to March. The Boland receives approximately 1.000 mm year-1 (on average), and is highly seasonal, peaking from May to August with a very dry summer. The soils in the Tsitsikamma region had larger silt and clay contents, resulting in larger plant-available soil water storage potentials. This decreases the susceptibility of these soils to pass into a deficit from seasonally fluctuating or drought-induced (abnormally low) precipitation rates. Clayey and loamy soils have a higher porosity than sandy soils due to the size and distribution of particles ([26]). This was evident in the Tsitsikamma, as the monthly and cumulative deficits were significantly lower relative to the other regions. The larger soil WD and lower water-retention capacities observed in sites B and F in the Tsitsikamma region can be attributed to the physical soil properties. These sites had shallower soils, with the occurrence of plinthite. Periodic flooding, followed by drier conditions, can lead to advanced cementation and plinthite development ([38], [25]), and these soils characteristically have dense subsoils that further inhibit the infiltration of water and root penetration ([15]). In podzols of which the clay content is less than 10%, soil texture ranges from sand to sandy loam and water-retention capacity can be as low as 50 mm m-1 ([36]). The lower than average water-retention ability of site I (Knysna region) was due to topographical and textural differences from the other sites, as this site contains a significantly higher medium-sand content. Soil texture significantly affects the water-retention ability of soils, and sandy soils have a smaller water-retention ability per unit of depth relative to predominantly silt and clay soils ([29], [26], [15]). The remaining sites in the Knysna region, J and K, showed signs of periodically waterlogged soil conditions, and K was naturally positioned at the base of a slope or floodplain. Topography and landscape positioning are also key indicators of a soil’s water-retention ability ([25]). The poor water-retention capacities of sites L and P in the Boland region can be attributed to soil texture. Both sites had a sand content of more than 95%, and site L had a substantial coarse sand content. Sandy and shallow soils naturally have poor water-retention capabilities, and the cultivation of such soils requires frequent precipitation events ([6]). The poor water-retention capabilities of both sites are due to the high sand contents and shallowness. The reasons for the observed water-storage capacity of site P was analogous to the observations made for soils that exhibit abrupt changes in soil texture, which result in periodically stagnant or waterlogged soil conditions ([20]).
Water dynamics
The degree of water loss from each site trailed the monthly precipitation significantly. Modelled soil water losses, following a significant decrease in monthly precipitation, relied on the water storage capacity of each site. Water storage capacities were larger in the Tsitsikamma, and it was only after a substantial or prolonged decrease in monthly or annual precipitation that the water availabilities changed from surplus to deficit values. Soil water availabilities were increasingly sensitive to the rainfall gradient ([14]) from the Knysna to Boland regions. Long-term water balance is determined by the interaction of precipitation and potential evapotranspiration and is regulated by soil water storage ([28], [16]). The temporal variation between sites, and the change from surplus to deficit values, hinged substantially on seasonal fluctuations in regional precipitation, and more specifically in the rainfall frequency and intensity, but edaphic properties and topographic positioning also affected the degree of soil water loss observed at all sites. The large deficits observed in several sites with shallow and/or sandy soils on saprolitic material were quickly changed to surplus values following one month of high precipitation. The loamy soils showed moderate resilience to water loss, and surplus values were maintained for several months on most sites following smaller successive precipitation events. Only after a significant reduction in monthly or annual precipitation did large deficit values appear. High precipitation in shallow soils may lead to excess water and losses may occur through runoff ([28]). Soil structural properties combined with the frequency and intensity of rainfall, as well as the seasonal cycles of wet and dry periods determines water availability to vegetation and should be considered simultaneously ([3], [16]).
Relationship between site index and soil water availability estimates
The relationship between site index and either MAP or AI was insignificant and weak, indicating that both MAP and AI will be poor predictors of growth. The AI is useful to contrast water availability among sites with the same seasonal patterns for ETp and MAP ([13]). However, when working across sites with more than one seasonal rainfall and evapotranspiration pattern, use of the AI to rank water availability of sites is bound to yield poor results, as we have shown in this study. The relationship between MGS and site index was much stronger, underscoring the importance of seasonal variation in evapotranspiration and seasonal distribution of rainfall. The MGS consists of the monthly rainfall, ETp estimates as well as a predefined threshold value to define water stress. The estimate shows the relationship between rainfall distribution and ETp throughout the year, whereas the soil WD includes a soil water storage component. The WD estimate showed significant correlations with the MGS, AI and adjusted site index. Water Deficit and MGS were the only estimates that correlated significantly with the adjusted SI values. The strongest (and highly significant) correlation was observed between the average annual soil WD and site index of each pine stand, and this was to some extent similar to the findings of Gonçalves et al. ([18]). Those authors reported a strong correlation (r = 0.68, p < 0.001) between the soil WD, in accordance with Thornthwaite & Mather ([42]), and mean annual increments of several Eucalyptus-afforested regions in Brazil. The research presented in this study, supported by that of Gonçalves et al. ([18]), advocates that soil WD could likely be used as a relatively simple, yet reliable, estimate of plant-available water for a given site, using datasets that are widely and readily available. The key appears to be the inclusion of a site-based estimate of potential evapotranspiration in the calculation that is used in combination with soil water storage capacity. It therefore appears that gridded and satellite data, such as LocClim (FAO), MODIS and Landsat, could potentially also be investigated as alternative estimates for the ETp and plugged into the methodology outlined by Pereira et al. ([31]) once soil water storage capacities have been calculated. In addition, the Southern African subcontinent has an abundance of historic and current monthly rainfall records, emphasising the practicality of using the WD estimate. Silvicultural decision making could potentially be improved further if the water deficit is used in combination with multiple estimates of resource availability, such as nutrient availability indices.
Conclusions
The findings of this study show that soil water storage is subject to the interaction of the supply (precipitation) and demand (evapotranspiration) of water in the ecosystem, and both are regulated by the ability of the soil to store water. In this experiment, soil WD was calculated on a monthly time-step and expressed annually on all sites (with varying intensities), regardless of optimal or suboptimal climatic conditions over the period of a decade. The climatic gradient produced variation between sites, however, the severity of the observed water deficits was equally affected by the soil storage capacity of each site. Soil WD was shown to be a superior estimate of plant-available water, relative to the use of MAP, AI and MGS. The soil WD provides an excellent index of plant-available water and requires input data that is currently quite readily available across Southern African forest site types. The WD should be advocated as a preferred measure of soil water availability with the currently available datasets and foresters should be educated to think in terms of water deficit rather than in terms of MAP when evaluating different site types.
Acknowledgements
The authors thank Phillip Fischer for providing soil and climate data on the Boland sites, José Rocha for his assistance with the Water Deficit methodology, as well as the THRIP programme of the National Research Foundation, the Dept. of Agriculture, Forestry and Fisheries and MTO Forestry for financial support.
References
Online | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Online | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Ben Du Toit
Department of Forest and Wood Science, Stellenbosch University, Private Bag X1, Matieland 7602 (South Africa)
Corresponding author
Paper Info
Citation
Scheepers GP, Du Toit B (2020). Soil water deficit as a tool to measure water stress and inform silvicultural management in the Cape Forest Regions, South Africa. iForest 13: 473-481. - doi: 10.3832/ifor3059-013
Academic Editor
Giustino Tonon
Paper history
Received: Feb 05, 2019
Accepted: Aug 17, 2020
First online: Nov 01, 2020
Publication Date: Dec 31, 2020
Publication Time: 2.53 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2020
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 39862
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 33779
Abstract Page Views: 2935
PDF Downloads: 2474
Citation/Reference Downloads: 3
XML Downloads: 671
Web Metrics
Days since publication: 1902
Overall contacts: 39862
Avg. contacts per week: 146.71
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2020): 3
Average cites per year: 0.50
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Soil respiration along an altitudinal gradient in a subalpine secondary forest in China
vol. 8, pp. 526-532 (online: 01 December 2014)
Research Articles
Dynamics of humus forms and soil characteristics along a forest altitudinal gradient in Hyrcanian forest
vol. 14, pp. 26-33 (online: 10 January 2021)
Research Articles
Soil fauna communities and microbial activities response to litter and soil properties under degraded and restored forests of Hyrcania
vol. 14, pp. 490-498 (online: 11 November 2021)
Research Articles
The effect of clear-cut age on soil organic carbon and nitrogen indices in Scots pine (Pinus sylvestris L.) stands
vol. 18, pp. 146-153 (online: 09 June 2025)
Research Articles
Effects of black locust and black pine on extremely degraded sites 60 years after afforestation - a case study of the Grdelica Gorge (southeastern Serbia)
vol. 9, pp. 235-243 (online: 22 August 2015)
Research Articles
Influences of forest gaps on soil physico-chemical and biological properties in an oriental beech (Fagus orientalis L.) stand of Hyrcanian forest, north of Iran
vol. 13, pp. 124-129 (online: 07 April 2020)
Research Articles
Growing season water balance of an inner alpine Scots pine (Pinus sylvestris L.) forest
vol. 11, pp. 469-475 (online: 02 July 2018)
Research Articles
Influence of soil and topography on defoliation intensity during an extended outbreak of the common pine sawfly (Diprion pini L.)
vol. 10, pp. 164-171 (online: 19 November 2016)
Research Articles
Effects of tree species, stand age and land-use change on soil carbon and nitrogen stock rates in northwestern Turkey
vol. 9, pp. 165-170 (online: 18 June 2015)
Research Articles
Spatial heterogeneity of soil respiration in a seasonal rainforest with complex terrain
vol. 6, pp. 65-72 (online: 07 February 2013)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword