Spatio-temporal modelling of forest monitoring data: modelling German tree defoliation data collected between 1989 and 2015 for trend estimation and survey grid examination using GAMMs
iForest - Biogeosciences and Forestry, Volume 12, Issue 4, Pages 338-348 (2019)
doi: https://doi.org/10.3832/ifor2932-012
Published: Jul 05, 2019 - Copyright © 2019 SISEF
Research Articles
Abstract
Spatio-temporal modelling of tree defoliation data from the German forest condition survey is statistically challenging, particularly due to irregular grids. In the present study, generalized additive mixed models (GAMMs) were used to estimate the spatio-temporal trends in defoliation of the main tree species spruce, pine, beech and oak from 1989 to 2015 and to examine the suitability of different monitoring grid resolutions (standard 16 × 16 km grid and denser grids). Although data has been collected since 1989, this is the first time spatio-temporal modelling for all of Germany has been carried out. GAMMs proved to be a statistically sound and highly flexible choice for spatio-temporal modelling of defoliation data. In addition to the space-time component, stand age showed a significant effect on defoliation. The mean age and the species-specific relation between defoliation and age determined the general level of defoliation. However, further investigations are necessary in order to understand what is behind the age effect. Adjustment for stand age was carried out for identifying hotspots of high defoliation that are not merely the result of the age effect. Fluctuations in defoliation were most likely related to weather conditions. South-western Germany has emerged as the region with the highest defoliation since the drought year 2003. This region was characterized by the strongest water deficits in 2003 compared to the long-term reference period (1961-1990). Furthermore, the spatio-temporal model was used to carry out a simulation study to compare different survey grid resolutions in terms of prediction error. The model-based approach for grid analysis turned out to be appropriate for the given data and sample design. The grid analysis indicated that an 8 × 8 km grid instead of the standard 16 × 16 km grid is necessary for spatio-temporal trend estimation and for detecting hotspots in defoliation in space and time, especially regarding oaks.
Keywords
Age Effect, Drought Stress, Forest Condition Survey, Generalized Additive Mixed Models, Grid Examination, Spatio-temporal Model, Survey Design, Tensor Product Smooth
Introduction
The forest condition survey represents a fundamental part of Europe-wide forest monitoring, which was initiated as consequence of the discussion on forest dieback in the 1980s. Anthropogenic air pollution, in particular by sulphur (S) and nitrogen (N) compounds, was considered as the main cause of the so called “new type of forest damage” ([31], [38]). Measures to mitigate air pollution as well as the establishment of the “International Co-operative Programme on Assessment and Monitoring of Air Pollution Effects on Forests” (ICP Forests) in 1985 were initiated under the Convention on Long-Range Transboundary Air Pollution (CLRTAP) by the Economic Commission for Europe of the United Nations (UNECE). Methods for the forest condition survey are widely harmonised and standardised throughout Europe and are recorded in the ICP Forests manual ([8]), which has continuously been subject to updates since its first publication in 1985. The survey is performed on wide-scale monitoring plots (Level I), which were established wherever forest coincided with a 16 × 16 km grid across Europe ([12]). The forest condition survey is primarily based on defoliation, which denotes the loss of needles or leaves in the crown of a tree compared to a local or absolute reference tree with full foliage. Defoliation represents a widely used indicator for the assessment of tree condition and vitality ([8]). Estimation of defoliation takes place visually using binoculars. A quality assurance programme including for example national training courses ([9], [8]) has been initiated in order to control consistency and reproducibility of defoliation data.
In Germany, the condition of forest trees was first recorded in 1984 and has been carried out annually throughout Germany since 1990. Grid densifications in addition to the 16 × 16 km grid are common within German federal states. In addition, changes of the grid over time have occurred. Irregular grids and thus irregular time-series represent one of several characteristics of the defoliation data which make spatio-temporal evaluation statistically challenging. Geoadditive models ([11], [14]) and generalized additive mixed models (GAMMs - [19]) have been proposed for the evaluation of defoliation data. Inference can be based either on full Bayesian posterior analysis using Markov chain Monte Carlo (MCMC) techniques or on empirical Bayesian posterior analysis using mixed model techniques. Approaches have been suggested for binary data ([11], [22]) and for ordinal data ([2], [16]). Up to date, spatio-temporal modelling of continuous defoliation data has been published by Augustin et al. ([3]) only for the German federal state Baden-Wuerttemberg. The authors used GAMMs and inference was based on mixed model methodology. These GAMMs are also promising regarding spatio-temporal modelling of defoliation throughout Germany, although this data comes along with new challenges such as shifts of the monitoring grid. One of the most important aspects of spatio-temporal modelling is the handling of the spatio-temporal trend and the interaction of space and time. In the proposed model, this aspect can be managed using the scale invariant tensor product, which is a three-dimensional smoothing function of space and time ([40], [43]). The tensor product allows modelling of data derived from irregular grids as well ([3]). Models using the tensor product are most likely superior compared to models in which the spatial and temporal effects enter the model additively, such as the models proposed by Kneib & Fahrmeir ([16]), since it is unlikely that the spatial trend of defoliation is additive in time ([3]). Another advantage of GAMMs is that (non-)linear effects of influencing parameters can also be modelled by using smoothing functions ([3], [43]). In the case of defoliation, it is well known that the level of defoliation depends on tree age ([15], [36]). Thus, tree age can be considered in the model and trends solely based on tree age can be separated from trends caused by other parameters (e.g., air pollution, weather conditions). GAMMs further support a wide range of correlation structures ([43]).
Annual descriptions of the time trend of defoliation, considering the 16 × 16 km grid only, are published by the Federal Ministry of Food and Agriculture ([4]). Statistical evaluations of the spatio-temporal development of defoliation in Germany are hitherto lacking. Age-adjusted spatio-temporal trends are crucial for identifying regions with high mean defoliation ascribed to other parameters than tree age. In addition, the suitability of the 16 × 16 km grid as well as of denser grid resolutions with respect to nationwide spatio-temporal modelling has not been examined for Germany to date and in general publications of the methods and results of grid examinations regarding the forest condition survey are rare ([17], [30]). We hypothesised that GAMMs represent an appropriate choice to cope with the challenges of this monitoring data. Therefore, the present study aims to use GAMMs to: (i) estimate the spatio-temporal trends of defoliation of the main tree species Norway spruce (Picea abies [L.] Karst), Scots pine (Pinus sylvestris L.), European beech (Fagus sylvatica L.) and pedunculated and sessile oak (Quercus robur L. and Q. petraea [Matt.] Liebl., treated together) in Germany from 1989 to 2015 and all available grid densities; and (ii) examine the suitability of different monitoring grid resolutions, which have been used in the past, for spatio-temporal modelling by comparing the respective prediction errors.
Materials and methods
Landscapes and distribution of tree species in Germany
The Federal Republic of Germany consists of 16 federal states including three city states. In the north of Germany, there are the North-German Lowlands. The North-eastern Lowlands are characterised by a more continental climate than the more maritime North-western Lowlands. Adjacent to the south, the Central Upland Range follows. Further in the south, the Southwest German Scarplands border and adjacent in the south-eastern part of Germany there are the Alpine Forelands and the Bavarian Alps.
Norway spruce represents the most common tree species in Germany and grows predominantly in moist and cooler regions of the low mountain ranges and the Alpine Forelands, but is rarely found in the Northern Lowlands. There are only few areas in Germany where spruce is native. Scots pine is the main tree species growing in the Northern Lowlands but it can also be found in the rest of Germany, though rarely in pronounced altitudes. European beech is the most common deciduous tree species in Germany and, similar to spruce, is distributed mainly in the moist low mountainous regions whilst is less represented in the Northern Lowlands. Beech usually develops from natural rejuvenation. Pedunculate and sessile oak together represent the less common of the main tree species. Oaks grow in areas from the Northern Lowlands to the low mountain ranges but rarely in pronounced mountainous, cooler regions.
Data from the forest condition survey
Annual data from the forest condition survey of Germany is available from 1989 to 2015. Tree defoliation represents the main parameter of the survey and is given in 5% classes from 0% (no defoliation) to 100% (dead tree). Additional parameters such as fructification and abiotic and biotic damage causes are also recorded. The investigated trees must belong to Kraft class 1 (dominant) to 3 (subdominant); hence no suppressed trees are considered. In Germany, the cross cluster is the most common design of the Level I plots. Cross clusters usually comprise 24 trees; six trees in all four directions of the compass in a distance of 25 m from the centre of the cross cluster. A detailed description of the methods can be found in Eichhorn et al. ([8]) and in Wellbrock et al. ([39]). The federal states are responsible for data collection, which is mandatory for the 16 × 16 km grid throughout Germany. From 2006 to 2008 during the second national forest soil inventory (NFSI II), the forest condition survey was conducted nationwide on a denser grid (usually 8 × 8 km). Further details on available grid densities of the federal states are given in Tab. 1. Two federal states changed their initial grid to coincide with the grid of the national forest inventory (Bavaria in 2006 and Brandenburg in 2009).
Tab. 1 - Available grid density (km × km) for spatio-temporal modelling of defoliation of the German federal states. The 16 × 16 km grid represents the standard grid. In the five federal states of former Eastern Germany, the forest condition survey started in 1990. (1): without three city states; (2): partial data set of 8 × 8 km grid.
| Federal state1 (Abbreviation) | 1989 | 1990 | 1991-2004 | 2005 | 2006-2008 | 2009-2010 | 2011-2015 |
|---|---|---|---|---|---|---|---|
| Baden-Wuerttemberg (BW) | 16 × 16 | 16 × 16 | 16 × 16 | 8 × 8 | 8 × 8 | 8 × 8 | 8 × 8 |
| Bavaria (BY) | 16 × 16 | 16 × 16 | 16 × 16 | 16 × 16 | 8 × 8 | 8 × 82 | 8 × 82 |
| Brandenburg (BB) | - | 16 × 16 | 16 × 16 | 16 × 16 | 8 × 8 | 16 × 16 | 16 × 16 |
| Hesse (HE) | 16 × 16 | 16 × 16 | 16 × 16 | 8 × 8 | 8 × 8 | 8 × 8 | 8 × 8 |
| Lower Saxony (NI) | 16 × 16 | 16 × 16 | 16 × 16 | 8 × 8 | 8 × 8 | 8 × 8 | 8 × 8 |
| Mecklenburg-Western Pomerania (MV) | - | 16 × 16 | 8 × 8 | 8 × 8 | 8 × 8 | 8 × 8 | 8 × 8 |
| North Rhine-Westphalia (NW) | 16 × 16 | 16 × 16 | 16 × 16 | 16 × 16 | 8 × 8 | 16 × 16 | 16 × 16 |
| Rhineland-Palatinate (RP) | 16 × 16 | 16 × 16 | 16 × 16 | 16 × 16 | 4 × 12 + 16 × 16 |
4 × 12 + 16 × 16 |
16 × 16 |
| Saarland (SL) | 16 × 16 | 16 × 16 | 16 × 16 | 16 × 16 | 2 × 4 | 2 × 4 | 2 × 4 |
| Saxony (SN) | - | 16 × 16 | 16 × 16 | 16 × 16 | 8 × 8 | 16 × 16 | 16 × 16 |
| Saxony-Anhalt (ST) | - | 16 × 16 | 16 × 16 | 8 × 8 | 8 × 8 | 8 × 8 | 8 × 8 |
| Schleswig-Holstein (SH) | 16 × 16 | 16 × 16 | 16 × 16 | 16 × 16 | 8 × 4 | 16 × 16 | 16 × 16 |
| Thuringia (TH) | - | 16 × 16 | 16 × 16 | 16 × 16 | 8 × 8 | 16 × 16 | 16 × 16 |
In the following evaluations, GAMMs were used only for the four main tree species. Norway spruce represented the most frequent tree species in Germany with 32.0% of all trees in the 16 × 16 km grid, followed by Scots pine with 29.1%, European beech with 16.2% and oaks with 6.2%. The two oak species Q. robur and Q. petraea were regarded together due to the occurrence of hybridization. However, it needs to be kept in mind that 16% of trees did not belong to the main tree species.
Evaluations were carried out on plot level. For age-adjusted spatio-temporal modelling, stand ages were necessary. The mean stand age for one tree species of one plot was estimated from the ages of individual trees. Different approaches for tree age estimation are valid, such as assured dates of stand establishment, estimates from increment borer and stem discs ([8]). Usually assured dates of stand establishment from forest inventory are used in Germany. The stands usually were relatively homogenous showing similar tree ages. In cases where the youngest or oldest tree of a plot deviated more than 20 years from the plot mean, the stand age was classified as “irregular”. For plots without individual tree age specification (25% of the plots, e.g., systematically for Bavaria from 1989 to 2005), the non-species-specific stand age of the plot given in the database was used. Hence, for 98% of the plots with at least one tree belonging to the main tree species, a stand age (other than “irregular”) was available. The mean stand age (median weighted according to the number of trees per plot) regarding the 16 × 16 km grid differed among the species and this was primarily due to more very old trees of the deciduous species. In 2015 (1989-2015, respectively), the mean stand ages of spruce, pine, beech and oaks amounted to 73 (70), 86 (70), 104 (90) and 110 (103) years, respectively. For all species, the increase in age from 1989 to 2015 was notably lower than 26 years. Pine trees growing in the Northern Lowland were on average slightly younger than pine trees in the remainder of Germany. Each plot having at least one tree belonging to the main tree species and having a stand age was used for the statistical evaluations. Therefore, the total number of unique plots ranged from 290 in 1989 (only 16 × 16 km grid without the former Eastern Germany) and 392 in 1990, respectively (only 16 × 16 km grid and all of Germany), to 1807 in 2008 (16 × 16 km grid and grid densifications in all federal states).
Spatio-temporal model for mean defoliation
We modelled the spatio-temporal defoliation monitoring data by species using a GAMM ([19], [40], [43]). Very good data in terms of covering age, space and time were available. In principle, data of further influencing variables could have been used but were not available to the same extent and the reduction in sample size lacks proportionality in terms of the small surplus regarding the explained variability. The spatio-temporal model was based on that developed by Augustin et al. ([3] - eqn. 1):
where yit is the mean defoliation of one of Norway spruce, Scots pine, European beech or oak for sample plot i =1, …, n and for year t = 1, …, 27, averaged over all trees of the respective species at sample plot i. We model mean defoliation at plot level rather than individual tree level because comparing variability of defoliation within and between plots showed that it was lower within plots than between plots. Before averaging defoliation, the defoliation class of a single tree was converted into a continuous variable by using the midpoint of the class. The logit link was used since defoliation represents an estimated percentage and the logit link ensured that fitted values were bounded in (0, 1). The function f1 is a one-dimensional smooth function of stand ageit using a penalized cubic regression spline basis. The function f2 is a three-dimensional smooth function of the year and of the coordinates (easting and northing of the Gauß-Krüger coordinate system, GK4), which is a tensor product smoother constructed from a two-dimensional marginal smooth for space and a marginal smooth for time ([3]). The marginal bases are a two-dimensional thin plate regression spline basis for easting and northing and a cubic regression spline basis for year. The tensor product of the two marginal smooths is used so that different penalties for space (metres) and time (years) are used ([40], [43]). For the error term ε a multivariate Normal distribution is assumed as N(0, σ2 Λ). The covariance matrix Λ is a block diagonal matrix with the ith subvector εi having covariance matrix Λi, which is related to the residuals of one plot i over time. The covariance matrix Λi further contains on the diagonal the weights 1/αit, where αit is the number of trees assessed at plot i and year t. The temporal correlation was modelled by a first order autoregressive-moving average process (ARMA(1.1) - [23]), i.e., εit = φεit-1 + pcit-1 + cit, where φ and p represented correlation parameters and cit follows a Normal distribution with an expected value of zero. The ARMA(1.1) process was most suitable for all four tree species according to model selection.
Parameter estimation can be carried out as for a GLMM using penalized quasi-likelihood with standard mixed modelling software ([19], [3], [43]). This is possible since the GAMM in eqn. 1 corresponds to a generalized linear mixed model (GLMM) because the smooth functions f1 and f2 can be rewritten as (eqn. 2):
The matrices X and Z are the design matrices containing the basis functions evaluated for each observation at plot i and year t. The matrix X contains the parts of the basis function to which the unpenalized coefficients β apply; e.g., for f1 this is a straight line and the matrix Z contains all parts of the basis functions to which the penalized coefficients b apply. The vector b is a vector of random effects following a normal distribution with mean zero and an unknown positive-definite covariance matrix Ψ.
For variance and trend estimation, we used the Bayesian representation of the GLMM in eqn. 2. This is done by interpreting the choice of smoother and penalty as making prior assumptions about the smoothness of the true function. Thus, the penalties can be expressed as prior distributions on the functions f1 and f2. Then, by using Bayes’ theorem, a posterior distribution of the model parameters is obtained ([37], [41], [3], [43]) and this is a multivariate normal distribution. Hence, the predictive distributions of any quantity of interest can be obtained by sampling from the multivariate normal posterior distribution of the model parameters; the lower and upper 95% quantiles constitute the credible interval for the quantity of interest. We used this type of interval because in the context of GAMMs the Bayesian credible intervals have been shown to have good coverage properties ([37]). All evaluations were performed using R ver. 3.2.2 ([26]). For the spatio-temporal modelling of defoliation, the R package “mgcv” ver. 1.8-10 ([42]) was utilized. In Appendix 1 (Supplementary material) we give an example R code for the described analysis.
Residual correlation was examined by using diagnostic plots in which normalized residuals were investigated in space and time ([3]). This included empirical semi-variograms (R package “geoR” - [27]) as well as empirical (partial) autocorrelation functions (R package “nlme” - [24]). Although stand age is confounded with space and time, collinearity between the parameters stand age and year did not occur as the correlation between stand age and year was low. The Bayesian information criterion (BIC) was used for model comparison and selection ([32]) due to its suitability for data with a high sample number compared to the number of model parameters. Further details on the statistical methodology are given in Augustin et al. ([3]).
Trend estimation
As described above, we generated predicted values for mean defoliation {hat} μitp = {hat} yitp from the posterior predictive distribution of yit and averaging over i, thus obtaining the mean defoliation in year t (eqn. 3):
for the pth draw from the posterior predictive distribution. The median and the 2.5% and 97.5% quantiles were calculated for the spatial ({hat} μitp) and temporal trend ({hat} μtp). For the trend estimation, plots were not weighted by number of trees per plot because on the one hand weighting would down-weight plots without pure stands, which would be an undesirable characteristic of the estimator ([3]), and on the other hand we were interested in a statement for the entire area of Germany. For parameter estimation of the spatio-temporal model shown in eqn. 1 and eqn. 2, available data at all grid resolutions were used. For time trend estimation, we generated a predictive distribution as described above using an area- and species-representative grid. We used the 16 × 16 km grid of the forest condition survey: (i) of 2015 (grid 1); and (ii) of the corresponding year (grid 2). In the first case (grid 1), the grid of 2015 was transferred to all other years (1989-2014). In addition, a defined stand age (median age of 2015, 50 years and 150 years, respectively) was transferred to all other years. This case offers the possibility to exclude the age and grid effect. In the second case (grid 2), the actual observed stand age of each plot was considered as well as changes in the 16 × 16 km grid (shift, elimination/addition of plots). The respective modelled defoliation values thus meet the actually assessed defoliation more closely.
Simulation study for the grid examination
German federal states are obliged to provide the forest condition data of the 16 × 16 km grid for the annual nationwide time trend evaluation by the BMEL. However, it is still unclear if this grid is sufficient for nationwide spatio-temporal trend modelling of defoliation. Therefore, the mean prediction error (MPE) of the defoliation estimates was estimated: (i) for the 16 × 16 km grid and the 8 × 8 km grid - the federal states having denser grids than 8 × 8 km (Rhineland-Palatinate, Saarland and Schleswig-Holstein) were not included for MPE estimations for the 16 × 16 km grid and the 8 × 8 km grid (approach I); and (ii) for the 16 × 16 km grid and for all grid resolutions available, which corresponded to the highest available grid density - all federal states were included for MPE estimations for the 16 × 16 km grid and for all grid resolutions available (approach II). We used the prediction error to compare the different survey grid resolutions as it estimates the difference between the estimated defoliation and the true defoliation. The parameters of the spatio-temporal model described in eqn. 1 and eqn. 2 were estimated using all available data from all federal states. For the simulation study, the estimates of the model fitted to the observed defoliation data were assumed to be the truth. As described above, data were simulated from the multivariate normal posterior distribution of these parameters. We draw s = 1, …, nsim (nsim = 40) set of parameters and the sth draw yields a realisation of the predictive distribution of the response for all possible grid points and all years (eqn. 4):
where {hat} ηits is the linear predictor simulated from the predictive distribution and thus the simulated data value of defoliation yits at plot i and year t is (eqn. 5):
For the generation of the error term, the parameter estimates relating to the ARMA error model εits ~ N(0, σ2Λi) were used. Moreover, the weights 1/αit were included. Under this simulation scheme, defoliation values lower than 0 and higher than 1 were possible and were truncated to 0 and 1, respectively. Exploratory plots showed that the simulated defoliation data reflected the actual observed data well. We simulated data for all sample plots available in 2008 (year with most plots); for approach I the federal states Rhineland-Palatinate, Saarland and Schleswig-Holstein were excluded. The stand age of each plot was set to the stand age in 2008, since the mean age was relatively constant over the whole period from 1989 to 2015. In the next step, a survey sample was taken from the simulated data and the GAMM was fitted to the survey sample data. The sample taken was either the sample obtained from the 16 × 16 km grid or from the 8 × 8 km grid of approach I or from the 16 × 16 km grid or from the denser grid of approach II. Subsequently, the time trend {hat} yts for Germany was estimated from the simulated sample data using eqn. 3. This was then compared with the assumed true µt, as estimated from the original data in eqn. 3, to estimate the MPE per year t (eqn. 6):
Finally, the MPE per plot i and year t was estimated by comparing the estimated mean defoliation {hat} yits with the assumed true µit from eqn. 1 where the parameters were replaced by their estimates from the model fitted to the actual data (eqn. 7):
In the following, the square root of the MPE is used (RMPE). The RMPEti > 5% was considered for the years 2006 to 2015 since we focused on the suitability of the present grid.
Results
Age-adjusted spatio-temporal trend of defoliation
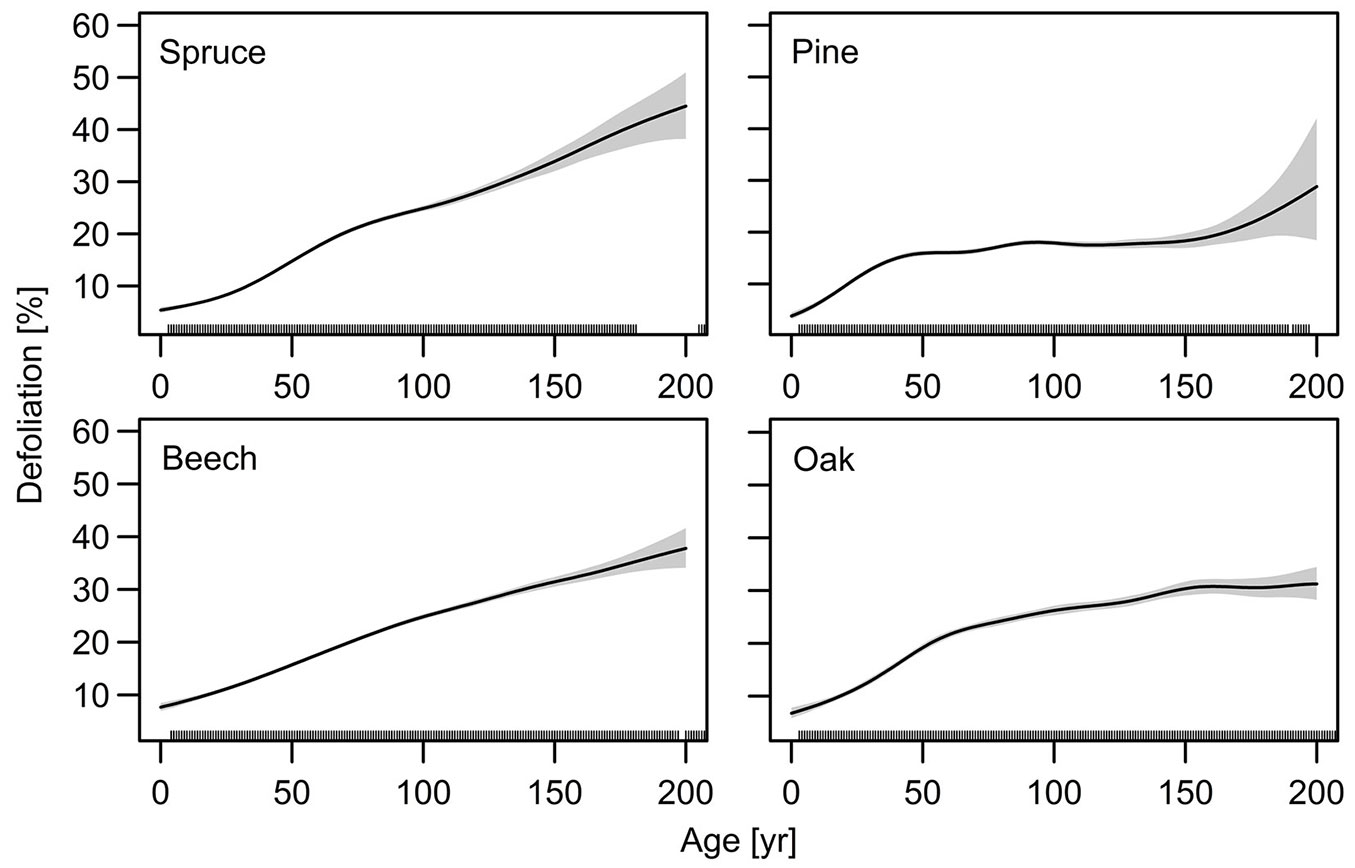
The best fit of the spatio-temporal model was obtained for spruce (adjusted R2 = 0.54; n = 10.182), followed by beech (adjusted R2 = 0.47; n = 9.283), oaks (adjusted R2 = 0.47; n = 6098) and pine (adjusted R2 = 0.41; n = 9252). Both the stand age and the space-time component showed a highly significant effect on defoliation (p < 0.0001). For comparison, adjusted R2 of models not including the stand age and space-time component ranged between 0.009 (spruce) and 0.031 (beech). The effect of stand age on defoliation differed among the tree species (Fig. 1). A nearly linear increase of defoliation with increasing stand age was observed for spruce and beech. For pine, defoliation increased until a stand age of approximately 40 years and hardly any dependency occurred for older pine trees. For oaks, as for pine, defoliation clearly increased until a stand age of approximately 60 years, whereas defoliation only slightly increased with further increasing stand age.
Fig. 1 - Effect of stand age on defoliation in spruce, pine, beech and oaks.The lines at the x-axis reflect the observed age values. The grey shaded area indicates the 95% credible interval. Please note that the same scaling was used for the x-axis for reasons of comparability.
Defoliation of spruce remained more or less the same from 1989 to 2015 (Fig. 2). The mean defoliation was 20.2% (grid 1, median age of 2015) and 18.9% (grid 2), respectively. The highest mean defoliation was observed in 1992 and in the two following years, as well as after 2003 (grid 1: 23.3% in 2004). The lowest defoliation was observed in 1989 (grid 1: 17.9%). At the beginning of the observations, the defoliation estimated for the grid and median age of 2015 (grid 1) was higher than the defoliation estimated for the actual observed grid and age (grid 2) due to differences in the grids and especially due to a lower actual stand age at the beginning of the time series. Over time both time trends overlapped. According to the association between defoliation in spruce and stand age (Fig. 1), defoliation of 150-year-old spruce was significantly higher than of 50-year-old spruce (grid 1 - Fig. 2). The course of the time trend was the same for both ages but it was more pronounced in the older spruce trees. The credible interval for the time trend of the 150-year-old trees was wider than that of younger trees because trees of 150 years are less common in spruce.
Fig. 2 - Estimated mean defoliation and credible interval (2.5% and 97.5% quantiles) for the four main tree species in Germany from 1989 to 2015. In black: observed 16 × 16 km grid and observed stand age per year (grid 2); in blue: 16 × 16 km grid of 2015 and weighted median stand age of 2015 (spruce: 73 years, pine: 86 years, beech: 104 years, oaks: 110 years - grid 1); in red: 16 × 16 km grid of 2015 and assumed stand age of 150 years (grid 1); in green: 16 × 16 km grid of 2015 and assumed stand age of 50 years (grid 1).
Pine showed the lowest mean defoliation of the four main tree species at 18.2% (grid 1, median age of 2015; 16.6% for grid 2). The highest defoliation was observed at the beginning of the 1990s (1991: 25.1% for grid 1 - Fig. 2). Defoliation decreased until the mid 1990s and stayed more or less unchanged up to 2015. A slight increase was observed in the years following 2003. Due to the weak association of defoliation in pine with stand age compared to the other species (Fig. 1), differences between the time trend of 150-year-old and 50-year-old pine were low compared to the other tree species (Fig. 2).
Defoliation of beech was higher than those of the two coniferous tree species (grid 1: 24.6%, grid 2: 21.3%). Defoliation on average showed no clear trend but pronounced fluctuations were observed (Fig. 2). Peaks of defoliation occurred in 1992, 2000, 2004-2006, 2010-2011, 2014, with the highest defoliation in the years 2004 and 2005 (grid 1: both years 29.1%). Beech trees of 150 years had notably higher defoliation than beech trees of 50 years (Fig. 2).
Oaks showed the highest mean defoliation of all species with 26.9% (grid 1; 23.0% for grid 2 - Fig. 2). Defoliation of oaks was lowest in 1989 (grid 1: 19.3%) and subsequently increased until 1993 (28.8%). In the following years, defoliation remained at a high level with a peak in 2004 (30.5%) but a slight decrease was observed in 2002 and after 2012 (Fig. 2). The credible intervals were wider compared to the other main species since oaks are less frequent. Differences between the time trend of 50-year-old and 150-year-old oak trees were evident but slightly lower than for spruce and beech (Fig. 2).
Defoliation varied spatially in Germany between 1989 and 2015 (Fig. 3; see also Fig. S1-S3 in Supplementary material). For spruce, defoliation was high in the North-eastern Lowlands at the beginning of the 1990s (Fig. S1). It continued to be slightly higher in south-eastern Germany in 1992. From 1994 to 2002, defoliation of spruce was comparably low everywhere in Germany. In 2003, defoliation slightly increased in southern Germany. Beginning in 2005, the highest defoliation was found in south-western Germany with the highest defoliation in 2006 and 2007 in particular in the area of the Black Forest, the highest low mountain range of Germany. Between 2005 and 2015, defoliation was generally lower in the eastern part of Germany (Mecklenburg-West Pomerania to Bavaria) than in the western part (Schleswig-Holstein to Baden-Wuerttemberg).
Fig. 3 - Results of spatio-temporal modelling of defoliation in beech from 1989 to 2015 using a nationwide consistent stand age of 104 years. Modelled defoliation is indicated in colour (see legend) and the isolines further reflect the modelled defoliation (e.g., 0.2 is 20%). The sample plots of the respective year are shown as points. Black points indicate plot defoliation < 25% and red points indicate plot defoliation ≥ 25% (observed defoliation at given actual stand age).
For pine, high defoliation >25% occurred in the North-eastern Lowlands as well as in parts of the border region of southern Germany at the beginning of the 1990s (Fig. S2). In the mid 1990s, a difference between the Northern Lowland with low defoliation and the remainder of Germany with slightly higher defoliation showed up and remained until 2015. Regarding the remainder of Germany, again south-western Germany appeared as the region with highest defoliation beginning in 2003.
For beech at the beginning of the time series, high defoliation was found in north-eastern Germany (Fig. 3). In 1992, defoliation > 25% occurred in central and southern Germany and in 2000 in north-western Germany. After 2003, high defoliation was observed in large areas of central and southern Germany. South-western Germany again emerged as a region of partly very high defoliation but comparably high defoliation also extended to Hesse and up to the south of Lower Saxony.
For oaks at the beginning of the 1990s, defoliation was also highest in north-eastern Germany but it was also high in south-eastern Germany (Fig. S3 in Supplementary material). Beginning in the mid 1990s, besides south-western Germany, the lowland north of the low mountain ranges (especially in North Rhine-Westphalia) emerged as an area of recurring high defoliation.
Summing up, a shift of high defoliation was demonstrated for all species with high defoliation in north-eastern Germany (North-eastern Lowlands) at the beginning of the time series and high defoliation in south-western Germany (western part of the Southwest German Scarplands) starting from 2003.
Grid examination
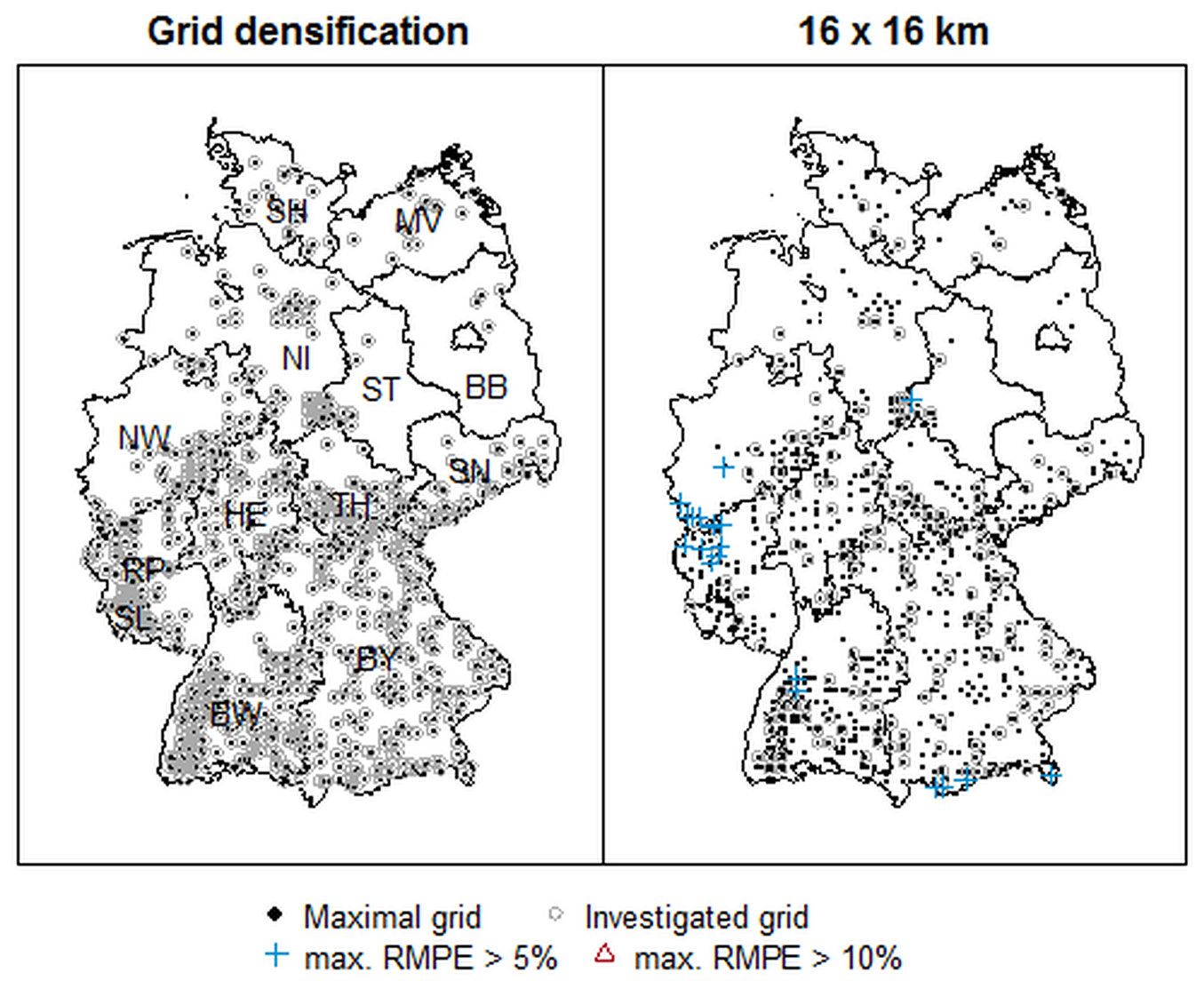
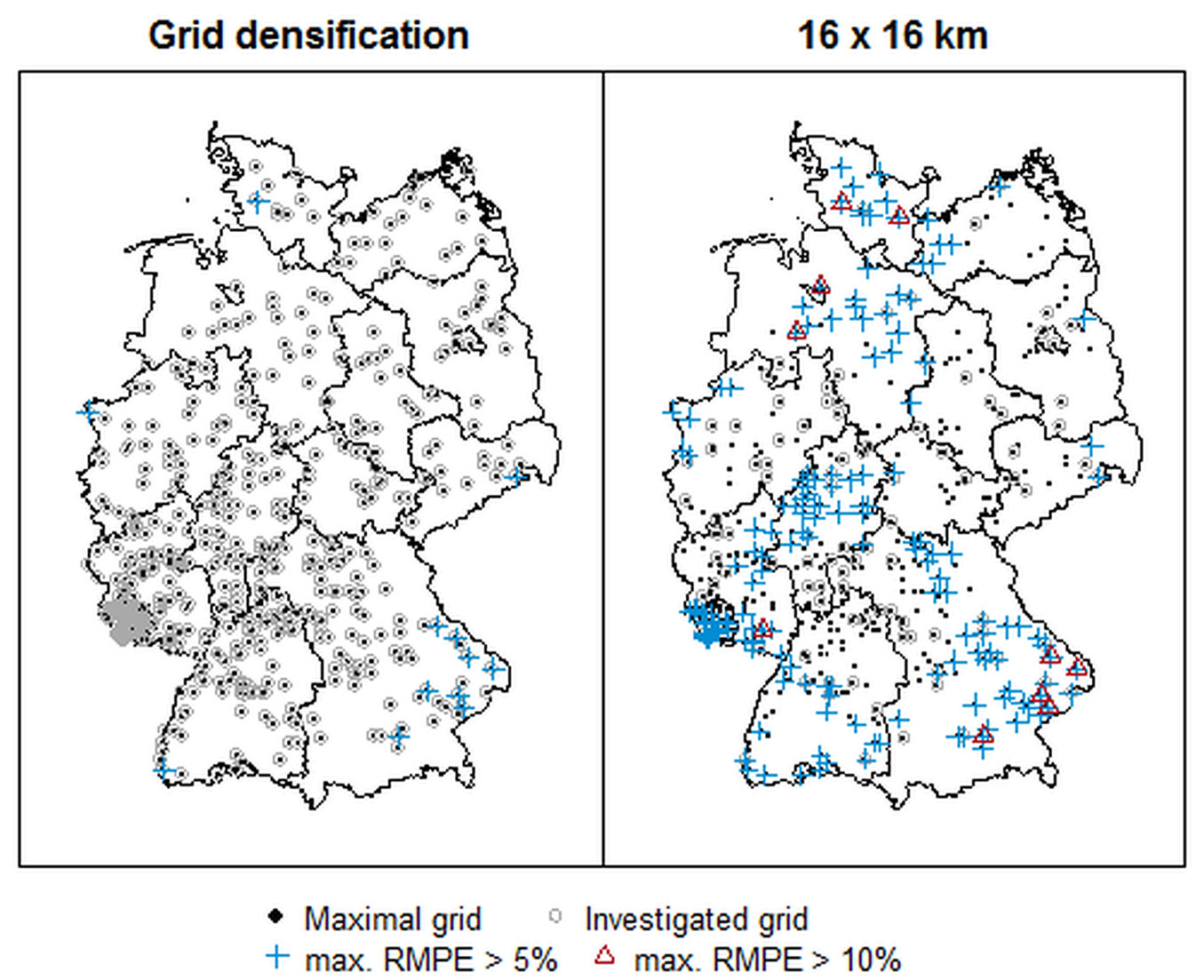
The RMPEt of the 16 × 16 km grid was lowest for pine at 0.9% (approach I and II) followed by spruce at 1.0% (approach I and II), beech at 1.6% (approach I) and 1.3% (approach II), respectively, and was highest for oaks at 1.9% (approach I) and 1.8% (approach II), respectively (Tab. 2, Tab. 3). The RMPEt of the 8 × 8 km grid (approach I) and of the grid densification (approach II) were lower in all cases and ranged from 0.5% to 1.1% (Tab. 2, Tab. 3). Through the years, no trend was observed for the RMPEt of the 16 × 16 km grid, whereas the RMPEt of the denser grids slightly decreased from 1989 to 2015 for all tree species. Although the mean RMPEt as well as the mean RMPEit (Tab. 2, Tab. 3) was low for the four main tree species and all grids (16 × 16 km grid and 8 × 8 km grid/grid densification), individual sample plots or regions showed RMPEit > 5% (Tab. 2, Tab. 3). No or only two plots with RMPEit > 5% were found for spruce, pine and beech for the 8 × 8 km grid and the grid densification, respectively (Tab. 2, Tab. 3). Moreover, only few oak plots had RMPEit > 5% regarding these densified grids. However, regarding the 16 × 16 km grid, in particular many oak plots had RMPEit > 5% (Tab. 2, Tab. 3). Spruce showed the lowest number of plots having RMPEit > 5%. Regional differences among tree species occurred regarding the RMPEit of the 16 × 16 km. For spruce, the highest uncertainties existed in the Eifel region, the Alpine region and in the north of the Black Forest (Fig. 4). These uncertainties did not occur if denser grids were used. For pine, different regions showing uncertainties were found regarding the 16 × 16 km grid. Weak points were particularly the southern and also northern parts of Germany (Fig. S4 in Supplementary material). For beech, high uncertainties occurred, especially at the borders of Germany, i.e., northern and north-eastern Germany, Saarland, south-western Baden-Wuerttemberg, the Alpine region and the Bavarian Forest (Fig. S5). In case of the denser grids, high uncertainties did not exist for pine and beech. For oaks, high uncertainties were found scattered over almost all of Germany regarding the 16 × 16 km grid (Fig. 5). The RMPEit of oak plots frequently amounted to even more than 10%. In the case of the denser grids, only isolated plots showed RMPEit > 5%, as well as the region of and around the Bavarian Forest. In conclusion, the 16 × 16 km grid was sufficient for the time trend calculation for the four main tree species, although higher uncertainty was observed for oaks. The most frequent species, spruce and pine, showed the lowest prediction error and the least frequent main tree species, the oaks, showed the highest error. For spatio-temporal trends, deficiencies occurred for all species regarding the 16 × 16 km grid.
Tab. 2 - Results of the simulation study for the grid analysis (approach I) presented for the four main tree species. The federal states Rhineland-Palatinate, Saarland and Schleswig-Holstein were not considered for approach I of the simulation study. RMPEit > 5% indicates the number of sample plots (counted once only) that had a root mean prediction error of > 5% defoliation between 2006 and 2015. The number in brackets shows the underlying total number of grid points.
| Tree species | Survey grid |
RMPEt [%] | RMPEit [%] | RMPEit > 5 % |
||
|---|---|---|---|---|---|---|
| Median | Range | Median | Range | |||
| Spruce | 8 × 8 km | 0.6 | 0.5 - 0.8 | 1.4 | 0.5 - 6.4 | 0 (745) |
| 16 × 16 km | 1.0 | 0.7 - 1.3 | 1.8 | 0.6 - 8.7 | 22 (745) | |
| Pine | 8 × 8 km | 0.5 | 0.4 - 1.0 | 1.7 | 0.5 - 6.1 | 0 (662) |
| 16 × 16 km | 0.9 | 0.5 - 1.2 | 2.2 | 0.7 - 9.4 | 76 (662) | |
| Beech | 8 × 8 km | 0.9 | 0.7 - 1.1 | 1.7 | 0.6 - 10.3 | 2 (604) |
| 16 × 16 km | 1.6 | 1.2 - 1.9 | 2.5 | 0.9 - 11.7 | 60 (604) | |
| Oaks | 8 × 8 km | 1.1 | 0.8 - 1.2 | 2.5 | 1.0 - 9.7 | 14 (381) |
| 16 × 16 km | 1.8 | 1.1 - 2.4 | 3.3 | 1.3 - 14.7 | 142 (381) | |
Tab. 3 - Results of the simulation study for the grid analysis (approach II) presented for the four main tree species. All federal states were considered for approach II of the simulation study. RMPEit > 5% indicates the number of sample plots (counted once only) that had a root mean prediction error of > 5% defoliation between 2006 and 2015. The number in brackets shows the underlying total number of grid points.
| Tree species | Survey grid |
RMPEt [%] | RMPEit [%] | RMPEit > 5 % |
||
|---|---|---|---|---|---|---|
| Median | Range | Median | Range | |||
| Spruce | Densification | 0.5 | 0.5 - 0.8 | 1.4 | 0.5 - 6.9 | 0 (869) |
| 16 × 16 km | 1.0 | 0.8 - 1.3 | 1.9 | 0.6 - 8.8 | 20 (869) | |
| Pine | Densification | 0.6 | 0.4 - 1.0 | 1.7 | 0.6 - 7.0 | 0 (733) |
| 16 × 16 km | 0.9 | 0.7 - 1.2 | 2.3 | 0.7 - 13.3 | 72 (733) | |
| Beech | Densification | 0.8 | 0.6 - 1.0 | 1.7 | 0.7 - 12.7 | 0 (775) |
| 16 × 16 km | 1.3 | 0.9 - 1.7 | 2.3 | 0.8 - 11.9 | 90 (775) | |
| Oaks | Densification | 1.1 | 0.7 - 1.5 | 2.4 | 0.7 - 9.5 | 12 (519) |
| 16 × 16 km | 1.9 | 1.3 - 2.5 | 3.3 | 1.3 - 14.9 | 166 (519) | |
Fig. 4 - Highest estimated root mean prediction error (RMPEit) of defoliation in spruce for the grid densification (at least 8 × 8 km grid) and 16 × 16 km grid (approach II) for the years 2006 to 2015. Black points indicate all possible sample plots (corresponds to the grid densification). The grey circles show the sample plots considered for the estimation of the RMPE (grid densification and 16 × 16 km grid, respectively). Blue crosses indicate RMPEit > 5% and red triangles RMPEit > 10%. The federal states Rhineland-Palatinate, Saarland and Schleswig-Holstein have grid densities that deviate from 8 × 8 km (denser grids). Abbreviations of the federal states of Germany (without city states) are indicated in the map for the grid densification. Abbreviations and full names are given in Tab. 1.
Fig. 5 - Highest estimated root mean prediction error (RMPEit) of defoliation in oaks for the grid densification (at least 8 × 8 km grid) and 16 × 16 km grid (approach II) for the years 2006 to 2015. Black points indicate all possible sample plots (corresponds to the grid densification). The grey circles show the sample plots considered for the estimation of the RMPE (grid densification and 16 × 16 km grid, respectively). Blue crosses indicate RMPEit > 5% and red triangles RMPEit > 10%. The federal states Rhineland-Palatinate, Saarland and Schleswig-Holstein have grid densities that deviate from 8 × 8 km (denser grids).
Discussion
Spatio-temporal modelling of defoliation
GAMMs proved to be a good choice for spatio-temporal modelling of defoliation data. They could cope with the challenges this monitoring data pose. Statistically sound estimates of mean defoliation in space and time with appropriate credible intervals could be produced. The use of a three-dimensional smoothing function of space and time allowed for high flexibility regarding changes in the grid, thus defoliation data from all available grid densifications could be included. Our study revealed that stand age was strongly associated with defoliation. Adjustment for stand age was possible using GAMMs and was carried out in order to identify hotspots of high defoliation not merely resulting from the age effect. The age effect primarily determined the general level of defoliation, whereas fluctuations in the time series of defoliation were most likely associated with weather conditions.
Age effect: determinant of the defoliation level
A pronounced effect of age on defoliation was common to all investigated tree species. This effect has frequently been mentioned in the literature, in particular for spruce ([29], [7], [35]). The species-specific age effects mostly corroborated results published by Klap et al. ([15]), Seidling ([33]) and Augustin et al. ([3]). The species-specific association between defoliation and age might be primarily attributed to the demand for light, stand situation, stand development and forest management (pruning, thinning, felling under mature canopy) typically found for the corresponding species. Beech is known to be shade-tolerant and the almost linear increase in defoliation with age might reflect the comparably slow but continuous vertical growth of beech ([25]). Young beech trees in Germany are usually shadowed and of lower social status, whereas old beech trees often grow in cleared stands with natural rejuvenation. Beech crowns shadowed by neighbouring trees or beech trees with lower social status were shown to have lower defoliation ([34]). This is in line with observations from the federal states Rhineland-Palatinate and Saarland, where old trees growing in canopy-closed stands were found to have lower defoliation than old trees growing in cleared stands ([21]). Oaks and pine are light-demanding tree species. Unlike for beech, Seidling ([34]) reported higher defoliation for oak and pine trees with lower social status. For both tree species, a similar asymptotic association between defoliation and age was found. Light-demanding tree species show notable vertical growth in young stands, whereas the growth rate decreases with increasing age ([25]). Pine trees grow faster vertically than oak trees but the time point of the decrease of growth rate is also reached earlier. Assessed pine trees mainly grew in pure stands (in particular in the Northern Lowland), whereas oak trees were mainly found in mixed stands. In Rhineland-Palatinate, old trees of both species were mainly found in canopy-closed stands ([21]), which is also true for other federal states such as Baden-Wuerttemberg. Spruce belongs to the semi-shade tree species and the age effect is similar to the curve progression of beech. Very old spruce trees were often found at sites having extreme climatic conditions or that were very poor quality, such as spruce trees growing in the Bavarian Alps. Hence, confounding between age and site conditions cannot be excluded and may partly be responsible for the linear increase of defoliation observed for very old trees of this species.
The estimated effects of age on defoliation represent associations as they were found on average for the tree species. However, old trees and plots having several old trees of one species for which low defoliation was observed in the long term could be found for each tree species. Natural senescence plays a role for the observed age effect. Changes in crown morphology, in part due to sexual maturity and accompanied recurring fructification, represent one aspect of natural senescence. However, trees probably do not age in close relation to time, but social status and stress factors determine their senescence ([6]). Several authors have proposed an accumulating effect of multiple stress factors with age resulting in enhanced sensitivity in older compared to younger trees ([15], [35]). The occurrence of healthy old trees is possible and old trees can regenerate under favourable conditions ([21]). However, selective vulnerability to a certain stress factor presumably does not increase in older trees compared to younger trees ([15]).
In the present study, it was shown that the general level of defoliation was primarily determined by the mean age and the species-specific association between defoliation and age. Hence, pine had the lowest and oaks the highest mean defoliation. The age adjustment for time trend estimation using a stand age of 50 years and 150 years, respectively, underlined that the differences in the mean level of defoliation among the tree species was primarily a result of the age effect. Oak, beech and spruce trees of 150 years on average showed the same level of defoliation, whereas old pine trees had a notably lower level of defoliation, which could be attributed to the species-specific association with age. Oak trees having a stand age of 50 years, however, exhibit a higher level of defoliation compared to spruce, pine and beech trees, which in turn had similar defoliation. Comparison of the existing time trend that arose using the true stand age of trees on the 16 × 16 km grid that was monitored in the respective year (grid 2) with the age- and grid-adjusted time trend (grid 1) further corroborated the effect of age on the defoliation level. Differences in the time course between both time series was mainly based on the different grids, whereas differences in the level of defoliation could be attributed to the differences in stand age. Both effects were strongest at the beginning of the time series since grids deviated most from the grid in 2015 (e.g., shift of grids) and trees on average were younger and thus less defoliated than in 2015. Thus, the present study underlines that an age adjustment is necessary for time trend as well as for spatio-temporal trend estimation in order to obtain time trends that do not mirror increasing defoliation as consequence of aging and to identify regions with longer-term high defoliation that cannot be ascribed primarily to the age effect.
Weather conditions: drivers of spatio-temporal defoliation trends
Investigations regarding the association between influencing parameters and defoliation were not examined in the present study but were simultaneously conducted in another study (“process study”) by our group using the same data and GAMMs ([10]). The results of the study are briefly summarized, because they contribute to the understanding of spatio-temporal developments observed in the present study. The “process study” revealed strong statistical associations between weather conditions, particularly deviations from the long-term mean (1961-1990), and defoliation in all four tree species. Besides weather conditions and indicators of drought stress, fructification of beech as well as insect infestation (pine, oaks) proved to be other stress factors associated with high defoliation ([10]).
A significant influence of climatic factors and an increase in defoliation with drought have been reported previously for different European countries ([15], [44], [36], [13]). These studies further reported that lagged effects, especially drought in the previous year and cumulative drought over several preceding years, show a major influence on defoliation in the following year. In summer 2003, an extreme heat wave and drought occurred in large parts of Europe, which had a strong impact on forest ecosystems ([20]). The severe drought stress in 2003 climaxed after the forest condition survey. In the present study, notably increased mean defoliation was observed in 2004 for all investigated tree species.
The nationwide mean defoliation of Norway spruce, which is known to be a tree species sensitive to water stress, remained elevated in 2005 to 2007. In 2009, the defoliation level prior to the drought event was reached again. In general, needle loss is still visible years after the event because spruce trees keep up several needle sets.
Defoliation of Scots pine, which is generally considered as relatively drought-tolerant in Germany, was only slightly higher between 2004 and 2006. Pine in general showed the lowest mean defoliation and hardly any temporal changes in defoliation were observed between the mid 1990s and 2015. The high defoliation that was observed in parts of north-eastern Germany particularly in 1991 was likely caused by severe insect infestation (data not shown). However, methodological differences in defoliation assessment after the introduction of the forest condition survey in former Eastern Germany cannot be ruled out as a reason for particularly high defoliation ([29]).
For European beech, it was not before 2008 that defoliation again reached the level of defoliation immediately before the drought. Mean defoliation of beech in general showed clear fluctuations that were primarily coincident with the occurrence of common to abundant fructification in beech trees ([7], [36], [10]). Regional differences in annual fructification intensity were found. For example, in 2000 common to abundant fructification occurred in western and north-western Germany. The combination of drought stress and substantial mast behaviour obviously required considerable time for regeneration of beech regarding defoliation.
Oaks tolerate a wide range of climatic conditions and soil water availability. Unlike for beech and the coniferous tree species, defoliation in oaks significantly increased only in 2004. In this year, insect infestation was widely observed in Germany (data not shown).
In 2004, the highest defoliation occurred in south-western Germany for all species and this region continued to be the area of highest defoliation until the end of the monitored period. Although all of Germany was affected by drought stress in 2003, the greatest water deficits compared to the long-term mean were found in south-western Germany and particularly in the area of the Black Forest ([1], [10]).
Model-based approach for grid examination
In Germany, the annual nationwide time trend evaluation of defoliation by the BMEL is based on the data of the 16 × 16 km grid, which is part of the Europe-wide Level I grid. The federal states are obliged to deliver data based on this grid. Our study revealed that in general the 16 × 16 km grid is sufficient to make a nationwide statement on time trends of defoliation for the four main tree species. Higher uncertainty exists for oaks, mainly due to being the least common main tree species. Spatio-temporal modelling is additionally necessary to identify hotspots of high mean defoliation at an early stage. For nationwide spatio-temporal trend estimation of defoliation using GAMMs, grids denser than 16 × 16 km (at least 8 × 8 km) are required for some regions for spruce, pine and beech and for all of Germany for oaks. Mostly since the start of the NFSI II, several federal states have already provided defoliation data based on their denser grids for the nationwide evaluations. In the present study, spatio-temporal modelling was based on data from all available grids. It needs to be considered that statements concerning the prediction error of defoliation trends can be made only with respect to the four main tree species, as other tree species were not investigated.
Although grid examinations have been carried out by federal states, results and methods have been published only rarely. For the federal state Lower Saxony, it was shown by means of sample error and 90% confidence intervals that a 4 × 4 km grid is sufficient for this federal state ([30]). For the federal state Baden-Wuerttemberg, a simulation study in 2006 revealed that the 16 × 16 km grid was not sufficient for spatio-temporal trend estimations (N. H. Augustin, personal communication). An 8 × 8 km grid including the 16 × 16 km grid points as fixed points with the remaining points as alternating subsets of the 4 × 4 km grid was suggested. For Switzerland, Köhl et al. ([17]) estimated sampling errors and reported that the loss of precision remained acceptable using an 8 × 8 km grid for nationwide evaluations, whereas a strong deterioration was observed when using a 12 × 12 km and 16 × 16 km grid, respectively. Design-based approaches ([17], [30]), as well as model-based approaches (N. H. Augustin, personal communication, [28]) were used for grid examinations. In the design-based approach, the observed values are regarded as a sample from a fixed population; that is, the observed values are regarded as fixed and the sample locations are regarded as the random quantity. Estimates and inference is based on a probability sample and is obtained from the resulting sampling distribution. This approach requires data to be derived from random sampling and to be independent from each other ([5], [18]). In contrast, in the model-based approach, the population is regarded as random and the sampling locations are fixed ([5]). Thus, random sampling and independence is not required but instead a spatial dependence needs to be modelled if present. Estimates and inference are based on the model and the model should mimic the data generating process. Data from the forest condition survey are obtained by systematic sampling on grids, which is a random sampling design and both the design-based and model-based approaches can be used for grid examination. Advantages of the model-based approach are that we can estimate the effects of explanatory variables on defoliation, we obtain spatio-temporal point estimates and we can predict, which makes it possible to estimate bias and prediction error, respectively, by means of simulation. Therefore, we applied the model-based approach using GAMMs. Since the simulation of the data and prediction on basis of the simulated data were based on the same model (which is believed to be the true model), the prediction error estimated would likely underestimate the true prediction error rather than overestimate it.
Conclusions
In the present study, generalized additive mixed models (GAMMs) were used for spatio-temporal modelling of tree defoliation data for the four main tree species of Germany from 1989 to 2015, as well as to examine the suitability of the 16 × 16 km grid, which represents the standard grid of the forest condition survey of Germany. This is the first time spatio-temporal modelling of defoliation has been carried out for all of Germany. GAMMs could cope with the statistical challenges this monitoring data come along with, like irregular grids, and proved to be a statistically sound and highly flexible choice for spatio-temporal modelling of defoliation data. The model-based approach for grid analysis turned out to be appropriate for the given data and sample design. Weak points occurred for all four tree species with respect to spatio-temporal trend estimation based on the standard 16 × 16 km grid. For oaks, we recommend using at least an 8 × 8 km grid. However, the standard grid was generally sufficient for nationwide time trend estimation. The study revealed a strong association between defoliation and stand age. The association between defoliation and age was species-specific but defoliation in principal increased with increasing age. Thus, the mean age and the species-specific relationship were mostly responsible for the general level of defoliation of the four tree species. The age effect was attributed to natural senescence, accumulation of stress with age and stand development as well as forest management. However, further investigations are necessary in order to understand what is behind the age effect and how it should be handled for evaluations of defoliation data. Data of the forest management and of the characteristics of the forest stand (e.g., competitive environment, DBH) are not available for the forest condition survey (Level I) since this survey focuses on the status and development of the forests. However, a detailed investigation could be done using data of the intensive forest monitoring (Level II), which amends the Level I survey to examine cause-effect-relationships. Adjustment for stand age was carried out in order to identify hotspots of high defoliation that are not merely the result of the age effect. Spatio-temporal fluctuations were most likely the result of weather conditions. The exceptional drought stress occurred in 2003 was associated with a notable increase in mean defoliation in the following years. Intensity and duration of the increase in defoliation were species-specific. In recent years, south-western Germany turned out to be the region with the highest mean defoliation of the four tree species. This region was affected by the strongest water deficit in 2003 compared to the reference period (1961-1990). Future measures should aim to a further reduction of soil acidification and mitigation of air pollution, as well as to adapted forest management in order to reduce stress factors for forest trees and facilitate a higher ability to regenerate and adapt to climate change.
Acknowledgments
We thank the responsible institutions of the federal states for providing the data from the forest condition survey based on their denser grids. We particularly acknowledge discussions with Inge Dammann (Northwest German Forest Research Institute), Friedrich Engels (Research Institute for Forest Ecology and Forestry Rhineland-Palatinate), Stefan Meining (Büro für Umweltüberwachung) and Hans Werner Schröck (Research Institute for Forest Ecology and Forestry Rhineland-Palatinate).
References
Gscholar
Gscholar
Online | Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Nicole Wellbrock
Thünen Institute of Forest Ecosystems, Alfred-Möller-Strasse 1, 16225 Eberswalde (Germany)
State Agency for Nature, Environment and Consumer Protection of North Rhine-Westphalia, Leibnizstrasse 10, 45659 Recklinghausen (Germany)
University of Bath, Claverton Down, Bath BA2 7AY (United Kingdom)
Corresponding author
Paper Info
Citation
Eickenscheidt N, Augustin NH, Wellbrock N (2019). Spatio-temporal modelling of forest monitoring data: modelling German tree defoliation data collected between 1989 and 2015 for trend estimation and survey grid examination using GAMMs. iForest 12: 338-348. - doi: 10.3832/ifor2932-012
Academic Editor
Matteo Garbarino
Paper history
Received: Jul 25, 2018
Accepted: Apr 10, 2019
First online: Jul 05, 2019
Publication Date: Aug 31, 2019
Publication Time: 2.87 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2019
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 43032
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 35268
Abstract Page Views: 3842
PDF Downloads: 3131
Citation/Reference Downloads: 18
XML Downloads: 773
Web Metrics
Days since publication: 2354
Overall contacts: 43032
Avg. contacts per week: 127.96
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2019): 11
Average cites per year: 1.57
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Height-diameter models for maritime pine in Portugal: a comparison of basic, generalized and mixed-effects models
vol. 9, pp. 72-78 (online: 11 June 2015)
Research Articles
First results of a nation-wide systematic forest condition survey in Turkey
vol. 4, pp. 145-149 (online: 01 June 2011)
Research Articles
Probabilistic prediction of daily fire occurrence in the Mediterranean with readily available spatio-temporal data
vol. 10, pp. 32-40 (online: 06 October 2016)
Research Articles
Large-scale spatial distribution of deer browsing damage to young tree plantations
vol. 14, pp. 34-40 (online: 14 January 2021)
Research Articles
Estimation of forest cover change using Sentinel-2 multi-spectral imagery in Georgia (the Caucasus)
vol. 13, pp. 329-335 (online: 07 August 2020)
Research Articles
Comparison of drought stress indices in beech forests: a modelling study
vol. 9, pp. 635-642 (online: 06 May 2016)
Review Papers
Monitoring the effects of air pollution on forest condition in Europe: is crown defoliation an adequate indicator?
vol. 3, pp. 86-88 (online: 15 July 2010)
Research Articles
Modeling stand mortality using Poisson mixture models with mixed-effects
vol. 8, pp. 333-338 (online: 05 September 2014)
Research Articles
Effect of drought stress on some growth, morphological, physiological, and biochemical parameters of two different populations of Quercus brantii
vol. 11, pp. 212-220 (online: 01 March 2018)
Research Articles
Estimation of stand crown cover using a generalized crown diameter model: application for the analysis of Portuguese cork oak stands stocking evolution
vol. 9, pp. 437-444 (online: 02 December 2015)
iForest Database Search
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords