Probabilistic prediction of daily fire occurrence in the Mediterranean with readily available spatio-temporal data
iForest - Biogeosciences and Forestry, Volume 10, Issue 1, Pages 32-40 (2016)
doi: https://doi.org/10.3832/ifor1686-009
Published: Oct 06, 2016 - Copyright © 2016 SISEF
Research Articles
Abstract
The prediction of wildfire occurrence is an important component of fire management. We have developed probabilistic daily fire prediction models for a Mediterranean region of Europe (Cyprus) at the mesoscale, based on Poisson regression. The models use only readily available spatio-temporal data, which enables their use in an operational setting. Influencing factors included in the models are weather conditions, land cover and human presence. We found that the influence of weather conditions on fire danger in the studied area can be expressed through the FWI component of the Canadian Forest Fire Weather Index System. However, the prediction ability of FWI alone was limited. A model that additionally includes land cover types, population density and road density was found to provide significantly improved predictions. We validated the probabilistic prediction provided by the model with a test data set and illustrate it with maps for selected days.
Keywords
Fire Occurrence, Prediction, Canadian Forest Fire Weather Index, Poisson Regression
Introduction
Predicting the occurrence of wildfire incidents is an important component of fire management. Due to the uncertainties in the influencing factors, as well as to random effects in the fire process, such a prediction must necessarily be probabilistic. Various probabilistic models are proposed in the literature, including Poisson models ([13], [27], [40]), logistic regression ([44], [35], [20], [40], [12], [4]), multiple regression ([37], [30]), neural networks ([44], [45]) and Bayesian networks ([15]). Recently, machine learning algorithms have been found to be well suited to modeling and predicting fire occurrences, due to their greater flexibility compared to classical regression analysis. In particular, the Maxent (maximum entropy) algorithm ([32]) and methods based on decision tree learning, such as the random forest algorithm ([28], [30]), have been applied. The choice of the appropriate model depends on the influencing factors selected and their spatial and temporal resolution, as well as the purpose of the model prediction.
Past probabilistic models of fire occurrence use weather factors, anthropogenic factors or combinations thereof as explanatory variables ([34]). The effect of climatic factors is often represented by components of the Canadian Forest Fire Weather Index System (CFFWIS - [24], [49], [1], [46]). In these studies, the temporal resolution is daily and the spatial resolution is regional, ranging from 1 to several km2 (except [46]). Although CFFWIS was originally developed for Canadian climates and vegetation, it is commonly used for predicting fire occurrence in the Mediterranean ([47], [8], [46]). Still, this necessitates that the CFFWIS indicators, in order to categorize fire danger level (e.g., low, moderate, high), be adjusted to the specifics of the Mediterranean climates ([29], [16], [14], [46]).
Various studies have looked into the combined effect of weather and anthropogenic factors ([9], [33], [3], [20], [40], [48], [31], [26], [30], [25]). The temporal resolution of these studies is seasonal or yearly, and thus the weather factors include mean, minimum and maximum temperatures, as well as cumulative precipitation. Common explanatory variables representing anthropogenic influences are population density, land use, distances to human-built infrastructures ([10]). However, many additional variables were studied, e.g., distance to campground ([11]), holidays ([27]), ownership of housing ([9]), proximity to urban areas and roads ([36], [1]), unemployment rate ([30]), rural exodus by means of population decrease ([25]), and hiking trail density ([4]). The spatial resolution in these studies varies from cellular (1 km2 grid - [33]) to regional.
The aim of this paper is the development of a daily probabilistic model for fire occurrences in Mediterranean climates, which includes both natural and anthropogenic factors. Such a daily predictive model with fine spatial resolution can eventually be helpful as a fire management tool. Here, we show that the fire risk prediction at the mesoscale can be improved with readily available data on weather and anthropogenic factors, combined with a sound probabilistic model.
In the proposed model, the potential influence of weather conditions is represented by the Canadian Forest Fire Weather Index System (CFFWIS - [43]). The anthropogenic influence is represented through spatial variables such as land cover type and road density, which was found to be a relevant indicator of fire occurrence in Amatulli et al. ([3]), Syphard et al. ([40]) and Oliveira et al. ([30]). The model is based on Poisson regression. Its results are daily maps of fire occurrence rates with 1 km2 spatial resolution. The use of readily available data make the model easy to integrate into existing fire prediction systems. This can improve fire occurrence predictions due to the high spatio-temporal resolution (daily, 1 km2) of the proposed model and the incorporation of both weather and anthropogenic factors.
The model is applied to the island of Cyprus, where the model parameters are calibrated from observed fire events. Cyprus is part of the Eastern Mediterranean region, which is drier and warmer than the more commonly studied areas of Spain, Southern France and Northern Italy. The data is separated into a learning set and a validation set, which allows to investigate the predictive power of the proposed model. It is found that the best prediction can be achieved by combining the natural and anthropogenic factors. The main factors describing anthropogenic influences are found to be land cover, population density and road density.
Methodology
Canadian Forest Fire Weather Index System
The Canadian Forest Fire Weather Index System (CFFWIS - [43]) was first introduced across Canada in 1971 and is meanwhile adapted in several national fire danger estimation systems ([41], [8]). The input parameters required by CFFWIS are daily values of easily observed weather parameters (dry bulb temperature, wind speed, relative humidity and precipitation). CFFWIS consists of six components: three fuel moisture codes (FFMC: Fine Fuel Moisture Code; DMC: Duff Moisture Code; DC: Drought Code) and three fire behavior indices (ISI: Initial Spread Rate; BUI: Build Up Index; FWI: Fire Weather Index). A detailed description of CFFWIS is available in Van Wagner ([43]) and Lawson & Armitage ([22]).
Probabilistic model for predicting fire occurrence
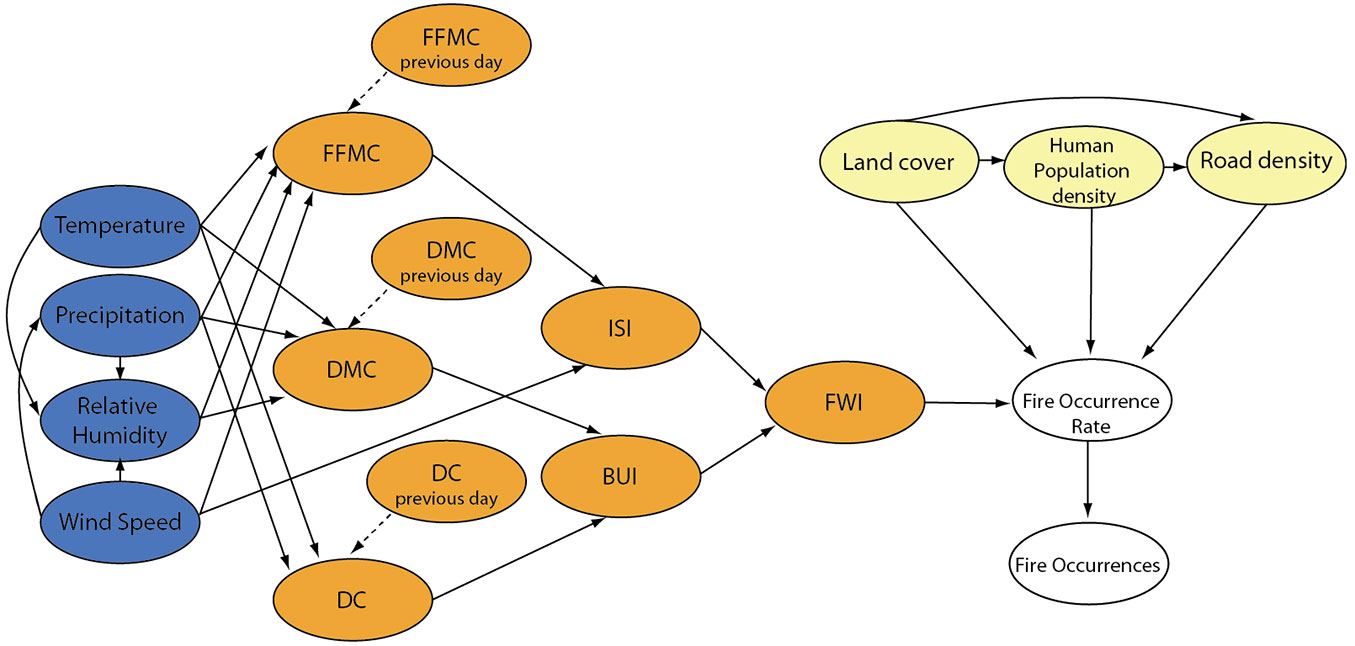
Fig. 1 summarizes the proposed probabilistic model by means of a Bayesian Network (BN). In the BN, probabilistic dependence among the variables is represented graphically by means of arrows. This makes it convenient not only for graphical communication of the model but also for quantitative probabilistic modeling. For these reasons, BN are increasingly applied for risk assessment of natural hazards, e.g., for wildfire occurrence ([15]), rock-fall hazards ([39]), avalanches ([17]), tsunamis ([7]) and earthquakes ([5], [21], [6]). For a detailed introduction to BN, the reader is referred to Jensen & Nielsen ([18]).
Fig. 1 - Bayesian Network for fire occurrence prediction. Blue nodes represent weather conditions; orange nodes are the components of the CFFWIS, which result in a FWI value; the variables in yellow represent the anthropogenic influence and the vegetation type; the variables in white are the predicted fire occurrence rate and the actual number of fires. The yellow variables change over space but are constant in time, whereas all other variables change both in time and space. Dashed arrows indicate a dependence on the value of the previous day.
The BN in Fig. 1 models daily fire occurrence in a cell of 1 km2, which is the spatial unit of this study. In the application presented in this paper, there is no difference between the BN model and the regression model. In fact, we use a regression approach to estimate the parameters of the BN model as explained later. However, when using the model for prediction, not all explanatory variables may be known with certainty. The BN allows modeling them as random variables, with a known distribution. As an example, the forecasted weather variables will be uncertain, which can be directly implemented in the BN.
In the presented study, data is available for all weather variables as well as all yellow variables. All these variables are continuous, with the exception of “land cover”, which has labeled states that are related to fuel type (e.g., forest, natural grasslands, olive groves, artificial surface, etc.). The orange variables are defined by the CFFWIS functions (see above). For given values of the weather variables, they are defined deterministically.
The fire occurrence rate λ, which is defined as the mean number of fires per day and km2, is estimated from the data. In our model, it is a function of land cover, human population density, road density and FWI. The variable “fire occurrences” N ∈ 0, 1, 2, … is the number of fires in one cell on one day. For a given daily fire occurrence rate λ, the number of fires follows a Poisson distribution, assuming independence among fire events for given occurrence rate. The conditional probability of observing n fires given λ is thus (eqn. 1):
where n = 0, 1, 2, …, λ [Nr. Fires day-1 km2] is the mean occurrence rate and α = 1 km2 is the area of the cell.
Observations of N are used to estimate λ based on eqn. 1, as described in the next section.
Poisson regression
The response variable is the number of fire occurrences N, which is a random variable described by the Poisson distribution with rate λ. This motivates the use of the generalized linear model of the Poisson regression for estimating λ ([27]). The rate λ is related to the explanatory variables x = [x1, …, xk] by means of the link function (eqn. 2):
where β = [β0, …, βk] is the vector of regression coefficients. This link function ensures that λ is a non-negative real number. The mean occurrence rate is then given as (eqn. 3):
Changing one of the explanatory variables from xi to xi+Δx, while keeping all other fixed, leads to a relative change in λ of (eqn. 4):
In the numerical investigations, several models are examined, which differ in the selection of the explanatory variables x. These are selected from a set of variables describing land cover, human population density, road density and components of the CFFWIS. Land cover is a categorical variable; therefore, a separate binary variable xi is defined for each of its categories. This variable takes value 1, if the land cover in this area belongs to this category, and value 0 otherwise.
Maximum likelihood estimation
Maximum likelihood estimation (MLE) is applied to determine the coefficients β. For the Poisson regression model, the likelihood function follows from eqn. 1 as (eqn. 5):
where md is the number of days with observations and ma is the number of spatial units with observations, nij is the number of fires observed on day i in the area j, xij are the values of the explanatory variables on day i in the area j.
The MLE is found as the value of β that maximizes L(β|n) (eqn. 6):
No analytical solution to this optimization problem exists. Numerical optimization must be applied. For this purpose, it is convenient to express the optimization problem in terms of the log-likelihood instead (eqn. 7):
In the numerical investigations, the simplex search method and the quasi-Newton method are used to solve eqn. 7, as implemented in the Matlab functions fminsearch and fminunc. The simplex search method is found to not converge in the models that include the categorical variable “land cover”.
Diagnostics
To compare different models, the Akaike Information Criterion (AIC) is employed ([2]). The AIC allows to compare models of different complexity. It is defined as (eqn. 8):
where ln L(βMLE|n) is the maximum log-likelihood and (k+1) is the number of coefficients βi of the model. The first term in the AIC accounts for the likelihood of the model, the second term punishes models with more parameters to avoid overfitting.
An additional comparison between models is performed with a validation data set nV, which is not used for estimating βMLE. The log-likelihood of βMLE calculated with the validation data set nV, i.e., ln L(βMLE|nV), provides an additional indication of model accuracy.
Numerical investigations
Study area: Cyprus
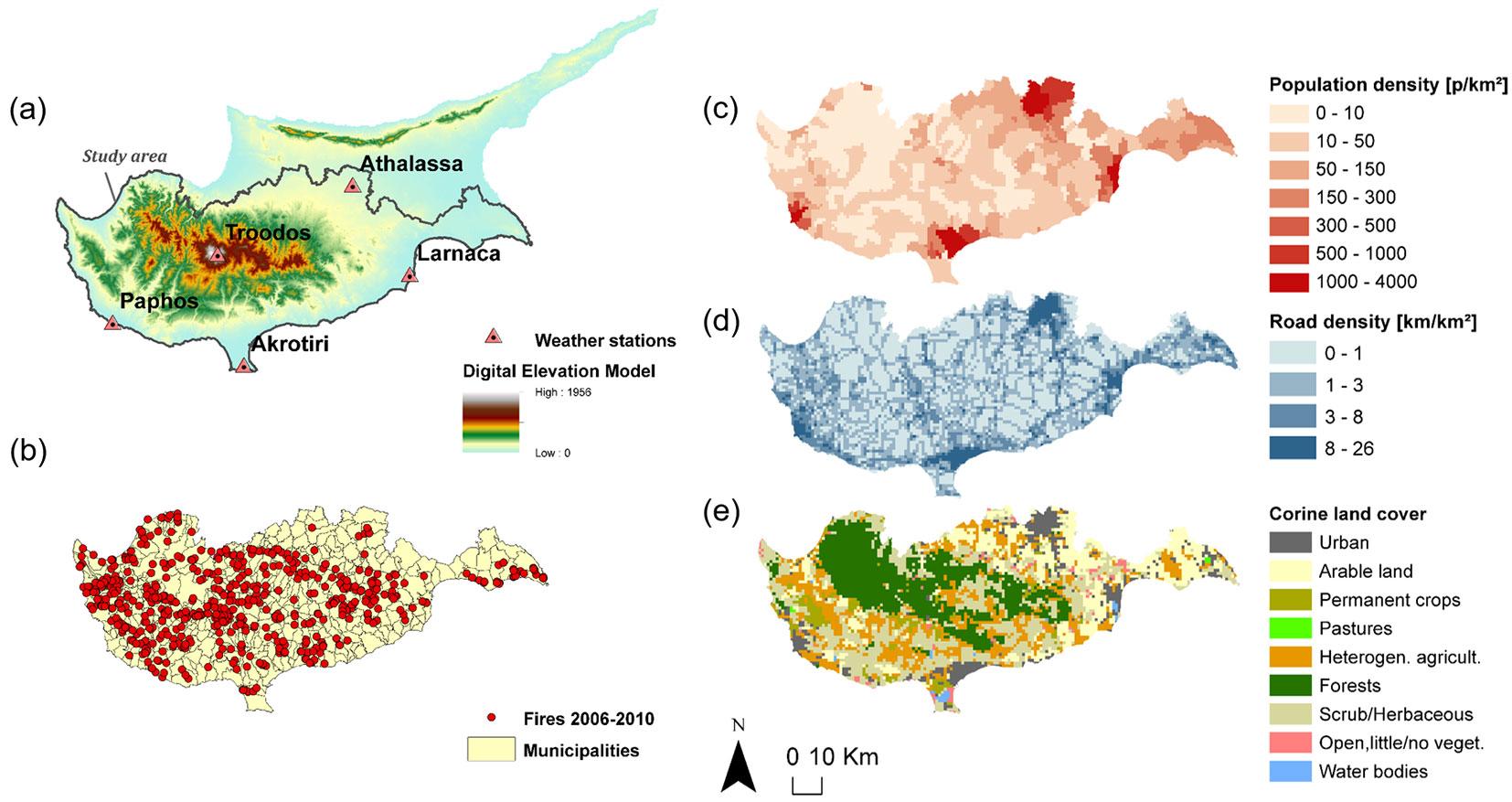
We employ data from the Republic of Cyprus, which is selected due to its representative Eastern Mediterranean climate (short cool winters followed by long hot and dry summers), vegetation and fire history and data availability. The study area and the five weather stations used in the analysis are indicated in Fig. 2a. The natural areas on the island are mainly covered by coniferous forests (e.g., Pinus brutia), whereas the permanent cultivated areas are dominated by vineyards. The highest peak of the study area is Olympus mountain of the Troodos massiv (1952 m a.s.l. - Fig. 2a). In the period 2001-2010, the mean annual number of fire occurrences in the study area was 215 and the mean annual burnt area was 29 km2 ([19]). Data of fires suppressed by the state forest agency (Department of Forests of Cyprus) for the period 2006-2010 is shown in Fig. 2b. The dataset includes records of fires of all sizes, with 10% of recorded fires being less than 0.01 ha. The total number of recorded fires is 616, which corresponds to a mean annual number of fire occurrences of 123.
Fig. 2 - (a) ASTER Digital Elevation Model (m) showing the highest peak of the Troodos massiv in white (1956 m a.s.l.) and the included five weather stations on Cyprus; (b) Municipality borders of the area of the numerical investigations and registered fire events during 2006-2010 (616 events); (c) population density; (d) road density; (e) land cover.
Data types and data sources
Both spatial and temporal explicit data are used in this study. Data are managed in a geodatabase processed with ArcGIS® 10.1 (ESRI, Redlands, CA, USA) and Python® 2.6.8 (Python Software Foundation, Wilmington, DE, USA) and are attached to a 1 km2 grid covering the whole area of the case study (6447 grid cells). The population density in each grid cell (people km-2) is determined from the municipality census data (Fig. 2c). The road density (km km-2) is computed from the actual length of roads in each cell (Fig. 2d). The land cover type assigned to each cell is the one covering the largest area within that cell (Fig. 2e). According to Corine land cover (2006), forests and semi-natural areas together with agricultural areas cover the largest part of the study area. The land cover type “Pastures” is included into the “Urban-Wetland” land covers, since it covered only a small area of the case study (7 km2).
Weather data interpolation and CFFWIS calculation
Daily weather observations (extracted from 3 hr and 6 hr observations) are interpolated using Inverse Distance Weighting (IDW - [38]). Daily values of the CFFWIS components are then calculated for each grid cell based on the interpolated values.
Temperature is additionally adjusted to the altitude based on the normal lapse rate (0.65 °C/100m - [23]). At each weather station i, the equivalent temperature at sea level is computed from the measured noon temperature Ti as T0,i=Ti +0.0065·hi, where hi is the altitude of the weather station in m. The IDW interpolation is performed using the T0,i values, resulting in a temperature value at sea level T0,c for each cell c. The daily noon value of temperature in each cell Tc is then computed as Tc =T0,c-0.0065·hc. Here, hc is the altitude at the center of cell c.
After the weather observations are interpolated, the daily FWI is calculated for each cell based on the formulation given in Van Wagner & Pickett ([42]). The starting values of the fuel moisture codes for the first day (Jan 1) are the ones proposed in Lawson & Armitage ([22]), i.e., FFMC = 85, DMC = 6, DC = 15. The starting values were reset every year.
Parameter estimation
After the data pre-processing, weather interpolation and FWI calculation, each of the 6447 grid cells is described by spatial information, noon daily weather conditions and FWI, and recorded fire events for the period 2006-2010 (11.772.222 records). Only the records of the period 2006-2009 (9.419.067 records) are used for parameter estimation.
Poisson regression with MLE is employed as described above. Various candidate models for the fire occurrence rate λ were learnt with the data. All models are of the form given in eqn. 3 and differ only in the selection of parameters employed. From these models, five were selected and are presented in this paper.
Results
Preliminary data analysis
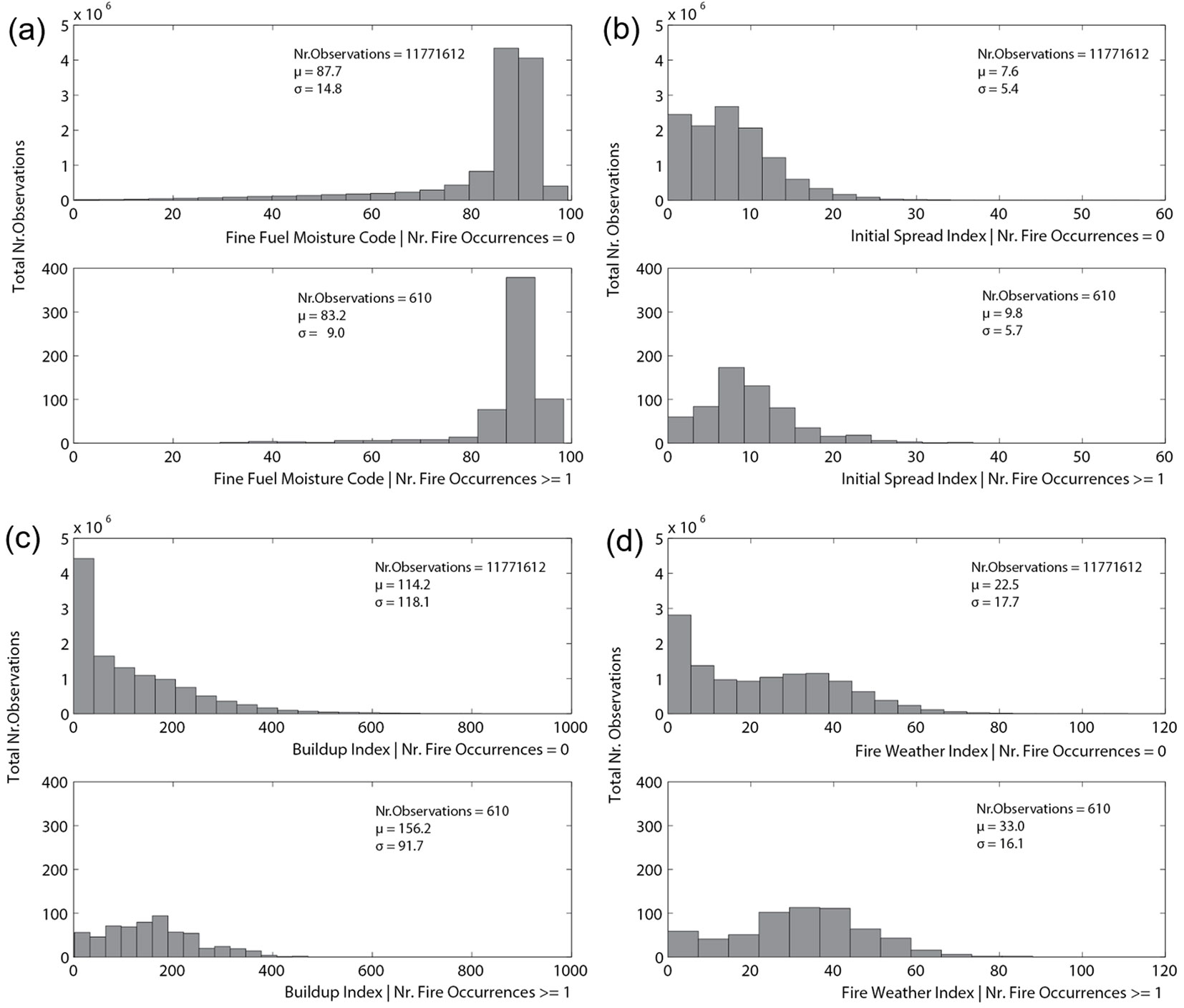
Preliminary analysis of the time series 2006-2010 is shown in Fig. 3 and in the Supplementary Material (Fig. S3, Fig. S4). As there are 616 recorded fires, the average occurrence rate of fires in this period is 5.5 × 10-5 fires d-1 km-2.
Fig. 3 - Histograms of (a) FFMC, (b) ISI, (c) BUI and (d) FWI (2006-2010) conditional on fire occurrence. CV=σμ is the coefficient of variation.
The results of Fig. 3 show that there is a statistically significant difference in the conditional means of ISI, BUI and FWI, which indicate their potential as explanatory variables in the regression model. However, by comparing the conditional distributions graphically, it is also clear that the components alone have only limited prediction ability. For example, fires occurred also on days and locations with FWI values close to zero.
Regression analysis
The investigated alternative candidate models included the components BUI, ISI and FWI of the CFFWIS. Maximum likelihood estimation (with respect to the learning set 2006-2009) results in the parameter values, which best explains the data for a given model. To compare the different models, the AIC is applied, which corresponds to the maximum log likelihood value and combined with a term that punishes the use of additional model parameters to avoid overfitting (see eqn. 8). The model including both BUI and ISI (M_BUI_ISI) performed better than M_BUI and M_ISI, and all three models proved to perform worse than M_FWI. For this reason, FWI is selected to express fire weather conditions in the further investigated models.
Tab. 1 - Selected models with explanatory variables and estimated parameters (2006-2009). (*): Permanent crops include olives, vineyards and fruits; (**): Urban-Wet-Past variable includes Urban areas, Wetlands and Pastures.
| Explanatory variables |
Param | Selected Models | ||||
|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | ||
| Intercept | β 0 |
-10.61 | -10.95 | -10.92 | -10.90 | -10.90 |
| FWI | β 1 |
0.0278 | 0.0282 | 0.0302 | 0.0327 | 0.0329 |
| Road density [km km-2] | β 2 |
- | 0.3236 | 0.3198 | - | 0.3217 |
| (Road density)2 [km km-2] | β 3 |
- | -0.0324 | -0.0276 | - | -0.0234 |
| Population dens. [people km-2] | β 4 |
- | - | -0.0018 | - | -0.0010 |
| Arable | β 5 |
- | - | - | -0.6501 | -0.9681 |
| Permanent* | β 6 |
- | - | - | 0.8383 | 0.3235 |
| Heterogeneous | β 7 |
- | - | - | 0.4098 | -0.0760 |
| Forest | β 8 |
- | - | - | 0.3497 | 0.1057 |
| Shrub/Herbaceous | β 9 |
- | - | - | 0.3279 | 0.0486 |
| Open spaces | β 10 |
- | - | - | -0.1310 | -0.1882 |
| Urban-Wet-Past** | β 11 |
- | - | - | -0.9556 | -1.1863 |
| log-likelihood (2006-2009) | - | -5198.4 | -5166.1 | -5151.2 | -5147.3 | -5111.9 |
| AIC (2006-2009) | - | 10400.8 | 10340.2 | 10312.4 | 10312.6 | 10247.8 |
In Tab. 1 models M1 to M5 are arranged according to their increasing number of explanatory variables, starting from M1 that includes FWI as the sole variable (M_FWI), to M5 with 12 variables, including FWI, road and population density and land cover types. As an example, the predicted rate of fires according to model M5 is (eqn. 9):
In models M2, M3 and M5, road density as well as (road density)2 are included as explanatory variables, to represent the non-linear effect of road density on the fire occurrence rate observed from Fig. S4c (in Supplementary Material). It is important to stress that road and population density are highly positively correlated, and are also dependent on land cover type.
Based on the learning data set, model M5 performs best, as it exhibits the lowest AIC, followed by M3 and M4. The estimated parameters of the explanatory variables FWI, road density and population density in all models M1-M5 are consistent. In models M4 and M5, the estimated parameters of the land cover types take slightly different values. They are higher in M4 due to the fact that in M5 the additional terms in the link function describing road and population density on average take a value slightly above zero.
It is also worthwhile noting that the variables describing road and population density in Model M5 are not independent of the land use type. Pearson’s correlation coefficient r between population density and urban & wetlands land cover type is 0.48 and between road density and urban & wetlands is 0.59. Therefore, the variables population and road density in model M5 partly express the fact that fires are less likely in urban areas. In M4, where these variables are not present, this effect is fully described by β11 alone. Because of this dependence, there is also a significant correlation (r = 0.56) between population and road density.
Eqn. 4 is used to compare the sensitivity of the studied models to changes in the explanatory variables. Tab. 2 shows the relative change of λ, as predicted by M5, when changing one explanatory variable and keeping all others fixed. For FWI, population density and road density, the change of the variable is equal to one standard deviation σ, whereas the land cover types change from 0 to 1. For higher FWI, λ increases and for higher population density λ decreases. These results agree with results in Fig. S4 (Supplementary Material).
Tab. 2 - Relative change of occurrence rate Δλ/λ with changing explanatory variables of model M5. For continuous variables FWI, population density and road density, the change of the variable is equal to one standard deviation σ. (*): (Δλ/λ)i=exp[Δx(β2 + 2 β3 μRD + β3Δx)], with μRD=2.09 being the mean value of road density.
| Explanatory variables | Δx | (Δλ/λ)i eqn. 4 |
|---|---|---|
| FWI | σ = 17.7 |
0.791 |
| Population density | σ = 316 |
-0.271 |
| Road density | σ = 3.23 |
0.614 * |
| (Road density)2 | ||
| Arable | 1 | -0.620 |
| Permanent | 1 | 0.382 |
| Heterogeneous | 1 | -0.073 |
| Forest | 1 | 0.111 |
| Shrub/Herbaceous | 1 | 0.050 |
| Open spaces | 1 | -0.172 |
| Urban-Wet-Past | 1 | -0.695 |
Prediction
Fire observations of the study area in 2010 are used to verify the predictive ability of the proposed models. The best model is the one that best discriminates the actual locations with fire occurrences from those without. This is described by the sum of the likelihood values for all cells and all days of the prediction data set. Model M5 predicts the highest log-likelihood for the entire data of 2010 (Tab. 3), which indicates that this model is the best in predicting fire occurrence among all investigated models.
Tab. 3 - Predicted fire occurrence rate at the locations of fires shown in Fig. 4.
| Day in 2010 | Fire locations |
Fire occurrence rate (× 10-5 d-1 km-2) | ||||
|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | ||
| Oct 8 | a | 7.2 | 7.1 | 7.8 | 9.1 | 9.4 |
| b | 6.4 | 4.6 | 5.1 | 8.1 | 6.4 | |
| c | 6.0 | 4.3 | 4.8 | 7.5 | 5.9 | |
| d | 5.7 | 6.3 | 7.0 | 7.0 | 8.8 | |
| e | 5.4 | 4.0 | 4.4 | 6.6 | 5.3 | |
| Jun 26 | a | 3.9 | 5.3 | 5.8 | 4.7 | 5.9 |
| b | 6.2 | 8.4 | 8.6 | 7.6 | 10.9 | |
| c | 5.1 | 8.0 | 8.0 | 6.0 | 10.7 | |
| 2010 | log-likelihood in study area | -1388.6 | -1383.2 | -1388.7 | -1380.6 | -1377.1 |
Two days in 2010 with the highest number of fires are selected to investigate and demonstrate the prediction of the fire occurrence rate with the model (whose parameters were learnt by data for 2006-2009). Fig. 4a shows the expected number of fires as predicted by the models on October 8, 2010 - the day with the highest number of fires in 2010 (5 fires) and for June 26, 2010. Urban centers are clearly visible in the maps as the areas with permanent low expected fires predicted by all models.
Fig. 4 - Expected occurrence rates of fires predicted by different regression models on (a) 8th October 2010 (day with maximum number of fires in 2010) and (b) on 26th June 2010 (day with second maximum number of fires and largest resulted burnt area (3.4 km2 = 340 ha) in 2010). Black dots represent the registered fires on this day (a - e). The predictions are estimated by the models M1, M2, M3, M4, M5. Occurrence rate results are in the order of 1e-5.
Models M4 and M5 generally predict higher occurrence rates than model M1, which includes only the influence of FWI (Tab. 3). However, it is reminded that to assess the predictive power of the model, it is not sufficient to focus on the prediction of fire occurrences. The prediction in all cells must be compared. To this end, one can compare the probability of the observed fire and no-fire events in the entire area on all days in 2010 as predicted by the models. This probability is equal to the likelihood of the final models computed with the 2010 data.
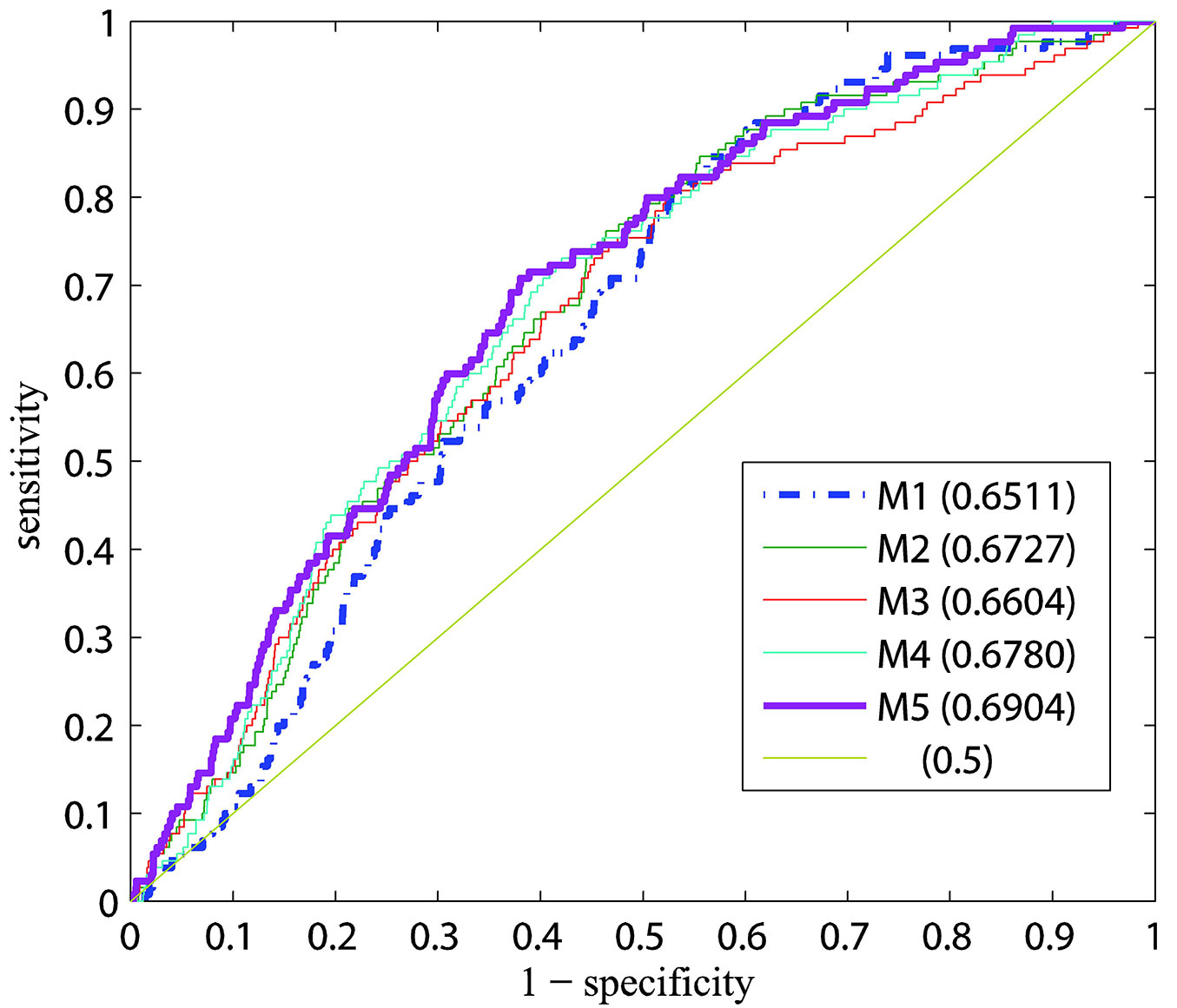
Since the likelihood is only a relative measure of prediction performance, additionally receiver operating characteristic (ROC) curves are computed for the dataset of 2010 and each model M1-M5 (Fig. 5). The ROC curves are computed by considering the binary variable, describing whether a fire occurred. The probability of one or more fires during one day is 1 - exp(-λ). Model M5 has the biggest area under the ROC curve, i.e., it performs best among the other models, whereas model M1 has the lowest AUC and performs worse among the models. ROC curves are worse, and AUC values are lower, when they are computed for the fine spatial resolution employed here, as opposed to an analysis of a larger area. However, this is a mathematical artefact, but it is important to realize when comparing the values to other published studies. In larger areas, random effects are reduced, as follows from the law of large numbers. It is straightforward to compute ROC curves for the entire study area, since the fire occurrence rate is simply the sum of the occurrence rates in all cells. The AUC values computed for prediction in the entire study area in 2010 is 0.74. This AUC value is the same for all models, because in this computation, the spatial differentiation is lost.
Discussion
This study is a step towards an improved prediction of fire occurrence in the Mediterranean for fire management purposes. The selected probabilistic modeling approach provides a quantitative metric of the ability of different explanatory variables to predict daily fire occurrence. Of particular interest is the ability of the FWI, which was developed for Canada, to predict fire danger in the Mediterranean. As we found in this study, the FWI is a good indicator for fire danger also in the Eastern Mediterranean, even if its prediction ability is lower than in Canada and similar climates. In previous empirical studies, the components of the CFFWIS (FFMC, expressing fine fuel moisture; ISI, representing relative fire spread expected immediately after ignition; and BUI, expressing moisture content of heavier fuels) were found to be relevant indicators for predicting people-caused fire occurrence in Canada ([24], [49]). FWI was here chosen to express fire weather conditions as it proved to be more expressive than the intermediated components of the CFFWIS. A likely reason for this is that the studied fire events are the ones registered and suppressed by the forest fire department. It can be thus assumed that not all ignited fires are included in the data set. Since the included fire events are those that initiated a threat and suppression efforts had to be undertaken, the proposed model is potentially more relevant for fire management planning. Nevertheless, the observed FWI values in the study area are mostly in a limited range only (Fig. 3), which limits the ability of the FWI alone to discriminate days and locations with high fire danger from those with low fire danger. This indicates that there might be potential in adjusting the definition of the FWI to local conditions. It may also be investigated if selected weather parameters should be included as explanatory variables in addition to the FWI.
In agreement with previous studies ([9], [33], [3], [20], [40], [48], [31], [26], [30], [25]), we found that including anthropogenic factors as explanatory variables can significantly improve the prediction of fire occurrence. The comparison of different models showed that a model with land cover types, population and road density has a significantly better predictive ability than one based on FWI alone. Since such data is readily available, it is straightforward to include it in forecasting systems.
Further explanatory variables describing anthropogenic factors may be included in the analysis (see also [9], [30], [25]). However, care should be taken not to introduce redundant variables. Already the three included explanatory variables (land cover type, population and road density) are partly redundant and inter-dependent, e.g., both population and road density are higher in urban areas. This dependency must be considered when transferring the model to other regions.
Due to the randomness of fire occurrence, there is a limitation to any prediction. This is evident in the results presented in this paper. Consider the predicted fire occurrence rate at locations and days where fires occurred, shown in Tab. 3: the rates predicted with the best models are approximately double the average rate of fires in the study area (5.5·10-5 day-1 km-2). Therefore, while the developed models are able to identify days and locations with higher fire risks, they are not - and of course will not - be able to deterministically predict fire occurrences in advance. Nevertheless, the predictions can support the planning of preventive and mitigating measures. Importantly, they also improve the understanding of influential factors.
Conclusions
A probabilistic model was developed for predicting fire occurrences in the Mediterranean based on readily available data on weather conditions, human presence and land cover at the mesoscale. The model was learned with data from Cyprus. In agreement with existing forecasting systems, components of the CFFWIS are included to represent daily weather conditions. Among these components, FWI proved to express best the conditions favoring relevant fires. The final model including environmental and social factors was shown to provide improved predictions compared to a forecast based solely on FWI.
Acknowledgements
We gratefully acknowledge the support of Stefan Peters in data preprocessing and of Florian Klein in weather interpolation. We thank Areti Christodoulou from the Department of Forests of Cyprus for supplying the fire data and the comments of Dr. Gavriil Xanthopoulos on the literature review. The comments of five anonymous reviewers to an earlier version are highly appreciated.
References
Online | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Daniel Straub
Engineering Risk Analysis Group, Technische Universität München , Theresienstr. 90, D-80333 München (Germany)
Corresponding author
Paper Info
Citation
Papakosta P, Straub D (2016). Probabilistic prediction of daily fire occurrence in the Mediterranean with readily available spatio-temporal data. iForest 10: 32-40. - doi: 10.3832/ifor1686-009
Academic Editor
Davide Ascoli
Paper history
Received: Apr 24, 2015
Accepted: Jul 07, 2016
First online: Oct 06, 2016
Publication Date: Feb 28, 2017
Publication Time: 3.03 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2016
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 51191
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 41442
Abstract Page Views: 3631
PDF Downloads: 4602
Citation/Reference Downloads: 69
XML Downloads: 1447
Web Metrics
Days since publication: 3431
Overall contacts: 51191
Avg. contacts per week: 104.44
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2017): 9
Average cites per year: 1.00
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Daily prediction modeling of forest fire ignition using meteorological drought indices in the Mexican highlands
vol. 14, pp. 437-446 (online: 28 September 2021)
Short Communications
Upscaling the estimation of surface-fire rate of spread in maritime pine (Pinus pinaster Ait.) forest
vol. 7, pp. 123-125 (online: 13 January 2014)
Research Articles
Fire occurrence zoning from local to global scale in the European Mediterranean basin: implications for multi-scale fire management and policy
vol. 9, pp. 195-204 (online: 12 November 2015)
Research Articles
Forest fire occurrence modeling in Southwest Turkey using MaxEnt machine learning technique
vol. 17, pp. 10-18 (online: 02 February 2024)
Research Articles
Assessing the performance of fire danger indexes in a Mediterranean area
vol. 11, pp. 563-571 (online: 01 September 2018)
Research Articles
Modeling human-caused forest fire ignition for assessing forest fire danger in Austria
vol. 6, pp. 315-325 (online: 16 July 2013)
Technical Reports
Comparison of fire danger indices in the Mediterranean for present day conditions
vol. 5, pp. 197-203 (online: 02 August 2012)
Research Articles
Differences of fire activity and their underlying factors among vegetation formations in Greece
vol. 6, pp. 132-140 (online: 08 April 2013)
Research Articles
The economic value of fire damages in Tuscan agroforestry areas
vol. 14, pp. 41-47 (online: 14 January 2021)
Research Articles
Wildland fire typologies and extreme temperatures in NE Spain
vol. 10, pp. 9-14 (online: 01 November 2016)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword