Height-diameter models for maritime pine in Portugal: a comparison of basic, generalized and mixed-effects models
iForest - Biogeosciences and Forestry, Volume 9, Issue 1, Pages 72-78 (2015)
doi: https://doi.org/10.3832/ifor1520-008
Published: Jun 11, 2015 - Copyright © 2015 SISEF
Research Articles
Abstract
Tree height is a key variable in forest monitoring studies and for forest management. However, tree height measurement is time consuming, and the recommended procedure is to use estimates from height-diameter models. Here, we compare height-diameter model forms and approaches for predicting tree height (h) as a function of tree diameter at breast height (d) and additional stand level covariates. Four model forms were evaluated: (i) basic models (which only used d as predictor variable); (ii) generalized models (which used d and stand-level predictor variables); (iii) a mixed-effects model based on the best basic model; and (iv) a mixed-effects model based on the best generalized model. Several alternatives aimed at minimizing height measurement effort were tested in terms of accuracy and applicability. From a practical point of view, the selected generalized model is recommended for estimating the height of maritime pine in Portugal. The results also show that a calibrated basic mixed model provides more accurate results than a basic model locally fitted when the number of h-d observations is limited.
Keywords
Pinus pinaster Ait., Sampling Design, Local Model, Stand Variables, Generalized h-d Relationship, Calibration
Introduction
Diameter at breast height (d) and total tree height (h) are key variables in forestry applications. These variables enable study of the horizontal and vertical forest structure, and they are used to estimate timber volume, site index and other important variables related to forest growth and yield, succession and carbon budget models ([30]). Although d is routinely measured in current forest inventories, h is usually measured in a subsample of trees to save time and expense. Hence, the diameter to height (h-d) relationship is widely used to overcome the lack of information about tree height. In even-aged stands, differences in the h-d relationship are mainly related to age, density and site ([8]). In a specific stand, the h-d curve shifts upwards with increasing age until reaching a certain age, which is particular to the species and the site (e.g., [25], [32]). The curve is generally sigmoid in shape over the full range of diameters, and the slope depends on the site quality, with steeper slopes indicating better sites and flatter curves indicating poorer sites. Since the first freehand curves were developed in the early 1930s, many h-d models have been proposed for describing the relationship between both variables (for a review of the models, see [8], [42], [17], [18]).
For height estimation using a basic model, which includes diameter at breast height as the sole independent variable [h = f(d)], the model must be fitted to data from each plot (representing a specific stand) and for each measurement occasion independently; this is usually referred to as a locally fitted basic model or simply a local model. Another option is the use of a generalized model that uses d and stand-specific variables as regressors [h = f (d, stand variables)], thus accounting for differences in the h-d relationship within stands and over time.
An alternative h-d modeling option is the development of a mixed-effects model ([22], [4], [38], [43]). Mixed-effects models allow for both mean and subject-specific responses and they have been found to be useful for repeatedly measured data ([9], [24]). The mean response considers only fixed parameters, common to the population, while the subject response considers both fixed parameters and random effects, specific to each subject. In forestry, the most common experimental subject is a permanent sample plot, in which some trees are measured repeatedly over time, or a stem analysis tree ([16]), in which the trajectories of height-age, diameter-age, and height-diameter can be reconstructed to determine how the height and diameter of trees change over time. As height and diameter data are generally obtained in plots, thus having a nested stochastic structure, there may be a lack of independence between observations, which yields biased estimates of confidence intervals for the parameter estimates ([37]). The use of mixed models is thought to help solve the lack of independence between observations ([19]). The inclusion of random effects, specific to each plot-inventory combination, allows the natural variability in the h-d relationship between different locations and time to be modeled, after defining a common fixed functional structure ([23]). In order to provide enhanced estimates, relative to those obtained when using a mean response in a new dataset, the random effects can be estimated when information about a sample of h-d pairs is available. This procedure is called calibration (or localization), and the resultant response is the calibrated response. Although there is no doubt about the advantages of the use of mixed models to avoid biased estimates for the covariance matrix, there is still some uncertainty about the advantage of its use for predictive purposes ([10]).
This paper analyzes different model forms and approaches for developing a h-d relationship for maritime pine (Pinus pinaster Ait.) in Portugal, i.e., the prevailing softwood species in this country. According to the National Forest Inventory (NFI - [1]), maritime pine covers around 885 000 ha of land in Portugal (27% of the mainland forest area), with a wood volume of 85.8 × 106 m3 and a total biomass of 49.7 × 106 Mg, which represents 24.8 × 106 Mg of sequestered carbon. Evaluation, comparison and selection of model forms and approaches were conducted with the purpose of identifying the optimal h-d model for incorporation in the ModisPinaster growth and yield model ([13], [14]). Briefly, the model addresses forest growth and yield, risks (wind related) and management procedures (such as thinning and harvesting) for pure maritime pine stands. The level of detail of the output is the diameter class, with the diameter distribution recovered by the Johnson SB distribution ([29]). The model can be downloaded from the CAPSIS (Computer-Aided Projection of Strategies In Silviculture) simulation platform (⇒ http://capsis.cirad.fr/capsis/mode l). Until recently, prediction of tree height using ModisPinaster simulations was based on the following provisional equation parameterized by Almeida ([2] - eqn. 1):
where N represents the number of trees per hectare, t refers to the stand age in years, hd is the dominant height, defined as the mean height of the 100 largest-diameter trees per hectare, and dd is the dominant diameter, defined as the mean diameter of the 100 largest-diameter trees per hectare.
The overall objective of the present study was to select an h-d model form and a model-fitting approach for application to maritime pine in Portugal, to replace the model of eqn. 1 previously included in ModisPinaster. The specific objectives of this research were as follows: (1) to compare basic, generalized and mixed-effects models; and (2) to test several alternatives for minimizing the height measurement effort in terms of accuracy and applicability.
Materials and methods
Data
This study used information from a large database on maritime pine collected in northern Portugal, mainly in the T’mega Valley, which is the most representative continuous area in the state (latitude range: 41° 15′ - 41° 52′ N, longitude range: 7° 20′ - 8° 00′ W). In the T’mega Valley, maritime pine occurs at an altitude between 100 and 900 m a.s.l. on hilly terrain. The soils are derived from granite and schist. The mean annual temperature varies between 13.1 °C and 16 °C at lower elevations (100-400 m), in an eastern direction. Above 400 m a.s.l, the mean annual temperature falls to 9.8 °C. The mean annual precipitation ranges between 660 and 1400 mm in the lower locations, and between 1000 mm and 2900 mm in higher locations ([27]). Most forests and woodlands in the region are community areas and are managed by the Portuguese Forest Service (the National Forest Authority).
In each sampled stand, circular plots of 0.05 ha were established as permanent sample plots. The first measurements were carried out in 1997 and the most recent in 2010. A total of 387 inventories of 133 plots, with 1 to 4 measurements - depending on the year of plot installation - were available for study. The data set includes tree and stand variables. Available tree characteristics were diameter outside bark at breast height (d, cm) of all living trees taller than 1.30 m, and total height (h, m) for a subset of trees (including the proportion of the 100 largest-diameter trees per hectare). The diameters were measured with a diameter or girth tape, to the nearest 0.1 cm.
Criteria for selection of a subset of trees for height measurements varied over time. In the earlier measurements, a systematic layout was followed and heights were measured with a Blume-Leiss hypsometer to the nearest 0.5 m. Subsequently, 1-3 average trees within each diameter class of 5 cm width were selected and the heights were measured with a Vertex hypsometer to the nearest 0.1 m. For a subset of plot-inventory combinations (47 %), the diameter and height of all trees were measured. The average value of h-d observations per plot equals 27. Stand age (t, years) was evaluated from the dominant trees by use of an increment core taken at 30 cm from ground level. To estimate the total age, the number of years that a seedling takes to reach this height (usually 2-5 years in the region) was added to the number of rings counted. Site index (S, m) at a reference age of 35 years was estimated using the model proposed by Marques ([27]). The diameter, height and stand variables are summarized in Tab. 1.
Tab. 1 - Summary statistics for the fitting data (10580 h-d observations in 387 plot-inventory combinations). (d): diameter at breast height (1.3 m above ground level) outside bark; (h): total tree height; (t): stand age; (N): number of trees per hectare; (dg): quadratic mean diameter; (G): stand basal area; (hm): mean height; (dd): dominant diameter, defined as the mean diameter of the 100 largest-diameter trees per hectare; (hd): dominant height, defined as the mean height of the 100 largest-diameter trees per hectare; (S): Site index, at a reference age of 35 years.
| Variable | Mean | Min. | Max. | Std. dev. |
|---|---|---|---|---|
| d (cm) | 21.4 | 0.7 | 53.8 | 8.7 |
| h (m) | 14.1 | 1.7 | 29.2 | 4.4 |
| t (years) | 40.3 | 12 | 70 | 12.5 |
| N (trees ha-1) | 1055 | 120 | 7680 | 913 |
| dg (cm) | 23.1 | 5.2 | 43.6 | 7.7 |
| G (m2 ha-1) | 32.1 | 6.0 | 57.3 | 9.9 |
| hm (m) | 14.8 | 4.8 | 26.7 | 4.3 |
| dd (cm) | 29.7 | 8.7 | 50.3 | 7.8 |
| hd (m) | 16.1 | 5.6 | 27.2 | 4.3 |
| S (m) | 15.9 | 9.7 | 30.4 | 2.6 |
Basic models
The 27 models proposed by Huang et al. ([18]) were evaluated in this study. The best locally fitted model for each plot-inventory combination was selected on the basis of the following criteria: (i) statistical significance of the parameters; (ii) visual inspection of the residuals; and (iii) goodness-of-fit statistics, which were averaged by model. The basic model with the best average goodness-of-fit statistics was again locally fitted by using different sampling designs (those evaluated for calibration of the basic mixed model, as explained below) for comparison with the other models and approaches tested.
Generalized models
Graphical analyses were performed to establish which stand variables were most closely related to the estimated local parameters of the best basic model, and to identify the type of relationship (e.g., linear, allometric, exponential). In addition, several generalized models selected from the literature ([21], [42], [2], [26], [39], [5], [38], [7]) were fitted to the dataset. These models include the most flexible equations for developing h-d relationships (i.e., the Bertalanffy-Richards, Weibull and Schnute models), which have been demonstrated as suitable for several species and types of stands. Some modifications were also tested, e.g., replacing the quadratic mean diameter and the mean height by dominant diameter and dominant height, respectively.
Mixed models
Mixed models can be applied to basic models ([43]), thus generating a basic mixed model, and to generalized models ([4], [5]), thus generating a generalized mixed model. The data used in this study comprised a sample of heights and diameters from different plots measured a maximum of four times. Thus, two hierarchical levels (trees in plots) and repeated measurements (several inventories of each tree) can be taken into account. Random effects for the tree measurement occasion were not included in this study, in accordance with Castedo Dorado et al. ([5]). This is not likely to have a notable effect on fitted mixed models because the number of measurement-occasions for one tree was small in comparison with the number of trees analyzed (10580).
Determining which parameters should be considered fixed and which should be considered mixed (also including random effects) is a key question when developing mixed models. Some authors ([31], [12]) suggest that all parameters in the model should be considered mixed if convergence is possible. Therefore, all parameters were first expanded with random effects in the selected basic and generalized models.
In this study, to evaluate the calibrated response the random effects were estimated using an approximate Bayesian estimator ([44] - eqn. 2):
where D is the estimated variance-covariance matrix for the random effects ui, Ri is the estimated variance-covariance matrix for the error term, Zi is the partial derivatives matrix with respect to random effects, and êk is the error matrix estimated using only the fixed parameters. When the random effects ui are introduced linearly and when the nonlinear function is linearized by the zero expansion method, the partial derivatives of the Zi matrix are equivalent to the partial derivatives with respect to the fixed parameters.
The calibrated response was then calculated as (eqn. 3):
The calibrated response was evaluated for different height sampling designs:
- Total height of randomly selected trees per plot-inventory. The mean and extreme values of the goodness-of-fit statistics after 100 simulations were obtained.
- Total height of quantile trees of the diameter distribution per plot-inventory (i.e., 1 tree = median-diameter tree; 2 trees = tercile-diameter trees; 3 trees = quartile-diameter trees; 4 trees = quintile-diameter trees, etc.).
- Total height of the smallest diameter trees per plot-inventory (this approach was only considered for the selected generalized mixed model).
Model fitting and comparison
The basic and generalized models were fitted with the NLIN procedure, while the mixed models were fitted with the NLMIXED procedure, both of SAS/STAT® ([34]). Statistical and graphical analyses were used to compare model performance. Three statistical criteria obtained from the residuals were examined: the coefficient of determination (R2), which indicates the proportion of the total variance that is explained by the model, the root mean square error (RMSE), and the Schwarz’s Bayesian Information Criteria (BIC - [36]).
Results
Basic models
Fitting statistics showed that the model evaluated by Burkhart & Strub ([3]) performed best (R2 = 0.995, RMSE = 1.027 m - eqn. 4):
where h represents total tree height (m), d is the diameter (cm) at breast height (1.3 m above ground level), and b0 and b1 are parameters to be estimated for each plot-inventory combination.
Model from eqn. 4 was also fitted locally using the different height sampling designs mentioned in the mixed models section. The use of quantile-diameter trees yielded a lower error than the average error obtained in the fitting with randomly selected trees up to five trees. When six or more trees were selected in both alternatives, the differences were not significant.
Generalized models
A modification of the model used by Tomé ([42]), in which the age term was omitted, yielded the best fit to the dataset (R2 = 0.933, RMSE = 1.149 m). The generalization of the best basic model (eqn. 4) yielded poorer results than the modified model of Tomé, and, although the quality of fit in the former model (eqn. 1 - [2]) was greatly improved by enlarging the dataset (with R2 from 0.805 to 0.929 and RMSE from 1.660 to 1.186m), it was poorer than the fit provided by the selected model. Therefore, the proposed generalized equation is as follows (eqn. 5):
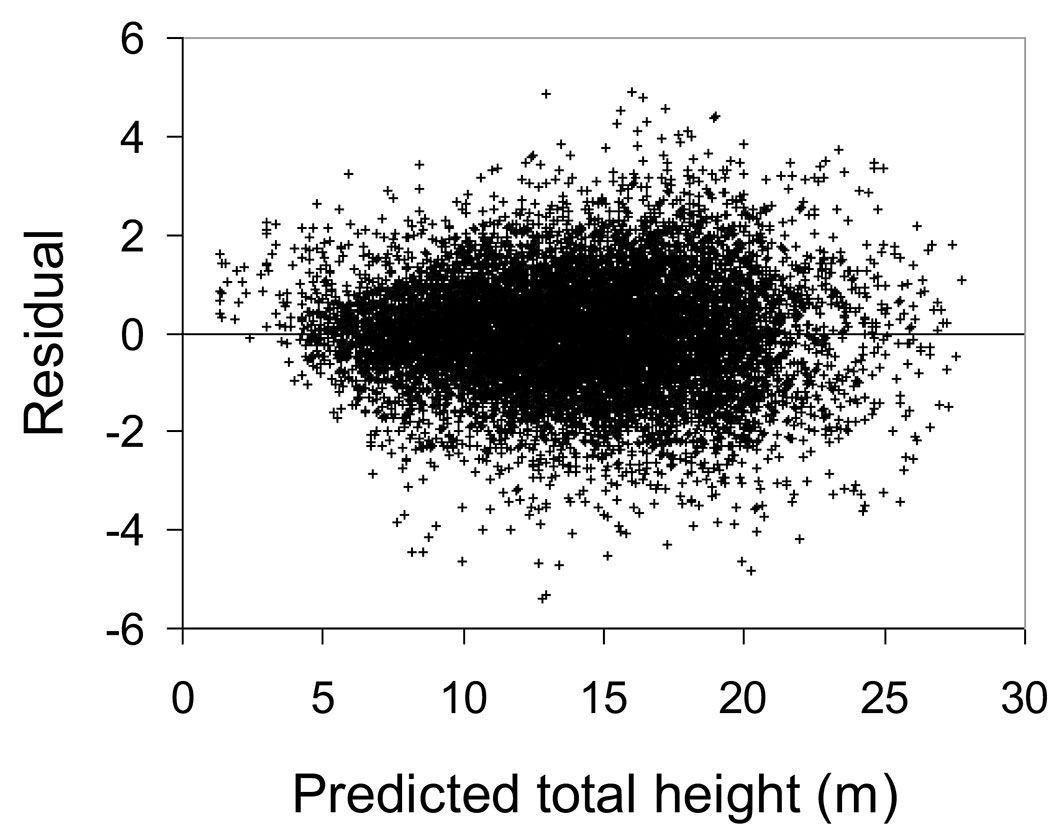
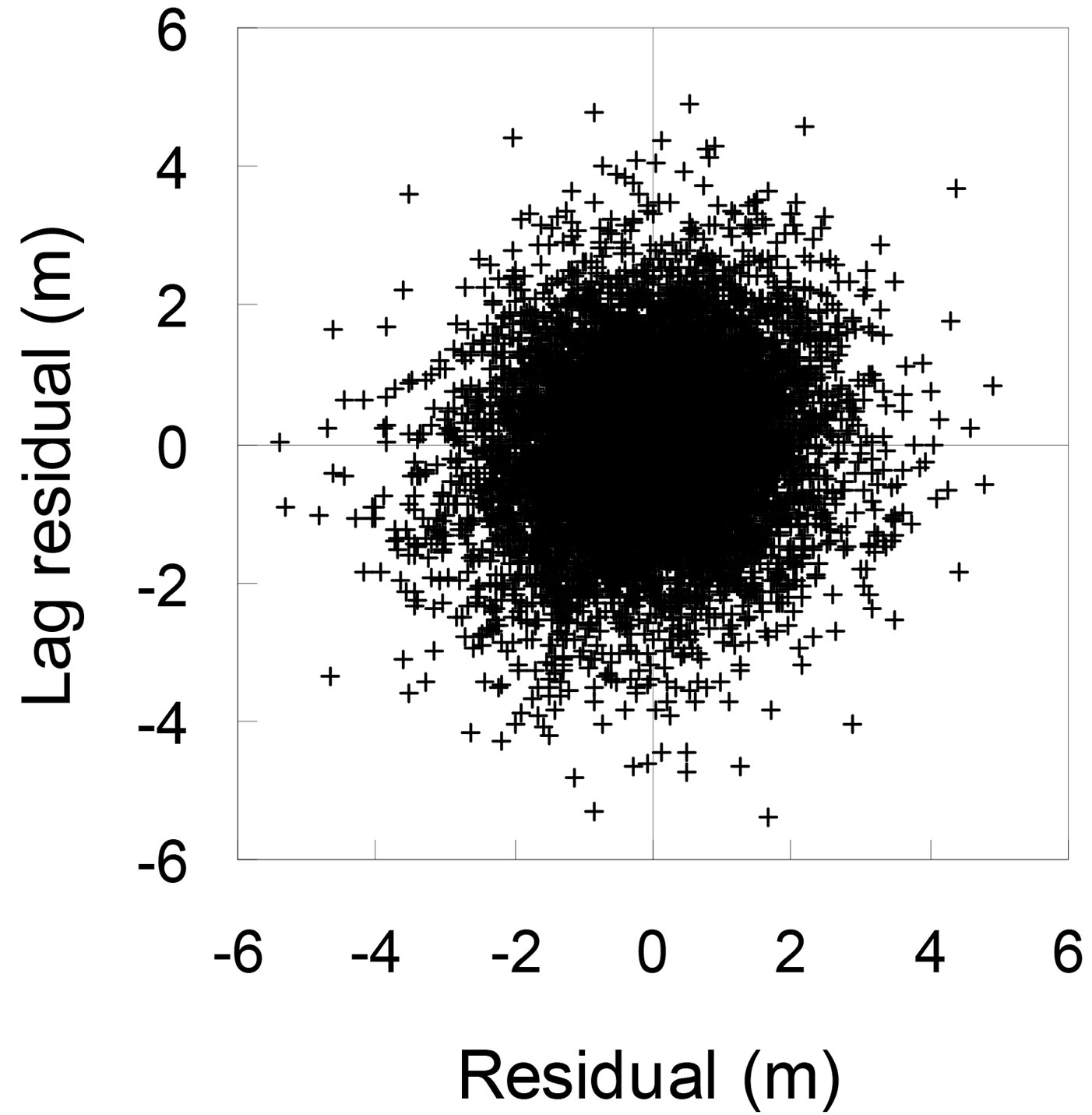
where b0 = -3.861, b1 = 0.2542 and b2 = 0.5326. All parameters from eqn. 5 were significant at the 5% level. The plot of residuals against predicted heights for the fitting data set did not show clear evidence of variation in residuals over the full range of predicted values (Fig. 1). The plot of residuals against lagged residuals within each plot-inventory combination (with the data ordered by ascending diameter) did not show any correlated errors (Fig. 2). Moreover, the predicted h-d curves (Fig. 3) showed appropriate trends and logical asymptotes.
Fig. 2 - Plot of residuals against lagged residuals of height for eqn. 5.
Fig. 3 - Predicted height-diameter curves obtained using eqn. 5 and the 387 plot-inventory combinations from this study.
Mixed models
The model of Burkhart & Strub (eqn. 4) was also selected to develop a basic mixed model. Both parameters of the model were linearly expanded with random effects as follows (eqn. 6):
Estimates of the fixed parameters and variance components for the random effects for eqn. 6 are shown in Tab. 2. All estimates were significant at the 5% level. In the calibration process, the use of quantile-diameter trees was preferable to the selection of random trees when only one tree is considered, but there were no differences in the other cases (note that the errors of randomly selected trees are average values).
Tab. 2 - Fixed parameter estimates, approximate significance tests and variance components for eqn. 6.
| Fixed Effect: Parameter |
Estimate | Approx. std. error |
t-value | Approx. p-value |
|---|---|---|---|---|
b 0 |
19.04 | 0.2889 | 65.91 | < 0.001 |
b 1 |
-7.352 | 0.1452 | -50.62 | < 0.001 |
| Random Effect: Variance component |
Estimate | Approx. std. error |
Z-value | Approx. Z-value |
var(u1) |
30.18 | 2.326 | 12.98 | < 0.001 |
var(u2) |
5.111 | 0.5437 | 9.401 | < 0.001 |
cov(u1, u2) |
-9.378 | 0.9959 | -9.416 | < 0.001 |
σ2(error variance) |
1.140 | 0.01627 | 70.06 | < 0.001 |
The selected generalized model (eqn. 5) was also used to develop a generalized mixed model. Convergence was not achieved when all parameters were considered as mixed and therefore all possible expansions of two fixed parameters with random effects were tested. The inclusion of random effects in the fixed parameters b0 and b2 generated the best results, producing the following model (eqn. 7):
Estimates for the fixed parameters and variance components for the random effects for eqn. 7 are shown in Tab. 3. All estimates were significant at the 5% level.
Tab. 3 - Fixed parameter estimates, approximate significance tests and variance components for eqn. 7.
| Fixed Effect: Parameter |
Estimate | Approx. std. error |
t-value | Approx. p-value |
|---|---|---|---|---|
b 0 |
-4.535 | 0.5459 | -8.307 | < 0.001 |
b 1 |
-0.2306 | 0.03012 | -7.656 | < 0.001 |
b 2 |
0.7753 | 0.08658 | 8.955 | < 0.001 |
| Random Effect: Variance component |
Estimate | Approx. std. error |
Z-value | Approx. Z-value |
var(u1) |
8.870 | 0.4068 | 21.80 | < 0.001 |
var(u2) |
0.6819 | 0.03157 | 21.60 | < 0.001 |
cov(u1, u2) |
-2.456 | 0.07077 | -34.70 | < 0.001 |
σ2(error variance) |
1.150 | 0.01609 | 71.43 | < 0.001 |
Calibration of the generalized mixed model using the total height of the smallest diameter trees per plot-inventory yielded better results than calibration with other designs for the same sampling effort. For comparison of eqn. 7 with the other alternatives, five additional trees should be measured to compute dominant height in this study (the size of the plots was 500 m2).
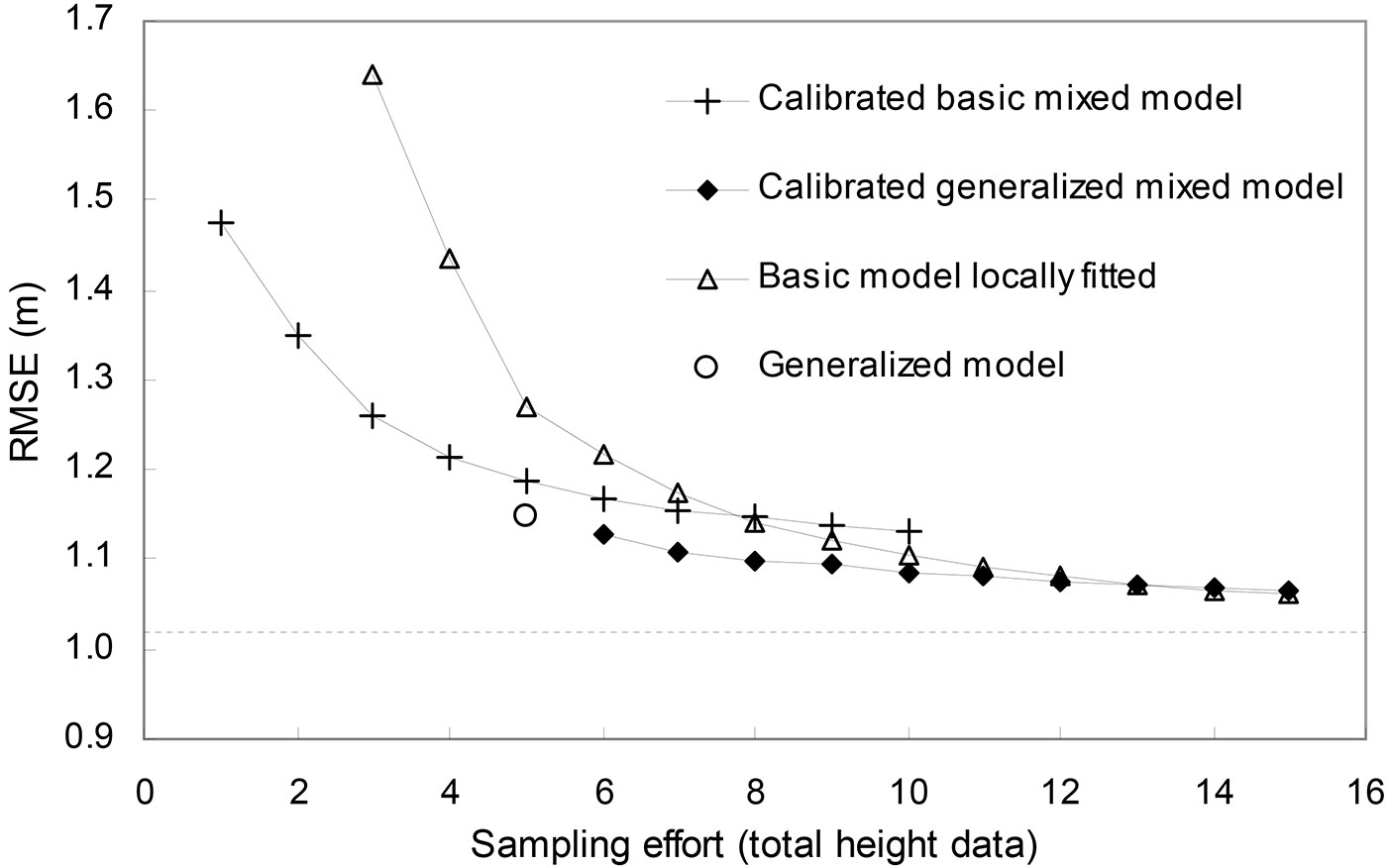
The relation between RMSE and sampling effort (number of measurements of total height) for the selected model forms and approaches is shown in Fig. 4. In each case, the option that generated the smallest RMSE is shown (i.e., the locally fitted basic model and calibration of the basic mixed model with quantile-diameter trees, and calibration of the generalized mixed model with the smallest diameter trees). In summary, the combination of model approach and sampling design yielding the lowest RMSE in relation to sampling effort is shown in Tab. 4.
Fig. 4 - Changes in RMSE with sampling effort for the different model forms and approaches tested in this study. The generalized mixed model was calibrated with data from the smallest diameter trees, and for calibration of the basic mixed model and local fit of the basic model were selected data from quantile-diameter trees. The horizontal dashed line represents the RMSE obtained in a local fit using all data and the selected basic model.
Tab. 4 - Model approach and sampling design yielding the lowest error in relation to sampling effort (number of measurements of total height). (d): diameter (cm) at breast height (1.3 m above ground level).
| Sampling effort | Model approach | Sampling design | RMSE (m) |
|---|---|---|---|
| 1 | Calibrated basic mixed model | Median d tree | 1.475 |
| 2 | Calibrated basic mixed model | Quantile d or randomly selected trees | 1.348 |
| 3 | Calibrated basic mixed model | Quantile d or randomly selected trees | 1.259 |
| 4 | Calibrated basic mixed model | Quantile d or randomly selected trees | 1.213 |
| 5 | Generalized model | Dominant trees | 1.149 |
| 6 to 13 | Calibrated generalized mixed model | Dominant trees + smallest d trees | 1.130 to 1.072 |
| 14 and so on | Basic model locally fitted | Quantile d or randomly selected trees | ≤ 1.067 |
Discussion
Several model forms and approaches for developing an h-d model for P. pinaster in northern Portugal were compared. In the first step, 27 basic models (h as a function of just d) were locally fitted. Height predictions with the selected basic model (eqn. 4) yielded a RMSE value of 1.027 m, which constitutes a reference minimum error for comparison with the other model approaches analyzed.
The selected generalized model (eqn. 5) includes the variable dominant height in its formulation. The use of this covariate may be preferred as it requires less sampling effort than accurate measurement of the mean height ([26]). Another advantage of this model is that it predicts a height equal to hd when the independent variable is a diameter equal to dd, and it predicts a height equal to 1.3 m when diameter is equal to 0. The model also includes a measure of stand density (i.e., trees per hectare). Stand density is the most obvious factor affecting the h-d relationship in a stand ([46], [45]): trees of the same height usually have smaller diameters in denser stands. Several variables have been proposed as additional predictor variables: stand age ([8], [40], [26]), crown competition factor ([41]), geographical features ([20], [33], [35]) or wind speed ([28]). Incorporation of additional predictor variables can improve the predictions, but it requires a greater sampling effort and limits the application of the model.
The reduction in RMSE with calibration was more evident when the mixed model was based on a basic model rather than on a generalized model (Fig. 4), because most of the variability was accounted for by the stand level variables included in the generalized model. According to Trincado et al. ([43]), the use of a basic mixed model in forest inventories by selecting a sub-sample of trees for height measurement enables the maintenance of a simple model structure without inclusion of additional predictor variables. The calibration of a basic mixed model with one tree (as done by [43]) did not yield very good results in this study, but it could be used in the absence of more observations. On the other hand, local fitting using the model proposed by Burkhart & Strub ([3]) is not possible with fewer than two observations because the model has two parameters. Although calibration using the total height of the smallest diameter trees per plot-inventory is not recommended for the basic mixed model, this calibration option produced the best results in relation to sampling effort when used with the generalized mixed model. This calibration method was also selected for other fast-growing species in the Iberian peninsula ([5], [7]) with generalized mixed models that also included dominant height and dominant diameter as stand-predictor variables. This can be explained by the fact that these models are restricted to passing through the point hd-dd, implying that the models will behave as quite invariant in the upper part of the h-d relationship, and that small trees will provide much more information for calibration in this case ([7]).
The use of the selected generalized model (eqn. 5) generated less error (RMSE) than the other options for the same sampling effort with five trees (Fig. 4 - note that in this study five trees were selected for estimating dominant height). Moreover, this equation has the advantage that it can be used for prediction purposes with data commonly measured in current forest inventories in Portugal, and it can easily be implemented in a statistical disaggregated dynamic growth model ([11], [6]) based on the state-space approach ([15]), in which the vector of state variables includes dominant height, as in ModisPinaster.
Numerous studies have shown that in the development of height-diameter models, the best approach depends on: (1) the data available; (2) the intended accuracy; and (3) the interest (or otherwise) in obtaining additional information. From a practical point of view (related to sampling effort, accuracy and practical applications), the use of the selected generalized model is recommended in preference to the other approaches tested. The dominant height (hd) must be known when using this model, and therefore it should be considered during the data collection process. If dominant height is not known and the total height of randomly or quantile-diameter selected trees is available, calibration of the basic mixed model rather than a local fit may be recommended (Fig. 4), specifically for a short range (up to 7-8) of h-d observations. The inclusion of random effects accounts for the natural variability in height at the stand level or in different time series for the same stand. However, as the number of observations increases (above 8 according to the results from the real case study), a local model will provide more accurate results than a calibrated basic mixed model.
Acknowledgements
This study was carried out during a stay by the first author at the Department of Forest Sciences and Architectural Landscape (CIFAP), University of Trás-os-Montes and Alto Douro (Portugal). We appreciate the cooperation of the staff who worked on data collection: technicians Carlos Brito and Carlos Fernandes of CIFAP. We also thank students who participated in the monitoring process: Carla Susana Ferreira, António Azevedo, Adelina Moreira, Alexandra Rodrigues, Susana Saraiva, Marco Ferreira and Teresa Enes.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Online | Gscholar
Authors’ Info
Authors’ Affiliation
Felipe Crecente-Campo
Ulises Diéguez-Aranda
Departamento de Ingeniería Agroforestal, Universidade de Santiago de Compostela, Escuela Politécnica Superior, R/ Benigno Ledo, Campus universitario, E-27002 Lugo (Spain)
Teresa F Fonseca
Luís R Almeida
Carlos P Marques
Department of Forest Sciences and Landscape Architecture, University of Trás-os-Montes e Alto Douro, Apartado 1013, 5001-801 Vila Real (Portugal)
Forest Management Branch, Alberta Ministry of Sustainable Resource Development, 8th Floor, 9920-108 Street, Edmonton, Alberta T5K 2M4 (Canada)
Corresponding author
Paper Info
Citation
Gómez-García E, Fonseca TF, Crecente-Campo F, Almeida LR, Diéguez-Aranda U, Huang S, Marques CP (2015). Height-diameter models for maritime pine in Portugal: a comparison of basic, generalized and mixed-effects models. iForest 9: 72-78. - doi: 10.3832/ifor1520-008
Academic Editor
Vicente Rozas
Paper history
Received: Dec 02, 2014
Accepted: Mar 04, 2015
First online: Jun 11, 2015
Publication Date: Feb 21, 2016
Publication Time: 3.30 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2015
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 52064
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 42937
Abstract Page Views: 3421
PDF Downloads: 4404
Citation/Reference Downloads: 35
XML Downloads: 1267
Web Metrics
Days since publication: 3811
Overall contacts: 52064
Avg. contacts per week: 95.63
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2016): 24
Average cites per year: 2.40
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Essential environmental variables to include in a stratified sampling design for a national-level invasive alien tree survey
vol. 12, pp. 418-426 (online: 01 September 2019)
Research Articles
Estimation of stand crown cover using a generalized crown diameter model: application for the analysis of Portuguese cork oak stands stocking evolution
vol. 9, pp. 437-444 (online: 02 December 2015)
Research Articles
A silvicultural stand density model to control understory in maritime pine stands
vol. 10, pp. 829-836 (online: 25 September 2017)
Research Articles
Influence of tree density on climate-growth relationships in a Pinus pinaster Ait. forest in the northern mountains of Sardinia (Italy)
vol. 8, pp. 456-463 (online: 19 October 2014)
Research Articles
Effects of defoliation by the pine processionary moth Thaumetopoea pityocampa on biomass growth of young stands of Pinus pinaster in northern Portugal
vol. 3, pp. 159-162 (online: 15 November 2010)
Research Articles
Nonlinear mixed model approaches to estimating merchantable bole volume for Pinus occidentalis
vol. 5, pp. 247-254 (online: 24 October 2012)
Research Articles
Is it needed to integrate mixture degree in Stand Density Management Diagram (SDMD)?
vol. 16, pp. 274-281 (online: 28 October 2023)
Research Articles
The use of tree crown variables in over-bark diameter and volume prediction models
vol. 7, pp. 132-139 (online: 13 January 2014)
Technical Advances
A simplified methodology for the correction of Leaf Area Index (LAI) measurements obtained by ceptometer with reference to Pinus Portuguese forests
vol. 7, pp. 186-192 (online: 17 February 2014)
Research Articles
Role of serotiny on Pinus pinaster Aiton germination and its relation to mother plant age and fire severity
vol. 12, pp. 491-497 (online: 02 November 2019)
iForest Database Search
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword