Using soil-based and physiographic variables to improve stand growth equations in Uruguayan forest plantations
iForest - Biogeosciences and Forestry, Volume 12, Issue 3, Pages 237-245 (2019)
doi: https://doi.org/10.3832/ifor2926-012
Published: May 03, 2019 - Copyright © 2019 SISEF
Research Articles
Abstract
Information provided by traditional growth models is an essential input in decision making processes for managing planted forests. They are generally fitted using inventory data guaranteeing robustness and simplicity. The introduction of explanatory factors affecting tree development in age-based sigmoidal growth and yield equations attempts not only to improve the quality of predictions, but also to add useful information underpinning forest management decisions. This study aimed to assess the use of the following soil-based and physiographic predictors: potentially available soil water (PASW), elevation (Elev), aspect (α) and slope (β) in a system of empirical stand equations comprising: dominant height (hdom), basal area (G), maximum diameter at breast height (dmax), and standard deviation of diameters (SDd). Augmented models were compared with the base models through precision and bias of estimations for two contrasting species: Pinus taeda (L.), and Eucalyptus grandis (Hill ex. Maiden), planted commercially in Uruguay. Soil-based and physiographic information significantly improved predictions of all the state variables fitted for E. grandis, but just hdom and G for P. taeda. Only PASW was consistently significant for the augmented models in P. taeda and E. grandis, while the contribution of other predictors varied between species. From a physiological point of view, predictors on the augmented models showed consistency. Models with such augmentation produced decrease of errors between 3 to 10.5%, however decreases in the prediction errors calculated with the independent dataset were lower. Results from this study contributed to add information to the decision-making process of plantations’ management.
Keywords
Forest Modelling, Soil Variables, Physiographic Variables, Pinus taeda, Eucalyptus grandis
Introduction
The afforested area in Uruguay grew at a fast rate since the Forestry Law of 1987 provided legal and tax incentives to the sector. Soils prioritized by law occupy 4,420,000 ha currently, and almost a quarter of this area has been planted. Eucalyptus grandis is the most commonly planted species in the country (over 250,000 ha), managed in long rotations for saw logs and plywood production in the North and part of the Central regions, and in short rotations for pulp mills in the West. Pinus taeda is the most planted species in the North (nearly 190,000 has), but it is also present in smaller areas in the West. In all cases the species is managed for saw logs.
To manage plantations efficiently, it is necessary to use tools that provide accurate growth and yield information, as well as an understanding of the main factors that help differentiate growth and yield between and within regions. It is of special interest to include information that would allow simulations on climate changing scenarios. Age-based sigmoidal equations representing tree growth and yield, fitted using sample plot data usually guarantee robustness and simplicity to these models, but at the expense of some explanatory ability. In this sense, the introduction of factors affecting tree development in growth and yield equations attempts not only to improve the quality of stand projections, but also to add useful information underpinning forest management decisions.
A selection of site-specific climatic, physiographic and/or soils-based characteristics, are often considered in assessing productivity ([39]) and also to improve growth and yield projections. Different strategies have been explored to use this information for augmenting mensurational equations: Woollons et al. ([41]) tested the inclusion of solar radiation, rainfall, minimum and maximum temperature, and soil type to project mean top height and basal area of Pinus radiata in New Zealand. There was improvement only for basal area when rainfall and solar radiation were included in equations fitted by soil type. Other approaches (as opposed to age) have used structural indices to make growth more dependent on climatic and soil inputs. Snowdon et al. ([32]) derived several climatic indices from two physiological models for incorporating annual variations in climatic factors into a Schumacher projection model for stand basal area of Pinus radiata. They compared different forms of a generalised Schumacher difference equation with these indices, and found that results were improved with an annual growth index derived from a “process-based” model. Based on this work, Henning & Burk ([13]) used growth indices derived from physiological models as factors to improve growth and yield estimates of an empirical model. They found that these external growth indices were effective in reducing bias in basal area estimations, but were less effective in improving precision. Maestri ([17]) studied the inclusion of modifiers for a von Bertalanffy-Richards equation for modelling dominant height in Eucalyptus grandis, concluding that rainfall, potential evapotranspiration, and maximum and minimum temperature were the most significant explanatory variables of annual increment. However, he also found that error reductions using water balance information were not higher than the error reductions obtained by using simpler environmental variables.
The objective of this work was to assess the contribution of soil-based and physiographic attributes such as: potentially available soil water (PASW), elevation (Elev), aspect (α), and slope (β), to a system of mensurational stand equations. Those variables are surrogates of key growth drivers such as radiation, soil moisture, and temperature, and have the advantage to be readily available for their use in forestry planning. Based on this background, we hypothesize that the inclusion of this information would improve precision and bias of predictions of height, basal area, and diameter dynamics for Eucalyptus grandis and Pinus taeda. Therefore, a comparison between models augmented with this information as opposed to base models without such augmentation is presented.
Methods
Growth and yield equations were fitted for predicting mean top height or dominant height (hdom), and basal area (the sum of basal area of all trees in a hectare, G) for two species commercially planted in Uruguay, namely: Pinus taeda and Eucalyptus grandis. Growth and yield equations for maximum diameter at breast height (dmax), and standard deviation of diameter at breast height (SDd) were also analysed since they are necessary to project diameters distributions by the method of moments using an inverse Weibull function ([15]).
Study area
Based on the Koppen-Geigen classification system, the climate in Uruguay is tropical-sub humid without marked variations across the country. This is caused by its position respect to both the Pacific and Atlantic Oceans, and the absence of prominent mountain ranges ([4]). Even though rainfall is well distributed during the year, it has a highly irregular pattern. The main climate features are presented in Tab. 1.
Tab. 1 - Climate characteristics: values corresponding to the period 1980-2009 ([4]). (Af): accumulated days with frosts; (RHy): annual air relative humidity; (ETP): Penman-Monteith evapotranspiration.
| Descriptor | Rainfall (mm) |
Temp. (°C) |
Af (days) |
Radiation (h day-1) |
RHy (%) |
ETP (mm month-1) |
|---|---|---|---|---|---|---|
| Mean | 1400 | 17.7 | 30 | 7 | 74 | 1100 |
| Maximum | 1600 | 22.6 | 40 | - | 78 | 1200 |
| Minimum | 1200 | 12.9 | 20 | - | 70 | 1000 |
The study was developed in the northern Uruguay, between 30° 50′ and 32° 49′ N and 53° 43′ and 58° 21′ W in three of the zones prioritized for forestry according to the Forestry Law of 1987 (no. 15939). Those areas were defined on production characteristics and limitations of the soils mainly oriented to cattle and wool. Soils with similar production characteristics are grouped in broad categories defined by a number, and plantations occur mainly in groups 7, 8, 9, and 2 (Fig. 1). Parent soil materials of the group 7 (North) comprise reddish sandstones to rose and white argillaceous sandstones. Soils are classified as leached and unsaturated (acrisols and luvisols - [3]). With some exceptions, soils are deep, reaching 1.5 to 3 m, acidic, with elevated levels of exchangeable aluminum, and low in base saturation ([22]). Very shallow weakly developed soils (lithosols) are also found mostly on the hill tops. Group 9 in the West (corresponding to group 9 and 09) is highly variable regarding parent geological material and this is reflected in the variability of soil characteristics. Nonetheless they are mostly sandy stones, developing soils classified as leached saturated, characterized by strong textural differentiation between A and B horizons (planosols and argisols), and melanic (brunosols - [3]). The Central area corresponding to group 8 comprises sandstones. Soils are generally sandy with low fertility. Classification varies from leached unsaturated (luvisols), leached saturated (argisols), melanic (brunosols), and weakly developed and shallow (lithosols - [3]). Soils of Groups 8 and 9 are comparatively shallower and more fertile than Group 7.
Fig. 1 - Prioritized soils for forestry and plots localization. Produced with spatial information of soils prioritized for forestry ([23]).
Data preparation
Information from 974 permanent sample plots (PSP) in geo-referenced locations in areas prioritized for forestry was used to fit the equations (Fig. 1). P. taeda’s plots (669) corresponded to commercial plantations while the E. grandis plots (305) were from commercial plantations and pruning, thinning, and breeding trials of the National Institute of Agricultural Research (INIA Uruguay). Only PSPs with more than two measurements and with locations geo-referenced were included in the dataset.
PSPs were linked to the following site characteristics: aspect (α), slope (β), elevation (Elev), and potentially available soil water (PASW), using information publicly available through the Ministry of Cattle, Agriculture, and Fisheries ([23]). For aspect, slope, and elevation, a digital elevation model with a precision of 30 × 30 m was used ([24]).
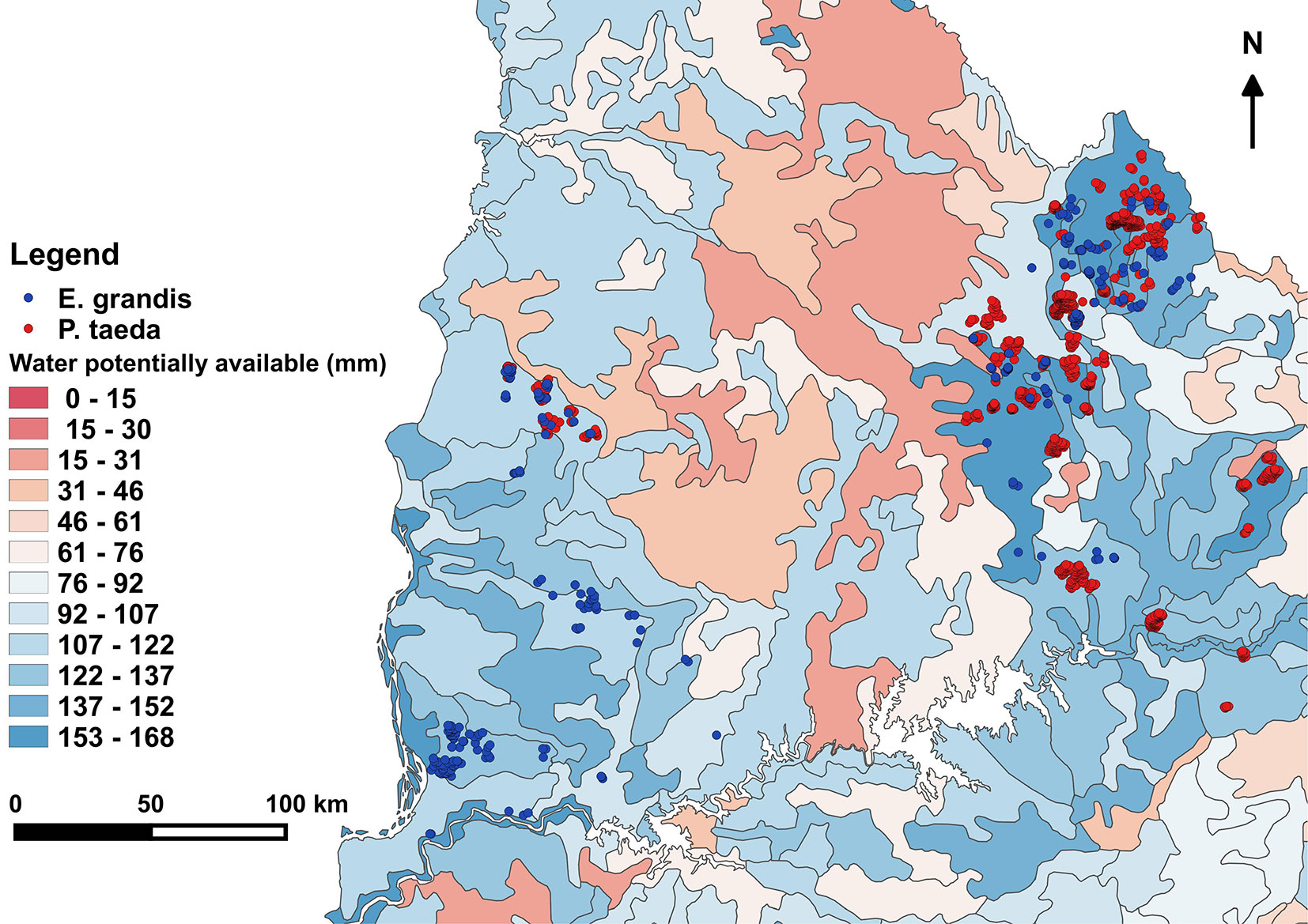
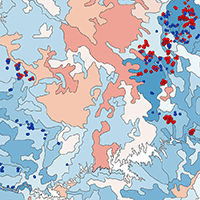
Aspect was decomposed to North-South and East-West components by calculating the sine and cosine of the azimuth angle, respectively. In this way sine values range from 1 to -1 from East to West, and cosine values range from 1 to -1 from North to South. Both components were weighted by the slope using the method proposed by Stage ([34]), so that the value for flat ground is 0 and it increases along with the slope. Therefore, variables obtained were αs = sin(α) · β, and αc = cos(α) · β. Potentially available soil water (PASW) was extracted directly from a digital national map (Fig. 2) developed by Molfino & Califra ([25]) based on the 1:1.000.000 Soil Classification Map of Uruguay ([21]). The cited authors calculated PASW for each soil profile type through pedotransfer functions developed for the country to compute water potentially available (between 1/10 to 15 atm). The values were calculated for each sub-horizon’s depth per soil type and weighted for the percentage that the soil type occupies on each of the 99 soil classification units. Finally, Molfino & Califra ([25]) applied a correction factor that accounts for limiting factors such as erosion, rockiness, stoniness, and salinity to get a value of net PASW. The range of all 4 studied predictors across the plots is depicted in Tab. S1 (Supplementary material).
Fig. 2 - Range of water potentially available for PSPs of both species. Produced with spatial information of potentially available soil water (1:1.000.000 scale map - [24]).
Procedures involving georeferenced information were developed using QuantumGis ([28]), and ArcGis for Desktop ([7]).
Datasets for both species were screened by graphical methods before and after computing the required variables, to assess the relationship between variables. The variable hdom was calculated as the mean height of the 100 trees with the largest d within a hectare using Garcia’s formula ([10]) to calculate the number of trees in each PSP equivalent to 100 trees per hectare. Seventy percent of the plots were used for fitting purposes while 30% were utilized for validation. A dataset was also prepared for hypothesis testing using only the longest interval of each plot of the entire dataset. The information of PSPs coverage is presented in Tab. 2.
Tab. 2 - Summary of the dataset used for modelling. (N): total number of sites; (n): mumber of plot measurements; (PSP): permanent sample plots; (G): basal area; (SD): standard deviation.
| Variable | P. taeda | E. grandis | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Min | Max | SD | Mean | Min | Max | SD | |
| N | - | - | 669 | - | - | - | 305 | - |
| n | 4.00 | 2.00 | 11.00 | - | 4.00 | 2.00 | 11.00 | - |
| t (years) | 7.13 | 2 | 25.9 | 3.2 | 6.95 | 1.18 | 18.7 | 3.47 |
| hdom (m) | 10.6 | 2.2 | 27 | 4.65 | 21.2 | 4.4 | 46.6 | 7.86 |
| dm (cm) | 17.2 | 2.3 | 41.9 | 7.56 | 17.6 | 3.1 | 45.2 | 7.18 |
| dmax (cm) | 21.1 | 4 | 46.7 | 8.71 | 24.3 | 5 | 62.6 | 8.77 |
| dmin (cm) | 12.8 | 0.48 | 36.6 | 6.92 | 10.1 | 0.1 | 41.1 | 6.64 |
| SDd (cm) | 2.2 | 0.11 | 8.42 | 0.96 | 3.42 | 0.64 | 10.5 | 1.43 |
| G (m2 ha-1) | 15.6 | 0.1 | 53.6 | 10.9 | 19.2 | 0.78 | 58.1 | 8.95 |
| N (stems ha-1) | 624 | 100 | 1667 | 180 | 886 | 87 | 1775 | 393 |
| PSP size (m2) | 338 | 200 | 500 | 84 | 682 | 400 | 2250 | 315 |
Growth equations
For modelling growth of hdom, G, dmax, and SDd, several differential equations in polymorphic and anamorphic form were tested (see Tab. S2 and Tab. S3 in Supplementary material). Those were fitted using non-linear least-squares as applied by Clutter ([5]) using all possible intervals within PSPs. Mixed effects models are sometimes employed to account for multiple measurements within plots, but in this study the problems related to data serial correlation were avoided by testing the inclusion of new variables using a correlation-free dataset where only one interval per plot was included. In this way, valid hypothesis testing was undertaken.
Candidate equations were compared through the root of the mean square error (RMSE), as a measure of precision; and the mean residual (MR) and mean absolute bias (MAB) as a measure of bias. All three statistics calculated using the modelling dataset were ranked and an overall rank for each model was computed by summing the rank values for all the statistics. The best ranked model for each state variable (hdom, G, dmax, and SDd) was selected. Normality was analysed graphically through histograms and Q-Q plots, and plots of residuals against the variables fitted and the independent variables were also assessed. After selecting the equation for each state variable, the inclusion of predictors was tested using the hypothesis testing dataset. Once the predictors to include were known all the equations were re-fitted using the modelling dataset. The behaviour of augmented models was assessed by plotting projections for contrasting growth conditions.
For the validation stage, plots of residuals (predicted vs. independent values) were examined to detect bias. Confidence intervals for the slopes of predicted vs. independent values with a level of significance of 5% were computed to compare the actual slope with the ideal slope of 1 ([11]). Comparisons of approaches were done through goodness of fit statistics as well as statistics of prediction (using the validation dataset) for each type of equation (simple and augmented) and comparing residuals.
Results
Growth equations
Correlations between the soil-based and physiographic variables and site index were initially assessed using the hypothesis testing dataset. High correlation between explanatory variables could interfere in determining the precise effect of each predictor and lead to large standard errors of the parameters. For P. taeda very low correlations were found between site variables; PASW and Elev, and Elev and β are the highest correlated with coefficients slightly over 0.3 in both cases. Moreover, none of the site variables showed high correlations with site index. Higher correlations were found with the eucalypt species; the same variables PASW and Elev, as well as Elev and β gave correlation coefficients of 0.84 and 0.60 respectively, whereas between PASW and β the coefficient was 0.47. Additionally, it was found that PASW and Elev had the highest correlations to SI (0.63 and 0.68 respectively). The use of correlated predictors was avoided.
For both species the inclusion of a dummy variable (Z7) to distinguish growth in Zone 7 compared to the rest (Zones 9 and 8) was assessed in base models as applied by Methol ([19]), for models currently available. For the pine species, Elev was the site variable most correlated with the dummy (0.59), whereas correlation with SI was very low (0.16). For E. grandis, correlation was high between Z7 and Elev (0.88) and PASW (0.80), while the correlation with β was less evident (0.54).
Base models
In general, models that showed the best fit were polynomial forms of von Bertalanffy-Richards and Schumacher. Base models selected for Pinus taeda were as it follows (eqn. 1 to eqn. 4):
whereas base models adjusted for Eucalyptus grandis were (eqn. 5 to eqn. 8):
For P. taeda there were very modest or no improvements of the hdom equations tested by adding the dummy variable, but for E. grandis its inclusion improved both precision and bias. For this species, a parameter (k) was added to t1 and t2 (eqn. 5), giving the equation known as the Johnson-Schumacher ([12]). This modification substantially improved bias and precision while the equation still preserved the properties of path invariance and consistency ([6]). For projecting basal area, the inclusion of a thinning modifier (ratio of stocking per hectare after thinning and before thinning divided by the time of thinning: [Na/Nb]/tt - [36], [19]) was also assessed. For the pine species, this term was not significant in the model and was not included. For E. grandis the term was significant. For modelling P. taeda’s dmax, site index (SI) was introduced in the equation to correct bias.
Augmented models
Augmented equations for hdom and G for Pinus taeda were as it follows (eqn. 9, eqn. 10):
where ω = a0 + a1 PASW.
An augmented form for dmax and SDd did not improved error for the pine species; hence those were not further tested. However, site variables would be indirectly introduced in dmax (eqn. 3) if SI was calculated using the augmented equation for hdom (eqn. 9).
For Eucalyptus grandis augmented models adjusted are as it follows (eqn. 11 to eqn. 14):
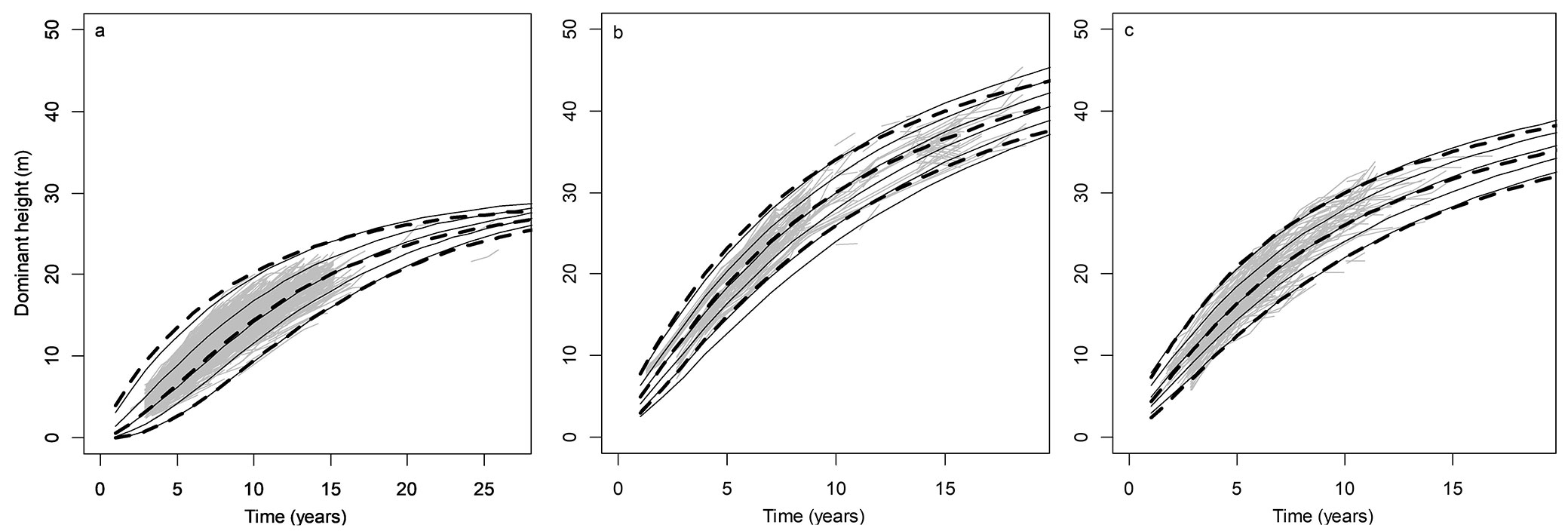
PASW was significant for all state variables except for SDd, whereas aspect modified by slope was not significant for G. The dominant height curves fitted corresponded to the trajectories of the entire dataset for each species (Fig. 3). For the case of E. grandis, plots located in the northern part of the country (Z7 = 1) reached greater dominant heights in general.
Fig. 3 - Dominant height curves using base equations (continued black lines), with original plot trajectories (grey lines), and a comparison with augmented equations (dashed lines), for P. taeda (a), and E. grandis planted in Zone 7 (b), and other Zones (c). Average values of site variables were applied for each Zone.
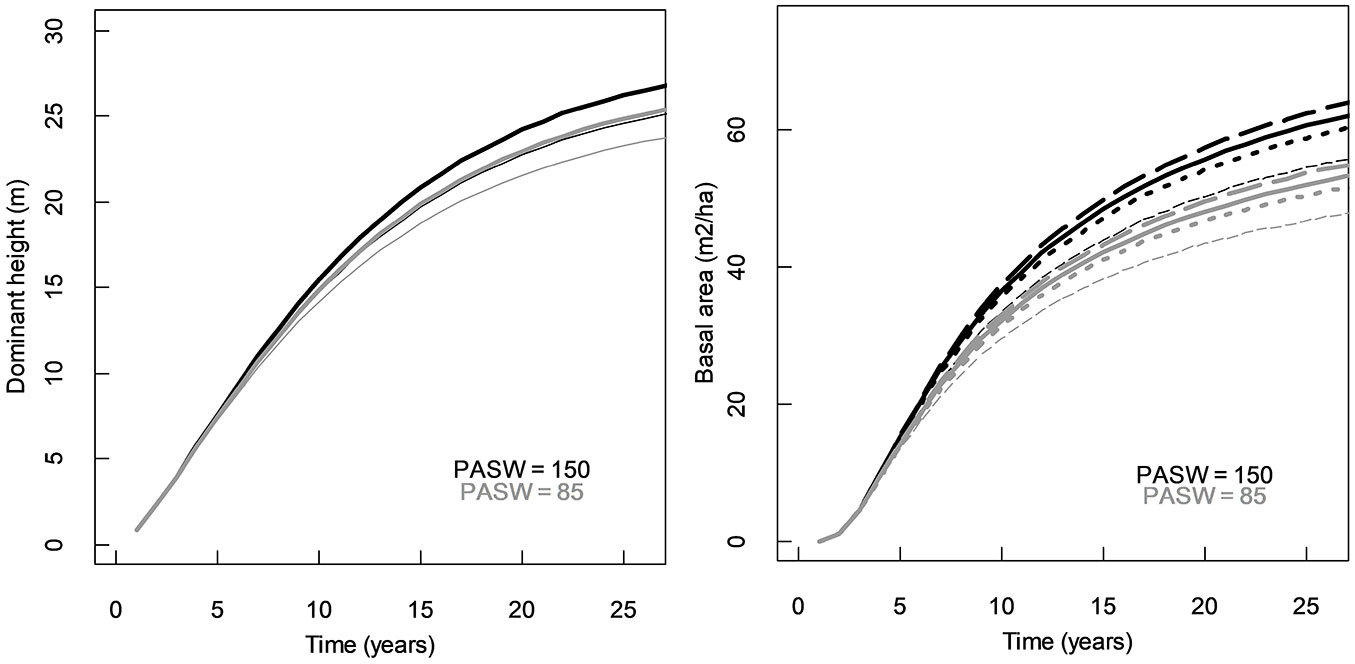
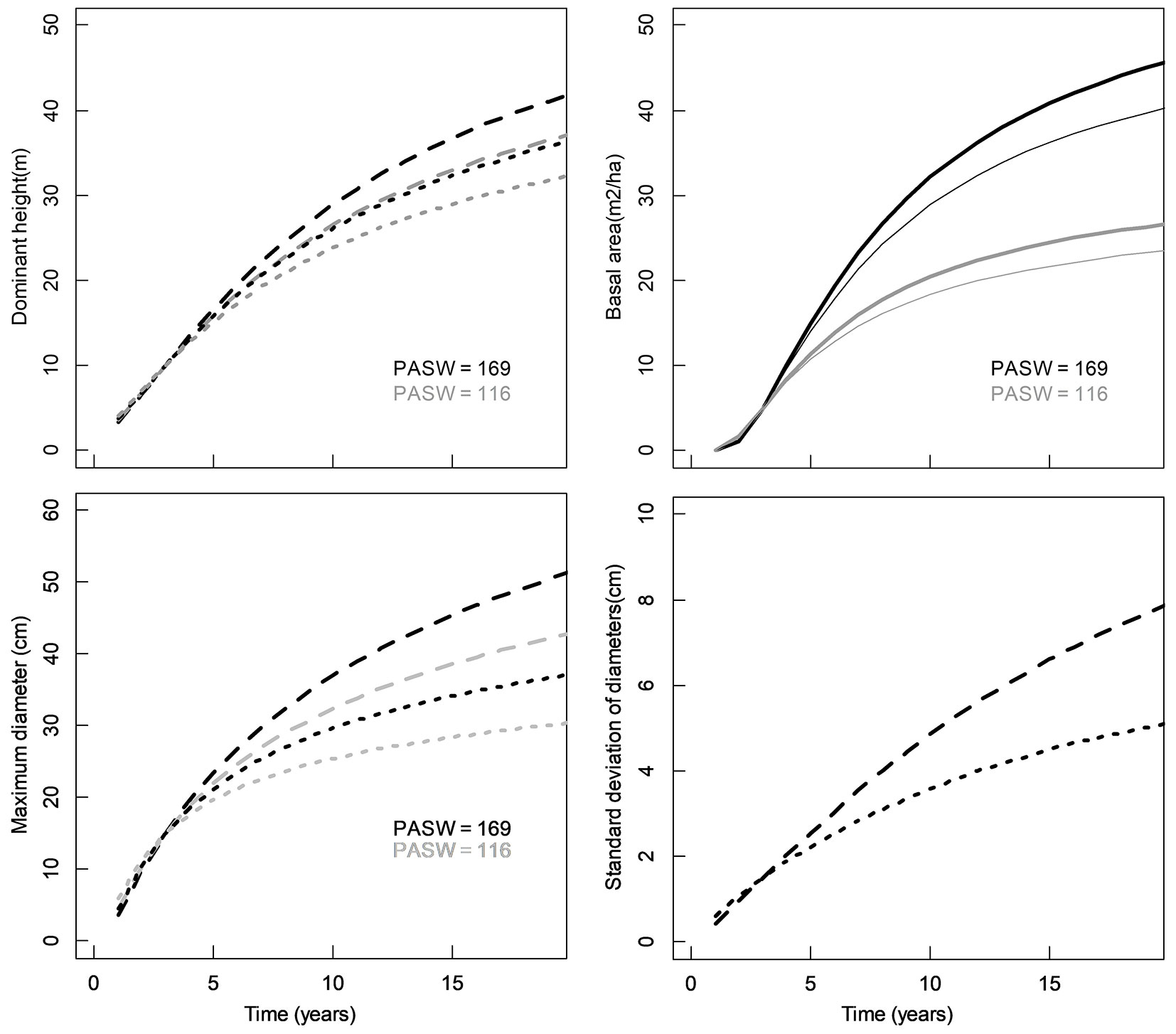
An analysis of the influence of the site variables included in P. taeda’s equations showed that higher growth rate was achieved for hdom in sites with higher elevation and higher PASW values (Fig. 4). For basal area, East aspects on steeper terrain and larger water storage capacity would favour growth (Fig. 4). For E. grandis, the hdom equation projects higher growth rate for NE orientation in steeper terrains with high values of PASW (Fig. 5). For basal area, the equation predicts higher growth in sites with higher values of PASW and lower Elev (Fig. 5). From a physiological point of view the model shows consistency, especially regarding the effect of water holding capacity of soils on growth for both species. The example plots also show differences in hdom growth with respect to PASW between both species; when for P. taeda the increase in growth by increasing 65 mm of PASW is approximately 2 m of height and 5 m2 ha-1 at the age 20, for E. grandis an increase of 53 mm represents around 5 m and 20 m2 ha-1 of increase in height and basal area, respectively. This reflects the differences in growth rate of those two species and the relationship between growth and potential availability of resources.
Fig. 4 - Effect of site variables on growth curves for P. taeda: dominant height for elevation values of 150 m (thick) and 65 m (thin). Basal area for elevation values of 150 m (thick line) and 65 m (thin lines), and 5% slopes facing E (dashed) and facing W (dotted).
Fig. 5 - Effect of site variables on growth curves for E. grandis: dominant height for slopes of 9% facing NE (dashed) and SW (dotted). Basal area for elevation values of 130 m (thick) and 172 m (thin lines); maximum diameter and standard deviation for 5% slopes facing East (dashed) and West (dotted).
For dmax, site variables PASW and αs included in the E. grandis’ equation affects such that stands located in soils with elevated levels of water storage capacity and steeper terrains facing East show larger maximum diameters (Fig. 5). SDd of this species increases its magnitude in sites facing East (Fig. 5). Statistics of fit and parameters of fitted models for each state variable are presented as Supplementary material (Tab. S4 to Tab. S7).
Validation of models and error comparison
Residual plots using the validation datasets did not show any strong patterns or bias (Fig. S1 to Fig. S5 in Supplementary material). The RMSE statistic using independent data was lower for enhanced equations with respect to the base counterpart with larger precision gains for E. grandis than the pine species (Tab. 3). RMSE was reduced up to 10 % when the models were adjusted. However, using an independent dataset precision gain observed was modest in general. Likewise, bias decreased when using physiographic and soil-based predictors for most of state variables (Tab. 4).
Tab. 3 - Comparison of RMSE for base and augmented models for each state variable, using the modelling dataset and an independent dataset.
| Species | Variable | Modelling dataset | Independent dataset | ||||
|---|---|---|---|---|---|---|---|
| Base | Augmented | ΔRMSE (%) | Base | Augmented | ΔRMSE (%) | ||
| P. taeda | hdom(m) | 0.894 | 0.867 | -3.0 | 0.860 | 0.850 | -1.0 |
| G (m2 ha-1) | 3.151 | 2.929 | -7.0 | 3.230 | 3.130 | -3.1 | |
| dmax (cm) | 1.789 | - | - | 2.080 | - | - | |
| SDd (cm) | 0.484 | - | - | 0.470 | - | - | |
| E.grandis | hdom (m) | 1.785 | 1.685 | -5.6 | 1.690 | 1.660 | -1.8 |
| G (m2 ha-1) | 2.847 | 2.677 | -6.3 | 2.760 | 2.650 | -4.0 | |
| dmax (cm) | 2.179 | 1.951 | -10.5 | 2.220 | 2.180 | -1.8 | |
| SDd (cm) | 0.516 | 0.494 | -4.3 | 0.556 | 0.560 | 0.7 | |
Tab. 4 - Comparison of MAB for base and augmented models for each state variable, using the modelling dataset and an independent dataset.
| Species | Variable | Modelling dataset | Independent dataset | ||
|---|---|---|---|---|---|
| Base | Augmented | Base | Augmented | ||
| P. taeda | hdom(m) | 0.69 | 0.67 | 0.67 | 0.66 |
| G (m2 ha-1) | 2.25 | 2.13 | 2.53 | 2.21 | |
| dmax (cm) | 1.32 | - | 1.52 | 1.49 | |
| SDd (cm) | 0.34 | - | 0.32 | 0.32 | |
| E. grandis | hdom (m) | 1.32 | 1.28 | 1.29 | 1.27 |
| G (m2 ha-1) | 2.00 | 1.90 | 2.05 | 2.05 | |
| dmax (cm) | 1.61 | 1.45 | 1.58 | 1.55 | |
| SDd (cm) | 0.38 | 0.37 | 0.41 | 0.41 | |
Discussion
Performance of physiographic variables
PASW was significant for most of the state variables modelled for P. taeda and E. grandis. This is consistent given that water availability is a key element for growth. Water stress leads to stomatal closure, and a decrease in carbon fixation efficiency. As a consequence, a reduction in cambial activity and foliage growth occurs, followed by a production decrease ([16]). For Eucalypt grandis hybrids Stape et al. ([35]) observed that an increase in water availability increases quantum efficiency and leaf area, and decreases carbon allocation to roots. Their results showed that for the species, water availability strongly influences the capture and use-efficiency of supplies. For P. taeda, Albaugh et al. ([1], [2]) found that stem growth efficiency (growth per LAI unit) as well as total biomass production efficiency increased by irrigation, and hypothesised that the increase occurred as a consequence of more biomass being allocated to photosynthesizing tissue. Given the importance of water availability for plant growth, a range of variables related to soil moisture, available water for stands, or rainfall has been tested before on differential equations or when modelling increments ([41], [32], [27], [30]) proving to be effective especially for improving G predictions. The tendency of a larger decrease in errors for G compared to hdom was also observed in this study.
The variable PASW used in this analysis is rather theoretical based on a coarse resolution 1:1.000.000 soil map, however it synthesises solidly a series of essential soil characteristics, yielding consistent results with respect to forest productivity. Furthermore, this variable represents potential water availability without interfering on the path invariance property of differential equations, which is a fundamental characteristic to provide robustness to mensurational models.
The effect of slope and aspect on growth varies depending on the species requirements and site characteristics that result from the interaction of mean annual temperature, rainfall regimes, altitude, and velocity and wind-direction ([40], [38], [14]). Aspect weighted by slope (αs and αc) was consistent for E. grandis equations, whereas for P. taeda it was significant only for G. NE and E aspect favoured growth and the effect was accented by the slope. We hypothesize that sunlight duration in northern slopes is longer in such latitudes (30° to 33° S), leading to longer period for photosynthesizing as well as warmer temperatures in winter, especially for E. grandis. Given that rainfall is abundant in general (1200 to 1600 mm year-1), desiccation would not pose a systematic problem for growth during warm months. Although this hypothesis should be tested, similar behaviour was reported by Running ([31]), who simulated growth of conifers in the northern hemisphere. He observed that in the cases when water was not restricted, energy was the factor limiting physiological activity; therefore, southern slopes produced higher seasonal photosynthesis. Although the use of sine and cosine of the azimuth angle as well as their association with slope has been used for predicting site index ([37], [34]) and stand volume ([33]), the use in differential growth equations is unusual.
Elevation has no explicit effect on growth but influences key growth factors such as temperature and soil moisture at a local scale. It has been used specifically in mountainous areas for forecasting site productivity ([26], [9]), being incorporated as an explanatory variable in yield equations for predicting hdom, G, and dmax ([18]). Because differences in altitude are relatively small in terms of the impact on site-specific temperature, an alternative hypothesis is that there is a negative influence of soil moisture in lower ground for P. taeda, since the species is frequently planted in marginal, low areas which are waterlogged for short periods. This was investigated graphically by using categorical information of drainage speed and results showed that plots located in sites classified as slow and medium drainage speed were associated with smaller values of altitude (e.g., less than 150 m), which would confirm the first hypothesis. Although elevation could be a surrogate of drainage for P. taeda, further research should be undertaken to confirm this hypothesis as well as testing the correspondence of altitude with climate variables such as temperature.
Advantages of augmented models
The augmented models represent an increase in flexibility of curves by including predictors on the shape parameters, the asymptote, or both. Although reductions of the prediction error (calculated using an independent dataset) were modest (2 to 4%), bias was reduced by augmentation of most equations.
To date, models used in Uruguay do not consider site characteristics explicitly. Prognosis systems for Eucalyptus grandis and Pinus taeda in the country use dummy variables to account for differences on growth curves. Dummy variables have been used by Methol ([19]) for modelling hdom and G for the same eucalypt species in Uruguay, distinguishing growth curves for zones 7, 8, and 9 (Fig. 1). Moreover, Methol ([20]) localized growth curves for hdom for Eucalyptus globulus ssp. globulus growing in the zones 2 and 9. Zonification has been used traditionally as a way to characterize a set of regional attributes related mainly to geology, topography, and soils. However, this has been traditionally developed for cattle production, and not for forestry, which poses limitations for characterizing potential forest productivity. For P. taeda, instead, zonification has not seemed to be effective and has not been applied in the past ([8], [29]). Main advantages in using augmented equations rely in the possibility to represent differences in site quality in a more descriptive way than with the localization strategy. This benefits the understanding of growth and allows the improvement of site and species management (e.g., assessing the benefits of improving water holding capacity of soils by subsoiling or assisting in the selection of pines vs. eucalypts). Further contribution of this work would be on the identification of areas where growth could be favoured or reduced due to variations in rainfall regimes under climate change scenarios and the quantification of such variations. It is expected that the methodology proposed here will be favoured with future improvements on the resolution of water holding capacity maps and digital terrain models.
Use of the equations and constraints
Explanatory components of the models add utilities for forest management, and the information needed is readily available with its quality tending to improve over time. However, care must be taken when using the equations when site variables border on the extremes of the range of values used in this study, especially when using a combination of extreme values. Representation of all possible combinations of explanatory variables’ values is a common issue in forest modelling since the set of PSPs used is restricted. To take a closer look to this potential problem, the extreme values of site variables were plotted against all the values of each of the remaining site variables used, to search for information gaps. Results showed that PSPs combining extreme values of the predictors were rare for the eucalypt species (i.e., extreme values of a site variable were commonly combined with average values of the rest); however, because the range of aspects in the plots presented no constraints, the main relationship to investigate was PASW and β extremes. In this sense, PSPs located in sites with β larger than 9% are very scarce; there are no PSPs with slopes larger than 9% in sites with low PASW (less than 100mm). For P. taeda, elevation should also be taken into consideration: extreme combinations were available in the dataset for PASW, β and large values of Elev, whereas low values of Elev were strictly associated with low PASW (100mm) and average β (5%). Forthcoming research should be directed to include permanent sample plots located in extreme sites to achieve more reliable models under such marginal sites.
Models for both species were adjusted using a dataset comprising a diverse genetic base, covering a large part of the variability for the country. This contributes to the generalization capacity of the models, however adaptations of certain genotypes to sites can occur. Interactions between genotypes and environments were not assessed and are not contemplated in the models.
An information gap was found for P. taeda near harvesting age, therefore care must be taken when performing projections beyond 16 years. Future work should consider updating datasets to include stands at harvesting age for this species.
Conclusions
Augmented stand level growth equations have been developed and can be recommended to be incorporated in a prognosis system to simulate height, basal area, and diameter dynamics for Pinus taeda and Eucalyptus grandis growing in northern Uruguay. Soil-based and physiographic information improved predictions of the variables fitted for E. grandis: hdom, G, dmax, and SDd, but were significant only for hdom and G in the case of P. taeda.
The use of explanatory variables (physiographic and soil variables) decreased the fitting error in a range from 3 to 10.5%, however decreases in the prediction errors calculated with the independent dataset were much lower ranging from 1.6 to 4%. In this sense, main advantage of the augmented models relies on the better description of site differences and their effect on tree growth, consequently adding new possibilities to the use of those models for plantations’ management.
Acknowledgements
The authors are indebted with the companies that generously have provided data for this study: Global Forest Partners LP and Cambium S.A., Cloverly S.A., Bosques del Sur S.A., and UPM-Forestal Oriental. We also acknowledge the Directorate of Renewable Resources (RENARE) of the Ministry of Cattle, Agriculture, and Fisheries (MGAP) for contributing with physiographic and soil information. Finally, we thank the reviewers whose valuable comments greatly improved this manuscript. Funding for this study was provided by the Ministry of Foreign Affair and Trade of New Zealand, through NZAid Scholarship, and INIA Uruguay.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Forestry Research Programme, National Institute of Agricultural Research (INIA Uruguay), Road 5, Km 386, 45000 Tacuarembó (Uruguay)
Richard C Woollons
School of Forestry, University of Canterbury, Private Bag 48000, Christchurch (New Zealand)
Corresponding author
Paper Info
Citation
Rachid-Casnati C, Mason EG, Woollons RC (2019). Using soil-based and physiographic variables to improve stand growth equations in Uruguayan forest plantations. iForest 12: 237-245. - doi: 10.3832/ifor2926-012
Academic Editor
Emanuele Lingua
Paper history
Received: Jul 19, 2018
Accepted: Mar 16, 2019
First online: May 03, 2019
Publication Date: Jun 30, 2019
Publication Time: 1.60 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2019
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 44325
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 37441
Abstract Page Views: 2860
PDF Downloads: 3270
Citation/Reference Downloads: 4
XML Downloads: 750
Web Metrics
Days since publication: 2424
Overall contacts: 44325
Avg. contacts per week: 128.00
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2019): 7
Average cites per year: 1.00
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Modelling taper and stem volume considering stand density in Eucalyptus grandis and Eucalyptus dunnii
vol. 14, pp. 127-136 (online: 16 March 2021)
Research Articles
Relationship between microbiological, physical, and chemical attributes of different soil types under Pinus taeda plantations in southern Brazil
vol. 17, pp. 29-35 (online: 28 February 2024)
Research Articles
Essential environmental variables to include in a stratified sampling design for a national-level invasive alien tree survey
vol. 12, pp. 418-426 (online: 01 September 2019)
Review Papers
Recent insights in soil nutrient cycling: perspectives from Pinus and Eucalyptus forest studies around the world
vol. 17, pp. 394-404 (online: 20 December 2024)
Research Articles
The use of tree crown variables in over-bark diameter and volume prediction models
vol. 7, pp. 132-139 (online: 13 January 2014)
Research Articles
Potential relationships of selected abiotic variables, chemical elements and stand characteristics with soil organic carbon in spruce and beech stands
vol. 14, pp. 320-328 (online: 09 July 2021)
Research Articles
Mid-rotation fertilization and liming of Pinus taeda: growth, litter, fine root mass, and elemental composition
vol. 14, pp. 195-202 (online: 24 April 2021)
Research Articles
Relationship between environmental parameters and Pinus sylvestris L. site index in forest plantations in northern Spain acidic plateau
vol. 9, pp. 394-401 (online: 16 January 2016)
Research Articles
Integrating area-based and individual tree detection approaches for estimating tree volume in plantation inventory using aerial image and airborne laser scanning data
vol. 10, pp. 296-302 (online: 15 December 2016)
Research Articles
Stability analysis and selection of optimal Eucalyptus urophylla × E. grandis families
vol. 18, pp. 293-300 (online: 20 October 2025)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword