Modelling taper and stem volume considering stand density in Eucalyptus grandis and Eucalyptus dunnii
iForest - Biogeosciences and Forestry, Volume 14, Issue 2, Pages 127-136 (2021)
doi: https://doi.org/10.3832/ifor3604-014
Published: Mar 16, 2021 - Copyright © 2021 SISEF
Research Articles
Abstract
Eucalyptus grandis and Eucalyptus dunnii are the most planted tree species in Uruguay. Anticipating information about the quantity and quality of wood is important for managing intensive forest plantation. The estimate of merchantable and total wood volume is an essential tool in forest planning and management. The aim of this study was to evaluate four systems of taper and merchantable volume that consisted in a taper, a merchantable volume and a total tree volume function. A modified second-order continuous autoregressive error structure corrected the inherent serial autocorrelation of different observations in one tree. Taper and volume equations were fitted simultaneously after autocorrelation correction by full information maximum likelihood method. The segmented system proposed by Fang et al. (2000) produced the best fit as it explained more than 98% of the taper, merchantable volume and total volume variability for both species. In addition, precision of the segmented system was compared with and without incorporating stand density as a variable. Results of this analysis showed that for E. grandis, the predictive accuracy of the model was improved by including the stand density variable, whereas for E. dunnii this variable was not statistically significant. This modelling framework provides an improvement in taper and tree volume predictions for E. dunnii and E. grandis in Uruguay. The possibilities offered by this methodology could be of interest for its application in countries where fast growing plantations are managed.
Keywords
Compatible Systems, Taper, Simultaneous Estimation, Intensive Silviculture, Eucalyptus
Introduction
The total volume of individual trees is commonly estimated using models that take into account the tree diameter and total height, but this method does not allow to estimate the distribution of products according to their final commercial use. To solve this problem, stem taper function equations are usually developed ([19], [4]). The use of taper functions ensures an accurate description of the diametric profile of the stem and facilitates the estimation of merchantable logs distribution at any arbitrary diameter or length ([45]).
Taper functions are equations that describe the diameter narrowing rate along the stem ([13]), which can be expressed as a function of the total height of the tree (H), and the diameter at the breast height (D - [7]). Taper equations utilize: (i) the diameter (with or without bark) at any point of the stem; (ii) the height at a certain diameter; and (iii) the commercial volume (with or without bark) at a given commercial height or minimum diameter from any stump height ([20]). According to Prodan et al. ([34]), the use of those functions allows to assess the combination of wood products that can be obtained from a stand, and they are usually applied along with simulations of different silvicultural regimes. The integration of the taper function from ground level to any height will provide an estimate of the merchantable volume at that height ([19], [4]).
These functions can also be compatible with volume equations that are used to estimate individual tree volumes; ideally, the volume computed by integrating the taper equation from the ground to the tree top should be equal to that calculated using the total volume equation ([7]). Following Diéguez-Aranda et al. ([8]), in the development of a compatible volume system, the most common approach is to express the α coefficient of a simplified Spurr’s volume equation ([42]) in terms of the taper equation coefficients, or vice versa, by using a compatibility relationship. This ensures that the taper function and the volume equation are analytically consistent ([39]). Another approach involves the development of a system that ensures compatibility between the taper function and a pre-established volume equation, by including this function in the mathematical expression of the taper function ([10]). Examples of volume equations used for this purpose are those proposed by Schumacher & Hall ([38]) and Spurr ([42]).
Compatible systems have been usually fitted using two different approaches: ordinary least squares (OLS) and simultaneously, using seemingly unrelated regression (SUR) or full information maximum likelihood (FIML - [8], [35]). In the classic OLS adjustment, it must be decided whether the error is minimized in the taper equations or in the merchantable volume. Then, the selected equation is fitted and the specific compatibility relationship is used to obtain the parameters of the non-fitted equation. On the contrary, the simultaneous fitting of the complete systems using FIML or SUR presents consistent estimators for all the equations of the system ([10]).
Data for adjusting taper models include multiple height and diameter measurements from each of the individuals in the sample, which determines a longitudinal data structure ([21]). Simultaneously, the variability of records within each tree is lower than the variability between trees; therefore, the assumption of independence is not fulfilled. Problems associated to the use of longitudinal data to taper functions fitting are related to multicollinearity, autocorrelation, and heteroscedasticity. In the presence of autocorrelation, the estimated parameters are not those of minimum variance since the mean square error of the model underestimates the variance of the error term, thus invalidating the significance contrasts. Although the estimators obtained in the regression adjustment remain unbiased, they are not the most efficient ([19]). For a correct analysis of longitudinal data, numerous studies propose to assume a particular error structure, expressing this autocorrelation among the errors as a stationary autoregressive model CAR(x) of order x ([11]). The advantages of this methodology are: (i) greater efficiency in obtaining parameters estimators of the model; (ii) adequate estimators for the standard errors of parameters; (iii) problems of lack of data or different number of measurements between individuals are solved; and (iv) it can be used even when the number of measurements is large compared to the number of individuals ([47]). According to Teshome ([45]) these systems should be designed to be simple, flexible and easy to handle so that they can accurately estimate merchantable volume of any log length or to any specific diameter, based solely on easily measurable individual parameters such as diameter at breast height and tree height.
Tree growth follows biological limitations; stem growth depends on complex multifactorial and site-specific factor combinations. Tree growth as well as stem shape depends on several intercorrelated stand specific factors, e.g., available resources, stand conditions, and structure attributes, which might potentially challenge the model’s predictive accuracy. This concern has been addressed in several studies by including stand density information in taper equations in order to improve model performance ([40], [41]). Calama & Montero ([5]) pointed out that the high level of random variability with respect to stem form indicated the presence of factors that acted both at plot (silvicultural treatment) and tree levels (competition).
Jacobs et al. ([16]) determined that when decreasing stand density, the lower part of the stem is conic instead of cylindrical. The lowering of stand density can cause a decrease in form factors, an increase in taper rates, and a decline in slenderness. Social status also affected stem shape: dominant trees increased in stem taper, while dominated trees in closed stands produced smaller crowns with less tapered stem ([16]).
To date, compatible systems of taper and volume equations are not widely used in Uruguay. The development of more accurate taper and volume models for intensive Eucalyptus plantations will significantly contribute to improve forest yield and planning. Therefore, the aim of the present study was to simultaneously fit a system of equations for predicting taper, merchantable volume and total tree volume, for Eucalyptus grandis (Hill ex. Maiden) and Eucalyptus dunnii (Maiden) growing in different zones of Uruguay. Specific objectives were: (i) to adjust four widely used stem taper profile models for predicting merchantable volume; (ii) to select and validate the best system; (iii) to assess the effect of stand density on stem taper and volume predictions. The present study involved simultaneous fitting, while addressing the autocorrelation, multicollinearity among independent variables, and heteroscedasticity.
Materials and methods
Study site
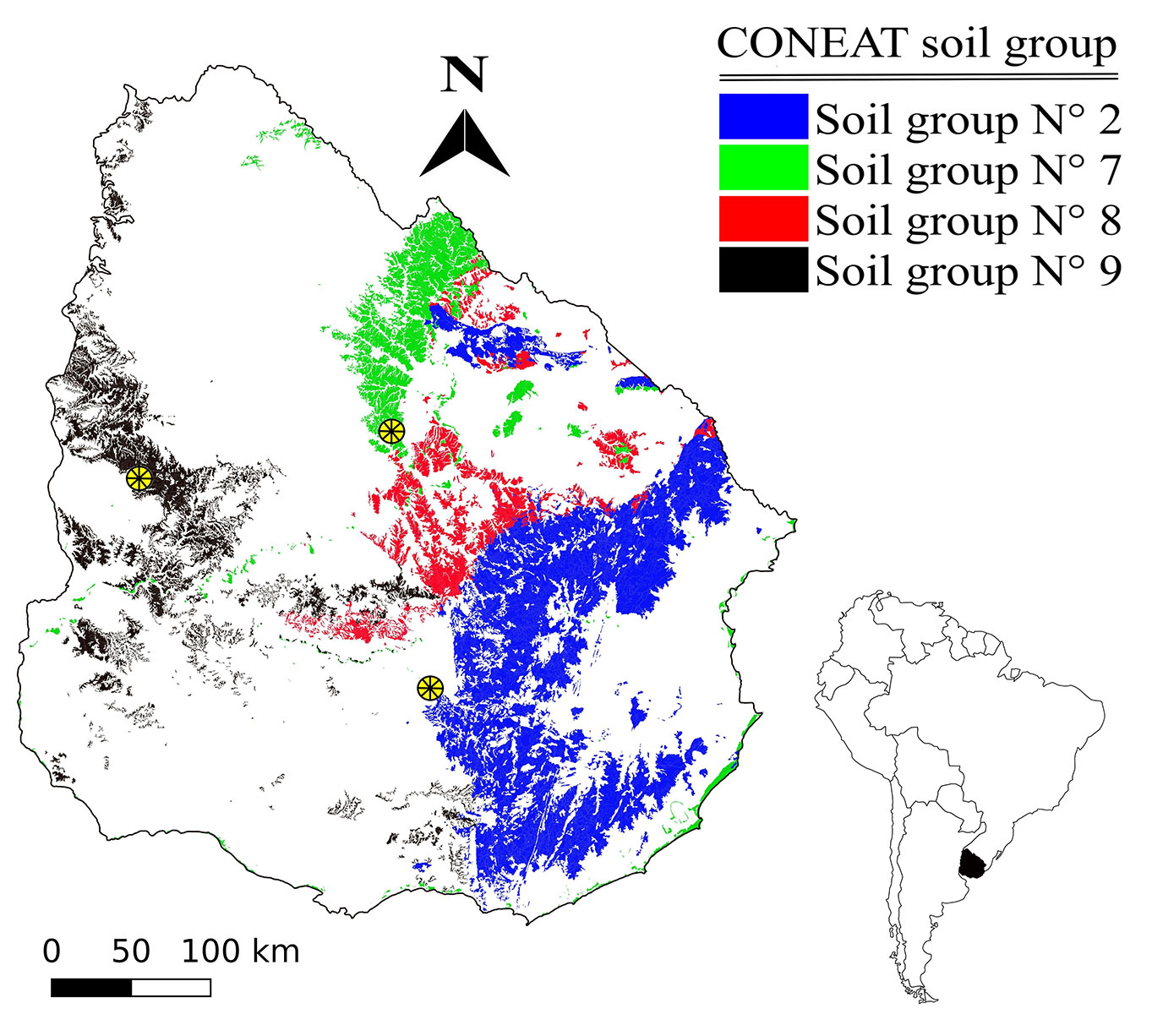
Data was collected in the trials of the National Institute of Agricultural Research (INIA) in 2015 ([33]), located in three different zones in Uruguay: northwest (32° 18′ 18″ S, 57° 44′ 06″ W, next to Guichon city, Paysandú); central east (33° 01′ 43″ S, 55° 31′ 08″ W, next to Sarandí del Yi, Durazno) and central west (33° 21′ 06″ S, 56° 41′ 17″ W, near Trinidad city, Flores - Fig. 1).
Fig. 1 - Location of the study area (yellow points) and soils forest classification sites in Uruguay.
The study zones have a temperate subtropical climate, with a mean annual temperature of 18 °C (12 °C in the coldest month, 24 °C in the warmest month) and mean annual rainfall between 1300 and 1400 mm ([6]). According to the classification of the National Commission for Agroeconomic Studies of the Land (CONEAT), Guichon predominant soils are planosols, with low fertility, horizon A 40-50 cm depth, weak structure, low level of organic matter, slopes of 1-3%, sandy texture, medium to low risk of drought, imperfect drainage, moderately-slow to slow permeability and good rooting ability. Trinidad soils are Vertisols, with medium fertility, horizon A 50-60 cm depth, weak structure, medium level of organic matter, slopes of 2-5%, loam franc structure, low risk of drought, moderate drainage, moderately permeability and good rooting ability. Sarandí del Yi presented soils corresponding vertisols ruptic and Brunosols with a horizon A 50-60 cm depth, sandy-loam, loam franc texture, low fertility, low risk of erosion, moderate slopes (1-3%), weak structure, low organic matter, imperfect drainage and good rooting capacity.
Data collection
A total of 60 trees of Eucalyptus dunnii and 113 trees of E. grandis were felled and measured for diameters at breast height (D), total height (H), and diameters (di) at the corresponding heights (hi = 0.2, 0.7, 1.3 m; and beyond this point, every 1.0 m up to total height - Tab. 1). The stump height was fixed at nearly 20 cm from the ground. Partial and total volumes of the stem (with and without bark), used for fitting the system, were estimated by Smalian method ([34]). The top section volume was estimated using the volume formula for a cone. Plots of relative height (hi/H) against relative diameter (di/D) for each species were carefully examined to detect possible anomalies, such as knots, bark defects, etc. (Fig. 2).
Tab. 1 - Summary statistics of the data for taper and volume of Eucalyptus grandis and E. dunnii in Uruguay. Variables and abbreviations: diameter over bark (dob, cm); diameter under bark (dubi, cm); diameter at breast height (D, cm); total height (H, m); total tree volume over bark (Vob, m3); total tree volume under bark (Vub, m3). (N): number of trees; (Sd): standard deviation; (Min): minimum; (Max): maximum.
| Species | Variable | N | Mean | Sd | Max | Min |
|---|---|---|---|---|---|---|
| E. dunnii | D (cm) | 60 | 18.21 | 3.55 | 24.40 | 9.90 |
| H (m) | 60 | 23.72 | 3.21 | 30.75 | 15.72 | |
| Vob (m3) | 60 | 0.28 | 0.13 | 0.65 | 0.05 | |
| Vub (m3) | 60 | 0.24 | 0.11 | 0.55 | 0.04 | |
| dobi (cm) | 1285 | 12.33 | 5.78 | 33.10 | 0.00 | |
| dubi (cm) | 1285 | 11.32 | 5.31 | 31.83 | 0.00 | |
| E. grandis | D (cm) | 113 | 22.71 | 5.82 | 36.90 | 10.95 |
| H (m) | 113 | 27.56 | 5.72 | 40.90 | 16.60 | |
| Vob (cm3) | 113 | 0.56 | 0.39 | 1.83 | 0.06 | |
| Vub (cm3) | 113 | 0.51 | 0.36 | 1.69 | 0.06 | |
| dobi (cm) | 2667 | 15.64 | 7.23 | 38.45 | 0.00 | |
| dubi (cm) | 2667 | 14.80 | 6.95 | 33.50 | 0.00 |
Fig. 2 - Relative diameter (quotient between an objective diameter and the diameter at breast height) against relative height (quotient between height to an objective diameter and total tree height) for Eucalyptus grandis (a) and E. dunnii (b) in Uruguay.
Compatible system fitting
Four compatible taper and volume systems widely used in forestry were selected from literature ([23], [8], [44]), to test and evaluate the taper and stem volume of both species (see Tab. S1 in Supplementary material). The compatible systems analysed had two components, a taper function and a total volume equation. In addition, the system proposed by Fang et al. ([10]) includes also a merchantable volume equation to or above any specified height or diameter limit.
Model fitting
Compatible taper and volume equations were fitted using a simultaneous method, where all parameter must be expanded through a compatibility relationship. This method reduces the total system squared error ([36]), minimizing prediction errors in diameter at different heights and volume ([8]). Parameter estimation was carried out using the “proc model” of SAS/ETS® ([36]). Systems were simultaneously fitted using the FIML method, that properly accounts for cross-equation correlation and is appropriate for systems of simultaneous equations ([36]). The full information of maximum likelihood estimation in the “proc model” procedure was considered. Simultaneous fitting of the systems applied requires an equal number of observations for all the equations. However, the number of observations in each equation was not equal, as there was more than one diameter observation for each tree but only one observation for total stem volume. Therefore, the structure of the data used ([8], [44]) includes the total volume and diameter of each tree and the inverse of the number of observations in each tree (1/ni) used as a weight when fitting total volume.
Multicollinearity, autocorrelation and heteroscedasticity
Main challenges when fitting stem taper and volume equations lay in the violation of the fundamental least squares assumption of independence and equal distribution of errors with zero mean and constant variance. The most important issues are multicollinearity, autocorrelation and heteroscedasticity, which affect the efficiency of the regression coefficients while the least-squares estimates remain unbiased and consistent.
Although the existence of multicollinearity does not seriously affect the predictive ability of the model ([19]), we evaluated the presence of multicollinearity between variables in the models analysed through the condition number (CN). According to Belsley ([3]), when 5 ≤ CN ≤ 10, multicollinearity is not a serious issue. If 30 ≤ CN ≤ 100, problems associated with multicollinearity may arise, and if CN>100 severe problems of multicollinearity exist. Thus, for CN values greater than 30, corrections must be made.
The data used in the study includes hierarchical relationships, with multiple observations for each tree; thus, autocorrelation within the residuals for each individual might be expected. To demonstrate the autocorrelation, residuals were analysed graphically and by assessing the Durbin-Watson statistic (Dw - [14]). Dw close to 2 allows the non-rejection of the null hypothesis (of non-existence of autocorrelation); Dw lower than 2 indicates positive autocorrelation of order one, while values between 2 and 4 indicate negative autocorrelation of order one ([9]).
One of the general methods proposed to deal with continuous, unbalanced, multilevel longitudinal data is to model the correlation structure directly. In the present study we considered a second-order continuous autoregressive error structure CAR (2), where h accounted for the distance between measurements, and their relative position on the stem was used to overcome the inherent autocorrelation of the longitudinal data. This structure was applied to data from the same sample unit measured at intervals that are not constant in time or space and with a different number of measurements in each sample unit, which is characteristic of taper functions. The CAR(x) error structure was programmed to enable dynamic updating of the residuals.
To account for second-order autocorrelation, we used a CAR (2) model form that expands the error terms in the following way ([47] - eqn. 1):
where eij is the j-th ordinary residual on the i-th individual (i.e., the difference between the observed and the estimated diameters of the i-th tree at j-th height measurement), d1=1 for j>k, k=1, 2 and it is zero for j≤k, ρk are the autoregressive parameters to be estimated, hij-hij-k are the distances separating the j-th from the j-k-th observations within each tree, hij>hij-k
When data from different sample units with different characteristics are used, a non-constant the variance of the errors (σι2) is expected which leads to heteroscedasticity. To detect the deviation of the homoscedasticity of the residuals, the Breusch-Pagan test was applied. To remove the restriction of the variance heterogeneity of errors, since variances are unknown, an alternative is to graphically identify those independent variables (or combinations thereof) that cause such variation. Neter et al. ([28]) suggested using the following formula (eqn. 2):
Prodan et al. ([34]), working with compatible taper and volume functions, proposed a power function of the variable D2iHti, (the square of the tree diameter multiplied by the total height tree) as a candidate for (eqn. 3):
To estimate the k-value (power term), we used the method suggested by Harvey (1976, in [30]), which consists of using the errors obtained with the unweighted model as a dependent variable in the power model of error variance.
The k parameter of eqn. 3 was estimated through linear regression using “proc reg” ([37]) following the methodology described above. According to Diéguez-Aranda et al. ([8]), the weighting factor for heteroscedasticity 1/(D2i Hti)k along with the correction for the special structure of the data, was multiplied and programmed in the model procedure of SAS/ETS® ([37]) by specifying the following (eqn. 4):
where ni is the number of observations in each tree, and res are the residuals.
The use of models with random effects parameters can handle autocorrelation and heteroscedasticity, but increases operating costs ([22]). This methodology involves additional measurements to estimate random effects parameters, as upper stem diameter-height measurements (calibration) for improving diameter prediction ([22]).
Model comparison and validation
The accuracy and precision of each model were compared through graphical and numerical analysis of their residuals. The statistical criteria applied were: the adjusted coefficient of determination (R²-adj, eqn. 5), coefficient of determination for nonlinear regression (R2, eqn. 6), root of the mean squared error (RMSE, eqn. 7), and mean absolute bias (MAB, eqn. 8 - [34]). These expressions are summarized as follows:
where r2 the correlation coefficient between the measured and estimated values (yi, hat{y}i, respectively), of the dependent variable, n is the total number of observations and p is the number of equation parameters.
The validation process was applied to assess whether the goodness-of-fit also reflects in the quality of predictions ([27]), which influences the selection of the best model. The use of cross validation in forestry is a common practice ([15]), and it is a method for model selection considering the predictive ability of the model. This is performed using the same data used for fitting ([27]), and consists of the calculation of the residuals of the i-th observation using parameters estimated by fitting the equation with all data except the i-th observation. This process is known as leave-one-out cross-validation, LOOCV ([17]).
The sum of squares of the eliminated residues is called PRESS (Predicted Residual Sum of Squares - [31]), and it is used to calculate the selection criteria or RMSE for cross-validation (RMSEcv - eqn. 9, eqn. 10):
A close agreement between RMSEcv and RMSE indicates that the model is not overfitting the data and has good predictive value ([2]). The Model Efficiency (ME) represents the proportion of variability observed in the original data that is explained by the model, and it varies between 0 (without adjustment) and 1 (perfect fit; [46] - eqn. 11):
Plots of residuals versus predicted values, as well as versus dependent and independent variables, were examined for detecting bias. Statistics and the graphical analysis of residuals are essential to describe the goodness-of-fit of a model and to understand which of the systems better represents observations, and therefore as criteria for recommending a model.
Model ranking
A classical procedure of ranking m models is to assign numbers (1, 2, 3, …, m) for model comparison. In this respective model order the exact place of a model with reference to other models is not known. Poudel & Cao ([32]) proposed a method where relative ranks were developed to display the relative positions of the models. This method was used to obtain the specific and relative position of each model, where the relative rank of method i is defined as follows (eqn. 12):
where Ri is the relative rank of model i (i =1, 2, 3, …, m), Si is the goodness-of-fit statistics produced by model i, Smin is the minimum value of Si, and Smax is the maximum value of Si. Assigned numbers by respective order of the model show that the best and the worst methods have relative ranks of 1 and m. Because the magnitude (and not only the order) of the Si’s are taken into consideration, this ranking method provides more information than the common ordinal ranks.
In our study the above ranking system was applied to R2, RMSE and MAB statistics for diameter, merchantable and total volume to calculate the mean rank. The overall rank was determined by taking the mean of the ranks (MR) for these variables.
Stand density effects
The stand density variable was tested into the selected system taper equations to improve the fitting. Liu et al. ([22]) in a study on Larix gmelinii showed the viability of including ecologically parameters (as stocking degree) and improving accuracy of taper equations by random effects.
Stand density was introduced through mathematical relationship between the resulting coefficients of volume equation and the density classes. For example, Schumacher & Hall ([38]) volume model included in Fang et al. ([10]) or its modified version in Sharma & Oderwald ([39]) for a compatible system (v = a0 dbha1 Ha2), has three parameters. Parameter a0 represents the estimated asymptotic volume at a determined dbh and H. Selecting parameter a0 as expanded parameter in the model can improve the estimation and indicates that the stand density has a significant effect on dbh and H individual volume relationship. The suitable taper system with stand density variable was fitted and evaluated by the whole fit data set and cross validation.
Tab. 2 - Values of the estimated parameters for simultaneous fitting for Eucalyptus grandis and Eucalyptus dunnii. Approximated standard errors are in brackets. All parameters significant at p-value < 0.0001.
| Species | Volume system | a 0 | a 1 | a 2 | b 1 | b 2 | b 3 | b 4 | p 1 | p 2 |
|---|---|---|---|---|---|---|---|---|---|---|
| E. grandis | Fang et al. ([10]) | 0.00005 (3.34E-7) | 2.136 (0.0014) | 0.761 (0.0014) | 3.88E-6 (3.69E-8) | 0.00003 (1.03E-7) | -0.0004 (0.0002) | - | 0.027 (0.0002) | 0.946 (0.0054) |
| Kozak et al. ([18]) | - | - | - | -2.9181 (0.008) | 1.0254 (0.004) | - | - | - | - | |
| Max & Burkhart ([24]) | - | 0.694 (0.026) | 0.038 (0.0006) | -2.667 (0.111) | 1.213 (0.062) | -0.887 (0.073) | 524.4 (15.31) | - | - | |
| Sharma & Oderwald ([39]) | 0.00003 (7.58E-9) | 2.207 (0.0003) | - | - | - | - | - | - | - | |
| Fang et al. ([10]) | 0.00002 (8.64E-7) | 1.860 (0.0063) | 1.194 (0.0095) | 4.20E-6 (4.91E-8) | 0.00003 (1.55E-7) | 0.00006 (8.44E-6) | - | 0.034 (0.0004) | 0.851 (0.006) | |
| E. dunnii | Kozak et al. ([18]) | - | - | - | -2.431 (0.023) | 0.789 (0.012) | - | - | - | - |
| Max & Burkhart ([24]) | - | 0.701 (0.104) | 0.0413 (0.001) | -2.261 (0.236) | 1.002 (0.133) | -0.410 (0.146) | 503.38 (25.86) | - | - | |
| Sharma & Oderwald ([39]) | - | 2.243 (0.0004) | 0.00003 (4.67E-8) | - | - | - | - | - | - |
We adjusted model compatible system taper and volume for E. grandis and E. dunnii with stand density into parameters used in the volume compatible equations (Tab. 2). The resultant parameter prediction equation for predicting a0 can be given by (eqn. 13 to eqn. 16):
where N is the stand density, and a01 and a02 are the parameters to be estimated. Equations (13 to 16) were substituted into selected model system to examine the effect of stand density on tree taper and volume. We named this modified version of the model as “Modified system”, to differentiate it from the original (“Original system”).
Results
Model fitting and selection
Parameter shared by both the taper and volume equations estimates and their approximated standard errors for each compatible volume system are listed in Tab. 2. The goodness-of-fit statistics for both species are shown in Tab. 3. All systems were initially fitted without expanding the error term to account for autocorrelation. As expected, because of the hierarchical nature of the data, the values of the Durbin-Watson (Dw) test for all functions of both species indicated that the residual trend could be described as a function of lag1- and lag2-residuals within the same tree. The error term was, therefore, expanded as a first order and a second order autoregressive structure. The correlation trend disappears with a first-order autoregressive error structure which was sufficient to eliminate the autocorrelation in the system for both species (Tab. 3).
Tab. 3 - Goodness-of-fit statistics of compatible volume systems for Eucalyptus grandis and E. dunnii in Uruguay. (R2-adj): adjusted coefficient of determination; (RMSE): root mean squared error; (MAB): mean absolute bias; (Dw): Durbin-Watson statistic; (MR): mean rank.
| Species | System | Taper equation | Dw | Volume equation | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (cm) | R2-adj | MAB (cm) | MR | RMSE (m3) | R2-adj | MAB (m3) | Dw | MR | |||
| E. grandis | Fang et al. ([10]) | 0.790 | 0.99 | 0.610 | 2.2 | 1.000 | 0.035 | 0.99 | 0.024 | 1.99 | 1.000 |
| Kozak et al. ([18]) | 1.789 | 0.93 | 1.255 | 2.08 | 2.000 | 0.035 | 0.99 | 0.024 | 1.98 | 1.100 | |
| Max & Burkhart ([24]) | 0.840 | 0.98 | 0.620 | 2.2 | 1.002 | 0.035 | 0.99 | 0.024 | 1.98 | 1.075 | |
| Sharma & Oderwald ([39]) | 1.146 | 0.97 | 0.816 | 1.9 | 1.382 | 0.036 | 0.99 | 0.025 | 1.96 | 4.000 | |
| E. dunnii | Fang et al. ([10]) | 0.787 | 0.99 | 0.612 | 2.0 | 1.000 | 0.021 | 0.98 | 0.015 | 1.9 | 1.000 |
| Kozak et al. ([18]) | 1.802 | 0.88 | 1.352 | 2.0 | 2.000 | 0.022 | 0.97 | 0.015 | 2.09 | 1.789 | |
| Max & Burkhart ([24]) | 0.898 | 0.97 | 0.624 | 2.2 | 1.001 | 0.023 | 0.97 | 0.015 | 2.0 | 1.711 | |
| Sharma & Oderwald ([39]) | 1.042 | 0.96 | 0.800 | 1.9 | 1.253 | 0.024 | 0.97 | 0.018 | 2.1 | 4.000 | |
Considering goodness-of-fit statistics and MR, the best models were Max & Burkhart ([24]) and Fang et al. ([10]) for both species. These equations exhibited the lowest values of RMSE (<0.8 cm), MAB (<0.62 cm), and the highest R2-adj (98.8%) for E. grandis and E. dunnii.
Concerning the total stem volume, the MR suggests that the models fall into two groups separated by a large gap. Fang et al. ([10]), Max & Burkhart ([24]) and Kozak et al. ([18]) models were included into a group with lower MR for E. grandis (MR=1.1) and E. dunnii (MR=1.8). Conversely, Sharma & Oderwald ([39]) appeared to be inadequate for both species (MR=4). R2-adj, RMSE and MAB show the same trend: all models except Sharma & Oderwald ([39]) were competitive and small differences were found. The total volume variance was similar for all the models for both species. However, the Fang et al. ([10]) model had the best MR for both species and was therefore selected. Based on the best fit, 99% of the total variation in predicting upper stem diameters and total volume was explained; RMSE was lower than 1 cm and 0.035 m3 in predicting stem diameter and total volume for both species. The model had an average absolute bias less than 0.0025 m3 for volume over bark and 0.61 cm for diameters.
In addition, the Fang et al. ([10]) model allowed the inclusion of a function to estimate merchantable volume; thereby, we readjusted a system with three equations: taper, merchantable volume (integration of taper equation to any height limit), and total stem volume (integration of taper equation to total tree height). The coefficient estimates for complete system after correction for autocorrelation, their approximated standard errors, and the goodness-of-fit statistics of the taper function, merchantable stem volume and total stem volume are given in Tab. 4.
Tab. 4 - Values of the estimated parameters for simultaneous fitting of Fang et al. ([10]) model. Approximated standard errors are in brackets. Goodness-of-fit statistics for taper, total volume and merchantable volume for Eucalyptus grandis and E. dunnii in Uruguay are reported. (R2-adj): adjusted coefficient of determination; (RMSE): root mean squared error.
| Equation | Parameters | Estimates | |
|---|---|---|---|
| E. grandis | E. dunnii | ||
| - | a 0 | 0.00004 (2.4E-7) |
0.00002 (5.4E-7) |
| a 1 | 2.09 (0.001) |
1.87 (0.005) |
|
| a 2 | 0.862 (0.001) |
1.233 (0.007) |
|
| b 1 | 4.2E-06 (3.3E-5) |
4.3E-6 (4.5E-8) |
|
| b 2 | 0.00003 (5.2E-5) |
0.00003 (1.3E-7) |
|
| b 3 | 0.0002 (0.00008) |
0.00018 (0.00002) |
|
| p 1 | 0.031 (0.0002) |
0.037 (0.0004) |
|
| p 2 | 0.941 (0.011) |
0.868 (0.0033) |
|
| Taper | RMSE (cm) | 0.71 | 0.87 |
| R2-adj | 0.98 | 0.98 | |
| Total Volume | RMSE (m3) | 0.04 | 0.02 |
| R2-adj | 0.99 | 0.98 | |
| Merchantable Volume | RMSE (m3) | 0.04 | 0.03 |
| R2-adj | 0.98 | 0.97 | |
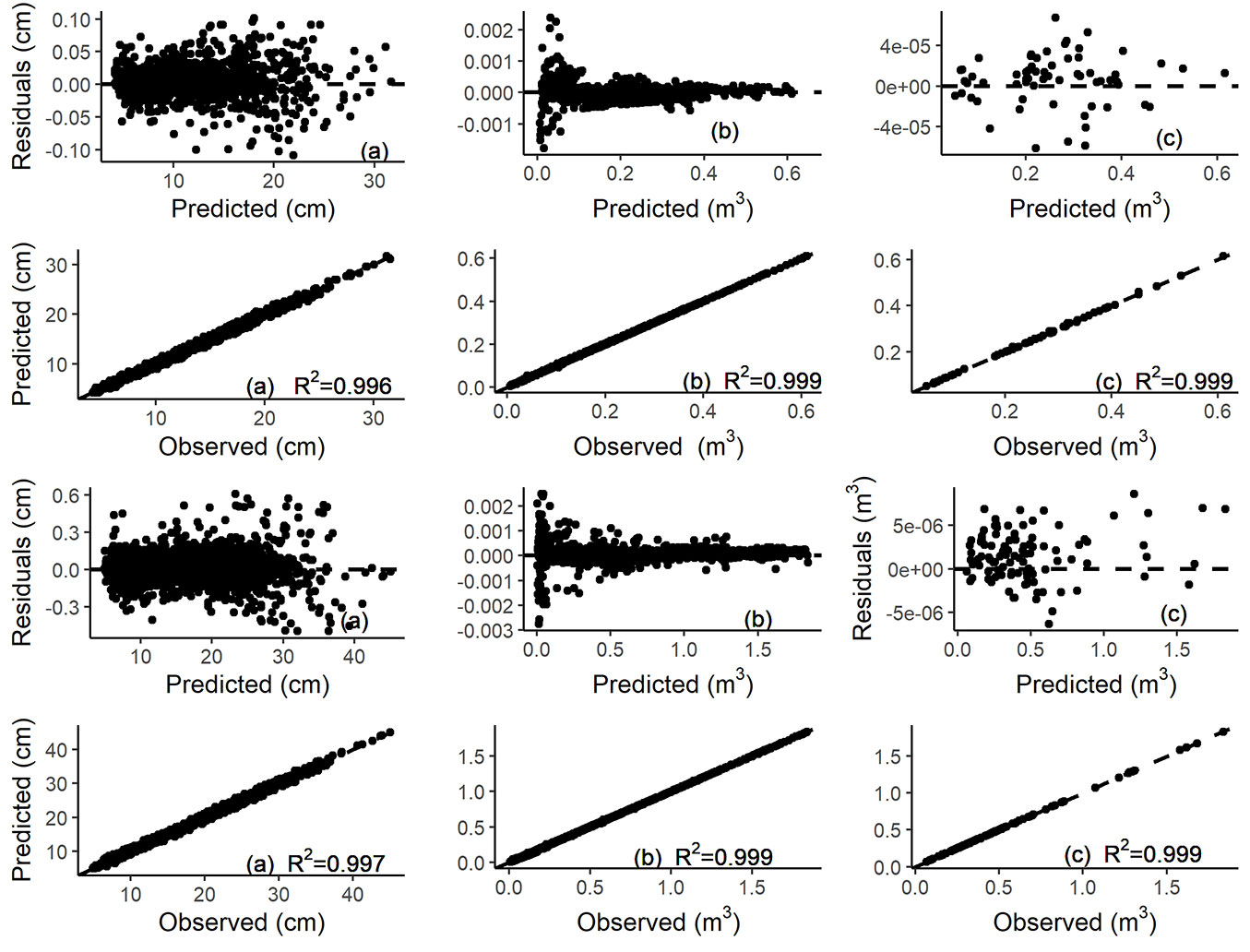
For Fang et al. ([10]) with three equation, mean average bias (MAB) were 0.610 and 0.659 cm for taper equation; 0.003 m3 and 0.016 m3 for total volume and 0.031 m3 and 0.022 m3 for merchantable volume for E. grandis and E. dunnii, respectively. Scatter plots of studentized residuals against predicted and observed values against predicted values for dub, merchantable volume and total volume are shown in Fig. 3. Residuals did not show a trend of increasing error variances, and the zero-studentized residuals cross the centre of the data points. This suggests that the taper and volume function were appropriately identified, and the error structure of the model is associated with the equal error variance. The multicollinearity was inferred by CN, 46 for E. grandis and 56 for E. dunnii.
Fig. 3 - Studentized residuals and observed values against predicted values for: (a) diameters under bark (dub, cm); (b) merchantable volume (m3); and (c) total volume (m3) obtained with the Fang et al. ([10]) model for E. dunnii (firsts row) and E. grandis (seconds row) in Uruguay. (R2): coefficient of determination.
The precision of predictions obtained by the Fang et al. ([10]) model through the LOOCV procedure was evaluated in terms of model efficiency (ME) and root mean square error (RMSEcv) of estimated diameters, merchantable volume, and total stem volume. For E. grandis, ME was 0.98, 0.98 and 0.87, and RMSEcv was 0.803 cm, 0.037 m3, 0.024 m3 for taper, total volume and merchantable volume, respectively. For E. dunnii, ME was 0.95, 0.98 and 0.87, and RMSEcv was 1.03 cm, 0.028 m3, 0.03 m3 for taper, total volume and merchantable volume, respectively. Mean average bias (MAB) values were 0.708 and 0.877 cm for taper equation, 0.026 m3 and 0.025 m3 for total volume, and 0.014 m3 and 0.019 m3 for merchantable volume for E. grandis and E. dunnii, respectively.
Model development and evaluation with density variable
When comparing the quotient between RMSEcv and RMSE of the selected model, we expected values lower or close to 1, indicating good predictive value of fitted models. For E. dunnii this was confirmed since the RMSE ratio was always lower than 1 (range: 0.80-0.88) for taper, total and merchantable volume. However, we found quotient values of 1.14 for total volume and 1.7 for merchantable volume for E. grandis, which indicates a possible overfitting.
The parameters p1 and p2 of Fang et al. ([10]) segmented model are the inflection points and marked differences between stems. To check the usefulness of an adjustment by species, the values of these parameters were compared with those obtained in a general model. These models were compared through R2-adj, RMSE and AIC values.
The calculated parameter p1 was 0.037, 0.031, 0.039, while p2 was 0.868, 0.941, 0.908 for E. dunnii, E. grandis and both species together, respectively. We obtained values of R2-adj = 0.98, 0.98, 0.96; RMSE = 0.8867 cm, 0.712 cm, 1.235 cm; ACI = 6099, 6093, 7269 for E. dunnii, E. grandis and both species together, justifying the adjustment by species.
The stand density range significantly affected the compatible system for E. grandis. The stand density in this study was 390, 453, 535, 850, 930 and 1090 tree ha-1. However, for E. dunnii there were not significant effects, probably because the study only covered a limited range of stand densities (930, 990, 1010 and 1100 tree ha-1) for this species.
Equations (13 to 16) were fitted and evaluated to the entire data set composed of different stand density by MR (calculated on R2-adj, RMSE and MAB values). Eqn. 13 obtained the first place into mean ranking (R2-adj = 0.98, 0.99, 0.99; RMSE = 0.895 cm, 0.034 m3, 0.031 m3; MAB = 0.668 cm, 0.024 m3, 0.025 m3 for taper, total and merchantable volume, respectively), followed by eqn. 14. Regarding bias, eqn. 13 had the lowest values: 0.18 cm, 0.0025 m3 and 0.021 m3.
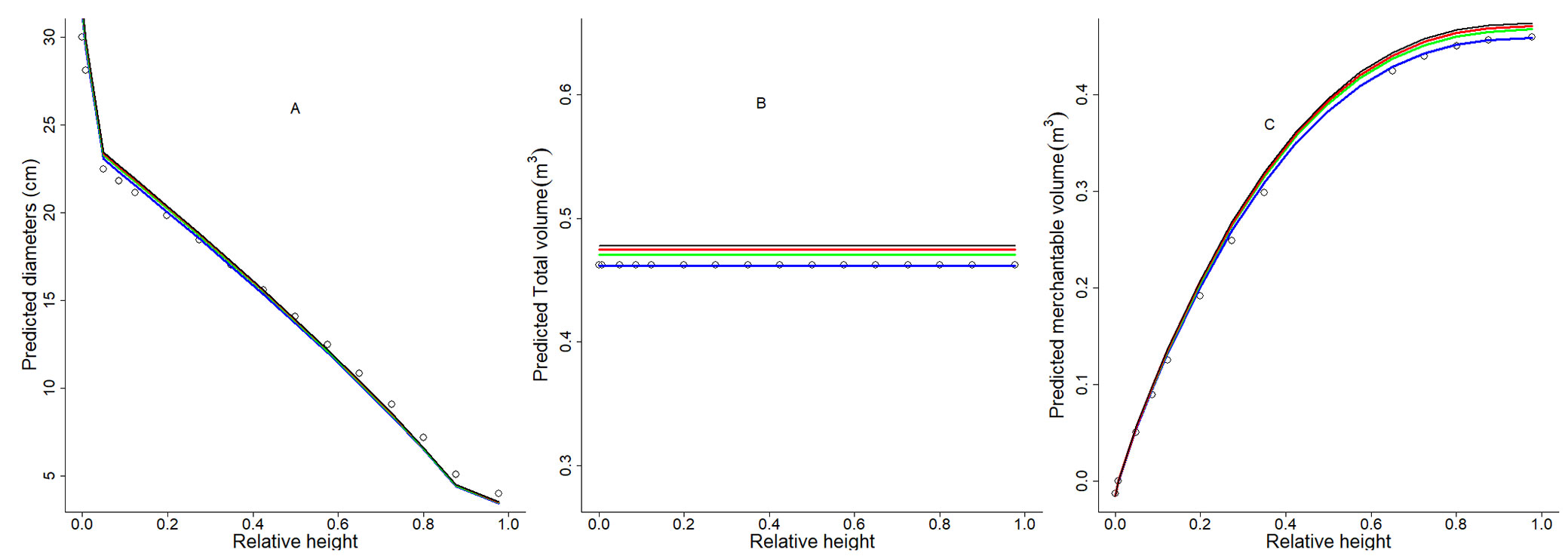
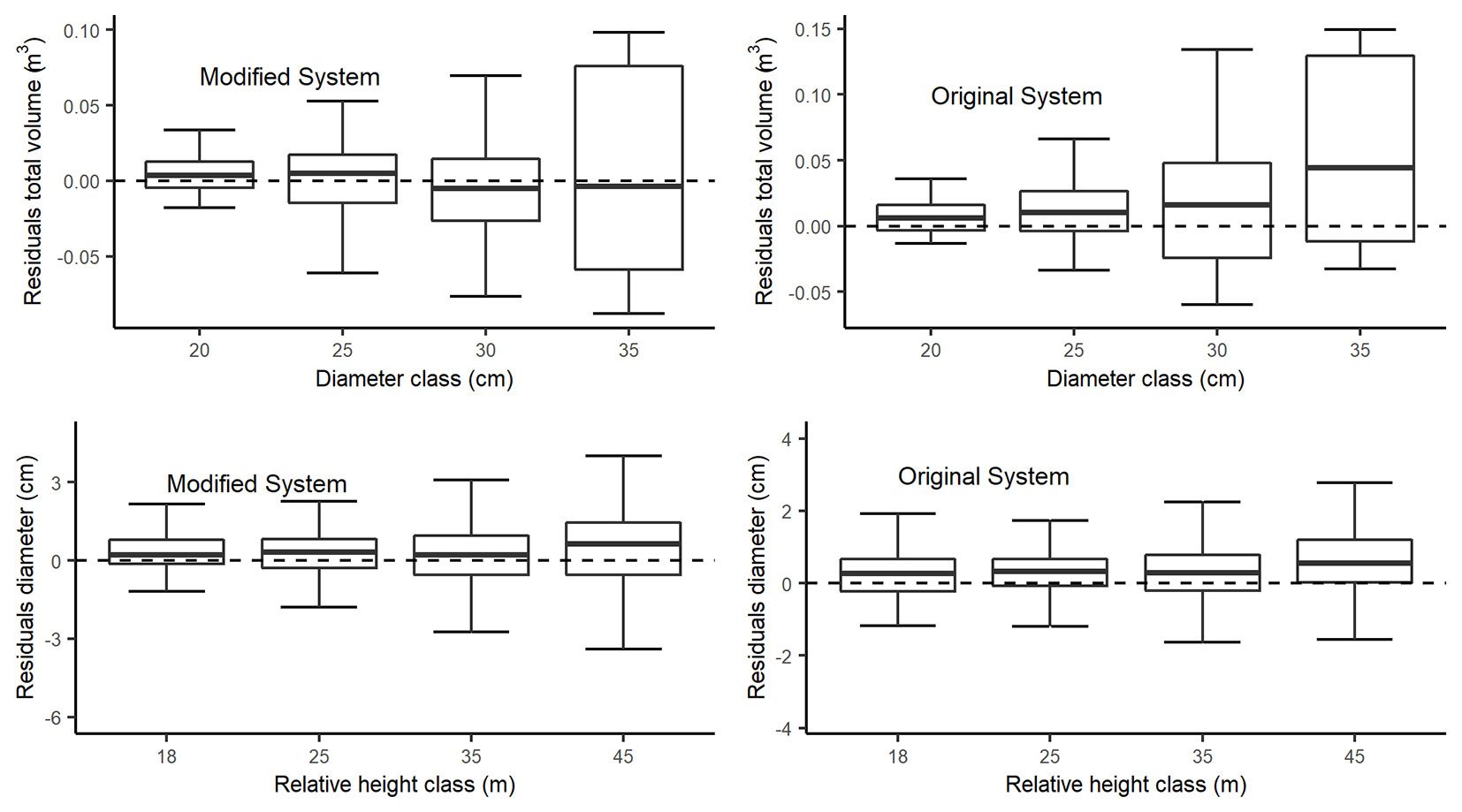
In reference to the Original system, Modified system improves in terms of R2-adj, RMSE and MAB for total and merchantable volume, while for the taper equation the goodness-of-fit was almost invariant (Tab. 5). The effect of stand density was analysed visually by generating tree profiles, total and merchantable volume using Original and Modified systems for an average tree with d = 22.7 cm and H = 26.6 m at different stand densities (Fig. 4). Box plots of residuals for both systems, Modified and Original, for total volume and diameter against relative height class and relative diameters class are reported in Fig. 5.
Tab. 5 - Values of the estimated parameters for the Modified model ([10]), approximated standard errors (Estd), and goodness-of-fit statistics for taper, total volume and merchantable volume for Eucalyptus grandis in Uruguay. (R2-adj): adjusted coefficient of determination; (RMSE): root mean squared error; (MAB): mean absolute bias.
| Equation | Parameters | Estimate | Estd | p-value |
|---|---|---|---|---|
| - | p 1 | 0.032 | 0.00026 | <0.0001 |
| p 2 | 0.942 | 0.00959 | <0.0001 | |
| a 01 | 0.000023 | 3.0E-7 | <0.0001 | |
| a 02 | 0.162 | 0.0045 | <0.0001 | |
| a 1 | 2.079 | 0.0015 | <0.0001 | |
| a 2 | 0.953 | 0.0019 | <0.0001 | |
| b 1 | 4.26E-06 | 3.4E-8 | <0.0001 | |
| b 2 | 0.000032 | 8.0E-8 | <0.0001 | |
| b 3 | 0.000401 | 1.5E-4 | 0.0086 | |
| Taper | RMSE (cm) | - | 0.795 | - |
| R2-adj | - | 0.98 | - | |
| MAB (cm) | - | 0.668 | - | |
| Total volume | RMSE (m3) | - | 0.034 | - |
| R2-adj | - | 0.99 | - | |
| MAB (cm) | - | 0.024 | - | |
| Merchantable volume | RMSE (m3) | - | 0.031 | - |
| R2-adj | - | 0.99 | - | |
| MAB (cm) | - | 0.025 | - |
Fig. 4 - Profiles (A), total volume (B) and merchantable volume (C) generated by Original (points) and Modified systems, for the average tree (d = 22.7 cm, H = 26.6 m) at different stand densities (blue line: 400 trees ha-1; green line: 850 trees ha-1; red line: 1200 trees ha-1; black line: 1600 trees ha-1) for Eucalyptus grandis in Uruguay.
Fig. 5 - Residuals boxplot of estimated total volume and estimated diameters by relative diameters classes of the Fang et al. ([10]) Original and Modified systems. The boxes represent the interquartile ranges. The maximum and minimum total volume and diameters prediction errors are represented respectively by the upper and lower whiskers.
Data for total volume was grouped into four diameter classes (20, 25, 30, and 35 cm). Original system has an overestimation trend while Modified system improved results for all classes, particularly at high diameters. For diameter data, height classes were 18, 25, 35 and 45 m, both Original and Modified system showed an overestimation for diameters in all classes. However Modified system residuals have a homogeneous distribution around zero.
Discussion
Original system model
After estimating the fit and cross-validation statistics of the four fitted models, the Fang et al. ([10]) model was selected and used in subsequent analysis. To ensure numeric consistency, a simultaneous fitting procedure based on the FIML estimation method was used. This method has been successfully used in several studies because it optimizes parameters of taper and commercial volume while it minimizes and homogenizes standard deviation. Results for the taper and volume equations fitted for both species indicated that Fang et al. ([10]) is the most precise and least biased model. This model had the first place in the model ranking. Previous research found that the modification of the Muhairwe variable exponent model was the best model to describe stem shape to E. grandis ([12]). Alternatively, Methol ([25]) adjusted the segmented model of Max & Burkhart ([24]) for both species. This model came second in our study.
The system of Fang et al. ([10]) is widely used for the description of stems form and estimated volume, and its implementation has been reported in biometric systems for a wide range of species and countries ([8], [43], [44], [14]). This model has the merits of being flexible and analytically integrable into a system providing high accurate estimates of stem volume for any stem segment. Rachid-Casnati et al. ([35]) adjusted for E. grandis the explicit model for total volume of Schumacher-Hall, and this model is integrated to the adjusted model in this study. The quality of fit in terms of ME was similar in both studies, but the RSME was slightly lower in Rachid-Casnati et al. ([35]), and the parameters values were similar, with small differences attributable to the simultaneous adjustment of the models.
Fang et al. ([10]) segmented model presents two inflection points on the relative height of the stem: p1 and p2 are the relative heights from the ground where the points are assumed by the model to occur, dividing the stem in three sections. The first inflection point (as percentage of the total height), where the neiloid changes to a paraboloid, and the second inflection point, at which the change from the paraboloid to a cone occurs. Inflection points for the selecting system occur at 3.1% and 94% for E. grandis and 3.7% and 86% for E. dunnii. The first inflection point were a very small percentage of total height in both species. These results are similar to those reported by previous studies, e.g., for E. grandis p1 was 3.6% in Ozçelik & Göçeri ([29]), al-though p2 was lower (45%) than that observed in this study. The presence of multicollinearity (correlations among variables) in the model has been examined by CN, its value for both species was in range of 30-100. This values are tolerated when models contain polynomial and cross-product terms ([3]). The equation systems of Fang et al. ([10]) showed weak multicollinearity for both Eucalyptus species, and Mora et al. ([26]) stated that multicollinearity does not seriously affect the predictive ability of the model. By comparing RSMEcv through LOOCV, and RMSE of the simultaneous adjustment, it was evidenced that the values were very close (Tab. 5), and this indicates that the model is not overfitting the data and has a good predictive performance.
Modified system model
Sharma & Parton ([41]) improved fit statistics and predictive precision by including stand density information into a variable taper equation. These studies identified tree competition as a relevant stand characteristic responsible for volume miscalculation. Liu et al. ([22]) assessed taper models and included both fixed-effects parameters, showing that age and stocking degree had significant effects on tree stem and improving the predictive taper equations. Traditional and simple volume functions do not consider the dependency of volume on competition or stem form. They generally involve dbh and H as predictors ([42]).
Including age and stand density in models, part of the site variability that affects the growing conditions of each individual tree is taken into account. This has proven to enhance predictions of the stem taper ([22]).
In our study the stand density had a statistically significant influence in volume estimation for E. grandis, while for E. dunnii the limited range of stand density compared to E. grandis could be too narrow to properly explore effects on volume.
Jacobs et al. ([16]) pointed out that the effect of competition was significant on both stem volume and stem taper in Picea abies. Sharma & Parton ([41]) reported that the difference in bole diameter between trees at lower and higher stand densities diminished increasing stand density, the density treatments only significantly affected the stem form of the smallest trees. According to Jacobs et al. ([16]), there is a lack of knowledge on how the stem form of trees with the same dbh and H is affected by the individual competition situation inside the stand. However, for the average tree no differences in stem profile were observed, while for merchantable and total volume the differences were considerable.
Results of the Original Fang et al. ([10]) model for merchantable volume showed an underestimation for densities greater than 400 tree h-1. The effect is stronger in the tree top section (0.8 to 1.0 relative height). For the total volume the trend in underestimation for all relative height classes is more evident. This means that the Original Fang et al. ([10]) model tends to underestimate the total volume regardless of the total height of the tree, while the underestimation of the merchantable volume is limited to the upper part of the tree.
Our results did not show difference in stem form by density range. Similar results were found by Ahnlund et al. ([1]) with Pinus sylvestris, where there were no significant differences in stem form for trees with dbh > 5 cm between density treatments. In a study on Eucalyptus in Congo with density range of 500-1300 tree h-1, Gomat et al. ([12]) reports that planting density had no significant influence on the stem profile. Unlike the findings of Jacobs et al. ([16]), who reports density effects in stem form, the butt logs of trees of the same size decreased in taper given increasing competition, and stem taper of the top log decreased with increasing competition, while the stem taper of the mid log increased with competition.
The inflection points for Modified system do not vary significantly compared to the Original system. These results show that a segmented model with two inflection points is appropriate to describe the stems of Eucalyptus species, and that stand density has no effects. Gomat et al. ([12]) studied factors affecting stem taper variation in Eucalyptus, reporting that the tree shape markedly changes between 1 and 2 years and is roughly stabilised afterwards. The plantations in this study had range between 7-17 years, therefore pronounced changes are not expected in the inflection points.
The overall form of the trees remains the same irrespective of the stand age and density, although slight volume differences can be observed (Fig. 5).
Results showed that stand density had an effect on volume parameters. Based on the fitting, validation statistics, and graphical analysis, the Fang et al. ([10]) system with stand density information is recommended for E. grandis. Thus, a system including stand density results in more accurate estimates for E. grandis, as stand density affects the volume and shape of stems. However, for E. dunnii, the inclusion of stand density was not significant and the variable was not included in compatible volume and taper systems.
Conclusions
The compatible volume system of Fang et al. ([10]) is the most adequate for describing the stem profile and predicting stem volume of E. dunnii and E. grandis. A modified second order continuous autoregressive error structure corrected the inherent serial autocorrelation of different observations within trees. In E. grandis, the model fit and the prediction performance of the taper and volume compatible systems were greatly improved by including stand density within the volume equation.
For E. dunnii no improvement was observed probably due to a narrow population range in the dataset. The inclusion of stand density in the model improved the efficacy of the system for E. grandis, while for E. dunnii no significant effects of stand density were found. Including stand density in taper and volume equations has practical implications, since for the same diameter and height a range of values are obtained depending on the population of the stand. This improves the characterization of stands associated to different management practices and subsequently assortment of products.
Acknowledgments
The authors thank the Instituto Nacional de Investigaciones Agropecuarias (INIA-Uruguay) for supporting fieldwork and the INIA Scholarship for PhD studies. We are particularly grateful for the support of Leonidas Carrasco Letelier, Roberto Scoz, Demian Gomez, Gonzalo Martinez, Jorge Basso (INIA) and Juan Gabriel Álvarez González (USC). We acknowledge the institutional support of the University of Cordoba - Campus de Excelencia CEIA3. We also thank the ERSAF group. We thank Dr. David Walker for his revisions of the manuscript versions, and the anonymous referees for their comments and corrections.
References
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Authors’ Info
Authors’ Affiliation
Fernando Requin
Cecilia Rachid-Casnati 0000-0002-8621-7061
National Institute of Agricultural Research (INIA) Tacuarembó, Ruta 5 km 386, Tacuarembó (Uruguay)
Department of Forestry Engineering, Laboratory of Silviculture, Dendrochronology and Climate Change, DendrodatLab- ERSAF, University of Cordoba, Campus de Rabanales, Crta. IV, km. 396, E-14071 Córdoba (Spain)
Senckenberg Biodiversity and Climate Research Centre (SBiK-F), Senckenberganlage 25, D-60325 Frankfurt am Main (Germany)
University of the Republic, Faculty of Agronomy, Paysandú (Uruguay)
Corresponding author
Paper Info
Citation
Hirigoyen A, Navarro-Cerrillo R, Bagnara M, Franco J, Requin F, Rachid-Casnati C (2021). Modelling taper and stem volume considering stand density in Eucalyptus grandis and Eucalyptus dunnii. iForest 14: 127-136. - doi: 10.3832/ifor3604-014
Academic Editor
Angelo Rita
Paper history
Received: Jul 31, 2020
Accepted: Jan 15, 2021
First online: Mar 16, 2021
Publication Date: Apr 30, 2021
Publication Time: 2.00 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2021
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 39013
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 31243
Abstract Page Views: 3427
PDF Downloads: 3678
Citation/Reference Downloads: 2
XML Downloads: 663
Web Metrics
Days since publication: 1783
Overall contacts: 39013
Avg. contacts per week: 153.16
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2021): 8
Average cites per year: 1.60
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Compatible taper-volume models of Quercus variabilis Blume forests in north China
vol. 10, pp. 567-575 (online: 08 May 2017)
Research Articles
Analyzing regression models and multi-layer artificial neural network models for estimating taper and tree volume in Crimean pine forests
vol. 17, pp. 36-44 (online: 28 February 2024)
Research Articles
Modeling compatible taper and stem volume of pure Scots pine stands in Northeastern Turkey
vol. 16, pp. 38-46 (online: 22 January 2023)
Research Articles
Comparative analysis of taper models for Pinus nigra Arn. using terrestrial laser scanner acquired data
vol. 17, pp. 203-212 (online: 22 July 2024)
Research Articles
Nonlinear mixed model approaches to estimating merchantable bole volume for Pinus occidentalis
vol. 5, pp. 247-254 (online: 24 October 2012)
Review Papers
Should the silviculture of Aleppo pine (Pinus halepensis Mill.) stands in northern Africa be oriented towards wood or seed and cone production? Diagnosis and current potentiality
vol. 12, pp. 297-305 (online: 27 May 2019)
Research Articles
Tree-oriented silviculture: a new approach for coppice stands
vol. 9, pp. 791-800 (online: 04 August 2016)
Research Articles
Effects of thinning and pruning on stem and crown characteristics of radiata pine (Pinus radiata D. Don)
vol. 10, pp. 383-390 (online: 16 March 2017)
Commentaries & Perspectives
Benefits of a strategic national forest inventory to science and society: the USDA Forest Service Forest Inventory and Analysis program
vol. 1, pp. 81-85 (online: 28 February 2008)
Research Articles
Integrating area-based and individual tree detection approaches for estimating tree volume in plantation inventory using aerial image and airborne laser scanning data
vol. 10, pp. 296-302 (online: 15 December 2016)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword