Dimensionless numbers for the net present value and the perpetual value of sustainable timber harvests from a monospecific uneven-aged forest
iForest - Biogeosciences and Forestry, Volume 12, Issue 1, Pages 35-42 (2019)
doi: https://doi.org/10.3832/ifor2715-011
Published: Jan 10, 2019 - Copyright © 2019 SISEF
Research Articles
Abstract
This paper proposes a simple and direct method to provide reliable approximations of the net present value (NPV) and the perpetual value (PV) of sustainable timber harvests from a monospecific uneven-aged forest based on dimensionless numbers. In addition, two new dimensionless numbers ρNPV and ρPV are introduced. These use the NPV or PV derived from the sale of timber throughout a harvest cycle, plus the final stocking value (as numerator), and the fair value of standing timber under IAS 41 (as denominator). They can be interpreted as economic performance indicators for forest management, inspired by the return on assets accounting concept, showing how profitable the forest is, relative to its total value, with sustainability and stability criteria. Those approximations to the variables NPV, PV, ρNPV and ρPV, were obtained under conditions of stable equilibrium from a matrix model. In order to exemplify and test the results, the model used data from uneven-aged managed Pinus nigra stands, considering three levels of tree diameter growth, six levels of basal area and 33 levels of recruitment, creating a total of 594 planning scenarios. Furthermore, the study revealed the existence of strong linear correlations between those variables and a dimensionless number.
Keywords
Dimensionless Numbers, NPV/PV, Equilibrium, Sustainable Harvesting, Matrix Model, IAS 41
Introduction
By applying conditions of stable equilibrium from a matrix model, a recent study ([15]) found dimensionless numbers λ0, š‚ and š′ to provide reliable approximations of, respectively, the population growth rate, λ0, the “sustainable/stable” harvest rate, s, where (eqn. 1):
and the proportion of trees that has to remain unharvested in order to retain the stable diameter distribution, s′ (where s′ = 1/λ0 = 1-s), of a forest stand, by means of the following expressions (eqn. 2, eqn. 3, eqn. 4):
where R is the global amount of recruitment, G the stand basal area, pi the transition probabilities between adjacent diameter classes, and n and w, respectively, the number and width of the diameter classes, as detailed below (the use of the circumflex above a variable here denotes a new object that represents an approximation to that variable, as defined in eqn. 2, eqn. 3 and eqn. 4).
Dimensionless numbers are numbers that represent a property of a system, but do not have physical units, such as length, area, mass or time, associated with them. Where such numbers exist for a specific system, they allow conclusions about the behaviour of the system to be extracted, without the need for a more detailed formulation relating all the different variables involved in the problem at hand. Hence, their importance and wide use in many fields, such as mathematics, physics, biology, engineering, and economics ([27]).
In financial sciences in general, indicators to quantify financial return have been widely applied, using the internal rate of return (IRR) and the return on assets (ROA - [1]). The IRR is defined as the discount rate that makes the net present value (NPV) equal to zero, and the ROA is expressed as the quotient between profit and the sum of invested capital. Attempts to derive similar return indicators for forests are discussed in detail in Knoke ([11]). Mills & Hoover ([20]) calculated the annual change in the market value of standing timber stock and land, divided by the market value of timber and land at the beginning of the year, to obtain an indicator for US timberland. Weber ([33]) computed a similar index for German tree species in order to define an indicator for “forest performance”, and Hyytiäinen & Penttinen ([9]) applied the same perspective in their analyses of forest assets in Finland.
In this context, the main aim of this study was to investigate whether there were relationships between those dimensionless numbers (in particular, eqn. 3) and the NPV and PV of sustainable timber harvests from a monospecific uneven-aged forest. In addition, we have introduced two new dimensionless numbers, ρNPV and ρPV, using the NPV or PV derived from the sale of timber throughout a harvest cycle, plus the final stocking value (as numerator), and the fair value of the standing timber under IAS 41 ([10]) as denominator. These can be interpreted as economic performance indicators for forest management, inspired by the ROA accounting concept, showing how profitable the forest is, relative to its total value, with sustainability and stability criteria. Moreover, we demonstrated that there are strong linear correlations between those numbers and š; to that end, it will be used the matrix model applied to uneven-aged managed Pinus nigra stands by López et al. ( [16], [17], [18]), which accurately describes the stand dynamics.
Matrix models, introduced by Leslie ([13]) and modified by Lefkovitch ([12]) by grouping organisms in terms of stage categories rather than age categories, have been applied to almost all the subject areas of forestry ([30], [3], [31], [14]). In forest management, matrix models have been applied, for example, to evaluate economic outcomes ([2], [5]) and ecological impacts ([32], [34]), or to optimise silviculture in mixed uneven-aged forests to increase the recruitment of browse-sensitive tree species without intervening in the ungulate population ([4]). A matrix population model works in discrete time, projecting a population from time t to t + 1 using a transition matrix (1 here represents the time step or projection interval). It is defined by the finite difference linear system of equations X(t+1) = AX(t), where X(t) and X(t+1) are column vectors containing the number of stems ha-1 within each diameter class at time t and t+1, respectively, and A is the transition matrix. In these models, the population growth rate (i.e., the temporal rate of exponential change of the population number of individuals in the long term) is the dominant eigenvalue, λ0 of A, and the equilibrium position (stable diameter distribution in this study) is determined by the right eigenvector, W0, corresponding to λ0. By asymptotic analysis (long term behaviour), we know that, independent of the initial conditions, when λ0 > 1, the total number of stems ha-1 of the tree population increases exponentially over time (unless harvests are conducted); when λ0 < 1 the population decays until extinction; and when λ0 = 1, a stable distribution proportional to W0 is obtained. Gotelli ([6]) referred to the special case of the stable distribution when λ0 = 1 as the “stationary distribution”; we considered the same case in reference to the stable diameter distribution of the stand W0.
Materials and methods
Stand population dynamics model
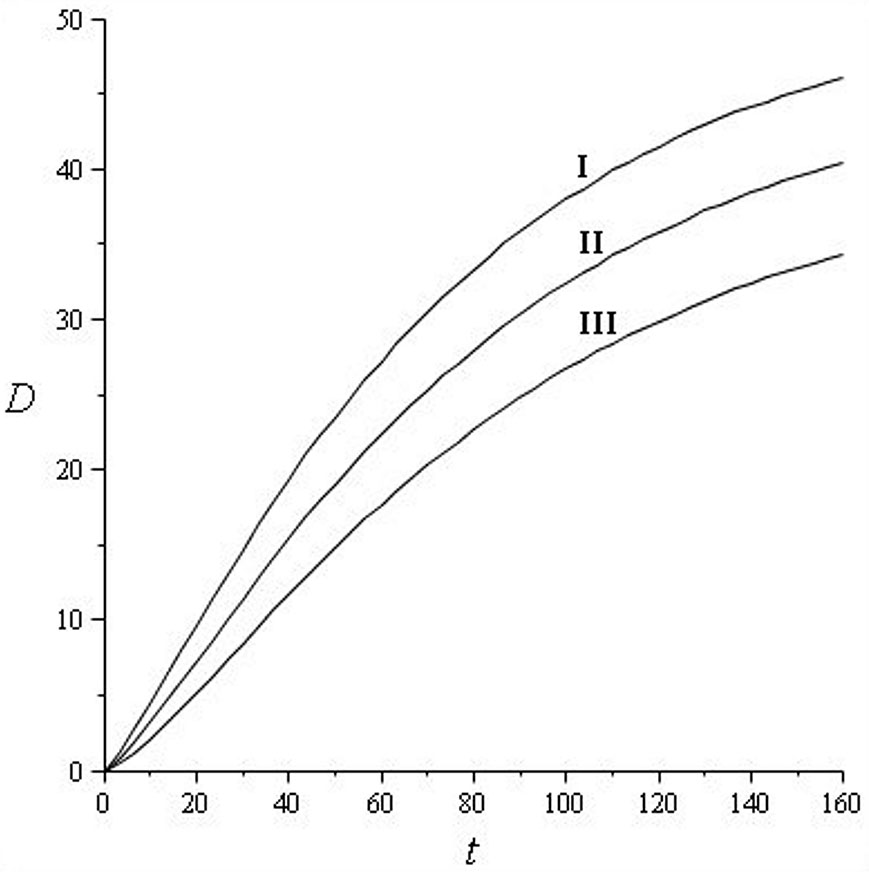
The matrix model uses the transition probabilities obtained in López et al. ([16], [17]) for uneven-aged managed Pinus nigra stands, considering three levels of tree diameter growth (Quality I, faster; Quality II, medium; and Quality III, slower diameter growth - Tab. 1, Fig. 1). The stands are located in the Spanish Iberian System, a mountain range extending about 400 km along the north-eastern edge of the central plateau, concentrating 60% of the area occupied by Pinus nigra in Spain ([7]). Based on data from those stands, the model simulates outcomes for 594 different forest management planning scenarios: three diameter growth levels (Qualities I-III) × six basal area levels (G = 21 to G = 26 m2 ha-1) × 33 recruitment levels (R = 200 to R = 840 stems ha-1). Group selection cutting was the silvicultural system used because Pinus nigra is not a shade-tolerant species, and the gaps opened in the canopy through single-tree selection cutting would not be large enough to ensure regeneration.
Tab. 1 - Transition probabilities between diameter classes for each quality. (n): number of diameter classes; (w): width of the diameter classes (= 6 cm).
| n | Quality I | Quality II | Quality III |
|---|---|---|---|
| 9 | 8 | 7 | |
| (0, 6] → (6, 12] | p1 = 0.7697 | p1 = 0.5951 | p1 = 0.4564 |
| (6, 12] → (12, 18] | p2 = 0.8602 | p2 = 0.6824 | p2 = 0.5326 |
| (12, 18] → (18, 24] | p3 = 0.7913 | p3 = 0.6200 | p3 = 0.4697 |
| (18, 24] → (24, 30] | p4 = 0.6828 | p4 = 0.5190 | p4 = 0.3692 |
| (24, 30] → (30, 36] | p5 = 0.5533 | p5 = 0.3971 | p5 = 0.2475 |
| (30, 36] → (36, 42] | p6 = 0.4106 | p6 = 0.2618 | p6 = 0.1119 |
| (36, 42] → (42, 48] | p7 = 0.2587 | p7 = 0.1171 | - |
| (42, 48] → (48,→) | p8 = 0.1000 | - | - |
| ∏ pk | 0.002104 | 0.001590 | 0.001168 |
Fig. 1 - Diameter growth models. I: site index 20, D = 51.68(1 - e-0.015259t)1.255111; II: site index 17, D = 46.645633(1 - e-0.014318t)1.337062; and III: site index 14, D = 40.644134(1 - e-0.013838t)1.456382. (D): dbh in cm; (t): time in years. The coefficient of determination was always greater than 0.999.
Since the harvesting operations in the study area generally took place every 10 years, this was the time step adopted in the model. Considering this time step, trees were grouped into n diameter classes of equal width, w = 6 cm: (0, 6), (6, 12), (12, 18), …, (30, 36), …, with the last class being (48,→; more than 48 cm) for Quality I, (42,→; more than 42 cm) for Quality II and (36,→; more than 36 cm) for Quality III. Therefore, an individual tree in class k could remain in class k or progress to class k+1 during the projection interval (t, t+1). The number of trees in each class changed in each projection interval, because some were harvested, some remained in the same diameter class and others grew past the boundary to the next diameter class. In such conditions, pk is the probability that an individual tree in class k at time t (initial) will appear in class k+1 at time t+1 (final time of projection); the recruitment coefficient, rk, is the number of offspring (stems ha-1) living at time t+1 produced in the interval of projection (t, t+1) by an average tree in class k at time t (similar to many standard size classified matrix models, r1 = 0 - [3]); hk(t) defines the proportion of harvested trees in class k, natural mortality included; xk(t) and xk(t+1) describe the stem densities in class k at the initial and final times of projection. Finally, R = r2 x2 + r3 x3 + … + rn xn denotes the global amount of recruitment at each time step, defined as the total number of trees entering into the first diameter class from t to t+1, generally above a certain threshold diameter. Notice that 0 < pk < 1 for k = 1, 2, …, n-1; rk ≥ 0 for k = 2, 3, …, n, with R = 0, if and only if rk = 0 for all k; and xk > 0 for k = 1, 2, …, n.
By analysing the dynamics of the projections, we found that the model is described accurately by the matrix model (eqn. 5):
where (eqn. 6):
I is the identity matrix of order n, H(t) = diag[h1(t), h2(t), …, hn(t)] is a diagonal matrix with the harvest rates hk(t), including natural mortalities, and X(t) and X(t + 1) are column vectors indicating the stem densities at the initial and final times of projection, respectively.
Sustainable/stable harvesting strategy and stable diameter distribution
The “sustainable/stable” harvesting strategy is aimed at reaching the stable diameter distribution of the stand for each harvest, yielding the harvest rate, s, shown in eqn. 1 for all the diameter classes and time steps; the population growth rate, λ0, is the dominant eigenvalue of the transition matrix without harvests (i.e., matrix A), and s also includes the natural mortalities. This is a sustainable harvesting strategy too (in the sense of population persistence over time) because s corresponds to the case in which the right eigenvector associated with the dominant eigenvalue equal to 1 of the transition matrix with harvests, i.e., matrix A(I-H), is W0.
On the other hand, the equilibrium is defined by the stable diameter distribution of the stand W0, which is simultaneously the right eigenvector of the matrices A and A(I-H) corresponding, respectively, to the dominant eigenvalues λ0 and 1. Thus the components of the stable diameter distribution of the stand N1, N2, …, Nn (stems ha-1) were obtained by solving the linear system AW0 = λ0 W0, yielding (proportional to) the vector W0 = (N1, N2, N3, …, Nn-1, Nn), where (eqn. 7):
for 1< i < n-1, and (eqn. 8):
NPV function
Considering that the main aim for the stands in the study area is the production of timber, the objective function is the NPV of all management operations over a planning horizon of T years, discounted to the beginning of the period, that is (eqn. 9):
where vk(t) is the stumpage value that corresponds to class k at year t (€ stem-1) and i is the discount rate ([17], [18]). The first summation represents the income derived from the sale of timber, and the second is the final stocking value. Harvesting costs are not considered because it is assumed that harvesting operations are not paid for the owner, but for the buyer of the stumpage. The costs for the owner of the land are the opportunity cost of invested capital and the opportunity cost of land. None of them are explicit costs, but they are incorporated into the NPV function. It is well known that the NPV is a justifiable management objective for a single economic goal ([26]).
The corresponding function of that management regime maintained in perpetuity is given by (eqn. 10):
In the case of the equilibrium defined by the “sustainable/stable” harvesting strategy, since hk(t) = s, xk(t) = Nk, for k = 1, 2, …, n and t = 0, 10, 20, …, the above equations become (eqn. 11, eqn. 12):
Since the stumpage prices of Pinus nigra in Spain remain fairly stable through time ([19]), simplifying eqn. 11 and eqn. 12 we obtain (eqn. 13, eqn. 14):
where ∑ Nk vk represents the fair value of standing timber under IAS 41 ([10]). By dividing eqn. 13 and eqn. 14 by this value, we obtain (eqn. 15, eqn. 16):
which means that, for previously defined values of i and T, there is a positive linear correlation between the NPV weighted by the fair value of standing timber, ∑ Nk vk, that is ρNPV, and s (resp. between the PV weighted by ∑ Nk vk, that is ρPV, and s). Note that ρNPV and ρPV are dimensionless numbers. Furthermore, given that there is a strong positive linear correlation between s and š‚ ([15]), it is expected that, for previously defined values of i and T, there must be a strong positive linear correlation between these variables ρNPV and ρPV, and š, as we demonstrate below.
Stumpage value model
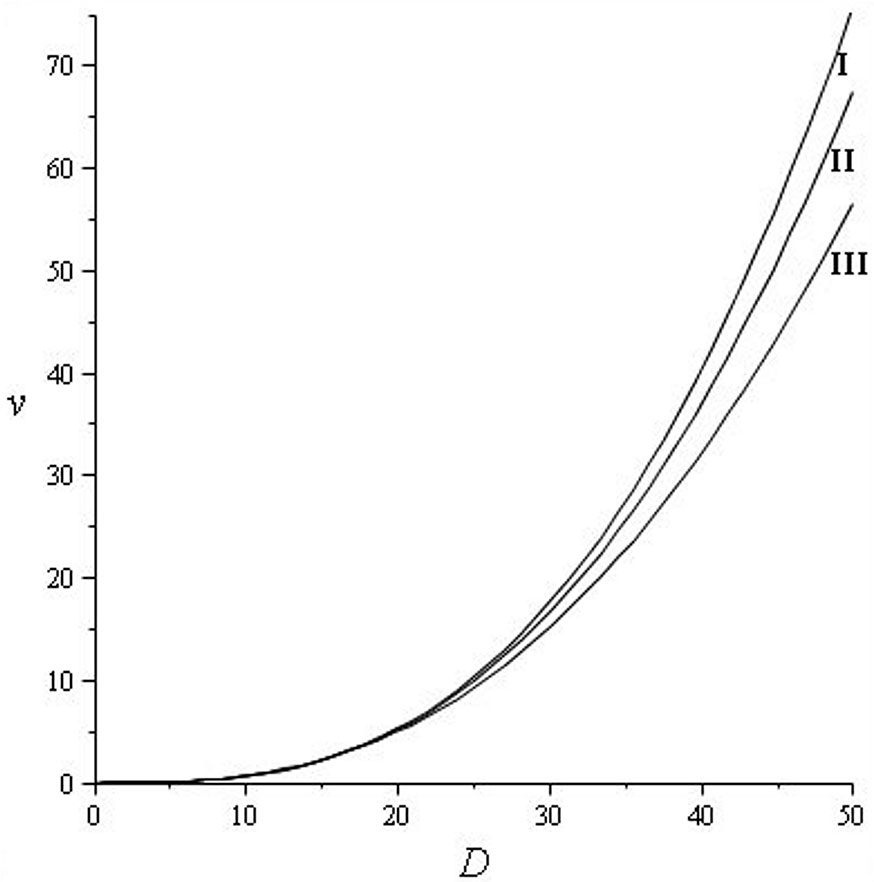
The stumpage value model applied in this study comes from López et al. ([17], [18]). In Tab. 2, we provide the stumpage values we used to obtain the economic data ([22], [29]). The regression models adjusted to these data appear in Fig. 2. The stumpage prices of Pinus nigra in Spain remained fairly stable between 1994 and 2011 ([19]).
Tab. 2 - Stumpage prices (€ m-3) of Pinus nigra in Spain according to diameter class and industrial destination.
| Products | Diameter classes (cm) | ||
|---|---|---|---|
| <20 | 20-40 | >40 | |
| Particle | 6 | 1.2 | 0.6 |
| Poles | 0 | 11.85 | 0 |
| Sawlog | 0 | 9.8 | 11.76 |
| High-quality sawlog | 0 | 0 | 9.96 |
| Total average price | 6 | 22.85 | 22.32 |
Fig. 2 - Stumpage value models: Quality I: v = D3.186471 exp(-7.704952 - 8.678687 · 10-3 D); Quality II: v = D3.114196 exp(-7.476506 - 9.903125 · 10-3 D); and Quality III: v = D2.987053 exp(-7.110977 - 1.078752 · 10-2D); stumpage values (v) in € stem-1 and diameter (D) in cm. The coefficient of determination was always greater than 0.9999.
The last row in Tab. 2 shows the average price per cubic metre for trees belonging to the different diameter classes. This price was obtained by adding up the four rows above in Tab. 2 that show the contributions to the final value of a tree for the four industrial destinations according to the percentage of wood of each diameter class going into each product type. The prices of particle board, poles, sawlogs, and high-quality sawlogs were 6.0, 39.5, 19.6 and 33.2 € m-3, respectively. It is necessary to point out that the demand for timber poles in Spain is very high, and therefore they reach a higher price than larger-sized sawlogs.
Results
By substituting transition probabilities pi, recruitment R, basal area G, together with w and n into the eqn. 3, we obtained š, as summarised in Tab. 3, for selected scenarios.
Tab. 3 - Numerical values of s and š (as defined in eqn. 4) for Qualities I, II and III.
| Quality | G (m2 ha-1) |
Variable | R = 200 stem ha-1 |
R = 520 stem ha-1 |
R = 840 stem ha-1 |
|---|---|---|---|---|---|
| Q I | 22 | s | 0.233770 | 0.323259 | 0.372742 |
| š | 0.350669 | 0.375210 | 0.387782 | ||
| 24 | s | 0.226305 | 0.314580 | 0.363570 | |
| š | 0.348471 | 0.372946 | 0.385489 | ||
| 26 | s | 0.219546 | 0.306683 | 0.355205 | |
| š | 0.346454 | 0.370868 | 0.383384 | ||
| Q II | 22 | s | 0.207665 | 0.292049 | 0.339704 |
| š | 0.318779 | 0.345258 | 0.358932 | ||
| 24 | s | 0.200729 | 0.283764 | 0.330816 | |
| š | 0.316422 | 0.342804 | 0.356433 | ||
| 26 | s | 0.194462 | 0.276245 | 0.322732 | |
| š | 0.314262 | 0.340553 | 0.354142 | ||
| Q III | 22 | s | 0.180733 | 0.259707 | 0.305332 |
| š | 0.278309 | 0.306537 | 0.321290 | ||
| 24 | s | 0.174348 | 0.251850 | 0.296767 | |
| š | 0.275820 | 0.303901 | 0.318585 | ||
| 26 | s | 0.168593 | 0.244738 | 0.288999 | |
| š | 0.273542 | 0.301487 | 0.316108 |
On the other hand, by applying eqn. 7 and eqn. 8, we obtained the components Nk of the stable diameter distributions W0 of the stand, as summarized in Tab. 4 for some scenarios. The λ0 values were obtained for each scenario under conditions of stable equilibrium from eqn. 5, using the transition matrix without harvests, and the s values came from eqn. 1.
Tab. 4 - Stable diameter distributions (W0). Components in stem ha-1, as defined in eqn. 7 and eqn. 8.
| Quality | G (m2 ha-1) |
R = 200 stem ha-1 | R = 840 stem ha-1 |
|---|---|---|---|
| Q I | 22 | [186.1, 122.9, 96.4, 77.2, 61.4, 47.5, 34.6, 22.1, 7.2] | [615.9, 325.9, 202.3, 125.4, 74.6, 41.1, 19.8, 7.4, 1.2] |
| 24 | [188.3, 125.7, 99.8, 81.0, 65.4, 51.4, 38.3, 25.3, 8.6] | [626.4, 336.8, 212.6, 134.2, 81.5, 45.9, 22.7, 8.8, 1.5] | |
| 26 | [190.3, 128.3, 102.9, 84.5, 69.1, 55.3, 42.0, 28.5, 10.1] | [636.1, 347.0, 222.4, 142.6, 88.2, 50.8, 25.7, 10.2, 1.9] | |
| Q II | 22 | [233.3, 147.0, 113.7, 90.3, 71.1, 53.9, 37.2, 16.6] | [757.0, 376.4, 226.4, 135.8, 77.3, 39.6, 16.4, 3.7] |
| 24 | [236.3, 150.7, 118.0, 95.0, 76.1, 58.9, 41.9, 19.5] | [771.0, 389.9, 238.8, 146.1, 85.0, 44.7, 19.1, 4.5] | |
| 26 | [239.1, 154.0, 122.0, 99.5, 80.9, 63.8, 46.6, 22.6] | [783.9, 402.5, 250.5, 156.0, 92.7, 49.8, 22.0, 5.4] | |
| Q III | 22 | [295.4, 179.0, 138.1, 110.0, 86.7, 64.6, 32.8] | [937.6, 440.2, 257.8, 149.7, 80.5, 36.1, 9.2] |
| 24 | [299.6, 183.8, 143.8, 116.4, 93.7, 71.8, 38.0] | [956.3, 457.2, 273.0, 162.1, 89.4, 41.4, 11.0] | |
| 26 | [303.4, 188.3, 149.1, 122.5, 100.4, 79.0, 43.6] | [973.6, 473.1, 287.6, 174.1, 98.3, 46.9, 12.9] |
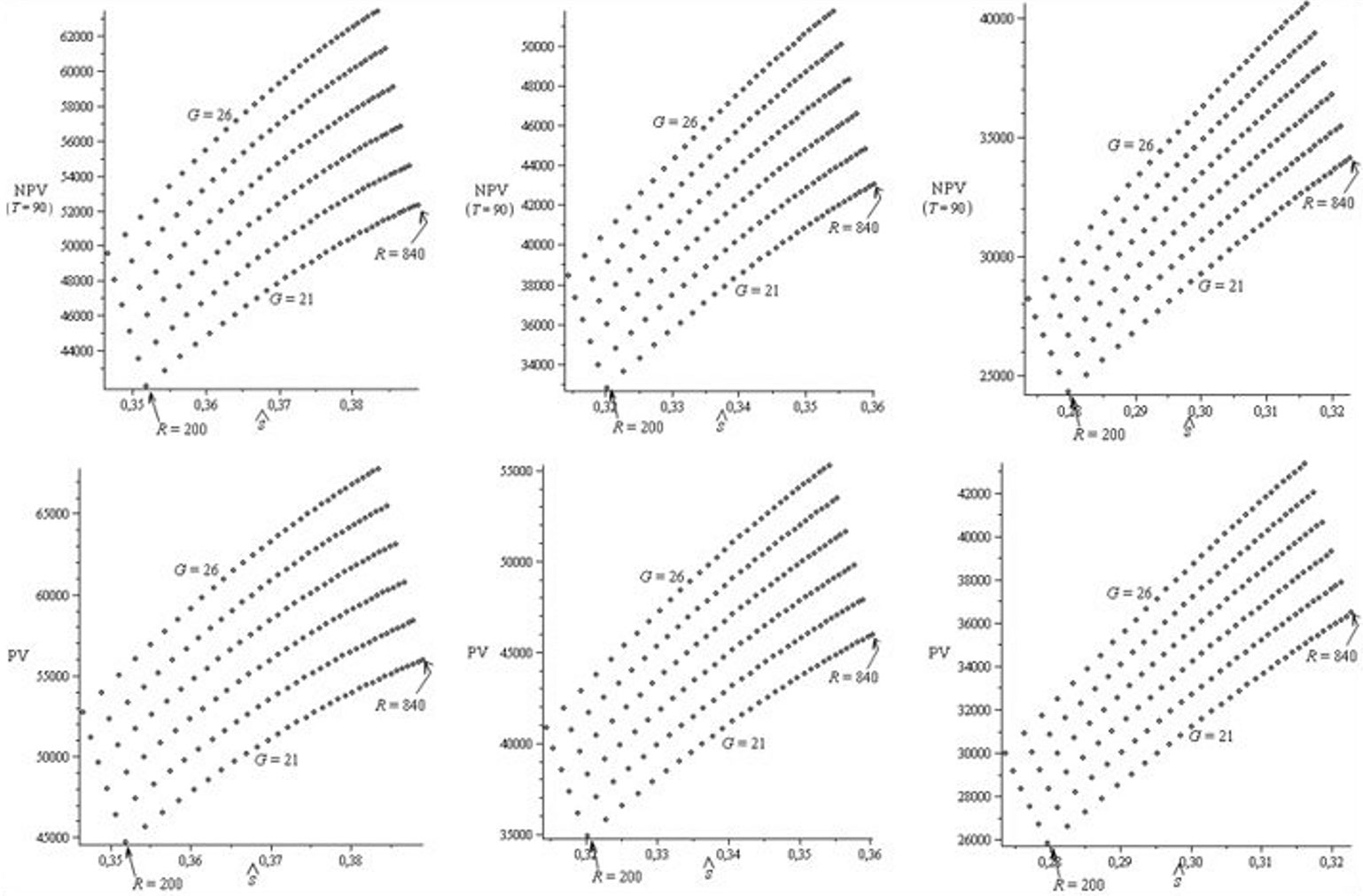
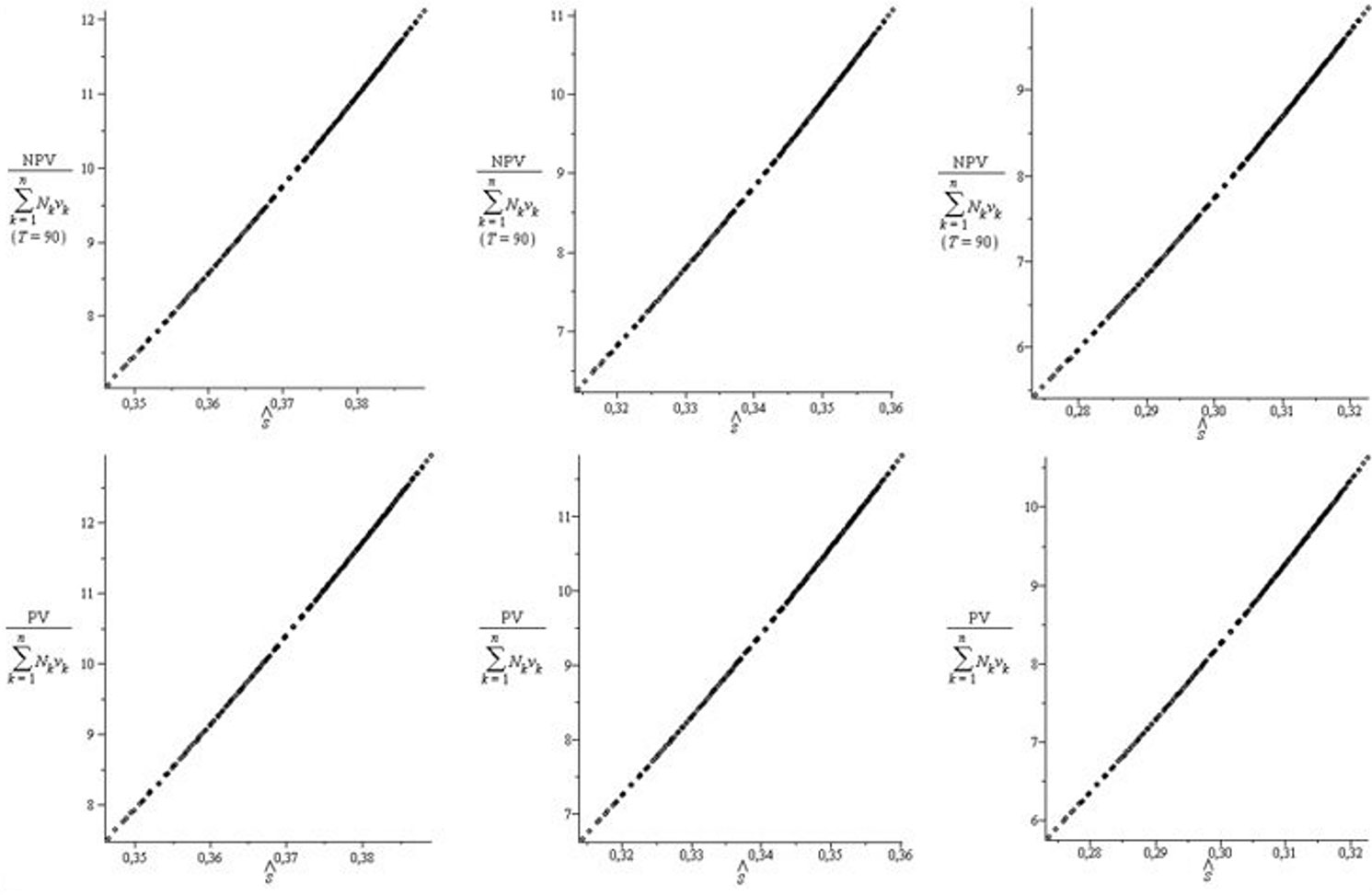
On the basis of the above data, by substituting Nk, s, š, i, T and vk into eqn. 13 to eqn. 16, we obtained NPV, PV, ρNPV and ρPV, as summarised in Tab. 5 and Tab. 6, for i = 3%, T = 90 years and several scenarios. Additionally, Fig. 3 and Fig. 4 depict the points (š, NPV) for T = 90, (š, PV), (š, ρNPV) for T = 90, and (š, ρPV), respectively (198 points for each case).
Tab. 5 - NPV (for T = 90 years) and PV values (€ ha-1) for the “sustainable/stable” harvesting strategies for i = 3% and Qualities I, II and III.
| Quality | G (m2 ha-1) | Param | R = 200 stem ha-1 | R = 520 stem ha-1 | R = 840 stem ha-1 |
|---|---|---|---|---|---|
| Q I | 22 | NPV | 5319.159 | 6191.831 | 6500.993 |
| PV | 5284.168 | 6283.379 | 6646.680 | ||
| 24 | NPV | 5701.675 | 6682.311 | 7038.929 | |
| PV | 5649.995 | 6770.617 | 7187.771 | ||
| 26 | NPV | 6074.394 | 7163.932 | 7569.088 | |
| PV | 6004.851 | 7247.846 | 7720.004 | ||
| Q II | 22 | NPV | 4185.287 | 5021.953 | 5359.973 |
| PV | 4118.386 | 5065.793 | 5454.054 | ||
| 24 | NPV | 4474.700 | 5404.061 | 5785.948 | |
| PV | 4390.309 | 5441.416 | 5879.039 | ||
| 26 | NPV | 4756.044 | 5778.243 | 6204.543 | |
| PV | 4653.231 | 5808.146 | 6295.701 | ||
| Q III | 22 | NPV | 3131.227 | 3909.704 | 4264.179 |
| PV | 3042.728 | 3913.709 | 4313.000 | ||
| 24 | NPV | 3336.493 | 4191.150 | 4584.694 | |
| PV | 3230.809 | 4186.435 | 4629.266 | ||
| 26 | NPV | 3535.449 | 4465.779 | 4898.460 | |
| PV | 3411.887 | 4451.574 | 4938.000 |
Tab. 6 - ρNPV (for T = 90 years) and ρPV dimensionless numbers for the “sustainable/stable” harvesting strategies for i = 3% and Qualities I, II and III.
| Quality | G (m2 ha-1) | Param | R = 200 stem ha-1 | R = 520 stem ha-1 | R = 840 stem ha-1 |
|---|---|---|---|---|---|
| Q I | 22 | ρ NPV | 0.9195 | 1.2448 | 1.4246 |
| ρ PV | 0.9135 | 1.2632 | 1.4566 | ||
| 24 | ρ NPV | 0.8924 | 1.2132 | 1.3913 | |
| ρ PV | 0.8843 | 1.2293 | 1.4207 | ||
| 26 | ρ NPV | 0.8679 | 1.1845 | 1.3609 | |
| ρ PV | 0.8579 | 1.1984 | 1.3880 | ||
| Q II | 22 | ρ NPV | 0.8247 | 1.1314 | 1.3046 |
| ρ PV | 0.8115 | 1.1412 | 1.3275 | ||
| 24 | ρ NPV | 0.7995 | 1.1012 | 1.2723 | |
| ρ PV | 0.7844 | 1.1089 | 1.2927 | ||
| 26 | ρ NPV | 0.7767 | 1.0739 | 1.2429 | |
| ρ PV | 0.7599 | 1.0795 | 1.2611 | ||
| Q III | 22 | ρ NPV | 0.7268 | 1.0138 | 1.1796 |
| ρ PV | 0.7062 | 1.0149 | 1.1931 | ||
| 24 | ρ NPV | 0.7036 | 0.9853 | 1.1485 | |
| ρ PV | 0.6813 | 0.9841 | 1.1597 | ||
| 26 | ρ NPV | 0.6827 | 0.9594 | 1.1203 | |
| ρ PV | 0.6588 | 0.9564 | 1.1293 |
Fig. 3 - First row: set of points (š, NPV) for T = 90; second row: set of points (š, PV). Left: Quality I; middle: Quality II; right: Quality III (198 total points for each case, 33 points for each basal area level, six points for each recruitment level, and i = 3%).
Fig. 4 - First row: set of points (š, ρNPV) for T = 90; second row: set of points (š, ρPV). Left: Quality I; middle: Quality II; right: Quality III (198 points for each case, and i = 3%).
The discount rates applied fell between 2% and 4%, as is typical in forest management studies, and the time horizon used to calculate the NPV ranged between 50 and 130 years. The influence of small variations in the discount rate i, or the time horizon T, on the results was minimal because they did not change the behaviour of the expressions shown in Materials and Methods (chapter “NPV functions”).
Regarding the regressions, we obtained the following results:
- As already mentioned, for previously defined values of i and T, the dimensionless numbers ρNPV and š have a strong positive linear correlation (see Fig. 4). For i = 3%, in particular, the total proportion of variance in ρNPV explained by š was r2 = 0.99974 for Quality I, r2 = 0.99965 for Quality II, and r2 = 0.99956 for Quality III. It is important to note that such r2 values do not depend on the planning horizon T.
- Similarly, for each discount rate i, the dimensionless numbers ρPV and š have a strong positive linear correlation, with the same r2 values as described above (Fig. 4).
- For previously defined values of basal area (between G = 21 m2 ha-1 and G = 26 m2 ha-1), i and T, the variables NPV and š have a strong positive linear correlation (Fig. 3). The same result holds for the variables PV and š. The best approximations always occurred for the lowest level of diameter growth and the highest basal area scenarios, with r2 being very close to 1 in all cases.
- For previously defined values of recruitment level (between R = 200 and R = 840 stems ha-1), i and T, the variables NPV and š have a strong negative linear correlation (Fig. 3). The same result holds for the variables PV and š. The best approximations always occurred for the lowest level of diameter growth and the lowest recruitment scenarios, with r2 being very close to 1 in all cases.
Discussion and conclusions
This paper proposes a simple and direct method based on dimensionless numbers, obtained under conditions of stable equilibrium from a matrix model, to provide reliable approximations of the NPV, PV, ρNPV and ρPV of a monospecific uneven-aged stand. In fact, these variables were related to š (see eqn. 3), which is a dimensionless number based on the following variables: (a) the transition probabilities pk, which can be calculated from counts of observed transitions between adjacent diameter classes from t to t+1; (b) the basal area of the stand G, and the global amount of recruitment R. Although Pinus nigra regenerates well in the study area under its own canopy ([23], [28]), there is a critical basal area that allows sufficient light transmittance for regeneration. This maximum value is around 20-30 m2 ha-1 ([24], [25], [21]). On the other hand, basal area clearly below 20 m2 ha-1 (before harvesting) could compromise natural regeneration ([25]). Consequently, in addition to three levels of diameter growth (Qualities I-III), we considered six levels of stand basal area from G = 21 to G = 26 m2 ha-1, and 33 levels of global recruitment, from R = 200 stems ha-1 (scarce recruitment) to R = 840 stems ha-1 (abundant recruitment), creating a total of 594 planning scenarios. The corresponding problems simulated a wide variety of typical management cases in the study area; and (c) the number n and width w of the diameter classes. As shown in López & Fullana ([15]), these scaling factors n and w could have a limited influence on š and therefore on the NPV, PV, ρNPV and ρPV values.
The ρNPV and ρPV dimensionless numbers should not be interpreted as a kind of IRR, but as economic performance indicators for forest management inspired by the ROA accounting concept, using the NPV or PV derived from the sale of timber throughout a harvest cycle, plus the final stocking value (as numerator), and the fair value of standing timber (as denominator), showing how profitable the forest is relative to its total value, with sustainability and stability criteria. Application of the NPV (or PV) implies the introduction of a discount rate exogenously defined. In this regard, we applied the same criteria as in the International Financial Reporting Standards (IFRS), in particular IAS 41 ([10]), to estimate that exogenous discount rate. In fact, IAS 41 ([10]), in applying the expectation value approach to forest valuation, when referring to the process of deriving the present value of expected net cash flows for a forest stand, prescribed the use of a determined discount rate in each case, recommending that assumptions about these rates should be internally consistent with the underlying economic factors of the sector. By using a discount rate in accordance with international accounting standards, the possibility of manipulation should be avoided or limited. Thus, to consider the incorporation of eventual risks, in this study we initially chose a wide range of discount rates from 2% to 4%, typical of forest management scenarios ([9], [8], [11]). Note that (eqn. 17):
It is not surprising therefore that the highest ρNPV and ρPV values were obtained for Quality I, followed by Quality II and Quality III (see Tab. 6 and Fig. 4). In fact, since there is a strong positive linear correlation between these numbers and š, and considering that the core of this dimensionless number š is given by the quotient (eqn. 18):
under the same conditions for R and G, the faster the flow of the stems through the diameter classes (i.e., the higher product of the transition probabilities), the greater š and consequently the greater the ρNPV and ρPV values. Likewise, within each site quality (where the product of the transition probabilities may be assumed to be constant), the key factor underlying the ρNPV and ρPV equations is the quotient R/G, which means that the greater R/G, the more profitable the forest will be (i.e., the G = 21 m2 ha-1 with R = 840 stems ha-1 is the most favourable scenario in this context). Two arrows in Fig. 4 point in the directions of the higher and lower R/G values.
Furthermore, the strong positive linear correlation between ρNPV and ρPV and š means that, stratifying the forest into uniform areas based upon tree diameter growths, the same linear regression line can be used in each stratum to estimate the ρNPV and ρPV dimensionless numbers. The same result holds for the variables NPV or PV and š for each basal area or recruitment levels, although, in the latter case, the corresponding strong linear correlation is negative.
Since the model rests on sustainability and stability criteria, it is important to investigate the sensitivity of the results to deviations from the equilibrium (stable diameter distribution); in particular, whether the strong linear relationship between the dimensionless numbers, ρNPV and ρPV, and š is sensitive to changes in the equilibrium position. In this regard, there have been two recent studies involving Pinus nigra stands in the study area ([17], [18]), both maximising the same NPV function, constrained by the same matrix model to describe the population dynamics, and with the same initial condition (the stable diameter distribution), as used in this study. Additionally, in the second one the final condition was assumed as the stable diameter distribution of the stand, and a wide variety of typical management scenarios in the study area, obtained by combining three rates of diameter growth (Qualities I-III), three levels of basal area (G = 22, 24 and 26 m2 ha-1), and three levels of recruitment (R = 200, 520 and 840 stems ha-1), were considered. The first one (hereafter S1) showed that the economically optimal harvesting strategies underlying the solutions for that model changed the stand towards distributions substantially deviated from the stable diameter distribution; and the second (hereafter S2) revealed that the stand diameter distribution did not deviate substantially from the equilibrium position over time. The NPV values obtained for the optimal harvesting strategies from S2 were always below those of the optimal harvesting strategies from S1 (where no restrictions were introduced for the final state), and above the NPV values obtained under sustainability and stability criteria.
In each case, the ρNPV and ρPV dimensionless numbers were computed, and a regression analysis was conducted, using the same š values as in this study. The results showed that, in both S1 and S2 strategies the strong linear relationship between the dimensionless numbers ρNPV and ρPV, and š was not sensitive to changes in the equilibrium position, with r2 values being very close to 1 in all cases. The lowest r2 values always occurred for the lowest level of diameter growth, with the minimum value of r2 being 0.9986 for the strategy S1.
In conclusion, this study showed that, under sustainability and stability criteria, there is a strong influence of the dimensionless number š on the NPV and PV of the forest harvesting strategies. Additionally, ρNPV and ρPV might be interpreted as economic performance indicators for forest management, inspired by the ROA accounting concept, showing how profitable the forest is relative to its total value, with sustainability and stability criteria. Those dimensionless numbers would also allow the extraction of conclusions about the behaviour of NPV of the forest harvesting, capturing information of all the global variables involved in the problem (e.g., recruitment, basal area and transition probabilities between diameter classes). Moreover, the study showed that there are strong linear correlations between the variables, NPV, PV, ρNPV , ρPV, and š.
Acknowledgments
The authors appreciate the helpful comments offered by the reviewers. The authors received no funding for this work, and have declared that no competing interests exist.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Universidad Politécnica de Madrid (UPM), Escuela Técnica Superior de Ingeniería de Montes, Forestal y del Medio Natural, Ciudad Universitaria, E-28040 Madrid (Spain)
Universidad Pontificia de Comillas, Alberto Aguilera 23, E-28015 Madrid (Spain)
Corresponding author
Paper Info
Citation
López Torres I, Belda Fullana C (2019). Dimensionless numbers for the net present value and the perpetual value of sustainable timber harvests from a monospecific uneven-aged forest. iForest 12: 35-42. - doi: 10.3832/ifor2715-011
Paper history
Received: Dec 21, 2017
Accepted: Oct 19, 2018
First online: Jan 10, 2019
Publication Date: Feb 28, 2019
Publication Time: 2.77 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2019
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 42075
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 36421
Abstract Page Views: 2464
PDF Downloads: 2372
Citation/Reference Downloads: 1
XML Downloads: 817
Web Metrics
Days since publication: 2533
Overall contacts: 42075
Avg. contacts per week: 116.28
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2019): 1
Average cites per year: 0.14
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Optimizing the management of uneven-aged Pinus nigra stands between two stable positions
vol. 9, pp. 599-607 (online: 01 March 2016)
Research Articles
Deploying an early-stage Cyber-Physical System for the implementation of Forestry 4.0 in a New Zealand timber harvesting context
vol. 17, pp. 353-359 (online: 13 November 2024)
Research Articles
Modelling the carbon budget of intensive forest monitoring sites in Germany using the simulation model BIOME-BGC
vol. 2, pp. 7-10 (online: 21 January 2009)
Research Articles
Incorporating management history into forest growth modelling
vol. 4, pp. 212-217 (online: 03 November 2011)
Research Articles
Comparison of alternative harvesting systems for selective thinning in a Mediterranean pine afforestation (Pinus halepensis Mill.) for bioenergy use
vol. 14, pp. 465-472 (online: 16 October 2021)
Research Articles
Spatio-temporal modelling of forest monitoring data: modelling German tree defoliation data collected between 1989 and 2015 for trend estimation and survey grid examination using GAMMs
vol. 12, pp. 338-348 (online: 05 July 2019)
Research Articles
Distribution factors of the epiphytic lichen Lobaria pulmonaria (L.) Hoffm. at local and regional spatial scales in the Caucasus: combining species distribution modelling and ecological niche theory
vol. 17, pp. 120-131 (online: 30 April 2024)
Research Articles
Local ecological niche modelling to provide suitability maps for 27 forest tree species in edge conditions
vol. 13, pp. 230-237 (online: 19 June 2020)
Research Articles
Modifying harvesting time as a tool to reduce nutrient export by timber extraction: a case study in planted teak (Tectona grandis L.f.) forests in Costa Rica
vol. 9, pp. 729-735 (online: 03 June 2016)
Short Communications
Dynamic modelling of target loads of acidifying deposition for forest ecosystems in Flanders (Belgium)
vol. 2, pp. 30-33 (online: 21 January 2009)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword