Optimizing the management of uneven-aged Pinus nigra stands between two stable positions
iForest - Biogeosciences and Forestry, Volume 9, Issue 4, Pages 599-607 (2016)
doi: https://doi.org/10.3832/ifor1298-008
Published: Mar 01, 2016 - Copyright © 2016 SISEF
Research Articles
Abstract
This study proposes a discrete optimal control model to obtain harvest strategies that maximize the net present value (NPV) of the timber harvested from uneven-aged Pinus nigra stands located in the Spanish Iberian System, between two stable positions. The model was constructed using an objective function that integrates financial data on the harvesting operations with a matrix model describing the population dynamics. The initial and final states are given by the stable diameter distribution of the stand, and the planning horizon is 70 years. The scenario analysis corresponding to the optimal solutions revealed that the stand diameter distribution does not deviate substantially from the equilibrium position over time and that the NPV for the optimal harvesting schedule was always greater than the NPV for the “sustainable/stable” harvesting strategy. The NPV increase for the different scenarios is between 5.36% and 14.43%, showing a greater increase in higher site index scenarios and higher recruitments.
Keywords
Sustainability, Stability, Equilibrium, Optimal Harvesting, Discrete Optimal Control, Matrix Model
Introduction
In a broad sense, a system is considered to be stable if it always returns to a reference position (equilibrium) after small disturbances. In a forest ecosystem the main factors influencing this equilibrium are recruitment, transitions between diameter classes, and mortalities (natural or induced by harvesting - [21]). These processes of evolution over time can be easily modeled using a matrix population model (e.g., [1], [2], [8], [30]), for which the population growth rate is the dominant eigenvalue λ of the transition matrix and the equilibrium position is determined by the stable diameter distribution W0. Stand management practices aimed at conserving this equilibrium are important because they represent the stand’s ability to persist in the face of external disturbances. Managing a stand by applying the “sustainable/stable” harvesting strategy ([9], [10], [12], [13]) is a good way to reach and maintain that equilibrium with sustainability. In fact, the “sustainable/stable” harvesting strategy is aimed at reaching the stable diameter distribution of the stand for each harvest, yielding for all the diameter classes and time steps the following “sustainable/stable” harvest rate (eqn. 1):
where λ0 is the dominant eigenvalue of the transition matrix without harvests, and s also includes the natural mortalities. This is a sustainable harvesting strategy too (in the sense of population persistence over time) because s corresponds to the case such that the right eigenvector associated with the dominant eigenvalue λ = 1 of the transition matrix with harvests, is W0.
By contrast, many harvesting strategies do not satisfy the requirements of sustainability or stability. In fact, using an objective function that integrates financial data of harvesting operations with a matrix model to describe the population dynamics, a recent discrete optimal control model proposed by López et al. ([13]) showed that the economically optimal harvesting strategies underlying the solutions of that model changed the stand towards distributions more characteristic of even-aged stands and substantially deviated from the stable diameter distribution. Moreover, the corresponding economically optimal harvesting strategies were always unsustainable, in the sense that the population growth rate λT for the whole harvest cycle was always λT < 1, being λT the dominant eigenvalue of the transition matrix from t = 0 to t = T, and T the planning horizon.
This study investigates the existence of a new sustainable, stable, and economically optimal harvesting strategy for uneven-aged Pinus nigra stands in the Spanish Iberian System. We rely on an objective function that integrates financial data of harvesting operations with a matrix model that describes the population dynamics, which creates a discrete optimal control model. In addition, it is investigated whether the sustainability and stability conditions can be satisfied by assuming the stable diameter distribution of the stand as the initial and final conditions, that is X(0) = X(T) = W0. Furthermore, we examine the effects of diameter growth, stand density, and recruitment on those strategies, considering a wide variety of typical management scenarios in the study area, obtained by combining three rates of diameter growth, three levels of stand basal area (G = 22, 24, and 26 m2 ha-1), and three levels of global recruitment (scarce: R = 200 stems ha-1; normal: R = 520 stems ha-1; and abundant: R = 840 stems ha-1). Finally, an economic comparison has been performed between this economically optimal harvesting strategy between two stable positions and the “sustainable/stable” strategy for each scenario.
In general, optimal control theory enables the solution of a wide variety of dynamic problems, for which the evolution of the dynamic system (discrete or continuous) can be partially controlled by the agent’s decision. In every moment t, the system can be described by a set of state variables xk(t) (e.g., stems ha-1 in diameter class k at year t), so the manager chooses a specific set of control variables hk(t) (e.g., harvest rate in diameter class k at year t). Different values for the control variables imply different paths in the phase space for the dynamic system and the manager must determine the control values that maximize the selected objective, according to the constraints of the problem.
Many authors have considered optimal control theory to model forest stands management both in continuous case ([5], [23]) and in discrete case ([7], [25], [11], [13]).
In the following sections, we describe the model and the estimates of the corresponding parameters. The general calculations, including regressions, employed the software Maple ([15]) version 18, and the solutions to the optimization problems were derived using the Solver® tool running under MS Excel 2013®.
Materials and methods
Discrete optimal control model
This model has three main features: (1) an underlying discrete time dynamic system, given by the stand population dynamics; (2) an objective function, which is in this case the net present value (NPV) of timber income over a fixed time horizon T; and (3) a set of constraints.
The combination of the objective function with the population dynamics model and the constraints produces a discrete optimal control problem, from which we have to determine control variables hk(t) that globally maximize the function NPV subject to the population dynamics and constraints.
Stand population dynamics
The stands of the study area are located in the Spanish Iberian System, a mountain range extending about 400 km along the north-eastern edge of the Central Plateau, including 60% of the area occupied by Pinus nigra in Spain ([4]). The management of Pinus nigra stands in this area is currently based on the growth and yield tables for Pinus nigra Arn. in the Spanish Iberian System ([3]). The data in these tables are classified according to growth rates into five site qualities, of which only the first three have been selected as our data source. These three qualities were defined by the dominant heights reached at the reference age of 60 years (20, 17, and 14 m, respectively). The study area is very large, covering the whole range of P. nigra in the Spanish Iberian System. Therefore, the spectrum of values taken by environmental variables such as slope, soil type, and even climatic characteristics is also very wide. This variability is captured in the growth and yield tables used by considering different site qualities that reflect variations in topography, height, slope, aspect, weather, and vegetation.
The population dynamics model that integrates recruitment, harvesting, and stem migration throughout the diameter classes over time is based on the model proposed by López et al. ( [9], [10]) for Fagus sylvatica L., and by López et al. ( [12], [13]) for Pinus nigra Arn. stands.
The starting assumptions were as follows: (a) the forest is in a steady state; (b) the average diameter growth curves for site indices 20 to 14 are defined by the Bertalanffy-Richards model ([31], [19]); (c) within each diameter class, the probability distribution for the diameter of the trees is uniform (rectangular); and (d) harvesting operations occur at the beginning of every projection interval. Group selection cutting is the silvicultural system used because P. nigra is not a shade-tolerant species, and the gaps opened in the canopy through single-tree selection cutting would not be large enough to ensure regeneration.
Harvesting operations in the study area generally take place every 10 years, thus we adopted this period as the range of the projection intervals in the model. Considering this time period and the diameter growth functions corresponding to site indices 20 to 14, trees were grouped into n diameter classes of equal width w = 6 cm: 0-6, 6-12, 12-18, …, 30-36, …, with the last class being more than 48 cm (48,→) for site index 20, more than 42 cm (42,→) for site index 17 and more than 36 cm (36,→) for site index 14 (note that n = 9 for site index 20, n = 8 for site index 17, and n = 7 for site index 14). Therefore, an individual tree in class k can remain in class k or progress to class k + 1 during the projection interval (t, t + 10). The number of trees in each class changed for each projection interval because some were harvested, some remained in the same diameter class, and others grew past the boundary to the next diameter class. In such conditions, pk refers to the probability that an individual tree in class k at time t will appear in class k + 1 at time t + 10. The term rk, or recruitment coefficient, is the number of offspring (stems ha-1) living at time t + 10, produced in the interval t, t + 10 by an average tree in class k at time t. Similar to many standard size classified matrix models, we did not consider the smallest diameter class to be fertile ([2]). The variable hk(t) defines the proportion of harvested trees in class k at year t, natural mortality included. Finally, xk(t) and xk(t + 10) describe the stem densities in class k at the initial and final projection times. By analysing the dynamics of the projections, we find that the model is described accurately by the following matrix model (eqn. 2):
where (eqn. 3):
and I is the identity matrix; H(t) = diag[h1(t), h2(t), …, hn(t)] is a diagonal matrix with the harvest rates hk(t); and X(t) and X(t + 10) are column vectors indicating the stem densities at the initial and final times of projection, respectively.
Objective function
Considering that the main goal for the stands in the study area is the production of timber, the objective function of the optimization problem is the NPV of all management operations over a planning horizon of T = 70 years, discounted to the beginning of the period and from the landowner’s perspective, that is (eqn. 4):
where vk(t) is the stumpage value that corresponds to class k at year t (€/stem) and i is the discount rate. The first summation represents the income derived from timber sale and the second is the final stocking value. It is well known that the NPV is a justifiable management objective for a single economic goal ([24]).
Harvesting costs are not considered because harvesting operations are not paid by the owner. The costs for the owner of the land are the opportunity cost of the invested capital and the opportunity cost of the land. None of them are explicit costs, but they are incorporated into the NPV obtained. This hypothesis is not restrictive since active forest management in the Mediterranean area is not frequent and the owner does not invest any effort in silvicultural actions.
The cost of harvesting operations would be paid by the buyer of the stumpage and that is the reason we did not consider it in the present study.
Set of constraints
As mentioned above, the initial and final conditions must represent the stable diameter distributions of the stand W0. Therefore, the first constraints are given by (eqn. 5):
We also set the following obvious constraints (eqn. 6):
for k = 1, 2, … , n and t = 0, 10, 20, 30, … , T - 10, where mk is the natural mortality in k-th class.
On the other hand, by applying the “sustainable/stable” harvesting strategy to each scenario and setting X(0) = W0 as the initial condition, the basal area of the stand continuously oscillates between values Gmin (after harvesting) and Gmax (before harvesting), and the stable diameter distribution is reached at each time step. Therefore, to compare the economically optimal and the “sustainable/stable” harvesting strategies, it is essential to assume an additional constraint to maintain the stand basal area throughout the harvest cycle within the range Gmin - Gmax during the optimization process, where Gmax was 22, 24, and 26 for the three levels G = 22, 24, and 26 m2 ha-1, respectively, and Gmin is the minimum basal area reached for each scenario under the “sustainable/stable” harvesting strategy.
Optimization method
For each discount rate, the tool Solver® of MS Excel 2013® was used to obtain a globally optimal solution of these nonlinear models by applying multistart methods. These methods provide a “convergence in probability” to a globally optimal solution, which means that as the number of runs of the nonlinear Solver routine increases, the probability that the globally optimal solution has been found also increases towards 100%.
The control variables hk(t) that maximize the objective function NPV (always under the population dynamics and the constraints mentioned above) are the solutions to the corresponding problem (one optimal solution for each scenario). Finally, the optimal harvesting schedules are defined by the combination of the control variables hk(t) corresponding to the scenario analyzed.
Input estimation
Transition probabilities
We calculated the transition probabilities by applying the method introduced in López et al. ([12]) considering that, given the basal area constraints and the low basal area scenarios of this study, stand density has a small influence on diameter growth. Thus, the diameter growths were defined by the Bertalanffy-Richards function ([31], [19] - eqn. 7):
adjusted using regression analysis to data points [t, D(t)] obtained from tables by Gómez Loranca ([3]). The main characteristics of these growth models are shown in Fig. 1.
Fig. 1 - Diameter growth models (dbh D in cm and time t in years). I: Site index 20, D = 51.68 (1 - e-0.015259t)1.255111; II: Site index 17, D = 46.645633 (1 - e-0.014318t)1.337062; III: Site index 14, D = 40.644134 (1 - e-0.013838t)1.456382 . The coefficient of determination was always greater than 0.999.
Using these diameter-growth models, the transition probabilities from class i to class (i + 1) or from interval [6(i- 1), 6i] to interval [6i, 6(i + 1)] are given by (eqn. 8):
for i = 1, 2, 3, 4, …, n-1, where f -1 is the inverse function of f in eqn. 7 defined as (eqn. 9):
where t is the age in years and D is the dbh in cm.
The above-mentioned transition probability equation is a direct application of the formula introduced by López et al. ( [9], [10]) for a Bertalanffy-Richards model. We provide the calculations for site indices 20, 17, and 14 in Tab. 1.
Tab. 1 - Transition probabilities (pk) between diameter classes for each site index.
| Transition | Site index 20 | Site index 17 | Site index 14 |
|---|---|---|---|
| (0-6) → (6-12) | p1 = 0.7697 | p1 = 0.5951 | p1 = 0.4564 |
| (6-12) → (12-18) | p2 = 0.8602 | p2 = 0.6824 | p2 = 0.5326 |
| (12-18) → (18-24) | p3 = 0.7913 | p3 = 0.6200 | p3 = 0.4697 |
| (18-24) → (24-30) | p4 = 0.6828 | p4 = 0.5190 | p4 = 0.3692 |
| (24-30) → (30-36) | p5 = 0.5533 | p5 = 0.3971 | p5 = 0.2475 |
| (30-36) → (36-42) | p6 = 0.4106 | p6 = 0.2618 | p6 = 0.1119 |
| (36-42) → (42-48) | p7 = 0.2587 | p7 = 0.1171 | - |
| (42-48) → (48,→) | p8 = 0.1000 | - | - |
According to the model assumptions and the methodology used, we had to consider that the same transition probability pk applies to all of the individuals in the same class k (where there might exist individuals under very different conditions), i.e., the transition probability pk is a global property shared by all of the individuals in the same class k, independently of their local conditions. We consider that the stratification into three site index classes must result in low variability around the mean pk values.
Recruitment and basal area
Pinus nigra regenerates well under its own canopy ([18], [26]), and recruitment may be very abundant even at high densities, as described by Tíscar Oliver et al. ([27]) who reported more than 1875 stems ha-1 during a regeneration event in Pinus nigra stands with G = 51.96 m2 ha-1. Nonetheless, there is a critical basal area for sufficient light transmittance for regeneration, approximately 20-30 m2 ha-1 ([20], [22]). Therefore, we have considered in the calculations three levels of stand basal area in that range, G = 22, 24, and 26 m2 ha-1. With these basal area values, we assumed the same three levels of recruitment (R) as in our previous studies: (i) 200 stems ha-1 (scarce recruitment); (ii) 520 stems ha-1 (normal); (iii) and 840 stems ha-1 (abundant). For these cases, similar to other matrix models for tree species ([29]), we attributed the global amount of recruitment R entirely to the last diameter class (r2 = r3 = … = rn-1 = 0; rn = R/[xn(0)]), which had no influence on the stable diameter distribution of the stand, which is established by transition probabilities, global amount of recruitment, and stand basal area ([9]).
Natural mortalit
We estimated natural mortalities based on previous studies. Specifically, Misir et al. ([16]) developed a mortality model for Pinus nigra subsp. pallasiana in Turkey from a logistic model and the observed data. They estimated an overall annual mortality rate of 1.41%, equivalent to a 13.24% mortality rate in a 10-year period. Trasobares & Pukkala ([28]) studied Pinus nigra Arn. in north-eastern Spain and suggested natural mortality rates of 2% (including minimal intermediate thinning) for the D > 30 cm diameter classes. Therefore, the following 10-year individual tree constant mortality rates for each diameter class were assumed: m1 = 0.20; m2 = 0.14; m3 = 0.08; m4 = 0.05; m5 = 0.03; and m6 = m7 = … = mn = 0.02.
“Sustainable/stable” harvesting strategy. Stable diameter distribution
As mentioned above, the “sustainable/ stable” harvesting strategy is aimed at reaching in each harvest the proportion of stems ha-1 in each class corresponding to the stable diameter distribution of the stand, yielding the following “sustainable/stable” harvest rate shown in eqn. 1, for all of the diameter classes and time steps. This rate corresponds to the case such that the right eigenvector associated with the dominant eigenvalue λ = 1 of the transition matrix with harvests is W0 for each time step.
By applying the “sustainable/stable” harvesting strategy to each scenario and setting X(0) = W0 (stable diameter distribution) as the initial condition, the basal area of the stand continuously oscillates between the values Gmin (after harvesting) and Gmax (before harvesting), and the stable diameter distribution is reached at each time step. The calculations for the 27 scenarios of this study, obtained by combining three rates of diameter growth with three levels of recruitment (R = 200, 520, or 840 stems ha-1), and three levels of stand basal area (G = Gmax = 22, 24, or 26 m2 ha-1), are shown in Tab. 2 along with the population growth rates λ0, the “sustainable/stable” harvest rates s, and the minimum basal areas Gmin.
Tab. 2 - Numerical values for λ0, s, and stable distributions (G in m2 ha-1, Est. Dis. in stems ha-1).
| Site Index | G | Variable | R = 200 stems ha-1 |
R = 520 stems ha-1 |
R = 840 stems ha-1 |
|---|---|---|---|---|---|
| 20 | 22 | λ 0 | 1.305091 | 1.477671 | 1.594240 |
| s | 0.233770 | 0.323259 | 0.372742 | ||
| G min | 16.857068 | 14.888296 | 13.799677 | ||
| Est. Dis. | [186.1, 122.9, 96.4, 77.2, 61.4, 47.5, 34.6, 22.1, 7.2] | [416.9, 239.8, 162.6, 110.9, 73.4, 45.7, 25.5, 11.4, 2.4] | [615.9, 325.9, 202.3, 125.4, 74.6, 41.1, 19.8, 7.4, 1.2] | ||
| 24 | λ 0 | 1.292499 | 1.458959 | 1.571264 | |
| s | 0.226305 | 0.314580 | 0.363570 | ||
| G min | 18.568685 | 16.450081 | 15.274322 | ||
| Est. Dis. | [188.3, 125.7, 99.8, 81.0, 65.4, 51.4, 38.3, 25.3, 8.6] | [423.2, 246.9, 169.9, 117.8, 79.4, 50.5, 28.9, 13.4, 2.9] | [626.4, 336.8, 212.6, 134.2, 81.5, 45.9, 22.7, 8.8, 1.5] | ||
| 26 | λ 0 | 1.281305 | 1.442342 | 1.550881 | |
| s | 0.219546 | 0.306683 | 0.355205 | ||
| G min | 20.291808 | 18.026241 | 16.764668 | ||
| Est. Dis. | [190.3, 128.3, 102.9, 84.5, 69.1, 55.3, 42.0, 28.5, 10.1] | [429.0, 253.5, 176.8, 124.3, 85.3, 55.3, 32.4, 15.5, 3.5] | [636.1, 347.0, 222.4, 142.6, 88.2, 50.8, 25.7, 10.2, 1.9] | ||
| 17 | 22 | λ 0 | 1.262093 | 1.412527 | 1.514472 |
| s | 0.207665 | 0.292049 | 0.339704 | ||
| G min | 17.431369 | 15.574919 | 14.526515 | ||
| Est. Dis. | [233.3, 147.0, 113.7, 90.3, 71.1, 53.9, 37.2, 16.6] | [516.1, 280.5, 185.4, 123.4, 79.1, 46.6, 23.0, 6.5] | [757.0, 376.4, 226.4, 135.8, 77.3, 39.6, 16.4, 3.7] | ||
| 24 | λ 0 | 1.251140 | 1.396188 | 1.494358 | |
| s | 0.200729 | 0.283764 | 0.330816 | ||
| G min | 19.182509 | 17.189656 | 16.060414 | ||
| Est. Dis. | [236.3, 150.7, 118.0, 95.0, 76.1, 58.9, 41.9, 19.5] | [524.6, 289.4, 194.4, 131.7, 86.1, 52.0, 26.5, 7.8] | [771.0, 389.9, 238.8, 146.1, 85.0, 44.7, 19.1, 4.5] | ||
| 26 | λ 0 | 1.241406 | 1.381684 | 1.476521 | |
| s | 0.194462 | 0.276245 | 0.322732 | ||
| G min | 20.943989 | 18.817621 | 17.608961 | ||
| Est. Dis. | [239.1, 154.0, 122.0, 99.5, 80.9, 63.8, 46.6, 22.6] | [532.4, 297.7, 202.8, 139.6, 93.0, 57.4, 30.1, 9.2] | [783.9, 402.5, 250.5, 156.0, 92.7, 49.8, 22.0, 5.4] | ||
| 14 | 22 | λ 0 | 1.220604 | 1.350816 | 1.439536 |
| s | 0.180733 | 0.259707 | 0.305332 | ||
| G min | 18.023866 | 16.286454 | 15.282699 | ||
| Est. Dis. | [295.4, 179.0, 138.1, 110.0, 86.7, 64.6, 32.8] | [644.2, 332.8, 216.0, 140.9, 87.0, 46.5, 14.8] | [937.6, 440.2, 257.8, 149.7, 80.5, 36.1, 9.2] | ||
| 24 | λ 0 | 1.211164 | 1.336630 | 1.422004 | |
| s | 0.174348 | 0.251850 | 0.296767 | ||
| G min | 19.815651 | 17.955611 | 16.877591 | ||
| Est. Dis. | [299.6, 183.8, 143.8, 116.4, 93.7, 71.8, 38.0] | [655.8, 344.3, 227.4, 151.3, 95.6, 52.8, 17.6] | [956.3, 457.2, 273.0, 162.1, 89.4, 41.4, 11.0] | ||
| 26 | λ 0 | 1.202780 | 1.324044 | 1.406468 | |
| s | 0.168593 | 0.244738 | 0.288999 | ||
| G min | 21.616583 | 19.636810 | 18.486024 | ||
| Est. Dis. | [303.4, 188.3, 149.1, 122.5, 100.4, 79.0, 43.6] | [666.3, 355.0, 238.2, 161.4, 104.2, 59.2, 20.4] | [973.6, 473.1, 287.6, 174.1, 98.3, 46.9, 12.9] |
On the other hand, to compare the economically optimal and the “sustainable/stable” harvesting strategies, the NPV values corresponding to the “sustainable/stable” strategies are given by (eqn. 10):
and the distance between these distributions can be evaluated with Keyfitz’s Δ (eqn. 11):
where xi and wi are the components of the diameter distributions X (optimal) and W0 (stable), scaled to 1 (i.e., Σ xi = Σ wi - [6]). The maximum value of Δ is 1, and the minimum of 0 occurs when the diameter distributions X and W0 (scaled to 1) are identical. Smaller values of Δ result when the distributions X and W0 (scaled to 1) become more similar.
Stumpage value model
The stumpage value model applied in this study comes from López et al. ([13]). It is a generalization of the model proposed for site index 20 in López et al. ([11]) for Pinus nigra in the Spanish Iberian System. In Tab. 3, we provide the stumpage values we used to obtain the economic data ([17], [28]). The regression models adjusted to these data appear in Fig. 2. The stumpage prices of Pinus nigra in Spain remained fairly stable between 1994 and 2011 ([14]).
Tab. 3 - Stumpage prices (€ m-3) of Pinus nigra in Spain according to its diameter class and industrial destination.
| Products | Diameter classes (cm) | ||
|---|---|---|---|
| <20 | 20-40 | >40 | |
| Particle | 6 | 1.2 | 0.6 |
| Poles | 0 | 11.85 | 0 |
| Sawlog | 0 | 9.8 | 11.76 |
| High-quality sawlog | 0 | 0 | 9.96 |
| Total average price | 6 | 22.85 | 22.32 |
Fig. 2 - Stumpage value models (stumpage values v in € stem-1 and diameter D in cm). (I) Site index 20: v = D3.186471 exp(-7.704952 - 8.678687 · 10-3 D); (II) Site index 17: v = D3.114196 exp(-7.476506 - 9.903125 · 10-3 D); (III) Site index 14: v = D2.987053 exp(-7.110977 - 1.078752 · 10-2D). The coefficient of determination was always greater than 0.9999.
The last row in Tab. 3 shows the average price per cubic meter for trees belonging to the different diameter classes. This price is obtained by adding up the four rows above showing the contributions to the final value of a tree of the four industrial destinations according to the percentage of wood of each diameter class going into each product type. The prices of particle board, poles, sawlog, and high-quality sawlog are 6.0, 39.5, 19.6, and 33.2 € m-3, respectively. It is necessary to point out that the demand for timber poles in Spain is very high and therefore they reach a higher price than larger size sawlogs.
Results
The transition probabilities in Tab. 1, the “sustainable/stable” harvest rates s, and the stable diameter distributions W0 in Tab. 2 were replaced into the proposed discrete optimal control model. Global optimal solutions to each corresponding optimization problem were found using Solver® by changing the hk(t) variables for k = 1, 2, …, n, and t = 0, 10, 20, …, 70 years. Using this procedure, we obtained the optimal state xk(t) and the control variables hk(t); basal areas before and after each harvest; optimal NPV and the NPV corresponding to the “sustainable/stable” harvesting strategy; and Keyfitz’s Δ for all of the scenarios considered. The discount rates applied fell between 2% and 4%, as is typical of forest management studies.
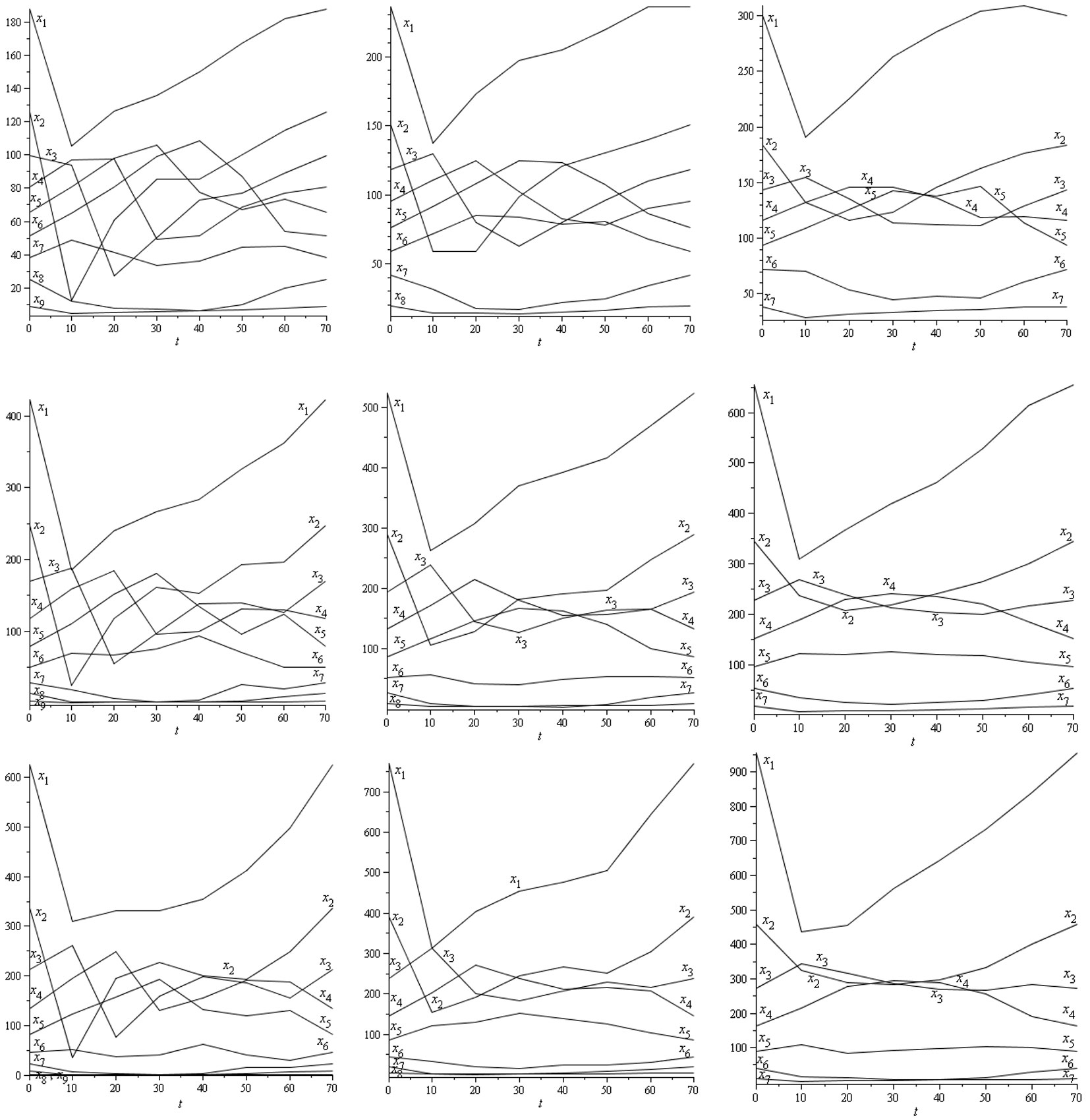
Fig. 3 - Population dynamics xk to maximize the NPV function throughout a harvest cycle of 70 years for G = 24 m2 ha-1 and i = 3% (left: Site index 20; middle: Site index 17; right: Site index 14; first row: R = 200 stems ha-1; second row: R = 520 stems ha-1; third row: R = 840 stems ha-1). The initial and final conditions are defined by the stable diameter distributions.
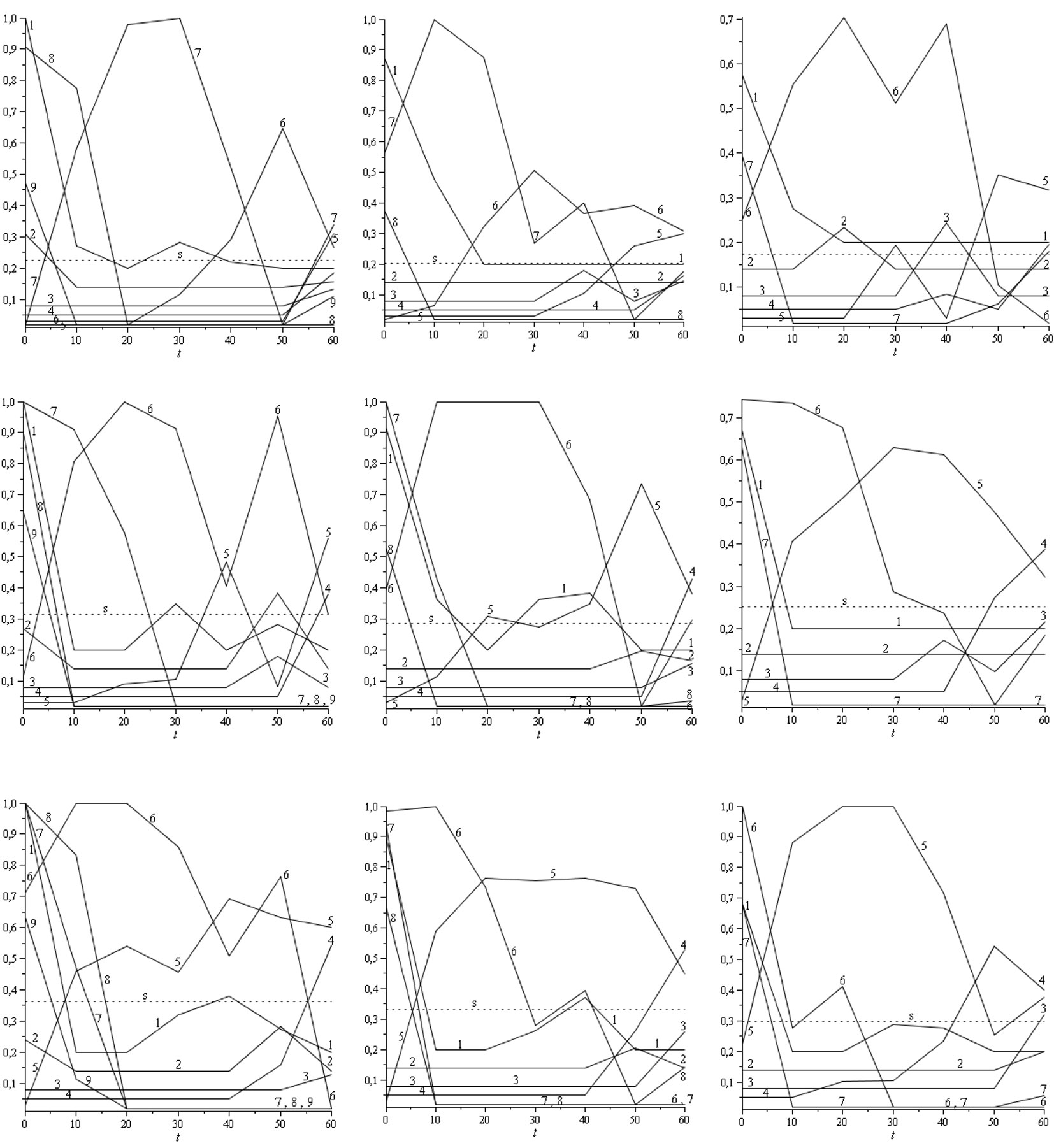
Fig. 4 - Optimal harvesting strategies hk(t) for G = 24 m2 ha-1 and i = 3% (left: Site index 20; middle: Site index 17; right: Site index 14; first row: R = 200 stems ha-1; second row: R = 520 stems ha-1; third row: R = 840 stems ha-1). The dashed lines depict the “sustainable/stable” harvest rates s.
Tab. 4 - NPV values (€ ha-1) for the “sustainable/stable” and the optimal harvesting strategies (Max. NPV) and NPV increase (%) for i = 3%, and different levels of site index, R, and G (G in m2 ha-1).
| Site Index | G | Strategy | R = 200 stems ha-1 | R = 520 stems ha-1 | R = 840 stems ha-1 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Value (€ ha-1) |
Increase (%) |
Value (€ ha-1) |
Increase (%) |
Value (€ ha-1) |
Increase (%) |
||||
| 20 | 22 | Sust/Stable | 5347.3646 | 12.48 | 6118.0328 | 14.33 | 6383.5522 | 14.43 | |
| Max. NPV | 6014.7773 | 6994.8646 | 7304.4446 | ||||||
| 24 | Sust/Stable | 5743.3336 | 12.24 | 6611.1260 | 14.36 | 6918.9460 | 14.35 | ||
| Max. NPV | 6446.4525 | 7560.6334 | 7911.8264 | ||||||
| 26 | Sust/Stable | 6130.4531 | 11.93 | 7096.2876 | 14.35 | 7447.4339 | 14.32 | ||
| Max. NPV | 6861.7018 | 8114.2591 | 8514.1776 | ||||||
| 17 | 22 | Sust/Stable | 4239.2159 | 9.69 | 4986.6137 | 12.75 | 5284.1332 | 13.84 | |
| Max. NPV | 4649.9201 | 5622.2967 | 6015.6138 | ||||||
| 24 | Sust/Stable | 4542.7283 | 9.31 | 5373.9477 | 12.61 | 5710.9061 | 13.65 | ||
| Max. NPV | 4965.6346 | 6051.5239 | 6490.3456 | ||||||
| 26 | Sust/Stable | 4838.9236 | 8.97 | 5754.1367 | 12.51 | 6131.0587 | 13.44 | ||
| Max. NPV | 5272.7622 | 6473.7901 | 6955.3522 | ||||||
| 14 | 22 | Sust/Stable | 3202.5660 | 6.20 | 3906.4753 | 10.12 | 4224.8230 | 11.44 | |
| Max. NPV | 3401.1319 | 4301.8564 | 4708.1096 | ||||||
| 24 | Sust/Stable | 3421.6868 | 5.77 | 4194.9510 | 9.74 | 4548.7650 | 11.36 | ||
| Max. NPV | 3619.2075 | 4603.4830 | 5065.3056 | ||||||
| 26 | Sust/Stable | 3635.0537 | 5.36 | 4477.2298 | 9.39 | 4866.5857 | 11.27 | ||
| Max. NPV | 3829.9429 | 4897.7062 | 5415.2350 | ||||||
Tab. 5 - Set of values for Keyfitz’s Δ corresponding to the distance between the diameter distribution associated with the optimal harvesting strategy and the stable diameter distribution (given by W0) for every period of the planning horizon (note that Δ = 0 for t = 0 and t = T = 70).
| Site Index | G | Year | R = 200 stems ha-1 |
R = 520 stems ha-1 |
R = 840 stems ha-1 |
|---|---|---|---|---|---|
| 20 | 22 | 10 | 0.2504 | 0.3052 | 0.3164 |
| 20 | 0.2374 | 0.2609 | 0.2422 | ||
| 30 | 0.1864 | 0.1775 | 0.1704 | ||
| 40 | 0.1433 | 0.1502 | 0.1777 | ||
| 50 | 0.0875 | 0.0939 | 0.1505 | ||
| 60 | 0.0364 | 0.0829 | 0.0986 | ||
| 24 | 10 | 0.25 | 0.3261 | 0.3195 | |
| 20 | 0.2377 | 0.2705 | 0.2433 | ||
| 30 | 0.19 | 0.1806 | 0.1597 | ||
| 40 | 0.1473 | 0.1432 | 0.1712 | ||
| 50 | 0.0889 | 0.0836 | 0.1409 | ||
| 60 | 0.0332 | 0.0794 | 0.1025 | ||
| 26 | 10 | 0.2356 | 0.3176 | 0.3247 | |
| 20 | 0.2365 | 0.2685 | 0.2455 | ||
| 30 | 0.1882 | 0.1815 | 0.1565 | ||
| 40 | 0.1512 | 0.1553 | 0.1655 | ||
| 50 | 0.0888 | 0.095 | 0.132 | ||
| 60 | 0.0331 | 0.0762 | 0.1044 | ||
| 17 | 22 | 10 | 0.2002 | 0.2585 | 0.2785 |
| 20 | 0.194 | 0.1997 | 0.2175 | ||
| 30 | 0.1588 | 0.1588 | 0.188 | ||
| 40 | 0.1088 | 0.1235 | 0.1623 | ||
| 50 | 0.081 | 0.1007 | 0.1489 | ||
| 60 | 0.0306 | 0.0576 | 0.0718 | ||
| 24 | 10 | 0.1882 | 0.2512 | 0.2843 | |
| 20 | 0.1912 | 0.1992 | 0.2168 | ||
| 30 | 0.1553 | 0.1571 | 0.1669 | ||
| 40 | 0.1083 | 0.1238 | 0.1435 | ||
| 50 | 0.0804 | 0.1013 | 0.1423 | ||
| 60 | 0.0319 | 0.0535 | 0.0691 | ||
| 26 | 10 | 0.1744 | 0.2457 | 0.2803 | |
| 20 | 0.1854 | 0.2029 | 0.2149 | ||
| 30 | 0.1549 | 0.1564 | 0.1661 | ||
| 40 | 0.1099 | 0.1246 | 0.1333 | ||
| 50 | 0.0794 | 0.1016 | 0.1316 | ||
| 60 | 0.0329 | 0.0494 | 0.0721 | ||
| 14 | 22 | 10 | 0.1245 | 0.1923 | 0.1985 |
| 20 | 0.1234 | 0.1881 | 0.2135 | ||
| 30 | 0.1183 | 0.1636 | 0.1754 | ||
| 40 | 0.0875 | 0.1311 | 0.136 | ||
| 50 | 0.0801 | 0.0907 | 0.1072 | ||
| 60 | 0.0358 | 0.0401 | 0.0482 | ||
| 24 | 10 | 0.1201 | 0.1889 | 0.1968 | |
| 20 | 0.1146 | 0.184 | 0.2063 | ||
| 30 | 0.1116 | 0.1569 | 0.1756 | ||
| 40 | 0.0837 | 0.1233 | 0.1441 | ||
| 50 | 0.0768 | 0.0864 | 0.1026 | ||
| 60 | 0.0349 | 0.037 | 0.0457 | ||
| 26 | 10 | 0.1141 | 0.1851 | 0.199 | |
| 20 | 0.1059 | 0.18 | 0.2094 | ||
| 30 | 0.1049 | 0.151 | 0.1893 | ||
| 40 | 0.0848 | 0.1165 | 0.1473 | ||
| 50 | 0.0742 | 0.084 | 0.1002 | ||
| 60 | 0.0339 | 0.0377 | 0.0448 |
The main results may be summarized as follows: (a) Fig. 3 shows the population dynamics xk needed to maximize the NPV function over 70 years with G = 24 m2 ha-1 and i = 3%; (b) Fig. 4 depicts the optimal harvesting strategies hk(t) for G = 24 m2 ha-1 and i = 3%; (c) the NPV values and the NPV increase between the “sustainable/stable” harvesting strategy s and the optimal harvesting strategy (maximizing NPV function) for i = 3% and different values of site index, R and G are displayed in Tab. 4; (d) Tab. 5 shows the set of values for Keyfitz’s Δ that correspond to the distance between the diameter distribution associated with the optimal harvesting strategy (for t = 70 years) and the stable diameter distribution (W0) for every period of the planning horizon. It is worth to notice that the values obtained were always very low and yielded Δ = 0 for t = 0 and t = 70, as expected. Moreover, it should be stressed that the transition matrix AT for the whole harvest cycle from t = 0 to t = 70 years is the following (eqn. 12):
and that λT = 1 for all of the scenarios, where λT denotes the population growth rate for the whole harvest cycle of T = 70 years. Thus, considering the whole harvest cycle, these optimal harvesting strategies are sustainable. In addition to that, the stable diameter distribution is recovered at the end of the harvest cycle.
The optimal harvesting strategy aimed at maximizing NPV subject to the initial and final stage conditions [X(0) = X(T) = W0], results in higher NPV figures than the “sustainable/stable” conditions. For i = 3%, this increment was always over 5.36% and reached a maximum of 14.43% for site index 20, R = 840 stems ha-1 and G = 22 m2 ha-1. The NPV increase was greater for site index 20 than for site index 17 and site index 14.
The influence of small variations in the discount rate or the natural mortality rates on the optimal harvesting strategies was minimal because they did not change the general pattern of the solutions found.
Discussion and conclusions
This study proposes a model that combines an objective function comprising the NPV of all the management operations in a planning horizon of T = 70 years with a matrix model for the population dynamics, constrained in the initial and final states to be the stable diameter distribution of the stand, i.e., X(0) = X(T) = W0. The resulting discrete optimal control model provides a simple tool for heuristic analysis to answer the “what if” questions in relation to forest management plans.
Following López et al. ( [9], [10], [12], [13]), we calculated the transition probabilities considering that pk is an average global property shared by all of the individuals in the same class k, and that, given the basal area constraints and the low basal area scenarios of this study, stand density has a small influence on diameter growth. Moreover, in the case of constrained optimization matrix models, in which the search for optimal paths throughout the phase space is mainly governed by the objective function, optimal decisions are essentially conditioned by the stumpage prices, i.e., by selective harvesting, and thus stand density has a minor influence on the objective function.
López et al. ([10]) also show that results obtained for λ0 are sensitive to the width w of the diameter classes, such that the most conservative values of λ0 and s result from the lowest values of w, which does not allow an individual tree to jump over more than one diameter class in a single projection. The minimum (integer) widths of the diameter classes compatible with this model assumption were w = 6 cm for site index 20, w = 5 cm for site index 17, and w = 4 cm for site index 14. However, because the dominant eigenvalue λ0 and the stable diameter distribution are not substantially affected by small or even moderate changes in the width of the diameter classes ([10]), we assumed a width of w = 6 cm for our study to facilitate the comparison and presentation of results.
As shown in Tab. 4, the NPV increase between the optimal and the “sustainable/stable” harvesting strategies was related to site quality. The highest NPV increments in absolute terms were obtained for the scenarios corresponding to site index 20, G = 26 and high to medium recruitment (R of 840 and 520 stems ha-1). Those increments were over 1000 € ha-1, with NPV values for the optimal strategies over 8000 € ha-1. However, the NPV increase in relative terms lies between 5.36% and 14.43%, showing a higher increase for higher quality sites and higher recruitments. For site index 20 and R between 520 and 840 stems ha-1, the NPV increase was always over 14%.
For high quality sites, the highest relative advance on the NPV between the optimal harvesting strategy and the “sustainable/ stable” is reached for medium and high recruitment (R between 520 and 840 stems ha-1), while for low-quality sites, this relative advantage is higher for high recruitment (R = 840 stems ha-1).
By applying the optimal harvesting strategies, the maximum value obtained for Keyfitz’s Δ was 0.32, with small deviations from the stable distribution throughout the harvest cycle. The highest Δ values were obtained for site index 20, R = 840 and 520 stems ha-1. On the other hand, the lowest values of Δ were obtained for site index 14, and R = 200 stems ha-1 (with Δ always less than 0.125).
In low-quality sites, the optimal management strategy leads to stand distributions that are closer to the stable distribution over the planning horizon than in medium- or high-quality sites. On the other hand, it is in these high-quality sites where the relative increase in the NPV is higher.
Regarding the optimal harvesting strategy (see Fig. 3, Fig. 4), the harvest rates are low for the first four diameter classes throughout the planning horizon. As expected, harvests for the seventh and eighth diameter classes are higher at the beginning of the planning horizon and lower during the last three periods. Most harvests for the fifth and sixth diameter class take place along the planning horizon. For medium and high recruitments, the highest harvest at the end of the planning horizon (t = 60) is performed mainly on the fourth and fifth diameter classes.
It is interesting to note that the optimal harvesting strategy results in a reasonable harvesting schedule, which follows from the dynamics of the stand, initial and final conditions, and the time preference stated by the NPV function, and that the NPV values obtained for the optimal harvesting strategies from this study lie always between those of the optimal (but not sustainable) harvesting strategies shown in López et al. ([13]), where no restrictions were introduced for the final state, and the NPV values for the “sustainable/stable” harvesting strategy.
In conclusion, the proposed optimization model was used in this study to determine economically optimal harvesting strategies of uneven-aged Pinus nigra stands in the Spanish Iberian System, when the population dynamics are governed by a matrix model, the initial and final diameter distributions are constrained to be the stable diameter distribution [X(0) = X(T) = W0], and a set of constraints is stated to maintain the stand basal area within narrow ranges commonly used in the management of this species. Under such conditions, this study shows that there are sustainable harvesting strategies that retain the stable diameter distribution of the stand at the end of the planning horizon, yielding a higher NPV than the “sustainable/stable” scenario, especially for high-quality sites, although these NPVs are lower than the corresponding values for the economically optimal harvesting strategies.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Sigfredo Ortuño Pérez
Fernando García Robredo
Universidad Politécnica de Madrid (UPM), ETSI de Montes, Ciudad Universitaria, E-28040 Madrid (Spain)
Universidad Pontificia de Comillas, Alberto Aguilera 23, E-28015 Madrid (Spain)
Corresponding author
Paper Info
Citation
López Torres I, Ortuño Pérez S, García Robredo F, Fullana Belda C (2016). Optimizing the management of uneven-aged Pinus nigra stands between two stable positions. iForest 9: 599-607. - doi: 10.3832/ifor1298-008
Academic Editor
Agostino Ferrara
Paper history
Received: Mar 26, 2014
Accepted: Nov 05, 2015
First online: Mar 01, 2016
Publication Date: Aug 09, 2016
Publication Time: 3.90 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2016
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 47310
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 40126
Abstract Page Views: 2496
PDF Downloads: 3469
Citation/Reference Downloads: 21
XML Downloads: 1198
Web Metrics
Days since publication: 3576
Overall contacts: 47310
Avg. contacts per week: 92.61
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2016): 6
Average cites per year: 0.60
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Dimensionless numbers for the net present value and the perpetual value of sustainable timber harvests from a monospecific uneven-aged forest
vol. 12, pp. 35-42 (online: 10 January 2019)
Research Articles
Use of LIDAR-based digital terrain model and single tree segmentation data for optimal forest skid trail network
vol. 8, pp. 661-667 (online: 22 December 2014)
Research Articles
Selection of optimal conversion path for willow biomass assisted by near infrared spectroscopy
vol. 10, pp. 506-514 (online: 20 April 2017)
Research Articles
Improving dimensional stability of Populus cathayana wood by suberin monomers with heat treatment
vol. 14, pp. 313-319 (online: 01 July 2021)
Research Articles
Comparison of genetic parameters between optimal and marginal populations of oriental sweet gum on adaptive traits
vol. 11, pp. 510-516 (online: 18 July 2018)
Research Articles
Distribution factors of the epiphytic lichen Lobaria pulmonaria (L.) Hoffm. at local and regional spatial scales in the Caucasus: combining species distribution modelling and ecological niche theory
vol. 17, pp. 120-131 (online: 30 April 2024)
Research Articles
Estimating the mechanical stability of Pinus nigra Arn. using an alternative approach across several plantations in central Italy
vol. 8, pp. 846-852 (online: 08 April 2015)
Research Articles
Modifying harvesting time as a tool to reduce nutrient export by timber extraction: a case study in planted teak (Tectona grandis L.f.) forests in Costa Rica
vol. 9, pp. 729-735 (online: 03 June 2016)
Research Articles
Deploying an early-stage Cyber-Physical System for the implementation of Forestry 4.0 in a New Zealand timber harvesting context
vol. 17, pp. 353-359 (online: 13 November 2024)
Research Articles
Stability analysis and selection of optimal Eucalyptus urophylla × E. grandis families
vol. 18, pp. 293-300 (online: 20 October 2025)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword