Evaluation of methods to improve the direct estimation of standing trees volume
iForest - Biogeosciences and Forestry, Volume 18, Issue 2, Pages 87-92 (2025)
doi: https://doi.org/10.3832/ifor4670-018
Published: Apr 17, 2025 - Copyright © 2025 SISEF
Research Articles
Abstract
Estimating timber volume in forests is crucial for effective management and commercial purposes, particularly for forest owners and managers. Accurate volume estimates inform management decisions, growth monitoring, and silvicultural treatments. Traditional methods often involve destructive sampling, which presents logistical and economic challenges. This study evaluates the non-destructive methods of Hossfeld’s, centroid sampling, and Pressler’s to estimate the volume of 42 Pinus pinaster and 50 Pinus radiata standing trees. For each species, the estimated volume was then compared with that calculated using precise measurements on felled trees and with the volume calculated using the simplified method F = 0.5. For both species, Pressler’s method showed the highest accuracy, with RMSE values of 28 and 102 dm³ for P. pinaster and P. radiata, respectively. However, the centroid and Hossfeld’s methods also showed satisfactory results: for P. pinaster the RMSE was 40 and 47 dm³, while for P. radiata it was 100 and 118 dm3, respectively. These estimates resulted largely more accurate than those obtained using the F=0.5 method (60 dm³ for P. pinaster and 432 dm³ for P. radiata). All the quick methods tested with F=0.5 show commendable accuracy, with Pressler’s method yielding the best results. According to the Percent Relative Bias, all the three methods slightly tend to underestimate the volume. Our results support the viability of non-destructive methods for rapid volume estimation without extensive felling and measurement. However, operational application in the field and validation across different tree species and growth habits are recommended. These methods offer viable alternatives to traditional approaches, reducing resource intensity and facilitating more frequent and detailed forest surveys. Our findings support the application of non-destructive techniques in forest management, potentially streamlining volume estimation and improving the accuracy of forest inventories.
Keywords
Tree Volume, Forest Measurements, Pressler Method, Hossfeld Method, Centroid Sampling
Introduction
Stand volume estimation methods and single tree volume estimation
Assessing the stock of wood in a forest is a crucial and expensive part of monitoring activities. This task is important for various reasons, ranging from local to global issues. It involves multiple stakeholders in the forestry sector, including forest owners, companies, and government agencies that primarily rely on wood as a commercial product. Additionally, it is relevant to institutions focused on environmental management, particularly in relation to CO2 sequestration and biodiversity conservation ([1], [19], [18], [3], [5], [6], [15]).
Estimating the timber resource of a forest requires estimating the volume of individual standing trees. The basic procedure is somewhat indirect, relying on volume tables or volume functions ([1], [9]). If such tools are available for the species and geographic area of interest, the estimation requires collecting specific information that these tools need as input. Typically, this includes the species, diameter at breast height (dbh), and some information about tree height.
The production and updating of volume tables and functions, especially in Italy, have practically stopped over the last few decades. The last major national effort was made in support of the 2nd National Forest Inventory (INFC 2005 - [17]). The collection of national-scale volume functions for Italian trees ([16]) encompassed all the major broadleaf and conifer species of the country. For many species, the number of sample trees was limited, although ultimately suitable for national-scale estimates. In contrast, for local assessments, estimates can be quite biased. The R package ForIT ([12]) enables the direct integration of functions in inventory estimations, highlighting the limited accuracy that can be obtained.
The creation of local volume tables for Sardinia has been nearly absent ([14]), and using national functions can lead to biased estimates.
Estimating the wood volume of a forest where reliable functions are not available must rely on direct measurements. To obtain an accurate measure of the tree bole volume, it is necessary to measure the diameter of many sections along the stem. Traditionally, this operation required cutting down the tree; however, modern laser technologies now allow measurements to be taken on standing trees. Nevertheless, this operation still demands a significant investment of time and resources ([2], [13]). Common operational requests for wood volume estimations in Sardinia cannot support such investments. As a result, an approximate stem volume estimate is obtained using the general average value of the “reduction factor” (F = 0.5). F represents the ratio of the stem volume to the volume of a cylinder with a section equal to the breast height section and height equal to the stem height (eqn. 1):
where dbh is the diameter at breast height, h is the tree height and Vstem is the real volume of the tree bole. The stand volume is then estimated by applying the average F value in the eqn. 2:
where G is the stand basal area, and hg is the height of a stem with an average basal area.
More accurate direct methods apply the same equation to groups of stems of different dimensions to account for the actual distribution of diameters. However, this improvement relies on evaluating the actual different F values for each group.
While felling and measuring the trunk, or evaluating the bole profile using terrestrial laser scanning (TLS) techniques, is a demanding operation, alternative methods have been developed over the years in Europe and North America to estimate the volume of a standing tree quickly yet reliably. These methods enable improved volume estimation for standing trees compared to the fixed F-value method, with the support of limited additional measurements. Despite their solid theoretical basis, they have been underutilized in forest mensuration due to the historical lack of tools to accurately measure diameters at specific heights along the stem ([9]). Today, advanced technologies make these tools readily available and widely used. Indeed, traditional instruments, such as the Spiegel Relascope and Finn caliper ([9]), and the Wheeler pentaprism tree caliper ([1]) have evolved into electronic devices and smartphone apps ([8]).
Improved quick estimation of the stem volume of single-standing trees
Among the non-destructive methods for estimating the volume of a standing tree based on measurements of trunk diameter at a given height, some have been more widely used and studied than others. Ducey & Williams ([4]) compared the accuracy of the centroid sampling method, the paracone method, and the Hossfeld’s method for estimating the volume of Pinus ponderosa trees in South Dakota. The results indicated that all three methods produced acceptably accurate results, with the paracone model being the most accurate for estimating the whole bole volume. Additionally, the Hossfeld’s method resulted slightly more accurate than centroid sampling for log volume estimation. In another study by Ozcelik et al. ([10]), six methods were tested for volume estimation of different species in Turkey, namely, Cedrus libani (18 trees), Abies cilicica (25), and Pinus brutia (27). The results showed that the Newton’s formula, the center of gravity method, and the centroid method were superior to the other methods in terms of accuracy. Wiant et al. ([20]) compared seven variations of the centroid, importance, and control variable methods for estimating the bole volume of over 5.400 trees, including both conifer and deciduous species in North America; the results showed that the centroid method was the easiest to apply in a forest setting and the most accurate among the tested methods, albeit with some bias.
In a study by Wood & Wiant ([21]) on more than 140 Australian hardwoods, centroid sampling yielded the best overall results. This suggests its potential applicability even for species with a deliquescent growth habit. Yavuz ([23]) compared the centroid sampling method with more sophisticated standard methods for estimating the stem volume of Fraxinus angustifolia (21 trees), Picea orientalis (38), and Fagus orientalis (33) in Turkey; the centroid sampling method showed no significant bias at the individual species level when compared to detailed measurements, and a significant improvement in estimation was observed when species were pooled.
The objective of this work is to make a preliminary evaluation of the accuracy of the centroid, Pressler’s, and Hossfeld’s methods in estimating the standing volume of a Mediterranean stand of Pinus radiata D. Don and P. pinaster Aiton.
Materials and methods
The study area is situated in central-eastern Sardinia (Italy) in the Gennargentu forest district, one of the 25 forest districts established under the Forest and Environmental Plan for the Sardinia Region ([11]). The district encompasses over 1500 km2 in a mountainous area (80% is above 600 m a.s.l., with 26% exceeding 1000 m a.s.l.) dominated by the Gennargentu massif. The artificial stands under investigation were established in the early 1970s between 830 and 900 m a.s.l. and currently cover over 10 ha. These stands are distributed across diverse slopes, ranging from flat to rather steep terraced terrains, and display different aspects, predominantly facing north, south, and east directions. Dominant species are Pinus radiata and P. pinaster. The measures were taken when the stands were over 40 years old, hence technically suited to produce economically valuable assortments.
The analysis was conducted on a set of 92 sample trees that were felled and accurately measured (Tab. 1). Sample trees were randomly selected within the strata defined, having extensively tallied all the stands. Before felling, species, dbh (diameter at 1.3 m), total height, health status, potential best withdrawable assortment, and eventual forking were recorded. After felling and limbing the main stem (usually the largest and most robust one, especially if forks were present) was measured. Attention was paid to preserve the whorl positions and any eventual secondary stems. Below 1.3 m above the ground, the measures were taken at heights of 0.15 and 0.50 m for approximately 9 out of 10 trees. Due to diverse constraints during the field work, auxiliary measurements were required for some trees. Above 1.3 m, the section heights were determined by branching measures, which were taken at each central section between two successive whorls up to a diameter of 5 cm.
Tab. 1 - Mean characteristics of the sample trees.
| Parameter | P. pinaster | P. radiata |
|---|---|---|
| n | 42 | 50 |
| dbhmin (cm) | 11 | 31 |
| dbhmax (cm) | 43 | 54 |
| dg (cm) | 22.4 | 42.5 |
| hmin (m) | 7.7 | 19 |
| hmax (m) | 16.4 | 29.5 |
| volmin (dm3) | 32 | 702 |
| volmax (dm3) | 836 | 2665 |
| volm (dm3) | 247 | 1493 |
Methods of volume estimation
The reference volume used for comparison was determined using Heyer’s formula, tailored to the tally protocol that was followed. As graphically displayed in Fig. S1 (Supplementary material), measured diameters were generally utilized as section central diameters (e.g., the diameter at 0.15 m was used to compute the volume from 0 to 0.3 m, and so on). The upper section of the stem was used as the base of the terminating cone. Generally, the 5 cm threshold diameter does not coincide with a whorl. To complete the volume, an additional cylinder was added, connecting the cone base to the top of the upper regular cylinder, using the diameter of the last section.
In this study, three methods were assessed for direct estimation of the volume of a standing tree, namely, Hossfeld’s, centroid sampling, and Pressler’s methods.
The Hossfeld’s method was proposed in the early 19th century but has been somewhat overlooked in the literature despite its demonstrated accuracy ([4]). This method enables the estimation of the volume for any specified section of the stem. The general formula is expressed as follows (eqn. 3):
In eqn. 3 VL represents the volume of a log of length L, A1/3L denotes the cross-sectional area measured at a distance 1/3·L from the larger end of the log, and AL corresponds to the cross-sectional area at the logs small end. When estimating the total tree volume AL= 0 and L = Htot = total tree height, thus the formula reduces to (eqn. 4):
The centroid sampling method is derived from the importance sampling method introduced by Gregoire et al. ([7]) and further developed by Kershaw et al. ([8]). Wood et al. ([22]) found that the variability in importance sample estimates was minimized when single-diameter measurements were taken at the height, splitting the predicted volume into two halves. They termed this point the “centroid point”, thus coining the term centroid sampling. This method requires the prior measurement of total tree height and upper stem diameter at centroid height. The height (Hs) of the upper stem sectional measurement (Ds) is calculated with eqn. 5 ([19] - simplified for total volume estimation):
where Htot is the total height of the standing tree. The application in the field can be carried out using instruments that allow the measurement of stem diameter at section heights that are not directly accessible. The requested section is relatively low and, hence, usually in clear sight.
The volume (Vtot) is expressed as follows (eqn. 6):
that, given eqn. 5 and As = Htot [(Ds2 π) / 4], can be simplified as (eqn. 7):
Eqn. 6 is based on the assumption that the stem conforms to the shape of a quadratic paraboloid ([19]). In practical terms, this formula is tightly related to Hossfeld’s formula because Hs is just below one-third of Htot.
The Pressler’s method requires estimating the height hP (Pressler’s height) of the stem section with a diameter equal to half the base diameter. La Marca ([9]) suggests that the area of the breast height section can be used as a substitute for the ground-level section area (S0). The latter approach was also adopted in this study.
Because the base section diameter (d0) is challenging to measure accurately due to butresses, it was not measured directly in the sample trees. We estimated the diameter of each tree using linear interpolation of all available diameter measurements below < 1.3 m, including the diameter at breast height (dbh). Initially, both variants of the formula are evaluated, searching for hp equal to half of d0 and equal to half of dbh. Also, hP is estimated by linear interpolation between the heights of the sections just above and below the searched diameter.
The volume of the standing tree is determined by the following equations (eqn. 8):
where d0 is the estimated ground level diameter and hp is the height where stem diameter equals d0/2 (eqn. 9):
Obviously, heights and diameters are assumed to be expressed in the same units in all the equations, and volume is estimated in the cube of that unit.
Estimation of additional measures required
As mentioned above, all the methods assessed in this study for directly estimating the volume of standing trees require additional measurements beyond the basic forest mensuration attributes, i.e., diameter at breast height (dbh) and total height (htot). The Hossfeld’s method requires D1/3L, that is the diameter of the section at 1/3 L; the centroid sampling method requires the Ds value, i.e., the diameter at “centroid height”; finally, the Pressler’s method requires hP, which is the height along the stem where the diameter is half the base section diameter (or the diameter at breast height).
Accuracy of the methods
The volumes estimated using the detailed measures taken on the sample trees served as a reference for the comparison of the different methods. The analysis aimed to evaluate the accuracy gain of the three methods tested with respect to the first approximation estimates. The comparison was conducted using the statistics reported in Tab. 2 (see also Tab. S1 in Supplementary material for the equations).
Tab. 2 - Accuracy statistics applied in this study. The corresponding formulas are reported in Tab. S1 (Supplementary material).
| Label | Statistics |
|---|---|
| MAE | Mean Absolute Error |
| Rsq | Coefficient of determination |
| RMSE | Root Mean Squared Error |
| PRB | Percent Relative Bias |
To verify and complement the results of the aggregate statistics, the volume estimates obtained by the three quick methods were compared with the reference estimates by linear interpolation, and the goodness-of-fit to the 1:1 relationship was assessed by graphical analysis. The intercept and slope were tested not significantly different from zero and one, respectively.
Results
In this study we evaluated the accuracy of three quick methods for volume estimation of standing trees and compared their accuracy with that of the oversimplified F = 0.5 approach currently used in Sardinia.
Graphical analysis
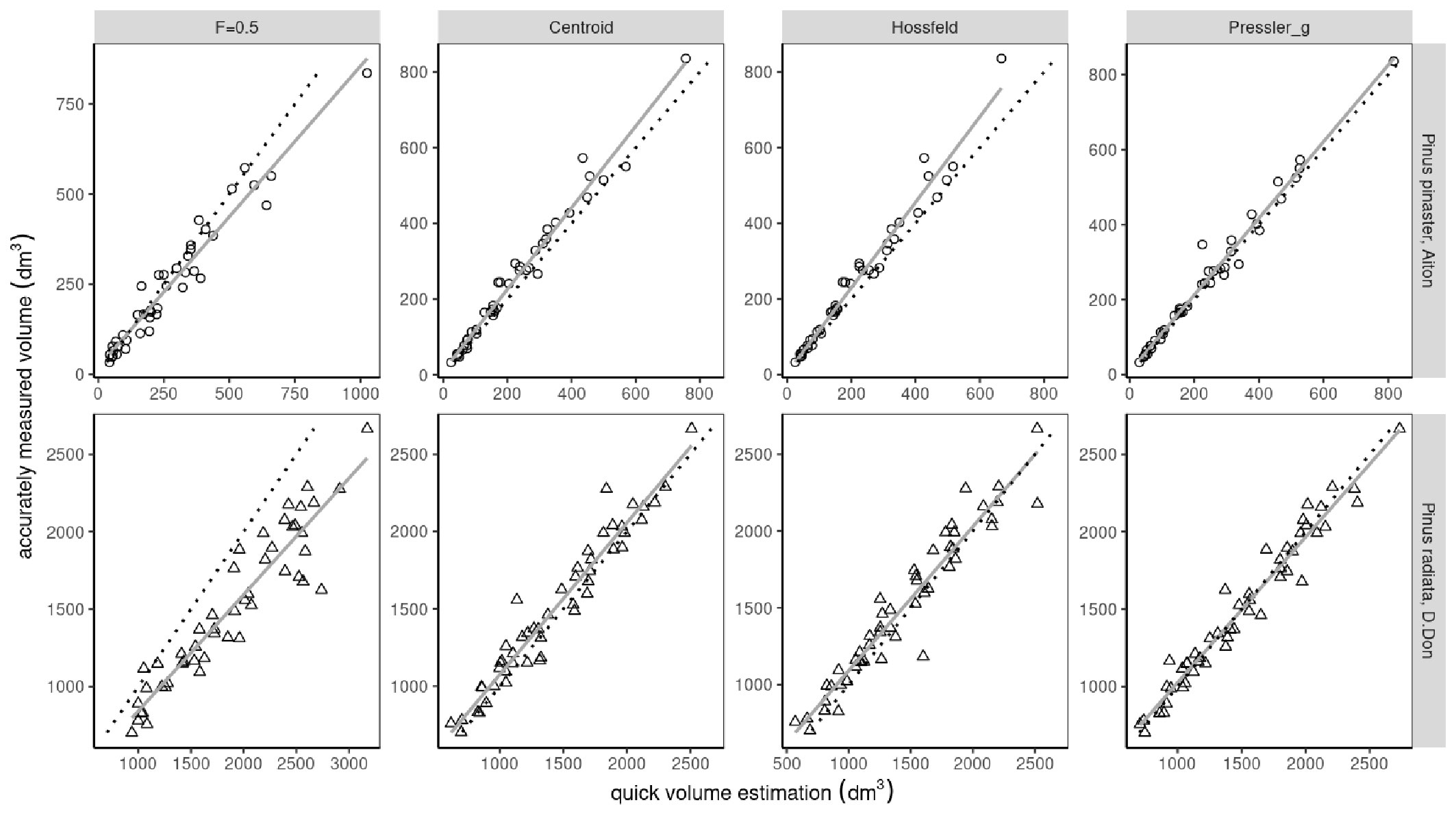
Fig. 1 shows the relationship between the reference volume calculated using Heyer’s formula on felled trees and the volume estimated by applying three quick methods to the same standing trees before they were cut down.
Fig. 1 - Graphical results of the quick volume estimation methods considered in this study for Pinus pinaster (upper row) and P. radiata (lower row).
Of the two variants of the Pressler’s method initially considered, the one using the base section was discarded due to its poor performances. Therefore, only the results of the Pressler’s method based the diameter at breast height are reported here.
Regarding Pinus pinaster, the performances of the Pressler’s method were superior, with minimal bias and a slope that is almost perfectly overlapping the 1:1 line. The centroid and Hossfeld’s methods also provided good estimates, showing a similar tendency to underestimate the volume as it increases, while a more pronounced underestimation was detected by using the Hossfeld’s method. While these methods generally underestimate the volume, the application of the F=0.5 approach results in a clear overestimation, especially as the tree size increases.
Regarding Pinus radiata, the F=0.5 simplification yields the poorest results, exhibiting the highest bias and a large overestimation of the standing tree volume, as clearly inferred by regression line that is distinctly not aligned with the 1:1 line. The Pressler’s method yielded the most accurate estimations of tree bole volume, while improvements were also observed using both the Hossfeld’s and centroid methods. The latter demonstrated a slight bias across the entire volume range, whereas the Hossfeld’s method showed a reduced bias as tree size increases.
Statistics
Tab. 3 reports the regression coefficients of the linear relationships (Fig. 1) between the reference values and the tree volume estimates obtained using the quick methods considered. Regarding the F=0.5 method, the slope was significantly different from 1 for both species, while the other methods exhibited varying fitting. Both the Centroid and the Hossfeld’s methods had a slope not significantly different from 1 only in P. radiata. Conversely, the slope of the regression line using the Pressler’s estimates was not significantly different from 1 only for P. pinaster. However, the probability is just below the threshold of significance while for P. radiata RMSE for this method presented the lowest value. The results of the comparison of the methods considered for each species are reported in Tab. 4 in terms of aggregate statistics. The error values resulted strongly affected by the different stem volume of the two species. Again, the Pressler’s method showed the best performance in P. pinaster, showing the lowest values of MAE and RMSE. Indeed, the RMSE for the Pressler’s method was 28 dm3, while Centroid and Hossfeld0s had 40 and 47 dm3, respectively. The F=0.5 method had an percentage relative bias (PRB) slightly lower than that of the Pressler’s method (approximately 5% vs. 8%, respectively). However, aggregate statistics do mask the uneven distribution of errors, as already displayed in Fig. 1. The Centroid and the Hossfeld’s methods yield quite similar results in terms of mean absolute error (MAE), which were significantly better than the F=0.5 results. PRB values were also similar, although slightly worse than for the F=0.5 simplified method.
Tab. 3 - Significance tests of the regression analysis coefficients. Regression model: Volreference = b0 + b1 · Volquick. (ns): not significatively different; (sig): significantly different (α = 0.05).
| Method | Species | p(H0: b0=0) | p(H0: b1=1) | ||
|---|---|---|---|---|---|
| F=0.5 | P. pinaster | 0.081 | ns | 0.000 | sig |
| P. radiata | 0.248 | ns | 0.000 | sig | |
| Centroid | P. pinaster | 0.153 | ns | 0.006 | sig |
| P. radiata | 0.077 | ns | 0.588 | ns | |
| Hossfeld’s | P. pinaster | 0.685 | ns | 0.000 | sig |
| P. radiata | 0.012 | sig | 0.115 | ns | |
| Pressler’s | P. pinaster | 0.204 | ns | 0.352 | ns |
| P. radiata | 0.068 | ns | 0.045 | sig | |
Tab. 4 - Summary of the accuracy of the different volume estimation methods. (MAE): mean absolute error; (Rsq): coefficient of determination; (RMSE): Root Mean Squared Error; (PRB): percentage relative bias.
| Species | Method | MAE | Rsq | RMSE | PRB |
|---|---|---|---|---|---|
| P. pinaster | Centroid | 30.0 | 0.948 | 40.6 | -14.5 |
| F=0.5 | 40.3 | 0.888 | 59.2 | 5.3 | |
| Hossfeld’s | 31.8 | 0.929 | 47.3 | -16.1 | |
| Pressler’s | 18.2 | 0.975 | 28.0 | -7.9 | |
| P. radiata | Centroid | 100.6 | 0.922 | 133.3 | -5.6 |
| F=0.5 | 374.9 | 0.177 | 432.5 | 19.4 | |
| Hossfeld’s | 118.5 | 0.902 | 149.0 | -5.9 | |
| Pressler’s | 79.3 | 0.954 | 102.4 | -0.4 |
Regarding P. radiata volume estimates, the Pressler’s method was the most accurate, demonstrating superior performance for all error statistics. Notably, there is a significant improvement in the PRB metrics compared to P. pinaster, reducing from 8 to 0.3% in absolute values. The accuracy of the estimates using the Hossfeld’s and the Centroid methods was notably similar also in this species. However, the Centroid method appears to exhibit slightly better performance in terms of RMSE. The F=0.5 method exhibited a sharp decline in performance for this species, as the RMSE was almost three times higher than that obtained using the Hossfeld’s method, and the PRB was three times higher than that from the Hossfeld’s and Centroid methods, with a very low R2 (0.18).
For both species, the F = 0.5 simplified method consistently showed a positive bias, while the Pressler’s method appears to yield the best approximation to the reference volume.
Discussions and conclusions
This study analyzed the efficacy of various methods for rapid tree volume estimation using non-destructing methods during forest surveys by comparing them with precise ground-thuth measurements.
A preliminary result of this study is the difference in the performances of the Pressler’s method when using dbh and d0. Indeed, using d0 we observed a significant performance decline, leading to the overestimation of the tree volume. The overestimation obtained using d0 compared to dbh may seem expected, but it is counterintuitive since the method was originally designed to be used based on d0. This finding supports the suggestion made by La Marca ([9]). It is worth noting that this does not significantly impact the application of the method, as it is easier to measure the dbh than an arbitrary diameter near ground level, especially when trying to avoid buttresses. This insight could potentially influence future practices in forest volume estimation using the Pressler’s method.
Overall, the methods compared in this study provide valid alternatives for estimating tree volume and calibrating existing tables. These non-destructive methods avoid the development of complex equations that require multiple tabulated parameters for application. Therefore, they can be considered as efficient and non-destructive alternatives for forest volume estimation and calibration processes. This could potentially streamline the process and reduce the reliance on more resource-intensive methods.
The plot of residuals (Fig. S3 in Supplementary material) showed a trend of incresing heteroscedasticity for values exceeding 500 dm³. This trend is observed in particular for Pressler’s using S0. Due to the method’s assumption of a quadratic paraboloid shape for the tree trunk, larger volumes may show significant deviations from this geometric estimate, increasing error variability.
In this study the height of standing trees was measured with an ultrasound hypsometer. Conversely, the reference volume was calculated using the length of the felled trees measured with a rolled meter. Due to potential differences between the two measurement methods, we compared the two height measures (Fig. S2, in Supplementary materials). In both species, the height of standing trees measured with the hypsometer is underestimated (the differences are significantly negative, Tab. S2), by less than 1 m on average. This underestimation becomes more pronounced with increasing tree height. Because the height measured with the hypsometer is directly utilized in the volume calculations for both the Hossfeld’s and the Centroid methods, any discrepancies in height measurements significantly affect the final volume estimates. As demonstrated in this study, this led to a more pronounced underestimation of volume for the abovementioned methods compared to the Pressler’s metod.
Although the three methods considered in this study are similar, their measurement approaches have essential differences that must be considered. In the Hossfeld’s method, the initial measurement is the total tree height; subsequently, one-third of the total tree height is calculated to determine the section at that point along the stem, resulting in three measurements and one straightforward calculation. The Centroid method requires more effort: after measuring the dbh and the total tree height, it is necessary to calculate both the k value and the height Hs along the stem where the second diameter must be measured, resulting in four measurements and two calculations. In contrast, Pressler’s method eliminates the need to measure total tree height. It requires measuring the diameter at breast height (dbh) and the height at which the stem diameter is half the diameter at breast height. Hence, the latter approach only requires two measurements and a straightforward calculation, while the first two methods require measuring an additional section at a precise height, allowing little margin for errors. Using the Pressler’s method, however, the specific height of the section is not explicitly defined. Identifying the section of a cylindric-shaped stem at which half the diameter at breast height (dbh) is reached can be challenging in the field, even when surveyors are instructed to stop as soon as they reach half dbh. Moreover, the height at which the second section along the stem is measured are similar in the Hossfeld’s and Centroid methods, and this may explain their comparable performances.
The observed differences between the two species considered can be attributed to differences in stem shape. Pinus pinaster typically exhibits a more irregular stem and smaller size compared to Pinus radiata. In this study, the latter species demonstrates a larger overall size and generally has a more regular stem profile.
The methods tested in this study show commendable accuracy. However, it is important to note that these methods were applied using measurements from felled trees, which allow for precise measurements of height, length, and section diameters. As mentioned earlier, the required sections and heights are calculated using linear interpolation. However, the application of these methods requires that measurements are taken from standing trees, which present a set of challenges. Therefore, the volume will be calculated using quick estimation methods, and when necessary, the trees will be felled to obtain detailed measurements and verify the accuracy of the estimates.
All of these methods require measuring the upper stem diameter of trees in the forest, which involves using appropriate tools, e.g., Bitterlich relascope, Wheeler caliper, or Finn caliper. While these tools can be difficult to find and somewhat expensive, their use in this context can provide a good return on investment. Additionally, measurements taken in the forest can be affected by operational challenges and the ability to accurately locate sections and heights in the upper stem, potentially leading to a lack of precision or systematic errors. Further research is needed to effectively apply these methods as they were originally intended.
Finally, it is worth remembering that these methods can be applied to the genus Pinus, which exhibits a typical excurrent habit. Although Wood & Wiant ([21]) successfully applied them to trees with a deliquescent habit, further research is needed to corroborate its validity. This is particularly important for low-density stands of broadleaved species, where large branches which contribute significantly to the volume may be inserted very low along the stem, and this may represent a potential problems in locating the upper stem sections.
Despite the limitations discussed above, this study supports the robustness of the theoretical framework underlying these methods for rapidly estimating the volume of standing trees, which demonstrated to yield accurate results for trees with an excurrent growth habit.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Roberto Scotti 0000-0001-7394-4473
NuoroForestrySchool, Department of Agricultural Science, University of Sassari, via Colombo 1, I-08100 Nuoro (Italy)
Corresponding author
Paper Info
Citation
Mura M, Mura M, Scotti R (2025). Evaluation of methods to improve the direct estimation of standing trees volume. iForest 18: 87-92. - doi: 10.3832/ifor4670-018
Academic Editor
Rodolfo Picchio
Paper history
Received: Jun 21, 2024
Accepted: Feb 11, 2025
First online: Apr 17, 2025
Publication Date: Apr 30, 2025
Publication Time: 2.17 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2025
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 6298
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 2695
Abstract Page Views: 1508
PDF Downloads: 1909
Citation/Reference Downloads: 1
XML Downloads: 185
Web Metrics
Days since publication: 250
Overall contacts: 6298
Avg. contacts per week: 176.34
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
(No citations were found up to date. Please come back later)
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Advantages of the point-intercept method for assessing functional diversity in semi-arid areas
vol. 8, pp. 471-479 (online: 31 October 2014)
Research Articles
Performance assessment of two plotless sampling methods for density estimation applied to some Alpine forests of northeastern Italy
vol. 16, pp. 385-391 (online: 19 December 2023)
Research Articles
A rapid method for estimating the median diameter of the stem profile of Norway spruce (Picea abies Karst) trees
vol. 10, pp. 328-333 (online: 11 February 2017)
Research Articles
Alternative methods of scaling Eucalyptus urophylla trees in forest stands: compatibility and accuracy of volume equations
vol. 11, pp. 275-283 (online: 29 March 2018)
Technical Advances
Improved estimates of per-plot basal area from angle count inventories
vol. 7, pp. 178-185 (online: 17 February 2014)
Research Articles
Optimizing line-plot size for personal laser scanning: modeling distance-dependent tree detection probability along transects
vol. 17, pp. 269-276 (online: 07 September 2024)
Research Articles
The recreational valuation of a natural forest park using travel cost method in Iran
vol. 2, pp. 85-92 (online: 10 June 2009)
Research Articles
Estimating changes in soil organic carbon storage due to land use changes using a modified calculation method
vol. 8, pp. 45-52 (online: 17 June 2014)
Research Articles
Simplified methods to inventory the current annual increment of forest standing volume
vol. 5, pp. 276-282 (online: 17 December 2012)
Research Articles
Quantifying forest net primary production: combining eddy flux, inventory and metabolic theory
vol. 10, pp. 475-482 (online: 12 April 2017)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword