The impact of land use on future water balance - A simple approach for analysing climate change effects
iForest - Biogeosciences and Forestry, Volume 14, Issue 2, Pages 175-185 (2021)
doi: https://doi.org/10.3832/ifor3540-014
Published: Apr 13, 2021 - Copyright © 2021 SISEF
Research Articles
Abstract
Regional climate change projections for Europe agree in predicting a statistically significant warming in all seasons. The most significant climate change effect is its impact on water cycle through altering precipitation patterns and evapotranspiration processes at multiple scales. The anticipated changes in the distribution and precipitation amounts together with continuously increasing temperatures may induce a higher rate of water consumption in plants, which can generate changes in soil moisture, groundwater, and the water cycle. Thus, climate change can cause changes in the water balance equations structure. A Thornthwaite-type monthly step water balance model was established to compare the water balance in three different surface land cover types: (i) a natural forested area; (ii) a parcel with mixed surface cover; (iii) an agricultural area. The key parameter of the model is the water storage capacity of the soil. Maximal rooting depth of the given area is also determinable during the calibration process using actual evapotranspiration (AET) and soil physical data. The locally calibrated model was employed for assessing future AET and soil moisture of selected land cover types using data from four bias-corrected regional climate models. The projections demonstrate increasing actual evapotranspiration values in each surface cover type at the end of the 21st century. Regarding the 10th percentile minimum soil moisture values, the forested area displayed an increasing trend, while the agricultural field and mixed parcel showed a strong decrease. The 30-year monthly means of evapotranspiration shows the maximum values in June and July, while the minimum soil moisture in September. Water stress analysis indicates water stress is expected to occur only in the agricultural field during the 21st century. The comparison of the three surface covers reveals that forest has the greatest soil water storage capacity due to the highest rooting depth. Thus, according to the projections for 21st century, less water stress is predicted to occur at the forested area compared to the other two surface covers which shows shallow rooting depth.
Keywords
Water Balance, Climate Change, Plant Available Water, Evapotranspiration, Soil Moisture, Water Stress
Introduction
The ongoing climate change can be characterized by a statistically significant warming trend in all seasons throughout Europe ([5], [45]). In the Carpathian Basin, the climate projections for the 21st century indicate an increase of temperature (expected in all seasons) and an increase of climatic aridity. The projected change could be between 2-5 °C, depending on the applied climate model and emission scenario ([36], [35]).
Higher temperatures reflect larger energy potentials in the atmosphere, which, therefore, contains more water at the same time and/or has a shorter water vapour retention time, both of which will accelerate the hydrological cycle ([7], [19]). This acceleration means temporal distribution changes of the precipitation, which often results in increased precipitation amounts during single events, though not affecting the annual rainfall amount which remains constant. Therefore, warming has also an effect on the hydrological cycle through precipitation intensity ([23]). The Carpathian Basin may experience a decrease of the precipitation amount in summer and an increase in winter ([35], [14]).
The most significant effect of climate change is its impact on the water cycle by altering precipitation patterns and evapotranspiration processes at multiple scales ([41]). The forecasted changes in the distribution and amount of precipitation along with the continuously increasing temperature may lead to a higher water consumption in plants (due to the longer growing seasons, and larger leaf area - [1]), which will generate changes in soil moisture, groundwater ([27]), and the water cycle. Thus, climate change can cause changes in the water balance equations structure ([21]).
In the Carpathian Basin, 90% of the precipitation is evapotranspired, while the remaining 10% is runoff ([24]). This large influence of vegetation on the water cycle makes modelling necessary to attain a quantitative understanding of the evapotranspiration process.
Previous studies modeling the impact of climate change on water balance ([25], [39], [46], [6]) revealed that evapotranspiration may increase, but soil water content may decrease in the future due to presumably increasing temperatures and decreasing precipitation, thereby leading to possible enhanced water scarcity towards the end of the 21st century. Thus, modelling the expected changes in water resources over different time scales can be crucial for water management, agriculture, forestry, and civil engineering in the Carpathian Basin region ([15], [18], [30]). Consequently, further studies at the regional scale are required ([40]).
The overall objectives of this study are to establish a monthly step water balance model for three different surface covers: (i) a forested area; (ii) a mixed parcel (1 km2 corn field plot with strips of poplar trees); (iii) an agricultural area. Using the calibrated model, the impact of climate change in the 21st century is analysed to compare the water balance of forest and two other land use types located at the north-western part of the Carpathian Basin.
Materials and methods
Study area
To test our model, we used three study areas in the Carpathian Basin, namely: a forested area, a mixed parcel, and an agricultural field. The first two are situated in the Western part of the Transdanubian Region of Hungary, while the third is in the eastern part of Austria next to Vienna (see Fig. S1 in Supplementary material).
Forested area
The forested area is an experimental catchment at the eastern foothills of the Alps near the city of Sopron. The elevation of the study area ranges from 370 to 550 m a.s.l.
This area has a subalpine climate, with an average annual temperature of 8.5 °C, and annual precipitation of 700-750 mm. The driest season is autumn, while the wettest is late spring and early summer ([11]).
The geological basis of the catchment is fluvial sediments deposited in five distinct layers in the tertiary (Miocene) period on crystalline bedrock. A finer-grained layer appears in the valley bottom, which is a good aquifer, giving rise to perennial streams ([22]). The soil texture of this area is loam. The dominant vegetation in the catchment comprises alder (Alnus glutinosa) in the bottom of the valley, spruce (Picea abies), and beech (Fagus sylvatica) on the northern slopes, whereas sessile oak (Quercus petraea) and beech (Fagus sylvatica) are on the southern slopes.
The investigation period was from January 2000 to December 2008, due to the availability of the data which originated from the AgroClimate.2 project ([8]).
Mean monthly temperature (TM) and monthly summed precipitation (PM) values are utilized as inputs for the forested area and measured (remote-sensing based) actual evapotranspiration values (ETCREMAP) for calibration and validation.
Szilágyi et al. ([43]) established a method called CREMAP to downscale the regional actual evapotranspiration values into spatially variable actual evapotranspiration rates. The CREMAP model is a modified, upgraded version of the ET estimation technique of Szilágyi & Józsa ([42]). The model provides a measure of actual evapotranspiration through a satellite-based, remote-sensed approach. Kovács ([24]) mapped the monthly actual evapotranspiration (ETCREMAP) for Hungary from 2000 to 2008 using the Szilágyi CREMAP method. The base of the method is a linear transformation of the eight-day composited MODIS (Moderate Resolution Imaging Spectroradiometer) daytime surface temperature values into actual evapotranspiration rates ([42]). These monthly actual evapotranspiration maps were prepared from March until November of each year.
Mixed parcel
The mixed parcel is basically used as an agricultural plot and was formerly a cornfield, except during the period 2003-2007 when it was used to grow barley and in 2004 when it was used for wheat. However, poplar (Populus × canadensis) trees can also be found along strips in this area. The parcel has a total area of about 1 km2, and the elevation is 120 m a.s.l.
The selected parcel is located in the Mosoni-sík microregion that is situated in Györ-Moson-Sopron County. It is basically (73.5%) plough-land. On the whole, this natural microregion is an alluvial plain ([11]).
The climate is continental, with temperature differences between the western and eastern part of the natural microregion. The average annual temperature is 9.7 °C and the annual precipitation is 560 mm ([11]).
The investigation period was from January 2000 to December 2008, the same as for the forested area. The data originated from the AgroClimate.2 project ([8]).
The input dataset contains mean monthly temperature (TM) and monthly summed precipitation (PM) values as well as measured (remote-sensing) actual evapotranspiration values (ETCREMAP) for calibration and validation.
Agricultural field
The agricultural field is an area of about 1000 km2 in the eastern part of Austria, between Vienna and the border of Slovakia. The elevation of this study area is 157 m a.s.l. It is characterized by a subhumid climate with a mean annual temperature and precipitation of approximately 10 °C and 550 mm, respectively. Typical summers are hot and dry, while winters are mainly cold with severe frost and limited snow cover ([16]). A typical soil type is chernozem, a black-coloured fertile soil ([16]). The favourable environmental conditions supported the development of large areas (650 km2) of intensive production of various crops in the past decades. As the region is prone to water deficit stress, irrigation is common and is expected to become even more important due to climate change effects ([31]).
Basic data for this study were obtained at the experimental farm of the University of Natural Resources and Life Sciences, Vienna (BOKU), in Groß-Enzersdorf (48° 12′ N, 16° 34′ E; 157 m a.s.l.). Regarding climate conditions, the location is representative for the agricultural field ([34]).
Mass changes of the surface-soil-vegetation system and, therefore, changes in soil water content can be estimated using weighing lysimeters ([3], [33]). Soil water balance components were determined using a large weighing lysimeter. During installation, a typical soil profile was created by re-packing soil in layers as follows: (i) sandy loam soil (0-140 cm, porosity 35-40% - 30 % sand, 50 % silt, 20 % clay; porosity: 43 %); (ii) gravel (140-250 cm, only macropores with negligible water holding capacity).
These soil characteristics and the consequent hydraulic properties were taken as the basis for the simulation. Although the input parameters are assumed to be typical for the region, a single soil profile cannot represent the characteristics of a large area like the agricultural field in general.
The utilized lysimeter and the surrounding area were permanently covered by grass and maintained to represent the standard conditions for the determination of reference evapotranspiration ([2]).
Eqn. 1 illustrates the relation between measured (Wlys, Wdrain) and unknown (Plys, Ilys, ETlys) water balance components based on daily changes (Δ - eqn. 1):
Therein, ΔWlys is the daily change of the soil water mass, determined by means of the weighing facility. ΔWdrain is the daily amount of drainage water (freely draining by gravity forces), measured at the bottom outlet by means of a tipping bucket device. Plys is precipitation and Ilys is irrigation on the lysimeter. Both were assumed to occur when net changes in soil water (ΔWlys + ΔWdrain) were positive. Consequently, evapotranspiration from the lysimeter surface (ETlys) was quantified as negative changes in soil water (ΔWlys + ΔWdrain). All units are millimetres per day (mm day-1). Specific smoothing functions were applied to improve measurement accuracy, which is 0.1 mm at average wind velocity. A detailed description of measurements and data processing can be found in Nolz et al. ([33], [34])
Mean monthly temperature (TM) and summed monthly precipitation (PM) values make the input dataset, and the actual evapotranspiration values (ETLYSIMETER) are for calibration and validation. Nevertheless, all input data refer to the experimental site in Groβ-Enzersdorf. In the given case, irrigation and precipitation comprise the input parameter.
The investigation period was from January 2004 to December 2011. It is important to note that the difference between the time series of the study areas is due to the availability of the input data.
The Thornthwaite-type hydrological model description
The Thornthwaite-type water balance model represents a 1-D system which considers only vertical fluxes. Input values are monthly precipitation (PM, mm) and temperature (TM, °C - [9]). To develop the Thornthwaite-type water balance model, we have chosen the R statistical software ([37]).
The first step in setting up the model was the calculation of the potential evapotranspiration (PET). PET is the amount of water that can be evaporated and transpired when soil water is sufficient to meet atmospheric demand ([2]). In this study, a temperature-based PET-model after Hamon ([17]) was applied. The calculation of potential evapotranspiration after Hamon (PETH) is described by the following equations (eqn. 2, eqn. 3):
where D is the day length (hr), TM is the average monthly temperature (°C), and e*m is the saturation vapour pressure (kPa).
The next step was a condition. If PM ≥ PETM then ETM = PETM and (eqn. 4):
where PETM is the calibrated monthly potential evapotranspiration (mm). Determination of PETM is part of the calibration, which will be described later. ETM (mm month-1) is the monthly actual evapotranspiration, and SOILM (mm) is the monthly soil moisture. Actual evapotranspiration is the amount of water evaporating from the surface and transpired by plants if the total amount of water is limited ([28]). SOILM represents the amount of soil water available for the vegetation (which is different from the total amount of soil water). Both ETM and SOILM denote the key components of this study.
For the simulation procedure, the first SOILM-1 value was set to a maximum value that corresponds with the soil-water storage capacity (SOILMAX, mm). The basic assumption was that soil is saturated before the beginning of the vegetative period. SOILMAX was introduced using unsaturated hydraulic parameters of the study areas’ soil types and setting a rooting depth of 1 m (eqn. 5):
where θfc is the water content at field capacity (dimensionless), θpwp is the water content at permanent wilting point (dimensionless), zrz is the rooting depth (vertical extent of root zone, in mm).
The following procedure illustrates how soil water storage is considered as a reservoir for evapotranspiration: if precipitation is less than the (calibrated) potential evapotranspiration in a certain month (i.e., PM < PETM), then (eqn. 6):
where (eqn. 7):
and ΔSOIL is the decrease in soil water storage [mm].
Model calibration and validation
Remote sensing based (for the forested area and mixed parcel) and grass-covered lysimeters (for the agricultural field) actual evapotranspiration data served as basis for calibration and validation. The available time series for the forested area and for the mixed parcel (2000-2008) was divided into two parts. The first part is used for calibration from 2000 to 2005, whereas the second is for validation from 2006 to 2008. In the agricultural field, the time series (2004-2011) was also divided into two parts. The first (from 2004 to 2008) was used for calibration and the second (from 2009 to 2011) for validation.
The calibration datasets were further divided into two parts considering both potential and actual evapotranspiration. The results of calibration and validation are reported in the Results section.
Fig. S2 (Supplementary material) schematically represents the functioning of the model and the relationships between the applied parameters in the modelling process for the forested area and mixed parcel.
Parameters of the calibration and the input data (TM and PM) of the validation period (2009-2011 for the agricultural field; 2006-2008 for the forested area and the mixed parcel) were used for the validation.
Projection procedure
As the basis for the projection procedure, the water balance model was re-calibrated for each study area using all available data (2000-2008 for the forested area and mixed parcel; and 2004-2011 for the agricultural field). This was done because model calibration using as much data as possible was assumed to deliver the best possible results.
Inputs for predicting future developments of actual evapotranspiration (ETM), soil moisture (SOILM), and the lower 10th percentile of soil moisture (SOILM_10Perc, i.e., mean of the values below the 10th percentile of the soil moisture) were the equations of the broken line regression (details in the Results section), the calibrated SOILMAX values, and projected temperature (TM) and precipitation (PM) values. The latter two originate from four grid-based, bias-corrected regional climate models (RCMs - FORESEE database).
FORESEE database
FORESEE is a bias-adjusted database that contains daily meteorological data (min/max temperature and precipitation) based on the simulation results of ten RCMs for 2015-2100, and observation based data for the period 1951-2014 interpolated to 1/6×1/6 degree spatial (horizontal) resolution grid (using inverse distance interpolation technique). Furthermore, all of the time series were converted to a 365-day calendar ([10]). It should be noted that each of the used RCM data are based on the A1B greenhouse gas emission scenario (i.e., a balanced emphasis on all energy sources).
Regional climate models
The four different RCMs illustrate the uncertainties, because all climate projections have inherent uncertainties. Data were extracted from the pixel including the study sites’ coordinates. The main properties of the RCMs can be found in Tab. S1 (Supplementary material). In the following, each model will be referred to by their model ID (first column of Tab. S1).
The time scale of RCMs covers a range from 2015 to 2100. Each contains temperature and precipitation data in monthly time intervals. To evaluate the results for the 21st century, four main investigation periods were designated: 1985-2015 (01.01.1985 - 01.01.2015), 2015-2045 (01.01.2015 - 01.01.2045), 2045-2075 (01.01.2045 - 01.01.2075), and 2070-2100 (01.01.2070 - 01.01.2100). The results of the first investigation period (1985-2015) are based on observation data (model ID “0”). As mentioned before, the FORESEE results for the RCMs were available from 2015; therefore, the investigation periods had to be shifted by five years compared to the investigation periods of the AgroClimate.2 project. With the data at hand, these 30-year-blocks with a five-year overlap in the last two periods seemed the best partitioning. The overlap in the last part of the 21st century was necessary because only 25 years of data were available.
Water stress
An appropriate and simple way to assess water stress is the calculation of the relative extractable water (REW, dimensionless) using the following equation ([12]) - eqn. 8):
When REW drops below 50% of SOILMAX, the transpiration is progressively reduced (because of stomatal closure); hence, plant water stress is assumed to occur. SOILMAX parameter is the maximal amount of water available to plants and, therefore, it reflects the maximum extractable water in the soil. The average soil moisture (SOILM) is the extractable water in the different periods of investigation.
Evaluating model performance
Model performance was tested using the coefficient of determination (R2) and the Nash-Sutcliffe model efficiency coefficient (R2NS). The latter is a criterion used for calibration and validation of hydrologic models (eqn. 9):
where ETMSR_i is the time series of measured values, ETSIM_i is the time series of simulated values, and mMSR_i is the average value for the considered period.
Results
Methodical results
Calibration of the potential evapotranspiration
The first step of calibration considered the potential evapotranspiration for actual land cover using ETCREMAP-values (for the forested area and mixed parcel) and Etlys values (for the agricultural field) at well-watered conditions. The latter were assumed to occur when precipitation or the actual evapotranspiration (ETCREMAP or ETlys) exceeded the potential evapotranspiration (PETH - eqn. 10):
The ETlys/ETCREMAP values selected in such a way are denoted PETlys/PETCREMAP. Measured (PETlys/PETCREMAP) and calculated (PETH) values were correlated with the second variable as the explanatory one. PET is known to be different between growing season and dormancy, therefore different relationships had to be established for the two periods ([38]). For this purpose, a software package named “segmented” of R software environment was applied ([37]). The bases are the so-called broken-line or segmented models that create a piecewise linear relationship between the response and one or more of the explanatory variables. This linear relationship is represented by two or more straight lines connected at unknown values called breakpoints ([29]).
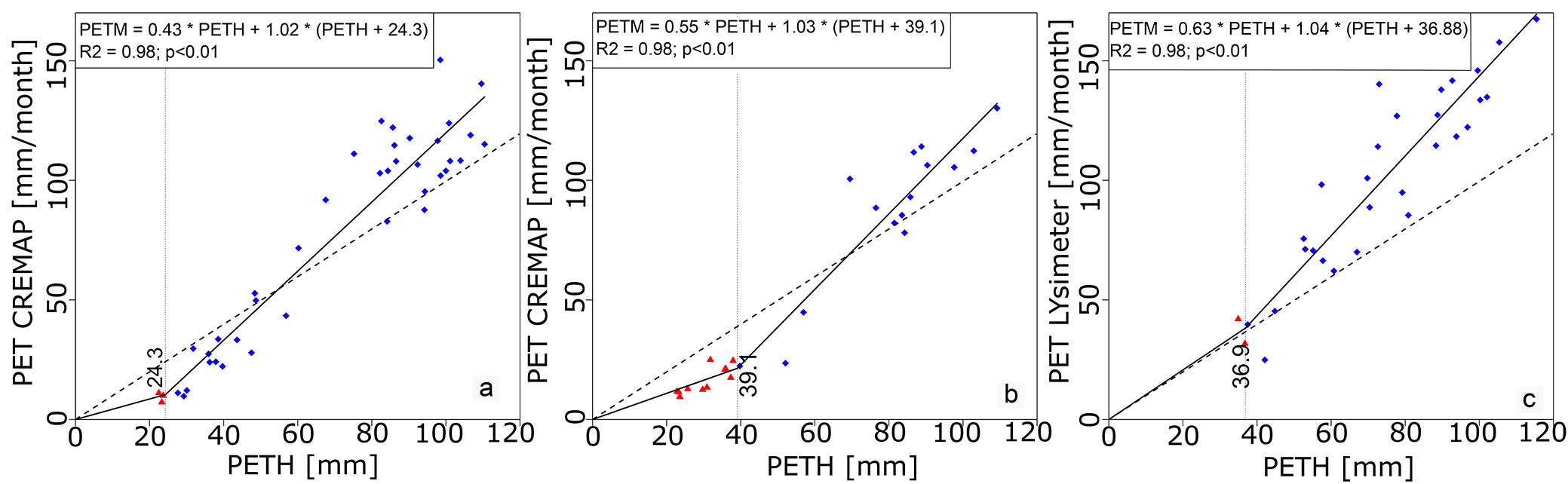
We compared the three study areas regarding PET calibration. Correlation between PETH and PETCREMAP/LYS during the period of dormancy is illustrated by the section on the left of the vertical dotted line (broken-line approach) in Fig. 1. This comparison revealed that each area has a high correlation between PETCREMAP/LYS and PETH, as reflected by the high coefficient of determination (R2 = 0.98 in each case).
Fig. 1 - Relationship between PETCREMAP/PETLYSIMETER and PETH in growing and dormant seasons with a 1:1 line (dotted), at forested area (a), at mixed parcel (b), at agricultural field (c) obtained after the calibration of PETH. The red triangles represent the values of the dormancy period, while blue dots represent the values of the growing season. The vertical dotted line is the separation of the two different vegetative states.
The 1:1 dotted lines exposed overestimation in the forested area (Fig. 1a) and mixed parcel (Fig. 1b), though only during the dormancy period. Therefore, the globally calibrated, calculated Hamon type PET has higher values than the measured PET in the winter seasons, as indicated by the lines of the first segment appearing under the 1:1 lines (Fig. 1a, Fig. 1b). Conversely, the agricultural field provides proper estimations for the dormant season, which means greater PETH values as well. However, only two values of lysimeter data (red triangles) could be related to this period, thus little could be concluded (Fig. 1c).
The breakpoint value obtained for the forested area (24.3 mm) is lower than the two other areas (mixed parcel: 39.1 mm; agricultural field: 36.9 mm). This can be attributed to the presence in the forested area of conifer species, the growing season of which begins earlier. Nevertheless, the value of albedo is also smaller in the case of the forested area; consequently the absorbed energy is higher, which can be manifested in higher evapotranspiration.
By contrast, each study area expresses greater or lesser underestimation in the growing season (i.e., the calculated PETH shows lower values than the measured values), particularly toward the higher values (Fig. 1). The largest underestimation occurred in the agricultural field during the growing season. However, the measured PET (PETCREMAP/LYS) removes the underestimations during the calibration of the calculated PET (PETH) because the measured PET was accepted as real data. Therefore, the measured PET (PETCREMAP/LYS) makes the calculated PET (PETH) surface dependent.
Calibration of the actual evapotranspiration
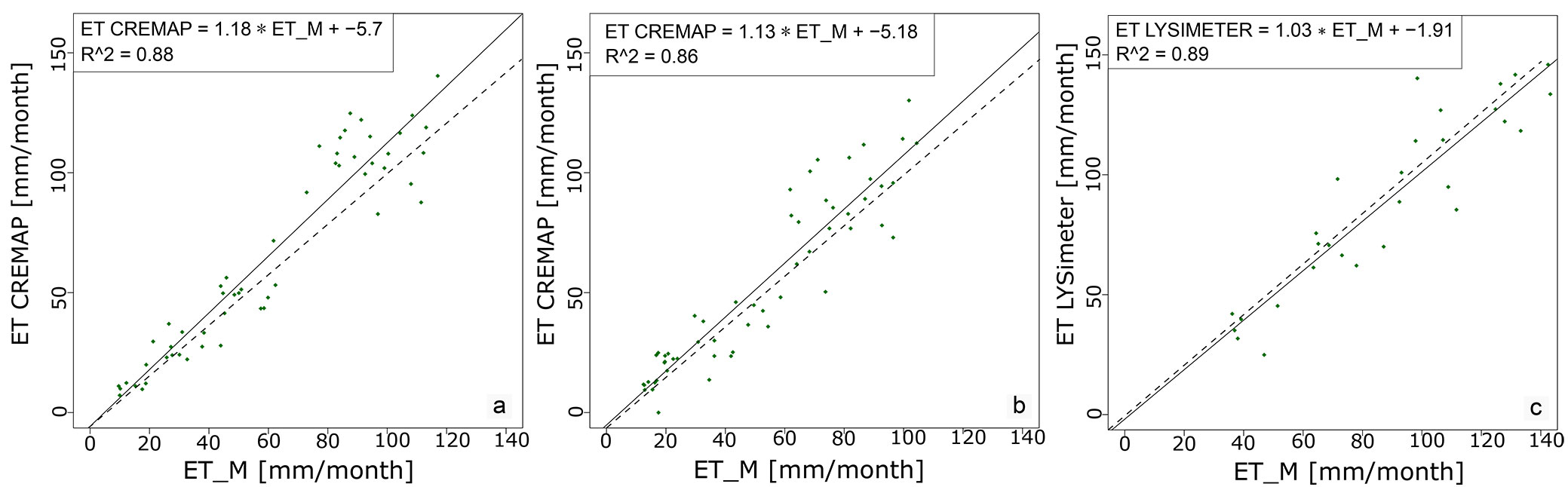
As the second step of the calibration, the calculated actual evapotranspiration (ETM) has been calibrated based on the parameter SOILMAX. In this case, the initial estimate of SOILMAX had to be adjusted in order to reach a maximal correlation between ETlys/ETCREMAP and ETM. To achieve this maximum correlation, the “optim” function of the mentioned R software was applied. Using the value of SOILMAX after calibration, the vertical extent of the root zone (and the maximum depth of tilth) can be calculated using soil texture data.
The Nash-Sutcliffe coefficient (R2NS) of the calibrated models were 0.85, 0.88 and 0.88 for the forested area, mixed parcel and agricultural field, respectively, while the coefficients of determination R2 were 0.88, 0.86, 0.89, respectively (Fig. 2). Consequently, the most accurate calibrated model was for the agricultural field, likely due to the homogeneous and permanent grass cover, which maintains reference conditions. Nonetheless, there were no significant differences between the calibrated models. Accordingly, our model calibration and the performance of our model are reliable.
Fig. 2 - Relationship between the calculated ETM and the measured ETCREMAP or ETLYSIMETER obtained after model calibration in each study area. (a): forested area; (b): mixed parcel; (c): agricultural field.
Results of validation
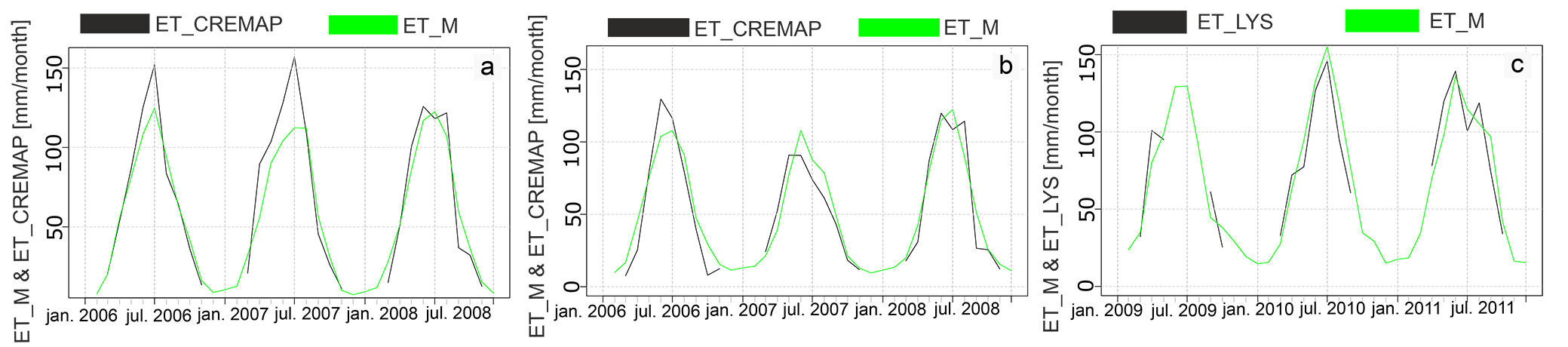
Fig. 3 displays the results of the model validation. The calculated ETM using the weather data over the validation period (forested area and mixed parcel: 2006-2008; agricultural field: 2009-2011) showed good accordance with the measured data (ETLYS/ETCREMAP). The R2NS values were equal with 0.88 (forested area); 0.89 (mixed parcel); 0.85 (agricultural field), therefore each model was accurate.
Fig. 3 - Comparison of the time series of measured ETCREMAP or ETLYS and calculated ETM values obtained after the validation step in each study area. (a): forested area; (b): mixed parcel; (c): agricultural field.
Greater difference was found between the measured ETCREMAP and the calculated ETM values in the forested area, particularly in the summer of 2007 (Fig. 3a). The greater difference is likely due to interception which is not included in the model. Nevertheless, there were larger sums of light precipitation at the forested area in the months of June and July in 2007, which results in higher interception. Therefore, there is an underestimation of the calculated actual evapotranspiration that causes the higher difference, particularly at the forested area in July 2007.
Although the curves of the agricultural field model fit each other the best visually, this model performed the “worst” regarding the Nash-Sutcliffe coefficient, due to the data loss caused by a thunderstorm in the summer of 2009.
Results of the model adjustments
As mentioned above, the model was re-calibrated for each study area using all available data as a basis for the projection procedure. The parameters of the re-calibrated models used in the projection phase are reported in Tab. 1. After comparison of the adjusted, re-calibrated, and the calibrated parameters, the R2 and R2NS values resulted more satisfactory in the case of re-calibrated models, although no significant differences between them were detected.
Tab. 1 - Results of the adjusted, re-calibrated model parameters in the study sites.
| Study sites | Re-calibrated PET parameter | Re-calibrated AET parameter | |||
|---|---|---|---|---|---|
| Model | R2 | Model | R2 | R2NS | |
| Forested area | PETM = 0.42 · PETH + 1.09 · (PETH - 26.04) | 0.98 | ETCREMAP = 1.14 · ETM - 4.79 | 0.89 | 0.88 |
| Mixed parcel | PETM = 0.50 · PETH + 1.05 · (PETH - 37.13) | 0.98 | ETCREMAP = 1.08 · ETM - 4.31 | 0.87 | 0.88 |
| Agricultural field | PETM = 0.54 · PETH + 1.04 · (PETH - 36.79) | 0.98 | ETLYS = 1.04 · ETM - 2.36 | 0.88 | 0.88 |
Tab. 2 displays the SOILMAX values after re-calibration with the calculated rooting depth as well as soil types with their field capacity and permanent wilting point. Much higher soil-water storage capacity (SOILMAX) was calculated for the forested area due to the presence of trees (tree cover is almost 100% in the area), which also means higher rooting depth and larger soil water reservoir as well. As explained earlier, the mixed parcel can be seen as a transition between the forested area and the agricultural field because of the presence of poplars. Therefore, the ≈2.5 m rooting depth is acceptable (the rooting depth can be determined with the help of the calibrated SOILMAX and soil sampling results).
Tab. 2 - Soil types, values of field capacity, permanent wilting point, re-calibrated SOILMAX and re-calibrated rooting depth in the study areas. Soil types were determined using the available data in the AgroClimate.2 project (forested area) or by soil sampling from borehole (mixed parcel). Field capacity (FC, dimensionless) and permanent wilting point (PWP, dimensionless) values of forested area and mixed parcel were used in accordance with Maidment ([26]). (*): see Tab. 3.
| Study sites | Soil type | FC | PWP | SOILMAX (mm) |
Rooting depth (mm) |
|---|---|---|---|---|---|
| Forested area | sandy loam | 0.207 | 0.095 | 502.4 | 4486 |
| Mixed parcel | sandy loam | 276.9 | 2472 | ||
| Agricultural field | sandy loam | * | * | 142.4 | 890 |
We used another method to determine the rooting depth at the agricultural field because θfc and θpwp parameters of the soil texture and plant available water (PAW) were available (Tab. 3). The rooting depth (zrz) was 890 mm for the agricultural field (Tab. 2). The exact value of the rooting depth was determined using iteration between PAW values of 126.2 and 161.0 mm (Tab. 3).
Tab. 3 - Main properties of the soil profile in the lysimeter. (PAW): plant available water; (PAWacc): PAW accumulated to the bottom of the given layer.
| Depth (cm) |
θfc (vol-%) |
θpwp (vol-%) |
PAW (vol-%) |
PAWacc (mm) |
|---|---|---|---|---|
| 0-20 | 30.1 | 14.9 | 15.2 | 30.4 |
| 20-40 | 32.7 | 17.2 | 15.5 | 61.4 |
| 40-60 | 30.4 | 14.7 | 15.7 | 92.8 |
| 60-80 | 30.2 | 13.5 | 16.7 | 126.2 |
| 80-100 | 29.7 | 12.3 | 17.4 | 161 |
| 100-140 | 30.0 | 11.9 | 18.1 | 233.4 |
| 140-250 | 1.7 | 0.8 | 0.9 | - |
Results and tendencies of the Regional Climate Models
The annual temperature means and the annual precipitation sums show an increasing tendency for each study site towards the end of 21st century. According to the RCM projections, the rate of increase of annual temperature in the period 2070/ 2100 (compared to the 1985/2015 reference period) is 1.9 °C for all the studied areas, while for precipitation the projections are: 68 mm (forested area); 69 mm (mixed parcel); 71 mm (agricultural field). Therefore, the rates of the expected temperature and precipitation increase are equivalent for the three study areas.
The different RCMs used for our projection provide different results, which influence the parameters (outputs) of the water balance. Compared to the averages of RCMs, the model with higher precipitation may indicate higher available water, while the greater temperature may cause greater potential evapotranspiration.
Results of the projections for the 21st century
Tab. 4 shows the results of RCM projections for the 4 investigation period. The mean values of actual evapotranspiration (ETM) will slightly increase at each study site by the end of the 21st century. However, the large standard deviations of ETM indicate a great uncertainty that is inherent to modelled data, particularly as four different RCMs were used. By the end of the 21st century, the anticipated rates of increase are +8% (+4 mm month-1) at the forested area, +8% (+4 mm month-1) at the agricultural field and +7% (+3 mm month-1) at the mixed parcel (Tab. 4). The highest absolute values of ETM were obtained for the agricultural field, since RCMs project the highest temperature for the grass covered surface among the study areas. During the 2015/ 2045 period the ETM values stagnate, reflecting the decrease in the projected temperatures (-0.2, -0.1 and 0 °C for the forested area, mixed parcel, and agricultural field, respectively). Conversely, there is a typical increasing trend in the second half of the century at each study area (the most considerable upward rate appears in the 2045/2075 period), since precipitation and temperature increases simultaneously (i.e., there is available water for the evapotranspiration process).
Tab. 4 - ETM, SOILM and SOILM_10Perc values (± standard deviation) obtained from the projection at the study areas.
| Study sites | Parameters | 1985/2015 | 2015/2045 | 2045/2075 | 2070/2100 |
|---|---|---|---|---|---|
| Forested area | ETM (mm month-1) | 48 ± 38 | 48 ± 37 | 51 ± 39 | 52 ± 40 |
| SOILM (mm) | 417 ± 92 | 416 ± 74 | 415 ± 76 | 394 ± 86 | |
| SOILM_10Perc (mm) | 208 ± 59 | 270 ± 32 | 271 ± 25 | 234 ± 37 | |
| Mixed parcel | ETM (mm month-1) | 43 ± 35 | 43 ± 33 | 45 ± 35 | 46 ± 35 |
| SOILM (mm) | 215 ± 57 | 210 ± 61 | 211 ± 63 | 199 ± 69 | |
| SOILM_10Perc (mm) | 109 ± 20 | 96 ± 15 | 96 ± 14 | 77 ± 21 | |
| Agricultural field | ETM (mm month-1) | 49 ± 34 | 49 ± 33 | 52 ± 34 | 53 ± 35 |
| SOILM (mm) | 58 ± 40 | 65 ± 43 | 66 ± 44 | 67 ± 48 | |
| SOILM_10Perc (mm) | 8 ± 3 | 7 ± 2 | 6 ± 3 | 5 ± 3 |
Contrary to the tendencies of ETM values, there are larger differences in the mean values of soil moisture (SOILM) among the study sites (Tab. 4), because of the larger differences in the SOILMAX values. The forested area has the highest and the agricultural field has the lowest soil moisture mean values. Compared to the 1985/2015 period, we found a decrease for the forested area (-6%; -23 mm) and the mixed parcel (-7%; -16 mm), but an increase for the agricultural field (+12%; +9 mm) by the end of the 21st century. These increases could be due to precipitation as a significant and continuous increasing is expected for the second part of the 21st century. Nevertheless, the shape of the graph for ETM monthly values at the agricultural field (Fig. 4) is flatter, i.e., lower ETM peak values for the summer period (though higher for annual means) that may lead to increasing SOILM values.
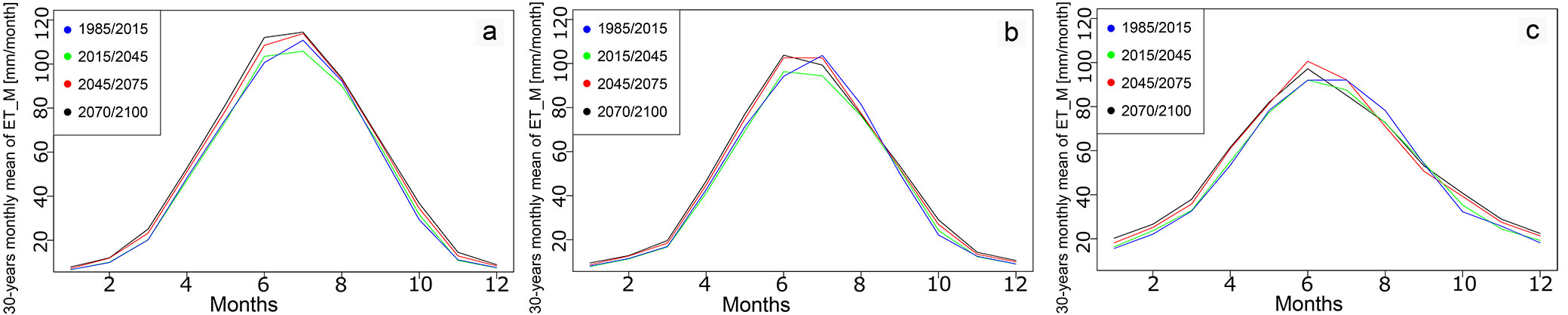
Fig. 4 - Monthly values of ETM for the study areas for the investigated 30-year means. (a): forested area; (b): mixed parcel; (c): agricultural field.
With regard to plant water uptake, the minimum soil moisture were calculated as 10th percentile minimum values (SOILM_10Perc - Tab. 4). The percentile analysis offers key information regarding water stress as it represents different results than SOILM values. Comparing the 2070/ 2100 period to the 1985/2015 reference period, the forested area shows increasing SOILM_10Perc values (+11%; +26 mm) by the end of 21st century, while there is a significant decreasing tendency at the mixed parcel (-29%; -32 mm) and the agricultural field (-37%; -3 mm). The predicted increase at the forested area is likely due to the deep root zone (~4.5 m) which allows a high SOILMAX, i.e., a greater amount of available water for the plants. It should be noted that SOILM_10Perc values of the agricultural field are really close to zero (Tab. 4) due to the lowest vertical extent of the root zone and the lowest SOILMAX value among the three study sites. At the forested area, a significant increase (+23%; +62 mm) appears in the period 2015/2045, constancy (+1%; +1 mm) occurs in the period 2045/2075, but a significant decrease (-16%; -37 mm) is expected in the period 2070/2100. Furthermore, nearly equal drop rates occur at the mixed parcel (-12%; -13 mm) and the agricultural field (-13%; -1 mm) in the 2015/2045 period. Stagnancy was found in the 2045/ 2075 period at the mixed parcel (0%; 0 mm) and a decrease at the agricultural field (-14%; -1 mm), while a downward trend can be observed at the end of the 21st century at the mixed parcel (-29%; -19 mm). However, nearly equal decreasing rates are expected at the agricultural field (-17%; -1 mm). The reason underlying the stagnancy in the middle of the 21st century (2045/ 2075) could be the simultaneous increase of temperature and precipitation, which, therefore, compensates for the decreasing SOILM_10Perc. Moreover, in the period 2070/ 2100 temperatures still shows a significant increase, while the increase of precipitation is less pronounced. Consequently, a remarkable decrease in SOILM_10Perc is expected in each study area. However, considering the uncertainty of the projected precipitation of the RCMs, a clear explanation cannot be given.
The previous analyses are based on annual mean values for the four 30-year-long investigation periods. These analyses, however, do not indicate the monthly development of output parameters of the models. Hence, a future research study that focuses on the 30-year monthly mean of ETM plus SOILM is required.
Fig. 4 emphasizes the changes in the 30-year monthly means of ETM, while Fig. 5 highlights the seasonal periodicity of SOILM. Considering the 30-year monthly mean of ETM, the greatest values at each study site occur in June and July, whereas the smallest in December and January. This can be attributed to the greater transpiration in the summer period, which can generates higher evapotranspiration values. In addition, a quick increase reflects the beginning of the biological activity of plants in April (Fig. 4). The values of ETM generally increase towards the end of 21st century, particularly in the summer period (10-15 mm month-1), i.e., 10-13% significantly upward rates; this could be due to the enhanced evapotranspiration constraint by the end of the 21st century due to the expected rising temperatures in the summer period. However, in the case of agricultural field, the largest values appear in the 2045/2075 period. Moreover, the greatest differences occur among the investigation periods in summer as well. Similar to the annual averages, the 1985/2015 period shows larger ETM values than the period 2015/2045. Although the agricultural field has the highest values of ETM regarding annual averages, the calculation of 30-year monthly mean of ETM reveals that the forested area and the mixed parcel have the highest ETM values in the summer period. Hence, the shape of the curves of the agricultural field (Fig. 4c) is flatter than the other two areas, with higher values in winter, but lower values in summer. These higher values at the agricultural field during dormancy are likely related to the earlier start of the growing season in areas with a grass surface. In addition, unlike forests, grass can transpire even in winter periods (as reflected by the higher values in winter at the agricultural field - Fig. 4c), while deciduous species at the forested area are leafless in winter. The maximums of ETM in summer were 115, 105 and 100 mm month-1 for the forested area, mixed parcel, and agricultural field, respectively. These values reflect the higher leaf area index of forests, leading to higher evaporative surface in the growing seasons.
Fig. 5 - Monthly values of SOILM for the study areas for the investigated 30-year means. (a): forested area; (b): mixed parcel; (c): agricultural field.
The 30-year monthly mean of SOILM shows a slight increase from January to March, when the soil is saturated and the values of SOILM are the closest to the water storage capacity (SOILMAX). From March to September, a decrease of soil moisture occurs due to the rising evapotranspiration. Consequently, the minimum values occur in early autumn (September) in each study area (Fig. 5). The increase observed in September is caused by the transition to the dormant season.
When the three study sites are compared, the most significant differences appear for the 30-year monthly mean of SOILM values rather than at the ETM values. The highest SOILM and ETM values are observed at the forested area. The forested area and mixed parcel show equal annual fluctuation (~150 mm), whereas the lowest values of ETM and SOILM and smallest fluctuation of SOILM (~90 mm) are found at the agricultural field. The rates of the annual soil moisture fluctuations and soil moisture storage capacity (SOILMAX) are lowest at the forested area (30%) but highest at the agricultural field (63%). Fig. 5 confirms that the highest SOILM values appear at the beginning of the investigation period, but lowest values are expected at the end of the 21st century.
Based on the above evidence, the water stress probability may increase towards the end of the 21st century.
Results of the water stress analyses
Tab. 5 summarises the mean values of REW (eqn. 8) derived from the four applied RCMs for each investigation period. A decrease of REW values towards the end of the 21st century is predicted at the forested area and the mixed parcel. However, the average REW values do not approach the 50% threshold of SOILMAX at both sites. Average REW values for the forested area range from 83% to 78% (i.e., water stress is predicted in 61 to 79 out of the 360 months considered), while for the mixed parcel range from 78% to 71% (79 to 104 months out of 360). REW values at the agricultural field decrease below the 50% threshold more frequently, i.e., water stress is likely to occur only at the agricultural field (Tab. 5). Indeed, there is an increase of REW values at the agricultural field from 42% (in the 1985/2015 observational based period) to 46%, which remains constant during the 21st century as a result of the similar increase in temperature and precipitation.
Tab. 5 - The values of relative extractable water (REW) in the 21st century for the study areas. Each 30-year period contains 360 months. The value 0.83 indicates that 83% of the 360 monthly REW values do not drop under the threshold of 50% SOILMAX.
| Study area | 1985/2015 | 2015/45 | 2045/75 | 2070/2100 |
|---|---|---|---|---|
| Forested area | 0.83 | 0.83 | 0.82 | 0.78 |
| Mixed parcel | 0.78 | 0.76 | 0.76 | 0.71 |
| Agricultural field | 0.42 | 0.46 | 0.46 | 0.46 |
Based on the above evidences, significant water stress is expected in the future at the agricultural field area, due to the relatively small SOILMAX value and small rooting depth detected.
Discussion
In this study, a Thornthwaite-type water balance model was adapted and applied to assess the future development of evapotranspiration and soil moisture in the western part of the Carpathian Basin.
Our study indicates an increasing tendency of actual evapotranspiration across the study areas towards the end of the 21st century, with high annual fluctuation and greater peaks for summer. The monthly average values of soil moisture, however, show no clear trend or a weak increase, whereas the lower 10th percentile minimums show a significant decrease and greater annual fluctuation (particularly in the early autumn) towards the end of the 21st century. The results showed that significant plant water stress is expected to occur only at the agricultural field.
In this study a relatively straightforward model approach was applied to regional conditions, though further research should refine our analysis, for example by considering crop characteristics, different soil, or land use changes. According to Bormann et al. ([4]) land use change (in addition to climate change) can have a strong impact on soil water balance, which they evaluated through the comparison of several hydrological catchment models. As stated by Bormann et al. ([4]), changes in soil properties (as a part of land use change scenario) should be considered to attain highly-reliable water balance models.
Granier et al. ([12]) established a daily lumped water balance model for forest stands with the aim of quantifying drought intensity and duration in different regions of France from 1951 to 1991. Compared to their results, we had relatively deep soil values (rooting depth of 4.5, 2.4, and 0.9 m for forested area, mixed parcel, and agricultural field, respectively). However, in this study only one soil layer was considered, as not enough information about soil characteristics was available ([12]). As a consequence of the deep soil estimates, the SOILMAX values in this study (502.4, 276.9 and 142.4 mm for forested area, mixed parcel and agricultural field, respectively) are much higher than those reported in Granier et al. ([12] - 180, 185 and 72 mm for coniferous and broad-leaved stands on deep soil, and for broad-leaved stands on shallow soil, respectively). Unlike these authors, we used a 0.5 (50%) value instead of 0.4 (40%) as REW threshold, mostly because we considered three different kinds of surface cover. Moreover, Allen et al. ([2]) advised a general threshold of 0.5 in the case of crops.
The monthly average of the modeled relative extractable water (REW) for the crop field showed an increasing trend (from 42% to 46%) towards the end of the 21st century, and values below the 50% threshold are expected to occur frequently. In contrast, REW values for forested area and mixed parcel do not approach such threshold (78% and 71%, respectively). According to Granier et al. ([12]), REW values did not lower below the 0.4 threshold in the wettest years in deep soils even in late summer (August and September), but can drop below such thresholds during the driest years.
Remrová & Císlerová ([39]) studied the impacts of climate change on the water balance of a grass-covered experimental catchment in the Czech Republic, finding that the vertical extent of the root zone was lower and the soil profile shallower (75 cm) compared to our agricultural field (140 cm). Nonetheless, they did not predict significant water stress (only 6 days in the summer of 2095), likely because their study area is more humid (1200 mm annual average precipitation) and cooler (8.1 °C annual air temperature). Moreover, they used a more pessimistic projection, particularly at the end of the 21st century (climate scenario A2, with a single RCM over the period 2071-2100), than those used in this study (scenario A1B, with 4 RCMs over the whole 21st century). Our annual AET increased over the period considered from 594 to 628 mm year-1 (+5%) in the case of agricultural field, which is lower than the +12% (from 400 to 450 mm) reported by Remrová & Císlerová ([39]). Furthermore, the absolute values of actual evapotranspiration (AET) in their study are lower, due to the aforementioned temperature difference.
Lutz et al. ([25]) developed a water balance model using a modified Thornthwaite-type method ([9]) on monthly step, with Hamon PET ([17]) approach, aimed at predicting the effect of changes in soil water balance on species ranges by mid-century in the Yosemite National Park (USA). They predicted an increase of 10% in AET across all plots over the 2020-2049 period, while in this study we found a substantial steadiness of AET values (572 mm year-1) in the forested area. Similar to Lutz et al. ([25]) results, the AET peaks occur in July, though we found a lower value (115 mm month-1). In our study sites, the water deficit (PET-AET) at the forested area shifts from 88 mm to 73 mm (-21%) over the period 2020-2049, while in their study the projected increase in deficit between the present and the future (2020-2049) was 23% across all plots, as a consequence of the increased temperature plus PET and decreased snowpack.
Regarding the annual tendency of AET rates, our results agree with those reported by Keables & Mehta ([20]) who used a monthly step Thornthwaite water balance approach in Kansas (USA). The AET rates in their study are small during the winter in response to lower temperatures, but increase in the spring with temperature and available water. AET peaks in July with 151-175 mm month-1 as the highest values of their study area. In our case, June basically has the highest AET values with 100-115 mm month-1. Similar to their results, the potential water deficit is predicted in the summer period (highest values in July and August).
Gulyás et al. ([13]) utilized a water balance model after Thornthwaite & Mather ([44]) to assess the water stress in a protected Pinus Sylvestris forest near Fenyöfö, Györ-Moson-Sopron county in Hungary. They calculated REW values using the soil moisture output data, which was estimated by the Thornthwaite-type water balance model after Granier et al. ([12]) as well. They reported that REW strongly decreased in the period 1961-2013. During the years of 1990-1991, 2001-2004, and 2011-2012, a huge water deficit occurred in the soil. The most significant water decrease was found at the beginning of the 1990s with extreme summer drought, and negative effects on the investigated forest. In our study, average REW values for the forested area showed a decreasing tendency over a different period (1985-2100), though they never approached to the 50% threshold. It should be noted that Gulyás et al. ([13]) applied 40% as a threshold.
Nistor et al. ([32]) evaluated the annual and seasonal crop evapotranspiration of the Carpathian Region from 1961 to 2010 using two datasets from 1961-1990 and from 1990 to 2010. They reported the same trends as in our study, with a rise in temperature and evapotranspiration values between their investigation periods. They found that absolute changes of annual crop evapotranspiration is insignificant, with a maximum value of 49 mm (0.06%) between 1961-1990 and 1991-2010.
Csáki et al. ([6]) presented a long-term, spatially distributed, Budyko-type climate-runoff model tested on the Zala River Basin (an essential runoff contributing region to Lake Balaton in Hungary). In their study, averaged long-term annual evapotranspiration and runoff were projected for the 21st century using precipitation and temperature as input data from 12 RCMs (A1B scenario). According to their projections, the long-term mean annual evapotranspiration may increase by 4.4% at the end of the 21st century (2071-2100) relative to their reference period (1981-2010), while in our case a 7-8% increase rate has been predicted (2070-2100 relative to the 1985-2015 period), but in a monthly step.
Climate simulations for the Rhine-Meuse drainage area in central-western Europe were carried out by Var Der Linden et al. ([46]) with a high spatial resolution (25 km) GMC model (EC-Earth V2.3 model) to study two model run over 30-year periods (2094-2098 vs. 2002-2006 as reference period) under low-to-moderate greenhouse gas forcing (RCP4.5). Large annual cycles of soil moisture with minimum values in September (860 mm) were indicated, which is higher compared to our study (300, 150 and 40 mm for forested area, mixed parcel, and agricultural field, respectively). Their model projections correspondingly result in soil drought during the growing season at the end of 21st century. Such difference could be attributed to the reduction of precipitation with soil moisture depletion at an average of 90 mm, while in our study we found 80, 70 and 20 mm for forested area, mixed parcel, and agricultural field, respectively. According to Var Der Linden et al. ([46]), the values of evapotranspiration may significantly increase by the end of 21st century, particularly in the summer period with 15 mm month-1 (+12%). Our results show similar upward rates (10-13%) in our study areas, with 10-15 mm month-1.
Conclusion
In this study, a Thornthwaite-type water balance model was applied to assess the impact of climate change on water balance components in a natural forested area, a mixed parcel, and an agricultural field in the western Carpathian Basin.
The main advantage of the developed model is the low amount of input data required (temperature and precipitation). This allows the model to be easily applied to other places where measured data are available for calibration/validation. This model system ensures fast impact analysis of climate change on evapotranspiration and soil water storage, along with the calculation of water stress parameters. Moreover, the model requires a significantly lower amount of work for input data pre-processing and baseline investigations than more complex models.
Based on standard future climate scenarios, an increase in ETM is expected in future decades, with a remarkable shift predicted for SOILM, indicating that less soil water will be available for plant growth during summer months in the studied region, and confirming the evidences reported by studies using similar methods ([25], [46], [6]). In the case of the forested area considered, a lower water stress for plants is expected to occur compared to the other two sites (mixed parcel and agricultural field) due to the larger soil moisture reservoir of forest stands. Nonetheless, critical periods of water shortage could lead to catastrophic effects on Carpathian forested areas, the restoration of which is much more difficult than that of crop fields.
List of abbreviations
AET: actual evapotranspiration (mm); CREMAP: Calibration-Free Evapotranspiration Mapping; D: daylength (hour); e*m:saturation vapor pressure (kPa); ETCREMAP: remote-sensing based actual evapotranspiration (mm); ETLYSIMETER: actual evapotranspiration values measured by weighing-lysimeter (mm); ETM: monthly actual evapotranspiration (mm · month-1): GCM: general circulation model; PAW: plant available water (mm); PET: potential evapotranspiration (mm); PETCREMAP: remote-sensing PET based on actual evapotranspiration at well-watered conditions (mm); PETLYSIMETER: actual evapotranspiration values measured by weighing-lysimeter at well-watered conditions (mm); PETH: Hamon type potential evapotranspiration (mm); PETM: calibrated monthly potential evapotranspiration (mm); PM: monthly summed precipitation (mm); R2: coefficient of determination (dimensionless); RCM: regional climate model; REW: Relative Extractable Water (dimensionless); R2NS: Nash-Sutcliffe coefficients (dimensionless); SOILM: monthly soil moisture (mm); SOILMAX: soil-water storage capacity (mm); SOILM_10Perc: 10th percentile soil moisture minimum values (mm); TM: monthly summed temperature (°C); zrz: rooting depth (vertical extent of root zone, mm); ΔWlys: daily change of soil water mass (mm day-1); Δwdrain: daily change of drainage water (mm day-1); Δplys: daily change of precipitation (mm day-1); ΔIlys: daily change of irrigation (mm day-1); ΔETlys: daily change of evapotranspiration (mm day-1): ΔSOIL: decrease in soil storage (mm); θfc: water content at field capacity (dimensionless); θpwp: water content at permanent wilting point (dimensionless).
Acknowledgement
This work was supported by the project EFOP-3.6.2-16-2017-00018 of the University of Sopron, Hungary. Fundings from the János Bolyai Scholarship of the Hungarian Academy of Sciences and from the Ministry of Agriculture in Hungary are gratefully acknowledged. The authors wish to thank Reinhard Nolz (University of Natural Resources and Life Sciences, Vienna, Austria) for supplying the lysimeter data.
References
Gscholar
Gscholar
Gscholar
Gscholar
Online | Gscholar
Gscholar
Gscholar
Online | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Péter Kalicz 0000-0003-0010-9519
Zoltán Gribovszki 0000-0003-3061-8912
Institute of Geomatics and Civil Engineering, University of Sopron, Sopron (Hungary)
Corresponding author
Paper Info
Citation
Herceg A, Kalicz P, Gribovszki Z (2021). The impact of land use on future water balance - A simple approach for analysing climate change effects. iForest 14: 175-185. - doi: 10.3832/ifor3540-014
Academic Editor
Raffaele Lafortezza
Paper history
Received: Jun 01, 2020
Accepted: Feb 05, 2021
First online: Apr 13, 2021
Publication Date: Apr 30, 2021
Publication Time: 2.23 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2021
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 35736
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 29978
Abstract Page Views: 2675
PDF Downloads: 2464
Citation/Reference Downloads: 3
XML Downloads: 616
Web Metrics
Days since publication: 1739
Overall contacts: 35736
Avg. contacts per week: 143.85
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2021): 3
Average cites per year: 0.60
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Soil water deficit as a tool to measure water stress and inform silvicultural management in the Cape Forest Regions, South Africa
vol. 13, pp. 473-481 (online: 01 November 2020)
Research Articles
Comparison of drought stress indices in beech forests: a modelling study
vol. 9, pp. 635-642 (online: 06 May 2016)
Research Articles
Growing season water balance of an inner alpine Scots pine (Pinus sylvestris L.) forest
vol. 11, pp. 469-475 (online: 02 July 2018)
Research Articles
Measured and simulated tree and stand water use of Douglas-fir along a climatic gradient across Germany
vol. 18, pp. 309-318 (online: 30 October 2025)
Review Papers
Quantifying and modeling water availability in temperate forests: a review of drought and aridity indices
vol. 12, pp. 1-16 (online: 10 January 2019)
Research Articles
Use of δ13C as water stress indicator and potential silvicultural decision support tool in Pinus radiata stand management in South Africa
vol. 12, pp. 51-60 (online: 24 January 2019)
Research Articles
Evaluation of fast growing tree water use under different soil moisture regimes using wick lysimeters
vol. 6, pp. 190-200 (online: 08 May 2013)
Research Articles
Comparative water balance study of forest and fallow plots
vol. 5, pp. 188-196 (online: 02 August 2012)
Research Articles
Model-based assessment of ecological adaptations of three forest tree species growing in Italy and impact on carbon and water balance at national scale under current and future climate scenarios
vol. 5, pp. 235-246 (online: 24 October 2012)
Research Articles
Spatial and temporal variation of drought impact on black locust (Robinia pseudoacacia L.) water status and growth
vol. 8, pp. 743-747 (online: 18 June 2015)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword