Model-based assessment of ecological adaptations of three forest tree species growing in Italy and impact on carbon and water balance at national scale under current and future climate scenarios
iForest - Biogeosciences and Forestry, Volume 5, Issue 5, Pages 235-246 (2012)
doi: https://doi.org/10.3832/ifor0634-005
Published: Oct 24, 2012 - Copyright © 2012 SISEF
Research Articles
Abstract
A semi-empirical model has been used to estimate total net primary productivity, canopy transpiration and the water use efficiency under actual and future climate projections (B1 and A2 IPCC Scenarios) of two deciduous (Fagus sylvatica, Quercus cerris) and one evergreen tree species (Quercus ilex) growing in Italy. In response to changes in the air temperature, the two deciduous species showed a strong reduction of NPP values, whereas the evergreen one showed very limited reductions. Under future warmer conditions, Q. ilex proved to be the best adapted species, probably for its drought-tolerant water-saving strategy, while Q. cerris suffered a reduction of transpiration, due to stomatal closure which was sensitive to the change of evaporative demand. Water Use Efficiency (WUE) values did not increase in the B1 and A2 scenarios, indicating a non-conservative water-saving strategy, which likely affected the distribution pattern of Q. cerris under these conditions. Similar functional behaviour have been noted for F. sylvatica, although this species adopted a water spending strategy, typical of species growing in mesic environments, that could represent a risk for survival of beech population under extreme air temperature change. In this respect, the reduced suitable area for this species under the A2 scenario could reduce the possibilities of an upward shift toward higher altitudes.
Keywords
Semi-empirical Model, Climate Change, Mediterranean Region, Net Primary Productivity, Water Use Efficiency
Introduction
Global air temperatures have increased by 0.7 °C during the 20th century and are projected to increase by between 1.1 and 6.4 °C during the 21st century, with the greatest increases expected to occur at more northerly latitudes ([33]). Furthermore, the outcomes of different climate change scenarios show regional variability of climate change. The changes in average temperatures that forests will have to face over the next 100 years, according to the latest projections ([33]), will be 2 °C increase in Ireland and the UK, up to about 3 °C increase in central Europe and 4-5 °C increase in northern Boreal and parts of the Mediterranean regions. All global circulation models agree that the warming will be greatest in eastern Europe during winter and in western and southern Europe during summer. In northern Europe the increase in temperature will be similar in all seasons. These increases will also be accompanied by changes in precipitation patterns that are much more difficult to forecast ([33]). However, many models predict that summer droughts in some central and southern European regions will become more prevalent ([63], [34]). Climate is therefore expected to become more variable with a greater risk of extreme weather events, such as prolonged drought, storms and floods.
Forests will be exposed to changes in mean climate variables but also to increased variability. The responses of plant productivity and other ecosystem processes to climate change are quite variable and increases, decreases, or no change at all have all been reported ([69], [64]). However, an overall positive response of aboveground plant productivity to warming has been reported for colder ecosystems ([69]). Furthermore, there is a large body of observational, satellite, and atmospheric data regarding plant species and ecosystems that shows clear biological responses to warming such as extended growing seasons and altitudinal and northward movement of species’ distributions in both northern and southern, cold-wet and warm-dry ecosystems ([52], [78], [61], [62], [49], [60]). Ecosystem processes and biological species may respond asymmetrically to climatic changes ([78]) and the overall effect on ecosystem functioning and species richness is, therefore, highly complex and determined by the relative sensitivity of the different processes to climate change.
The accounting of biological carbon sequestration requires adequate knowledge of inter and intra-annual variation in ecosystem carbon exchange with the atmosphere. Large variations in the C sequestration capacities of various forest ecosystems have been reported ([53]). These variations depend on climate, species, site productivity and disturbances, including management. Drought represents one of the main source of inter-annual variation in terrestrial carbon sequestration as it causes large reductions in gross primary productivity (GPP) as well as in net ecosystem exchange (NEE) of terrestrial ecosystems ([12], [29], [66]). Although this is true for most terrestrial biomes, it is especially relevant in seasonally dry climates, where there is often a large variability in seasonal and annual precipitation. The Mediterranean climate has a marked seasonality with a dry and hot summer, when low precipitation is coupled to high atmospheric evaporative demand, leading to a decrease in moisture availability to plants. If the dry season lasts too long plant water deficits may negatively affect the capacity for carbon assimilation as a result of lower photosynthetic rates and reduced leaf areas (or shorter life span of annual plants) induced by limited water availability. It is generally expected that elevated CO2 will promote reductions in stomatal conductance (g s) that can ameliorate the negative effects of drought in many species through decreased water use ([51]), and it may have important consequences for forest water dynamics ([8], [42]). However, growing experimental evidence suggests that many forest tree species show small or non-significant changes in stomatal conductance under long-term elevated CO2 ([22], [10], [15], [71]), suggesting that stomata acclimate in parallel to, and possibly depending on, photosynthetic acclimation ([31], [1]).
Carbon (C) pool and fluxes estimations are required at a regional level to assess carbon exchange under the ongoing climatic change in order to establish suitable polices for mitigation of and adaptation to climate change. The interest in modelling C exchange reflects the growing attraction in using models as vehicles to integrate knowledge, research activities, experimental results, and to test hypotheses ([27]), and as the most flexible tools to address how climate change (especially for temperature and soil water availability) will affect the process-based forest functionality ([25], [9], [38]). An example of simplification of models applied to the forest systems is the use of the so-called “big leaf” model ([46], [76]), that describes the response of vegetation as a whole (big leaf) in terms of variations of the main environmental factors ([74], [3]). The aim of this paper is to show simulations of total net primary production, transpiration and water use efficiency for tree species as Fagus sylvatica, Quercus cerris and Quercus ilex, forming widely diffused forest-types in the Mediterranean area, under actual climatic scenario and CO2 concentration “1961-90” and two climatic scenarios representing low and high CO2 emission trajectories: B1 (stabilization at 550 ppm atmospheric CO2) and A2 (no stabilization of atmospheric CO2) storylines ([54]), for the temporal frame “2071-2100”. Results will be presented for the Italian territory, with an evaluation of the consequences on total net primary productivity and distribution patterns of these tree species.
Material and methods
Study area and tree species
The study area includes the Italian Peninsula, an area of 301 338 km2, geographically divided from the rest of Europe by the Alps. The forest landscape changes according to latitudinal and altitudinal gradients. Mountains forests - characterized by conifers such as Abies alba, Picea abies, Larix decidua and Pinus sylvestris are common in the Alps. Below this belt and along the Apennine chain forests are dominated by Fagus sylvatica. Sub-mountain and hill areas are characterized by deciduous species, mainly Quercus cerris, Quercus pubescens, Ostrya carpinifolia and Fraxinus ornus. Typical Mediterranean species such as Quercus suber, Quercus ilex, Pinus halepensis and Pinus pinaster can be found along the coasts and become more and more common towards the south of the peninsula. In this study, we considered three populations of tree species characterizing the Italian forest ecosystems, from temperate to Sub- and Mediterranean species: Fagus sylvatica (European beech), Quercus cerris (Turkey oak), and Quercus ilex (Holm oak). All three species are widely represented in Italy, forming pure or mixed woods covering extensive areas.
Environmental variables
Current (average of time period lasting from 1961 to 1990) and future (average of time period lasting from 2071 to 2100) climate scenarios are derived by using the HadCM3 model ([50]). The HadCM3 model projected the average climate under the two scenarios A2 and B1 storylines ([54]) as reported in the Intergovernmental Panel on Climate Change Special Report on Emissions Scenarios ([34]). Climatic data are statistically downscaled through a bilinear interpolation so as to obtain raster data with a spatial resolution of 3 km (for a total of 33 432 grid cells over-imposed on Italy), that is corresponding to the grid map of the forest data used in this paper. Only the temperature data are interpolated after detrending at sea level by using a normal lapse rate of 0.6 °C for each 100 m of altitude ([4]).
Climatic variables are chosen among those believed to be more meaningful for their influence on the physiology of tree species. We used annual mean temperature (MeanT, °C), minimum temperature of the coldest month (MinT, °C), maximum temperature of the hottest month (MaxT, °C), summer (SP) and winter (WP) precipitations (mm), and total annual precipitation (PTot, mm).
The MOCA model
The MOCA (MOdelling for Carbon Assessment) model has been mainly developed to estimate the total net primary production of forest stands (NPP, tC ha-1 yr-1) by using climatic and physiological parameters as guide variables. This model has been previously used to calculate the NPP variation according to the foreseen temperature change for an evergreen Mediterranean forest ([77]), and to quantify and simulate the residence of Phillyrea angustifolia maquis after a fire event ([76]). MOCA is based on the big-leaf approach ([40], [16], [77]), which considers the canopy structure as a big leaf that is functionally defined by time-dependent Leaf Area Index (LAI, m2leaf m-2ground). MOCA can be adapted to different species and vegetation types, basically requiring annual mean air temperature (MeanT) and geographical coordinates for each site as input, in order to calculate both daily values of light intensity above canopies [Q o(t), µmole photons m-2 s-1] and air temperature [Tair(t)]. Additional parameters must be obtained by a set of parameters acquired by laboratory and field data in order to adapt the model to different species.
Daily net photosynthetic rate [A(t), μmol CO2 m-2 s-1] is calculated as a response to the mean light radiation inside the canopy at the t th day of year [Q i(t), µmole photons m-2 s-1], according to De Wit et al. ([18] - eqn. 1):
where A max is the maximum rate of net photosynthesis at light saturation (µmolCO2 m-2 s-1 - Tab. 1), Rd is the dark respiration rate (µmolCO2 m-2 s-1 - Tab. 1) integrated for the darkness period, and QY is the quantum yield efficiency of photosynthesis (µmolCO2 µmole photons-1 - Tab. 1).
Tab. 1 - Input and simulated parameters utilised by the MOCA model. All input parameters except light extinction coefficients and NPP repartition coefficient to the leaves come from leaf gas exchange measurements performed plant species; in particular, F. sylvatica and Q. cerris forests growing in the Italian Central Apennine - Abruzzi and Molise Regions, whereas values concerning Q. ilex derived from [48], [47], [21].
| Parameter Type | Parameter Name | Symbol | Fagus sylvatica | Quercus cerris | Quercus ilex | Units |
|---|---|---|---|---|---|---|
| Input | Rate of respiration in the dark | Rd | 1.03 | 1.03 | 0.50 | μmol CO2 m-2 s-1 |
| Maximum rate of net photosynthesis at light saturation |
A max | 20 | 21 | 15 | μmol CO2 m-2 s-1 | |
| NPP repartition coefficient to the leaves | α | 0.301 | 0.280 | 0.230 | - | |
| Quantum yield efficiency |
QY(T) | 0.055 | 0.036 | 0.044 | μmol CO2 μmol photons-1 | |
| Light extinction coefficient | k | 0.71 | 0.60 | 0.69 | Dimensionless | |
| Simulated | Total net primary productivity | NPP | - | - | - | gC m-2 y-1 |
| Daily net photosynthetic rate |
A(i) | - | - | - | μmol CO2 m-2 s-1 | |
| Leaf Area Index | LAI(t) | Initial value: 0 | Initial value: 0 | Initial value: 2.2 | m2 leaf m-2 ground |
Total net primary productivity (gC m-2 yr-1) is calculated by an integration with time (from 100th to 281st Julian Day, JD for deciduous species, and the overall JDs for the evergreen species) of A(t) as (eqn. 2):
where Kc(t) is the maintenance respiration calculated as a function of leaf temperature by the Q 10 temperature coefficient (that is a measure of the rate of change of a biological or chemical system as a consequence of increasing the temperature by 10 °C - eqn. 3):
where R 10 is the respiration rate at 10 °C (1.5 µmolCO2 m-2 s-1) and Q 10 is 1.7, which was in the range found by Granier et al. ([28]) for the beech (1.6 ≤ Q 10 ≤ 1.8), and applied also for Quercus cerris. Q 10 was set to 2.2 for Q. ilex.
The foliage emission period has been calculated by analysis of fifteen NDVI images acquired from Terra satellite (from 14 May to 18 December 2005) through the GRASS-GIS software ([81]), thus deriving the annual NDVI curve, approximated by the Richard’s equation, for each plant species.
Light attenuation through the canopy Q i (t) (µmole photons m-2 s-1) is assumed to be depending on the LAI(t) according to the Beer-Lambert law (eqn. 4):
where K (=0.72) is the coefficient of light extinction through the canopy. The LAI tot (m2leaf m-2ground) is modelled by the following equations (eqn. 5-eqn. 6):
where A g(t-1) is the net photosynthetic rate (gDry Weight m-2 day-1) of previous year-day (t th-1), β is the leaf partition coefficient of the accumulated biomass (=0.25), and SLA(t) is the specific leaf area at the t th day of the year (m2 g-1 Dry Weight) defined by a saturation growth equation fitting empirical data derived from measurement campaigns in beech and mixed forests of the Apennine mountains (eqn. 7):
where c and d are fitted parameters (c = 0.0116 and d = -52.563 for Q. cerris; c = 0.0059 and d = -95.250 for F. sylvatica). The SLA is kept constant during the year (0.005 m2 g-1 Dry Weight) only for Quercus ilex.
Daily stomatal conductance to water vapour [gs(t), mol m-2 s-1] is calculated as function of A(t), ambient CO2 (Ca, 380 ppm) and relative humidity [RH(i), dimensionless] after Ball et al. ([7]) and Harley et al. ([30]). Daily canopy transpiration [E(t), g H2O m-2 day-1] is then calculated as function of diurnal average leaf temperature, vapour pressure difference [VPD(i), mbar], photoperiod [ph(t), h], and LAI ([35] - eqn. 8):
where VPD(t) is the daytime mean atmospheric vapour pressure deficit calculated by air and leaf temperature-based empirical functions ([2]), gc(t) is the diurnal average canopy stomatal conductance (m s-1), cp is the specific heat of air at constant pressure (1.012 J g-1 °C-1), ρ(T air) is the air density (g m-3), λ(T air) is the latent heat of vaporisation of water (J g-1), and γ(λ, cp) is the psychrometric constant (mbar °C-1) ([26]). Saturation water vapour pressure is calculated according to Dilley ([20]). The water vapour conductance of the canopy [gc(t), m s-1] is calculated as function of the stomatal conductance, gs(t), and the LAI(t), for each t th day of year ([35] - eqn. 9):
where fc transforms the stomatal conductance expressed in molar units (mmol m-2 s-1) to non-molar units (mm s-1) as function of the leaf temperature (eqn. 10):
where T leaf is a linear function of T air empirically found by leaf gas exchange measurements.
Total canopy transpiration (Et - tH2O m-2 yr-1) is calculated by an integration with time (from 100th to 281st Julian Day, JD for deciduous species, and the overall JDs for the evergreen species) of E(t) as (eqn. 11):
The water use efficiency (WUE) has been calculated as NPP Et -1ratio (tC tH2O-1) to characterise the differences in the water use under several climate scenarios.
Finally, MOCA implemented a sub-routine generating pseudo-random numbers for each day which fluctuated between 0 and 1. These numbers were used to simulate the daily clouds coverage, adopting an average of 42% for the Italian annual cloudiness, regarding the time-frame 1961-1990 ([73]), and affecting thus the irradiance above the canopy Q o(t). It is assumed that the Italian average cloudiness did not change in the future. The randomly assessment of daily cloudiness implied that one run of the model was slightly different to another. For this reason, the NPP values utilised in the paper were average values coming from 10 runs of the MOCA model for each different climatic scenarios.
The MOCA validation
MOCA results have been validated with the NPP data coming from eddy covariance flux towers of the CarboEurope Programme such as Roccarespampani (42°23’ N, 11°51’ E, Q. cerris forest - [39]), Collelongo (41°52’ N, 13°38’ E, F. sylvatica forest - [72]), and Castelporziano estate (41°45’ N, 12°22’ E, Q. ilex forest - [75]) for the 2000-2005 period. The latter two sites are also included in the Italian Long Term Ecosystem Research network (LTER-Italy - ⇒ http://www.lteritalia.it/defaultuk.php).
For site based validation, NPP values have been calculated from Gross Primary Production (GPP) measured by towers multiplied by: (a) the NPP/GPP ratios reported from Mediterranean warm evergreen (0.542) and temperate humid deciduous (0.537) biomes ([45]); and (b) the ratio (NEP+Rh)/GPP reported in the same paper, where NEP is the net ecosystem production and Rh is the heterotrophic respiration. In case (b), Fagus sylvatica and Quercus cerris showed a (NEP+Rh)/GPP ratio of 0.514, whereas Q. ilex value was 0.639. The denominator of ratios (a) and (b) are independent as NPP comes from biometric estimates, NEP from fluxes and Rh from various measurements techniques ([45]).
MOCA model has been applied for each eddy covariance test site and run for ten times for each year (2000-2005). Averages values of measured and modelled net primary productivity have been reported and compared by the one-way ANOVA test and using a Newman-Keuls test as post-hoc test.
Furthermore, the values estimated by MOCA model have been compared to the above-ground net primary production data derived by remote sensing studies carried out on the same plant species formations distributed over the Italian territory ([11]).
Maps of the total net primary productivity
MOCA model has been applied on a range of latitudinal bands with a width of 0.25°, lasting from forty-two to forty-seven depending on the species specific distribution of plant species analysed here and ranging from north (47°39’12”) to south (35°51’54”) of Italy (Tab. 2). NPP, Et and WUE values have been calculated for each latitudinal band by using proper climatic and environmental maps characterising each band. In details, climatic parameters used in these simulations were of the “average year” of both “1961-1990” (for current scenario) and “2071-2100” (for B1 and A2 scenarios) temporal ranges, coming from the downscaled climatic data of the HadCM3 model. MOCA routines run for one full year (365 JD) at a daily time step. Current and future potential distributions of plant species analysed here ([5], [6] - see [19] for technical details) have been used as template to generate the NPP distribution maps. The distribution of plant species is based on the Importance Value (IV) which is an indicator of abundance based on the density and dominance of a tree species ([32]). Finally, the NPP values have been geographically represented for all cells of the Italian grid at the resolution of 3 × 3 km.
Tab. 2 - Latitudinal ranges for mean annual temperature (mean T) and their differences with the mean temperature of the coldest month, used as input for the MOCA model.
| F. sylvatica | Q. cerris | Q. ilex | ||||||
|---|---|---|---|---|---|---|---|---|
| LAT ranges | MeanT | ΔT | LAT ranges | MeanT | ΔT | LAT ranges | meanT | ΔT |
| 36.89-37.14 | 15.90 | 9.70 | 35.51-35.76 | 18.10 | 9.90 | 35.51-35.76 | 18.10 | 9.90 |
| 37.14-37.39 | 15.50 | 10.30 | 35.76-36.01 | 18.10 | 9.70 | 35.76-36.01 | 15.87 | 10.16 |
| 37.39-37.64 | 15.00 | 10.50 | 37.01-37.26 | 17.00 | 8.20 | 36.76-37.01 | 18.65 | 9.90 |
| 37.64-37.89 | 12.90 | 9.90 | 37.26-37.51 | 15.30 | 10.80 | 37.01-37.26 | 16.35 | 10.01 |
| 37.89-38.14 | 12.60 | 10.00 | 37.51-37.76 | 14.30 | 11.50 | 37.26-37.51 | 15.30 | 9.99 |
| 38.14-38.39 | 11.40 | 9.50 | 37.76-38.01 | 14.20 | 10.80 | 37.51-37.76 | 15.60 | 10.40 |
| 38.39-38.64 | 11.40 | 9.50 | 38.01-38.26 | 14.30 | 10.00 | 37.76-38.01 | 14.95 | 10.41 |
| 38.64-38.89 | 11.40 | 9.60 | 38.26-38.51 | 15.80 | 9.20 | 38.01-38.26 | 14.42 | 9.98 |
| 38.89-39.14 | 11.50 | 9.60 | 38.51-38.76 | 14.30 | 10.30 | 38.26-38.51 | 15.70 | 9.13 |
| 39.14-39.39 | 11.50 | 9.60 | 38.76-39.01 | 14.30 | 10.60 | 38.51-38.76 | 14.16 | 10.10 |
| 39.39-39.64 | 11.40 | 9.60 | 39.01-39.26 | 14.50 | 10.70 | 38.76-39.01 | 14.23 | 10.58 |
| 39.64-39.89 | 11.40 | 9.60 | 39.26-39.51 | 12.30 | 10.00 | 39.01-39.26 | 14.68 | 10.75 |
| 39.89-40.14 | 11.40 | 9.50 | 39.51-39.76 | 12.60 | 10.00 | 39.26-39.51 | 13.39 | 10.17 |
| 40.14-40.39 | 11.20 | 9.50 | 39.76-40.01 | 13.50 | 9.90 | 39.51-39.76 | 13.42 | 10.10 |
| 40.39-40.64 | 11.20 | 9.50 | 40.01-40.26 | 12.10 | 9.60 | 39.76-40.01 | 13.57 | 9.91 |
| 40.64-40.89 | 11.10 | 9.50 | 40.26-40.51 | 12.90 | 9.80 | 40.01-40.26 | 12.49 | 9.66 |
| 40.89-41.14 | 11.10 | 9.50 | 40.51-40.76 | 12.86 | 10.24 | 40.26-40.51 | 13.18 | 9.77 |
| 41.14-41.39 | 11.50 | 9.70 | 40.76-41.01 | 12.81 | 10.58 | 40.51-40.76 | 14.02 | 10.47 |
| 41.39-41.64 | 10.40 | 10.50 | 41.01-41.26 | 12.48 | 10.92 | 40.76-41.01 | 13.76 | 10.74 |
| 41.64-41.89 | 10.40 | 10.50 | 41.26-41.51 | 13.08 | 11.49 | 41.01-41.26 | 13.35 | 10.90 |
| 41.89-42.14 | 10.50 | 10.50 | 41.51-41.76 | 13.16 | 11.30 | 41.26-41.51 | 13.82 | 11.41 |
| 42.14-42.39 | 9.20 | 11.30 | 41.76-42.01 | 12.81 | 11.42 | 41.51-41.76 | 14.07 | 11.10 |
| 42.39-42.64 | 9.20 | 11.30 | 42.01-42.26 | 12.68 | 11.45 | 41.76-42.01 | 13.20 | 11.42 |
| 42.64-42.89 | 9.20 | 11.20 | 42.26-42.51 | 12.92 | 11.78 | 42.01-42.26 | 13.48 | 11.46 |
| 42.89-43.14 | 10.00 | 10.50 | 42.51-42.76 | 12.96 | 11.88 | 42.26-42.5 | 13.28 | 11.81 |
| 43.14-43.39 | 8.70 | 11.00 | 42.76-43.01 | 12.60 | 11.94 | 42.51-42.76 | 13.37 | 11.96 |
| 43.39-43.64 | 10.00 | 10.50 | 43.01-43.26 | 12.80 | 11.90 | 42.76-43.01 | 13.35 | 12.01 |
| 43.64-43.89 | 10.00 | 10.50 | 43.26-43.51 | 12.89 | 11.79 | 43.01-43.26 | 13.44 | 11.89 |
| 43.89-44.14 | 8.90 | 11.00 | 43.51-43.76 | 12.78 | 11.69 | 43.26-43.51 | 13.20 | 11.79 |
| 44.14-44.39 | 8.90 | 11.00 | 43.76-44.01 | 12.64 | 11.82 | 43.51-43.76 | 13.12 | 11.65 |
| 44.39-44.64 | 8.80 | 10.90 | 44.01-44.26 | 12.14 | 11.72 | 43.76-44.01 | 13.39 | 11.92 |
| 44.64-44.89 | 8.80 | 10.90 | 44.26-44.51 | 10.81 | 11.66 | 44.01-44.26 | 13.46 | 11.57 |
| 44.89-45.14 | 8.80 | 10.90 | 44.51-44.76 | 10.72 | 11.69 | 44.26-44.51 | 12.90 | 11.41 |
| 45.14-45.39 | 8.70 | 10.90 | 44.76-45.01 | 10.94 | 11.75 | 44.51-44.76 | 12.70 | 11.84 |
| 45.39-45.64 | 6.60 | 10.50 | 45.01-45.26 | 11.54 | 13.01 | 44.76-45.01 | 12.98 | 12.06 |
| 45.64-45.89 | 6.50 | 11.50 | 45.26-45.51 | 11.22 | 13.11 | 45.01-45.26 | 13.07 | 13.29 |
| 45.89-46.14 | 5.90 | 11.50 | 45.51-45.76 | 11.31 | 13.67 | 45.26-45.51 | 12.48 | 13.83 |
| 46.14-46.39 | 6.00 | 11.50 | 45.76-46.01 | 10.66 | 12.73 | 45.51-45.76 | 12.99 | 13.86 |
| 46.39-46.64 | 7.90 | 11.00 | 46.01-46.26 | 10.80 | 12.55 | 45.76-46.01 | 12.41 | 13.13 |
| 46.64-46.89 | 7.80 | 11.00 | 46.26-46.51 | 10.20 | 12.94 | 46.01-46.26 | 12.80 | 13.19 |
| 46.89-47.14 | 5.60 | 11.50 | 46.51-46.76 | 9.75 | 13.75 | 46.26-46.51 | 11.93 | 13.49 |
| 47.14-47.39 | 5.60 | 11.50 | 46.76-47.01 | 8.96 | 14.18 | 46.51-46.76 | 11.27 | 14.72 |
| - | - | - | 47.01-47.26 | 8.50 | 14.61 | 46.76-47.01 | 9.88 | 14.73 |
| - | - | - | - | - | - | 47.01-47.26 | 9.40 | 15.03 |
Results
Validation of the modelled NPP outputs
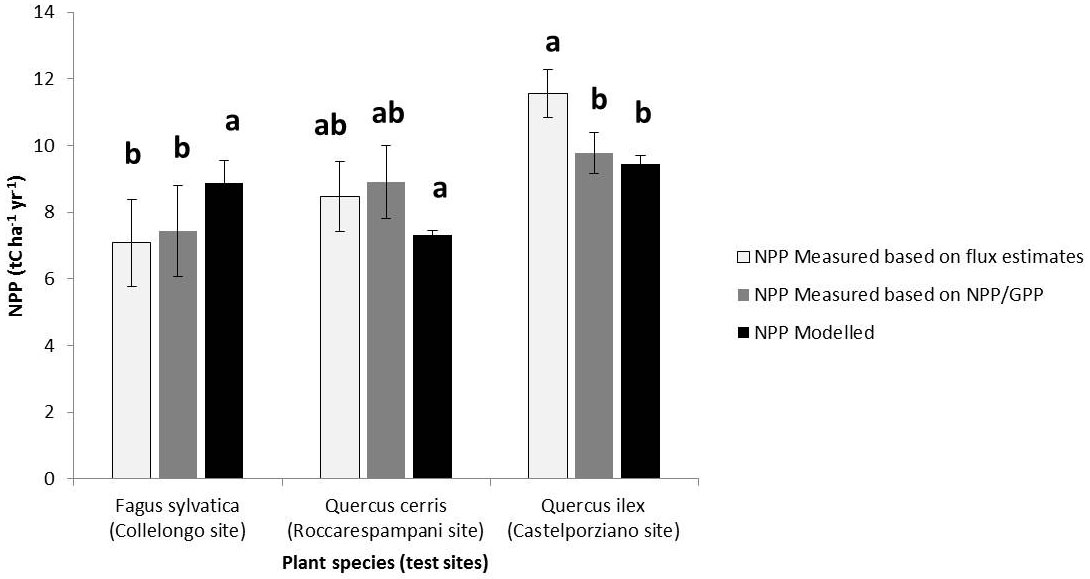
For specific locations where the eddy covariance flux towers are placed, the modelled NPP values are in agreement to the calculated ones (Fig. 1). Statistical analysis demonstrates that the modelled NPP values are included in range of variation of the measured ones, although it should be taken into account that the climate parameters used by MOCA are based on both current climate scenario “1961-1990” and astronomical algorithms which, in turn, are depending on geographical coordinates of each measuring site, so can be considered independent from the actual climate of the years when the fluxes were measured (2000-2005). Indirect estimations of NPP made by remote sensing approach or hybrid methodologies highlight a strong correspondence with average values modelled by MOCA model and represented in the annual NPP maps. Chirici et al. ([11]) reported modelled NPP values by C-Fix model for Italy as 4.26 tC ha-1 yr-1 for beech forests, compared to 2 to 4 tC ha-1 yr-1 as modelled by MOCA, whereas Mediterranean broad-leaves forests showed an averaged NPP value of 4.27 tC ha-1 yr-1 in C-fix vs. 5.43 tC ha-1 yr-1 for MOCA. Finally, values from the two modelling approaches for the Holm oak forests are very similar (4.96 tC ha-1 yr-1 and 4.97 tC ha-1 yr-1).
Fig. 1 - Comparisons between modelled and measured NPP average values regarding three woody plant species. Eddy covariance flux measurements have been performed in the 2000-2005 time period for Castelporziano (Q. ilex forest), Collelongo (F. sylvatica forest) and Roccarespampani (Q. cerris forest) sites. Different letters denote significant differences between NPP values assessed by the Newman-Keuls test performed at p≤0.05.
Time and latitudinal dynamics
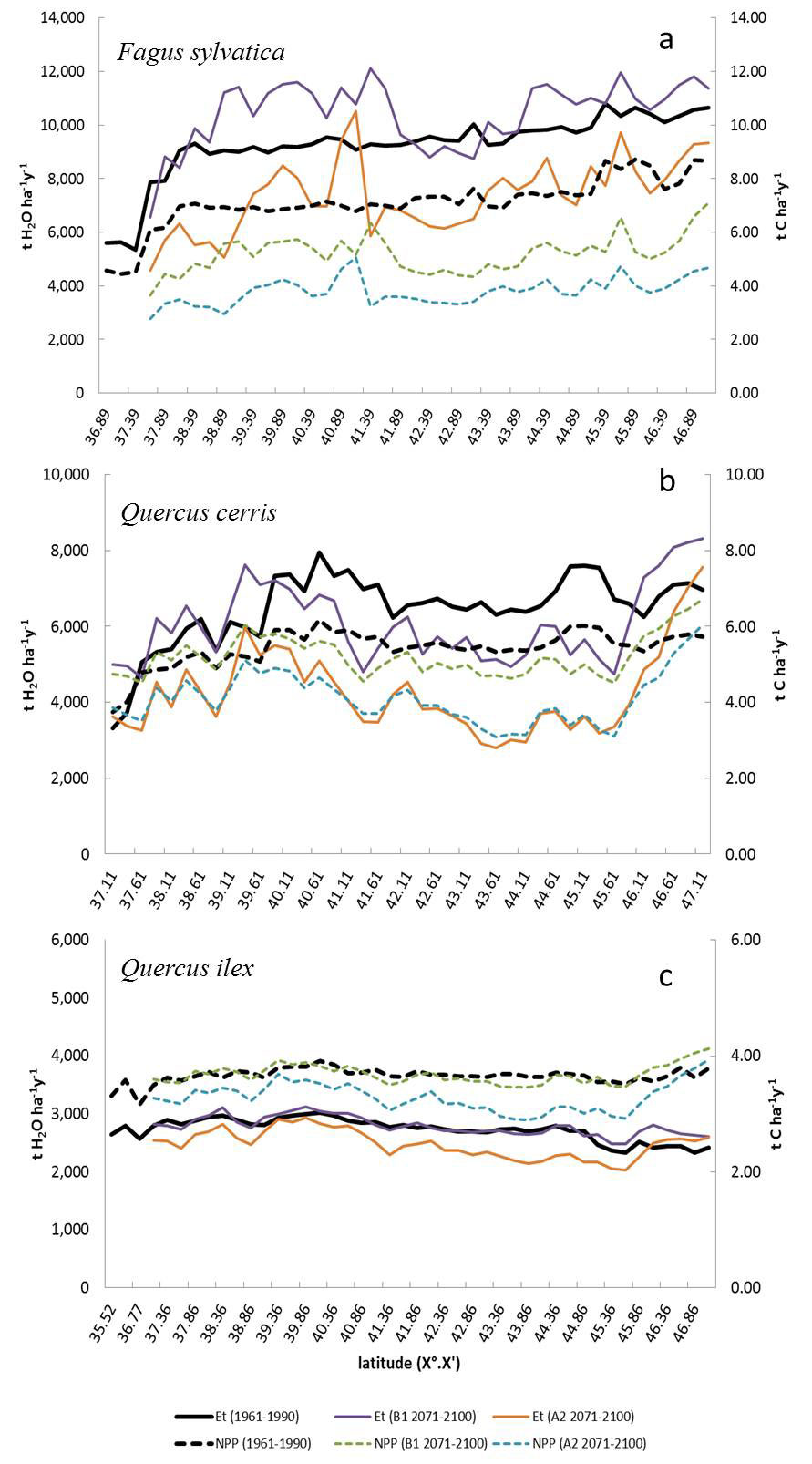
Fig. 2a-c shows the NPP and transpiration rates (Et) along latitudinal ranges from south to north of Italy. Fagus sylvatica (Fig. 2a) has a NPP (“1961-90”) trend growing similarly to a power regression model, showing the lowest values for Sicily and the southern Apennines (4.51 ± 0.06 tC ha-1yr-1), constant values for the beech populations located along the south-central to the northern Apennines (7.11 ± 0.96 tC ha-1), and highest ones for the Alps (8.38 ± 0.43 tC ha-1yr-1). However, NPP decreases when climatic scenarios change, which is of about -26% in the “2071-2100” B1 scenario and -40% in the “2071-2100” A2 scenario (Fig. 2a). Quercus cerris shows similar trends for the NPP values, although it seems to maintain higher NPP values than F. sylvatica under limiting climatic scenarios (Fig. 2b). The NPP values of Quercus ilex are lower than the other two species, but it keeps its trend and values, also under limiting environmental conditions (Fig. 2c).
Fig. 2 - Latitudinal trends of net primary productivity (NPP, tC ha-1) and transpiration rate (Et) estimated under actual (1961-90) and future scenarios (B1 and A2 - 2071-2100) for (a) Fagus sylvatica, (b) Quercus cerris and (c) Quercus ilex.
On average, F. sylvatica shows an increase of canopy transpiration (Et) under the “2071-2100” B1 climate scenario (+7.8%) and a reduction in more limiting A2 scenario (-22.9%) with respect to the “1961-90” scenario (9843 ± 631 tH2O ha-1 yr-1). Differently, Q. cerris shows a progressive reduction of Et values (-13.9% and -40.7% for the B1 and A2 scenarios, respectively), compared to the “1961-90” (6758±528 tH2O ha-1 yr-1), especially for central and northern Italy. Q. ilex shows a clear water conservative strategy pointed out by a very slight reduction of the transpiration rates (-0.8% and -6.3% for the B1 and A2 scenario, respectively) compared to the reference period of “1961-90” (2782 ± 131 tH2O ha-1 yr-1). It is worth noting that Q. ilex has reduced NPP between foliage and atmosphere for all locations of its distribution in Italy, resulting thus more tolerant to the increasing drought stress.
Annual net primary productivity maps
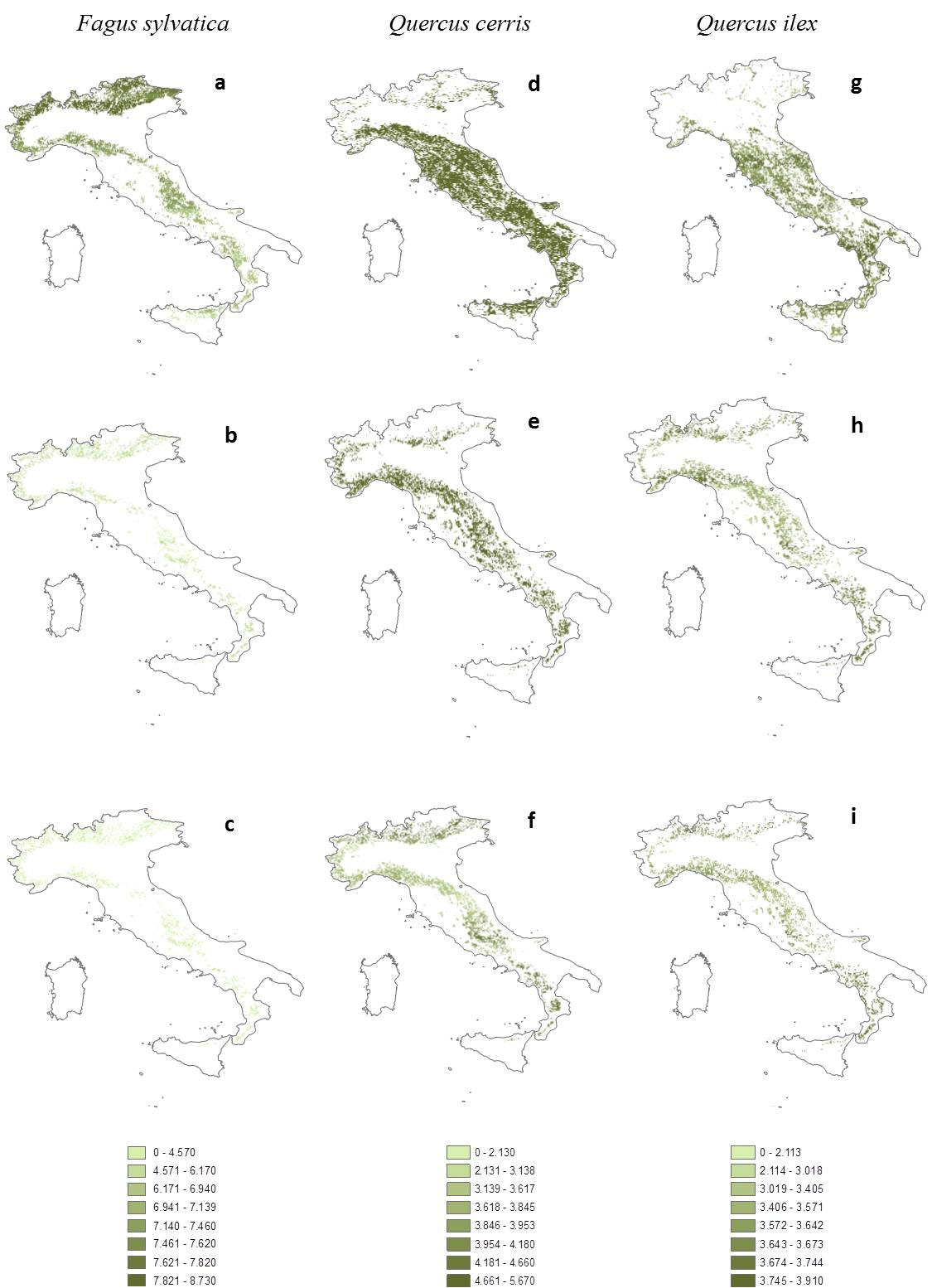
Fig. 3a-i reports the geo-spatial representation of the NPP values for Italy. The map represents the distribution of potential NPP distribution, that refers to the potential distribution of plant species as defined by Attorre et al. ([6]) and determined by the bioclimate envelope in the current and changed climatic conditions. Each pixel represents a cell of 3 x 3 km (900 ha), which is returned to a value of productivity in tC ha-1. Each cell holds the Importance Value (IV) index and the territorial suitability. Fig. 3a shows the primary productivity of beech, according to its current potential distribution. The net primary productivity ranges from 2 to 4 tC ha-1 yr-1, and in some favourable and suitable areas, where the species is dominant, the primary productivity of the beech reaches values of 6-8 tC ha-1 yr-1. However, an overall reduction of the beech’s distribution area throughout the country is evident under the climate “2071-2100” B1 scenario (Fig. 3b). The beech coverage tends to become scarce in central and southern Italy, and potentially increases in the Alps. In this climatic scenario, beech reduces the estimated NPP values to 3 tC ha-1 yr-1. The reduction in NPP would justify the reduction of the potential distribution area, whereas a good productivity is kept in areas which are less affected by the rise of temperature. Under the “2071-2100” A2 scenario (Fig. 3c) beech responds in a negative way, experiencing a strong impact on its potential distribution and, consequently, on primary productivity reducing both their values, mainly due to more limiting climatic conditions, being more critical for the species.
Fig. 3 - Italian distribution of net primary productivity (NPP, tC ha-1) under different climatic scenarios. Fagus sylvatica: (a) actual climate 1961-90; (b) B1 2071-2100; (c) A2 2071-2100. Quercus cerris: (d), (e), (f) as for F. sylvatica. Quercus ilex: (g), (h), (i) as for F. sylvatica.
Q. cerris covers large part of central Italy under the “1961-90” climatic scenario with NPP values ranging from 3.7 to 6.2 tC ha-1 yr-1 and an average value of 5.57 ± 0.27 tC ha-1 yr-1 (Fig. 3d). The “2071-2100” B1 scenario exerts a negative impact on the potential distribution of Q. cerris and the higher productivity areas shift to the Apennines, reaching a maximum value of 6.3 tC ha-1 yr-1 (Fig. 3e). Primary productivity is greatly reduced (3.92 ± 0.55 tC ha-1 yr-1) along with the potential distribution of the species in the A2 scenario (Fig. 3f , -20.3% - [6]).
Quercus ilex is a Mediterranean sclerophyllous species growing along the Italian coasts and south-facing limestone slopes of the hinterland. In the “1961-90” scenario, NPP map points out appreciable values (4 tC ha-1 yr-1) for regions of the central Italy, and a range between 1 and 3 tC ha-1 yr-1 for Italian southern regions (Fig. 3g). Interestingly, under climate change, this species would be able to potentially expand and to establish itself in the northern regions of Italy. Nuclei of Q. ilex are evident in several regions of the pre-Alps (Piedmont, Valle d’Aosta, Lombardy, Trentino, Veneto and Friuli Venezia Giulia), where Q. ilex has the opportunity to grow, preferring the hottest exposures. In the “2071-2100” B1 scenario, Q. ilex moves to the innermost areas of the Italian peninsula (Fig. 3h), where the primary productivity reaches values of 3.64 ± 0.15 tC ha-1 yr-1. Under the “2071-2100” A2 scenario (Fig. 3i), the presence on the Apennine ridge and pre-Alps becomes more evident. The diffusion in the regions of the Po valley, those with the greatest climatic variations in raising the temperature, appears to favour the occupation of territory by Q. ilex. Productivity values are low, but similar to the B1 climate scenario ones (3.58 ± 0.14 tC ha-1 yr-1). Nuclei in the southern regions (Campania and Calabria) are also preserved, showing a primary productivity of about 3.5 tC ha-1 yr-1.
Water use efficiency maps
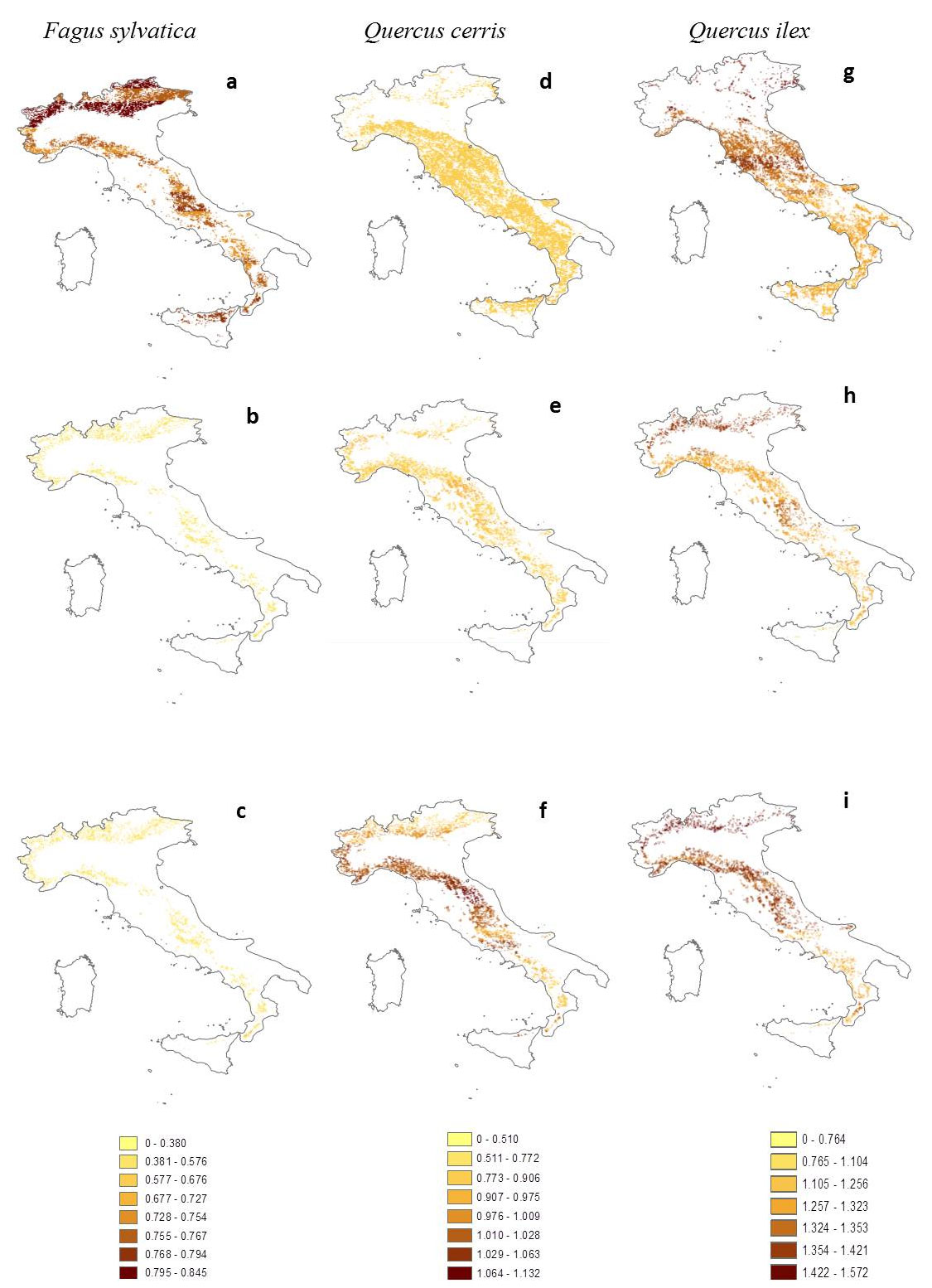
Water use efficiency (WUE) maps of Fagus sylvatica highlight a reduction of values induced by climate changes (Fig. 4a-c). The difference percentages calculated between “1961-90” and “2071-2100” B1 scenarios range from -42% to -26%, showing greater reduction in the pre-Alps areas (-41%) and northern Apennines (-37%). Similar values have been calculated for difference between “1961-90” and “2071-2100” A2 scenarios. Averages values of WUE are progressively decreasing from 0.772 ± 0.029 kgC tH2O-1 (“1961-90” scenario) to 0.486 ± 0.016 kgC tH2O-1 and 0.507 ± 0.025 kgC tH2O-1 (“2071-2100” B1 and A2 scenarios, respectively). Quercus cerris shows increasing difference percentages of WUE in the “2071-2100” B1 scenario compared to the reference “1961-90” one (Fig. 4d-f). The most representative frequency class of percentage change ranges between 7% and 15%, characterizing the northern and central Apennines, whereas these difference percentages range from -5% to 3% in the southernmost part of Apennines. The increasing trend in percentage differences appears also under the “2071-2100” A2 scenario with the most representative frequency class ranging from 25% to 30% and similar geographical localizations to the B1 climatic scenario. Average values of WUE are higher than beech ones, being 0.825 ± 0.026 kgC tH2O-1, 0.875 ± 0.039 kgC tH2O-1 and 0.991 ± 0.065 kgC tH2O-1 for the “1961-90”,” 2071-2100” B1 and A2 scenarios, respectively. The difference percentages calculated for Quercus ilex between “1961-90” and “2071-2100” B1 scenarios are more limited, ranging from -7.9% to -1.7%, showing greater reduction in the central and southern Apennines (Fig. 4g-i) than in the northerners. However, these differences remain at similar values for the “2071-2100” A2 scenario, although they are higher than the difference between “2071-2100” B1 and “1961-90” scenarios, ranging between -3.8% and 5.6%. As a consequence, the average values of WUE for Q. ilex are rather constant as 1.326 ± 0.053 kgC tH2O-1, 1.318 ± 0.046 kgC tH2O-1 and 1.375 ± 0.061 kgC tH2O-1 for “1961-90”, “2071-2100” B1 and A2 scenarios, respectively. This increase of WUE is parallel to the reduction of geographical distribution of Q. ilex, where only the 13% of current potential distribution (1961-90) is maintained ([6]). Overall, it is worth noting that the more drought-tolerant and adapted species is also the one showing the highest WUE in all scenarios.
Fig. 4 - Italian distribution water use efficiency (WUE, kgC tH2O-1) under different climatic scenarios. Fagus sylvatica: (a) actual climate 1961-90; (b) B1 2071-2100; (c) A2 2071-2100. Quercus cerris: (d), (e), (f) as for F. sylvatica.Quercus ilex: (g), (h), (i) as for F. sylvatica.
Discussion
Ecological considerations on the dynamics and physiology of the species
Climate change projections indicate an increased likelihood of droughts ([37]) and variability of precipitation - in time, space, and intensity - that would directly influence water resource availability. The combination of long-term changes (e.g., warmer average temperatures) and greater extremes (e.g., droughts) can have decisive impacts on water demand, with further impact on the ecosystems. An increase in air temperatures and a slight decrease in precipitations are forecast for the Mediterranean area by General Circulation Models (GCMs, Fourth Assessment Report - [33]). Lower water availability is also projected for this region by eco-physiological models such as GOTILWA ([70], [63]). In fact, increased temperatures and lower water availability have been already experienced in the last decades ([41], [67], [17], [62], [63]). Several studies have described reduced plant performance in the Mediterranean area during summer months due to heat and drought stress ([23], [79], [57], [65]).
Ecosystem responses to climate change are driven by complex multifactor influences ([56]). In the Mediterranean area, the future presence of a species is thus likely determined by the complex balance of temperature change, soil water availability, species-specific photosynthetic capacity, seasonal fires, air-free pollutants and land use changes. Moreover, species-specific responses may affect the structure and functioning of ecosystems through altered relationships with other plant-competitors on mineral resources and vital spaces. Comprehensive analysis of gas exchanges of each species can be made on the basis of data simulated by MOCA model. Two deciduous species show a strong reduction of NPP values as responding to the climate change, whereas evergreen Mediterranean oak shows a much lower NPP reduction. These responses may be affected by the non-consideration of the possible different impact of the increase of CO2 atmospheric concentration on the three studied species in the future scenarios. As reported by Keenan et al. ([36]), the increase of CO2 may counteract the reduction of NPP due to the climatic limitations induced by alteration of species-specific climate envelopes. Furthermore, a decreased suitability for a pixel (niche-based) to host a species was reflected in less NPP for the same site, if no CO2 effect was taken into account (semi-empirical modelling). NPP simulations made by a process-based model, GOTILWA+ showed that NPP increased as CO2 raised in the future climatic scenario, although the root mean squared error (RMSE) increased by a factor of three between GOTILWA+ simulations considering atmospheric CO2 as constant and those considering a CO2 increment ([36]). However, studies have also identified interspecies variability in responses to increasing atmospheric CO2 concentrations, and importantly have highlighted the possibility of species-specific response saturation rates. For these reasons, we have maintained the air CO2 concentration at 380 ppm also in the future climate changing scenarios and compared the response of the three species. As a consequence, the reduction of NPP values observed in all tree species examined here is due mainly to the influence of the bioclimatic envelope (distribution of the species) and changed climate.
Also transpiration rates and water use efficiency differed among tree species under climate change scenarios. Q. ilex was the best adapted to drought stress among plant species considered here. The higher drought resistance of Q. ilex is based on a drought-tolerant water-saving strategy ([43]), due to the morpho-anatomic characteristics of the sclerophyllous leaves and their longer physiological functioning in time ([47]), on generally low transpiration rates, and on the root system which is able to adapt and to resist to dehydrated soils ([47]). Furthermore, the higher WUE values of Q. ilex under limiting climatic scenarios with respect to the other two species point out a well-adapted functional mechanisms to maintain a positive carbon gain by the activation of “alternative ways” to dissipate the excess of incoming radiant energy ([80], [68]). Increases in WUE have also been found in rainfall exclusion experiments ([58], [44], [24]), although uncertainty remains in terms of how long such increases can be sustained. Q. cerris showed a progressive reduction of NPP and transpiration rates under limiting scenarios, due to the closure of stomata which are sensitive to change of evaporative demand between plant and atmosphere. However, under water stress the stomatal closure could be justified by the reduction of the stem/root hydraulic conductance and to the variation of soil water availability ([13], [14], [55]) for oaks. An integrated mechanism seems to be involved for the limitation of water loss when soil water dehydration becomes more intense; high evaporative demand becomes just as important as the state of dehydration of the soil, which directly affects the root ability to water uptake ([47]). Nevertheless, WUE values do not increase in the 2071-2100 B1 and A2 scenarios, pointing out a non-conservative water strategy under limiting climate conditions for this species. This could affect the distribution pattern of Quercus cerris and, in turn, its ability to fix carbon under these conditions. Q. cerris has potentially the possibility to shift to higher altitudes ([6]), towards cooler conditions and closer to its favourable climatic niche, although it may be limited by the presence of F. sylvatica. Functional similarities with Q. cerris have been noted in F. sylvatica, although beech shows different adaptive abilities to counteract the climate change, adopting a water spender strategy, that is typical for species growing in mesophilous environments. This strategy could represent a risk for survival of plant populations when environmental conditions extremely change. However, it has been reported that beech can show inter-annual and seasonal adaptation and relatively flexible changes in WUE, allowing the maintenance of carbon gain in relatively dry years (Matteucci, personal communication, Scartazza et al. submitted). It is worth noting that the remaining beech suitable surface area under the 2071-2100 A2 scenario is 65% compared to the reference “1961-90” period ([6]), pointing out a scarce possibility to shift to higher altitudes. As a consequence, F. sylvatica may be seriously threatened by climate change in Italy, being also subjected to a strong reduction of NPP.
However, it seems that in a warmer and drier environment, as the one projected for the Mediterranean areas for the following decades, the performance of the dominant species could be less competitive with respect to the other more drought and heat resistant species such as the co-dominant Phillyrea latifolia for Q. ilex (see [59]); as a general rule, the temporal dynamics of progressive physiological adjustments counteracting the environmental limiting factors (high temperature and drought increase) seem to play a fundamental role for determining competitive abilities against other co-occurring plant species under Mediterranean limiting conditions, conditioning thus the final distribution patterns of plant species.
Finally, it is also important to stress that our results are restricted to tree species in Italy, and thus we cannot be certain to what extent any patterns or results observed here may be either affected by species (co-)occurrences in other regions, or extrapolated to other topo-climatic scenarios.
Conclusions
The resulting spatial representation of the net primary productivity under two climatic scenarios was consistent with what is known about the eco-physiological response to environmental stresses (high temperature, drought) of the species analysed here. The use of multivariate statistical models to assess the different distribution areas of the species under different climatic conditions ([6]) has been very important to address the geo-referring of the MOCA’s output. This combined approach allowed also to deduce some aspects on the use environmental resources (water, solar radiation) in relation to north-south latitudinal gradient and two different climate scenarios. These suggestions may be helpful to identify priority areas to be managed in an adaptive way, so as to preserve the actual forest resource and mitigate or minimize the effects of climate change.
Acknowledgements
This work has been funded by the “Sapienza” University of Rome grant (MIUR Ateneo 2009) and the Italian Ministry of Environment, in collaboration with CONECOFOR (CONtrollo ECOsistemi FORestali), the intensive monitoring programme of forest ecosystems in Italy coordinated by the National Forest Service of Italy (CFS). The programme is framed within the Pan-European Level II Monitoring of Forest Ecosystems and was co-sponsored by the European Union under the Regulation no. 2152/2003 “Forest Focus”.
The work of MM and GM was funded by the FP6 European Integrated Project CIRCE (contract no. 036961).
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
M Mancini
F Francesconi
R Valenti
F Attorre
Department of Environmental Biology, “Sapienza” University of Rome, p.le Aldo Moro 5, I-00185 Rome (Italy)
Institute of Agroenvironmental and Forest Biology, National Research Council of Italy, v. Salaria km 29.300, I-00015 Monterotondo Scalo, RM (Italy)
Institute for Agricultural and Forestry Systems in the Mediterranean, National Research Council of Italy, v. Cavour 4-6, I-87036 Rende, CS (Italy)
Corresponding author
Paper Info
Citation
Vitale M, Mancini M, Matteucci G, Francesconi F, Valenti R, Attorre F (2012). Model-based assessment of ecological adaptations of three forest tree species growing in Italy and impact on carbon and water balance at national scale under current and future climate scenarios. iForest 5: 235-246. - doi: 10.3832/ifor0634-005
Academic Editor
Marco Borghetti
Paper history
Received: Aug 08, 2012
Accepted: Oct 10, 2012
First online: Oct 24, 2012
Publication Date: Oct 30, 2012
Publication Time: 0.47 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2012
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 61117
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 50327
Abstract Page Views: 4371
PDF Downloads: 4908
Citation/Reference Downloads: 32
XML Downloads: 1479
Web Metrics
Days since publication: 4846
Overall contacts: 61117
Avg. contacts per week: 88.28
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2012): 23
Average cites per year: 1.64
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Potential impacts of regional climate change on site productivity of Larix olgensis plantations in northeast China
vol. 8, pp. 642-651 (online: 02 March 2015)
Review Papers
Climate change impacts on spatial distribution, tree-ring growth, and water use of stone pine (Pinus pinea L.) forests in the Mediterranean region and silvicultural practices to limit those impacts
vol. 14, pp. 104-112 (online: 01 March 2021)
Research Articles
Modeling of early stage litter decomposition in Mediterranean mixed forests: functional aspects affected by local climate
vol. 8, pp. 517-525 (online: 18 November 2014)
Research Articles
Perceptions of forest experts on climate change and fire management in European Mediterranean forests
vol. 7, pp. 33-41 (online: 14 October 2013)
Research Articles
Predicting the effect of climate change on tree species abundance and distribution at a regional scale
vol. 1, pp. 132-139 (online: 27 August 2008)
Research Articles
Seeing, believing, acting: climate change attitudes and adaptation of Hungarian forest managers
vol. 15, pp. 509-518 (online: 14 December 2022)
Research Articles
An assessment of climate change impacts on the tropical forests of Central America using the Holdridge Life Zone (HLZ) land classification system
vol. 6, pp. 183-189 (online: 08 May 2013)
Research Articles
Is Pinus pinea growth affected by climate change in western Anatolia?
vol. 18, pp. 93-101 (online: 28 April 2025)
Research Articles
Role of forest cover, land use change and climate change on water resources in Marmara basin of Turkey
vol. 8, pp. 480-486 (online: 31 October 2014)
Research Articles
Responses of European forest ecosystems to 21st century climate: assessing changes in interannual variability and fire intensity
vol. 4, pp. 82-99 (online: 05 April 2011)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword