Intra-annual tree growth responds to micrometeorological variability in the central Amazon
iForest - Biogeosciences and Forestry, Volume 14, Issue 3, Pages 242-249 (2021)
doi: https://doi.org/10.3832/ifor3532-014
Published: May 21, 2021 - Copyright © 2021 SISEF
Research Articles
Abstract
Intra-annual distribution of precipitation in central Amazonia leads to a short mild dry season, which is associated with an increase in irradiance and temperature and a decline in relative humidity; however, the independent effect of each individual climatic variable on tree growth is still under investigation. The objective of this study was to determine how tree growth (inferred from radial stem increment) responds to monthly variations of micrometeorological variables in the central Amazon. During five years (2013-2017) we measured tree growth in 51 trees from nine species and, above the forest canopy, collected environmental data, such as photosynthetically active radiation (PAR), air temperature (T), precipitation, air relative humidity (RH), air vapor pressure deficit (VPD), reference evapotranspiration (ETo), and soil water content (SWC). We used principal component regression to evaluate the effect of micrometeorological variability on tree growth. Mean tree growth across species was responsive to variations in almost all the micrometeorological variables examined, with the exception of mean and minimum temperature, maximum RH, and minimum VPD. Mean tree growth across species increased with increasing precipitation, RHmean, RHmin and SWC, while it decreased with increasing PAR, Tmax, and ETo. It was also shown that an increase in VPDmean and VPDmax has a negative effect on tree growth. These results contribute to improve our understanding of effect of climate variability on tree growth, and shed light on the potential effect of severe droughts in the central Amazon.
Keywords
Atmospheric Evaporative Demand, Tropical Rainforest, Wood Density
Introduction
The Amazon rainforest covers a large area (about 5.3 × 106 km2) and plays an important role in the global carbon and water cycle, storing about 86 Pg C in total biomass ([36], [23]). Even when an increase in atmospheric CO2 can enhance the ecosystem photosynthesis ([20]), the impact of droughts can alter the integrity of the rainforest ecosystem in the Amazon region ([23]). Tree growth is defined as the gain in biomass and is often estimated by measuring the stem diameter increment over time ([38] [41], [28]). It can be limited by several factors, including nutrient availability, irradiance, precipitation and soil water content. Variations in irradiance ([40], [35]), precipitation ([28], [42]), and leaf nutrient content ([26]) have been reported to affect either photosynthesis or tree growth in the Amazon region. In central Amazonia the positive effect of precipitation on tree growth is less evident or not significant in the wettest years ([38], [9]), because the cloudiness associated with the rainy season, greatly reduces incoming radiation.
Actually, in the wettest part of the Amazon (north and central Amazon), it has been reported that ecosystem photosynthesis tends to increase in the dry season, following a slight increase in vapor pressure deficit (VPD - [10]). Likewise, Rowland et al. ([35]) also reported that at an eastern Amazonian forest with a strong rainfall pattern, carbon accumulation was greater in the dry season than in the wet season, in that case, accompanying an increase in solar radiation. The effect of temperature on tree growth is also still to be elucidated. For instance, Laurance et al. ([17]) reported that in the central Amazon tree growth increased with an increase in maximum temperature (Tmax), while the opposite was found by Méndez ([28]).
In the central Amazon, evapotranspiration (ET) tends to increase in the dry season ([15], [12], [8], [4]). A rise in VPD and transpiration during the dry season can lead to a drop in stomatal conductance (and hence in photosynthesis), as stomatal conductance often decreases with increasing VPD ([25]). While in southeastern Amazonia a sustained increase in VPD seems to be the trend of last three decades, in the north and central Amazon, a substantial increase in VPD has only been reported during prolonged dry seasons ([5]). Indeed, the increase in VPD observed during the drought of 2015 was associated with a drop in sun-induced fluorescence, an indicator of photosynthesis over the whole Amazon region ([42]).
Although much research has been carried out to assess the effect of climatic parameters on tree growth in tropical rainforest ([40], [9], [28]), there is still no consensus on the relative importance of each individual climatic parameter on tree growth. In fact, as the climatic variables are correlated, the individual effects of climatic variables on tree growth or plant functioning are difficult to be demonstrated ([11]). Therefore, to evaluate the relative contribution of each climatic variable on tree growth, it is essential to remove the effect of collinearity. This is important, because in tropical rainforests the effect of micrometeorological variability on tree growth can be as low as 9% of the total variance ([41]). An accurate estimate of the effect of micrometeorological variability on tree growth is of paramount importance because of the great influence of the Amazon forest on the global carbon balance and water cycle. The main objective of this study was to determine how tree growth (as inferred from radial stem increment) responds to monthly variations of micrometeorological variables in the central Amazon. In this study we hypothesize that, in the central Amazon, mean tree growth positively responds to an increase in vapor pressure deficit (VPD), temperature and photosynthetically active radiation (PAR), and negatively to an increase in precipitation.
Materials and methods
Study site
The study was conducted at the Tropical Forest Experiment Station (ZF2 Reserve), located at a terra-firme rainforest plateau in central Amazonia, about 60 km north of Manaus (02° 36′ 21″ S, 60° 08′ 11″ W, ≈ 120 m above sea level). In this area the leaf area index varies from 4.7 in dry season to 5.0 in the wet season ([27]) and tree density is high. In a tree inventory conducted in the central Amazon, Rankin-De-Mérona et al. ([33]) found a tree density (>10 cm diameter at breast height - DBH) of 636 trees per ha, canopy height was 35-40 m (most of trees with < 30 cm in diameter), while the mean stem length (height to the first branch) was 11.6 m. In the region, tree species diversity is very high; for instance, at an experimental site (km 30 of Manaus), Prance et al. ([32]) recorded 179 species of trees in one hectare (≥ 15 cm DBH), while the production of new leaves tends to be more concentrated in the dry season ([2], [22]).
The mean annual precipitation is 2420 mm ([9]), with a mild dry season which extends from June to October, being July-September the driest months (≤ 100 mm per month, rainfall data for Manaus over the 1930-2010 period - [13]); while the rainy season prolongs from November to May. At a nearby site (K34 - 60° 13′ W, 02° 36′ S), the actual evapotranspiration (ET) is about 3.4 mm day-1 in the wet season and 3.7 mm day-1 in the dry season (mean of 1300 mm yr-1); VPD and surface conductance (a proxy of canopy conductance in dense forests) vary from 7.1 hPa and 0.018 m s-1 (~0.72 mol m-2 s-1) in the dry season to 4.9 hPa and 0.022 m s-1 (~0.89 mol m-2 s-1) in the wet season ([8]). Mean temperature and RH are about 26 °C and 76%, respectively ([4]), while net radiation is 130 W m-2 (wet season) and 140 W m-2 in the dry season, with a mean net radiation of 11.7 MJ day-1 ([8]). The soil type is an Oxisol (Yellow Latosol) of clay texture and low fertility. The soil water content (SWC) held at tension of -1.5 MPa (often called the permanent wilting point) is about 0.30 v/v ([34]), and although soil water from the top layers supplies most of the transpirational demand, under prolonged drought roots can extract water from deep soil layers (> 4.8 m depth, [7]).
Micrometeorological environment, plant material and tree growth
During the 2013-2017 period, air temperature (T), PAR, RH, and precipitation (Pr) data were daily recorded above the forest canopy, at the top of a 40-m-tall observation tower (02° 35′ 21″ S, 60° 06′ 53″ W). PAR was measured using a quantum sensor (Li-190SA, Li-Cor, NE, USA), and air temperature and RH with a temperature-humidity sensor (Humitter 50y, Oy Vaisala, Finland) connected to a data logger (LI-1400, Li-Cor, Lincoln, NE). Data were collected at 15 min (PAR) or 30 min intervals (T and RH). PAR data were integrated over time to obtain daily PAR values (mol m-2 d-1). Precipitation data were recorded using a rain gauge (Em5b, Decagon, WA, USA). We used RH (%) and air temperature (T, °C) to compute vapor pressure deficit (VPD, in hPa) as previously described ([21]). VPD was obtained from RH and air temperature (T) data, VPDmin from RHmax and mean minimum T (Tmin), while VPDmax was obtained from mean RHmin and mean maximum T (Tmax) data. Reference evapotranspiration (ETo) was calculated as: ETo = 0.0023(Tmean + 17.8)(Tmax - Tmin)0.5 Ra, where Ra is the extraterrestrial radiation ([3]). In addition, we also measured soil water content SWC (%, v/v) at about two-week intervals, by collecting undisturbed soil samples at 10-20 cm depth, which were oven-dried at 105 °C as previously described ([21]).
In this study we collected data from 51 trees of nine evergreen species; each of the selected species had at least four replications (Tab. 1). In these trees we measured stem diameter increment (an estimator of tree growth, TG) at breast height (DBH, 1.3 m above the ground) at monthly intervals during 60 months (2013-2017). TG was measured using stainless steel dendrometer bands installed at least two years before the beginning of the current experiment. We also measured wood density (WD, dry mass to fresh volume ratio) by extracting one core sample per tree (3 to 5 cm in length and 5.15 mm in diameter) with an increment borer (Haglöf, Sweden). The core sample was extracted at about 1.3 m from the ground and at random days during the experimental period. Tree height was estimated using a regression model developed for trees of the central Amazon ([31]).
Tab. 1 - Mean wood density (WD, ± SE), mean monthly growth rates (TG, ± SE), tree height (± SD) and mean diameter at breast height (± SD) of trees. (Abbr): abbreviation; (n): number of trees; (Ecol): Eschweilera collina (Lecythidaceae); (Garg): Geissospermum argenteum (Apocynaceae); (Ilau): Inga laurina (Fabaceae); (Lmic): Licania micrantha (Chrysobalanaceae); (Pmac): Pouteria macrophylla (Sapotaceae); (Pdec): Protium decandrum (Burseraceae); (Smic): Scleronema micranthum (Malvaceae); (Stom): Swartzia tomentifera (Fabaceae); (Tven): Tachigali venusta (Fabaceae). In WD and TG columns, means followed by a different letter are significantly different (p ≤ 0.01) after Tukey test.
| Species | Abbr | n | Height (m) |
Diameter (cm) |
WD (g cm-3) |
TG (mm month-1) |
Some uses |
|---|---|---|---|---|---|---|---|
| Eschweilera collina | Ecol | 7 | 22.25 ± 3.5 | 20.7 ± 6.1 | 0.79 ± 0.01 bc | 0.058 ± 0.068 b | Timber potential |
| Geissospermum argenteum | Garg | 6 | 27.1 ± 5.3 | 34.1 ± 13.4 | 0.80 ± 0.01 bc | 0.099 ± 0.074 ab | Pharmacological potential |
| Inga laurina | Ilau | 5 | 21.2 ± 4.1 | 18.9 ± 6.6 | 0.73 ± 0.02 cd | 0.132 ± 0.08 ab | Shading tree in agroforestry |
| Licania micrantha | Lmic | 4 | 23.9 ± 3.8 | 23.7 ± 9.8 | 0.79 ± 0.02 bc | 0.258 ± 0.09 ab | Timber potential |
| Pouteria macrophylla | Pmac | 4 | 24.9 ± 5.8 | 28.3 ± 14.9 | 0.92 ± 0.02 a | 0.110 ± 0.09 ab | The tree produces edible fruits |
| Protium decandrum | Pdec | 6 | 21.5 ± 1.6 | 18.6 ± 2.6 | 0.59 ± 0.01 e | 0.106 ± 0.07 ab | The tree produces essential oils |
| Scleronema micranthum | Smic | 5 | 28.5 ± 3.2 | 36.8 ± 10.4 | 0.67 ± 0.02 c | 0.243 ± 0.08 ab | Timber industry |
| Swartzia tomentifera | Stom | 6 | 23.4 ± 4.9 | 24.1 ± 9.5 | 0.82 ± 0.01 b | 0.086 ± 0.07 ab | Timber potential |
| Tachigali venusta | Tven | 8 | 25.2 ± 6.5 | 29.7 ± 17.0 | 0.54 ± 0.01 e | 0.473 ± 0.06 a | No information |
| Mean or total | - | 51 | 24.2 | 26.1 | 0.74 ± 0.04 | 0.173 ± 0.01 | - |
Statistical analyses
To assess differences among species, the effects of months and years on TG, and the effect of interactions, we conducted a repeated-measures analysis of variance using the following hierarchical model (eqn. 1):
where Yijkl is the observation that represents the growth of a tree; µ a constant; αi, ßj, and γk represent the effect of i-th species, j-th years, and k-th months; (αß)ij, (αγ)ik, (ßγ)jk, and (αßγ)ijk denote the effect of the interactions; and εijk indicates the error term.
We used principal component regression (PCR - [30]) to evaluate the effect of monthly variations of micrometeorological variables on detrended tree growth (TGC). By performing PCR the collinearity among regressors was removed, and hence the variance inflation factor (VIF, a measure of collinearity between the predicting variables) became unity. The VIF is 1/(1-R2); thus, when the correlation (R) among regressors in null (R2 = 0), VIF = 1.0 ([30]). In the PCR analysis, we used TGC instead of raw tree growth data (TG), because a time-related trend in tree growth can affect PCR results ([29]). This step was accomplished by using a first-order autoregression ([30]). Prior to subjecting the TGC to PCR, the climatic data were standardized (observed value minus the mean divided by the standard deviation). In matrix notation, a standard multiple linear regression (MLR) model can be represented by eqn. 2 ([30]):
In eqn. 2, Y is the observation vector (dependent variable), X the matrix of regressors (also called design matrix), b the vector of coefficients, and ε the vector of random error terms. Likewise, a PCR model can be represented by eqn. 3, while the calculations required to compute the regression coefficients and test their significance are given in eqn. 4-15 ([30]):
In eqn. 3, the columns of Z represent a new set of orthogonal scores (z-scores). In eqn. 4, T is a matrix whose columns represent eigenvectors (derived from X data), while in eqn. 5, α represents a vector of regression coefficients. In eqn. 6, Λ denotes a diagonal matrix (p × p, being p is the number of regressors in matrix X) of the eigenvalues (λ1, λ2, … λp) of X′X. In eqn. 7, the orthogonal z-scores (z1, z2, …, zu) are often termed principal components. The estimator of α‚ and its variance-covariance are computed as shown in eqn. 8 -eqn. 9.
For standardized regressors (eqn. 10, eqn. 11):
The standardized regressors (bpc), the variance, and standard error of bpc (SE) are given by eqn. 12-14. In eqn. 12 , the “pc” subscript indicates that the principal components corresponding to near-zero eigenvalues have been removed from the analysis; likewise, the “u” in the second part of eqn. 12 is the number of principal components retained in the reduced PCR model (i.e., after discarding principal components associated with near-zero eigenvalues).
The significance of bpc can be tested on individual coefficients by using the statistic tn-k-1, where k represents the number of principal components in the reduced model, as described in eqn. 15:
In eqn. 14, the MSE is obtained as the regression of Y on the u-principal components retained in the model, while tjm denotes the j-th element of the eigenvector tm (m = 1, …, u). As supplementary information, the bivariate Pearson’s correlations between climate variables were also determined. Statistical analyses were carried out using Statistica® v. 7.0 (StatSoft, Inc., Tulsa, OK, USA).
Results
Micrometeorological variables and tree growth
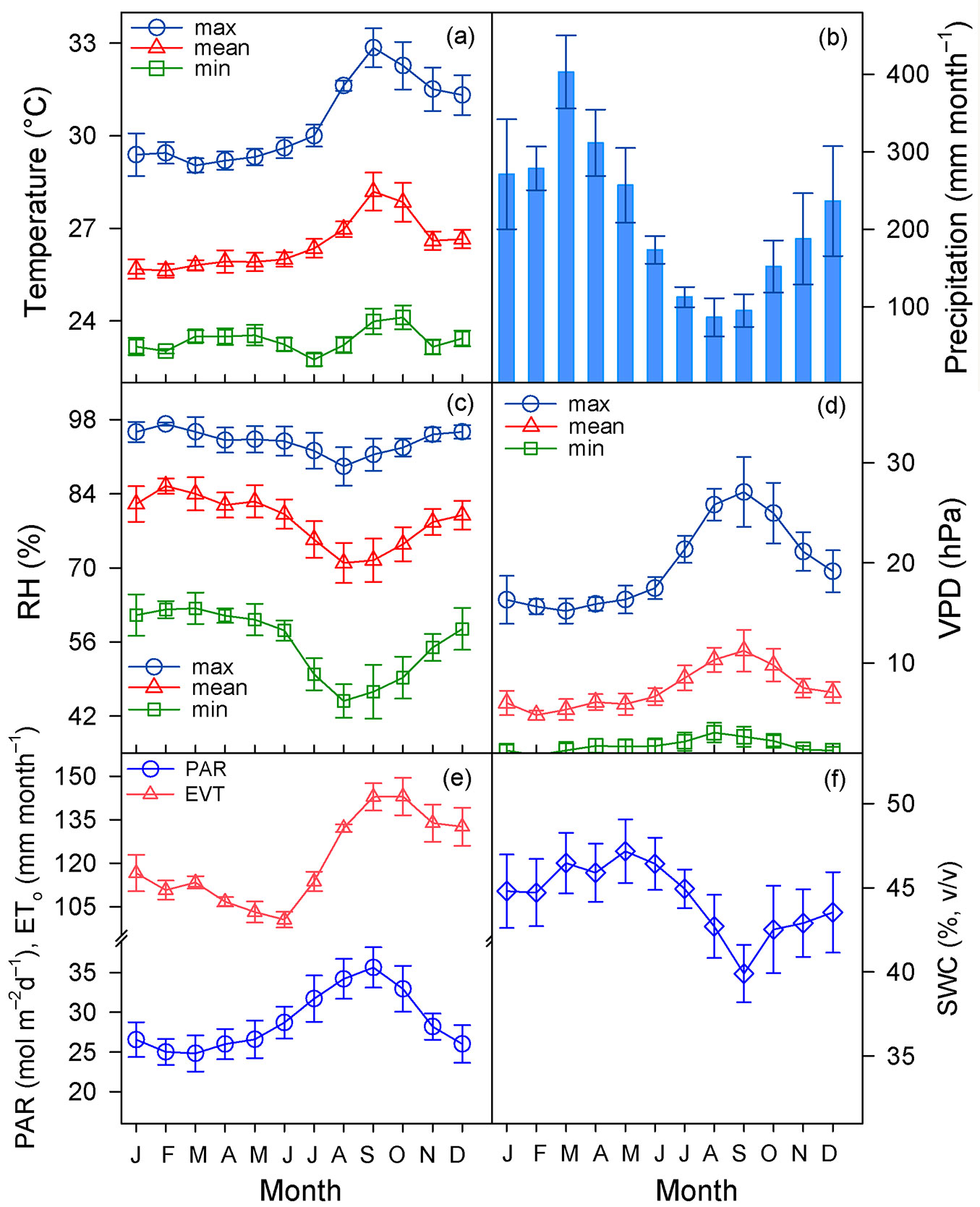
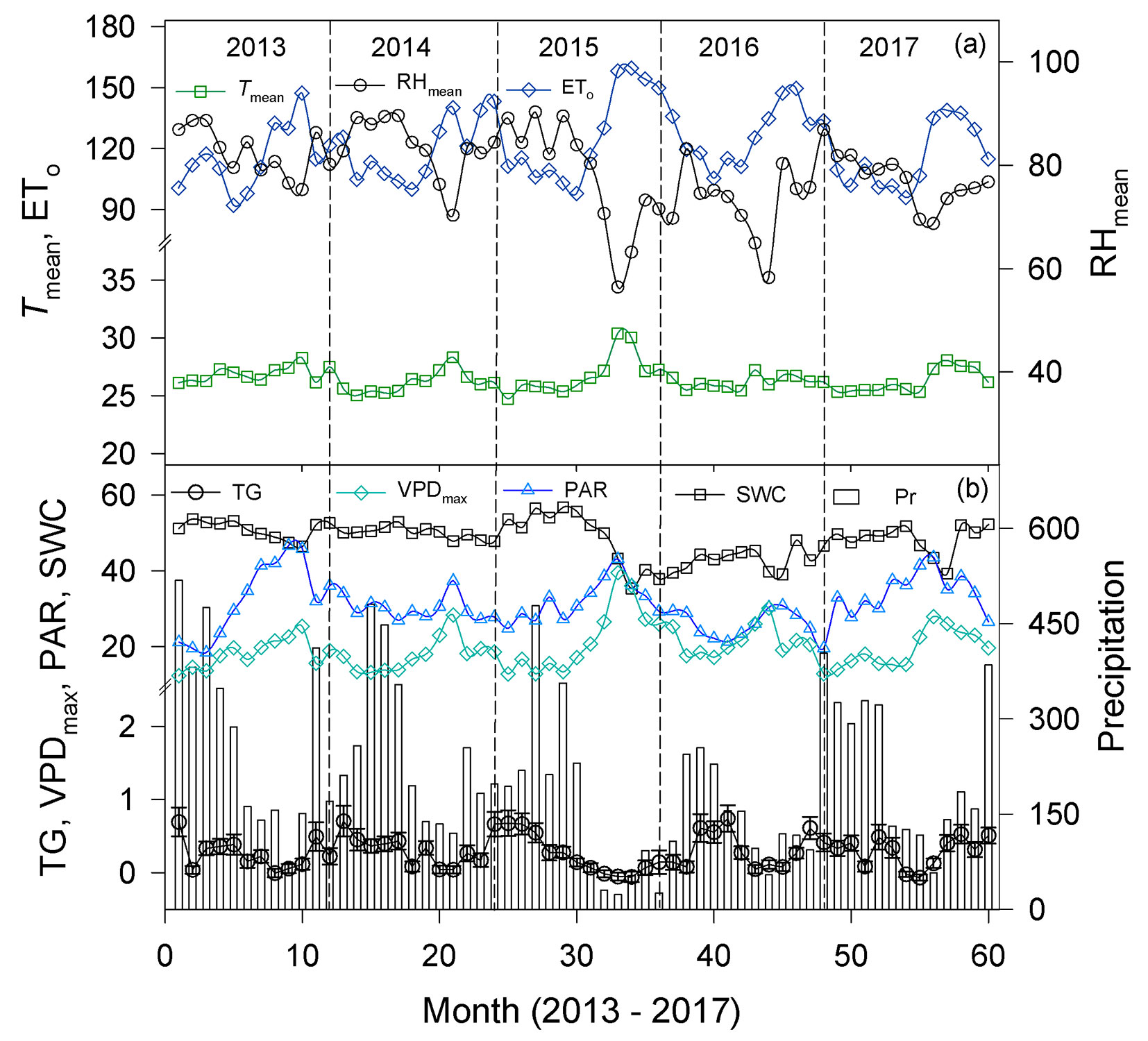
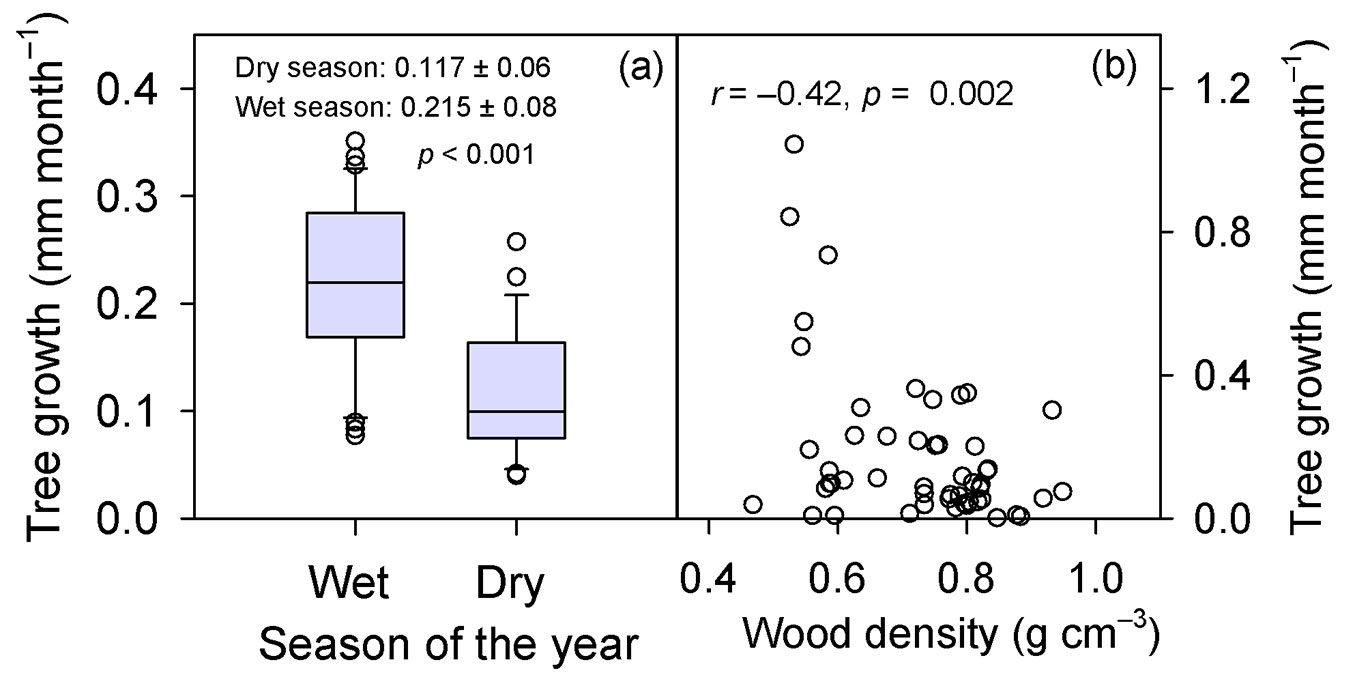
During the study period Tmean was 26.5 °C, RHmean 78.9%, and PAR 28.9 mol m-2 d-1, with variations in minimum and maximum values as described in Fig. 1. Mean SWC was 44.3% and mean values of VPD and ETo were 7.4 hPa and 120.8 mm month€’1, respectively (Fig. 1). Although the mean precipitation of the 2013-2017 period was close to the historical mean (2420 mm yr-1), it was irregularly distributed (Fig. 2), and as expected, the climatic variables were correlated (Tab. S1 in Supplementary material). Tree growth significantly differed among years (p = 0.025), species (p = 0.003), and months (p < 0.001 - see ANOVA in Tab. S2), and within a year the trees grew more slowly in the dry season than in the wet season (0.117 vs. 0.215 mm month-1, respectively; p < 0.001 - Fig. 3A).
Fig. 1 - Monthly variation of air temperature (a), precipitation (b), relative humidity (RH, c), and vapor pressure deficit (VPD, d), photosynthetically active radiation (PAR), and reference evapotranspiration (ETo, e), and soil water content (SWC, f). Each symbol or bar represents the mean (± standard error) of the indicated month over the years (2013-2017).
Fig. 2 - (a) Monthly variation of Tmean (°C), ETo (mm month-1), and RHmean (%), and (b) VPDmax (hPa), PAR (mol m-2 d-1), SWC (%, v/v) , precipitation (Pr, mm month-1, bar), and radial mean monthly growth rate (TG, mm month-1) across species. Each symbol represents the mean value of the indicated month over the years (2013-2017). The vertical dashed line indicates the year. Other acronyms are as described in Fig. 1 and Tab. 2.
Fig. 3 - (a) Radial mean monthly growth rates (TG, raw data) across species (51 trees) recorded in the wet seasons (November-May) and dry seasons (June-October) throughout the experimental period (2013-2017). (b) The relationship between mean growth rate (TG) per tree and wood density, WD. In panel (a), the boundaries of the box indicate the 25th and 75th percentile, and the solid line within the box denotes the median; the mean value (mm month-1) within a season is also shown. In panel (b), each symbol corresponds to the mean growth rates of one tree over the five years (mean of 60 months), while WD represents the value of one sample per tree.
The highest growth rates were recorded in Tachigali venusta (0.473 mm month-1) and the lowest one in Eschweilera collina (0.058 mm month-1), while the other seven species comprised a group with rather similar growth rates (Tab. 1). Tachigali venusta was the species with the lowest wood density (WD) and the highest growth rates, and across species tree growth was negatively correlated with wood density (r = -0.42, p = 0.002 - Fig. 3B).
Effect of micrometeorological variability on tree growth
In this section, we used the mean TGC across species (TGC-mean) to describe the statistical procedure. The principal component analysis showed that the first four factors explained 92.9% of the total variance of the climatic data. The eigenvectors and eigenvalues associated with these four factors were used to compute the z-cores (eqn. 4) more closely associated with TGC. The regression of the first four z-cores (z1, z2, z3 and z4) on the TGC-mean yielded four α-coefficients (i.e., α1= -0.012, p < 0.001; α2 = -0.012, p = 0.08, α3 = - 0.020, p = 0.02, and α4 = -0.003, p = 0.68). Therefore, by observing the p values of the α1-4-coefficients we were able to select the z-scores (i.e., z1 and z3) more closely related with TGC-mean (i.e., α1= -0.012, p < 0.001 and α3 = - 0.020, p = 0.02 - Tab. S3 in Supplementary material). Thus, in the next step we only used z1 and z3 (PCR reduced model) to obtain the PCR-beta coefficients (bpc) associated with each of the climatic variables, as described in eqn. 12. The regression of the z1 and z3-score on TGC-mean yielded the mean square error (MSE = 0.0050, R2 = 0.264, p < 0.001 - Tab. S3), which was required to compute the standard error (eqn. 14) and for testing the significance of the beta coefficients -bpc (eqn. 15). By using this approach, the bpc described in Tab. 2 were obtained.
Tab. 2 - Regression coefficients (Beta) obtained by Principal Component Regression (PCR) of the effect of climatic variables on detrended tree growth (TGC) of the studied species. The R2 (determination coefficient) of PCR is also shown. Abbreviations are shown in Tab. 1 and Fig. 1. The standard error and p value of coefficients are shown in Tab. S4 (Supplementary material). (*): p < 0.05.
| Species | Ecol | Garg | Ilau | Lmic | Pmac | Pdec | Smic | Stom | Tven | TGC-mean |
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | 0.08 | 0.06 | 0.18 | 0.12 | 0.17 | 0.1 | 0.1 | 0.22 | 0.22 | 0.26 |
| PAR | -0.0072* | -0.0077 | -0.0164* | -0.0139 | -0.0106 | -0.0062 | -0.0158 | 0.0072* | -0.0352* | -0.0126* |
| Pr | 0.0003 | 0.0069 | 0.0149* | 0.0134 | 0.0104* | 0.0062 | 0.015 | 0.0006 | 0.0346* | 0.0121* |
| Tmean | -0.0036 | 0.0023 | 0.0044 | 0.0017 | 0.0009 | 0.0001 | 0.0026 | -0.002* | 0.0027 | 0.0016 |
| Tmin | -0.0058* | 0.008 | 0.0164* | 0.012 | 0.0088 | 0.0047 | 0.0143 | 0.0031* | 0.029 | 0.0109 |
| Tmax | 0.0019 | -0.0013 | -0.0031* | -0.0044* | -0.0037* | -0.0025* | -0.0044* | -0.0104* | -0.0072* | -0.0039* |
| RHmean | 0.0001 | 0.0016 | 0.0039* | 0.0052* | 0.0043* | 0.0029* | 0.0052* | -0.0016 | 0.0003* | 0.0046* |
| RHmin | 0.0021 | 0.0023 | 0.0053* | 0.0063* | 0.0051* | 0.0033* | 0.0065* | -0.0028 | -0.0036* | 0.0056* |
| RHmax | -0.0028 | -0.0016 | -0.0029 | -0.0006 | -0.0001 | 0.0004 | -0.0013 | -0.0009 | 0.0001 | -0.0006 |
| VPDmean | -0.0009 | -0.0007 | -0.002 | -0.0038 | -0.0033* | -0.0023 | -0.0036 | 0.001 | -0.0111* | -0.0034* |
| VPDmin | 0.0024 | 0.0021 | 0.0039 | 0.0013 | 0.0006 | -0.0001 | 0.0022 | 0.0009 | 0.0018 | 0.0012 |
| VPDmax | -0.0011* | -0.0016 | -0.0039* | -0.0052* | -0.0044* | -0.003* | -0.0053* | -0.0015 | -0.0147* | -0.0047* |
| SWC | -0.0058 | 0.0017 | 0.0039* | 0.0047* | 0.0038* | 0.0025* | 0.0048* | 0.0105* | 0.0129* | 0.0042* |
| ETo | 0.0036 | -0.0022 | -0.005* | -0.0057* | -0.0046* | -0.003* | -0.006* | -0.0133* | -0.0153* | -0.0051* |
We found that most of the species were responsive to variations in SWC, ETo, VPDmax, RHmin, RHmean and Tmax, four species responded to variations in PAR and three species to changes in precipitation, while only two species responded to variations in VPDmean (Tab. 2). It was also found that three species were responsive to variations in Tmin, while only Swartzia tomentifera was affected by variation in Tmean, whereas none of the species responded to variations in either VPDmin or RHmax (Tab. 2). The mean tree growth across species (TGC-mean) was responsive to variations in almost all micrometeorological variables investigated, the exceptions were Tmin, Tmean, RHmax and VPDmin, and together micrometeorological variability accounted for 26.4% of total variation in TGC-mean (Tab. S3 in Supplementary material). The TGC-mean as a function of standardized climatic variables can be represented by eqn. 16, whose coefficients are described in Tab. 2.
Because climatic variables were affected by seasonality, the variables that increased during the dry season, such as PAR, Tmax, VPDmean, and VPDmax (Fig. 1) negatively affected tree growth. For instance, across species the reduction in tree growth in the dry season vs wet season (Fig. 3a) occurred simultaneously with a decrease (dry season vs. wet season) in precipitation (123.9 mm month-1 vs. 277.9 mm month-1 - Fig. 1) in combination with a rise in Tmax (31.3 vs. 29.9 °C), PAR (32.6 vs. 26.2 mol m-2 d-1), VPDmean (9.3 vs. 6.1 hPa), and VPDmax (23.3 vs. 17.1 hPa).
Response of individual species to micrometeorological variability
On the responsiveness of individual species to micrometeorological variability, we found that Inga laurina and Tachigali venusta were the most responsive species, as they were affected by the variation of nine climatic variables (p ≤ 0.05 - Tab. 2). Protium decandrum, Pouteria macrophylla, Scleronema micranthum, Licania micrantha and Swartzia tomentifera responded to variations in 6-8 micrometeorological variables, and hence, they constituted a second group, while the other two species (Eschweilera collina and Geissospermum argenteum, a third group) were less responsive to variations in the measured climatic variables. In fact, G. argenteum was only barely responsive to variation in precipitation, RHmin, SWC and ETo (p < 0.085). In comparison with the species that grew more slowly, there was a slight trend for species with faster growth rates (mm month-1) to be more responsive to micrometeorological variability, e.g., T. venusta (0.473) and I. laurina (0.132) were more responsive to climatic variability than E. collina (0.058) or G. argenteum (0.099).
The majority of species responded to microclimatic variability in the same way, the exception were S. tomentifera, which positively responded to variations in PAR, and E. collina, which was negatively affected by an increase in Tmin. On average, PAR, Tmax, VPDmean, VPDmax and ETo had a negative effect on TGC-mean (negative beta values in Tab. 2), while the effect of SWC, precipitation, RHmin, and RHmean was positive. Swartzia tomentifera responded to variation in Tmean, but the combined effects over species was too small to have a significant effect on TGC-mean. Although three species responded to variations in Tmin, the overall effect of Tmin on TGC-mean was insignificant. This occurred because while I. laurina and S. tomentifera responded positively to Tmin, the opposite effect was observed in E. collina (Tab. 2).
Discussion
On average, tree growth was responsive to variations in nine out of the 13 micrometeorological variables studied, and we found that PCR explained 26.4 % of the total variance. When the effect of climate variability on tree growth is under evaluation, a R2 value of 0.26 is not unexpected, as many factors can affect tree growth ([6]). For instance, Wagner et al. ([41]) found that only 9% of the variation in tree growth can be ascribed to seasonal climate variability. Because climatic parameters were greatly influenced by micrometeorological seasonality, climatic variables that increased during the dry season negatively affected tree growth. For instance, taking the wet season as the base line, the reduction in tree growth (45.6%) in the dry season occurred in parallel with a decrease in precipitation (55.4%) and RHmin (17.1%), and with a rise in PAR (24.7%), VPDmean (52.5%) and VPDmax (36.5%). The decline in tree growth in the dry season is in agreement with the results reported by Wagner et al. ([40]) for the central Amazon. Méndez ([28]) also found a decline in tree growth during the drought of 2015-2016 in the central Amazon (02° 35′ S, 60° 12′ W). Likewise, by using sun induced florescence, Lee et al. ([18]) and Yang et al. ([42]) found that leaf fluorescence (an estimator of photosynthesis) decreased during the dry season in the Amazon region, which ultimately can lead to a decline in biomass accumulation.
It has been reported that several climatic parameters, such as solar radiation, VPD and ET increase in the dry season. However, because the increase in VPD and ET during the dry season ([8]) occurs simultaneously with a decrease in precipitation ([4]) and SWC ([7]), it is difficult to separate their respective contributions on tree growth by using standard multiple regression.
Even though reduced precipitation is one of the major climatic parameters associated with the dry season, our results clearly show that the increase in VPD (mean and maximum) and ETo have a significant effect on tree growth, which cannot be statistically ascribed to the influence of other climatic parameters, as the contribution of collinearity was removed. At same time, it is also shown that, irrespective of the direct influence of temperature on VPD, Tmax by itself seems to have an effect on tree growth that cannot be attributed to the effect of VPD. This is important because it shows that when highly correlated variables are under investigation, as it often occurs with climatic variables, disregarding collinearity between variables can lead to imprecise results. In this work we hypothesized that mean tree growth positively responds to an increase in VPD, temperature and PAR, and negatively to an increase in precipitation, which was not supported by data, as across species a rise in PAR, Tmax, VPDmax and VPDmean had a negative effect on tree growth across species, while an increase in precipitation and SWC had a positive effect.
Studies that aim to assess the effect of the dry season on tree growth in the Amazon have led to different conclusions, perhaps because the impact of drought on tree growth depends on the length of the dry season. For example, Silva et al. ([38]) and Dias & Marenco ([9]) did not find a negative effect of the dry season on tree growth, whereas Wagner et al. ([40]) reported that tree growth decreases in the dry season. In this study we found that the decrease in tree growth was essentially associated with an increase in PAR, Tmax and VPDmax, and with decline in precipitation and SWC.
A negative effect of PAR on tree growth is in contrast with the results reported by Rowland et al. ([35]) who concluded that tree growth increased in the dry season when irradiance is more intense. The discrepancy can be ascribed to the length of the dry season, as it has been reported that root water uptake can be enhanced during drought ([24], [7]), which can help to withstand the effect of water stress in mild dry seasons.
It has been postulated that in the Amazon, precipitation can limit ecosystem photosynthesis up to about 2000 mm yr-1, and that above this threshold solar radiation can be the limiting factor of photosynthesis ([1]). In this study, the trees grew more slowly with a reduction in precipitation and SWC, irrespective of an increase in PAR with decreasing precipitation, which shows that the distribution of precipitation within a year is of paramount importance for the effect of PAR on tree growth. We have shown that a decline in VPDmax (also VPDmean) was associated with an increase in tree growth (Fig. 2, Tab. 2), and that VPD increased in the dry season (Fig. 1). It is known that stomatal conductance (and hence photosynthesis) is a function of VPD, being the most common response a decline in stomatal conductance with increasing VPD ([14], [25]). Thus, it is plausible to infer that the effect of VPDmean and VPDmax on tree growth occurs via its effect on stomatal conductance. This is consistent with the findings of Lee et al. ([18]) and Yang et al. ([42]) who reported a decline in sun induced fluorescence in the dry season, which occurred in parallel with an increase in VPD.
We found a negative effect of Tmax on tree growth, whereas over a wide range of tropical forest sites Wagner et al. ([40]) reported that Tmax has no significant effect on tree growth, and concluded that temperature variations are of secondary importance for tropical tree growth. This suggests that in comparison with other major drivers of tree growth, such as precipitation and solar radiation ([40], [28]), the effect of temperature is more difficult to detect. In tropical rainforests, the optimum temperature for photosynthesis is about 29 °C ([19]), with decreasing photosynthetic rates at higher temperatures. Beside the indirect effect of temperature and relative humidity on photosynthesis (via its effect of VPD), an increase in temperature has also a direct effect on transpiration via the effect of temperature on water viscosity (Darcy’s Law), and cuticular transpiration ([16]). Similarly, RH has also a direct effect on transpiration, as it may affect the hydration of cuticle components ([16]). An increase in Tmax may have also a direct effect on tree growth via the effect of temperature on leaf respiration, isoprene emission and photorespiration ([37], [39]). As most of the species negatively responded to a decrease in SWC (the exception was G. argenteum; E. collina was barely responsive, p =0.06), it can be inferred that even when root water uptake can be enhanced under drought ([24], [7]), the increased water absorption during the dry season did not keep pace with the transpirational demand, which ultimately resulted in a reduction in tree growth.
One of the difficulties in assessing the individual effect of climatic variability on tree growth is to remove the effect of collinearity between the climatic drivers. By using PCR we show that the mean tree growth was responsive not only variation in precipitation, temperature (Tmax), and PAR, but also to variation in relative humidity (RHmean and RHmin) and vapor pressure deficit (VPDmean and VPDmax). This result is important because due to global warming (temperature is increasing about 0.16 °C per decade over the Amazon region), the rainfall pattern in the Amazon is changing, ranging from lower rainfall intensity (longer dry seasons) in eastern and southern Amazonia to higher rainfall intensity in the northern Amazon ([23]). It has also been reported an increase in vapor pressure deficit, from a steady increase in southern Amazon (over last three decades) to episodic increases during drought events in the northwest of the Amazon region ([5]), when a decline in photosynthesis can occur ([42]). Therefore, an increase in VPD often leads to an increase in transpiration, which associated with a decline in precipitation can lead to severe water deficit and thereby to decline in photosynthesis -except in the wettest part of the Amazon where a mild increase in VPD can enhance photosynthesis ([10]). Moreover, under severe drought, high VPD can greatly reduce hydraulic conductivity, which can eventually affect the survival of trees ([25], [5]). Thus, if the dry season becomes longer and dryer, as predicted by models ([23]), it may be expected that trees currently more sensitive to droughts will be the more affected by climate changes. These results contribute to improve our understanding of the ecophysiology of Amazonian trees and provide further information regarding the potential effects of increased drought in the Amazon region.
Conclusions
In this study we assessed the effect of several climatic parameters on tree growth, and we were able to remove the effect of collinearity among climatic variables by using principal component regression. On average, tree growth increased with increasing precipitation, SWC, RHmin, and RHmean, while it decreased with increasing PAR, Tmax , and VPDmax and ETo, which conflicts with our working hypothesis. Thus, it seems plausible to conclude that the decline in tree growth that occurs during the dry season could reflect a decrease in the capacity of the tree to extract water from deeper soil layers to meet the increased transpirational demand during the dry season. A contribution of this study is to clearly demonstrate the effect of variations in VPDmean and VPDmax on tree growth of Amazonian trees. These results enhance our understanding of the ecophysiology of Amazonian trees and provide insights into the potential effects of severe droughts foreseen by climate models for the Amazon region.
Acknowledgments
We acknowledge the Ministry of Science, Technology and Innovations - National Institute for Research in the Amazon (MCTI-INPA), the Foundation for Research Support of the State of Amazonas (FAPEAM), Coordination for the Improvement of Higher Education Personnel (CAPES code 0001) and the National Council for Scientific and Technological Development - CNPq (303907/2018-5). We greatly appreciate the reviewers for their valuable comments, which greatly improved the quality of the manuscript.
Abbreviations
DBH: tree diameter at breast height; ETo: reference evapotranspiration; ET: evapotranspiration (actual); TG: tree growth (inferred from radial stem increment); TGC-mean: mean of detrended TG across species; PAR: photosynthetically active radiation; PCR: principal component regression; Pr: precipitation; R2: square of correlation (determination coefficient); RH: relative humidity; RHmax: mean maximum RH; RHmin: mean minimum RH; RHmean: mean RH; SWC: soil water content; T: air temperature; Tmax: mean maximum T; Tmin: mean minimum T; Tmean: mean T; VPD: vapor pressure deficit; VPDmax: mean maximum VPD; VPDmin: mean minimum VPD; VPDmean: VPD mean. VIF: variance inflation factor; WD: wood density.
Species: Ecol: Eschweilera collina; Garg: Geissospermum argenteum; Ilau: Inga laurina; Lmic: Licania micrantha; Pdec: Protium decandrum; Pmac: Pouteria macrophylla; Smic: Scleronema micranthum; Stom: Swartzia tomentifera; Tven: Tachigali venusta.
Conflict of Interest
The authors declare that they have no conflict of interest.
Author contributions
SAAV collected data and conducted statistical analysis; RAM secured funding, collaborate in the analysis of data, supervised the experimental work, and wrote the article with contributions of the first author.
References
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Instituto Nacional de Pesquisas da Amazônia - INPA, Botany Graduate Program, Avenida André Araújo, 2936, 69067-375 Manaus, AM (Brazil)
Instituto Nacional de Pesquisas da Amazônia - INPA, Coordination of Environmental Dynamic, Tree Ecophysiology Laboratory, 69067-375 Manaus, AM (Brazil)
Corresponding author
Paper Info
Citation
Antezana-Vera SA, Marenco RA (2021). Intra-annual tree growth responds to micrometeorological variability in the central Amazon. iForest 14: 242-249. - doi: 10.3832/ifor3532-014
Academic Editor
Rossella Guerrieri
Paper history
Received: May 21, 2020
Accepted: Apr 08, 2021
First online: May 21, 2021
Publication Date: Jun 30, 2021
Publication Time: 1.43 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2021
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 35338
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 29987
Abstract Page Views: 2459
PDF Downloads: 2259
Citation/Reference Downloads: 3
XML Downloads: 630
Web Metrics
Days since publication: 1742
Overall contacts: 35338
Avg. contacts per week: 142.00
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2021): 6
Average cites per year: 1.20
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Links between phenology and ecophysiology in a European beech forest
vol. 8, pp. 438-447 (online: 15 December 2014)
Research Articles
Quantifying the vertical microclimate profile within a tropical seasonal rainforest, based on both ground- and canopy-referenced approaches
vol. 15, pp. 24-32 (online: 27 January 2022)
Research Articles
Analysis of canopy temperature depression between tropical rainforest and rubber plantation in Southwest China
vol. 12, pp. 518-526 (online: 09 December 2019)
Research Articles
The potential of using xylarium wood samples for wood density calculations: a comparison of approaches for volume measurement
vol. 4, pp. 150-159 (online: 11 August 2011)
Research Articles
Variation of wood and bark density and production in coppiced Eucalyptus globulus trees in a second rotation
vol. 9, pp. 270-275 (online: 08 September 2015)
Short Communications
Effect of intensive planting density on tree growth, wood density and fiber properties of maple (Acer velutinum Boiss.)
vol. 9, pp. 325-329 (online: 22 October 2015)
Research Articles
Validation of models using near-infrared spectroscopy to estimate basic density and chemical composition of Eucalyptus wood
vol. 17, pp. 338-345 (online: 03 November 2024)
Research Articles
Earlywood vessel features in Quercus faginea: relationship between ring width and wood density at two sites in Portugal
vol. 8, pp. 866-873 (online: 27 April 2015)
Research Articles
Physical, chemical and mechanical properties of Pinus sylvestris wood at five sites in Portugal
vol. 10, pp. 669-679 (online: 11 July 2017)
Research Articles
Density, extractives and decay resistance variabilities within branch wood from four agroforestry hardwood species
vol. 14, pp. 212-220 (online: 02 May 2021)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword