Validation of models using near-infrared spectroscopy to estimate basic density and chemical composition of Eucalyptus wood
iForest - Biogeosciences and Forestry, Volume 17, Issue 6, Pages 338-345 (2024)
doi: https://doi.org/10.3832/ifor4516-017
Published: Nov 03, 2024 - Copyright © 2024 SISEF
Research Articles
Abstract
Determining the wood properties is fundamental because these properties are directly related to wood quality. The near-infrared (NIR) spectroscopy technique has been used to determine various properties of wood. However, even with promising results, NIR spectroscopy needs to be further investigated to evaluate the robustness of its estimates. The objective of this study was to develop regression models from NIR spectra to estimate the basic density and the extractive and lignin contents of wood as well as to verify their robustness through independent and cross-validation. NIR spectra were initially obtained through an integration sphere and optical fiber for the transverse and radial faces of solid wood and through an integration sphere for powdered wood. The wood basic density and the extractive and lignin contents were determined by conventional methods in 180 and 143 specimens, respectively. The samples were collected from Eucalyptus urophylla × Eucalyptus grandis clones aged 5 years. The basic density and extractive and lignin content values were correlated with the NIR spectra by a partial least squares regression. The best models for estimating the basic density of the wood were generated from the spectra obtained on the transverse surface, both with the integration sphere pathway and in the optical fiber pathway. For estimating the chemical properties of wood, the best models were developed from the powdered wood via the integration sphere for assessing the extractive content, Klason lignin, acid-soluble lignin content and total lignin. In all the models, the mathematical treatment of the data by the first derivative was essential for better fitting the models and reducing the error. We concluded that NIR spectroscopy was effective for the estimation of basic density and extractive and lignin contents of wood.
Keywords
Introduction
The different analysis techniques used to investigate wood quality (physical, mechanical, chemical, and anatomical properties) usually require large amounts of time and substantial investment. Recently, near-infrared (NIR) spectroscopy has been shown as an increasingly promising tool for evaluating wood quality ([17], [18], [7], [8], [9], [27]).
NIR spectroscopy is based on electromagnetic radiation that extends in the wavelength range from 750 nm to 2.500 nm or from 13.300 to 4.000 cm-1. It is also based on vibrational spectroscopy, which measures the interaction between light and material ([25]). With the aid of multivariate statistics and computer systems, NIRS can be used to perform quantitative analyses and qualitative applications, such as the classification of wood and other biological materials ([35]). To extract information using this technique, calibrations have been developed that relate the NIR spectra of a large number of samples of a material, such as wood, and the property being studied, such as cellulose yield or content ([11]).
NIR spectroscopy is a fast and nondestructive technique with a measurement time of approximately 1 minute or less, and is applicable to any biological material, requiring little or no sample preparation ([24]). However, NIRS is sensitive to the moisture conditions of the sample. Fresh wood, bark, fruits, seeds, and leaves may have high moisture levels, and the NIR spectra are very sensitive between 1400 and 1900 nm, where the main hydroxyl absorption peaks occur. In addition, portable NIR equipment capable of recording spectra with low noise and low sensitivity to temperature and humidity, as well as other common sources of variation in the forest environments, is needed ([18]).
NIR spectroscopy has already been satisfactorily used in studies of wood properties ([12], [38], [7], [8], [19], [6]) and is a promising tool for determining information about wood quality and its control. During wood formation, internal and external factors lead to variations in the type, number, size, shape, physical structure, and chemical composition of wood elements. According to Larson ([22]), wood quality is the classification of these variations in the elements when they are counted, measured, weighed, analyzed, or evaluated for a specific purpose.
Many studies are reported in the literature presenting NIR-based calibrations developed in order to predict wood density and its chemical composition. Regarding models for estimating chemical properties, part of the models have been developed using as reference values that represent a composite sample ([4], [38], [19], [23]). In other words, discs or wedges are converted into powder, without distinction of region within the wood, and the whole (grounded) wedge is considered in modeling. In this study, we assumed that the model would perform better if the reference analyses were carried out considering the radial variation of the analyzed property instead of using a sample composed of dust from all regions of the disk.
The objective of this study was to develop multivariate predictive models for estimating the basic density and extractive and lignin contents of wood considering the radial variation of properties. To this purpose, the wedges were subdivided into 3 parts (pith, intermediate, and sapwood), and the wood from each region was converted into powder separately and submitted to chemical analysis, thereby considering the radial variation. The wood chemical composition and radial variations of density, lignin, and extractive content (EXT) of Eucalyptus trees were previously presented in Pimenta et al. ([26]). In the present study, NIR spectra were recorded in wood dust from each region and the predictive model took into account the radial variation that occurred in the wood discs.
Materials and methods
Origin of the material and sampling
The trees used in the study were clones of Eucalyptus urophylla ×E. grandis hybrids from the experimental planting of a cellulose pulp company located in the municipality of Itamarandiba, MG, Brazil (17° 51′ S, 42° 51′ W; altitude: 910 m asl). The average annual rainfall of the region is 1000 mm, with the soil classified as Yellow Latosol ([20]).
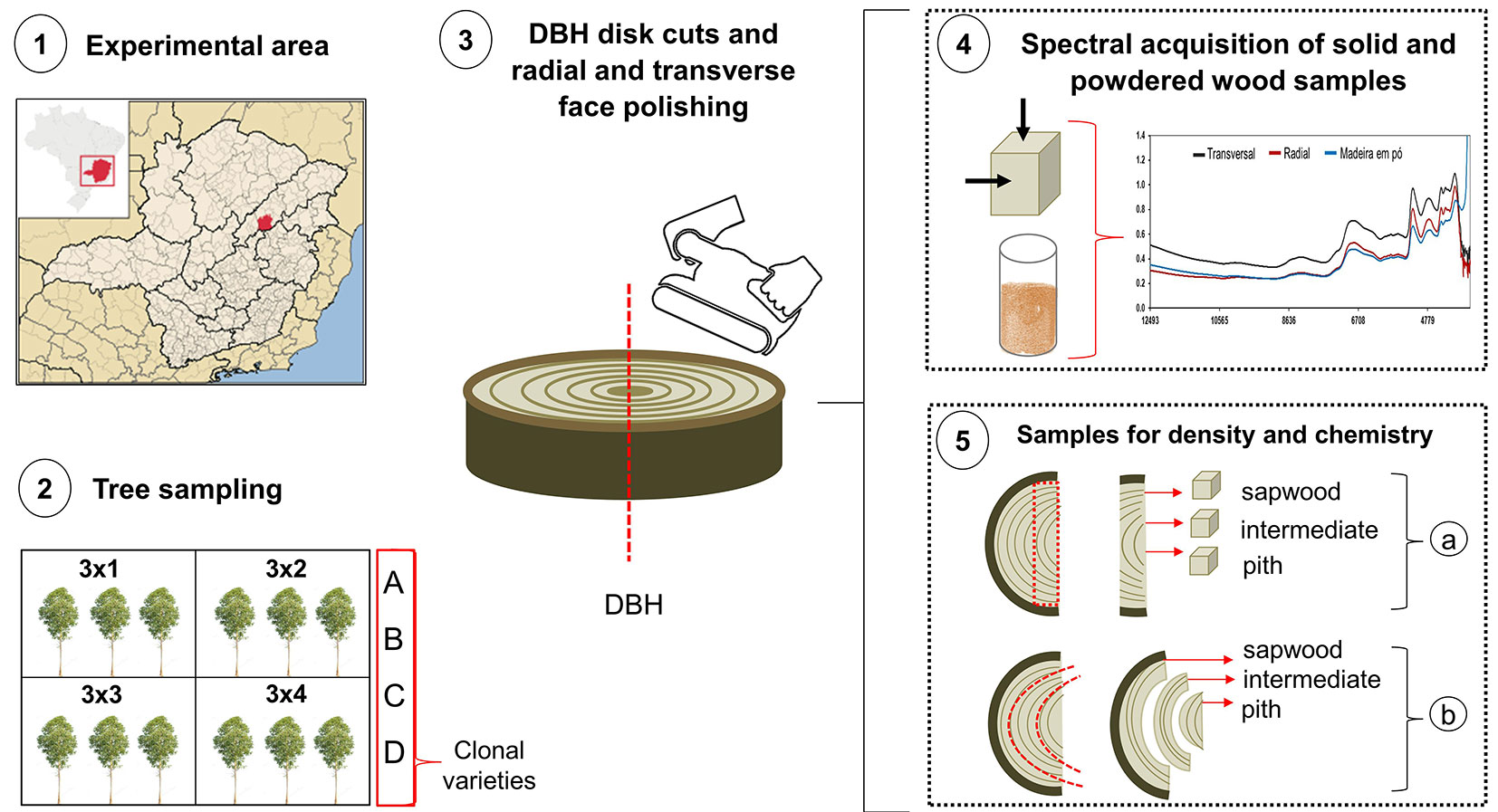
In the experimental area, four different clones (A, B, C, and D) were planted in four spacing arrangements (3 × 1 m, 3 × 2 m, 3 × 3 m, and 3 × 4 m). The mean diameter of the trees within the experimental plots was determined based on forest inventory data, and this mean value was used in selecting the collected trees. The sampling consisted of cutting three trees in each planting spacing arrangement for each clone at the age of 5 years, totaling 48 trees. Transverse discs approximately 3 cm thick were collected at the diameter at breast height (DBH) of each tree, totaling 48 discs, which were used for the chemical characterization and density analyses. The sampling scheme adopted is shown in Fig. 1. The wood of these trees was previously studied by Pimenta et al. ([26]), who investigated how planting spacing and the genetic material (clone) affect the radial variation of basic density and chemical composition of wood.
Fig. 1 - Sampling scheme of Eucalyptus urophylla × Eucalyptus grandis trees. (a) Location of the experimental area; (b) sampling of three trees at each planting spacing for each clone; (c) disc cutting of each tree; (d) dividing the disks into two opposite wedges, polishing the radial and transverse surfaces, and acquiring the spectra; and (e) preparation of the specimens for (1) density determination and (2) chemical characterization.
Sample preparation
To determine the basic density, 180 specimens with dimensions of 2 × 2 × 2 cm were taken from the DBH discs of the 48 selected trees; those with the presence of defects, such as cracks and knots or any other type of defect that compromised the use of material for the study were discarded. The transverse and radial faces of specimens were sanded before spectral acquisition. Specimens were selected from the pith, sapwood, and intermediate regions. To determine the chemical composition (lignin and extractives), the other half of the same DBH discs of the 48 trees sampled were also divided into pith, sapwood, and intermediate regions, totaling 143 samples. These samples were ground and the produced powder was used for spectral acquisition and chemical analysis (Fig. 1, Fig. 2).
Fig. 2 - Sample preparation for the physical and chemical analyses of the reference: (a) cut the discs into two opposite wedges; (b) prepare the prismatic specimens to determine the basic density of the wood; (c) divide the radial regions for chemical characterization; (d) manual coking of the samples; (e) chips separated by the radial position along the disc; and (f) powdered samples obtained by grinding.
After cutting, the samples were kept in a climate-controlled room (temperature at approximately 20 ± 1 °C and a relative humidity of approximately 60 ± 2%). Under these conditions, the moisture content of the wood samples stabilized at approximately 12%.
Determination of wood properties
The basic density was determined using the immersion method according to NBR 11941 ([1]). The samples taken from the wedges of each tree were reduced to chips and subsequently transformed into sawdust in a Wiley mill, and the sawdust that passed through the 40 mesh sieve was retained in the 60 mesh sieve and selected for analysis. From the sawdust, extractives were determined in ethanol-toluene according to the ASTM D1107-96 standard ([3]). The determination of insoluble lignin was performed according to the Klason method, modified as proposed by Gomide & Demuner ([15]), which was derived from the TAPPI T 224 om-88 standard and soluble lignin, and determined by spectrometry, according to Goldschimid ([14]). The total lignin (TL) content consisted of the sum of the two values.
Acquisition of spectra in the NIR
The acquisition of the spectra from the 180 solid specimens and 143 powdered samples was performed in diffuse reflection mode in a Bruker spectrometer Model Vector 22/N (Bruker Optik GmbH, Ettlingen, Germany) together with OPUS software ver. 7.0. The equipment consisted of acquisition pathways: integration sphere and optical fiber. Both were used to perform the spectral analysis of the wood samples.
The acquisition of the spectra occurred in the NIR between 12.500 and 3.600 cm-1 (800 to 2.780 nm), with a spectral resolution of 8 cm-1 (a spectrum is composed of 1.125 absorbance values) and 32 specimen readings. As a reference, a base with a gold-plated surface was used to calibrate the absorption of NIR light. Before obtaining the spectra, the room where the spectrometer was located was fully acclimatized to stabilize the humidity, with a temperature of approximately 20 °C and a relative humidity of approximately 60%.
The spectra were obtained for the 180 specimens made to predict the density in the radial and transverse faces via optical fiber (Fig. 3a) and in the transverse face via the integration sphere (Fig. 3b). The 143 powdered samples were analyzed using the integration sphere (Fig. 3c).
Fig. 3 - Measurement of wood samples on Fourier transform NIR spectrophotometer. (a) Solid wood specimens via optical fiber and (b) via integration sphere, and (c) powdered wood samples via integration sphere.
Multivariate analysis of the data
The Unscrambler® software (ver. 9.7) was used for multivariate analysis of the data. Principal component analysis (PCAs) were performed to explore the data and evaluate their dependence through the clusters. The models were fitted by the partial least squares regression (PLS-R) method, which related the dataset obtained from the NIR spectra and the analyzed properties. The number of principal components and the number of latent variables (LVs) were chosen by the software based on both the minimization of the standard error and the maximization of the coefficient of determination (R2) of the validation.
The calibrations were performed from the original spectra and the spectra were treated mathematically by the first derivatives (13-point filter and a second-order polynomial) using the Savitzky & Golay ([29]) algorithm and Standard Normal Variate (SNV) transformations. These treatments were performed to exclude noise and improve the quality of the calibration signal. For the PLS-R, 180 samples were used to obtain the basic density models, and 143 samples were used for the extractive and lignin content models. Model calibrations were validated by the method of complete cross-validation (leave-one-out) and external validation (test set). The cross-validation was performed by the random method from ten segments. In this type of validation, each calibration sample is taken individually; then, the model is constructed, the retained sample is estimated, and it is repeated for all samples. The external validation was based on two datasets, using 70% of the samples for the calibration set and 30% of the samples for the validation set (randomly selected).
The outliers were identified and excluded during the adjustment of the models to improve the quality of the calibration; no more than 5% of all the data were excluded. The criteria adopted to choose the best prediction models were the R2 of the cross-validation model (R2cv), the number of LVs used in the calibration, and the root-mean-square error (RMSE) of the cross-validation (RMSECV).
According to Costa et al. ([7]), the RMSE measures the efficiency of the calibration model to predict the variable of interest in many unknown samples, while the ratio of performance to deviation (RPD), i.e., the ratio between the standard deviation of the reference values and RMSE, was calculated to assess the accuracy of the calibration. Calibrations with RPD values between 2 and 3 indicate that the predictions are approximate, and values between 3 and 5 indicate that the calibration is satisfactory for the predictions ([36]).
Results and discussion
Physical and chemical analyses of the wood from the calibration set
The Eucalyptus samples had an average basic density of 462 kg m-3, ranging from 365 to 578 kg m-3. The coefficient of variation was 8.34%. The basic density values shown in Tab. 1 are compatible with those obtained in several studies on Eucalyptus wood ([33], [13], [10], [32]). Tab. 1 also shows the mean, minimum, and maximum values obtained from the physical and chemical analyses of wood in the calibration set, in addition to the coefficients of variation (CVs).
Tab. 1 - Summary of the physical and chemical analyses of the wood from the calibration lot. (CV): coefficient of variation; (n): number of samples.
| Stats | Basic density (kg m-3) |
Klason lignin (%) |
Acid soluble lignin (%) |
Total lignin (%) |
Extractives (%) |
|---|---|---|---|---|---|
| Average | 462 | 22.38 | 4.91 | 27.27 | 6.34 |
| Minimum | 364 | 20.28 | 3.85 | 24.92 | 0.75 |
| Maximum | 577 | 24.58 | 6.75 | 29.22 | 18.58 |
| CV (%) | 8.34 | 4.09 | 11.84 | 3.40 | 60.57 |
| n | 144 | 144 | 144 | 144 | 144 |
The Klason lignin (KL) content varied significantly, ranging from 20.28% to 24.58%. The TL content also varied, with an average value of 27.27%. The acid-soluble lignin (ASL) showed the largest variation, with an average value of 4.91% and a CV of 11.84%. The average extractive content was 6.34%, ranging from 0.75% to 18.58%, with a CV of 60.57%. This range of variation may be due to differences in the extractive content along the radial position in the pith-bark direction, as the samples were taken from these regions separately and not in composite samples. In addition, extractives comprise a wide class of chemical compounds, and their composition can vary significantly between different wood species and within different parts of the tree ([5], [28], [2]). It is important to note the amplitude of variation in the property values; thus, the calibrations were adjusted. As NIRS calibrations performed using PLS-R do not allow extrapolations, it was important that the samples from the calibration lot represented all the samples to be analyzed.
NIR spectra of wood
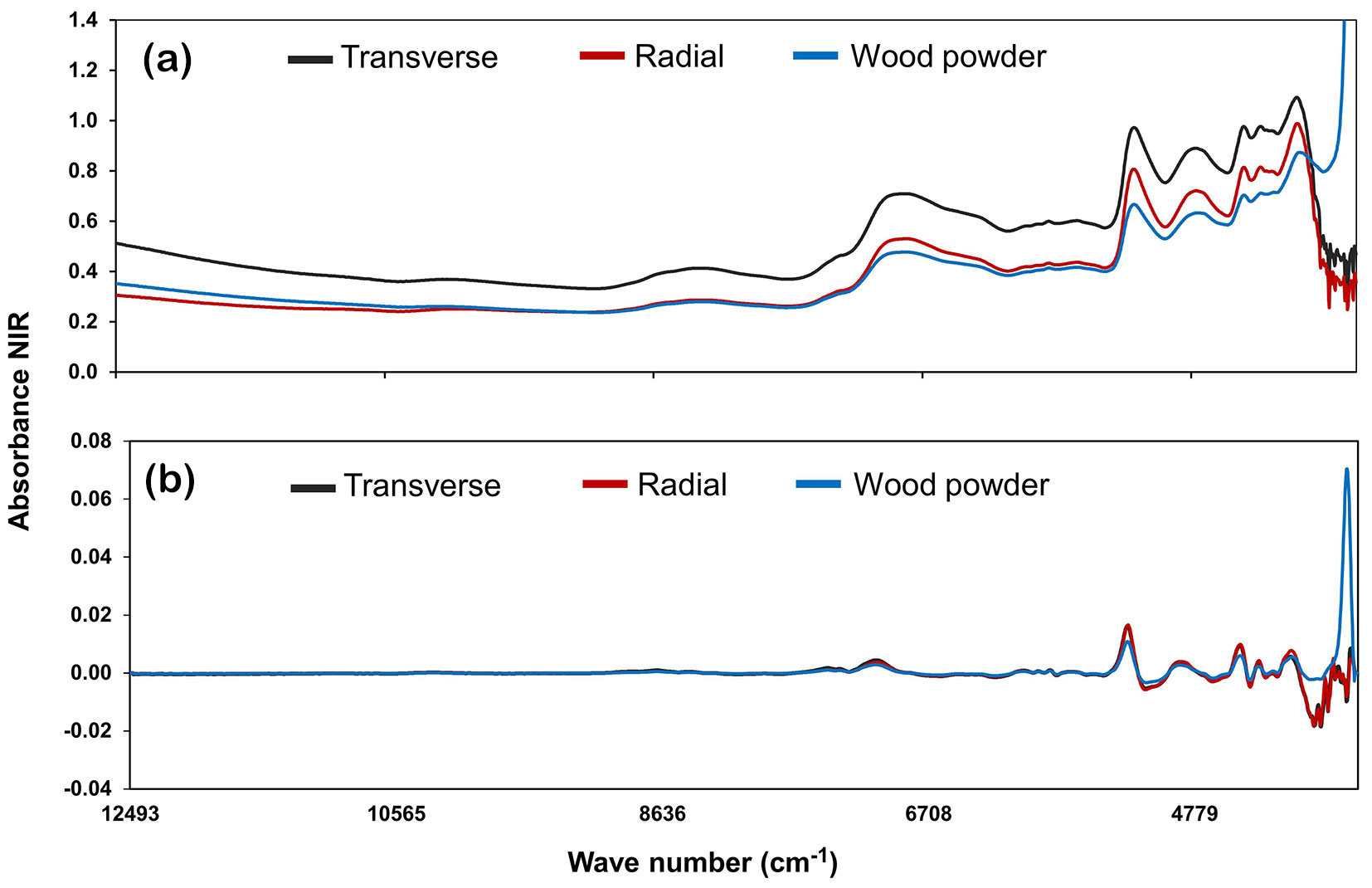
The spectral signatures of the Eucalyptus wood are shown in Fig. 4. The spectral information is presented in the range of 12.500 to 3.500 cm-1, with a resolution of 8 cm-1. It was observed that the first half of the spectral region (from 9.500 cm-1 to 12.000 cm-1) was noisy, making it difficult to obtain useful information. The absorbance peaks were observed from the second half of the spectrum (from 9.500 cm-1 to 3.500 cm-1), where the information of interest for the calibration of the models was included.
Fig. 4 - Mean diffuse reflection spectra obtained from the samples of solid wood and wood powder; (a) original data and (b) data treated by the first derivative for basic wood density, lignin content, and extractive content.
Spectra can usually present noise and imperfections, which can be addressed through mathematical approaches ([12], [7]). Fig. 4a shows the spectra obtained from the samples of solid wood (radial and transverse faces) and powdered wood from the original data, and Fig. 4b shows the spectra of these same data treated by the first derivative. The treatment of the data reduced the noise in the spectra and indicated the most informative regions for calibrating the predictive models.
Calibration and cross-validation models for basic wood density
The calibration results to predict the basic density of the wood are shown in Tab. 2. Both the radial and transverse surfaces provided accurate calibrations; however, the transverse surface resulted in the best model performance through the integration path. In addition, compared to the radial surface, the transverse surface also provided better calibration for basic density models in other studies ([21], [7], [9]).
Tab. 2 - Calibrations and cross-validations to estimate the basic wood density from NIR spectra obtained through the integration sphere and optical fiber. (Treat): treatment; (RadF): radial surface through the optical fiber; (TransF): transverse surface through optical fiber; (TransIS): transverse surface through the integration sphere; (1dv): first derivative; (SNV): normal standard deviation correction; (R2c): coefficient of determination of the calibration; (R2cv): coefficient of determination of the cross-validation; (RMSEC): root-mean-square-error for the calibration; (RMSECV): root-mean-square error for the cross-validation; (Out): number of samples eliminated; (%): percentage of eliminated data; (LV): latent variables; (RPD): ratio of performance to deviation of the cross-validation.
| Model | Acquisition route/face |
Treat | R2c | R2cv | RMSEC | RMSECV | LV | Out | % | RPDCV |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | - | 0.71 | 0.60 | 24.52 | 28.84 | 9 | 9 | 5.0 | 1.84 |
| 2 | RadF | 1dv | 0.82 | 0.70 | 19.47 | 25.27 | 10 | 9 | 5.0 | 2.10 |
| 3 | - | 1dv+SNV | 0.82 | 0.70 | 19.01 | 25.09 | 10 | 12 | 6.6 | 2.12 |
| 4 | - | - | 0.67 | 0.54 | 26.73 | 31.71 | 10 | 9 | 5.0 | 1.67 |
| 5 | TransF | 1dv | 0.82 | 0.69 | 18.91 | 25.15 | 10 | 9 | 5.0 | 2.11 |
| 6 | - | 1dv+SNV | 0.85 | 0.71 | 17.29 | 24.46 | 10 | 9 | 5.0 | 2.17 |
| 7 | - | - | 0.75 | 0.60 | 24.08 | 30.97 | 10 | 9 | 5.0 | 1.97 |
| 8 | TransIS | 1dv | 0.94 | 0.81 | 12.22 | 22.04 | 10 | 9 | 5.0 | 2.54 |
| 9 | - | 1dv+SNV | 0.93 | 0.81 | 13.74 | 22.27 | 9 | 9 | 5.0 | 2.74 |
The calibrations obtained with the radial and transverse faces through the fiber optic acquisition path showed similar performances, and among them, the calibration for the transverse face with data treated by the first derivative and the normal standard deviation correction (SNV) performed better, with an R2 of 0.71 and an error performance ratio of 2.17. Calibrations obtained with the transverse face through the integration sphere acquisition path, with data treated by the first derivative, showed the best performance. With an R2 of 0.81 and a RPD of 2.54, this face provided satisfactory calibrations for predicting the basic wood density. This mathematical treatment was essential to optimize the calibration models’ fitting. Models treated by the first derivative and the first derivative followed by the Standard Normal Variate (SNV) transformations showed close and satisfactory performances. For forest science applications, an RPD value greater than 1.5 is considered acceptable for preliminary readings and predictions ([30]).
Fig. 5 shows the relationship between the basic density determined in the laboratory and the basic density estimated by the models using NIRS. In general, the calibration values were very close to the basic density values measured in the laboratory. It was observed that the transverse face had less data dispersion through the integration sphere acquisition pathway, in addition to the highest R2cv.
Fig. 5 - Basic wood density values determined in the laboratory and estimated by models. Models 2 and 6 (optical fiber) and Model 8 (integration sphere) in Tab. 2.
Jiang et al. ([21]) investigated the precision of fir wood sample density predictions by comparing the tangential, radial, and transverse surfaces. The results showed that the best predictive model was obtained with the transverse surface. Costa et al. ([7]) reported the calibrations to predict the basic density of eucalyptus wood, achieving a better performance using the wood cross-section obtained through the integration sphere.
Calibration and cross-validation models for lignin and extractive contents
The calibration with the best performance to predict the KL content had an R2 of 0.98 for the calibration set, 0.81 for the cross-validation set, and an RPD of 2.31. Moreover, the treatment of the data with the first derivative was essential to achieve a better fit of the model. The statistics associated with the calibrations to predict the levels of KL are shown in Tab. 3.
Tab. 3 - Calibrations and cross-validations for estimating lignin content and wood extractives from NIR spectra obtained through the integration sphere. (Treat): treatment; (KL): Klason lignin; (ASL): Acid soluble lignin; (TL): Total lignin; (EXT): Extractives; (1 dv): first derivative; (SNV): normal standard deviation correction; (R2c): coefficient of determination of the calibration; (R2cv): coefficient of determination of the cross-validation; (RMSEC): root-mean-square-error for the calibration; (RMSECV): root-mean-square error for the cross-validation; (Out): number of samples eliminated; (%): percentage of eliminated data; (LV): latent variables; (RPD): ratio of performance to deviation of the cross-validation.
| Model | Property | Treat | R2c | R2cv | RMSEC | RMSECV | LV | Out | % | RPDCV |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | - | - | 0.76 | 0.63 | 0.44 | 0.55 | 10 | 7 | 5.0 | 1.77 |
| 11 | KL | 1 dv | 0.98 | 0.81 | 0.13 | 0.42 | 7 | 4 | 2.8 | 2.31 |
| 12 | - | 1 dv+SNV | 0.97 | 0.81 | 0.16 | 0.43 | 6 | 5 | 3.5 | 2.26 |
| 13 | - | - | 0.74 | 0.61 | 0.24 | 0.29 | 10 | 7 | 5.0 | 1.80 |
| 14 | ASL | 1 dv | 0.98 | 0.80 | 0.07 | 0.22 | 7 | 4 | 2.8 | 2.37 |
| 15 | - | 1 dv+SNV | 0.98 | 0.81 | 0.06 | 0.22 | 8 | 7 | 5.0 | 2.37 |
| 16 | - | - | 0.76 | 0.65 | 0.42 | 0.51 | 10 | 7 | 5.0 | 1.79 |
| 17 | TL | 1 dv | 0.98 | 0.84 | 0.10 | 0.35 | 7 | 7 | 5.0 | 2.61 |
| 18 | - | 1 dv+SNV | 0.98 | 0.83 | 0.13 | 0.36 | 6 | 7 | 5.0 | 2.54 |
| 19 | - | - | 0.70 | 0.53 | 1.74 | 2.21 | 10 | 7 | 5.0 | 1.89 |
| 20 | EXT | 1 dv | 0.97 | 0.75 | 0.52 | 1.59 | 7 | 4 | 2.8 | 2.63 |
| 21 | - | 1 dv+SNV | 0.97 | 0.75 | 0.51 | 1.51 | 6 | 7 | 5.0 | 2.77 |
For the prediction of the acid-soluble lignin (ASL) content, the calibration with the best performance from the powder showed an R2 of 0.80 for the cross-validation set and a RPD of 2.37. In addition, the treatment of the data with the first derivative also provided a better fit of the model, requiring to discard only four samples which were considered outliers.
The performance of the calibrations to predict the TL content was also very similar to that of prediction models for acid-soluble KL (Tab. 3). Once again, the treatment of the data with the first derivative was essential to better fit the model; the calibration with the best performance had a R2 of 0.84% and a RPD of 2.61.
The models for estimating the extractive content were also satisfactory and had an RPD greater than 1.5. The model showing the best performance had an R2 of 0.75%, and its RPD of 2.63 was considered satisfying. The calibrations for the EXT are shown in Tab. 3. In general, the analysis in Tab. 3 showed that predicting the chemical properties of wood (lignin and extractive contents) requires a high number of principal components for their calibration. In addition, it was observed that when the data were mathematically treated, the number of principal components decreased (10, 8, 7, and 6), and the RPD increased (1.77 to 2.77).
If the RPD value suggested by Schimleck et al. ([30]), in which an RPD greater than 1.5 is considered satisfactory for preliminary readings and predictions, then all fitted models were considered satisfactory for predicting the content of the KL, ASL, TL, and extractives. These calibrations had statistical results similar to those for calibrations developed in other studies (Tab. 4).
Tab. 4 - Predictive models from the literature for the estimation of extractive content (EXT), Klason lignin (KL), acid-soluble lignin (ASL), and total lignin (TL) in Eucalyptus wood. (Rcv2): coefficient of determination of the cross-validation; (RPD): ratio of performance to deviation.
| Reference | Species | Property | Rcv2 | RPD |
|---|---|---|---|---|
| Hein et al. ([16]) | Eucalyptus urophylla | KL | 0.86 | 2.85 |
| ASL | 0.72 | 1.99 | ||
| KL | 0.93 | 2.83 | ||
| Hodge et al. ([19]) | Eucalyptus spp. | ASL | 0.66 | 1.11 |
| TL | 0.98 | 3.20 | ||
| [23] | Eucalyptus and Acacia | TL | 0.74 | 2.47 |
| Zhou et al. ([38]) | Eucalyptus dunnii | EXT | 0.94 | 4.27 |
| TL | 0.87 | 2.47 | ||
| Baillères et al. ([4]) | E. urophylla × E. grandis | EXT | 0.87 | 2.20 |
| KL | 0.87 | 2.30 |
Fig. 6 shows the relationship between the wood chemical properties determined in the laboratory and those estimated by the models using the NIR technique. Overall, the calibration values were very close to the values measured in the laboratory.
Fig. 6 - Comparison of the wood chemical property values determined in the laboratory and estimated by models. Models 2, 5, 8, and 11 in Tab. 3 for the levels of Klason lignin (LK), acid-soluble lignin (ASL), total lignin (TL), and extractive content (EXT).
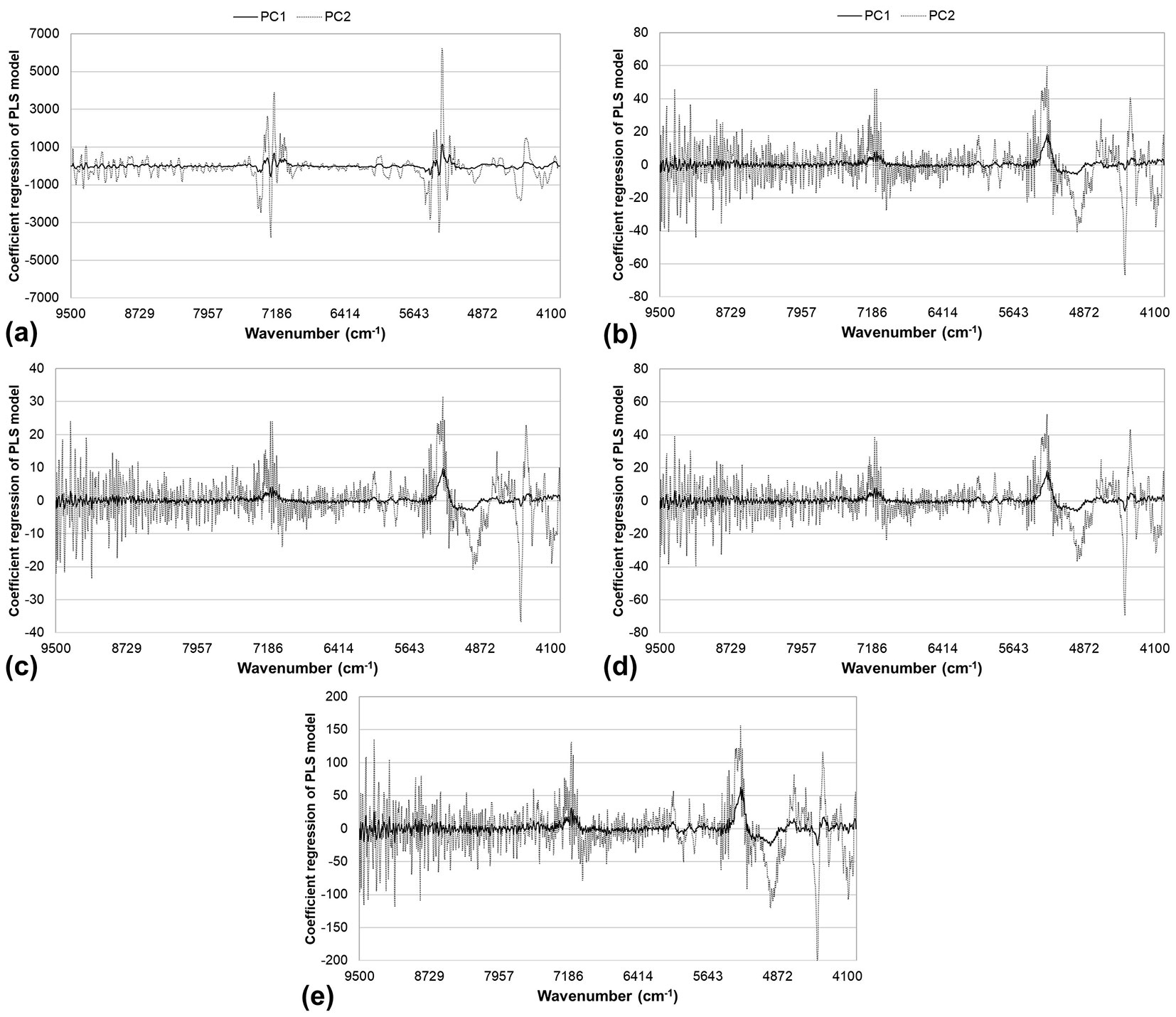
It is widely acknowledged that key wood components such as cellulose, hemicellulose, lignin, and extractives significantly influence calibrations ([34]). However, certain components might exert more influence on specific bonds than others. The regression coefficients derived from NIR-based models offer insights into the significance of particular wavenumbers (or wood components) in modeling wood density and chemical composition based on their NIR absorbance patterns.
Fig. 7 shows the plot of weighted regression coefficients for the model for estimating wood density (a, model 8), Klason lignin (b, model 11), acid-soluble lignin (c, model 14), total lignin (d, model 17) and extractive content (e, Model 20) contents.
Fig. 7 - Regression coefficients of PLS-R models that estimate wood basic density (a), Klason lignin content (b), acid-soluble lignin (c), total lignin (d), and extractives (e) from spectra first derivative NIR.
In the regression models for estimating Lignin (models 11, 14, and 17) and extractive contents (model 20), wavelengths around 4405, 4872, 5250, and 7186 cm-1 display significant regression coefficients. These crucial absorption bands correspond to O-H, C-O, C-H, and C-C stretching, commonly observed in the crystalline regions of cellulose, as well as C-O stretching and C=O combination observed in aromatic groups of lignin ([31]).
The spectral range spanning from 4000 to 5000 cm-1 comprises the combination band region ([37]). In this range, absorbance peaks exhibit considerable overlap due to interactions between various chemical bonds. The range from 5000 to 9000 cm-1 represents the first and second harmonic regions, offering valuable information with minimal noise ([31]). The presence of high regression coefficients at 7186 cm-1 and 5250 cm-1 suggests the importance of lignin molecules in the wood density model.
External validation
External validation is recommended by Pasquini ([24]). In this study, the best models according to the selection criteria were validated using this approach. Tab. 5 shows the results of the models for predicting the studied wood properties using the entire database.
Tab. 5 - Independent calibrations and validations to estimate the wood basic density, lignin content, and extracts from spectra in the NIR. (RF): radial surface through the optical fiber; (TF): transverse surface through optical fiber; (TE): transverse surface through the integration sphere; (KL): Klason lignin; (ASL): Acid soluble lignin; (TL): Total lignin; (EXT): Extractives; (od): original data; (1dv): first derivative; (SNV): normal standard deviation correction; (R2c): coefficient of determination of the calibration; (R2cv): coefficient of determination of the cross-validation; (RMSEC): root-mean-square-error for the calibration; (RMSECV): root-mean-square error for the cross-validation; (LV): latent variables; (RPDCV): ratio of performance to deviation of the cross-validation.
| Model | Type of model | R2c | R2p | RMSEC | RMSEP | LV | RPDCV |
|---|---|---|---|---|---|---|---|
| 22 | RF 1dv | 0.85 | 0.65 | 17.34 | 26.69 | 10 | 1.99 |
| 23 | TF 1dv + SNV | 0.87 | 0.66 | 16.28 | 25.94 | 10 | 2.05 |
| 24 | TE 1dv | 0.96 | 0.78 | 10.20 | 23.00 | 10 | 2.65 |
| 25 | KL 1dv | 0.95 | 0.71 | 0.22 | 0.50 | 10 | 1.94 |
| 26 | ASL 1dv | 0.81 | 0.77 | 0.23 | 0.23 | 7 | 2.27 |
| 27 | TL 1dv | 0.84 | 0.71 | 0.34 | 0.46 | 7 | 1.99 |
| 28 | EXT 1dv | 0.98 | 0.74 | 0.32 | 1.52 | 6 | 2.75 |
When comparing the cross-validation results (Tab. 2, Tab. 3) and the external validation results (Tab. 5), it was observed that the parameters of the cross-validation model were similar to those for the external validation for the evaluated properties. The performance of the models in both validation processes was similar and satisfactory, thus showing the efficiency of the calibrated models.
Concluding remarks
The calibrations obtained from spectra in the NIR allowed an accurate estimation of the wood basic density and the content of extractives and lignin through the integration sphere and optical fiber acquisition pathways. Moreover, the integration sphere pathway had better performances as showing better statistical parameters.
The cross-sectional surface was the most suitable for estimating the basic density and extractive and lignin contents. The spectra obtained from the radial surface provided lower but acceptable regression models, thus showing the potential to estimate the analyzed properties.
The application of mathematical treatments of the data, the detection and disposal of anomalous samples, and the selection of specific wavelengths reduced the standard error of the calibration and cross-validation (RMSEC and RMSECV, respectively) and increased the coefficient of determination (R²) and the ratio of the performance deviation (RPD).
Finally, this study showed that the NIRS technique was effective in predicting the basic density and extractive and lignin contents of eucalyptus wood, regardless of the genetic material and the planting spacing.
Acknowledgments
We thank the Wood Science and Technology Graduation Program (PPGCTM) of the Universidade Federal de Lavras (Brazil). Special thanks to Suzano SA Company for providing the wood samples. This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001, by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq - grants no. 406593/2021-3) and by the Fundação de Amparo aÌ€ Pesquisa do Estado de Minas Gerais (FAPEMIG. APQ-00742-23).
References
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Emilly Gracielly Dos Santos Brito 0000-0003-3854-2692
Paulo Ricardo Gherardi Hein 0000-0002-9152-6803
Federal University of Lavras, Forest Science Department, Trevo Rotatório Professor Edmir Sá Santos, 37203-202, Lavras, MG (Brazil)
LD Celulose S.A., Rodovia BR 365 km 574, S/N, 38490-000, Indianópolis, MG (Brazil)
Klabin SA Company, São Paulo, SP, Brazil (Brazil)
Corresponding author
Paper Info
Citation
Mesquita Pimenta E, Dos Santos Brito EG, Ramalho FMG, Hein PRG (2024). Validation of models using near-infrared spectroscopy to estimate basic density and chemical composition of Eucalyptus wood. iForest 17: 338-345. - doi: 10.3832/ifor4516-017
Academic Editor
Petar Antov
Paper history
Received: Nov 04, 2023
Accepted: Jun 27, 2024
First online: Nov 03, 2024
Publication Date: Dec 31, 2024
Publication Time: 4.30 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2024
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 6909
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 3839
Abstract Page Views: 1348
PDF Downloads: 1498
Citation/Reference Downloads: 1
XML Downloads: 223
Web Metrics
Days since publication: 406
Overall contacts: 6909
Avg. contacts per week: 119.12
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
(No citations were found up to date. Please come back later)
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
NIR-based models for estimating selected physical and chemical wood properties from fast-growing plantations
vol. 15, pp. 372-380 (online: 05 October 2022)
Research Articles
Estimation of total extractive content of wood from planted and native forests by near infrared spectroscopy
vol. 14, pp. 18-25 (online: 09 January 2021)
Research Articles
Improving sustainability in wood coating: testing lignin and cellulose nanocrystals as additives to commercial acrylic wood coatings for bio-building
vol. 14, pp. 499-507 (online: 11 November 2021)
Research Articles
Interaction between planting spacing and wood properties of Eucalyptus clones grown in short rotation
vol. 14, pp. 12-17 (online: 02 January 2021)
Research Articles
Physical, chemical and mechanical properties of Pinus sylvestris wood at five sites in Portugal
vol. 10, pp. 669-679 (online: 11 July 2017)
Research Articles
Characterization of technological properties of matá-matá wood (Eschweilera coriacea [DC.] S.A. Mori, E. odora Poepp. [Miers] and E. truncata A.C. Sm.) by Near Infrared Spectroscopy
vol. 14, pp. 400-407 (online: 01 September 2021)
Research Articles
Variation of wood and bark density and production in coppiced Eucalyptus globulus trees in a second rotation
vol. 9, pp. 270-275 (online: 08 September 2015)
Research Articles
Comparison of extractive chemical signatures among branch, knot and bark wood fractions from forestry and agroforestry walnut trees (Juglans regia × J. nigra) by NIR spectroscopy and LC-MS analyses
vol. 15, pp. 56-62 (online: 08 February 2022)
Research Articles
Density, extractives and decay resistance variabilities within branch wood from four agroforestry hardwood species
vol. 14, pp. 212-220 (online: 02 May 2021)
Short Communications
Effect of intensive planting density on tree growth, wood density and fiber properties of maple (Acer velutinum Boiss.)
vol. 9, pp. 325-329 (online: 22 October 2015)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword