When a definition makes the difference: operative issues about tree height measures from RPAS-derived CHMs
iForest - Biogeosciences and Forestry, Volume 13, Issue 5, Pages 404-408 (2020)
doi: https://doi.org/10.3832/ifor3411-013
Published: Sep 03, 2020 - Copyright © 2020 SISEF
Short Communications
Abstract
Tree height (H) survey is a fundamental step in forest mensuration. The error affecting tree height measure, necessarily influences the correspondent tree estimates. The remotely survey of vegetation using PHODAR (PHOtogrammetric Detection And Ranging) or LiDAR (Light Detection And Ranging) techniques generates very high-density point clouds, that result into Canopy Height Models (CHMs) having GSD (Ground Sampling Distance) of few centimetres. This GSD value potentially allows to survey single crown apexes, which, from a forestry point of view, do not represent the actual tree height. Apex height value, in fact, does not represent the prevailing dendrometric height (PDH) but the maximum tree value. In this study we propose a new approach aimed at measuring dendrometric height by PHODAR derived CHM, taking care about this issue. The proposed method defines a correcting factor (found equal to 95% percentile of CHM values distribution within a given crown) for the tree height extraction from CHM based on the PDH concept. The method could be implemented to single crown approach in forest parameters extraction algorithms permitting more reliable results, especially in terms of tree volume and related estimations (e.g., carbon stock quantification, allometric models).
Keywords
Tree Height, Prevailing Dendrometric Height, CHM, PHODAR, LiDAR
Introduction
Tree height (H) survey is a fundamental measure in forest characterization; H is required to define a stand site index measuring the local fertility and give an estimate of standing trees volume. Especially tree stem volume has a key role in forest estimates being related to the amount of wooden commodity. Stem volume is ordinary calculated as ([22] - eqn. 1):
where DBH is the tree diameter at the breast height; f is the tree shape factor, i.e., the ratio between the real tree volume and the theoretical volume of a cylinder having the same height. According to eqn. 1 the error affecting tree height measure necessarily impacts the accuracy of the correspondent tree volume computation. Standard approach to measures tree height operates by hypsometer ([22], [26]), where angle and distance measures are coupled within simple trigonometric formulas. H is obtained by collimating the top and the basis of trees determining the correspondent angle and the horizontal distance separating observer and tree. This method suffers from different errors mainly related to the collimation process. Bragg ([6]) found that errors mainly depend on the wrong detection of tree tops and stem inclination. Another error is related to the operator’s hand motion during the collimation step that, in the most of cases, is operated with no fixed support. The uncertainty that this operational conditions can determine in angular measures is estimated to range between ± 0.5° and ± 2°, determining H errors between 1% to 10% ([1]). The introduction of RPAS (Remotely Piloted Aircraft System) have enriched the survey of vegetated surfaces ([5]). RPAS-based acquisitions can provide information about surfaces with a very high geometric resolution ([19], [15]). Remote survey of vegetation can be operated by PHODAR (PHOtogrammetric Detection and Ranging) or LiDAR (Light Detection and Ranging) techniques. Both of them have largely improved the possibility of accurately measuring morphometric and structural parameters of forest stand or individual trees ([25], [9], [17]), thus supporting forest inventories. Many studies and practical experiences demonstrated that tree counting and tree height measure can be achieved with high accuracy ([23], [24], [20], [10], [8]). In this context, these parameters are derived by tree crown segmentation from Canopy Height Models (CHMs - [11], [13], [27]), i.e., raster maps obtained by grid differencing between a Digital Surface Model (DSM) and Digital Terrain Model (DTM), possibly derived from point clouds. When trying to obtain tree measures from CHM, the Local Maxima approach, applied within the same segment (representing the entire tree crown), is often used to locate the top of the tree ([1], [18], [21]). When working with high geometric resolution CHMs, possibly obtained by PHODAR/LiDAR point clouds, the reference Ground Sampling Distance (GSD) sizes few centimeters. Such a value potentially allows to survey points representing single crown apexes that, according to the Local Maxima approach, can be labelled as the top when measuring tree height. Unfortunately, from a forestry point of view, apexes are not representatives of the actual tree height, since they do not represent the prevailing dendrometric height (PDHCHM) but, conversely, the maximum height value (HCHMmax - Fig. 1). Consequently, HCHMmax could not be used to estimate tree volume or site indices, as a not negligible overestimation would occur. In this work, PDH is suggested to be newly defined as that height value corresponding to the most frequently one occurring within tree upper canopy.
Fig. 1 - A new definition of prevailing dendrometric height (PDH) is proposed, corresponding to the most frequent height value occurring within upper tree crown.
Materials and methods
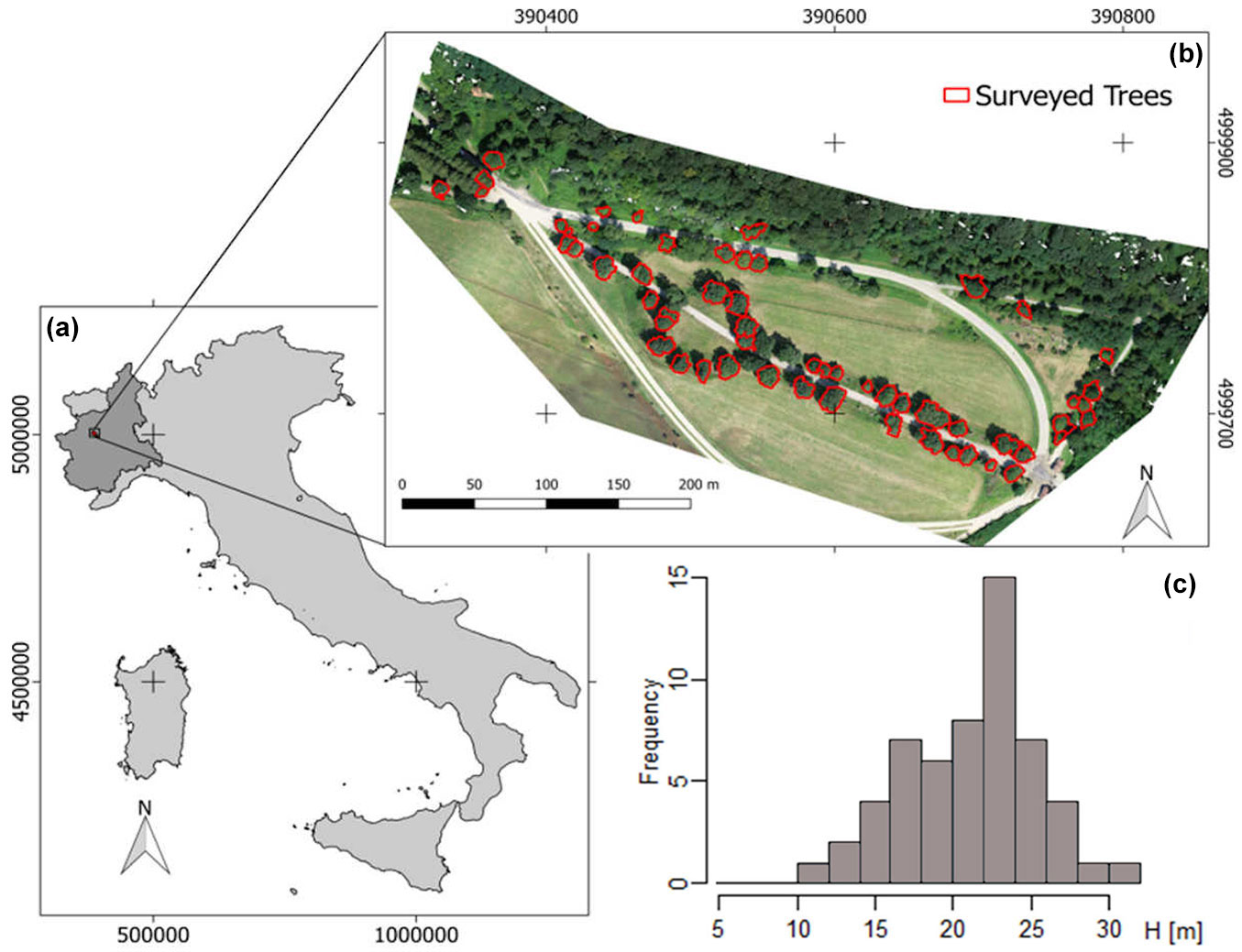
In this study, we propose a new definition of prevailing dendrometric height; consequently, a different approach, other than the Local Maxima one, has been considered to process CHM. A small and highly controllable CHM of 60 mixed broadleaf trees (Quercus robur L. 45%, Fraxinus excelsior L. 12%, Alnus glutinosa L. 7%, Ulmus campestris Mill. 8%, Robinia pseudoacacia L. 20%, Tilia spp. 8%) was processed. The study area is located in the “La Mandria” regional park (Piemonte, NW Italy). This study area was chosen for the presence of both ancient and young trees with different apexes length representing various ontological phases ([3]). A ground survey was conducted to obtain a reference dataset. For each of the 60 surveyed trees the correspondent crown ground projection was mapped by Field-map© tools ([28]) and recorded as georeferenced vector layer P (Fig. 2). Tree height was measured by Vertex IV-360® ultrasound hypsometer (Haglof, Sweden) at 40 m distance having a nominal accuracy of ± 0.25° for angles and ± 0.2 m for distances. HGmax was measured by collimating tree top (maximum visible height), while PDHG was estimated with reference to the main development of the crown (i.e., pointing to the basis of the highest apexes). HGmax and PDHG values were, finally, recorded into the attributes table of P. The test CHM was generated by grid differencing between a DSM generated by regularization of a PHODAR-derived point cloud surveyed by RPAS. A DJI Phantom4 RPAS equipped with a 12.4 Megapixel RGB camera was used for data acquisition. Flight and sensor’s technical features are reported in Tab. 1. Obtained images (about 700) had a GSD of about 5 cm. Photogrammetric block bundle adjustment and point cloud generation were achieved by the software Photoscan® v. 1.2.4 (Agisoft LLC, St. Petersburg, Russia). Image block bundle adjustment was achieved using 9 ground control points (GCPs) surveyed in correspondence of target panels (markers) distributed over the area before the flight. GCPs survey was achieved by VRS-NRTK (Virtual Reference Station - Network Real Time Kinematic) GNSS mode using a Leica 1200® receiver (3D positioning accuracy was ~ 3 cm). Leave-one-out procedure ([7]) was adopted to test bundle adjustment accuracy using the previous 9 GCPs without requiring additional survey and Mean Absolute Errors (MAE) were calculated. Point cloud was exported in .LAS format, filtered, classified as ground/not-ground, and regularized to generate the correspondent DSM (Digital Surface Model). Filtering, classifying and rasterizing processes were preformed using LAStools libraries ([12]). CHM was computed by grid differencing between the above-mentioned DSM and an available DTM (Digital Terrain Model) obtained from the Piemonte Region geoportal (ICE dataset - ⇒ http://www.geoportale.piemonte.it/geocatalogorp/). DTM had a GSD = 5 m and a precision σzDTM= 0.60 cm ([4]). DTM was oversampled by nearest neighbor method at 5 cm to make it consistent with the PHODAR derived DSM.
Fig. 2 - (a) Study area is located in “La Mandria” regional park (Piemonte - NW Italy); (b) RPAS-derived orthomosaic and surveyed tree crowns (reference frame is WGS84 UTM 32N); (c) Frequency distribution function of ground measured tree height (HGmax ).
Tab. 1 - Parameters of DJI Phantom4 RGB camera and flight parameters adopted for the photogrammetric survey.
| Flight/Sensors Parameters | Size | Units |
|---|---|---|
| Focal length | 8.6 | mm |
| CMOS sensor size | 13.2 × 8.8 | mm |
| Physical pixel | 2.2 | mm |
| Forward image overlap | 93 | % |
| Side image overlap | 83 | % |
| Flight relative altitude (above ground level) | 90 | m |
Results and discussions
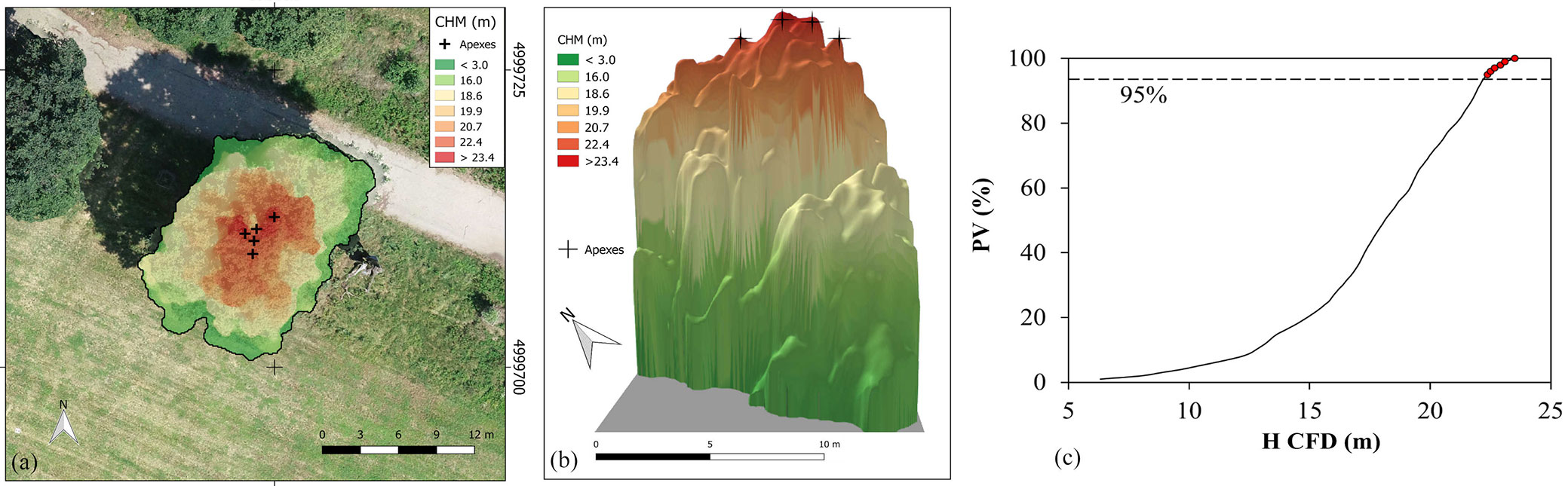
The following positioning errors (MAE) were obtained for GCPs after image block adjustment adopting leave-one-out procedure: 0.267 m (σx,y), 0.229 m (σz) and 0.352 m (σx,y,z). A high-density point cloud was generated (about 36 million points, 250 pts m-2), filtered, classified and regularized to generate the correspondent DSM with a cell size of 0.1 m. After regularization DSM height accuracy was tested with reference to the GCPs to exclude a degradation of the native accuracy. Results proved that height accuracy of DSM was the about same (σzDSM = 0.236 m) as the above mentioned one (σz = 0.229 m). CHM accuracy (σzCHM) was finally estimated by the Variance Propagation Law (VPL - [2]) involving σzDTM and σzDSM; σzCHM resulted to be equal to 0.64 m. Such accuracy is higher than that obtainable using hypsometer and adopted in ordinary forest inventory ([16]). An object-based approach aimed at mapping tree crowns from CHM was used, adopting the watershed segmentation algorithms (available in SAGA GIS v. 7.4 - ⇒ http://www.saga-gis.org/). The following parameters were used: segmentation criterion was the local minima one; joining segment threshold (minimum difference between neighbored segments) was set to 0.8. For each segment, assumed as tree crown perimeter (hereafter called Detected Crown - DC), the correspondent CHM zonal statistics (average, standard deviation, minimum and maximum) were computed and the cumulative frequency distribution of H (H CFD) generated. H CFD was used as descriptor of the inter-crown variability and comparing tree CHM-based height with ground-based one. With reference to the above-mentioned H CFD (one for each of the segmented crowns) the percentile value (PV) correspondent to the local PDHG was computed. Sixty different PVs were found depending on the assessed crown. PV mean value (μPV) was assumed as reference threshold, for broadleaves, to filter out apexes while measuring PDHCHM from CHMs. The computed μPV value was 95%; consequently, PDHCHM was found equal to the value within DC which corresponds to the 95 percentile of H CFD (Fig. 3). In Fig. 4the frequency distributions of HCHMmax and PDHCHM are compared, figuring out the effect on tree height measure given assuming PDHCHM in place of HCHMmax. The Kolmogorov-Smirnov test was run to test significance the similarity of the two distributions with a normal one. D-value was 0.075 (p = 0.871, Skewness: 0.046) and 0.069 (p = 0.957, Skewness: 0.020) for PDHCHM and HCHMmax, respectively, demonstrating that distributions did not significantly differ from a normal one. Since the two distributions were strictly correlated (r = 0.998, p < 0.001) a two-tailed paired t-test ([14]) was performed too, to determine if HCHMMax was significantly different from PDHCHM. A t = -17.58 (p < 0.001) was found indicating a significant difference between mean values of the two compared distributions, i.e., tree height values computed as PDHCHM are significantly different from those ordinarily computed in forestry (HCHMMax - [11], [1], [17]).
Fig. 3 - An example of oak crown in the study area. (a) CHM and apexes positions; (b) 3D view of CHM showing the role of outliers played by apexes within the crown; (c) H CFD of DC considered; dotted line represent the threshold value (95% PV) used to filter out apexes (red dots).
Fig. 4 - HCHM (left) and PDHCHM (right) frequency distributions computed considering all surveyed trees in study area.
Relative difference (ΔHs) between HCHMmax and PDHCHM was calculated for each tree and the correspondent cumulated frequency distribution generated. σzCHM value was used as threshold to test if differences were significant or not (Fig. 5). The 57% of ΔHs resulted to be greater than σzCHM further demonstrating that tree height computed according to PDHCHM is significantly different from that computed with reference to HCHMmax in more than a half of cases.
Fig. 5 - ΔHs cumulative distribution function and correspondent box-plot (min, Q1, median, Q3, max) computed with reference to all the trees in the study area. Red line shows CHM estimated accuracy (σzCHM).
Conclusions
PHODAR will represent a potential tool for more suitable and accurate forest inventories in the next future. Nevertheless, it introduces new ambiguities (i.e., potential errors) during forest parameters measurement (e.g., tree height, stem volume, etc.). With special concerns about tree height measures, we propose an approach based on the new concept of PDH. The value of tree height measure is an operative convention that, depending on the context, can be interpreted differently. In this study a new definition of tree height is proposed that is thought to be an alternative to the ordinary approach based of local maxima, with the aim of minimizing the effect of apexes within the crown, which can significantly affect the final accuracy of estimates. In particular, the prevailing dendrometric height within the crown (PDH) involves the use of a correcting factor based on the frequency distribution function of the CHM height values contained within the crown perimeter. We found that the 95th percentile of this distribution can be assumed as PDHCHM. Results showed that differences between PDHCHM and HCHMMax (i.e., ordinary approach) were significant. Future developments are expected to be addressed to quantify the absolute accuracy of this method and the eventual improvements it can determine while estimating wood volume in forest stands with reference to different species.
Acknowledgements
We thank Dr. Martina Zucaro for the help in ground surveys, Dr. Claudio Rizzo for the RPAS flight, and La Mandria natural park technicians for the project support.
References
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Online | Gscholar
CrossRef | Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Roberta Berretti 0000-0002-1944-8855
Filippo Sarvia 0000-0003-4556-446X
Enrico Borgogno Mondino 0000-0003-4570-8013
DISAFA - Department of agriculture, forest and food sciences, University of Torino, Largo P. Braccini 2, Grugliasco, TO (Italy)
Corresponding author
Paper Info
Citation
De Petris S, Berretti R, Sarvia F, Borgogno Mondino E (2020). When a definition makes the difference: operative issues about tree height measures from RPAS-derived CHMs. iForest 13: 404-408. - doi: 10.3832/ifor3411-013
Academic Editor
Carlotta Ferrara
Paper history
Received: Mar 23, 2020
Accepted: Jun 24, 2020
First online: Sep 03, 2020
Publication Date: Oct 31, 2020
Publication Time: 2.37 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2020
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 37139
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 31776
Abstract Page Views: 2155
PDF Downloads: 2489
Citation/Reference Downloads: 0
XML Downloads: 719
Web Metrics
Days since publication: 1929
Overall contacts: 37139
Avg. contacts per week: 134.77
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2020): 3
Average cites per year: 0.50
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Review Papers
Accuracy of determining specific parameters of the urban forest using remote sensing
vol. 12, pp. 498-510 (online: 02 December 2019)
Research Articles
Estimation of aboveground forest biomass in Galicia (NW Spain) by the combined use of LiDAR, LANDSAT ETM+ and National Forest Inventory data
vol. 10, pp. 590-596 (online: 15 May 2017)
Review Papers
Analysis of full-waveform LiDAR data for forestry applications: a review of investigations and methods
vol. 4, pp. 100-106 (online: 01 June 2011)
Review Papers
Remote sensing-supported vegetation parameters for regional climate models: a brief review
vol. 3, pp. 98-101 (online: 15 July 2010)
Research Articles
A LiDAR-based approach for a multi-purpose characterization of Alpine forests: an Italian case study
vol. 6, pp. 156-168 (online: 08 April 2013)
Research Articles
High resolution biomass mapping in tropical forests with LiDAR-derived Digital Models: Poás Volcano National Park (Costa Rica)
vol. 10, pp. 259-266 (online: 23 February 2017)
Research Articles
Identification and characterization of gaps and roads in the Amazon rainforest with LiDAR data
vol. 17, pp. 229-235 (online: 03 August 2024)
Technical Reports
Detecting tree water deficit by very low altitude remote sensing
vol. 10, pp. 215-219 (online: 11 February 2017)
Review Papers
Remote sensing of selective logging in tropical forests: current state and future directions
vol. 13, pp. 286-300 (online: 10 July 2020)
Research Articles
Classification of xeric scrub forest species using machine learning and optical and LiDAR drone data capture
vol. 18, pp. 357-365 (online: 07 December 2025)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword