Qualitative evaluation and optimization of forest road network to minimize total costs and environmental impacts
iForest - Biogeosciences and Forestry, Volume 5, Issue 3, Pages 121-125 (2012)
doi: https://doi.org/10.3832/ifor0610-009
Published: Jun 05, 2012 - Copyright © 2012 SISEF
Technical Reports
Abstract
An efficient and low-cost transportation network is necessary for sustainable management. Roading and log skidding are the most expensive and destructive operations in forest environment, unless carefully planned and evaluated. A transportation network has to be assessed and optimized to minimize the total cost of road construction and its environmental impact. The aim of this study was determining the optimum forest road network density, and evaluating the quantity and quality of the existing forest road network. In order to determine the optimum forest road network density, skidding cost, road construction and maintenance costs, and harvesting volume in each compartment were considered. Then optimum skidding distance was calculated with regard to optimum road density and total correction factors. The relative openness and efficiency coefficient of the existing forest road network were determined for the calculated optimum skidding distance, using ArcGIS. The results showed that the optimum road density, relative openness and road network efficiency coefficient were 21.5 m ha-1, 90% and 32%, respectively. As a result, when the quality of a forest road network has to be evaluated, road network efficiency coefficient is more efficient than relative openness, that per se cannot be considered as an appropriate indicator.
Keywords
Forest road network, Environmental impact, Qualitative evaluation, Optimum road density, Efficiency coefficient, GIS
Introduction
Forests support a lot of ecosystem services, including primary products, secondary products, water supply, hydrological regulation, environmental purification, soil formation, soil conservation, biodiversity conservation, recreation, etc. ([12], [10]). One of the main objectives of forest management is the sustainable utilization of natural resources ([25]). Forest road planning plays an important role in forest management and logging practices. Roads are essential structures to provide access to the forest for wood production and logging ([1]). On the other hand, road construction and log skidding are the most expensive and destructive operations in the forest environment, leading to soil compaction and increasing surface runoff and soil erosion along the skidding path. Therefore, the viability and profitability of operational forest management plans are deeply influenced by road construction and maintenance costs, as well as the road network structure ([20]). A large area of forest is destroyed during road construction, provoking not only economic losses, but also changes in the environmental conditions ([19]). Road construction in forest may also cause biodiversity loss as a result of habitat fragmentation ([17], [36], [7]), making forest communities more prone to impoverishment and depletion. As the high density of forest road network will lead to the excessive economical and environmental costs, forest road managers have to carefully evaluate and optimize the forest road network density for minimizing the total costs and environmental impacts of these infrastructures. Average log skidding distance is an important component to evaluate the quality of forest road network, and should be considered for computing the optimal forest road network density ([39]).
Matthews ([26]) was the first who developed a two dimensional model for skidding distance, with assumptions of flat terrain condition, regular road distribution, and provided that logs are carried out on the shortest path to the nearest road. Segebaden ([34]) improved the road spacing model by introducing network and transport correction factors. Heinimann ([14]) reported that the above mentioned assumptions do not apply in mountainous conditions with sloped terrain, and introduced a slope correction factor to compute the real skidding distance.
Road technical specifications and wood extraction methods are two main factors affecting optimum road spacing and density, aimed to minimize the total cost of roading and skidding ([32], [27]). Moreover, the timber volume to be harvested is an important factor affecting the quantity and quality of forest road network density. Sedlak ([33]) calculated road spacing with regard to volume of annual growth and reported lower average road spacing in parts of forest with higher annual growth and larger harvesting volume.
There are many researches aimed to determine road and skidding costs, road spacing and generally optimal road network under different logging practices ([21], [37], [38], [6], [15], [8], [3], [4], [29], [28]).
Chung & Sessions ([6]) introduced the Network 2001 program for the analysis and selection of optimum forest road network. Pentek et al. ([29]) used forest road relative openness and efficiency coefficient to analysis forest road network with determination of optimum road density and average skidding distance.
In the Caspian forests, most of harvested timbers are extracted by ground-based skidding system. In that context, optimal average skidding distance must be determined as first step in order to get the optimum forest road network density. However, Caspian forests are mainly located in mountainous area, where studies based on the theoretical skidding distance (namely, those based on Matthews’s model) do not apply.
The present study aimed to evaluate the quantity and quality of the existing forest road network, with estimation of optimum road density and road network efficiency coefficient in ArcGIS, with respect to road construction, maintenance and skidding cost, and harvest volume in Namkhaneh district, Kheyroud Educational and Research Forest, northern Iran.
Material and methods
Study site
The temperate deciduous forests of northern Iran, known as the Caspian forests, cover an area of around 2 million hectares, ranging from the level of the Caspian Sea up to 2200 m a.s.l. Oriental beech (Fagus orientalis Lipsky) is the most important broadleaved deciduous species in the Caspian region, forming natural pure and mixed forests ([2]). The study site is located in Nowshahr (latitude: 36°33’ N, longitude: 50°33’ E). The research was carried out on road network of Namkhaneh district, which covers 1083 ha, ranging from 350 to 1350 m a.s.l.; slope varies between 0 to 80%. Only 788 ha of the district area are considered as harvesting area, while the rest (295 ha) were excluded as protected area. The management in the district is mixed un-even aged high forest, with single and group selective cutting regime. Forest roads are categorized as permanently main forest roads used for trucking, with an average width 6.5 m and longitudinal slope 3 to 8% ([24]). Overall raod length is 15.8 km and current forest road density is 20 m ha-1. Ground skidding using wheeled cable skidders (Timber Jack 450C, 174 hp and 12 tn) is the most common method of wood extraction in this mountainous, uneven aged hardwood forest. Cable systems are not available and not used in the Caspian forest.
Determination of the average real means skidding distance
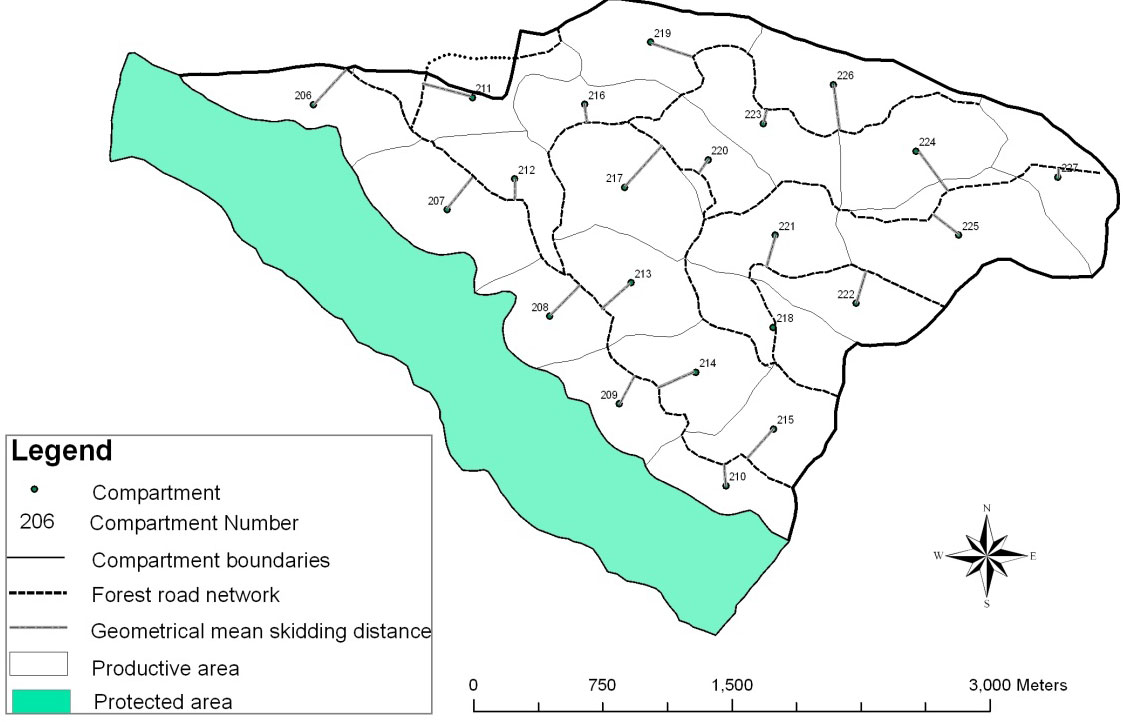
In order to determine average real means skidding distance, the center of gravity of each compartment was defined, and its distance to the nearest road was measured in an ArcGIS environment. Indeed, this distance is the geometrical mean skidding distance for each compartment (Fig. 1), which has to be multiplied by the network correction factor to obtain the real mean skidding distance (Tab. 1). To obtain the average real means skidding distance at the district level, averages were weighted on the log volume to be harvested in each compartment.
Tab. 1 - Harvesting volume, SDEG (existing geometrical mean skidding distance) and SDER (existing real mean skidding distance) of each compartment in the study area.
| Compartment | Area (ha) |
Harvesting volume (m3) |
SDEG (m) |
SDER (m) |
|---|---|---|---|---|
| 206 | 39.9 | 297.5 | 271.1 | 428.3 |
| 207 | 49.7 | 178.5 | 233.6 | 369.1 |
| 208 | 29.3 | 195.5 | 243.2 | 384.3 |
| 209 | 26.2 | 246.5 | 176.7 | 279.2 |
| 210 | 23.6 | 85 | 120.7 | 190.7 |
| 211 | 31.1 | 238 | 284.9 | 450.1 |
| 212 | 25.4 | 170 | 108.7 | 171.8 |
| 213 | 35.3 | 212.5 | 209.2 | 330.5 |
| 214 | 35.6 | 246.5 | 222.6 | 351.7 |
| 215 | 32.2 | 221 | 219 | 346 |
| 216 | 24 | 59.7 | 93 | 146.9 |
| 217 | 48.6 | 238 | 308.4 | 487.3 |
| 218 | 34.1 | 119.2 | 12.7 | 20.1 |
| 219 | 40 | 347.8 | 245 | 387.1 |
| 220 | 26.5 | 212.5 | 85 | 134.4 |
| 221 | 35.6 | 297.5 | 175.2 | 276.8 |
| 222 | 28.6 | 103 | 187.7 | 296.5 |
| 223 | 35.2 | 246.5 | 82.1 | 129.7 |
| 224 | 44 | 255 | 244.1 | 385.7 |
| 225 | 66.1 | 261 | 186.8 | 295.1 |
| 226 | 41.3 | 314.5 | 253 | 399.6 |
| 227 | 35.3 | 212.5 | 55 | 86.6 |
Optimum forest road network density estimation and comparison with the existing density
The optimum forest road network density was calculated using the following equation ([31]) that consider road construction, maintenance, skidding costs and harvesting volume (eqn. 1):
where DO is the optimum forest road network density (m ha-1), E is the average annual quantity of extracted log (m3 ha-1); TP is the cost of skidding 1 m3 of log at the distance of 1 m (US$ m-3 m-1); F is the walking cost factor, that Rebula ([31]) estimated as 51.7% of skidding cost per skidder (see below); KS is the overall correction factor of the theoretical mean skidding distance; TA is the average annual amortization of 1 m of forest road (US$ m-1); TO is the average annual maintenance cost of 1m of forest road (US$ m-1); dS is the secondary profit from the forest road network (US$ m-3). Depending on the region considered, this parameter may include profits from mushrooms, resins, ornamental seeds and pods, aromatic plants or plants for pharmaceutical products, and other non-wood forest products. As wood harvesting is the main and the only profit in the study area, this parameter was not taken into account in our estimation.
To obtain the value for the walking cost factor F in eqn. 1, several parameters need to be preliminarily defined, such as the number of workers, the average walking speed, the payment of workers per hour, the intensity of work. Considering the wheeled skidder used in the study area and the topographic conditions in this study, fairly similar to those previously reported in the literature ([31], [29]), the value of 51.7% was used.
Average optimum geometrical mean skidding distance
In order to calculate the average optimum geometrical mean skidding distance, the following equation was used (eqn. 2):
where SdOR is the average optimum real means skidding distance, DO and KS were already defined above.
Dividing th SdOR by network correction factor (KG), the average optimum geometrical mean skidding distance may be obtained (eqn. 3):
Determination of the forest road relative openness
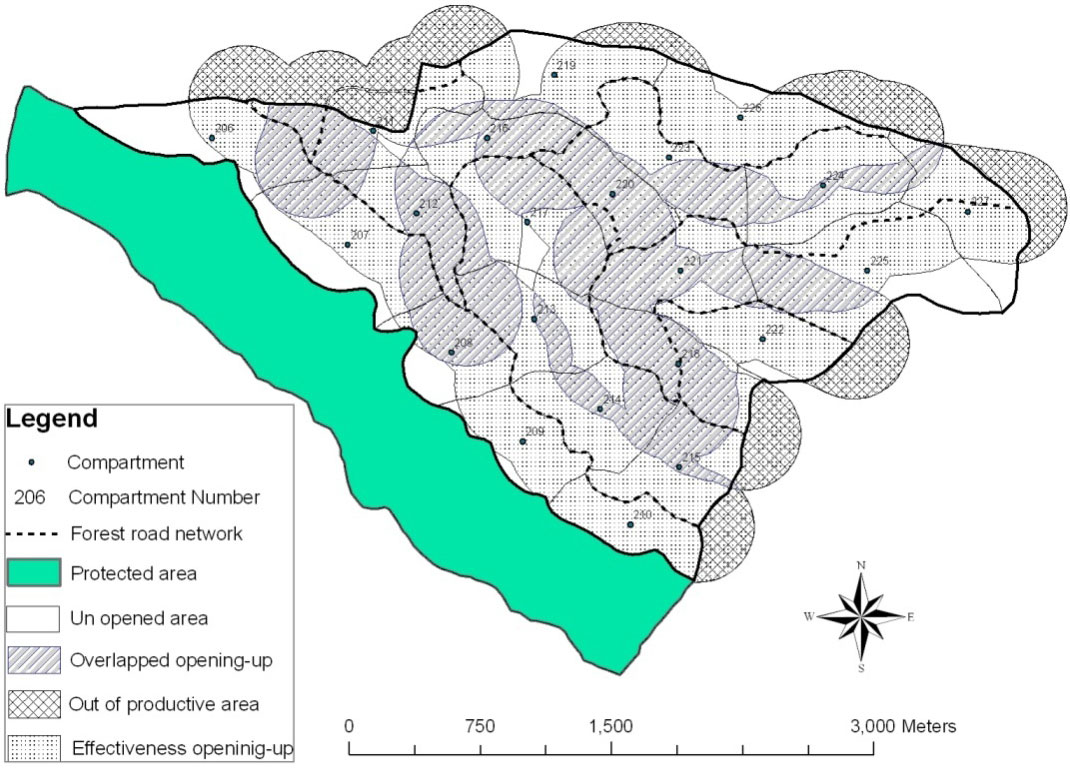
Buffer zones wrapping the existing roads on both sides and extending twice the optimum average geometrical mean skidding distance were created in the ArcGIS environment (Fig. 2). Indeed, the buffer zone represents the maximum skidding distance. Then, the relative openness was calculated using the following equation (eqn. 4):
where OR is the relative openness of forest road, AT is the total area of the district (ha) and OE is the effective opening-up area (ha). The buffer opening-up zone falling outside the district area and the overlapped buffer opening-up were excluded from this analysis.
Evaluation of the forest road network efficiency coefficient
Opening-up effectiveness indicates the effectiveness of the forest road location. In the presence of a regular road network, the effective opening-up would be at the maximum level with regard to road density. However, an ideally distributed road network does not occur in practice ([16]). In order to calculate the forest road network efficiency coefficient, the following equation was used (eqn. 5):
where KU is the efficiency coefficient of forest road network, OE is the effective opening-up area (ha), and OI is the ineffective opening-up area, i.e., the overlapped buffer opening-up and the part of buffers falling outside the district area (ha).
Results
Average existing real mean skidding distance
To calculate the existing real mean skidding distance, the existing geometrical mean skidding distance in each compartment was multiplied by the correction factor (KG) of 1.58, as reported by Pentek et al. ([29]). The average existing real mean skidding distance (SdER) at district level was estimated taking into account the harvesting volume (E) and existing real mean skidding distance (SdER) in each compartment (Tab. 1), obtaining a value of 310 m (eqn. 6):
Optimum road network density
The forestry center of the Kheyroud Educational and Research Forest has defined and reported the costs of road construction and maintenance. To have a set of comparable costs - as different road sections have been constructed in different times -, the cost of each section was actualized to a certain year, using the average interest rate of the Iran Central Bank. According to the above forestry center report, the annual road construction cost and road maintenance cost were estimated 52.5 US$ m-1 year-1 and 1.1 US$ m-1 year-1, respectively. Value of the annual road amortization cost over a period of 50 years was 2.2 US$ m-1 year-1. The average harvesting volume calculated using weighted averages was 6.2 m3 h-1. Skidding operations in the study area is carried out by a contractor company, whose costs are 25 US$ m-3, with no variable or fixed skidding cost. Considering the skidding cost (25 US$ m-3) and distance (310 m), the parameter F takes the value of 0.042 (eqn. 7):
Majnounian et al. ([23]) reports values for the total correction factor (KS) for Kheyroud Forest from 2 (gentle slope) to 2.63 (steep terrain). We used KS = 2.3, because Namkhaneh district area extends over low and steep terrain (mean slope angle 35%) and due to the both sides skidding, a value of 0.575 was used in the eqn. 1. Finally, the optimum road density value obtained (DO) was 21.5 m ha-1.
Average optimum geometrical mean skidding distance
Considering, DO = 21.5 m ha-1 and KS = 0.575, the average optimum real mean skidding distance was 267 m (eqn. 8):
As the buffers are formed on the road network layout using the geometrical skidding distance, the average optimum geometrical mean skidding distance (SdOG) was calculated using KG = 1.58 (eqn. 9):
Relative openness
Tab. 2 - OR and KU of existing forest road network. (OT): total opening-up area; (OD): double opening-up area; (OO): outer opening-up area; (OI): ineffective opening-up area; (OE): effective opening-up area; (OR): relative openness; (KU): efficiency coefficient.
| Harvesting area (ha) |
OT (ha) |
OD (ha) |
OO (ha) |
OI (ha) |
OE (ha) |
OR % |
KU % |
|---|---|---|---|---|---|---|---|
| 788 | 1192 | 328 | 154 | 482 | 710 | 90 | 32 |
The relative openness was calculated dividing effective opening-up by the total district area (Tab. 2 - eqn. 10):
Efficiency coefficient of the forest road network
Effective opening-up was 710 ha and ineffective opening-up (the area of buffers either overlapping or falling outside the district area) was 482 ha. Therefore, the forest road network efficiency coefficient obtained was 32% (Tab. 2 - eqn. 11):
Discussion
The popular method by Matthews ([26]), commonly used to assess a forest road network efficiency, is unsuitable for Caspian forests because its assumptions do not hold in the context analyzed. In this study, to calculate the real skidding distance and optimum road network density, two correction factors were considered. The current road density was 20 m ha-1 and the current average mean skidding distance using the center of gravity method was 310 m. The obtained value for optimal road density (21.5 m ha-1) considering road construction and maintenance costs, skidding cost and the harvesting volume, was a slightly higher than the actual road density. According to the Iranian Plan and Budget Organization (IPBO), a value of 20 m ha-1 is considered as the optimum road density for the current logging and transportation system in the Caspian forests ([18]). Moreover, Lotfalian ([22]), considering a ground skidding system (Timber Jack 450C) and different characters (i.e., slope, skidding cost, correction factors, soil type, etc.) in the Sangdeh forest (northern Iran), reported an optimum forest road density (21 m ha-1) comparable with the results of this study. Therefore, the value 21.5 m ha-1 can be suggested as an optimal and economical density for road network in the Caspian forests, as well as in regions with terrain conditions, logging and wood extracting methods similar to our study area.
Optimal average mean skidding distance, relative openness and efficiency coefficient of the studied forest road network were 267 m, 90% (excellent openness) and 32%, respectively. Based on the results obtained, the actual road density in the area (20 m ha-1) is roughly adequate. However, the low value of the efficiency coefficient (32%) suggests that the studied road network do not present a proper distribution. In other words, road networks with a low efficiency coefficient may lead to habitat and biodiversity losses in the future, due to forest fragmentation into smaller and more isolated patches as a consequence of sub-optimal harvesting practices ([5], [9], [11], [17]). Based on the relative openness only, the forest road network seems to show a well opening-up and function. On the other hand, the road network efficiency coefficient obtained indicates a fairly high level of ineffective opening-up. Therefore, it can be concluded that road network efficiency is lower than the value that of relative openness indicated. Analogously, Pentek et al. ([29]) reported the relative openness (81.4%) and the efficiency coefficient (42.37%) of a forest road network in Croatia.
In the Caspian forest, the relative openness is commonly used as a suitable indicator for the selection of the best road network variants (e.g., [13], [35], [30]). Nonetheless, in this investigation, despite a very good relative openness (90%), the efficiency coefficient of the studied road networks were not satisfactory (32% only). It may thus be suggested that the road network efficiency coefficient, that considered the ratio of ineffective to effective opening-up, is a more reliable indicator of the forest road network quality and efficiency.
Conclusion
Forest road network plays an important role in sustainable forest management, which has to be planned as much optimally as possible. To achieve an optimal road network with low-costs and high-quality, the following points are recommended:
- taking into account all the economical parameters such as the skidding costs, road construction and maintenance costs for the road network optimization;
- taking into account the harvesting volume and the possible secondary forest products, because they can also increase road network density;
- considering the efficiency coefficient to analyze the quality of the forest road network variants, as showed in this study, it is a more precise indicator for the qualitative evaluation and optimization of a forest road network;
- considering other functions of forest roads like ecotourism, forest fire extinction, etc, in forest road network assessment.
Acknowledgments
The authors wish to thank Eng. J. Fathi, manager of the Kheyroud Educational and Research Forest, University of Tehran, for his helpful assistance in data and maps supply. We also would like to express our thanks to Dr. I. Potočnik, University of Ljubljana, Biotechnical Faculty, for his kind collaboration. This work was financed by University of Tehran. The authors also express their appreciation to two anonymous reviewers for their helpful and valuable comments and suggestions.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
B Majnounian
E Abdi
Forestry and Forest Economics Department, Faculty of Natural Resources, University of Tehran, Karaj (Iran)
Corresponding author
Paper Info
Citation
Hayati E, Majnounian B, Abdi E (2012). Qualitative evaluation and optimization of forest road network to minimize total costs and environmental impacts. iForest 5: 121-125. - doi: 10.3832/ifor0610-009
Academic Editor
Agostino Ferrara
Paper history
Received: Sep 23, 2011
Accepted: Mar 19, 2012
First online: Jun 05, 2012
Publication Date: Jun 29, 2012
Publication Time: 2.60 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2012
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 60583
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 48489
Abstract Page Views: 4274
PDF Downloads: 6118
Citation/Reference Downloads: 33
XML Downloads: 1669
Web Metrics
Days since publication: 4933
Overall contacts: 60583
Avg. contacts per week: 85.97
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2012): 36
Average cites per year: 2.57
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Technical Reports
Decision making in forest road planning considering both skidding and road costs: a case study in the Hyrcanian Forest in Iran
vol. 6, pp. 59-64 (online: 21 January 2013)
Research Articles
Temporal analysis of the traffic loads on forest road networks
vol. 6, pp. 255-261 (online: 13 June 2013)
Research Articles
Assessment of timber extraction distance and skid road network in steep karst terrain
vol. 10, pp. 886-894 (online: 06 November 2017)
Research Articles
Impact of rainfall intensity and cutslope material on sediment concentration from forest roads in northern Iran
vol. 7, pp. 48-52 (online: 21 October 2013)
Research Articles
Large scale semi-automatic detection of forest roads from low density LiDAR data on steep terrain in Northern Spain
vol. 12, pp. 366-374 (online: 05 July 2019)
Research Articles
Exploring the reliability of CAN-bus data in assessing forwarder rolling resistance under real working conditions
vol. 17, pp. 360-369 (online: 13 November 2024)
Research Articles
Use of LIDAR-based digital terrain model and single tree segmentation data for optimal forest skid trail network
vol. 8, pp. 661-667 (online: 22 December 2014)
Research Articles
Examining the evolution and convergence of wood modification and environmental impact assessment in research
vol. 10, pp. 879-885 (online: 06 November 2017)
Research Articles
Evaluation of urban forest landscape health: a case study of the Nanguo Peach Garden, China
vol. 13, pp. 175-184 (online: 02 May 2020)
Research Articles
Roadside vegetation: estimation and potential for carbon sequestration
vol. 3, pp. 124-129 (online: 27 September 2010)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword