Temporal changes of forest species composition studied by compositional data approach
iForest - Biogeosciences and Forestry, Volume 10, Issue 4, Pages 729-738 (2017)
doi: https://doi.org/10.3832/ifor2187-010
Published: Aug 01, 2017 - Copyright © 2017 SISEF
Research Articles
Abstract
Many ecological data are compositional and different quantitative techniques have been used to analyze such data, albeit some of them being methodologically wrong. The aim of this contribution is to apply the compositional data approach to forestry data and demonstrate the strengths of this method for percentage or relative data with infrequent zero values. Basal areas of three dominant tree species (Abies alba, Picea abies, Fagus sylvatica) in 119 forest compartments in some of the Omphalodo-Fagetum forests in Slovenia in 1954 and 2004 were used to investigate the dynamics of forest species composition over a 50-year period. For the investigated period some additional data about geomorphology and harvesting rates within the compartments were used as explanatory variables of compositional change. The species composition of each forest compartment was subjected to several methods within a compositional analysis framework: descriptive, ternary diagram-based graphical presentations, significance of compositional differences between management classes, significance of perturbation differences (the indicator of forest compositional change) and relation of the compositional change with the explanatory variables by means of compositional linear model. Results indicated that the silver fir was the dominant species in both years, but a clear reduction in silver fir proportion was observed after 50 years. The perturbation differences indicated comparatively large relative increase in the proportion of Norway spruce between 1954 and 2004. Subsequently, the perturbation differences were subjected to isometric log-transformation (ilr) and two derived ilr coordinates were further used as dependent variables in the multivariate linear model. The initial stand structure correlated well with the perturbation differences. These were also significantly correlations with salvage cutting, a consequence of silver fir decline in the 1954-2004 period. This study demonstrated that the compositional data approach can be successfully used to study forest dynamics yielding some insights into data which are not possible or even not valid using some alternative methods.
Keywords
Percentage Data, Data Transformation, Compositional Change, Compositional Linear Model, Forest Dynamics, Vegetation Shift, Omphalodo-Fagetum
Introduction
Many ecological data are compositional (composed of only relative information) or may be regarded as compositional. The forest species composition is expressed as the number of trees, the basal area, or the biomass of each species in a given area. These data may be viewed as absolute values when studying biomass increment, tree density, or diameter structure ([8], [13], [29], [19]) and are related to environmental factors or management regime. Often, it is more reasonable to consider such data in a relative manner, i.e., as part of a whole. Vegetation data may be directly assessed or estimated with percentages or percentage classes, such as the Braun-Blanquet, Londo, and Domin cover scale ([11]). This approach is prevalent in community ecology where the structure of biological community is primarily characterized by the relative abundance of species ([51]).
Different quantitative techniques have been used to analyze patterns in community species composition and dynamics ([31], [40]). Different dimension reduction (ordination) techniques are commonly utilized to analyze multiple species in a community; these approaches include principal component analysis (PCA - [43], [28]), correspondence analysis (CA - [36], [12], [52], [53]), and non-metric multidimensional scaling (NMDS - [40], [9], [52], [44], [30], [17], [25]). These techniques have been widely applied in community ecology, for which data are often characterized by scarcity (many zero values - [31]). Other approaches reduce the community composition to certain values that can be analyzed by univariate statistics, such as various diversity indices ([43]) and importance values ([6], [28]). Both ordination and univariate indices are the methods of choice when a large number of species are studied and data on many infrequent species are scarce ([8]). The main disadvantage of these predominantly descriptive approaches is the large loss of information that occurs when the community composition is reduced to a few dimensions or one value ([3]).
However, zeros are very rare and do not occur in some instances, such as during the investigation of the occurrence of a small number of dominant tree species, plant functional groups, or diameter classes. In these cases, it is desirable to use all of the information available in the data, i.e., to use linear modeling, which can more powerfully explain community composition, dynamics, and species interactions ([3]). Past studies utilized linear models to study shifts in dominant species composition, and each species was separately analyzed with repeated ANOVA or paired t-tests preceded by an arcsin square root transform of percentage data ([36], [17], [41]). As will be discussed, the forest species composition is compositional by nature and demands an approach specific to these data. Compositional data are intrinsically multivariate. One or more other components inevitably exist when only one component is known, and thus special multivariate methods are needed ([1], [18]).
Compositional data contain only relative information and present certain peculiarities that preclude traditional statistical methods. The mathematical foundations of compositional data analysis and terminology are explained in Aitchinson ([1]), and Egozcue & Pawlowsky-Glahn ([15]). These peculiarities arise from use of the closed data, i.e., data summing to a constant, mainly 1 or 100%. Compositional data are always positive and constrained to a constant sum. The parts do not vary between -∞ and +∞ which is generally the assumption when using ordinary statistical methods. Any increase of one component inevitably leads to the decrease in one or more other components. This bias toward negative correlations leads to unusual properties of the variance-covariance matrix ([39], [7]). The distribution of compositional data are often rightly skewed ([18]) and differs considerably from the normal distribution central to classical statistical estimation. Calculation of the arithmetic mean for right-skewed data will result in a biased and excessively high estimate of the central value. Another issue is the subcompositional incoherence that results from the changed correlations between the raw values of components following the analysis of some parts of a composition (i.e., subcomposition - [1], [27]). The approach presented in this paper successfully addresses all of these issues.
The purpose of this contribution is to introduce the compositional data approach to forest science and demonstrate its applicability in forest dynamics research. The forest species composition of uneven-aged forests in the Snežnik area in southwest Slovenia was analyzed using different methods within compositional data framework. A brief theory of compositional data analysis is first presented, followed by an example of its application to 3-component tree species forest compositions. The graphical representations of the compositional data and descriptive statistics are presented and interpreted. Statistical analyses were applied in a compositional context, including MANOVA and compositional linear modeling.
Material and methods
Brief theory of compositional data analysis
Basic concepts
Based on the nature of compositional data, which seeks to describe the parts of some whole and provide only relative information between components, three principles can be derived ([1], [16]):
- The results of any statistical analysis must be the same if all components of the composition are scaled with a positive number (scale invariance). This relationship is ensured by closing the data to 1 or 100% prior to any analysis. Changing the units of the components does not change the results of the compositional data analysis.
- The results of any statistical analysis must be the same if previously unmeasured components are added to the composition (subcompositional coherence); the statistical result for some components may not be dependent on the other reported components.
- Any statistical result for compositions may not be dependent on the sequence of the reported components (permutation invariance).
Composition is presented as a real vector x = [x1, x2, …, xD] of positive components, in which the sum of positive constant κ is usually taken as 1 or 100% (eqn. 1):
where C is called the closure operator, i.e., each component of the vector is divided by the sum of all its components and multiplied by a constant κ ([1]). The closure operation ensures the principle of scale invariance. When investigating soil texture, for example, the total soil volume is irrelevant and is only used to calculate the relative values of components. Changing the total soil volume cannot change the relative values of the soil texture classes. Two compositions are considered identical when proportional, so the expression of a composition in different units does not change the results of the analysis of such data. For identical compositions, the equation holds: x = y, if x = c y, where c is a positive real number.
Simplex and simplicial geometry
The sample space of compositions is the D-part simplex (SD), which is a restricted space of a real vector space (eqn. 2):
where i = 1, …, D. In the case of a 2-dimensional real space, the simplex within this space is a line segment (1-simplex); in the case of a 3-dimensional real space, the simplex is a 2-dimensional triangle, and so on. The closure operation is the projection of a vector with positive components onto the simplex. The only relevant information given by the composition is the relative one, i.e., the ratios between its parts. This relation gives the D-part composition an intrinsically multivariate nature of D-1 degrees of freedom.
Simplicial geometry does not follow ordinary Euclidean rules observed in real vector space. Nevertheless, concepts such as distance between points, straight lines, orthogonality, norm, and inner vector product exist for a simplex vector space, although these concepts are highly non-intuitive (see [16] for details). These concepts, however, are needed when we investigate the compositional difference between compositions or a linear compositional process.
The compositional operations perturbation and powering satisfy the properties required to give a simplex SD the vector space structure ([1], [37]).
Perturbation plays the same role in SD as the sum of vectors in real space. Given two D-part compositions x = [x1, x2, …, xD] and y = [y1, y2, …, yD], with x, y ∈ SD, their perturbation x⊕y is defined as follows (eqn. 3):
The neutral element of the simplicial vector space is the identity composition I = C[1,…, 1] = [1/D, …, 1/D] (in the case of a 2-simplex in the barycenter of the triangle), and the inverse x-1 of a composition x = [x1, …, xD] is given by the composition x-1 = C[1/x1,…,1/xD].
The perturbation of a composition x with the inverse of a composition y is denoted by symbol “•” (eqn. 4):
This operation is equivalent to subtraction in real vector spaces and is called the perturbation difference. For instance, the inference about mean difference between paired compositions is based on the inference about perturbation differences ([2]).
The powering of composition x = [x1, x2, …, xD] is an operation by a real number or scalar c, defined by (eqn. 5):
Powering plays the same role in SD as multiplication by scalars in real space.
Transformation of compositional data and the use of coordinates
Aitchinson ([1]) pioneered the analysis of compositional data and introduced two transformations, additive log-ratios (alr) and centered log-ratios (clr), which transform values constrained by simplex into real space and facilitate the application of classical statistics. Both transformations, however, have important drawbacks: the alr transformation is permutation invariant and not isometric (the distances between points are not preserved), and the clr transformation lacks subcompositional coherence and yields a singular covariance matrix. Egozcue et al. ([14]) introduced an isometric log-ratio transformation that successfully overcomes the above-mentioned problems. This approach reduces compositional operations to ordinary vector operations when representing compositions by their coordinates. Egozcue et al. ([14]) showed that a simplex is a part of the real space that has a different geometric structure. An orthonormal base (perpendicular, unit vectors) can be defined in simplex and compositions can be expressed as coordinates with respect to this base. Fortunately, these coordinates have an ordinary Euclidean vector structure, permitting the application of ordinary statistics such as linear modeling and hypothesis testing, among other statistical methods.
The principle of working in coordinates states that each composition in D-part simplex (x ∈ SD) can be expressed as a perturbation linear combination ([34] - eqn. 6):
where coefficients xi* (i = 1, …, D-1) are coordinates with respect to the orthonormal basis [e1, e2, …, eD-1] of the simplex SD. The isometric log-ratio transformation (ilr) assesses coordinates x* to x. Given a basis, the coordinates of x are uniquely determined. The vector x* of D-1 coordinates is the real vector in RD-1, and the values of coordinates are not constrained to be positive or less than 1. In a 2-simplex, the composition is expressed with two ilr coordinates, while a 3-simplex using three ilr coordinates, and so on. Similar to real space, many orthogonal bases exist; no unique approach dictates the definition of the most appropriate base. The main criterion to select an orthonormal basis is the enhancement of interpretability of the representation in coordinates. Some special orthonormal bases are associated with the sequential binary partition of the compositional vector ([15]), in which the parts of compositions are divided into 2 groups of parts (subcompositions) in D-1 sequential steps. The method of partitioning the groups of parts can be related to the nature of the parts. In that case, the generated coordinates, or balances, are more easily interpreted.
The corresponding general equation for isometric log-ratio transformation from simplex to real space y = ilr(x) is defined using orthonormal basis, e1, e2, …, eD-1 ([14] - eqn. 7):
with i = 1, 2, …, D-1. The components of y = ilr(x) with respect to orthonormal basis of eqn. 7 are (eqn. 8):
where g(x1, …, xi) = g(x) = [x1·x2···xD]1/D is the geometric mean of the parts of composition x with D parts, and i = 1, 2, …, D-1.
Descriptive statistics of compositional data
Standard descriptive statistics, such as the arithmetic mean and the variance of the individual components, do not fit with Aitchison geometry as measures of central tendency and dispersion. The closed sample geometric mean is a measure of the central tendency for compositional data. For a data set n compositions, all with D parts, the central tendency is called the centre and is defined as follows (eqn. 9):
with gi (i = 1, …, D) as the geometric mean of all the parts of a composition.
The variability of a set of compositions can be expressed using various measures. One can either use metric (or total) variance based on simplicial distances be tween a composition and the geometric mean of a set of compositions ([16]). Another option is to use either variation matrix or variance matrix of centered log-ratios ([1]) both of which contain information on codependence between compositional parts but lack simpler one-value representation.
Compositional linear modeling
Compositions can evolve dependence on one or more external co-variables such as time, space, or different environmental variables. The explaining variable can be continuous, discrete, real, or even compositional data. The strategy of linear modeling of compositional processes in the simplex can be replaced with linear modeling of compositional coordinates in real space ([38]). The use of log-ratio transformed compositions (e.g., ilr and alr) instead of raw values can make the linear combinations meaningful with respect to the geometry of the simplex ([37], [48]). Aitchinson ([1]) argues that the conditional distribution is the normal distribution of the simplex. The multivariate nature of the data set is preserved when the applied methods are linear ([48]).
Application of the approach
Study area
The study site is situated in the predominantly forested Natura 2000 Snežnik area in southwest Slovenia (Lon. 14° 26′ E, Lat. 45° 35′ N). The area is located in the Dinaric Mountains, which range from Slovenia to Montenegro. The forest management unit Leskova dolina (2.392 ha) was chosen as the research area. The altitude ranges from 610 m to 1796 m a.s.l. The topography of the area is very diverse, with abundant sinkholes typical of high Karst geology with limestone and dolomite as the parent material. Due to the high variability in topography, different pedogenetic associations developed primarily litosols, rendzic leptosols, cambisols, and luvisols. The soil depth varies between 10 and 300 cm, depending on the micro-topographic position, and precipitation is evenly distributed throughout the year, with a mean annual precipitation of 2150 mm. The average mean temperature is 6.5 °C, and late spring and early autumn frosts are common. The prevalent plant community in the study area is the Dinaric silver fir - European beech forest (Omphalodo-Fagetum Mar. 93). The main tree species are silver fir (Abies alba Mill.), Norway spruce (Picea abies Karst.), and European beech (Fagus sylvatica L.). Sycamore (Acer pseudoplatanus L.) and elm (Ulmus glabra Huds.) are also present but in a much lower percentage. Most of the stands are managed with a selective cuts (single-tree or group) or shelterwood system, leading to considerable within-stand variation in tree age and tree species composition. The close-to-nature forest management prevents forest clear cuts or intensive forest shifts, making the Snežnik forests very suitable for the study of forest community structure and dynamics. Tree ingrowth largely results from natural processes rather than tree planting.
Data sources
The analysis utilized the basal area, expressed as m2 ha-1, which represents the area of a given section of land that is occupied by the cross-section of silver fir, Norway spruce and European beech trunks measured at the diameter at breast height (1.3 m above ground) per forest compartment in 1954 and 2004. In the 1890s, the forests in the Snežnik area were divided into forest compartments, and each has relatively homogenous site characteristics and stand type. The shapes of the compartments have not changed throughout the last century. Forest compartments with similar site and stand characteristics (parent material, soil, vegetation community, stand structure, etc.) determine forest management system and are thus grouped into forest management classes (FMCs). These classes were named after the prevalent vegetation units in this area of Dinaric silver fir and European beech forests: Omphalodo-Fagetum typicum (TYPC), Omphalodo-Fagetum homogynetosum (HOMO), Omphalodo-Fagetum mercurialetosum (MERC), and Omphalodo-Fagetum lycopodietosum (LYCO - [24]).
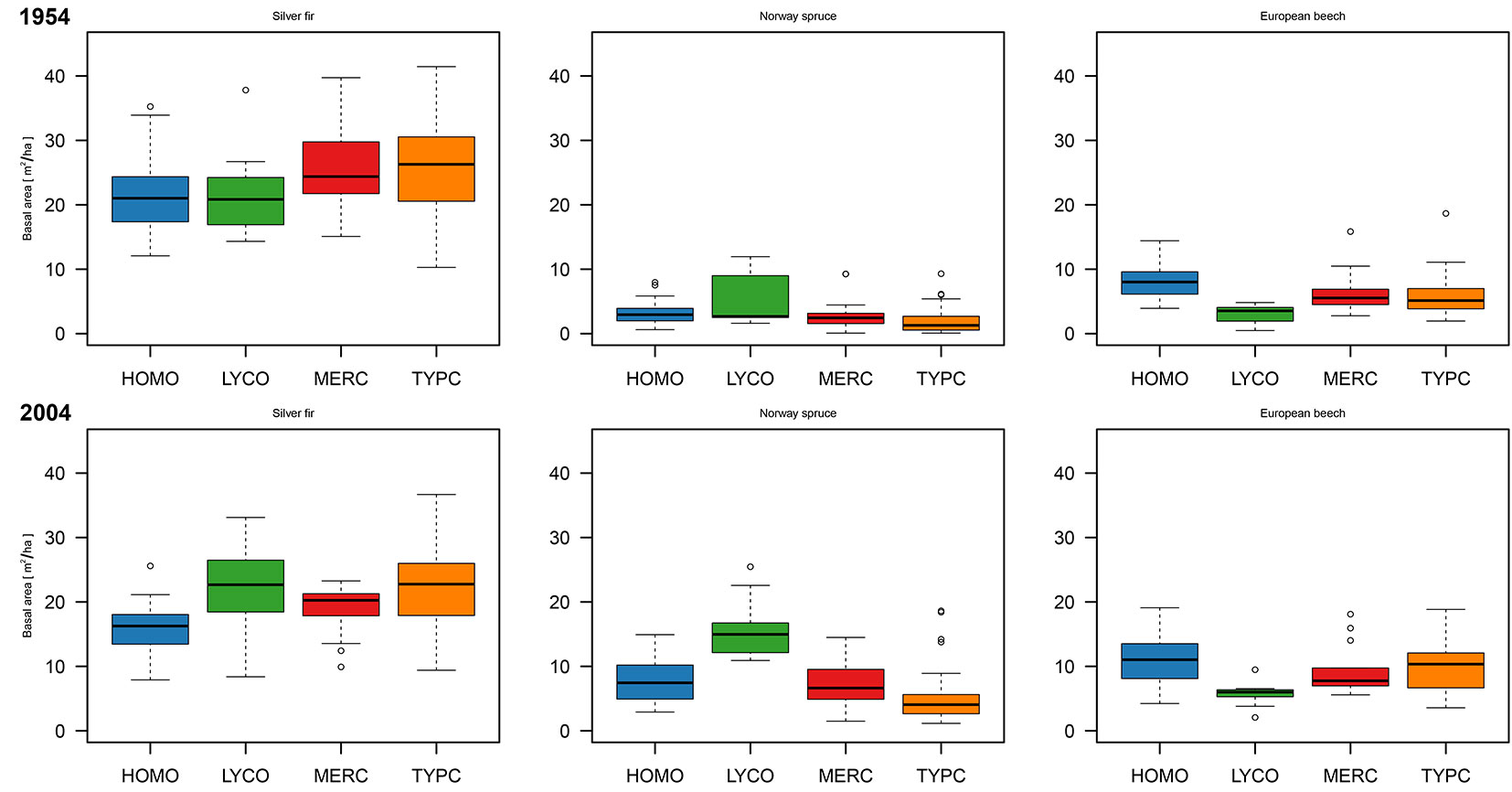
In each compartment, all trees with a diameter greater than 10 cm were measured (full calipering) at breast height in 1954, and the trees were classified into 5-cm DBH classes for each tree species ([20]). The basal area of each tree species was calculated from the DBH frequency distribution using the means of DBH classes as class representatives and dividing the values by the compartment size. Personnel limitation necessitated a different, indirect approach of basal area determination in 2004. In each forest compartment, several homogenous forest stands were delineated with orthophotographies at 1:5000 scale ([24]). In each forest stand, several temporary sampling plots (minimum 7 per stand) were established. The basal area of each tree species in each plot was estimated with Bitterlich’s angle-count method with basal area factor k = 2. Sample plot data were averaged for each forest stand. To obtain information on tree species composition in each forest compartment, the basal area of certain tree species within a forest stand belonging to the specific compartment was weighted according to the proportion of the forest stand in the specific forest compartment. The validity of 2004 indirect basal area estimation per forest compartment was additionally tested using permanent sampling plots of forest inventory (n = 471 plots). No significant deviation between indirect basal area estimation and forest inventory data were ascertained. Fig. 1 presents the basal area data for both observed periods among FMCs. In addition, explanatory forest structure variables and terrain topography were defined (Tab. 1) for each compartment.
Fig. 1 - Basal area of 119 forest compartments according to 4 different forest management classes (FMCs) for 1954 and 2004.
Tab. 1 - Explanatory variables and data sources of forest structure and terrain topography specified for each forest compartment. ([20], [21], [22], [23], [24]).
| Data source | Explanatory variable per forest compartment | Units |
|---|---|---|
| Calculated from full calipering from 1954 data | Median silver fir diameter at DBH | cm |
| Median Norway spruce diameter at DBH | cm | |
| Median European beech diameter at DBH | cm | |
| Species composition of trees with diameter < 30 cm | - | |
| Records of harvested trees in 1954-2004 | Harvesting rates | m3 |
| Salvage logging relative to total harvesting rates | % | |
| Broadleaf logging relative to total harvesting rates | % | |
| Conifers logging relative to total harvesting rates | % | |
| Digital elevation model 12.5 × 12.5 m | Mean altitude | m |
| Mean terrain curvature | - | |
| Mean slope | degrees |
Analysis of sample data
We utilized several consecutive steps to perform the compositional analysis of this example data set. First, some descriptive statistics, such as means and variation, were shown and coupled with general graphic data representation. A ternary diagram was most suitable for our 3-part compositions. In a ternary diagram, each point represents a 3-part composition in a forest compartment. The vertices of the ternary diagram correspond to the three components or, in this study, species. The components are proportional to the lengths of the perpendicular segments from the vertex to the opposite side of the triangle.
Second, we separately assessed the relative differences in the mean species compositions between the 4 FMCs for each year (1954 and 2004) by classical MANOVA of the ilr transformed data. The first ilr coordinate (ilr1) represents the balance between silver fir and Norway spruce, and the second ilr (ilr2) represents the balance between conifers and broadleaves. The MANOVA assumptions were verified. The Box test was used to test the equality of the covariance matrices and univariate normality of the individual ilr coordinates to ensure multivariate normality. The assumptions are only marginally accepted because of the outliers. A univariate ANOVA was performed to assess the significance of individual ilr coordinates. The Waller-Duncan K-ratio post-hoc test was used for multiple comparisons between FMC means. Because of the marginally accepted assumptions for MANOVA, we additionally utilized the Kruskal-Wallis non-parametric analysis of variance and post-hoc test for medians of the ilr coordinates between FMCs, and we obtained the same results.
Third, the compositional change was evaluated with a calculation of perturbation differences (eqn. 4). In the case of no change in tree species composition, the perturbation difference should match the identity composition (composition with equal portions of each part). In our research, the perturbation differences were tested against the identity I = (1/3, 1/3, 1/3).
Finally, to obtain a deeper explanation of the compositional change, we related the compositional change to the explanatory variables by regression of the perturbation-differences against these variables. We modeled the perturbation differences against FMC; tree species composition of thin trees (DBH < 30 cm) in 1954; median DBH of silver fir, Norway spruce, and European beech; and percentage of salvage cut in 1954-2004 period. The dependent variables in the multivariate linear models included both ilr coordinates of perturbation differences that measure forest compositional changes between 1954 and 2004. Prior to the analysis, the tree species composition of thin trees (DBH < 30 cm) in 1954 was transformed by isometric log-ratio transformation (ilr).
The data were analyzed in the R environment ([42]) using the package “compositions” ([49], [50]).
Results
Descriptive statistics
The subcomposition of the three dominant tree species included in this analysis represents 97.6% of the total basal area. The tree species abundance in each compartment was expressed as part of the total basal area of all trees. The D = 3-part composition describes the relative abundance of three tree species, silver fir, Norway spruce, and European beech, in 119 forest compartments. Our data did not include zero values, indicating that no tree species was absent in any forest compartment.
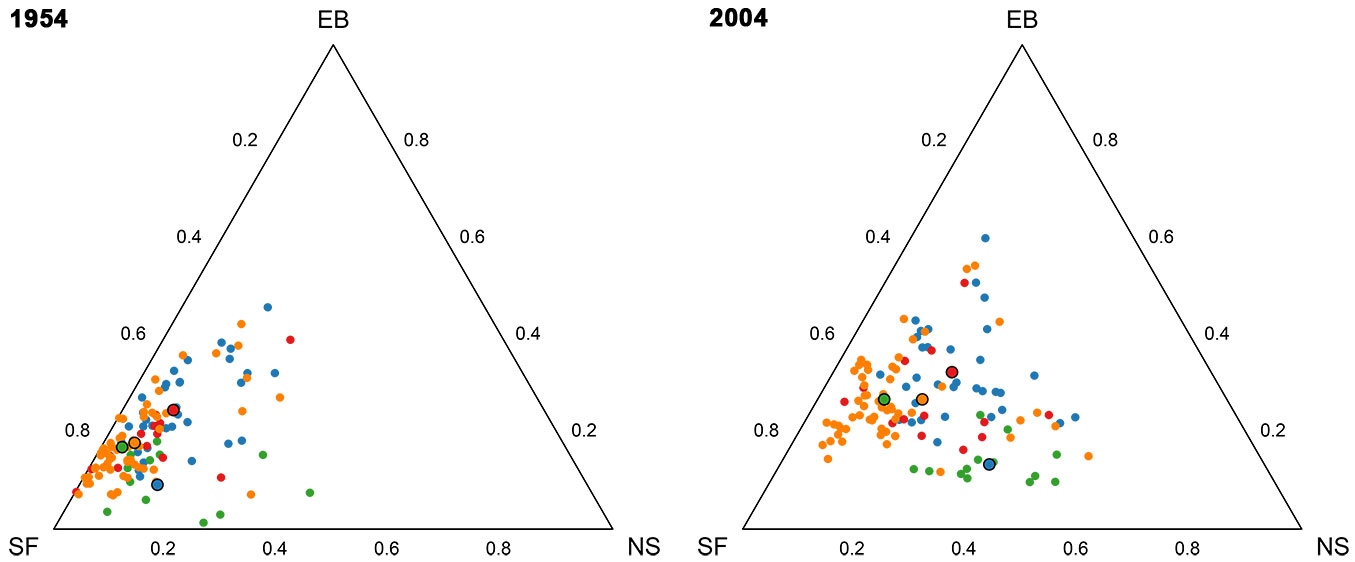
Fig. 2 presents the forest compositions in two ternary diagrams. The centers (closed geometric means) of the compositions for each FMC are presented in the ternary diagrams and in Tab. 2. Silver fir is generally the dominant species in both years, but a clear reduction of the silver fir portion is observed after 50 years. There is an increase in Norway spruce and European beech. The total relative variability expressed by the total variance (Tab. 2) decreased from 1954 to 2004 in all FMCs (Tab. 2).
Fig. 2 - Ternary diagrams of tree species compositions determined in 1954 (left) and 2004 (right). Each symbol represents a single forest compartment (n = 119). Different color symbols represent different FMCs: (blue) Omphalodo-Fagetum homogynetosum (HOMO); (green) Omphalodo-Fagetum lycopodietosum (LYCO); (red) Omphalodo-Fagetum mercurialetosum (MERC); (orange) Omphalodo-Fagetum typicum (TYPC). Bold symbols present the corresponding geometric means of FMC classes.
Tab. 2 - Mean percentages per tree species (SF: silver fir; NS: Norway spruce; EB: European beech), total variance of the dataset, and significance of differences between four FMCs in 1954 and 2004. Significant differences between FMCs are described for each ilr-coordinate separately using letters; FMCs with same letters are not significantly different at 0.05 confidence level for a given ilr-coordinate.
| Year | Parameter | Species / irl | HOMO | LYCO | MERC | TYPC |
|---|---|---|---|---|---|---|
| - | No of compartments | - | 33 | 13 | 13 | 60 |
| 1954 | Mean portion of | Silver fir (SF) | 0.66 | 0.77 | 0.77 | 0.79 |
| Norway spruce (NS) | 0.09 | 0.14 | 0.05 | 0.04 | ||
| European beech (EB) | 0.25 | 0.09 | 0.18 | 0.17 | ||
| Total variance | - | 0.43 | 0.98 | 1.30 | 1.04 | |
| Homogenous groups | ilr1 ( SF / NS ) | a | a | b | b | |
| ilr2 [ ( SF * NS )/ EB] | a | b | a | a | ||
| 2004 | Mean portion of | Silver fir (SF) | 0.46 | 0.49 | 0.54 | 0.61 |
| Norway spruce (NS) | 0.21 | 0.37 | 0.19 | 0.12 | ||
| European beech (EB) | 0.32 | 0.13 | 0.27 | 0.27 | ||
| Total variance | - | 0.30 | 0.14 | 0.49 | 0.46 | |
| Homogenous groups | ilr1 ( SF / NS ) | b | a | b | c | |
| ilr2 [ ( SF * NS )/ EB] | a | b | a | a |
Comparing species compositions among FMCs
We applied a classical MANOVA test to the ilr-transformed data to assess the relative differences in mean species compositions between the 4 FMCs for each year (1954 and 2004). The differences in species composition between FMCs were statistically significant (p1954 < 0.001, p2004 < 0.001) in both investigated periods. The results indicate that the ratio between silver fir and Norway spruce in 1954 is significantly higher in TYPC and MERC compared to HOMO and LYCO. The second ilr coordinate represents the ratio between the geometric mean of the subcomposition of silver fir and Norway spruce (conifers) and European beech (broadleaves). This ratio in LYCO is significantly different from that in other FMCs in 1954 and 2004. TYPC in 2004 displays the significantly highest ratio between silver fir and Norway spruce, but the ratio is smaller than in 1954. In short, LYCO is distinctly different from other FMCs because of a lower proportion of European beech.
Temporal changes in tree species composition
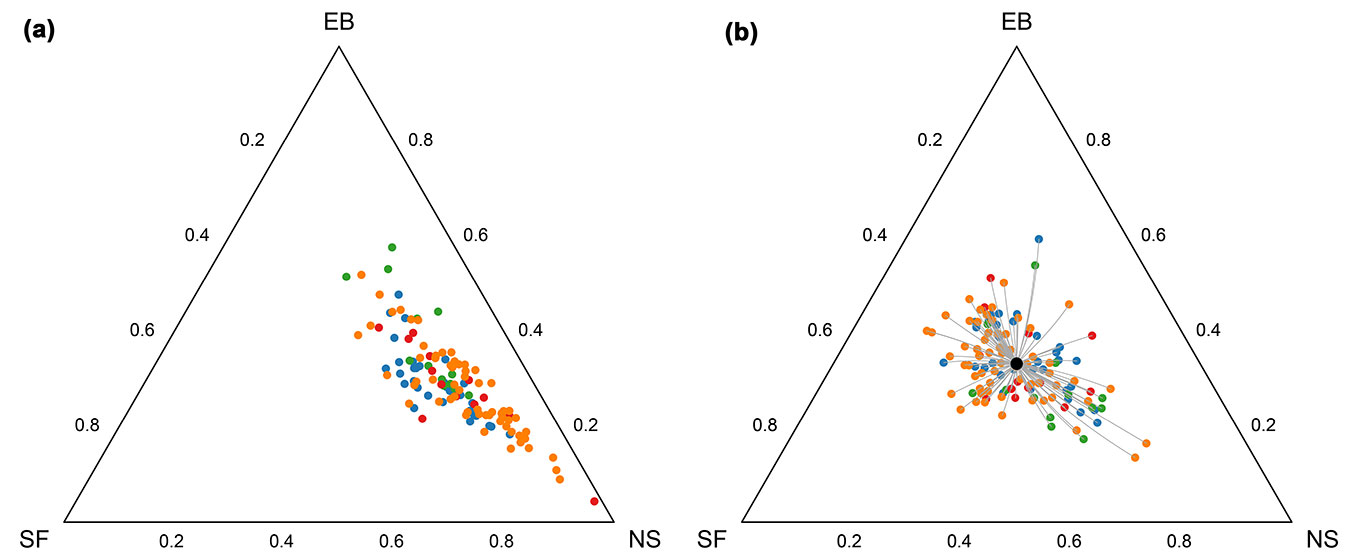
The perturbation differences for all forest compartments were calculated to analyze the difference (distance) between forest compositions in 1954 and 2004 (Fig. 3). The perturbation differences are concentrated in the right part of the ternary graph, with the mean perturbation (silver fir = 0.14, Norway spruce = 0.57, European beech = 0.29) indicating the comparatively large relative change in Norway spruce. This result is caused by the low proportion of Norway spruce in the majority of the forest compartments in 1954 and by the increase of the abundance of spruce in the study period.
Fig. 3 - (a): Shift in tree species composition between 1954 and 2004 shown on ternary diagram. The circles are forest compartments in 1954, and the line segments are compositional straight lines toward the 2004 forest compositions. (b): The perturbation differences between the two observation periods. The magnified symbols in both plots represent two compartments shown as compositional change and the corresponding perturbation difference. Different color symbols represent different FMCs (see Fig. 2 for color codes).
The significant compositional change is quite evident in Fig. 3. However, we tested the significance with the Hotelling T2 test, which is a multivariate extension of the paired t-test. The Hotteling T2 test indicated that the compositional change (ratios between species percentages) is highly significant (F-stat = 244.08, p = 0.000).
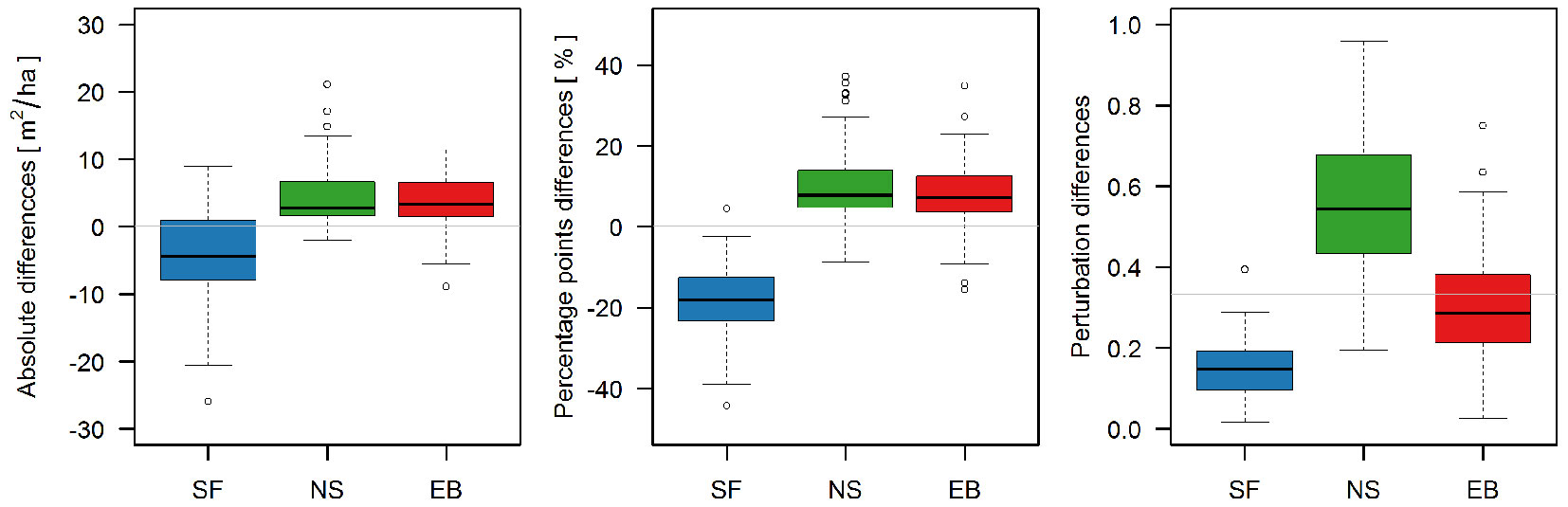
We also compared change in 1954-2004 period of each of the dominant three species using three different measures, namely change in absolute terms (in basal area per hectare), in percentage points and in perturbation differences. Fig. 4 shows that the magnitude of change for each species is much different for perturbation difference than for the other two measures of change. Change in absolute terms and in percentage points was the largest for silver fir (decrease), whereas perturbation difference was the largest for Norway spruce and smallest for silver fir.
Fig. 4 - A comparison of different measures to evaluate forest species compositional change during the investigated period between 1954 and 2004. Grey horizontal lines indicate no change.
Linear modeling of compositional change
The initial stand structure was well correlated with the perturbation differences. The site characteristics, expressed as FMC, seem to play an important role in the forest species composition dynamics. In both cases, the first and second ilr coordinates are significantly correlated with salvage cuts, as a consequence of silver fir decline. The compositional coefficient of determination (R2) is 0.56, and residuals are uniformly distributed around the barycenter of the ternary diagram (Fig. 5).
Fig. 5 - Predicted perturbation differences from final model (a) and the distribution of model residuals (b). Different color symbols represent different FMCs (see Fig. 2 for color codes).
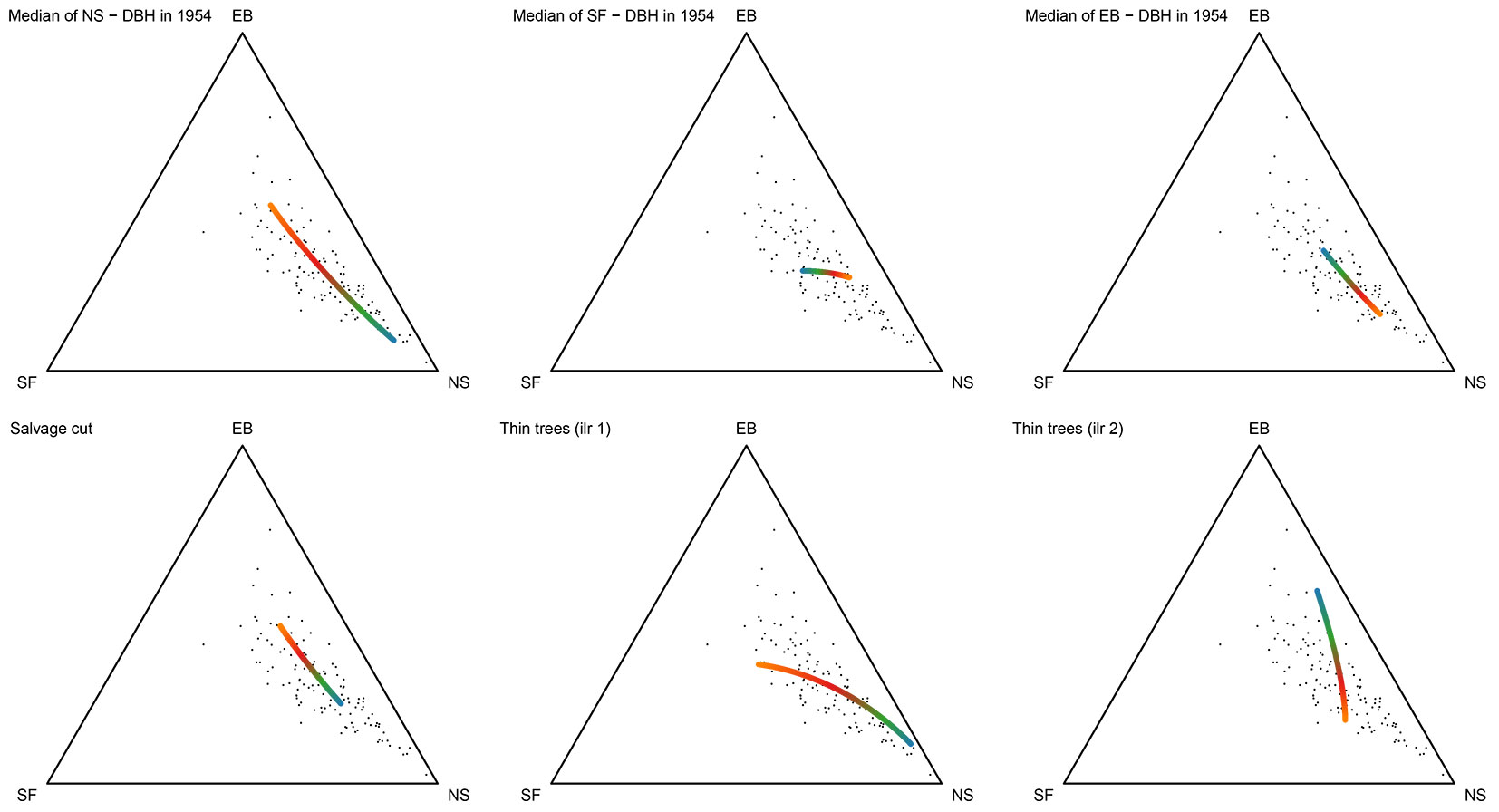
The effect of unique variables on perturbation differences is presented in Fig. 6 and Tab. 3. The changes in the share of Norway spruce are highest in the forest compartments with the lowest median DBH of Norway spruce in 1954, while an increase in the European beech portion is observed in compartments with larger DBH of Norway spruce trees in 1954. In these compartments, there is no ingrowth of young silver fir trees, bigger Norway spruces trees were cut, and the share of European beech increased (triangle 1 in Fig. 6). The salvage cut created a similar effect. Greater incidences of salvage cut increase the proportion of European beech.
Fig. 6 - The component effect for each co-variable in a linear model of perturbation differences in the forest composition between 2004 and 1954. The small points indicate perturbation differences. The color ramp represents the component effect (orange and blue colors represent high and low values of the explanatory variable, respectively).
Tab. 3 - Estimates of the parameters, residual standard error, and adjusted coefficients of determination for modeling perturbation differences.
| Coordinate | Coefficients | Estimate | Std. Error | t value | p value | Res. Std. Error | Adj. R2 |
|---|---|---|---|---|---|---|---|
| ilr 1 | (Intercept) | -0.692 | 0.434 | -1.592 | 0.114 | 0.358 | 0.588 |
| TT ilr 1 | -0.488 | 0.051 | -9.531 | 0.000 | |||
| TT ilr 2 | -0.078 | 0.064 | -1.223 | 0.224 | |||
| NS median | -0.039 | 0.009 | -4.642 | 0.000 | |||
| SF median | 0.038 | 0.011 | 3.553 | 0.001 | |||
| EB median | 0.056 | 0.017 | 3.377 | 0.001 | |||
| Salvage cut | -0.004 | 0.001 | -2.861 | 0.005 | |||
| ilr 2 | (Intercept) | 0.069 | 0.379 | 0.182 | 0.856 | 0.312 | 0.437 |
| TT ilr 1 | 0.034 | 0.045 | 0.754 | 0.452 | |||
| TT ilr 2 | -0.354 | 0.056 | -6.336 | 0.000 | |||
| NS median | 0.039 | 0.007 | 5.236 | 0.000 | |||
| SF median | 0.008 | 0.009 | 0.905 | 0.367 | |||
| EB median | -0.063 | 0.015 | -4.324 | 0.000 | |||
| Salvage cut | 0.004 | 0.001 | 3.742 | 0.000 |
Compartments with a small silver fir DBH do not change greatly (a colored line begins near the center of the ternary diagram on Fig. 6), but compartments with a higher silver fir DBH value tend to have an increasing share of Norway spruce. The proportion of Norway spruce increases in compartments with a high mean value of European beech trees. This result is most likely due to the selective cutting of the larger European beech trees and the more efficient regeneration and ingrowth of Norway spruce compared to silver fir. The first ilr coordinate of tree species composition of thinner trees (DBH < 30 cm) in 1954 represents the ratio between Norway spruce and silver fir and can be interpreted as follows: in forest compartments in which the Norway spruce/silver fir ratio is high, the perturbation differences are minor (the line ends near the center of the ternary diagram), but a low Norway spruce/silver fir ratio leads to a high relative increase in Norway spruce.
Discussion
We have outlined the fundamentals of compositional data analysis and have presented some examples of its application in the study of forest structure and forest dynamics. Aitchinson ([1]) noted that the ratios, not the differences, between parts provide information when using closed data. Our research utilized a 3-component forest species composition. Prior to the application of traditional methods, the isometric log-ratio transform (ilr) of the data was utilized to determine the differences between uncorrelated samples (differences in tree species composition between FMC), paired samples (temporal changes in tree species composition), and linear modeling of time changes expressed as the perturbation difference of compositions dependent on covariables that describe the forest condition. The ilr transformation preserves the distances between compositions when mapping the data from the Aitchinson geometry to the Euclidean geometry, in which the calculations and graphical representations are normally calculated ([14]). Within the Aitchinson geometry, other methods such as cluster analysis or principal component analysis may be applied to the untransformed closed data ([49]).
Compositional data analysis presents two common challenges: (i) characterizing a change in composition; and (ii) testing hypotheses concerning the nature of the change. In general, a lack of change in a value indicates that the expected difference between two paired samples is zero. For compositions, the perturbation difference is the corresponding measure of change. In our 3-species Sneznik forest composition, we showed that the forest composition change over the last 50 years is highly significant. The interpretation of perturbation differences as compositions is somewhat complicated when investigating the bidirectional dynamics of forests, in which trees are simultaneously eliminated (felled or dying trees) and growing (recruitment of new trees). The perturbation difference characterizes the net change in species composition. The forest species composition in the forest compartment 10a in 1954 is x1954 = [0.77, 0.16, 0.07] and x2004 = [0.48, 0.24, 0.29] in 2004, where the first, second, and third parts are silver fir, Norway spruce, and European beech, respectively. The compositional change expressed as the perturbation difference is xdif = C[0.48/0.77, 0.24/0.16, 0.29/0.07] = [0.10, 0.24, 0.66,], indicating a 6.6-fold larger change in European beech than silver fir and a 2.4-fold larger change in Norway spruce than in silver fir. Compositional data analysis results require careful interpretation. The perturbations in studies of temporal dynamics do not single-handedly indicate anything about the absolute change. Like any other composition, perturbation only possesses relative information, and only the ratios between parts are important and interpretable. Additional information external to compositional data (e.g., forest cut inventory or ingrowth estimation) are needed to reach conclusions about absolute change. Utilization of linear modeling necessitates the interpretation of the regression coefficients within a simplex vector space.
The species composition of the investigated forests displayed relative increases in Norway spruce and European beech and decreases in silver fir. To explain this change some historical facts should be presented. Mature forests of European beech and silver fir prevailed in the Dinaric parts of Slovenia and beyond in the middle of 19th century, and young trees below the canopy mainly consisted of shade-tolerant silver fir, which was capable of effective regeneration due to low ungulate densities. Adult beech trees were intensively harvested for firewood and charcoal production until the middle of the 20th century, while silver fir became a dominant tree species, desired for its timber and suitability for selection management ([26], [4]). The abundance of silver fir faced the turning point in the last decades of 20th century with substantial silver fir dieback. Recent studies have offered some possible explanations for this event ([47], [35]). Those studies suggest that silver fir decline occurred due to interplay of different abiotic effects (air pollution with sulphur and nitrogen compounds, acid rain leading to nutrient deficiencies and imbalances and drought effects). Besides, natural regeneration and recruitment of silver fir was largely hindered due to increasingly high densities of ungulates, browsing young silver fir trees ([10]). The decrease of silver fir might also be at least partly explained by the observed natural alternation between silver fir- and European beech-dominated phases. During silver fir dieback Norway spruce was promoted as its substitute.
Using linear modeling we showed which direct and indirect variables were substantially related to forest compositional change. The perturbation differences identified in this study demonstrate the advantage of this approach for ecological studies. Fig. 6 shows that the relative change is highest for Norway spruce, indicating that the method is sensitive to changes in rare, minor tree species, which are usually difficult to be assessed ([52]).
In general, in the case of forest species composition, the total sum of forest basal area (m2 ha-1) is not irrelevant, since the total wood biomass or tree coverage of a site tells a lot about forest productivity and structure ([46]). Our analysis of compositional data considered that the total of parts of composition is irrelevant, since relative amounts of tree species are of larger importance ([3]) in forest community studies. When dealing with the basal area per hectare, we can think of it being the composition of n-parts (n represents number of all tree species) plus the remaining part which is the area, not covered by tree trunks. All the parts sum to a constant (a forest hectare), which indicates that the data are closed according to physical laws ([45]). The subcompositional coherence principle of compositional data analysis indicates that the results of any subcomposition analysis (e.g., the three common forest species in our study) are the same in a relative context.
This paper does not consider null values, which are the principal problem that can arise in compositional data analysis of ecological data ([32]). The ratios cannot be computed in this situation. Null values are a main characteristic of ecological data, particularly species composition data ([51]). To overcome the null value problem, plant community dynamics research traditionally utilizes multivariate methods that are not sensitive to missing data (e.g., correspondence analysis or CA). These essentially descriptive methods, however, lack the predictive power of linear models. Subcompositional incoherence is a key pitfall when utilizing CA instead of the compositional data approach. This problem occurs when the addition of parts (species) into the analysis subsequently changes the result of the analysis. Much of the specialized literature discusses different methods of null replacement ([32], [33]), but a common assumption argues that a sensitivity analysis should follow value imputation. Greenacre ([27]) proposed a method to actually evaluate the subcompositional incoherence and decide whether this factor is small enough to be neglected.
Conclusions
This paper presents a natural and mathematically clean framework to deal with closed data, particularly when the data are subjected to physical constraints, such as mass or area conservation ([45]). Multiple reports have cautioned against analysis of raw percentage data or closed data ([5]) with the possibility of wrong conclusions when analyzing compositions directly. Even traditional transformations (e.g., log or arcsin-sqrt) and separate component analyses are now regarded as outdated. Basically, the same statistical methods, such as descriptive statistics, linear modeling, spatial analysis, time series analysis or classification methods can also be used on compositional data, but only if such data is properly (ilr) transformed. However, some difficulties still persist with the approach used in our study; the ilr coordinates, gained after the transformation, are somewhat difficult to interpret and the problem of zeros and missing values is still not fully resolved.
We showed that certain aspects of forest dynamics such as species composition can be successfully evaluated using compositional data approach. For the investigated forests of SW Slovenia we showed significant compositional change in a 50-year period caused by the interplay between environmental factors and forest regime with their differential effects on three dominant tree species. In absolute terms, the amount of silver fir changed the most; decrease could be attributed to fir dieback and poor regeneration/recruitment due to ungulates. In relative terms, expressed in perturbation differences, largest change was showed for Norway spruce with its increase being predominantly the effect of promotion through forest management measures.
Acknowledgements
We thank the anonymous reviewers for their valuable comments which greatly contributed to the quality of the paper. We acknowledge the financial support from the Slovenian Research Agency (Young Researcher’s programme [MK] and research core funding No. P4-0059 and No. P4-0085).
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
University of Ljubljana, Biotechnical faculty, Večna pot 83, 1000 Ljubljana (Slovenia)
Klemen Eler
University of Ljubljana, Biotechnical faculty, Jamnikarjeva 101, 1000 Ljubljana (Slovenia)
Corresponding author
Paper Info
Citation
Kobal M, Kastelec D, Eler K (2017). Temporal changes of forest species composition studied by compositional data approach. iForest 10: 729-738. - doi: 10.3832/ifor2187-010
Academic Editor
Luca Salvati
Paper history
Received: Aug 02, 2016
Accepted: May 10, 2017
First online: Aug 01, 2017
Publication Date: Aug 31, 2017
Publication Time: 2.77 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2017
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 47653
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 41404
Abstract Page Views: 2177
PDF Downloads: 3064
Citation/Reference Downloads: 16
XML Downloads: 992
Web Metrics
Days since publication: 3058
Overall contacts: 47653
Avg. contacts per week: 109.08
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2017): 6
Average cites per year: 0.67
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Single-tree influence on understorey vegetation in five Chinese subtropical forests
vol. 5, pp. 179-187 (online: 02 August 2012)
Research Articles
Modelling the carbon budget of intensive forest monitoring sites in Germany using the simulation model BIOME-BGC
vol. 2, pp. 7-10 (online: 21 January 2009)
Research Articles
Incorporating management history into forest growth modelling
vol. 4, pp. 212-217 (online: 03 November 2011)
Research Articles
Post-fire effects and short-term regeneration dynamics following high-severity crown fires in a Mediterranean forest
vol. 5, pp. 93-100 (online: 30 May 2012)
Research Articles
Mapping the vegetation and spatial dynamics of Sinharaja tropical rain forest incorporating NASA’s GEDI spaceborne LiDAR data and multispectral satellite images
vol. 18, pp. 45-53 (online: 01 April 2025)
Commentaries & Perspectives
The role of plant sociology in the study and management of European forest ecosystems
vol. 6, pp. 55-58 (online: 21 January 2013)
Research Articles
Compatible taper-volume models of Quercus variabilis Blume forests in north China
vol. 10, pp. 567-575 (online: 08 May 2017)
Research Articles
Spatio-temporal modelling of forest monitoring data: modelling German tree defoliation data collected between 1989 and 2015 for trend estimation and survey grid examination using GAMMs
vol. 12, pp. 338-348 (online: 05 July 2019)
Research Articles
Distribution factors of the epiphytic lichen Lobaria pulmonaria (L.) Hoffm. at local and regional spatial scales in the Caucasus: combining species distribution modelling and ecological niche theory
vol. 17, pp. 120-131 (online: 30 April 2024)
Research Articles
The missing part of the past, current, and future distribution model of Quercus ilex L.: the eastern edge
vol. 17, pp. 90-99 (online: 22 March 2024)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword