A comparison of models for quantifying growth and standing carbon in UK Scots pine forests
iForest - Biogeosciences and Forestry, Volume 8, Issue 5, Pages 596-605 (2015)
doi: https://doi.org/10.3832/ifor1403-008
Published: Feb 02, 2015 - Copyright © 2015 SISEF
Research Articles
Abstract
Scots pine is the most abundant native conifer in the UK. A stand level dynamic growth (SLeDG) model is parametrised for British Scots pine stands for the first time. This model predicts stands annually based on their current state, and allows for changes in forest management. Stand growth and carbon storage predictions using this model were compared with those of the yield look-up package ForestYield, and a process-based model (3PGN). Predictions were compared graphically over an 100 year rotation, and strengths and weaknesses of each were considered. The SLeDG parametrisation provided forecasts of Scots pine growth with percentage mean absolute difference < 12% for all state variables. The model comparison showed that similar outputs were predicted by all three models, with the greatest variation in the yield table based prediction of volume and biomass. Future advances in data availability and computing power should allow for greater use of process-based models, but in the interim more flexible dynamic based growth models may be more useful than static yield tables for providing predictions which extend to non-standard management prescriptions and estimates of early growth and yield.
Keywords
Growth, Yield, Carbon, Modelling, Dynamical-systems, 3PG, ForestYield
Introduction
The combination of both spatial scale and rotation length of forest stands mean that models of forest growth are essential for sustainable management ([4]). Historically this has been achieved using yield models which use empirical relations between state variables such as top height, basal area, and number of stems to forecast stand development and timber volume production ([53]). For example, in the UK there is widespread use of the yield tables of Edwards & Christie ([10]) provided through a lookup package ForestYield. Increased emphasis on providing a multi-function forest resource ([38]) has meant that such models have had to be applied to activities such as carbon storage reporting ([9]). However, forest managers focusing on multi-function management are in turn more likely to deviate from management regimes aimed only at maximising timber production. Another shortcoming of such yield tables is that they fail to be linked causally to the drivers of productivity such as climate and nutrient availability, and are unable to account for changes in these drivers as might be expected in a changing climate ([35]). A shift to more flexible forest models is appropriate to accommodate for changes in environment or management objectives.
Hybrid models combine both empirical and process based modelling approaches: using simple mathematical relationships between stand variables, and representations of the underlying ecophysiological processes in stand development respectively. Through the combination, shortcomings of the empirical and process-based approaches may be ameliorated ([26], [35]), providing both traditional outputs for forest managers as well as estimates of carbon sequestration, whilst reducing the uncertainty in model outputs that occurs in complex process modelling ([50]). Additionally, prediction precision may be improved by using a hybrid approach which can deal with changes in growing environment not represented in empirical models ([40]).
There are a number of hybrid models which have been applied for varied species and locations globally ([50], [54], [31]). Perhaps the most widely applied hybrid model is Physiological Principles Predicting Growth (3PG) developed by Landsberg & Waring ([25]). It uses physiological principles as the basis for a relatively simple process-based model that can provide forest managers with stand variables as well as estimates of carbon fixation. The model works in three stages: derivation of primary production, partitioning the production to above and below ground portions, and derivation of output variables ([27]). It has been parametrised successfully for a number of species, including: eucalyptus (Eucalyptus spp.) in Australia ([45]), Brazil ([1]), Spain ([43]) and Portugal ([34]); ponderosa pine (Pinus ponderosa Douglas ex C.Lawson) and Douglas fir (Pseudotsuga menziesii (Mirb.) Franco) in the Pacific Northwest ([49]), and in the UK for Scots pine (Pinus sylvestris L. - [58]) and Sitka spruce (Picea sitchensis (Bong.) Carr. - [33]). However, while 3PG has the potential to be used over large areas where it has not been calibrated ([1]), it still requires a large number of parameters to be measured or estimated (both climatic and in the stand). This may increase both model uncertainty and the cost of parametrisation, especially in cases with limited data availability.
Another class of models which can have elements of flexibility in the sense described above are dynamic yield models as suggested by Pretzsch ([41]). Dynamic yield models allow forecasting of a stand based on its current state, as measured by a number of state variables (such as top height, basal area, and number of stems per hectare). Changes in a state variable are a function of only the current state of the stand. Thus variation in forest management strategies can easily be modelled by adjusting state variables accordingly. For example, a thinning may be modelled by reducing the number of stems and the basal area in the state vector, creating an adjusted state vector. The trajectory of this adjusted state vector is then forecast. This would not be possible with a static yield model, where only predetermined points for thinnings can be simulated.
A number of stand level dynamic growth (SLeDG) models have been developed for a variety of species based on the initial work of García ([14]): for eucalypts (Eucalyptus globulus Labill.) in Spain ([15]), Sitka spruce in Ireland ([5]), interior spruce - a mix of white spruce (Picea glauca [Moench] Voss), and Engelmann spruce (Picea engelmannii Parry) and their hybrids - in British Columbia ([17]), loblolly pine (Pinus taeda L.) in the Piedmont region of the USA ([18]), and trembling aspen (Populus tremuloides Michx.) in Western Canada ([19]). This approach has an advantage in that SLeDG models may be parametrised providing acceptable extrapolations with relatively small Permanent Sample Plot (PSP) datasets ([17]). As the UK has a robust but not particularly extensive network of PSPs (Scots pine n = 196; Sitka spruce n = 488), such models are advantageous. Changes in stand-level variables are predicted with biologically consistent differential equations. Recent SLeDG style models have moved towards more of a hybrid style, including variables which account for reduction of productivity following thinning or topping in turn reducing the stand’s photosynthetic (and nutrient capture) apparatus ([18]). In the most recent implementation of the model framework it is suggested that the model may allow for estimating the root, leaf, and branch biomass of stands ([18]), thus providing both timber growth estimates, and a standing biomass estimate for forests. It is also suggested that the model productivity may be modulated by climate and nutrient parameters, allowing for predictions in a changing climate ([18]). However, neither the standing carbon nor climate change predictions have been tested yet. Additionally, unlike 3PG there has been no work on integrating the model with routines of soil carbon dynamics ([59]), which are an important component of the forest carbon cycle ([22]).
While there can be no “perfect model”, certain models will lend themselves better than others to certain tasks. Here we do not aim to determine a perfect model, but instead compare model utility for different tasks. This paper has two objectives. Firstly, we introduce the use of the SLeDG approach in UK forests. The model is described and parametrized for Scots pine. Scots pine is the most abundant native conifer in the UK, and the second most abundant overall species - occupying over 17% of the UK forest area ([13]). With current forest strategy aiming to afforest with native species, Scots pine’s importance in UK forestry looks set to increase ([57]). Timber outputs, as well as standing carbon outputs are estimated and reported for the first time with a SLeDG model.
Secondly, forecasts of forest growth and standing carbon estimates of the SLeDG model are compared with those of the ForestYield package and the 3PGN model. Although versions of 3PG have previously been compared with other growth models ([40], [54]), the ForestYield model has not previously been compared to alternative modelling methods for forest carbon accounting. This therefore allows a comparison of the outputs of these forest growth models, as well as identifying the potential for improving the current methodology for stand level forest growth and carbon reporting estimations.
Methods
Data
The data for the parametrisation of the models were provided by the Forest Research Forest Mensuration, Modelling and Forecasting Group, consisting of 51 PSPs across Scotland. The measurement statistics taken from these PSPs are summarised by age group in Tab. 1.
Tab. 1 - Summary of measurements from Permanent Sample Plots by age group.
| Plots | Parameter | Mean | SD | Min | 1st Quartile |
Median | 3rd Quartile |
Max |
|---|---|---|---|---|---|---|---|---|
| Young plots (Age < 40 years, n=88) |
Age | 31.2 | 6.42 | 14.0 | 28.0 | 32.0 | 37.0 | 39.0 |
| Top height (m) | 12.6 | 2.11 | 6.80 | 11.1 | 12.6 | 14.1 | 16.6 | |
| Stems ha-1 | 2059 | 1150 | 608 | 1212 | 1755 | 2606 | 6125 | |
| Basal area (m2) | 31.4 | 8.26 | 16.9 | 26.5 | 29.9 | 34.9 | 53.5 | |
| Volume (m3) | 168 | 65.2 | 45.9 | 118 | 175 | 209 | 290 | |
| Yield Class (m2 ha-1 yr-1) | 10.2 | 1.68 | 7.0 | 9.0 | 10.0 | 11.0 | 14.0 | |
| Initial Spacing (m) | 1.50 | 0.48 | 0.90 | 1.20 | 1.40 | 1.80 | 2.40 | |
| Middle-aged plots (40 ≤ Age < 70 years, n=140) |
Age | 53.1 | 7.75 | 40.0 | 46.0 | 51.0 | 60.0 | 69.0 |
| Top height (m) | 18.1 | 2.48 | 12.0 | 16.5 | 18.3 | 19.8 | 23.9 | |
| Stems ha-1 | 1196 | 792 | 792 | 561 | 934 | 1703 | 3948 | |
| Basal area (m2) | 40.1 | 9.64 | 23.7 | 32.1 | 37.75 | 49.0 | 63.9 | |
| Volume (m3) | 304 | 78.5 | 165 | 245 | 295 | 354 | 553 | |
| Yield Class (m2 ha-1 yr-1) | 9.67 | 1.66 | 4.0 | 9.0 | 10.0 | 10.0 | 14.0 | |
| Initial Spacing (m) | 1.45 | 0.47 | 0.90 | 1.20 | 1.40 | 1.80 | 2.40 | |
| Old plots (Age ≥ 70 years, n=38) |
Age | 87.37 | 11.8 | 71.0 | 79.0 | 87.0 | 94.8 | 115 |
| Top height (m) | 21.26 | 4.12 | 13.0 | 19.3 | 21.7 | 24.2 | 27.9 | |
| Stems ha-1 | 631 | 337 | 259 | 368 | 496 | 787 | 1473 | |
| Basal area (m2) | 43.9 | 13.2 | 25.1 | 32.1 | 41.0 | 55.7 | 68.4 | |
| Volume (m3) | 397 | 144 | 173 | 294 | 385 | 502 | 487 | |
| Yield Class (m2 ha-1 yr-1) | 8.0 | 2.27 | 4.0 | 8.0 | 8.0 | 9.0 | 12.0 | |
| Initial Spacing (m) | 1.02 | 0.22 | 0.90 | 0.90 | 0.90 | 0.90 | 1.40 |
These plots were planted with Scots pine between 1878 and 1965. Measurements were taken from stands ranging in age between 14 and 125 years, with at least two mensurational surveys per plot. Plots varied in their management with a variety of thinnings undertaken.
Thirteen plots were unthinned controls. Four soil types were selected on Ecological Site Classification ([42]): podzol, brown earth, sand and podzol/brown earth mixture; and 45 soil sample plots were collected as part of an earlier study ([58]). The elevation of both PSP and soil plots ranged from 3 to 364 m a.s.l., and were located between latitude 56° 63.1′ and 57° 69.3′ N and longitude 5° 19.7′ and 3° 07.0′ W.
Model efinitions
SLeDG
This version of the SLeDG model is an adaptation of the model by García et al. ([18]), which is an evolution of the model first suggested by García ([14]). This family of models uses a state-space approach to forecast the stand development based on a description of stands using four state variables: top height, number of stems per hectare, cylindrical stem volume (the product of basal area and top height), and occupancy. Occupancy is analogous to an interception efficiency: an index of the rate of gross photosynthesis versus a maximum potential rate, where a stand has enough leaves to intercept all photosynthetically available radiation (PAR - [36]).
Changes in the state variables through time are estimated by differential functions. The model variables are listed in Tab. 2. The SLeDG model was parametrised for Scots pine in three stages similar to García et al. ([18]): height (site index, SI), mortality, and basal area with occupancy. Additionally, model outputs for merchantable volume were also parametrised. The biomass expansion factors (BEF) and root:shoot ratios of Levy et al. ([29]) were used to provide standing biomass outputs based on the merchantable volume. Details of the model structure and parametrisation are available in Appendix 1.
Tab. 2 - Growth model variables and units.
| Variable | Units | Definition | Kind |
|---|---|---|---|
| H | m | Top height | State variables |
| N | stems ha-1 | Number of stems (per hectare) | |
| W | m3 ha-1 | Stem wood; product of B and H | |
| Ω | - | Occupancy | |
| H s | m | Site index | Additional variables |
| B | m2 ha-1 | Basal area | |
| R | - | Relative closure | |
| V | m3 ha-1 | Merchantable volume (stem to 7cm diam.) |
Model statistics were calculated to provide an initial benchmark of the model fits to the data. As the dataset was small the statistics were only calculated with the PSP data used in model calibration, i.e., no independent data were used. Therefore a bootstrap analysis was used to provide a validation of the model as suggested by Vanclay & Skovsgaard ([52]).
One thousand bootstraps were run for each part of the model parametrisation resulting in confidence intervals for calibrated parameters. Variance inflation factors were calculated for each part of the model to assess multicollinearity between state variables. Mean absolute difference, percent mean absolute difference, and the modelling efficiency were also calculated. Mean absolute difference is simply the average of all deviations of PSP data points from the model, which can also be expressed as a percentage. Modelling efficiency is described by Vanclay & Skovsgaard ([52]). It provides a statistic analogous to R2, whereby 1.00 represents “perfect” fit between model and measured data, and 0.00 represents a poor fit (negative values indicate very poor fit).
3PGN
The 3PGN model is described in Xenakis et al. ([59]) as a process based model structure coupling the 3PG model ([25]) with the introductory soil carbon model (ICBM - [2]).
The 3PG model can be broadly separated into three parts. The first part deals with the derivation of the primary production: gross primary production is calculated using photosynthetically available radiation (PAR). PAR is estimated as half of incoming shortwave radiation ([25]). PAR is adjusted to available photosynthetically available radiation (APAR), scaled by a function of leaf area index. Dimensionless modifiers for vapour pressure deficit, soil water, temperature and age determine the utilisable APAR. Gross primary production is calculated by multiplying the utilisable APAR by an apparent canopy quantum efficiency which is usually assigned the value of 0.03 mol C (mol photon)-1 (cf. review of published literature by [25]). Finally gross primary production is simply scaled by 0.48 ± 0.05 to give Net Primary Production.
The second part determines the partitioning of the production to above and below ground portions ([27]). The production may be allocated to either the roots, stem, or foliage of a stand. Changes in biomass of roots, stem, and foliage is therefore the balance of the production allocated to each minus root dieback, stem mortality, and litterfall. The below ground portion of carbon allocation is determined by a fertility rating (a percentage site productivity rating), water content, and stand age. The above ground allocation of carbon is divided between stem and foliage using a ratio determined by basal area.
The third part produces outputs from the model such as stand volume, stem number, and basal area which may be of use to managers. Stem number change (mortality) is estimated by a version of the -3/2 self-thinning rule ([61]) which sets maximum number of stems (Nmax) proportional to stem mass (Mmax) according to Mmax = kNmax-3/2, where k is a coefficient to be estimated. Increases in stem mass are scaled to stand volume for output using an allometric relationship.
The Introductory Soil Carbon Model (ICBM - [2]) is incorporated by including three carbon and three nitrogen pools for soil carbon. Each pool has different rates of decomposition, which may be further modulated by environmental conditions. Litterfall, root turnover and natural mortality calculated by 3PG are used as inputs to the soil carbon pools.
A previous calibration of 3PGN parameters for Scots pine ([59]) was used for this study. This used the same 51 plot dataset as the SLeDG parametrisation. The calibration was performed using an application of the Bayesian theorem with the implementation of a Monte Carlo Markov Chain. Calibration was performed for different plots and a mean parameter vector was extracted. For more details see Xenakis et al. ([59]).
The model was run for each yield class. Average climatic and site conditions for each yield class (YC) were estimated based on mean climate for each yield class and a mean soil type estimated from 45 soil samples collected by Xenakis et al. ([60]) from across Scotland. Solar radiation was estimated from temperature, humidity and site information using the algorithm given by Xenakis et al. ([59]).
Thinning in 3PGN is represented as a fraction of the biomass of foliage, wood and root of the mean tree removed in each intervention. To calculate the fractions for each yield class from the tables of Edwards & Christie ([10]), the biomass of the three structural pools before and after thinnings was calculated using the allometric equations developed by Xenakis et al. ([60]). Thus the ratio of the biomass removed from thinnings to the biomass before thinnings was estimated. The model was run with and without thinnings.
Forest Yield
ForestYield ([12]) is a computerised version of the yield tables of Edwards & Christie ([10]). It outputs top height, basal area, stem number, and volume for stands of given planting density, site quality (YC), and thinning regime. The equations used to calculate the yield tables are not utilised in ForestYield. Instead, it includes the data from the yield tables, and points in between table cells are mathematically interpolated. Stands that do not match these predetermined YCs, planting, and thinning regimes, are estimated by using the closest regime. To estimate stand whole tree biomass, ForestYield outputs were expanded with the biomass expansion factors estimates of Levy et al. ([29]) as is performed in the land use, land use change and forestry (LULUCF) reporting in the UK ([9]), and in a similar manner to the SLeDG model.
Model comparison and initiation
Such different models are not easily compared statistically. Previous model comparisons have looked at errors when models have been validated against common data ([54], [40]). However, as all available Scots pine data were utilised in parametrisation of SLeDG and 3PGN, a similar comparison was not possible.
Instead, all three models were compared by looking at how each predicts a range of productivity classes (defined by YC) over one rotation of one hundred years. These represented hypothetical stands, rather than looking at specific stands which have been measured.
In order to compare the models predictions of stands through time a standard of site quality is needed. ForestYield utilises yield class (YC) as its measure of site quality, however 3PGN and SLeDG require a conversion between their site quality measures and YC. In this study, even YCs ranging between 4 and 14 m3 ha-1 yr-1 were used. The YC is the estimated mean annual increment of a stand of trees which occurs at the intersection between the idealized curves for mean annual increment and current annual increment plotted against stand age ([10]).
In the SLeDG model, SI is used as a measure of site quality. The relationship between YC and SI is given as (eqn. 1):
with a reference age of 50, α1 = -5.507 and α2 = 0.867 (RMSE = 0.428, R2 = 0.981) for Scots pine ([11]).
In 3PGN site quality is represented by the fertility rating. The link between 3PG and ICBM which calculated the fertility rating parameter from ICBM’s output was removed and so fertility rating was re-introduced as a parameter ([33]).
The model was run using the parameter set of Xenakis et al. ([59] - fit to the same 51 PSPs) for each soil type. The fertility rating parameter was calibrated manually to achieve the closest fit of predicted against observed diameter at breast-height (dbh). The calibrated values of fertility rating were assigned to the different yield classes based on mean YC for a given soil type. For two YC (8 & 10) values for fertility rating were interpolated between the fitted fertility rating due to lack of stand data.
The predictions were initiated as follows: initial planting density was fixed at 2500 stems ha-1; a previous average for Scots pine planting in the UK (Forestry Commission, pers. comm.) and previously used in 3PGN forecasts by Xenakis ([58]). It should be noted however that current grant applications for Scots pine forest establishment requires a density of 3000 stems ha-1 at establishment ([46]). Assuming a constant initial planting density across modelling platforms provides a common starting point for forecasting hypothetical stand growth. Even YCs ranging between 4 and 14 m3 ha-1 yr-1 were forecast with each model.
Differences in outputs of top height, basal area, stem numbers, volume, and whole tree biomass were compared graphically over the range of productivity commonly seen in the UK. Similarities and differences in how the models forecast growth were considered and potential causes discussed. Additionally the requirements of the models in order that they may be run were compared, what parameters and variables are required in order to run a simulation of a stand, and how that relates to model purpose and utility.
Results
SLeDG
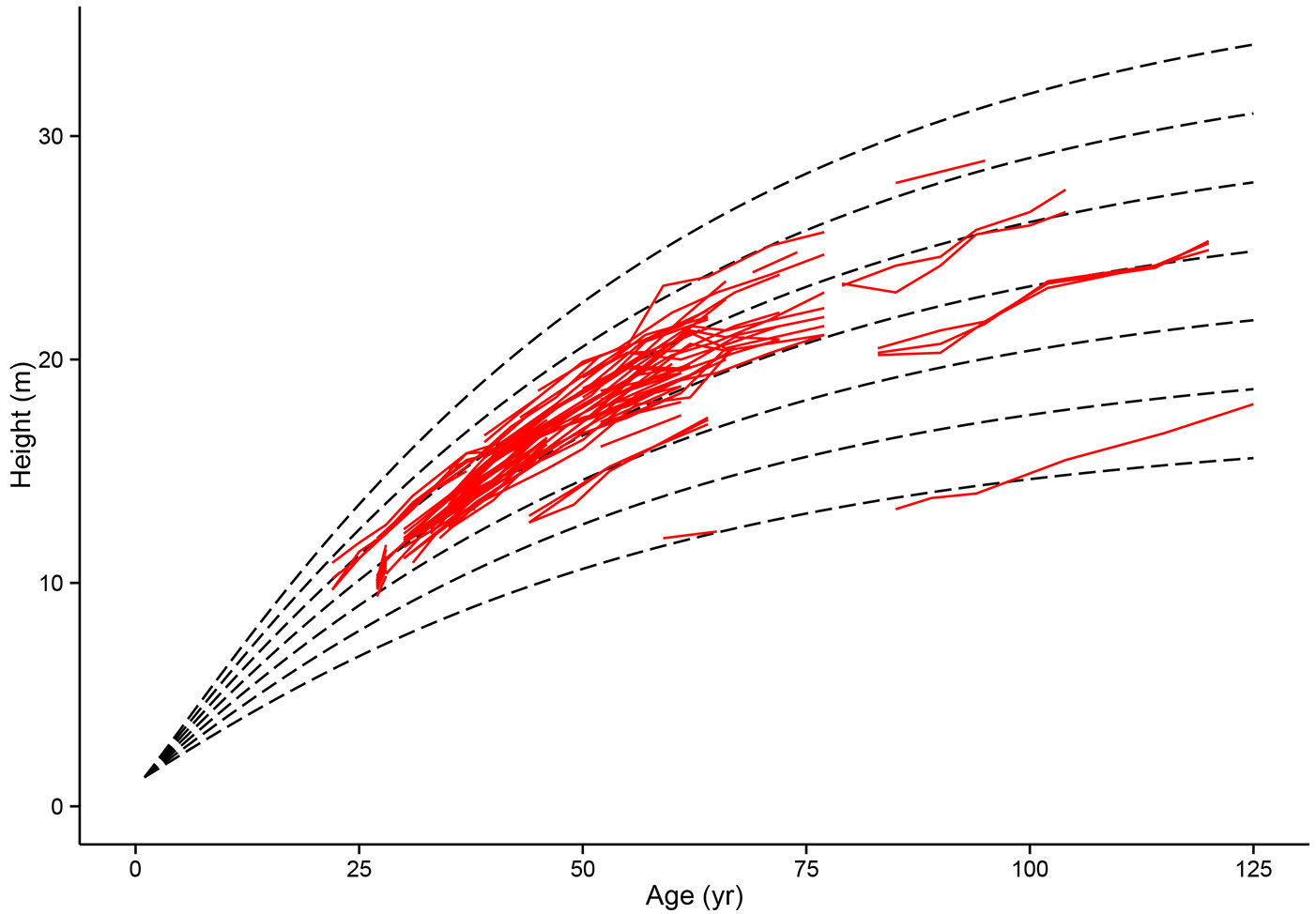
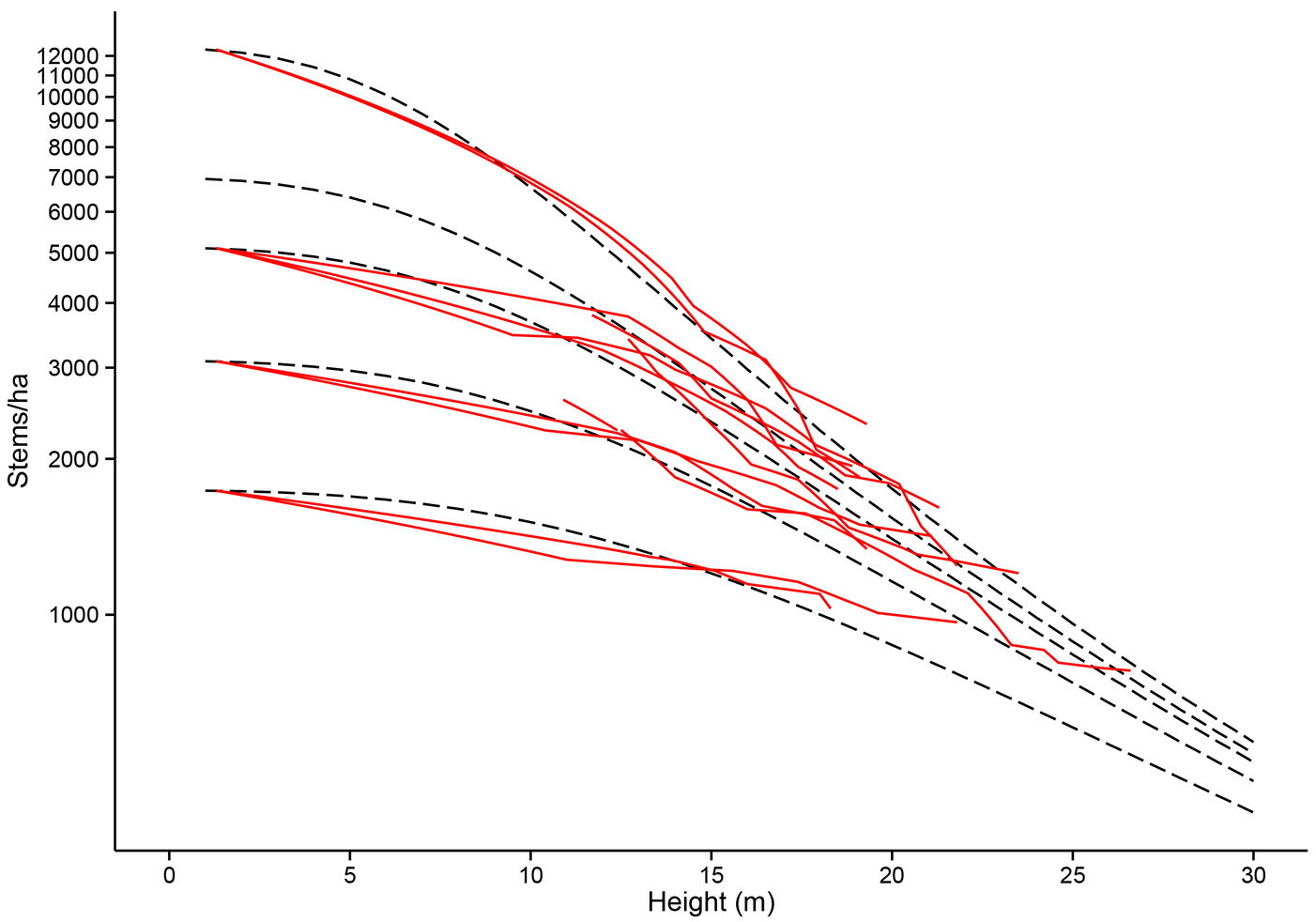
The fitted parameters, their error, and bootstrap derived confidence intervals for the height-age and mortality sub-models are given in Tab. 3. The fit of these sub-models to the PSP data is shown in Fig. 1 and Fig. 2.
Tab. 3 - Stand Level Dynamic Growth (SLeDG) model parameter estimates, errors, and confidence intervals calculated from bootstrap analysis for Scots pine. (†): indicates fixed parameters (that were not adjusted in parametrisation).
| Parameter | Value | Standard Error |
95% Confidence Interval |
Definition |
|---|---|---|---|---|
| b 1 | q | - | - | Height parameters |
| b 2 | 0.0200 | 1.31 × 10-3 | 0.0121 - 0.0227 | |
| b 3 | 0.859 | 2.98 × 10-2 | 0.804 - 0.901 | |
| q | - | - | - | Site quality measure |
| b 4 | 7.57 × 10-7 | 4.61 × 10-7 | -1.43 - 1.46 | Mortality parameters |
| b 5 | 1.83 | 0.32 | 0.151 - 2.36 | |
| b 6 | 1.86 | 0.17 | 1.13 - 2.34 | |
| b 7 | 0.249 | 0.464 | 0.142 - 0.274 | Gross increment parameters |
| b 8 | 1.04 | 0.72 | 0.965 - 1.24 | |
| b 9 | 0.4† | - | - | |
| k | b 9 | - | - | Relative size mortality parameter |
| b 10 | 2.4† | - | - | Occupancy exponent |
| b 11 | 0.105 | 0.368 | -2.79 - 0.943 | Occupancy scalar |
| b 12 | 2.778× 104† | - | - | Planting density for full closure at planting |
| β v | 0.394 | 2.84 × 10-3 | - | Merchantable volume scalar |
| c v | 11.0 | 1.94 | - | Merchantable volume intercept7 |
Fig. 1 - Model-data comparison of top height growth in Scots pine permanent sample plots. Modelled top height growth (dashed lines) for even site indices 10-22 (age 50) based on Scots pine PSP (permanent sample plot) data.
Fig. 2 - Model-data comparison of mortality in Scots pine permanent sample plots. Mortality of stands as top height increases for different initial planting densities. PSP (permanent sample plot) data is shown with the fitted model (dashed lines).
In the parametrisation for basal area and occupancy, the values for loblolly pine relating to occupancy and relative size of mortality loss (b9 = 0.4, b10 = 2.4, b12 = 2.778 × 104 - [18]) performed well due to the similarities in shade tolerance and thus self thinning between the pine species. Therefore, values for b9, b10 and b12 were fixed in the parametrisations, as preliminary investigations showed no statistical improvement when these parameters were allowed to vary. These fixed values and the other estimated values for all parameters relating to basal area and occupancy are given in Tab. 3. The errors are estimated from the Hessian calculated in the parametrisation, and confidence intervals are based on the bootstrap analysis.
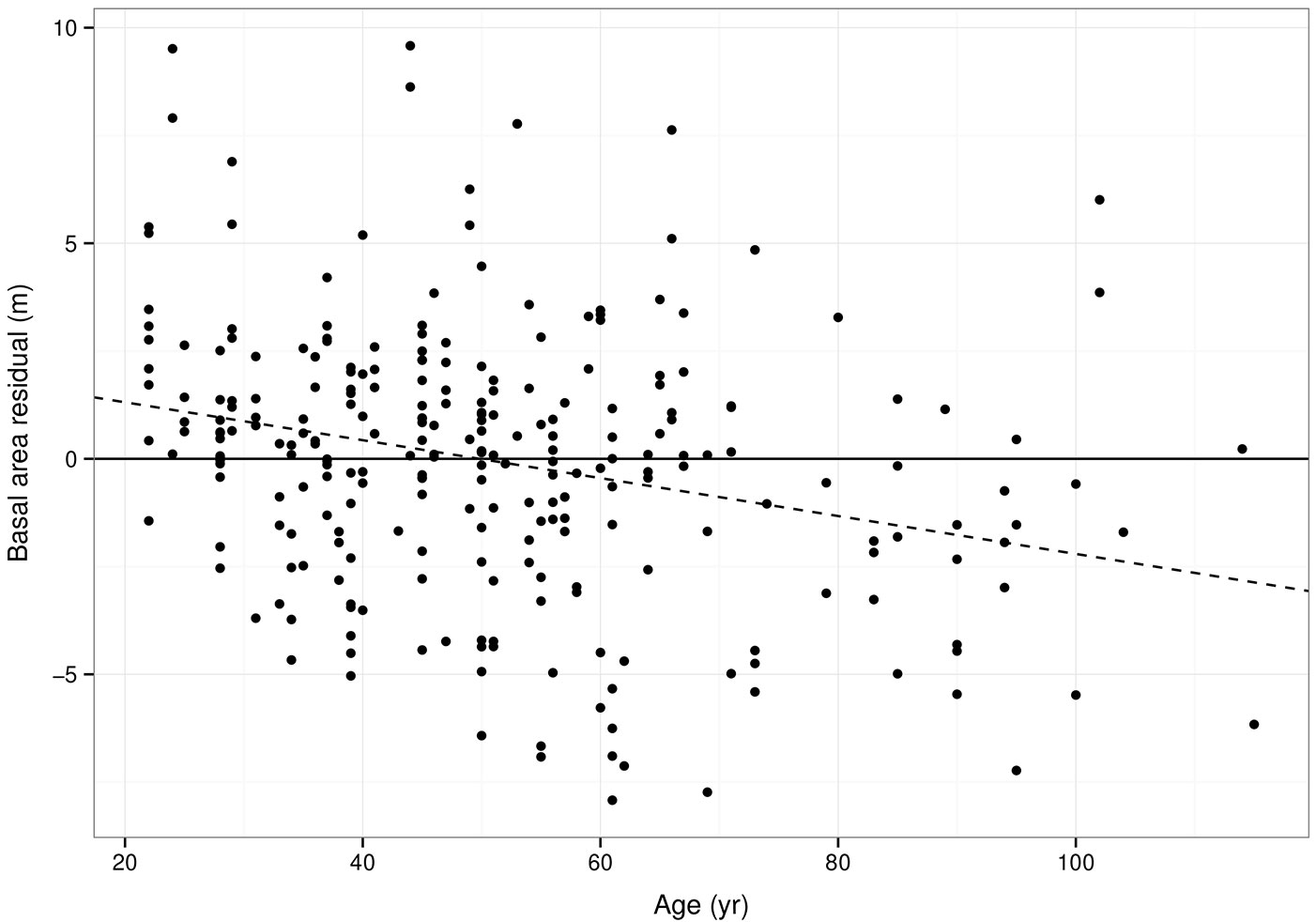
The errors in the predicted value of basal area (B) over the range of ages are given in Fig. 3. The linear model fitted to the errors has a slope significantly different to zero (P = 2.13 × 10-4), indicating consistent overestimation in the first 50 years and underestimation in years after.
Fig. 3 - Error in basal area predictions using estimated parameters. Dashed line indicates a linear model fitted to the residuals.
The estimates of the coefficients from a linear regression of merchantable volume (V) on the product of basal area and top height (W) on aggregated data from the tree pulling database were βv = 0.394 and cv = 11.01. The regression had a R2 value of 0.978.
The model for projecting forest stands can be summarised by the following equations (eqn. 2, eqn. 3, eqn. 4, and eqn. 5):
where H, N, W, and Ω are top height, number of stems per hectare, product of basal area and top height, and occupancy respectively. The local productivity is defined by the parameter q. The latter three equations may be multiplied by the first equation to express the variability in N, Ω, and W in terms of dt instead of dH, and eqn. 3 may be substituted into eqn. 5 for a more standard form.
All variance inflation factors in the model were less than 5 with the exception of top height in the stem wood accumulation function (eqn. 5) which was had a value of 7.40. This value is still below the threshold value of 10 suggested as a sign of high collinearity by Kutner et al. ([24]). The statistics of model fit for SLeDG are given in Tab. 4 for H, N, and B. Overall there is high modelling efficiency for all three variables, indicating a good agreement between observed and estimated values. Although the lowest modelling efficiency is seen in B, it has a lower percentage mean absolute difference than N. Predictions of H show the best agreement between observed and estimated values, with high modelling efficiency and the smallest percentage mean absolute difference.
Tab. 4 - Statistical measures of model fit in calibration against Permanent Sample Plot (PSP) data.
| Variable | Top Height (m) |
Stems (ha-1) |
Basal area (m2 ha-1) |
|---|---|---|---|
| Mean absolute difference | 0.3521 | 130.1 | 2.551 |
| % Mean absolute difference | 2.128 | 11.83 | 7.317 |
| Modelling efficiency | 0.9875 | 0.9334 | 0.9092 |
3PGN Calibration
All of the parameters but one used in this instance for 3PGN can be found in the calibration for Scots pine by Xenakis et al. ([59]) and Xenakis ([58]). The only difference here is in the values of fertility rating. The range of fertility rating for given YC (and associated soil type) is given in Tab. 5. The proportion of explained variance by the regression of measured versus predicted dbh was always greater than 0.7 for all YC which had representative plots.
Tab. 5 - Fertility rating values (percentage site productivity rating) for given soils and associated yield class (YC) based on regression between modelled and observed diameter at breast-height (dbh). (‡): interpolated values.
| Soil type | YC | Fertility rating |
Adjusted R2 |
|---|---|---|---|
| Podzol | 4 | 0.100 | 0.898 |
| Regosol | 6 | 0.265 | 0.747 |
| Gley | 8 | 0.300‡ | - |
| Humicgley | 10 | 0.335‡ | - |
| Podzol/Brownearth | 12 | 0.370 | 0.928 |
| Brownearth | 14 | 0.550 | 0.971 |
Model predictions
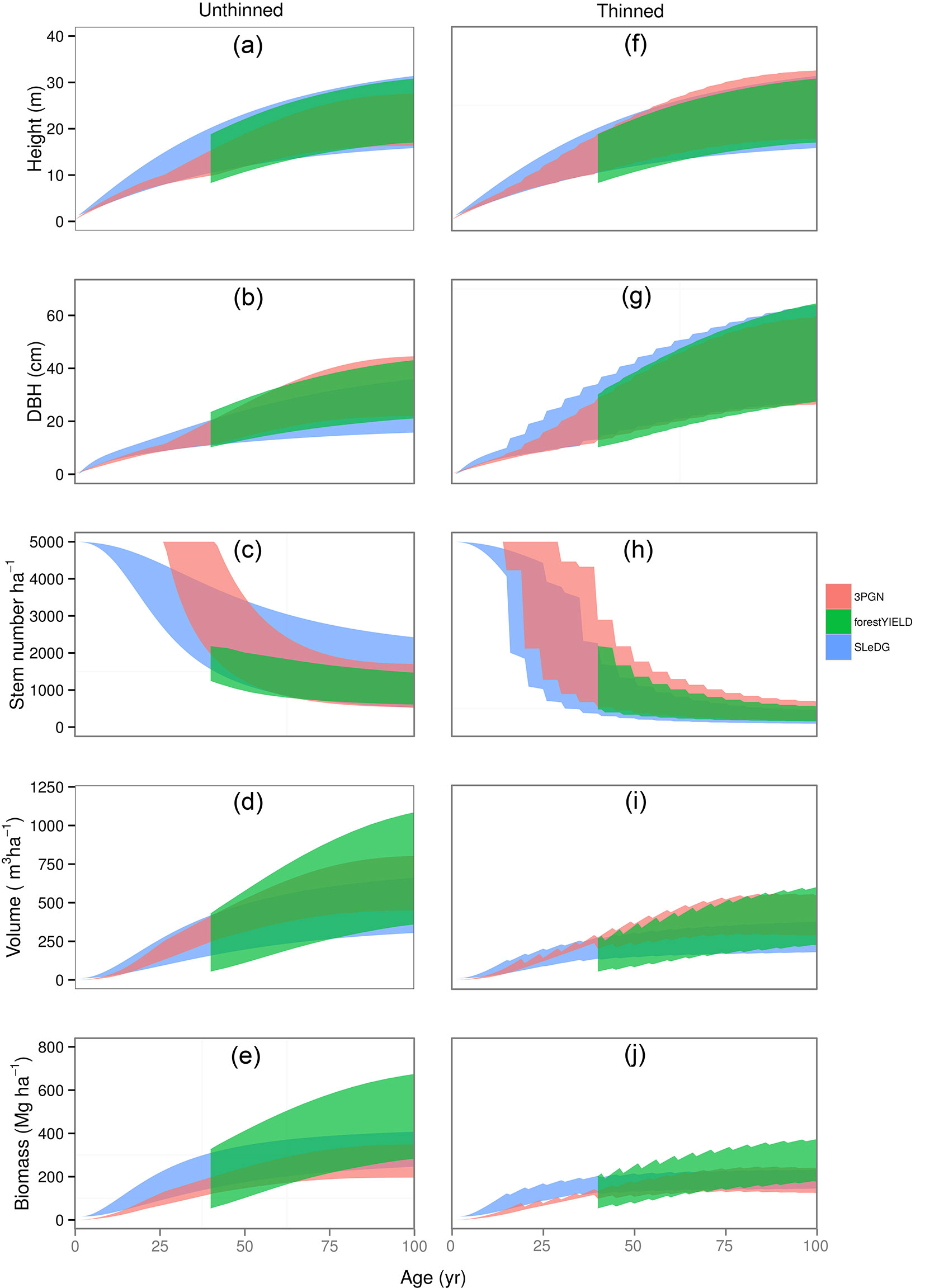
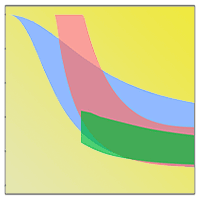
The variable output for unthinned and thinned stands for all three models can be seen in Fig. 4. The range of productivity between YC 4-14 is represented for each model by a different coloured ribbon. As ForestYield predictions only begin at age 40 for YC 4 stands, the ribbon representing ForestYield was truncated. Height and average dbh show similar trajectories over the range of productivities for all three models, in both thinned and unthinned stands.
Fig. 4 - Plots of SLeDG, 3PGN, and ForestYield thinned and unthinned stand predictions through time. Ribbons indicate range of productivity equivalent to YC 4 to 14. DBH denotes diameter at breast-height.
There was no early mortality predicted by 3PGN until the age of 25 years or even later in less productive stands. As previously noted, ForestYield does not produce any mortality predictions before 40 years in YC 4. ForestYield does produce mortality predictions for higher productivity stands younger than 40 years, though the earliest mortality is predicted at 25 years in YC 14 ([10]). Only SLeDG was able to predict early stand mortality (Fig. 4c, Fig. 4h). In the unthinned stand simulation, 3PGN and ForestYield show reasonable agreement, with less than 1000 stems difference between most and least productive stands. The SLeDG model predicts a much wider difference in stem numbers between most and least productive YCs. When the thinned stands are simulated, there is better agreement between models (Fig. 4h).
Although 3PGN predicts on average a greater volume than SLeDG over the period of an unthinned rotation (Fig. 4d), it also predicts the lowest biomass of the three models, with the exception of the lowest productivity stands predicted by ForestYield (Fig. 4e). Although 3PGN predicts much higher volume growth than SLeDG for thinned stands, its biomass prediction follows a different trajectory, with either lower or comparable biomass relative to SLeDG. ForestYield shows the largest difference between highest and lowest YC in its prediction of volume and biomass. It also predicts a much greater volume and biomass in higher yield class stands than both SLeDG and 3PGN.
Discussion and conclusions
SLeDG
The SLeDG model as summarised by eqn. 2-5 provides an alternative method for yield prediction in British stands of Scots pine. Although parametrised with a small dataset, the model provides reasonable forecasts of Scots pine growth throughout the range of productivity observed in the UK.
Simultaneous parameter estimation has previously been identified as the best way to minimize model errors ([48], [52]). The three stage fitting of SLeDG could therefore introduce additional error compared to a simultaneous fitting operation. However, it could equally be stated that the co-variation of model parameters can often make it difficult to identify the true optimum parameter configuration.
The site index model selected in the parametrisation produces an anamorphic set of curves (Fig. 1). While anamorphic height growth curves have been criticized in the past for their single point productivity classification ([62]), the selection versus alternative curve forms in the parametrisation indicates that this simple function is sufficient. Anamorphic curves have also been shown to be useful for UK Sitka spruce stands ([44]).
The mortality section of the SLeDG model (Fig. 2) is an example of a self-thinning “law”, as explained by García ([16]). Thus, like other self-thinning laws such as the -3/2 law used in 3PGN, there is a maximum stem number for a stand of a given height or mass. However, unlike the -3/2 law the SLeDG mortality parametrization provides a species specific mortality law. This is of benefit as previous studies have shown that the -3/2 exponent is inadequate in representing species specific shade tolerances ([56], [55], [3]). In this parametrization of SLeDG the trajectory of mortality for most stands is not dependent on this self-thinning line until greater heights are reached. This can be seen in Fig. 2 as the point when the models mortality projections come close together past stand heights of 20 m.
Occupancy is an implicit (or latent) variable in this model as in previous parametrisations of SLeDG for other species ([18]). As such the values predicted by the model cannot be benchmarked against empirical data. Despite the fact that it is not a direct physical measure, occupancy is useful to provide a physiological limitation on stand productivity, similar to the PAR modulation by LAI in 3PGN, taking into account reductions in productivity at initial planting or following thinnings. In the future, it may be possible to estimate occupancy based on relative stand closure using Light Detection and Ranging (LiDAR) measurements. Alternatively, a method similar to that of Duursma et al. ([8]) for estimating light use efficiency in woody plants may be scaled from individual plants to stand scale using LiDAR measurements to estimate occupancy directly.
Although the linear model fitted to the basal area residuals indicates a consistent bias which is a function of stand age, the linear model is likely to be affected by the few oldest plots (> 70 years) in the dataset. The older plot measurements in the PSP dataset tend to be less productive plots (Tab. 1), with more productive plots having been harvested. Thus the dataset is not representative of all productivity classes over the range of ages. As lower productivity stands are expected to have lower basal area in earlier stages of growth, this trend is likely to continue in later stages of the model, hence the potential for underestimation of basal area in older stands. Ideally PSP data from more productive, older stands would be included in a future parametrisation to remedy this.
The statistical tests to benchmark SLeDG (Tab. 4) reveal an excellent fit between the data and the model that has been fit to the data. A modelling efficiency so close to 1.0 is consistent with a graphical assessment of the model as can be seen in Fig. 1 and Fig. 2, where the model follows closely the measured values. Ideally independent data would have been used in a benchmark analysis. However, because of the small size of the PSP dataset, the decision was made to use all data in parametrisation. Bootstrap simulations are suggested as an alternative to independent validation in cases of data scarcity ([52]). Results of the bootstrap analysis were consistent with the parameter estimates when the whole dataset was used (Tab. 3). The parameter estimates for b7 and b8 do not sit in the middle of the bootstrap confidence intervals, which could be a result of bias in sampling of the bootstrap. Non-overlapping time intervals used in the parametrisation are assumed independent. However, plots with more measurements are more likely to be sampled repeatedly in the bootstrap which uses sampling with replacement.
Further improvements to SLeDG may include modulating the site index part of the model by a climate index (similar to the climate variables used in 3PGN) to allow for predictions in a changing climate. Equally, a soil model may be integrated with the model as in 3PGN with a variable similar to fertility rating modulating the site index, and the occupancy providing values for fine root turnover and litter production. With this a measure of soil carbon accumulation may be obtainable.
Model comparison
Despite their differences in structure, the three models show reasonable agreement in variables and outputs over the years predicted. This is especially true in the thinned stand projections. The main differences occurred in the predicted volume and biomass forecasts. The higher biomass estimates of SLeDG compared to 3PGN in unthinned stands (Fig. 4e) may be similar to overestimates of biomass seen when using BEF based on only one variable ([28]), as the BEF is only based on top height ([29]).
Additionally, this discrepancy may be explained by the underestimation in biomass previously observed when using 3PGN to estimate Scots pine growth, due to an underestimated foliage biomass pool ([59]). As before, the cause of the underestimate of 3PGN may be better understood given a more complete dataset with foliage and root carbon storage in chronosequences. Regardless of the cause, both models forecast a smaller range of volumes and biomass than ForestYield. It is possible that the lower variation in stem numbers observed in ForestYield (Fig. 4c, Fig. 4h) does not represent the variation one might expect between very high and low productivity sites. If lower fertility sites had a higher stem number for a given height, the range in stand volume may be reduced to a range similar to that observed in the other two models.
In thinned stands, SLeDG and 3PGN arrive at a similar biomass estimate across the range of YC, despite an earlier biomass accumulation predicted by SLeDG. However, SLeDG still predicts lower volumes in thinned stands. This may also be a symptom of the low number of older high productivity stands in the PSP dataset.
Alternative models for producing biomass outputs could be considered to estimate biomass both from SLeDG or ForestYield yield estimates instead of simple BEFs. EFISCEN ([37]) and CBM-CFS3 ([23]) are two models for estimating forest carbon driven by yield outputs that could potentially utilise the yield predictions of either SLeDG or ForestYield.
Despite the limited PSP data available for Scots pine in the UK the benefit of using the SLeDG approach is that it still provides a reasonable forecast of stand growth across a range of sites. There is a reduction in time and effort required to parametrise SLeDG versus 3PGN, which requires 50 parameters to be estimated ([59]) compared to the 13 in this parametrisation of SLeDG. Additionally, climatic variables including maximum and minimum monthly temperatures and precipitation may not be easily obtained, being dependent on the nearest weather station. However, improved data availability reduces this advantage of SLeDG over 3PGN. With increasing data availability from remote sensing sources, which may easily be utilised by 3PGN in a similar way to 3PGS ([7], [6]), the potential for using 3PGN in UK forests can only increase. Indeed, the potential of 3PGN is that it may utilise a wider range of data for calibration should it become available: as well as forest growth variables, carbon fluxes measured by eddy covariance may be utilised by 3PGN for calibration and validation ([33]).
In this model comparison, we provide no indication of the uncertainty in model predictions. Both SLeDG and 3PGN provide parameter error values, allowing for error in variables and output to be propagated to the state variables. ForestYield does not provide any uncertainty in its parameters, and the yield tables that it is based on also provide no error values ([10]). In financial terms, a measure of uncertainty is highly desirable for estimating optimum harvest ([30]). Equally for carbon storage, a measure of uncertainty is important for both policy makers and managers, with uncertainty in parameters identifying parts of models requiring further attention ([47]). Indeed, quantification of uncertainties features heavily in the guide for LULUCF reporting ([21]).
Bayesian approaches to forest model calibration such as those of Van Oijen et al. ([51]), Patenaude et al. ([39]), and Xenakis et al. ([59]) are one approach which could lead to better understanding of model uncertainty, and future work on models for stand level development should consider this as an option. More generally, greater transparency in the relationships, assumptions and limitations of empirical yield models used for timber estimation and as drivers for other models (e.g., carbon reporting - [32]), and wind risk estimation ([20]) can lead to wider utility and application.
While this paper has concentrated on Scots pine in particular, the calibration of both SLeDG and 3PGN to other species both in the UK and beyond is possible. Both models are aimed at forecasting even-age monocultures, limiting their use in more complex forest stand structures. As a counterpoint both models forecast stands based on the current state of the system without requiring historical measurements to estimate productivity, particularly useful in countries where details of forest establishment are not widely known. With hybrid models it is possible to allow for a greater range of forest management strategies than static tables. Forecasts can be based on the current state of a forest stand, rather than fitting a given stand to a predetermined growth trajectory. Thus, improved estimates of forest stand-level metrics in the UK should allow for flexibility in predictions following any alterations in forest management; the ability to utilise as much data as possible whilst being robust enough to be able to run efficiently with minimal data available; and also be fully documented in order that various sources of error may be accounted for. None of the models considered here reach such lofty goals. However, it seems of benefit to move towards dynamic models of forest growth for carbon stock estimation. With current data availability a dynamic model such as SLeDG can account for changes in forest management. Replacing the static yield table approach currently used in C-FLOW with growth predictions from a dynamic statistical model could provide growth estimates for forest management in cases where management has deviated from the traditional schemes included in the tables of Edwards & Christie ([10]). In addition it is then possible to run model based scenarios of alternative management approaches to inform management. In the future, when data from multiple sources (for example remote sensing, and sensor networks) become more available, models such as 3PGN may become more appropriate, providing both forecasts and insight into the underlying processes driving changes in forest growth. Indeed, it may be most appropriate to consider the use of both SLeDG and 3PGN in concert to provide forest growth forecasts in the future. Such an approach allows the ensemble of models to continue to benchmark check each other, whilst providing more information about the uncertainty of predictions.
Acknowledgements
We wish to thank the Forest Research Forest Mensuration, Modelling and Forecasting Group for the provision of ForestYield predictions and provision of PSP data. This work was funded by the UK National Environmental Research Council and Forestry Commission UK.
References
CrossRef | Gscholar
CrossRef | Gscholar
Online | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Online | Gscholar
Online | Gscholar
Gscholar
CrossRef | Gscholar
Online | Gscholar
Gscholar
Gscholar
Gscholar
Supplementary Material
Authors’ Info
Authors’ Affiliation
School of Geosciences, University of Edinburgh, Edinburgh EH9 3JN (UK)
ICREA at CREAF, Cerdanyola del Valles, Barcelona (Spain)
Corresponding author
Paper Info
Citation
Lonsdale J, Xenakis G, Mencuccini M, Perks M (2015). A comparison of models for quantifying growth and standing carbon in UK Scots pine forests. iForest 8: 596-605. - doi: 10.3832/ifor1403-008
Academic Editor
Emanuele Lingua
Paper history
Received: Jul 21, 2014
Accepted: Jan 09, 2015
First online: Feb 02, 2015
Publication Date: Oct 01, 2015
Publication Time: 0.80 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2015
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 56598
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 46474
Abstract Page Views: 3510
PDF Downloads: 5314
Citation/Reference Downloads: 41
XML Downloads: 1259
Web Metrics
Days since publication: 4027
Overall contacts: 56598
Avg. contacts per week: 98.38
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2015): 8
Average cites per year: 0.73
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Modelling the carbon budget of intensive forest monitoring sites in Germany using the simulation model BIOME-BGC
vol. 2, pp. 7-10 (online: 21 January 2009)
Research Articles
Local ecological niche modelling to provide suitability maps for 27 forest tree species in edge conditions
vol. 13, pp. 230-237 (online: 19 June 2020)
Research Articles
Distribution factors of the epiphytic lichen Lobaria pulmonaria (L.) Hoffm. at local and regional spatial scales in the Caucasus: combining species distribution modelling and ecological niche theory
vol. 17, pp. 120-131 (online: 30 April 2024)
Research Articles
Spatio-temporal modelling of forest monitoring data: modelling German tree defoliation data collected between 1989 and 2015 for trend estimation and survey grid examination using GAMMs
vol. 12, pp. 338-348 (online: 05 July 2019)
Short Communications
Dynamic modelling of target loads of acidifying deposition for forest ecosystems in Flanders (Belgium)
vol. 2, pp. 30-33 (online: 21 January 2009)
Research Articles
Incorporating management history into forest growth modelling
vol. 4, pp. 212-217 (online: 03 November 2011)
Research Articles
Heuristic forest planning model for optimizing timber production and carbon sequestration in teak plantations
vol. 10, pp. 430-439 (online: 24 March 2017)
Research Articles
Comparison of drought stress indices in beech forests: a modelling study
vol. 9, pp. 635-642 (online: 06 May 2016)
Research Articles
Yield of forests in Ankara Regional Directory of Forestry in Turkey: comparison of regression and artificial neural network models based on statistical and biological behaviors
vol. 16, pp. 30-37 (online: 22 January 2023)
Research Articles
Properties and prediction accuracy of a sigmoid function of time-determinate growth
vol. 8, pp. 631-637 (online: 13 January 2015)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword