Heuristic forest planning model for optimizing timber production and carbon sequestration in teak plantations
iForest - Biogeosciences and Forestry, Volume 10, Issue 2, Pages 430-439 (2017)
doi: https://doi.org/10.3832/ifor1733-009
Published: Mar 24, 2017 - Copyright © 2017 SISEF
Research Articles
Abstract
We developed a forest planning model integrating two operational scales (single-stand and forest levels) for the optimization of timber production and carbon sequestration in forest teak (Tectona grandis L. f.) plantations. At the stand level, growth and yield simulations using a heuristic thinning optimizer provided a set of near-optimal thinning regimes for individual stands differing on initial spacing and site quality, given biological, silvicultural, and financial constraints. The set of near-optimal thinning regimes obtained were then used as input of the forest-level model, which generated optimal harvest plans for the whole plantation by simultaneously maximizing the net present value of merchantable wood and carbon sequestration. The net amount of carbon captured by the biomass and the emissions produced by decomposition of woody debris and timber products after harvest were estimated. The growth and yield model was based on a system of differential equations incorporating heuristics (genetic algorithms) to optimize age and intensity of thinnings. The full model can handle the optimization of harvest schedules for projects up to 10.000 ha and 200 stands and was tested on a validation dataset including teak plantations from Venezuela and other Latin American countries. Results indicated that regimes favoring carbon sequestration reduce the benefits of timber production, and equal profitability of carbon sequestration and timber production was obtained for carbon prices over 40 $US Gg-1. Sensitivity analysis showed that the proposed model is sensible to variation in growth rates, carbon and timber prices, and production quotas, and barely sensible to harvest and transport costs. The developed model has a modular structure that allows its calibration to incorporate data from a wide range of management regimes for teak and other forest species.
Keywords
Forest Planning, Harvest Scheduling, Optimization, Heuristics, Carbon Sequestration, Tectona grandis
Introduction
Teak (Tectona grandis L. f.) is a tropical species with high commercial value due to its quality, appearance, durability, resistance to fungus attack and insects. Because of its excellent characteristics and the wide range of uses, it is regarded as a valuable wood all over the world ([17]). Until recent times, the main sources of teak timber were the old-growth tropical forests of Southeast Asia; however, overexploitation led to exhaustion, and all producer countries (except Myanmar) banned teak logging. Yet, the demand for teak timber is currently increasing, driven by India and China markets. This has led to the development of many teak plantation projects in Asia, Africa, and Latin America ([26]). By 2010, Latin America had almost 250000 ha of teak, 80% of them less than 20 years-old.
Despite its long history as a planted species, reliable information regarding growth and productivity of teak is lacking, and gaps still exist regarding short rotations, growth dynamics and thinning regimes ([17], [33]). Most research has focused on the optimization of single stand management schedules based on field trials and permanent plots. More recently, growth and yield simulation models were developed to assess the effect of various management options in teak by integrating data from several studies ([5], [21], [41], [23]). Nonetheless, forest planning aimed at optimizing management for timber production and carbon sequestration in multiple stands of teak plantations has not been published yet. Forest planning consists in the selection of the best management option to achieve one or several objectives, including biological, ecological, economic, social, and environmental variables. Several techniques are used to develop optimization models and find efficient solutions to forest planning problems, like mathematical programming (e.g., Linear, Integer, Goal, and Dynamic programming). The large number of variables and constraints involved, the existence of non-linear relationships between variables, and the need to simultaneously optimize for different objectives often make the optimization of models an arduous task. In this case, heuristic techniques can be applied as they can handle the model complexity more efficiently ([6], [37], [29]). Among these techniques, Simulated Annealing, Genetic Algorithms, Tabu Search, Threshold Accepting, and Ant Colony Algorithms were successfully applied in forest planning ([37], [29], [43], [44], [40]).
Different algorithms use different strategies for seeking the optimal solution through the solution space and various criteria allow to evaluate the quality of the solutions obtained. The maximization of profitability and monetary benefits is usually the optimal solution in industrial forest plantations. However, optimizing for carbon sequestration has lately become a major goal of many forest planning models, due to the significant role of forests in the reduction of atmospheric CO2 and climate change mitigation. The adoption of the Kyoto protocol and the creation of carbon markets stimulated the scientific community to focus on the assessment of the CO2 amount stored by forest ecosystems, thus bringing this issue to the attention of forest managers. Indeed, carbon uptake is currently considered a new goal of silvicultural management ([35]).
Many forest planning models that incorporate carbon sequestration as optimization criteria have been reported in the literature ([19], [15], [2], [14], [36], [25], [3], [8], [42], [9]). In addition, several models quantifying carbon stored in teak trees have been developed ([12], [27], [18]). However, to our best knowledge, no models have been developed for optimizing timber production and carbon sequestration in teak plantations.
The aim of this work was to optimize management plans of multiple-stand teak plantations by developing a heuristic model which simultaneously maximizes financial benefits from timber production and carbon sequestration.
Material and methods
Model structure
The model simulates a teak plantation project comprising many stands differing in age, site quality, and initial spacing. Time of thinning and final harvest for each stand depend on the trade-off between wood production and carbon storage to maximize financial benefits for the project over a planning period of 40 years. Two optimization models working at different planning levels were developed. The first one (sub-model 1) operates at the stand level, and provides a set of “best thinning schedules” for each stand, assuming a fixed final harvest after 30 years. The second model (sub-model 2) operates at the forest level, by choosing for each stand the “best schedules” that maximize financial gains for the whole project, taking into account both carbon and timber goals subject to various constraints. Although the rotation age initially assigned to all stand is 30 years, the forest-level sub-model can modify the optimal harvest age of each stand (i.e., stands could be clear-cut before or after age 30). Single-stand development is simulated by using a yield and growth model, while a second module calculates the carbon budget, comprising storage and emissions (Fig. 1).
Stand-level optimizer (sub-model 1)
Sub-model 1 generates a set of thinning regimes for each stand with different initial spacing and site quality, and selects a subset of eight “best” thinning schedules, including the “no thinning” option. The objective function maximizes the financial gain, considering at the same time the merchantable timber production and the carbon sequestration in terms of Net Present Value (NPV, in US$). For each stand, several simulations are done taking into account the desired number of thinnings. The best schedules for each stand are the inputs for sub-model 2.
Forest-level optimizer (sub-model 2)
Sub-model 2 searches for the optimum harvest schedule (Maximum NPV) for the entire plantation, indicating which stands to thin or harvest each year, and considering both timber production and carbon sequestration. The objective function takes into account the incomes from timber and carbon capture, the cost of planting, maintenance, and transport of timber products. Constraints include a yearly timber production goal varying from year to year. In order to consider the additional costs due to spreading of harvest activities (moving personnel and machinery across the planted area), a spatial index seeks for minimizing the displacement of equipment within the plantation, and assumes no spatial adjacency constraints.
Growth and yield model
A whole-stand growth and yield model based on differential equations simulates the stand production by projecting stand variables such as basal area, stand density, average diameter, height, and volume for various combinations of site quality, initial spacing, and thinning regime. Basal area growth is calculated as (eqn. 1):
where Gt is the stand basal area at time t (m² ha-1), Gp is the maximum basal area supported by a given site (m² ha-1), to is the initial time for running the simulations (yrs), k and m are parameters related to growth rate and scale.
Simulation data set
Top height growth was derived from a site index (base age 16) family of anamorphic curves derived from the Schumacher-Hall model ([22]). Stand density was modeled using a simple negative exponential model to account for density-dependent mortality, and a random function that depends on stand age to describe density independent mortality ([23]). Quadratic diameter growth is an output from basal area and stand density.
Model parameters were estimated based on a data set from trials and permanent/ temporal plots in plantations ranging from 2 to 32-yrs-old and located in the Western Plains of Venezuela (Tab. S1 and Tab. S2 in Supplementary material). Trials and plots were established on adequate climatic conditions for teak, i.e., precipitation 1500-2000 mm, a dry season of three to four months, average temperature of 26-28 °C; soil of alluvial origin (entisols, inceptisols, alfisols, and entisols), where the physiographic position determines soil physical and chemical properties and drainage. Plantations were different in soil quality, as reflected by the site index equations and management (initial spacing and thinning schedules). Over (Vob) and under bark (Vub) total volumes were estimated for standing trees according to Moret et al. ([30] - eqn. 2, eqn. 3)
where d is diameter at breast height (cm) and h is the total height (m).
Carbon balance
For each year of the planning horizon, the net carbon balance (i.e., storage minus emissions) for each stand was calculated based on the amount of carbon stored in aboveground and belowground biomass. Carbon emissions during the rotation period included the decomposition of carbon stored in woody and foliage debris remaining in the stand after thinning or harvest, as well as the emissions from decomposition of merchantable products after harvest and processing. The model does not explicitly describe the carbon stored or released from the soil, emissions from harvest operations, products transport (i.e., carbon emitted by trucks and machinery), product recycling, or effects of substituting fossil fuels by wood. Similar approaches were used in other forest planning works ([14], [3]).
Carbon storage from the biomass
To estimate the stem biomass, the outputs of the growth and yield model were taken as inputs for the sub-model 2. Woody biomass dry weight was assessed from stem timber volume based on the basic density of teak wood (0.54 Mg m-3 - [34]). Further, a biomass expansion factor (1.33) was used to estimate the total aboveground biomass (leaves, branches, and stem) as a function of the stem biomass ([27]). Dry belowground biomass (roots and fine roots) was derived from the aboveground biomass using a shoot-root ratio of 0.16 ([20]); finally, the carbon content was estimated as a fraction (0.495) of the total dry biomass (see Tab. S3 in Supplementary material).
Carbon emissions
The estimation of carbon emissions from the decomposition of harvest residues (such as roots, branches, stumps, and dead wood) was included in sub-model 2. The rates of carbon emissions generated by the forest products after harvesting or thinning were projected according to product classes: (i) long (i.e. large solid wood products), (ii) medium, and (iii) short duration. According to Hoen & Solberg ([19]), carbon emission processes were simulated by considering future carbon emissions as a function of decomposition rates and the organic lifetime of harvested wood products (“anthropogenic” time). According to this model, the removal in each period was assigned to a certain number of final “use categories”, each with different emission rates. In the time period i+j, the carbon emission Eik,i+j from biomass of category k removed at time i was calculated as follows (eqn. 4):
where BEi is the removed biomass at time i, ek is the fraction of removed total biomass assigned to the use category k, and Qk,i+j is the emission rate of product k in the time interval i+j, which was calculated as (eqn. 5):
where ATk is the “anthropogenic” time for the use category k, qk is the annual fraction of decomposition for category k, which can be obtained using eqn. 6:
Eqn. 6 implies that the biomass in each category decomposes as a constant proportion of the remaining biomass. For each use category, emission and decomposition will stop when a very tiny fraction (<0.01 MgC ha-1) is emitted. Thus, a small fraction of biomass will not further decompose, e.g., soil organic carbon ([19]). In addition, carbon emission patterns are not appreciably affected by carbon mineralization processes.
Seven use categories were considered in the model: (1) roots; (2) deadwood; (3) branches and stumps; (4) bark and debris; (5) short duration wood products (small poles for fencing); (6) midterm duration products (struts and large poles); and (7) long term duration products (sawn timber). Decomposition time (DT) and anthropogenic time (AT) were taken from Hoen & Solberg ([19]) and are summarized in Tab. S4 (Supplementary material). The proportions of wood products per category for teak trees were taken from Osorio ([32]), and are listed in Tab. S5 (Supplementary material).
Optimization of the stand-level model
We developed a restricted optimization model using integer variables to represent ages of thinning, and continuous variables for thinning intensities (percentages of the stand basal area).
The objective function was (eqn. 7):
where NPVwood and NPVcarbon are the net present value (US$) of merchantable wood and the net present value (US$) of carbon stored, respectively. The decision variables were: (i) the number of years from planting (year 0) to first thinning, or the number of years between successive thinnings (Aj), where j represents the j-th thinning; (ii) the thinning intensity, expressed as the percentage of the stand basal area removed by the j-th thinning (Ij).
The model constraints were (eqn. 8 to eqn. 14):
where Goi is the basal area at the beginning of the i-th year (m2 ha-1), Gfi is the basal area at the end of the i-th year (m2 ha-1), Gthini is the basal area thinned in the i-th year (m2 ha-1) and ΔGi+1,i is the current annual increment of basal area (m2 ha-1).
Constraint in eqn. 11 indicates that the minimum age for the first thinning is five year-old. This is a common practice used to obtain a small amount of commercial products. Sometimes thinning is done at age 3 to favor early diameter growth; however, there are no studies indicating that this is a financially optimal decision. eqn. 12 implies that at least three years must elapse between successive thinnings. From a practical point of view, there are logistical problems to organize and execute thinnings too often. Constraint in eqn. 13 avoids the removal of very few trees in a given thinning, because the growth response of remaining trees would be negligible and the operational costs high.
Optimiztion of the forest-level model
A binary variable constrained optimization was modeled to achieve the optimum harvest plan. The objective function was (eqn. 15):
where NPVwood is the net present value of cash flows incoming during the planning period due to timber harvested, NPVcarbon is the NPV of cash flows due to positive net carbon storage, and SI is a “spatial index” that aggregates forest operations, in such a way the stands to be cut at a given time are as close as possible to each other and to the main road.
The net present value of merchantable timber was calculated as follows (eqn. 16):
where nr is the number of stands considered, mi is the number of alternative management regimes for the stand i, a is the number of years of the planning period, r is the interest rate. The term Iijk represent the incomes from timber harvested in the stand i for the year k when the management regime j is applied. These incomes result from multiplying the harvested volume by the price per cubic meter of timber. Prices are for roundwood and vary depending on log average diameter. The term Cijk is the total costs for stand i in year k for a given management j, and include the harvest costs which vary according to the extracted volume, costs of stand establishment and tending, and transporting timber to the sawmill.
The net present value of carbon was calculated as follows (eqn. 17):
where Pc is the carbon price (US$ Mg-1 of C), nr is the number of stands considered, mi is the number of alternative management regimes for stand i, Td is the time (years) at which 90% of carbon of the product with the largest organic life span has been emitted to the atmosphere. Fijk is the carbon fixed (Mg of C) in the stand i in year k under the management regime j; and Eijk is the carbon emitted (Mg of C) by the stand i in year k if the management regime j is applied; and r is the interest rate.
The spatial index (SI) proposed by Chen & Gadow ([10]) was calculated for each year k of the planning period (eqn. 18):
with i ≠ w, where SIk is the spatial index for the year k, nr is the number of stands, Riwk is a binary variable taking the value of 1 if the stands i and w are cut in the year k and 0 in any other case, diw is the distance between the stands i and w. Thereafter, the SI’s for all years were added up to obtain a SI for the harvest plan (eqn. 19):
where Pie is the weight or penalty imposed to the SI for balancing its value with NPVwood and NPVcarbon in the objective function, and a is the number of years of the planning period.
The decision variables (Xij) were binary variables taking the value of 1 (Xij =1) when the management regime j is assigned to the stand i, and Xij =0 otherwise.
Management regime was defined based on initial spacing, thinning regime, and the final harvest age. Thinning ages and intensities were determined by sub-model 1 depending on the planting year of stands and the age of last thinning, which must be done at least three years before the final harvest. The constraints were (eqn. 20 to 22):
with k = 1, 2, ..., a; i = 1, 2, …, nr; and j = 1, 2, …, mi, where nr is the number of stands, mi is the number of alternative regimes for stand i, VEijk is the volume harvested from the stand i in year k under the j-th management regime, CPk is the timber production quote for year k and a is the number of years of the planning period.
Constraint in eqn. 20 refers to the annual quota of timber. Constraint in eqn. 21 implies that a given stand can undergo only a unique management regime. Constraint in eqn. 22 indicates that decision variables must be binary.
Optimization techniques and implementation
The existence of nonlinear relationships among integer and continuous decision variables, and the model structure make extremely difficult to solve the above equations with classic mathematical techniques; therefore, heuristic techniques were used.
For solving sub-model 1, we used Genetic Algorithms (GA), a robust and efficient technique successfully applied to find optimal or close-to-optimal solutions when exact methods are difficult to implement ([16]). To obtain the best thinning regimes for each stand, we developed a GA using a roulette wheel selection, two point crossover, and mutation of the solutions.
An optimization algorithm based on Simulated Annealing (SA) was incorporated in sub-model 2 in order to search for the best management plans at the forest level. The SA technique has been previously applied to forest harvest planning ([37], [29], [39], [40]), and has proven to achieve solutions very close to a mathematical optimum. The SA algorithm uses random initial solutions and a geometric cooling schedule. We implemented the model in Visual Basic 2010.
Study case
Description and assumptions
We used the data set obtained from teak plantations in Venezuela (described above) to simulate a teak plantation covering 10.000 ha and comprising 200 stands (50 ha each). Simulated stands differed in initial spacing, with 100 stands having an initial density (Di) of 1600 trees ha-1 (2.5×2.5 m) and the remaining 100 stands having Di = 1111 trees ha-1 (3.0×3.0 m). Moreover, the simulated stands differed in site quality: for each type of initial spacing, 50 stands were assigned to site quality I (SQ I), with a site index of 27 m (base age 16 years) and maximum basal area (Gp = 37.5 m2 ha-1), while 50 stands were assigned to site quality II (SQ II - site index = 24 m; Gp = 32.0 m2 ha-1).
The planning project spanned 40 years, from initial planting of the first stand until the final harvest of the last stand. Stand planting took place in the first ten years of the project (0 to 10). The timber goal was to obtain merchantable wood from logs ≥ 20 cm in diameter. At the end of the planning period (40 years), all stands should have been harvested. We assumed that stands were not replanted after harvest, thus allowing for secondary vegetation to recover and some teak trees to re-sprout; however, the additional carbon sequestration of these abandoned stands was not considered in the project.
A different associated transport cost (in US$ m-3) was assigned to each stand, depending on its distance from the sawmill. Roundwood prices were assigned according to diameter classes (between 53 and 400 US$ m-3 - see Tab. S6 in Supplementary material), and base carbon price was 10 US$ Mg-1 of C, as commonly used in financial analyses ([1]).
Optimization objectives
Three alternative management scenarios were set with the objective of maximizing: (A) total NPV for merchantable timber production only; (B) total NPV for both timber and carbon sequestration; (C) total NPV for carbon sequestration only.
Sensitivity analysis
We carried out a three-stage sensitivity analysis for scenario B only (Timber production + C sequestration). The stage 1 consisted of a sensitivity analysis for individual stands (sub-model 1). The magnitude of changes in the optimal solution was analyzed considering changes in harvest costs, interest rates, growth rates, timber prices, and carbon prices. Sensitivity was tested for: (i) growth rate (k) at intervals of ± 1%, within a biologically reasonable range (e.g., possible increase in growth rates due to fertilization); (ii) thinning and harvest costs between ± 10 and ± 50% from the base value (14.24 US$ m-3) at 10% intervals; (iii) interest rate from 2 to 14 % (base value 10%), which is the common range of discount rates in forestry projects; (iv) price carbon increments of 20, 30, 40, 50, 100, 150, and 200 US$ Mg-1; and (v) differences in timber prices per cubic meter due to log dimensions. The price of teak timber depends largely on log size and age, as large logs with a high proportion of heartwood are best for teak products (e.g., furniture, plywood). For young teak plantations, wood quality and log dimensions are highly correlated. Four scenarios were considered: (1) all diameter classes have the same price in US$ m-3 (i.e., no premium for large diameter logs); (2) logs with diameter (d) ≥ 25 cm are twice the value of logs 10 ≤ d ≤ 25 cm; (3) logs with d ≥ 25 cm are three times the value of 10 ≤ d ≤ 25 cm logs; and (4) logs with size d ≤ 10 cm have no value as timber product.
At stage 2 we carried out a sensitivity analysis for changes at forest level considering the sensitivities obtained in stage 1 (stand level), as changes in the optimal solution at stand level propagate to the forest level changing the optimum harvest plan. If no changes occurred at the stand level for a given variable, then the sensitivity analysis was carried out at the forest level for that variable. Finally, in stage 3 we carried out an additional sensitivity analysis at forest level, but considering only forest-level input variables such as transport costs from the stands to external roads and production quotas. Transport costs were changed from the base costs up to ±50%, at 10% intervals for each of the four categories. We tested the model sensitivity to modifications of the annual production quota by raising or lowering the quota in certain periods (Tab. S7 in Supplementary material).
Model validation
Bettinger et al. ([7]) proposed a classification of validation approaches for forest planning models according to problem particularities, model complexity, and availability of exact solutions. We carried out a “level 2” validation (known as “self-validation”) by assessing the robustness of the solution through a statistical approach. Using this method, a sample set of solutions is required, each having a different objective function value easily obtainable from heuristics using stochastic processes such as simulated annealing and genetic algorithms ([7]). This type of validation is considered appropriate when a well-understood heuristic technique is applied to a new management problem, as it is our case.
The above validation approach was carried out at both stand and forest levels for the scenario of simultaneously optimizing timber production and carbon sequestration (scenario B). Fifty runs at each planning level were done and the optimum NPV and its basic statistics were recorded.
Results
Stand level
The developed model simulated the best thinning regimes for each stand according to initial spacing and site quality under the optimization scenarios. For those scenarios that included timber production, either alone (scenario A) or combined with carbon sequestration (scenarios B), the best thinning regimes were the same, but they differed only in the magnitude of NPVtotal, which was larger when both objectives were considered. On the other hand, when NPVcarbon was the only optimization/maximization goal (scenario C), thinnings were prescribed at later ages and lower intensities. For example, for scenario A (Di = 1600 trees ha-1, SQ = I, harvest age = 30), the best thinning regime for scenarios A and B consisted of three thinnings at ages 5, 10, and 19, removing 46.5%, 47.7%, and 29% of the total basal area, respectively (Tab. 1). Contrastingly, when the goal was carbon sequestration (scenario C), the best option was no thinning.
Tab. 1 - Net present value (NPV) of the best thinning regimes for teak stands (initial density: 1600 trees ha-1; Site quality: I; Rotation age: 30) for scenarios: A (wood production only); B (wood production and carbon sequestration); C (carbon sequestration only). (NT): number of thinnings for each regime. For each thinning, the age (years) and the percentage of removed basal area (in parentheses) are reported.
| Scenario | NT | Thinnings | NPV (US$ ha-1) |
|||
|---|---|---|---|---|---|---|
| First | Second | Third | Fourth | |||
| A/B | 0 | - | - | - | - | A: 7100; B: 1390 |
| A/B | 1 | 9 (79.9) | - | - | - | A: 6290; B: 6780 |
| A/B | 2 | 5 (55.8) | 14 (53.7) | - | - | A: 8980; B: 9470 |
| A/B | 3 | 5 (46.5) | 10 (47.7) | 19 (29.0) | - | A: 9090; B: 9580 |
| A/B | 4 | 8 (44.6) | 16 (25.6) | 20 (47.7) | 25 (26.7) | A: 7900; B: 8470 |
| C | 0 | - | - | - | - | 680 |
| C | 1 | 27 (27.9) | - | - | - | 672 |
| C | 2 | 23 (25.2) | 27 (25.7) | - | - | 670 |
| C | 3 | 20 (26.2) | 24 (27.4) | 27 (48.1) | - | 666 |
| C | 4 | 17 (26.0) | 21 (25.4) | 24 (36.3) | 27 (39.0) | 651 |
Forest level
We ran the model to obtain the optimal harvest sequence for 200 stands during the planning period under the proposed scenarios. For each year, the model indicated which stands should be thinned or harvested to maximize the expected benefits. Again, the simulated NPVtotal value obtained for the scenario B (both optimization criteria) was higher than those obtained for either scenario A (maximizing timber production) or scenario C (maximizing carbon sequestration) alone. In addition, there were no changes in the optimal harvest sequence between scenarios A and B.
The average rotation age obtained by optimizing for NPVwood was shorter than that obtained by maximizing for NPVcarbon only (Tab. 2). Moreover, the majority of the best thinning regimes obtained by the model consisted of two or three thinnings (Tab. 3). When the objective was to maximize NPVcarbon, the number of thinnings decreased. In this case, 62 (31%) out of 200 stands were not thinned, and for most stands two thinnings or less were required (Tab. 3).
Tab. 2 - Rotation age for stands under optimal planning schedules for each management scenario: (A) Wood production; (B) Wood production + carbon sequestration; (C): Carbon sequestration.
| Scenario | Clearcut age (years) | Clearcut stands (age < 25 years) |
Clearcut stands (age ≥ 25 years) |
||||
|---|---|---|---|---|---|---|---|
| Average | Min | Max | N | % | N | % | |
| A and B | 27.2 | 20 | 38 | 61 | 30.5 | 139 | 69.5 |
| C | 30.5 | 20 | 39 | 25 | 12.5 | 175 | 87.5 |
Tab. 3 - Number of stands with a given number of prescribed thinnings under the optimization scenarios: (A) wood production only; (B) wood production + carbon sequestration; (C): carbon sequestration only.
| Scenario | Number of thinnings | Total | ||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| A and B | 29 | 39 | 55 | 55 | 22 | 200 |
| C | 62 | 39 | 38 | 31 | 30 | 200 |
For the base scenarios (i.e., base prices for timber and carbon), the NPVtotal value obtained by maximizing for NPVwood almost doubled the NPVtotal value obtained by maximizing for NPVcarbon (Tab. 4). Maximizing only for NPVcarbon increased NPVcarbon by 3.47 US$ millions, while NPVwood decreased by 22.95 US$ millions. Hence, when the maximization of NPVcarbon was the sole objective of the teak plantation project, the potential benefits of wood production predicted by the model decreased by 73.9%. Contrastingly, maximizing NPVwood as the sole objective decreased the predicted benefits from carbon sequestration by 29%. Thus, given the base scenarios and the model assumptions, it seems not attractive to manage teak plantations with the only aim of carbon sequestration.
Tab. 4 - Net present value for wood (NPVwood) and carbon sequestration (NPVcarbon) according to optimization objectives.
| NPV | Optimization objectives | Difference (US$ million) |
|
|---|---|---|---|
| Wood production |
Carbon sequestration |
||
| NPVwood (US$ million) | 31.03 | 8.08 | -22.95 |
| NPVcarbon (US$ million) | 8.47 | 11.94 | +3.47 |
| Total NPV | 39.50 | 20.04 | - |
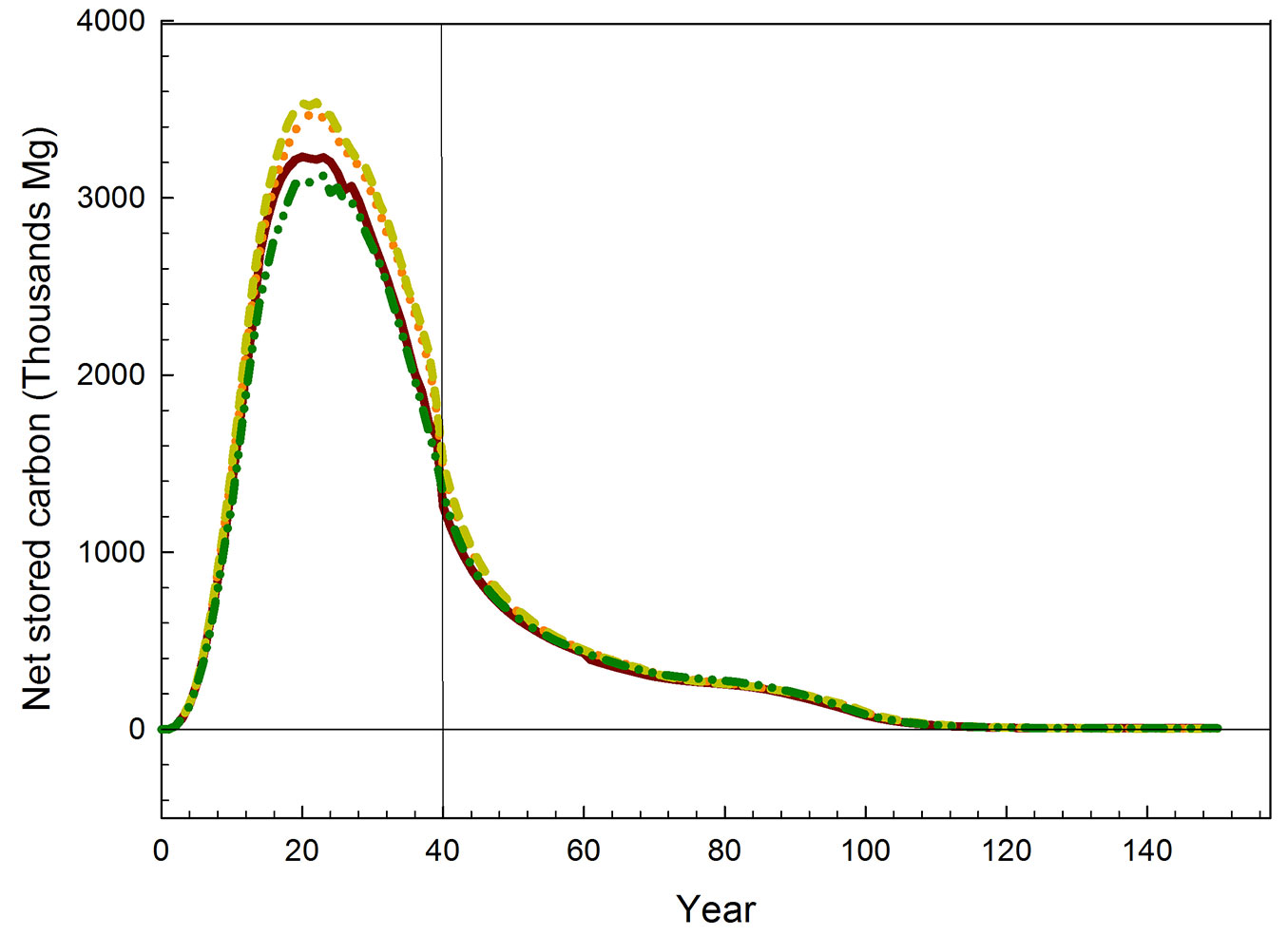
The developed model provided estimates of the carbon stored in standing trees, died trees, forest products, harvest residues, and woody debris for each year of the planning period (Fig. 2). As expected, the quantity of carbon stored through the 40 years of the planning period were higher when maximizing for NPVcarbon (eqn. 17), as compared with scenarios that included wood production. Under this scenario, the model tended to minimize the number and intensity of thinnings, and to delay the thinnings and final harvest ages to defer the beginning of C emissions. In other words, the model favored net C storage to increase the value of the objective function, by avoiding large C emissions due to cutting operations, as emissions due to mortality of standing trees were small.
Fig. 2 - Dynamics of net carbon storage (from total accumulated biomass). Average life cycle of carbon stored as wood in standing trees, forest products, and harvest residues for a 10.000 ha teak plantation under the base optimization scenarios (maximum NPV criteria). Carbon price 10 US$ Mg-1of C and timber prices between 53 and 400 US$ m-3 according to log size categories (Tab. S6 in Supplementary material). (Scenario 1): maximizing NPV for carbon sequestration (green dashed line); (scenario 2): maximizing NPV of wood production only (orange dashed line); (scenario 3): Maximizing NPV of wood and carbon simultaneously (brown line).
In our model, at the year 40 all stands not harvested during the project life were cut (76.879 m3 in the A-B scenarios, and 273.600 m3 in scenario C), thus the largest part of the carbon previously sequestered was kept as merchantable products and as debris from harvest and wood processing. In scenario C (max NPVcarbon), the amount of carbon stored remained larger until year 69, because the final harvest was much larger than in scenario A, but as short to medium duration products. On the other hand, in scenario A (max NPVwood), the total amount of C stored as harvested products was lower, but as long duration products. In both scenarios, the remaining fraction of carbon returned to the atmosphere, according to decomposition and anthropogenic times for products and debris; hence, the curve for scenario C decreased gradually (Fig. 2). Likewise, during this period, emissions before year 40 continued according to the assumed decomposition rates. After that year, most C stored in short and medium duration products has been released back to the atmosphere. Thus, the total carbon that remains stored in scenario C is the largest, because it comprises long duration products. After year 116 almost all C has been released, remaining a small fraction that never decomposes or is incorporated into the soil as organic C ([19]). Consequently, the curves for scenarios A and B were similar (Fig. 2).
Sensitivity analysis
The model was very sensitive to changes in growth rates of basal area and in timber prices, as very small changes generated different optimum harvest plans. In addition, the model was sensitive to changes in interest rates by changing the optimal solutions in terms of thinning regimes and harvest ages (Tab. 5). Nevertheless, for interest rates between 6 and 10% the optimum harvest plan did not change. Regarding carbon prices, the sensitivity analysis indicated that the optimal solution (harvest plan) changed when the prices reached 40 US$ Mg-1 C. In such case, the optimum thinning ages occurred later and thinning intensities were lower.
Tab. 5 - Sensitivity analysis for selected variables. Data indicate the ranges in which the optimal solution (harvest patterns) is modified with respect to the base solution.
| Variable / Parameter | Model sensitive to changes (range) |
Model not sensitive to changes (range) |
|---|---|---|
| Basal area growth rate | [0.10, 0.25] | None |
| Harvest cost | None | [7.12, 21.36] US$ m-3 |
| Interest rate | > 10% | < 10% |
| Wood prices | All scenarios | No scenarios |
| Carbon price | ≥ 40 US$ Mg-1 of C | [0, 40] US$ Mg-1 C |
| Transport cost | None | All scenarios |
| Production quotas | Scenarios 1-4 | Scenarios 5-8 |
Changes in allowable production quotas for the whole project modified the optimal harvest plan. When annual quotas were raised from five to 10.000 m3 between the years 7 and 20 (scenarios 1, 2, 3 - Tab. S7 in Supplementary material), the optimum harvest plan changed because thinning regimes and final harvest for each stand changed to meet the new quotas. When the quota for years 21-40 rose from 60 to 65.000 m3, an optimal solution could not be found. For scenarios where production quotas were reduced (scenarios 5, 6, 7, 8 - Tab. S7 in Supplementary material), the optimal solutions were the same as the base scenario; yet, volume yield per year surpassed the assigned annual quotas. Changes in harvest and transport costs did not change the optimal solution, thus the proposed model is not sensitive within the range of changes assumed for these variables.
Model validation
To validate the model, descriptive statistics for a sample of 50 solutions for the thinning regime sub-model (stand level) were produced considering one to four thinnings (Tab. 6). In all cases, the lowest NPVtotal differed by less than 28% from the maximum NPV (optimum). The percent difference between the lowest and highest NPV increased when more thinnings were carried out, indicating that the genetic algorithm was more precise when only one or two thinnings were prescribed (6.9 and 14.5%, respectively). Furthermore, the variability of the solutions was larger in scenarios with more thinnings. This could happen because there are two types of decision variables: integer variables (representing thinning age) and continuous variables (representing thinning intensity); hence, an infinite number of combinations does exist. As more variables were included in the model, its complexity increased reducing the precision of the genetic algorithm.
Tab. 6 - Model validation. Net present value (NPV) statistics from 50 runs for the stand-level model and for the forest-level model. Study case: 10.000 ha teak plantation project. Statistics for NPV are: average, minimum (Min), maximum (Max), standard deviation (SD) in thousand US$; and coefficient of variation in percentage (CV); (D1): percentage difference between the maximum value and the minimum value; (D2): percentage difference between the average and the maximum value; (NT): number of thinnings.
| Statistics | Stand level | Forest level |
|||
|---|---|---|---|---|---|
| NT = 1 | NT = 2 | NT = 3 | NT = 4 | ||
| Average | 6.55 | 8.83 | 8.70 | 7.12 | 38185.53 |
| Min | 6.32 | 8.10 | 7.29 | 6.13 | 39500.00 |
| Max | 6.78 | 9.47 | 9.58 | 8.47 | 37649.18 |
| SD | 0.20 | 0.37 | 0.47 | 0.52 | 384.99 |
| CV | 3.12 | 4.18 | 5.40 | 7.23 | 1.01 |
| D1 | 6.87 | 14.48 | 23.95 | 27.67 | 4.68 |
| D2 | 3.53 | 6.76 | 9.14 | 15.90 | 3.33 |
At forest level, model validation showed that the difference between the highest and lowest NPV was 4.68 % (Tab. 6). Thus, there is a strong confidence that the value obtained by just one model run falls within 5% of the best solution, therefore indicating a satisfactory performance of the simulated annealing algorithm. In addition, the small percent difference between the best value and the average value supports the robustness of the heuristic technique applied. The coefficient of variation of solutions produced for the forest level model (sub-model 2) was lower than that for the stand level sub-model (Tab. 6).
Discussion
The model proposed in this study simulates a full teak plantation project at the stand and forest levels and provides a optimized harvest plan by identifying which stands to thin or harvest each year in order to both maximize the benefits and meet the operating constraints. The simulation carried out in this study (200 stands, 10.000 ha) was solved by the model in a few seconds. The results obtained were satisfactory, considering the model complexity, assumptions and constraints. For example, for maximizing NPVwood, the model increased the number of thinnings and their intensities to favor larger diameter growth and logs with higher value as sawn timber. Moreover, the simulated dynamics of the stand variables (diameter, basal area, stand density) were within the expected limits for acceptable quality teak stands in terms of both growth and yield ([5], [34]). Model sensitivity analysis indicated that stand growth rates and timber prices strongly influence optimal management plans obtainable, while interest rates, carbon price, and annual production goals had a lesser influence. Transport and plantation management costs appeared to have a low impact on the optimization of management plan. Chiari et al. ([11]) found similar results when analyzed the sensitivity of a linear programming model for a large eucalyptus plantation project devoted to pulpwood production in Venezuela.
The proposed model can be usefully applied to optimize harvest plans in teak plantations by maximizing wood production and/or carbon sequestration as separate objectives or simultaneously. According to the model results, for a price of 10 US$ Mg-1 of C and the current timber prices (53-400 US$ m-3, depending on log diameter) there were no differences in cutting patterns (best thinning regimes and optimal harvest plan) between the scenario optimizing timber production (scenario A) and that maximizing both wood production and C sequestration (scenario B). This is because timber prices were much higher than the market carbon prices. The lack of differences between the above scenarios can be explained because the model is not sensitive to changes in C prices between 0 and 40 US$ Mg-1 (Tab. 5). C prices above 40 US$ Mg-1 could make teak plantations for carbon sequestration a more profitable option. Further, larger C prices could allow stocking larger C amounts before harvest, thus changing the harvest patterns and the net C storage curves between the aforementioned scenarios (Fig. 3).
Fig. 3 - Dynamics of net carbon storage under scenarios of wood production only (dark green dashed line), wood + carbon sequestration (40 US$ Mg-1 - brown solid line); wood + carbon sequestration (100 US$ Mg-1 - orange dotted line), wood + carbon sequestration (150 US$ Mg-1 - green dashed line). Timber prices are reported in Tab. S6 (Supplementary material).
When maximization of NPVcarbon was set as the only management goal in the model, the generated harvest plans had lesser, later, and lower intensity thinnings, as well as longer rotations. Raymer et al. ([42]) found similar results analyzing several management strategies for increasing the benefits from carbon sequestration in a forestland in Norway. Likewise, Bateman & Lovett ([4]) suggested to avoid thinnings for increasing carbon sequestration of plantations. Similarly, other authors found that carbon sequestration in plantations can be increased by delaying the final harvest ([28], [38], [24]). Therefore, the management regime may influence the capacity of a forest plantation to sequester carbon.
The simulations carried out revealed that maximizing for NPVcarbon C stock in the plantation was larger until year 69 as compared to scenarios maximizing NPVwood; however, for the latter scenarios a larger fraction of C remained stored in long duration products until the year 116.
Our results showed that implementing management plans to favor carbon sequestration reduce the economic benefits from timber production, and vice-versa, indicating that these objectives are in conflict, which is consistent with previous studies ([2], [42], [31]). According to the model’s results, with C prices of US$ 10 Mg-1 managing teak plantations for carbon sequestration only is not attractive, because of the high market value of teak timber. For other tropical species with lower timber value used in plantations, such as pine or eucalyptus, optimizing for carbon sequestration could be more attractive, especially if environmental concerns are important. In such cases, considerations on the land value could be more critical to determine the feasibility of implementing carbon sequestration projects.
Our results suggest that teak has a good potential for carbon storage due to its fast growth and wood durability. Additional benefits could be obtained from C sequestration only by optimizing the NPVwood, as long as C prices are below 40 US$ Mg-1. Managing teak projects as infinite rotation plantations would transform them in permanent carbon sinks, also increasing their capacity for soil carbon storage.
Most teak plantations, especially in Latin America, are small to medium size private-owned projects (i.e., 3.000-10.000 ha) made by several stands of different age, site quality, and extension. In addition, they are planned for limited time horizons (e.g., 30-40 years) and for only one rotation. Although the present study is based on simulations, such characteristics are similar to those implemented in the proposed model. However, the information required to model teak plantation management is mainly limited by two reasons: (i) companies are not willing to make public information on operational activities; and (ii) more than 80 % of teak plantations in Latin America are less than 20 years old ([13]), thus no company has completed the first rotation.
Although our model is calibrated on teak trees growing in the Venezuelan Western Plains (alluvial soils), growth and yield performances of teak stands are comparable with those observed in other countries, like Brazil, Mexico, Colombia, Ecuador, and other states of Central America, in terms of growth rates, mean annual increments (8-20 m3 ha-1 yr-1), yield, and financial results for a given site index. Moreover, volume and yield tables from Venezuela have been successfully extrapolated to other countries. However, we caution to extrapolate our results to Asian or African Countries, or to clonal plantations under intensive management. Furthermore, as the growth and yield model used is based on the basal area, its calibration to more site specific conditions and management regimes can be done with no risk of obtaining unrealistic results. Finally, the modular structure of the proposed model allows for changes in the growth and yield model without affecting the other model components.
So far, the high prices of high quality teak timber has reduced the need of harvest optimization techniques for increasing efficiency in timber production and planting operations. As many teak plantations are reaching commercial ages in Latin America, timber supply could exceed the demand, thus lowering timber prices. Further, certification of sustainability is increasingly required on the market for timber products from plantation projects, which implies many environmental requirements. In addition, many projects receive subsidies in their initial phases and are subject to enter the incipient carbon market. Thus, optimizing carbon sequestration and timber production in teak plantations is going to be crucial in the upcoming years.
Conclusions
In this study, a model was developed for optimizing both thinning regimes in individual teak stands and the harvest plan for the whole plantation, aimed at simultaneously maximizing timber production and carbon sequestration. The adopted modeling approach allowed the integration of both stand and forest planning levels. At the stand level, we approached the stocking-regime optimization problem using a heuristic model based on Genetic Algorithms. Production curves were generated according to stand characteristics by a forest stand growth and yield simulator. At forest level, we used a simulated annealing heuristic technique to determine optimal harvest ages and assign an appropriate thinning regime to each stand matching the annual production quotas.
The proposed harvest planning model may help managing small to large scale teak plantations, by providing information on plantation growth and yield, and considering the impact of stocking and harvest regimes. The possibility of quickly running and examining several potential harvest plans under various scenarios makes the model useful as a starting point for designing management plans, fieldwork task assignments, road construction, and equipment displacement.
Acknowledgements
This work was supported by the Consejo de Desarrollo Científico, Humanístico, Tecnológico y de las Artes (CDCHTA), Universidad de Los Andes (ULA), Mérida, Venezuela [Grant FO-705-11-01-B] and by the Genética and Silvicultura Research Team, Instituto de Investigaciones para el Desarrollo Forestal, ULA. We are grateful to Dr. Thomas J. Dean, Dr. Lawrence W. Vincent, Dr. Magdiel Ablan and Dr. Miguel Acevedo. We also thank two anonymous reviewers for their useful comments and advices.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Escuela de Ingeniería Forestal, Facultad de Ciencias Forestales y Ambientales. Universidad de Los Andes, Mérida 5101 (Venezuela)
Centro de Estudios Forestales y Ambientales de Postgrado, Facultad de Ciencias Forestales y Ambientales. Universidad de Los Andes, Mérida 5101 (Venezuela)
Corresponding author
Paper Info
Citation
Quintero-Méndez MA, Jerez-Rico M (2017). Heuristic forest planning model for optimizing timber production and carbon sequestration in teak plantations. iForest 10: 430-439. - doi: 10.3832/ifor1733-009
Academic Editor
Giorgio Matteucci
Paper history
Received: Jun 05, 2015
Accepted: Oct 30, 2016
First online: Mar 24, 2017
Publication Date: Apr 30, 2017
Publication Time: 4.83 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2017
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 52480
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 41679
Abstract Page Views: 2992
PDF Downloads: 6462
Citation/Reference Downloads: 42
XML Downloads: 1305
Web Metrics
Days since publication: 3160
Overall contacts: 52480
Avg. contacts per week: 116.25
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2017): 14
Average cites per year: 1.56
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Climatic fluctuations trigger false ring occurrence and radial-growth variation in teak (Tectona grandis L.f.)
vol. 9, pp. 286-293 (online: 28 September 2015)
Research Articles
Density management diagram for teak plantations in Tabasco, Mexico
vol. 10, pp. 909-915 (online: 01 December 2017)
Research Articles
Roadside vegetation: estimation and potential for carbon sequestration
vol. 3, pp. 124-129 (online: 27 September 2010)
Research Articles
Outlook of the European forest-based sector: forest growth, harvest demand, wood-product markets, and forest carbon dynamics implications
vol. 11, pp. 315-328 (online: 18 April 2018)
Review Papers
Tectona grandis Linn. f. secondary metabolites and their bioactive potential: a review
vol. 15, pp. 112-120 (online: 26 March 2022)
Research Articles
Forest management with carbon scenarios in the central region of Mexico
vol. 14, pp. 413-420 (online: 15 September 2021)
Research Articles
Estimating biomass and carbon sequestration of plantations around industrial areas using very high resolution stereo satellite imagery
vol. 12, pp. 533-541 (online: 12 December 2019)
Commentaries & Perspectives
Forest plantations with public subsidies: to harvest or not to harvest, this is the question
vol. 15, pp. 229-233 (online: 12 July 2022)
Research Articles
Modeling air pollutant removal, carbon storage, and CO2 sequestration potential of urban forests in Scotlandville, Louisiana, USA
vol. 9, pp. 860-867 (online: 22 September 2016)
Research Articles
Aboveground tree biomass of Araucaria araucana in southern Chile: measurements and multi-objective optimization of biomass models
vol. 14, pp. 61-70 (online: 09 February 2021)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword