Forest management with carbon scenarios in the central region of Mexico

doi:10.3832/ifor3630-014

Forest management with carbon scenarios in the central region of Mexico

iForest - Biogeosciences and Forestry, Volume 14, Issue 5, Pages 413-420 (2021)
doi: https://doi.org/10.3832/ifor3630-014
Published: Sep 15, 2021 - Copyright © 2021 SISEF

Research Articles

Abstract

Article

Authors’ Info

Info & Metrics

References

Images & Tables

The search for mechanisms to mitigate global warming has generated a series of proposals to reduce deforestation and promote conservation of forests as carbon stocks through financial or in-kind support. However, the economic implications of including carbon sequestration in forest for timber production have not been dealt with in depth, and the conditions in which combined production might be a profitable option to forest owners, particularly in Mexico, are unknown. The aim of this study was to quantify carbon sequestration in a central region of Mexico and evaluate the profitability of selling carbon credits as well as timber products. Data and information used comes from three inventories (2013, 2014 and 2016) taken in 160 permanent sampling plots of 400 m²each; forest management costs per hectare were obtained through interviews to the landowners, and the profitability was assessed using the economic indicators Net Present Value (NPV), Internal Return Rate (IRR), Benefit-Cost Ratio (BCR), and Land Expected Value (LEV). The results indicate that, in areas of low productivity, carbon sequestration is profitable only at a low discount rate (3.5%) and a high price of the ton CO₂e (USD 100 ha^-1 year^-1). However, under combined production, the optimal rotation periods are longer, depending on the discount rate and price of sequestered carbon. Therefore, timber production will continue to be the main economic activity, until the rules of operation of the different mechanisms created for carbon sequestration become more flexible and the carbon markets offer more attractive incentives.

Climate Change, Carbon Sequestration, Productivity, Financial Profitability, Optimal Rotation

Climate change (CC) is a statistical variation in the mean state of the climate over a prolonged period. It is produced by natural processes or by persistent anthropogenic changes ([20]). Today, it is undoubtedly one of the issues attracting the most interest and will continue over the upcoming decades. According to Joos & Spahni ([21]), the concentration of carbon dioxide (CO₂) in the atmosphere at the beginning of the industrial age (1970) was approximately 277 parts per million (ppm), a value that has increased to 407.38 ± 0.1 ppm in 2018 ([13]). This has intensified the search and development of mechanisms to balance the concentrations of CO₂ and other greenhouse effect gases (GEG) and compounds in the atmosphere to detain or reduce global warming.

One of these mechanisms is the Kyoto Protocol, in which developed countries committed to reducing their emissions of GEG by at least 5.2 %, relative to 1990 levels, for the period 2008-2012. In addition, in 2015, 195 countries signed the Paris Agreement, whose objective is to detain the temperature increase in this century to less than 2 °C ([49]). In such agreement, it is recognized that forests play a central role in achieving this goal, since they store large amounts of carbon in both vegetation and soils, and have an important role in the exchange of carbon dioxide between the biosphere and the atmosphere ([3]); therefore, their conservation and restoration are unpostponable. As a result, international policy instruments and programs have emerged such as REDD+ projects, that are based on the provision of financial incentives to conserve forests, improve forest carbon stocks and sustainable forest management ([35]), or the Clean Development Mechanism (CDM), which is an instrument designed to reduce greenhouse gas emissions through the purchase of Certified Emission Reduction Units (CERs) from afforestation or reforestation projects in developing countries ([51]). Under the CDM, several Latin American countries have participated in afforestation and reforestation projects, such as Bolivia, Peru, Paraguay, Uruguay, Brazil, Argentina, Chile. While in REDD+, in 2011, Peru and Brazil had more than 40 pilot projects, being among the countries with the largest number of projects worldwide; Nicaragua, El Salvador, Belize, Panama, Costa Rica have also taken part in this initiative ([26]). Likewise, some countries have made various commitments to contribute to the mitigation of climate change, for example, Colombia and Brazil which committed to restoring 1 and 12 million forest hectares, respectively ([44]), through the Bonn Challenge, which aims to restore 150 million global hectares of degraded lands by 2020.

In 2009, the government of Mexico, through its Special Climate Change Program (Programa Especial de Cambio Climático - PECC), committed to reducing its GEG emissions by 50% to 2050, relative to the quantity emitted in 2000 ([37]). In addition, in the Paris Agreement, the government committed to reducing GEG by 22% and short-lived climate pollutants (SLCPs) by 51% for the year 2030, relative to the base scenario.

Despite the environmental and social benefits obtained under this approach, in Latin America there are few studies related to CC, timber production and carbon sequestration; most of them have been directed only to the quantification of biomass and carbon stocks in natural forests ([38]), forest plantations ([27]) or in determining the climate change mitigation potential of forest ecosystems ([17]). It is therefore necessary to carry out studies to address the production of more than one good or service, such as the production of timber plus the benefits of carbon sequestration, the production of water and biodiversity conservation. Specifically, the inclusion of carbon sequestration benefits to forest harvesting has various implications such as an extended rotation period ([12], [46]). To this respect, Nepal et al. ([32]) found that for Mississippi forest landowners to be willing to extend the rotation period by 5 and 10 years, the prices for captured carbon must be USD 50 and USD 110 per Mg CO₂e, respectively. On the other hand, Köthke & Dieter ([24]) mention that including the benefits of carbon sequestration in forest management could be an opportunity to achieve profitability in forest sites that until now were not profitable. Therefore, the economic analysis of alternative scenarios of the joint production of timber plus carbon sequestration through financial indicators represents an adequate alternative to analyze the profitability of forestry and to determine the conditions under such production would be profitable.

The objective of this study was to quantify the carbon sequestration in managed forests in the central region of Mexico, and to evaluate the financial profitability of timber production combined with carbon credits in different alternative scenarios.

Study area

The study was conducted in the Intensive Carbon Monitoring Site Atopixco, which is located in a forested region of Zacualtipán, Hidalgo state, in the Sierra Madre Oriental (Mexico). It covers portions of ejidos Atopixco, La Mojonera, El Reparo, Tzincuatlán, Zahuastipán and Santo Domingo, and small private land with an area of 900 ha (3 × 3 km - [33]). The site is part of the “Red Méx-SMIC, Intensive Carbon Monitoring Sites network”, established in 2012 in forest landscapes of Mexico, with the aim of obtaining information for the calibration-validation of models of forest carbon dynamics ([4]). The main vegetation types at the regional level are pine-oak forests, oak forests and tropical montane cloud forest.

Forest management in these forests began in the early 1980’s using the Method of Silvicultural Development (MSD), which is a planning scheme based on rotation age ([31]). The regeneration method is a seed tree method prescribing 3 to 4 thinnings evenly spaced during a rotation of 40 to 80 years. The goal is to regenerate forest stands whose age composition and density achieve the maximum average production ([48]). In the last four decades, forest management has been oriented toward developing even-aged forests dominated by Pinus patula, a fast growing species that is endemic to Mexico. The topography of the site is hilly with a mean altitude of 2100 m a.s.l. The predominant soil is Feozem, with good drainage. Climate is humid temperate [C(m)] and subhumid temperate [C(w2)], mean annual temperature is 13.5 °C, and mean annual precipitation is 2050 mm.

Field data

The dataset was obtained from three measurements (2013, 2014 and 2016) of 40 clusters, each consisting of four 400 m² sampling plots distributed in an inverted “Y” within one hectare. The registered variables were total height (H, m), diameter at breast height (DBH, cm), dominant height (HD, m), number of live trees (NL) and stand age (years) obtained in the field and from the forest management plan.

Financial characterization and discount rate

Average costs per hectare of timber production were obtained through interviews with the agents of forest activity (ejido president, forest administrator, and forest workers), for the stages of stand establishment, maintenance, and harvest, which are the main activities of the forest management process. Fixed costs were obtained from establishment and maintenance, while variable costs were defined in function of timber production.

Discounting future cash flows is an economic practice of long tradition in forest economics, due to the long period of time between stand regeneration ([43]) and final harvest. According to Bettinger et al. ([5]), the discount rate can be nominal or real; the first includes inflation, while the second does not and may or may not incorporate a risk factor. Klemperer ([23]) remarks that there is no risk factor universally used, and its selection will depend on the payment period, the amount of risk in incomes and the degree of aversion to risk of the decision-maker. Worldwide, reported discount rates used in forest investments oscillate between 6% in the northern hemisphere and 15% in the southern hemisphere ([10]). For Mexico, of the few studies conducted to date, Masera et al. ([28]) analyzed the forestry options for carbon sequestration by comparing three study cases and using four real discount rates (0, 3, 5 and 10%). Based on that study and given the high variability of the discount rates used, we opted for real rates of 3.5% and 4.5% without considering a risk factor.

Forest growth systems, timber and carbon yield

Information on growth systems and yield per hectare were obtained from the prediction and projection models of Ramírez et al. ([36]). Aboveground biomass per hectare was estimated from the timber volume of Pinus patula and broadleaf species with factors of direct proportionality of 0.433 and 0.817, respectively ([36], [33]). Aboveground carbon ratio for Pinus patula and broadleaf species were 0.507 and 0.494, respectively ([15]). Carbon estimations in MgC ha^-1 were multiplied by 3.667 (ratio between molecular weights of CO₂ and carbon, 44/12) because the carbon markets operate in metric tons of carbon equivalent (MgCO₂e). In addition, we did not consider the penalty for the re-emission of CO₂ into the atmosphere at the time of harvest, since the proportions of the final products are not known of short or long life that the harvested timber will become.

Diameter distribution modeled with the Weibull function

The stand variables proposed were dominant height (HD, m), site index (SI, m), basal area (BA, m² ha^-1), number of trees ha^-1 (NT) and quadratic mean diameter (Dq, cm). The height (H, m) by diameter class (D), growth in quadratic mean diameter and total volume (V) were obtained with eqn. 1, eqn. 2 and eqn. 3, respectively:

\begin{equation} H=1.3+0.241315 \cdot HD^{1.085389} D^{ \left (0.711527 \cdot HD^{-0.26345} \right )} \end{equation}

\begin{equation} Dq=5.663274 \cdot exp \left (\frac{-14.54899}{Age} \right) \cdot SI^{0.572138} \end{equation}

\begin{equation} V=0.0000253 \cdot D^{1.6939421} H^{1.4175090} \end{equation}

The parameters that are part of the Weibull function were recovered using the moment method ([42]), while percentiles were estimated with Ordinary Least Squares (OLS - eqn. 4, eqn. 5, eqn. 6):

\begin{equation} p_0=0.319277 Dq^{1.715867} HD^{-0.60877} Age^{0.173854} \end{equation}

\begin{equation} p_{65}=1.006196 Dq^{1.029508} \end{equation}

\begin{equation} p_{93}=1.865844 \cdot Dq^{0.89569} \end{equation}

The parameter location a was estimated as follows (eqn. 7):

\begin{equation} a= \left \{ \matrix {p_0 = 2.5 & \text{when}\;\; P_0 \ge 5 cm \cr \frac{p_0}{2} & \text{otherwise}} \right . \end{equation}

while parameter c was calculated as (eqn. 8):

\begin{equation} c= \frac{\ln[-\ln (1-0.93)/-\ln (1-0.65)]}{\ln [(p_{93}-a)/(p_{65}-a)]} \end{equation}

and parameter b was estimated with the expression of the second moment of the Weibull distribution (eqn. 9):

\begin{equation} b=a \cdot {\frac{\Gamma_1}{\Gamma_2}} + { \left [{ \left (\frac{a}{{\Gamma_2}} \right)}^2 \cdot \left({\Gamma_1}^{2} - \Gamma_2 \right ) + \frac{Dq^2}{\Gamma_2} \right]}^{\frac{1}{2}} \end{equation}

where Γ(.) is the Gamma function, Γ₁ = Γ[1+(1/c)] and Γ₂ = Γ[1+(2/c)].

Distribution and prices by type of timber product and Mg CO₂e

Products were allocated with the equation of Fang et al. ([14]) reported in the Forest Biometric System corresponding to the Unit of Forest Management 1302 Zacualtipán-Molango ([50]). The products considered were: cellulosic (10 ≥ d < 20 cm); secondary (20 ≥ d < 25 cm); and primary products (d ≥ 25 cm). The nominal price by type of product was obtained through interviews in the study region: cellulosic (USD 15 m^-3), secondary (USD 40 m^-3) and primary (USD 80 m^-3). Since the prices per carbon credit (MgCO₂e ha^-1 year^-1) were below USD 75, there were no profitable scenarios. The exchange rate was $20.00 MXN to one dollar.

Updating production costs

To deflate the different values, 2013 was used as the base year because it had the following characteristics: it is a recent year, abundant information is available, reasonable historic economic behavior was registered, normal market conditions, uniformity in price variations, and no catastrophic events occurred (natural disasters, political elections, special events, etc. - [19]).

Present production values (PV) were estimated by type of product discounted at interest rate i with eqn. 10. Wood prices were deflated with eqn. 11, while costs (fixed and variable) of timber production were deflated with eqn. 12 and updated with eqn. 13:

\begin{equation} PV= \frac{Pr_{j} \cdot Q_{j}}{{(1+i)}^t} \end{equation}

\begin{equation} P_{r} = \frac{Pc}{INPP} \cdot 100 \end{equation}

\begin{equation} Cr_{k} = \frac{Cc_{k}}{INPP} \cdot 100 \end{equation}

\begin{equation} Ct_{k} = \frac{Cr_{k}}{{(1+i)}^t} \end{equation}

where PV is the discounted production value (USD), Pr_j is the real price by product type (USD m^-3), Q_j is the product amount (m³of timber), Pc is the nominal price of timber (USD m^-3), INPP is the National Index of Prices to the Producer with base year 2013, Cc_k is the nominal cost (USD), Cr_kis the real cost (fixed or variable, USD), Ct_k is the total discounted cost (USD), i is the real discount rate (3.5% and 4.5%), t is the number of years, beginning with the present, in which production is registered, j are the primary, secondary or cellulosic products, k are the stages of forestry process (establishment, maintenance, and timber harvest).

Reineke density index

The Reineke’s stand density index (SDI - eqn. 14) and the equation that represents the number of trees with 1 cm diameter per hectare (eqn. 15) were fit with OLS using 26 sites equivalent to 20% of all the sites of the dataset (130 sites - [41]):

\begin{equation} SDI=NT \cdot { \left (\frac{19}{Dq} \right )}^{-1.605} \end{equation}

\begin{equation} NT = \alpha_0 \cdot Dq^{ \alpha_1 } \end{equation}

where NT is the number of trees ha^-1, Dq is the quadratic mean diameter ha^-1, α_i are the parameters to be estimated.

Components of the evaluated scenarios

The different scenarios included the following variables and conditions: (i) productivity, site index (SI) of 18 and 30 m; (ii) silvicultural treatments, two thinnings and one regeneration cutting at the end of the rotation period (40 years), and one regeneration cutting at the end of the rotation period; (iii) final product: wood, carbon and a combined production (wood plus carbon); (iv) discount rate: 3.5% and 4.5%, and finally, the price of MgCo₂e ha^-1, which was USD 75 and USD 100. The combination of these gave rise to different scenarios. The percentage of trees to remove in each thinning was obtained through a density management diagram. The density management diagram is one of the most efficient methods of silvicultural planning and management in even-aged forests ([30]). This enables maximizing individual growth and total biomass production ([41]). Although the MSD considers 3 to 4 thinnings during the rotation period, we limited to two thinnings at 10 and 20 years, and a regeneration cutting at the end of the rotation (40 years). Pinus patula reaches its maximum volume growth between 24 and 27 years ([36]), and another thinning at 30 years of age would not have little effect on the species growth. The scenarios were evaluated based on the final product, timber and captured carbon (Tab. 1).

Tab. 1 - Scenarios evaluated for the condition of pine forest and timber as end product under the silvicultural treatment of two thinnings and one regeneration cutting. (SI): site index.

Scenario	SI	Discount rate (%)	Price Mg Co₂e (USD)	Product
1	18	3.5	100	Timber
2	18	4.5	75
3	30	3.5	100
4	30	4.5	75
5	18	3.5	100	Carbon sequestration
6	18	4.5	75
7	30	3.5	100
8	30	4.5	75

Enlarge/Reduce Open in Viewer

Financial indicators

The financial indicators used were Net Present Value (NPV), Internal Return Rate (IRR), Benefit-Cost Ratio (BCR) and Land Expected Value (LEV). Eqns. 16 to 19 show the respective algebraic expressions ([9], [39]):

\begin{equation} NPV=\sum_{t=0}^{n} {\frac{B_{t} -C_{t}} {(1+i)^t}} \end{equation}

\begin{equation} IRR=\sum_{t=0}^{n} {\frac{B_{t} -C_{t}}{(1+i^{ \text{*}} )^t}}=0 \end{equation}

\begin{equation} BCR=\frac{\sum_{t=0}^{n} {{B_{t}}/(1+i)^t}}{\sum_{t=0}^{n} {{C_{t}}/(1+i)^t}} \end{equation}

\begin{equation} LEV= \frac{\left [PVc+PVf - (Ad + Ma + \text{Re}) \cdot \delta - (Gr+Mr) \cdot e^{-iT} \right ]}{ \left (1- e^{-iT} \right )} +S \end{equation}

where B_t, C_t are the benefits and costs in the time period t (USD ha^-1); t is the time in years; i is the real discount rate (3.5% and 4.5%); i^* is the rate that makes the cash flow equal zero; LEV is the land expected value; PVc, PVf are the net present value of the benefits for carbon sequestration and sale of wood; Ad, Ma, Re, Gr, Mr are, respectively, the regeneration administrative costs (USD ha^-1), road maintenance costs of regeneration (USD ha^-1), regeneration land rent (USD ha^-1), costs of regeneration protection, and costs of stand maintenance (USD ha^-1), regeneration (USD ha^-1); S are the government support granted to the ejidos (USD ha^-1); δ is the parameter that expresses the discount factor for annuity; T is the rotation age (40 years).

Determination of the optimal rotation age for combined production

To determine the optimal rotation age for combined production, the equi-marginality criteria were used, that is, when the marginal benefit (MB) and the marginal cost (MC) associated with the decision to harvest are equal. Its mathematical expressions are presented in eqn. 20 and eqn. 21 ([46]):

\begin{equation} MB= \sum_{i} p_{i}V_{i}^{\prime}(T) + \left [pc \cdot \alpha \cdot V^{\prime}(T) \right ] \end{equation}

\begin{equation} MC=r \sum_{i} p_{i} V_{i} (T) + d(LEV) \end{equation}

where i = [cellulosic (ce), secondary (se), and primary products (pr)]; p_i is the price of the i-th product; V′_i(T) is the marginal increase in volume of the i-th product; V_i(T) is the volume of the i-th product at the end of the planning horizon; V′(T) is the increase in total volume; d is the real discount rate (3.5% and 4.5 %); pc is the price of carbon; α is a constant that expresses the proportion of CO₂e per m³ of wood.

Financial characterization

The costs and percentages during stand establishment (year 1) are shown in Tab. 2. Firebreaks, which are opened on the perimeter of the regeneration area with a minimum width of 3 m, was the costliest (USD 79.16), followed by purchase of seedlings (USD 63.32) and forest tools (USD 48.34 - machetes, axes, hoes, rakes and shovels). The total average cost for the stand establishment was USD 352.54 ha^-1, which was equivalent to 45.49% of the total costs (i.e., stages of establishment and maintenance).

Tab. 2 - Activities and real average cost (USD ha^-1) for the stand establishment during the first year.

Establishment	Total (USD ha^-1)	Percentage
Fencing material	29.92	3.86
Labor for fencing	27.49	3.61
Cost of seedlings	63.32	8.17
Transportation costs of seedlings	5.28	0.68
Labor for seedling establishment	54.19	6.99
Opening roads	44.33	5.72
Opening fire-breaks	79.16	10.21
Tools	48.34	6.24
Total	352.54	45.49

Enlarge/Reduce Open in Viewer

Maintenance involved six activities (Tab. 3) and accounts for 54.51% of the total fixed costs (not considering harvesting costs). Costs of land rent and protection against pests and fires are covered throughout the rotation period (40 years) and add up to USD 101.98 ha^-1year^-1. Cleaning of the planted land (chapeo), pruning and liberation cutting are carried out during the first 8 years of the stand with an annual cost of USD 120.49 ha^-1. Maintenance of firebreaks and roads has a cost of USD 133.40 ha^-1 in the second year and USD 66.60 ha^-1 year^-1 from the third and successive years. The total cost, considering the establishment and maintenance stages for the planning horizon was USD 775.03 ha^-1.

Tab. 3 - Activities and real average cost (USD ha^-1) for the maintenance stage.

Maintenance	Total (USD ha^-1)	Periodicity	Percentage
Land rent	65.65	Yearly	8.47
Protection against pests	28.24	Yearly	3.64
Protection against fires	8.09	Yearly	1.04
Clearing	69.43	Until year 8	8.95
Pruning and liberation cutting	51.05	Until year 8	6.58
Maintenance of fire-breaks	87.35	Only during the 2nd year	11.27
Maintenance of roads	46.05	Only during the 2nd year	5.94
Maintenance of fire-breaks	43.57	As of the 3rd year	5.62
Maintenance of roads	23.03	As of the 3rd year	2.97
Total	422.48	-	54.51

Enlarge/Reduce Open in Viewer

Harvest activities had a total cost of USD 12.23 m^-3extracted and includes the cost of forest technical services (USD 1.50 m^-3); on site processing (felling, sectioning and moving logs to the drag track) costs USD 8.07 m^-3, while for final cutting and thinning (regardless of the type of product) and costs of administration was USD 2.68 m^-3.

During the rotation period, the ejido receive diverse subsidies from the federal government through the National Forestry Commission (CONAFOR) to achieve different activities including a payment for environmental services destined to conservation of forested areas that have been excluded from timber production (Tab. 4).

Tab. 4 - Average Mexican government subsidy, in real terms (USD ha^-1), in support of forestry activity in the region.

Subsidy	Total (USD ha^-1)	Periodicity
Fencing	49.68	First year
Planting	73.26	First year
Road maintenance	34.72	Every year
Cleaning of the planted land (chapeo) and pruning	44.24	Until 8 years
Payment for environmental services	78.24	Every year
Total	280.17	-

Enlarge/Reduce Open in Viewer

In the harvesting stage, an aspect that called our attention was the high cost of administration. Every cubic meter of extracted timber had a cost of USD 2.68 (21.97% of the total cost of this stage), added to the costs of in site processing of USD 0.07 (65.99 %) and USD 1.50 (12.04 %) for forest technical services, making a total of USD 12.23 m^-3. The costs of administration during timber harvest are considered high. On average, this harvest activity is carried out by four people, who work approximately four months, but with adequate organization, it could be done by two people. However, trying to reduce these costs is complicated because the ejidos highly value the social features (i.e., job generation).

The Reineke’s stand density index and thinning regime

Fitting of the Reineke’s stand density index model had an R²-adj of 0.96, as well as statistical significance in its parameters. The following is the final model (eqn. 22):

\begin{equation} NT = 198260.27 \cdot Dq^{-1.74} \end{equation}

where NT is the number of trees ha^-1, Dq is the quadratic mean diameter (cm).

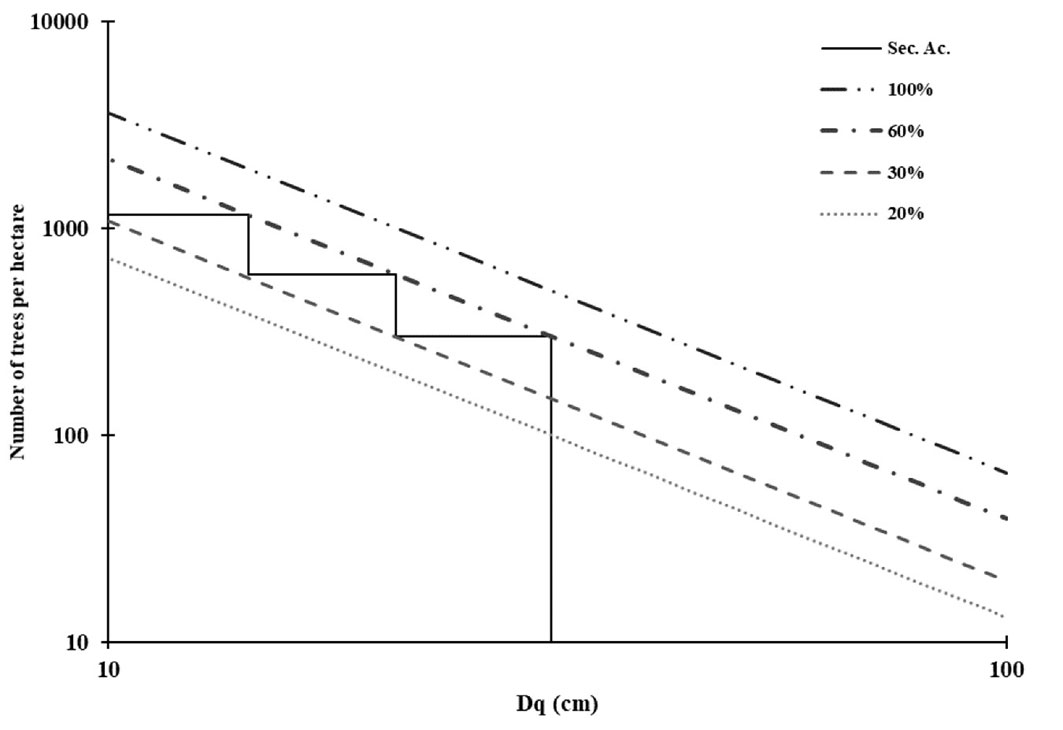
The density management diagram generated for an initial 1200 trees suggests two intensive thinnings before harvest (40 years - Fig. 1). This result coincides with Santiago et al. ([41]), who indicated that in Pinus patula stands in a geographic area near our study site, thinning intensity should be 50% at each intervention.

Fig. 1 - Thinning prescription for Pinus patula stands in Zacualtipán, Hidalgo. (Sec. Ac.): thinning intensity; (100% and 60%): upper and lower limit of the area of self-thinning; (30%): upper limit of the area of constant growth; (20%): lower limit of growth free of mortality.

Enlarge/Shrink Download Full Width Open in Viewer

Thinnings occur at a Dq of 14.34 and 20.90 cm, while the final cutting is at 31.5 cm at the age of 10, 20 and 40 years, respectively. The thinning intensity suggested is 48% and 50% for the first and second thinnings. This does not consider natural mortality since in natural stands with densities below 1000 threes ha^-1, the mortality rate is low (0.81% - [36]). Therefore, decreasing the number of individuals was the consequence of only silvicultural interventions.

Scenarios for pine forest

Tab. 5presents the financial indicators obtained for the scenarios generated for timber as the final product. For all the scenarios in which two thinnings and one regeneration cutting are applied (scenarios 1, 2, 3, and 4), the results indicate that timber production is profitable, with PNV of 735.79 to USD 1838.31 ha^-1, IRR of 6.09 to 6.51% with BCR of more than one, and positive LEV values. Undoubtedly, the scenarios with SI 30 have better results than those with SI 18 and are even better when low interest rates are considered, as was shown with an interest rate of 3.5%. Application of thinnings is of great importance in forest management because it permits redistribution of growth and manipulation of tree spacing, favoring growth of the target individuals and species ([29]).

Tab. 5 - Financial indicators obtained for the scenarios of SI 18 and SI 30, with timber as the end product.

Scenario	SI	Discount rate (%)	NPV (USD)	IRR (%)	BCR	TT (yrs)	LEV (USD)
1	18	3.5	1512.54	6.09	1.25	29	650.16
2	18	4.5	735.79	6.09	1.14	29	-114.47
3	30	3.5	1838.31	6.51	1.28	27	920.74
4	30	4.5	974.84	6.51	1.17	27	51.76

Enlarge/Reduce Open in Viewer

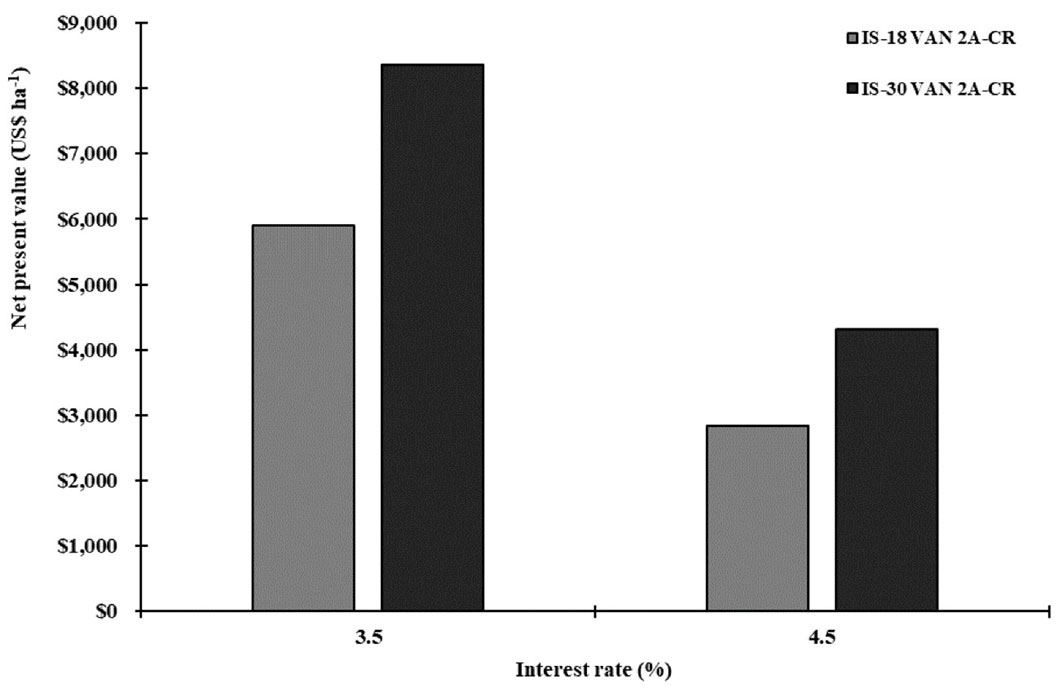
For the scenario of not harvesting at the rotation age and entering to the market of carbon credits to commercialize sequestered CO₂e stored in the forest stand, estimated financial indicators are optimistic under certain conditions. Fig. 2 shows the NPV for the different scenarios; the highest value is obtained in SI 30, with two thinnings and one regeneration cutting, a discount rate of 3.5% and a price of USD 100 per MgCO₂e ha^-1 year^-1 (scenario 7), while the lowest value occurred in SI 18 with two thinnings and the regeneration cutting, a discount rate of 4.5% and a price of USD 75 (scenario 6).

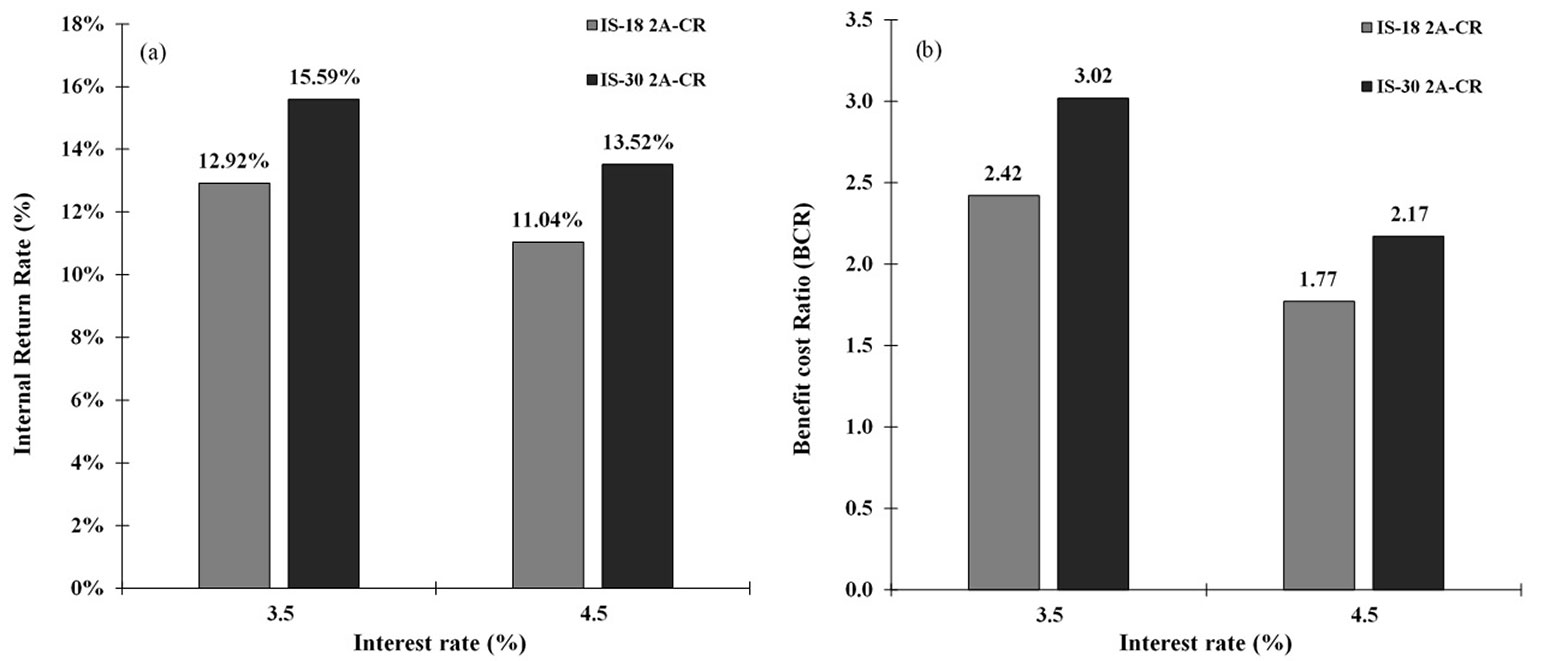
Fig. 2 - Net present value (NPV) for different scenarios and SI of 18 and 30.

Enlarge/Shrink Download Full Width Open in Viewer

The values obtained for IRR ratify the finding for NPV (Fig. 3a). The proposed scenarios (no. 5, 6, 7, and 8) for SI 18 and SI 30 had values above 10%. Under the defined conditions, the discount rate used can increase to 10% and, even then, the project would still be profitable. On the other hand, Fig. 3b shows the BCR for different scenarios. The highest value was obtained in scenario 7, in which USD 2.02 would be received for every dollar invested, while in scenario 6, there would be a profit of USD 0.77 for each dollar invested.

Fig. 3 - (a) Internal return rate (IRR - %) and (b) benefit cost ratio (BCR) obtained in the scenarios with SI of 18 and 30.

Enlarge/Shrink Download Full Width Open in Viewer

Optimal rotation period for timber production plus carbon sequestration

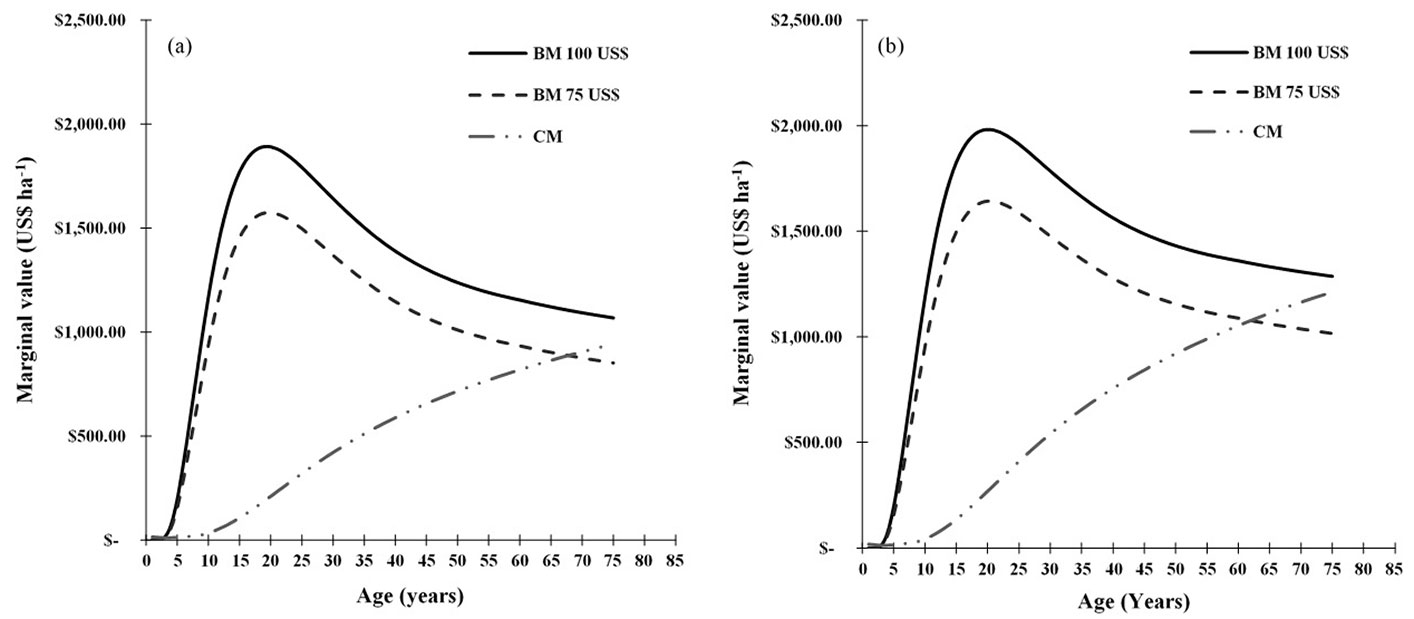
The technical rotation determined for SI 30 was 37 years, but if a combined production is selected, the optimal rotation period (i.e., when BM = CM) lengthens. With a discount rate of 3.5% and a price of USD 100 per MgCO₂e ha^-1 year^-1 captured, the optimal rotation period was more than 75 years. However, using the same discount rate, but at a price of USD 75, the rotation period is 69 years (Fig. 4a). Using a discount rate of 4.5% with a price of USD 100 and USD 75 per MgCO₂e ha^-1 year^-1 captured, the optimal periods are 75 and 63 years, respectively (Fig. 4b). This implies that when the discount rate increases, the optimal rotation period decreases. This behavior was also reported by Abedi et al. ([1]) and Keles ([22]). The extent of the rotation age, including carbon sequestration benefits, has been documented by several authors. Abedi et al. ([1]) evaluated two Populus deltoides plantations in northern Iran and found that, by including carbon sequestration, the rotation ages increased from 10 to 14 years for tree density of 3 by 3 m and from 8 to 11 years for the 3 × 4 m. Similarly, Keles ([22]) determined the optimal cutting ages in plantations of Turkish pine (Pinus brutia Ten.), under different crop spacing and found that without considering the benefits from carbon sequestration, the optimal cutting ages were between 29 and 32 years; however, when these benefits were included, the optimal ages were between 33 and 39 years. Likewise, Gutrich & Howarth ([18]) explored different types of forest in the state of New Hampshire, USA and found that the optimal rotation period without considering carbon sequestration varied from 34 to 44 years, depending on the type of forest, and when considering low marginal benefits from carbon sequestration, the optimal rotation period was 53 to 177 years.

Fig. 4 - Optimum rotation period in a SI of 30 for combined production. Prices for MgCO₂e ha^-1 year^-1 of USD 100 and USD 75 with a discount rate of (a) 3.5% and (b) 4.5%.

Enlarge/Shrink Download Full Width Open in Viewer

Timber production or carbon sequestration

In general, timber production involves a series of high costs attributable to establishment and maintenance over the rotation period (40 years). In productive areas with SI of 24, 30 and 36, this activity is profitable, but in poor sites (SI 18), it is not. Therefore, productive zoning of the forest becomes fundamental since forest exploitation is usually carried out on relatively large areas and the above is not considered.

The Mexican government endeavors to encourage ejidos to conserve their forests through a series of programs ([7]). However, these efforts have not had the expected results, nor have they been able to totally cover the demand. There are several conditions and requirements that hinder the access to some of the support intended for forest activity. For example, incorporating a project under the Clean Development Mechanism (CDM) requires that additionality be demonstrated ([11]), meaning that the reduction of CO₂ emissions of a new project are higher than those that would occur without the project. In addition to approaching baseline problems of the project and possible leaks, the compensations occasionally continue to be the same. This has influenced the forest owners’ decisions to not include carbon sequestration as a viable alternative ([16]).

Regarding REDD+, Stern ([45]) mentions that decreasing emissions from degradation and deforestation by 50% in developing countries by 2030 could cost between 15 and 33 billion dollars annually. For this reason, implementing actions in the short term aimed to decrease these emissions would be profitable, especially when it is contrasted with the enormously high environmental and economic costs resulting from inaction.

An alternative to CDM is the voluntary market, where the exchange of emissions certificates is not regulated by specific legal norms and have been, to date, the only source of funding for projects to reduce emissions from deforestation and forest degradation (REDD+ - [40]). In this panorama, forming part of a voluntary market might be the best option. However, the average price per MgCO₂e is USD 10 ([25]). According to our results, it is not enough to cover maintenance costs. Therefore, going from timber production to combined production is still uncertain and complicated.

Postponing harvest of a stand is profitable when the forest growth rate is higher than the defined discount rate. If not, it is better not to delay harvest and sell ([2]). However, delaying harvesting, even if it is not profitable, would increase social benefit since all the carbon stored would remain sequestered for a longer time. In Mexico, 60% of the forested area is owned by ejidos and indigenous communities ([47]), and these areas have an important role in reducing poverty, dealing with social exclusion, and jobs generation ([34]). The owners of these forests, who mostly belong to middle and poor economic classes, are highly dependent on the products they harvest, and ceasing to use the forest would bring consequences in terms of opportunity costs, while people with more resources would be willing to pay for improving their health and development through the supply of fresh air, water, scenery ([8]), and other benefits the forest provides. According to Blomley & Iddi ([6]), forests have a much more important role as sources of cash for poor homes than for relatively rich homes. For this reason, it is difficult to destine forests only to carbon sequestration and storage given the conditions of the ejidos and communities of Mexico.

Destining low-productive areas to carbon sequestration is profitable only if payment for MgCO₂e is at least USD100 per ha^-1 year^-1, and if the discount rate is less than 3.5%. Combining timber production with carbon sequestration would involve extending the rotation period, which are sensitive to the discount rate and to the price of MgCO₂e captured. Longer optimal rotation aged implies that the CO₂stored in the forest stands to be intervened would remain for a longer time, and the benefits it would generate would be more of a social than economic nature.

Timber production will remain as the main economic option at least the rules to operate of the different national and international carbon mechanisms become more flexible, and the carbon markets offer better economic incentives.

The characterization of the costs incurred in each stage of forest management allowed detecting areas of opportunity for the forestry enterprises studied, which can help them becoming more efficient, effective and competitive.

(1)

Abedi T, Mohammadi S, Bonyad A, Torkaman J (2018). Optimal rotation age of Populus deltoides considering economic value of timber harvesting and carbon sequestration. Austrian Journal of Forest Science 135: 315-342.
Online | Gscholar

(2)

Ackerman F (1993). The natural interest rate of the forest: macroeconomic requirements for sustainable development. Ecological Economics 10: 21-26.
CrossRef | Gscholar

(3)

Ajete I, Mercadet D, Alvarez D, Toirac I, Conde I (2012). Estimación del contenido de carbono en los bosques de la empresa forestal integral Guantánamo [Estimation of the carbon content in the forests the forest integral company Guantanamo]. Revista Forestal Baracoa 31: 3-8. [in Spanish]
Gscholar

(4)

Angeles G, Méndez B, Valdez R, Plascencia O, De los Santos HM, Chávez G, Ortiz D, Soriano A, Zaragoza Z, Ventura E, Martínez A, Wayson C, López D, Olguín M, Carrillo O, Maldonado V (2015). Estudio de caso del sitio de monitoreo intensivo del carbono en Hidalgo. Fortalecimiento REDD+ y Cooperación Sur [Case study of the site of intensive carbon monitoring in Hidalgo. Strengthening REDD + and South Cooperation]. CONAFOR, COLPOS, Mexico, pp. 105. [in Spanish]
Gscholar

(5)

Bettinger P, Boston K, Siry JP, Grebner DL (2017). Forest management and planning (2nd edn). Academic Press, New York, USA, pp. 349.
Online | Gscholar

(6)

Blomley T, Iddi S (2009). Participatory forest management in Tanzania. 1993-2009: lessons learned and experiences to date. Ministry of Natural Resources and Tourism - URT, Forestry and Beekeeping Division, Dar es Salaam, Tanzania, pp. 72.
Online | Gscholar

(7)

Chagoya JL, Iglesias G (2009). Esquema de pago por servicios ambientales de la Comisión Nacional Forestal, México [Payment scheme for environmental services of the National Forestry Commission, Mexico]. In: “Políticas Públicas y Sistemas de Incentivos Para el Fomento y Adopción de Buenas Prácticas Agrícolas: Como Medida de Adaptación al Cambio Climático en América Central” (Sepúlveda C, Ibrahim M eds). Primera Edición, Turrialba, CATIE, Costa Rica, pp. 291-292. [In Spanish]
Online | Gscholar

(8)

Chaudhary M (2009). Assessing the protection of forest based environmental services in the Greater Mekong sub-region. Asia-Pacific Forestry Sector Outlook Study II, Working Paper Series vol. 14, FAO/UN, Bangkok, Thailand, pp. 67.
Gscholar

(9)

Clutter JL, Forston JC, Pienaar LV, Brister GH, Bailey RL (1983). Timber management: a quantitative approach. John Wiley and Sons, Inc., New York, USA, pp. 333.
Online | Gscholar

(10)

Cubbage F, Donagh PM, Balmelli G, Olmos VM, Bussoni A, Rubilar R, De La Torre R, Lord R, Huang J, Hoeflich VA, Murara M, Kanieski B, Hall P, Yao R, Adams P, Kotze H, Monges E, Pérez CH, Wikle J, Abt R, Gonzalez R, Carrero O (2014). Global timber investments and trends, 2005-2011. New Zealand Journal of Forestry Science 44: 1-12.
CrossRef | Gscholar

(11)

De Olivera FLP, Lemme CF, Leal RPC (2011). Cost of equity capital and additionality of Brazilian renewable energy projects under the clean development mechanism. Latin American Business Review 12: 233-253.
CrossRef | Gscholar

(12)

Díaz L (2002). Los sistemas forestales y la provisión de bienes ambientales [Forest systems and the provision of environmental goods]. In: Jornada Temática “Aspectos Medioambientales de la Agricultura”. Libro Blanco de Agricultura, Madrid, Spain, pp. 12. [in Spanish]
Gscholar

(13)

Dlugokencky E, Tans P (2018). Trends in atmospheric carbon dioxide. National Oceanic and Atmospheric Administration, Earth System Research Laboratory - NOAA/ESRL, Boulder, Colorado, USA, Web Site.
Online | Gscholar

(14)

Fang Z, Borders BE, Bailey RL (2000). Compatible volume-taper models for loblolly and slash pine based on a system with segmented-stem form factors. Forest Science 46: 1-12.
Online | Gscholar

(15)

Figueroa C, Angeles G, Velázquez A, De los Santos HM (2010). Estimación de la biomasa en un bosque bajo manejo de Pinus patula Schltdl. et Cham. en Zacualtipán, Hidalgo [Biomass estimation in a managed Pinus patula Schltdl. et Cham. forest at Zacualtipan, Hidalgo state]. Revista Mexicana de Ciencias Forestales 106: 105-112. [in Spanish]
Gscholar

(16)

Foley T (2009). Extending forest rotation age for carbon sequestration: a cross-protocol comparison of carbon offsets of North American forests. Masters Project, Nicholas School of the Environment, Duke University, Durham, NC, USA, pp. 51.
Gscholar

(17)

Fonseca W, Villalobos R, Rojas M (2019). Potencial de mitigación del cambio climático de los ecosistemas forestales caducifolios en Costa Rica: modelos predictivos de biomasa y carbono [Potential mitigation of climate change of deciduous forest ecosystems in Costa Rica: predictive models of biomass and carbon]. Revista de Ciencias Ambientales 53: 111-131. [In Spanish]
CrossRef | Gscholar

(18)

Gutrich J, Howarth R (2007). Carbon sequestration and the optimal management of New Hampshire timber stands. Ecological Economics 62: 441-450.
CrossRef | Gscholar

(19)

INEGI (2018). Sistema de cuentas nacionales de México año base 2013 [System of national accounts of Mexico base year 2013]. Instituto Nacional de Estadística Geográfica e Informática, DF, México, pp. 593. [in Spanish]
Gscholar

(20)

IPCC (2013). Glossary. In: “Climate change 2013. Physical bases. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Group of Experts on Climate Change” (Stocker TF, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM eds). Cambridge University Press, Cambridge, UK, pp. 185-204
Gscholar

(21)

Joos F, Spahni R (2008). Rates of change in natural and anthropogenic radiative forcing over the past 20.000 years. Proceedings of the National Academy of Sciences USA 105: 1425-1430.
CrossRef | Gscholar

(22)

Keles S (2017). Determining optimum cutting ages including timber production and carbon sequestration benefits in Turkish pine plantations. Sains Malaysiana 46: 381-386.
CrossRef | Gscholar

(23)

Klemperer WD (1996). Forest resource economics and finance. McGraw Hill, New York, USA, pp. 551.
Online | Gscholar

(24)

Köthke M, Dieter M (2010). Effects of carbon sequestration rewards on forest management - an empirical application of adjusted Faustmann formulae. Forest Policy and Economics 12: 589-597.
CrossRef | Gscholar

(25)

Lobos A, Vallejos GO, Caroca C, Marchant C (2005). El mercado de los bonos de carbono (“bonos verdes”): una revisión [The carbon credit market (“green bonds”): a review]. Revista Interamericana de Ambiente y Turismo 1: 42-52. [in Spanish]
Online | Gscholar

(26)

Locatelli B, Evans V, Wardell A, Andrade A, Vignola R (2011). Forests and climate change in Latin America: linking adaptation and mitigation. Forests 2: 431-450.
CrossRef | Gscholar

(27)

López L, Domínguez M, Martínez P, Zavala J, Gómez A, Posada S (2016). Carbono almacenado en la biomasa aérea de plantaciones de hule (Hevea brasiliensis Müell. Arg.) de diferentes edades [Stored carbon in the aboveground biomass of rubber (Hevea brasiliensis Müell. Arg.) plantations at different ages]. Madera y Bosques 22: 49-60. [in Spanish]
CrossRef | Gscholar

(28)

Masera O, Bellon MR, Segura G (1997). Forestry options for sequestering carbon in Mexico: comparative economic analysis of three case studies. Critical Reviews in Environmental Science and Technology 27: 227-244.
CrossRef | Gscholar

(29)

Mead JD (2005). Opportunities for improving plantation productivity. How much? How quickly? How realistic? Biomass and Bioenergy 28: 249-266.
CrossRef | Gscholar

(30)

Müller U, Rodríguez R, Gajardo P (2013). Desarrollo de una guía de manejo de la densidad en bosques de segundo crecimiento de roble (Nothofagus obliqua) en la región del Biobío [Stand density management diagrams for roble (Nothofagus obliqua) in the Biobío Region, Chile]. Bosque 34: 201-209. [in Spanish]
CrossRef | Gscholar

(31)

Musálem LF (1979). Las bases y primeras acciones del programa nacional de mejoramiento silvícola en bosques de coníferas [The bases and first actions of the national silvicultural improvement program in coniferous forests]. SAG-SFF, DF, México, pp. 102. [in Spanish]
Gscholar

(32)

Nepal P, Grala R, Grebner D (2012). Financial feasibility of increasing carbon sequestration in harvested wood products in Mississippi. Forest Policy and Economics 14: 99-106.
CrossRef | Gscholar

(33)

Palacios DJ, De los Santos HM, Angeles G, Fierros AM, Santiago W (2020). Sistema de crecimiento y rendimiento para evaluar sumideros de carbono en bosques de Pinus patula Schiede ex Schltdl. et Cham. bajo aprovechamiento forestal [Growth and yield system to evaluate carbon sinks in managed Pinus patula Schiede ex Schltdl. et Cham. forests]. Agrociencia 54: 241-257. [in Spanish]
Online | Gscholar

(34)

Patel T, Dhiaulhaq A, Gritten D, Yasmi Y, Bruyn TD, Paudel NS, Suzuki R (2013). Predicting future conflict under REDD+ implementation. Forests 4: 343-363.
CrossRef | Gscholar

(35)

Phelps J, Guerrero M, Dalabajan D, Young B, Webb E (2010). What makes a “REDD” country? Global Environmental Change 20: 322-332.
CrossRef | Gscholar

(36)

Ramírez A, De los Santos HM, Angeles G, González MJ, Santiago W (2020). Densidad inicial en el rendimiento maderable y biomasa de Pinus patula con especies latifoliadas [Initial density in the timber yield and biomass of Pinus patula with hardwood species]. Agrociencia 54: 555-573. [in Spanish]
CrossRef | Gscholar

(37)

Reyes JA, Gómez JP, Osaland R, Zavala R (2012). Potencial de servicios ambientales en la propiedad social en México [Potential of environmental services in social property in Mexico]. Instituto Interamericano de Cooperación para la Agricultural, Secretaría de la Reforma Agraria, México, pp. 103. [In Spanish]
Gscholar

(38)

Rodríguez L, Guevara F, Reyes L, Ovando J, Nahed J, Prado M, Campos R (2016). Estimación de biomasa y carbono almacenado en bosques comunitarios de la región Frailesca de Chiapas, México [Estimation of the biomass and stored carbon in community forest of La Frailesca region of Chiapas, Mexico]. Revista Mexicana de Ciencias Forestales 7: 77-94. [In Spanish]
CrossRef | Gscholar

(39)

Romero C, Ríos V, Díaz L (1998). Optimal forest rotation age when carbon captured is considered: theory and applications. Journal of the Operational Research Society 49: 121-131.
CrossRef | Gscholar

(40)

Sabogal J, Moreno E, Ortega GA (2009). Procesos de certificación de proyectos de captura de gases de efecto invernadero (GEI) En los Mercados Internacionales de Carbono [Certification processes for greenhouse gas (GHG) capture projects in the International Carbon Markets]. Gestión y Ambiente 12: 07-20. [In Spanish]
Online | Gscholar

(41)

Santiago W, De los Santos HM, Angeles G, Valdez JR, Del Valle DH, Corral JJ (2013). Self-thinning and density management diagrams for Pinus patula fitted under the stochastic frontier regression approach. Agrociencia 47: 75-89.
Online | Gscholar

(42)

Santiago W, De Los Santos HM, Angeles G, Corral JJ, Valdez JR, Del Valle DH (2014). Prediction of Pinus patula Schl. et Cham. timber yield through diameter distribution models. Agrociencia 48: 87-101.
Online | Gscholar

(43)

Sauter PA, Mußhoff O (2018). What is your discount rate? Experimental evidence of foresters’ risk and time preferences. Annals of Forest Science 75 (1): 239.
CrossRef | Gscholar

(44)

Schwartz N, Aide T, Graesser J, Grau H, Uriarte M (2020). Reversals of reforestation across Latin America limit climate mitigation potential of tropical forests. Frontiers in Forests and Global Change 3: 85.
CrossRef | Gscholar

(45)

Stern N (2007). The economics of climate change: the Stern Review. Cambridge University Press, Cambridge, UK, pp. 662.
CrossRef | Gscholar

(46)

Telles E, González MJ, De los Santos HM, Fierros AM, Lilieholm RJ, Gómez A (2008). Rotación óptima en plantaciones de eucalipto al incluir ingresos por captura de carbono en Oaxaca, México [Optimal timber rotation lenghts in eucalyptus plantations including revenues from carbon capture in Oaxaca, Mexico]. Revista Fitotecnia Mexicana 31: 173-182. [in Spanish]
CrossRef | Gscholar

(47)

Torres JM (2015). Desarrollo forestal comunitario: la política pública [Community forestry development: public policy]. Cide, DF, México, pp. 238. [in Spanish]
Online | Gscholar

(48)

Torres JM, Moreno R, Mendoza MA (2016). Sustainable forest management in Mexico. Current Forestry Reports 2: 93-105.
CrossRef | Gscholar

(49)

UNFCCC (2015). París agreement. United Nations Framework Convention on Climate Change, United Nations, Paris, France, pp. 40. [in Spanish]
Online | Gscholar

(50)

Vargas B, Corral JJ, Aguirre OA, López JO, De Los Santos HM, Zamudio FJ, Treviño EJ, Martínez M, Aguirre CG (2017). SiBiFor: forest biometric system for forest management in Mexico. Revista Chapingo Serie Ciencias Forestales y del Ambiente 23: 437-455.
CrossRef | Gscholar

(51)

Zomer R, Trabucco A, Bossio D, Verchot L (2008). Climate change mitigation: a spatial analysis of global land suitability for clean development mechanism afforestation and reforestation. Agriculture, Ecosystems and Environment 126: 67-80.
CrossRef | Gscholar

Authors’ Affiliation

(1)

0000-0003-1814-4320
0000-0003-4076-5043
0000-0002-9550-2825
Colegio de Postgraduados, km. 36.5 Carr. Mexico-Texcoco, Montecillo, Texcoco, C.P. 56230 (México)

(2)

0000-0003-1958-1696
Instituto de Estudios Ambientales-División de Estudios de Postgrado-Ingeniería Forestal, Universidad de la Sierra Juárez, Avenida Universidad s/n, C. P. 68725, Ixtlán de Juárez, Oaxaca (México)

Corresponding author

Manuel de Jesús González-Guillén
mgonzalezg60@gmail.com

Citation

Ramírez-Martínez A, González-Guillén MJ, De Los Santos-Posadas HM, Ángeles-Pérez G, Santiago-García W (2021). Forest management with carbon scenarios in the central region of Mexico. iForest 14: 413-420. - doi: 10.3832/ifor3630-014

Academic Editor

Marco Borghetti

Paper history

Received: Aug 19, 2020
Accepted: Jul 13, 2021

First online: Sep 15, 2021
Publication Date: Oct 31, 2021
Publication Time: 2.13 months

Open Access

This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Breakdown by View Type

(Waiting for server response...)

Article Usage

Total Article Views: 21885
(from publication date up to now)

Breakdown by View Type
HTML Page Views: 18745
Abstract Page Views: 1120
PDF Downloads: 1733
Citation/Reference Downloads: 6
XML Downloads: 281

Web Metrics
Days since publication: 954
Overall contacts: 21885
Avg. contacts per week: 160.58

Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Feb 2023)

(No citations were found up to date. Please come back later)

(no records found)

Publication Metrics

by Dimensions ^©

List of the papers citing this article based on CrossRef Cited-by.

iForest Similar Articles

Research Articles

Heuristic forest planning model for optimizing timber production and carbon sequestration in teak plantations

Quintero-Méndez MA, Jerez-Rico M

vol. 10, pp. 430-439 (online: 24 March 2017)

Research Articles

Potential impacts of regional climate change on site productivity of Larix olgensis plantations in northeast China

Shen C, Lei X, Liu H, Wang L, Liang W

vol. 8, pp. 642-651 (online: 02 March 2015)

Research Articles

Voluntary carbon credits from improved forest management: policy guidelines and case study

Vacchiano G, Berretti R, Romano R, Motta R

vol. 11, pp. 1-10 (online: 09 January 2018)

Research Articles

Roadside vegetation: estimation and potential for carbon sequestration

Da Silva AM, Braga Alves C, Alves SH

vol. 3, pp. 124-129 (online: 27 September 2010)

Research Articles

Modelling the carbon budget of intensive forest monitoring sites in Germany using the simulation model BIOME-BGC

Jochheim H, Puhlmann M, Beese F, Berthold D, Einert P, Kallweit R, Konopatzky A, Meesenburg H, Meiwes K-J, Raspe S, Schulte-Bisping H, Schulz C

vol. 2, pp. 7-10 (online: 21 January 2009)

Research Articles

Climate-wise models of biomass productivity for hybrid poplar clones in Europe

Bianchi S, Lee D, Bergante S, Facciotto G, Hynynen J, Nervo G

vol. 16, pp. 188-194 (online: 30 June 2023)

Research Articles

Modeling air pollutant removal, carbon storage, and CO₂ sequestration potential of urban forests in Scotlandville, Louisiana, USA

Ning ZH, Chambers R, Abdollahi K

vol. 9, pp. 860-867 (online: 22 September 2016)

Editorials

Change is in the air: future challenges for applied forest research

Tognetti R, Cherubini P

vol. 2, pp. 56-58 (online: 18 March 2009)

Research Articles

Identifying priority conservation areas for above-ground carbon sequestration in Central Mexico

Cruz-Huerta C, González-Guillén MDJ, Martínez-Trinidad T, Escalona-Maurice M

vol. 10, pp. 923-929 (online: 07 December 2017)

Research Articles

First vs. second rotation of a poplar short rotation coppice: leaf area development, light interception and radiation use efficiency

Broeckx LS, Vanbeveren SP, Verlinden MS, Ceulemans R

vol. 8, pp. 565-573 (online: 27 April 2015)

iForest Database Search

Search By Author

Search By Keyword

Google Scholar Search

Citing Articles

GScholar

Search By Author

Search By Keywords

PubMed Search

Search By Author

Search By Keyword

iForest - Biogeosciences and Forestry

Contents

Search

Journal Info

Journal Subjects and Fields

For Authors

For Reviewers

For Readers

SISEF Publishing

Search iForest Contents