Allometric relationships for predicting the stem volume in a Dalbergia sissoo Roxb. plantation in Bangladesh
iForest - Biogeosciences and Forestry, Volume 3, Issue 6, Pages 153-158 (2010)
doi: https://doi.org/10.3832/ifor0554-003
Published: Nov 15, 2010 - Copyright © 2010 SISEF
Research Articles
Abstract
Allometric relationships for estimating stem volumes of Dalbergia sissoo Roxb. (Sissoo) trees were investigated in monoculture plantations in Bangladesh. The various allometric relationships between stem volume and different dimensions were tested and the coefficient of determination R2 values were used to compare the strength of the relationships. Although the allometric equations were highly significant (P<0.01) there was considerable variation among them as indicated by the R2 values. Our results suggested that tree volume is more correlated with basal area than with simple D (stem diameter at 1.3 m height above the ground). The allometric relationships of stem volume to the tree diameter at 10% of tree height (D0.1) did not improve the allometric strength in comparison with simple D as reported in case of some other tree species. The multiplication of tree height H with D in the allometric equation gives a little improvement in the degree of fitness of the allometric equations. However, for the Sissoo plantations studied the stem dbh alone showed a very strong accuracy of estimation (R2 = 0.997) especially when used as D2. It is concluded that the use of tree height in the allometric equation can be neglected for the species, as far as the present study area is concerned. Therefore, for estimating the stem volume of Sissoo, the use of D2 as an independent variable in the allometric equation with a linear or quadratic equation is recommended. The paper describes details of tree volume allometry, which is important in silviculture and forest management.
Keywords
Allometry, Monoculture plantation, Regression, Rosewood, Sissoo, Stem volume
Introduction
Sissoo is known as a premier timber species of the rosewood genus with the common name sissoo in Bangladesh. It is native to Sub-Himalayan zone including India, Pakistan and Afghanistan ([35], [20]). It is also recognized as an important species for fuel wood, shade tree, agroforestry and fodder in the region ([35], [34], [13]). Foresters traditionally derive timber volumes by employing allometric techniques. Allometric relationship for estimating stand volume as well as forest biomass is very important for managing any natural and artificial forest resources ([5], [10], [22], [24]). In the estimation of stand volume, the uncertainties appear due to the measurements of basal area and the use of a mean form factor, which is related to mean tapering ([24]). Thus, allometric relationships offer better estimates of the forest standing volume, which is also an important parameter in further research such as biomass and carbon-emission estimates avoiding the uncertainties in the bole-volume estimates ([16], [24]). Therefore, choosing a suitable functional variable in the allometric equation is very important for allometric techniques in forest science ([16], [17]).
There are various independent variables in the allometric relationships to estimate biomass. In most studies, D (dbh, stem diameter at 1.3 m height above the ground) was taken as the only independent variable in the allometric equation (e.g., [23], [29], [12], [1], [11], [26]). However, incorporation of the variable H (tree height - i.e., the use of D2H) ensures higher accuracy of allometric estimation in some tree species ([32], [33], [18], [28]). Moreover, the use of the new variable D0.12H (D0.1, diameter at one-tenth of H) instead of D2H has been suggested to improve the accuracy of estimation ([25], [14], [17]). Attiwill ([3]) found a strong allometric relationship between the girth (at the point immediately before branching) of main branches of a tree and branch dry weight in a stand of Eucalyptus obliqua L’ Herit. The use of DB (stem diameter at a height of clear bole length) provides better results in estimating the weight of branch and leaf, and leaf area per tree, as described by the pipe model theory of Shinozaki et al. ([30]). Various allometric equations have been developed from different tropical species ([7], [27], [6], [2], [9], [16], [10]). It is evident that mainly species of dicotyledonous trees differ in allometry because of distinctive bole shape. The allometric equations developed from various species yield useful estimates for large-scale inventories.
In this paper, we seek to establish the allometric relationships of the stem volume of individual trees to different dimensions, such as D, D2, D2H, D0.1, D0.12 and D0.12H and to propose a standard method for predicting the stem volume of Sissoo.
Materials and methods
Study site and species description
The study was carried out in block plantations at Khulna located in the southern part of Bangladesh (Fig. 1). The area belongs to subtropical region. Dalbergia sissoo is one of the important plantation species in the region.
The species is a strong-light demander and shows good coppicing ability ([35]). The development of seedling is better in full overhead light than under partial shade. It is capable of growing under adverse soil and moisture conditions ([34]). Though, D. sissoo is a frost hardy species, its young leaves are adversely affected by severe frost and even the poles get completely defoliated ([31]). It has a complex root system that consists of a deep tap root and long lateral roots. Root suckers are produced from the lateral roots. Root suckers develop towards the end of the rainy season and may attain a height of more than 2 m on good soil ([15]). The species can grow naturally up to 1500 m elevation. The temperature in its native range averages 12-22 °C, but varies from just below freezing to nearly 50 °C with an average annual rainfall of 500 to 2000 mm with a monsoonal pattern and drought period of 3-4 months ([35]). The growth of the bole is crooked and straight logs of any great length are difficult to obtain. The heartwood is brown with darker streaks and because of its strength and durability, the wood is highly valued for furniture, constructional and general utility purposes.
Sampling, data collection and analysis
All the studies were carried out in May 2006 in a monoculture plantation of D. sissoo where the canopy was completely closed. A destructive sampling of 30 individual trees with a wide range of diameter and height were used for this study (Tab. 1). The following measurements were carried out: tree height H, stem diameter at a height of H/10 (D0.1 - [17]), stem dbh D and stem diameter at 1.0 m interval thereafter up to the merchantable height (stem height at 10 cm diameter). For measuring the diameter, girth values were converted to diameter after divided with π. Stem volume was calculated using the Smalian’s formula ([4]).
Tab. 1 - Description of sissoo sample trees used for this study. H: Tree height; D0.1: stem diameter at a height of H/10; D: stem diameter at 1.3 m height (dbh); V: stem volume.
| Tree No. | D (cm) | D0.1 (cm) | H (m) | V (cm3) |
|---|---|---|---|---|
| 1 | 9.549 | 10.027 | 9.01 | 10403.4 |
| 2 | 9.708 | 10.504 | 8.01 | 17653.9 |
| 3 | 10.134 | 11.141 | 8.02 | 25678.3 |
| 4 | 10.663 | 10.982 | 9.01 | 20521.2 |
| 5 | 10.759 | 11.459 | 8.07 | 27829.2 |
| 6 | 11.141 | 11.937 | 9.03 | 14610.4 |
| 7 | 11.513 | 12.414 | 7.50 | 36859.9 |
| 8 | 11.678 | 13.051 | 8.02 | 37520.3 |
| 9 | 11.937 | 11.937 | 9.75 | 38089.3 |
| 10 | 12.321 | 12.573 | 8.50 | 41628.1 |
| 11 | 12.614 | 12.892 | 8.50 | 46894.1 |
| 12 | 12.984 | 12.796 | 12.01 | 51629.2 |
| 13 | 13.210 | 13.528 | 11.03 | 62953.1 |
| 14 | 13.242 | 13.210 | 11.02 | 56349.9 |
| 15 | 13.687 | 13.433 | 10.25 | 57361.4 |
| 16 | 13.866 | 14.006 | 10.25 | 36131.8 |
| 17 | 14.006 | 14.324 | 8.50 | 60054.8 |
| 18 | 14.961 | 14.801 | 14.01 | 89369.7 |
| 19 | 15.597 | 15.756 | 14.04 | 101757.4 |
| 20 | 16.470 | 16.870 | 14.02 | 128149.9 |
| 21 | 16.999 | 17.666 | 11.01 | 139271.9 |
| 22 | 17.189 | 17.507 | 10.75 | 122993.6 |
| 23 | 21.963 | 22.282 | 12.50 | 206910.6 |
| 24 | 26.897 | 26.420 | 15.10 | 411254.8 |
| 25 | 27.056 | 26.420 | 15.00 | 390567.9 |
| 26 | 27.693 | 27.693 | 14.75 | 437078.1 |
| 27 | 29.155 | 28.254 | 20.05 | 569421.1 |
| 28 | 31.210 | 29.155 | 20.02 | 665874.1 |
| 29 | 32.675 | 30.152 | 20.50 | 759421.1 |
| 30 | 33.423 | 31.831 | 21.75 | 819421.1 |
The simple allometric equation is generally written using the power curve ([17]) in the form (eqn. 1):
where y is the dependent variable and x is the independent variable, and a the coefficient and b the allometric constant. The equation is linearized by taking logarithms, as follows (eqn. 2):
where ln a and b are the intercept and slope of the regression line, respectively. The ln a and b are obtained by the method of least squares. In this study, the allometric relationships of the volume and different dimensions such as D, D2, D2H, D0.1, D0.12 and D0.12H were also established using following equations (eqn. 3, eqn. 4, eqn. 5, eqn. 6, eqn. 7):
The coefficient of determination R2 was calculated using the following equation (based on the real data before logarithmic transformation - eqn. 8):
where yi is the observed value, yei is the corresponding values calculated from the regression line, and ymi is the mean of the observed values ([19]). The R2 value (coefficient of determination) is a measure of the goodness-of-fit between the observed and calculated values ([17]).
Results
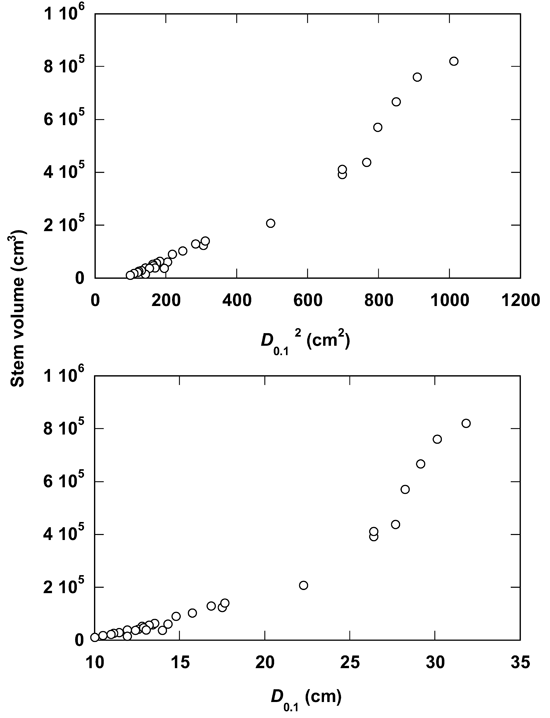
Various allometric equations were developed for data fitting. The allometric relationships of stem volume of sissoo trees to D and D2 are illustrated in Fig. 2. The scatter plot shows a non-linear trend when D is used as independent variable. This trend is changed to linear distribution if D2 is used (Fig. 2). This is also illustrated by the coefficient of determination using D, where the power equation (R2 = 0.970) shows better fitting than linear equation (R2 = 0.944). When D values are squared, the linear equation shows stronger relationship (R2 = 0.983) than power equation (R2 = 0.970 - Tab. 2). In this case, the polynomial cubic equation showed the best fit for both D (R2 = 0.997) and D2 (R2 = 0.996) with a very close estimate by the quadratic equation for D (R2 = 0.993) and D2 (R2 = 0.996).
Tab. 2 - Summarized coefficients of the relationships between individual tree volumes of Sissoo to different independent variables. H: Tree height; D0.1: stem diameter at a height of H/10; D: stem diameter at 1.3 m height (dbh). The units: D = [cm], D0.1 = [cm], H]= [m]. LIN = Linear, LOG = Logarithmic, QUA = Quadratic, CUB = Cubic, POW = Power, EXP = Exponential.
| Variable | Equation | a | b | c | d | R2 | F | Sign. |
|---|---|---|---|---|---|---|---|---|
| D | LIN | -342298 | 30629.2 | - | - | 0.944 | 474.4 | < 0.01 |
| LOG | -1E+06 | 561873 | - | - | 0.869 | 186.3 | < 0.01 | |
| QUA | 145717 | -24827 | 1322.63 | - | 0.993 | 1925.9 | < 0.01 | |
| CUB | -203182 | 34316.7 | -1754.7 | 49.327 | 0.997 | 2588.8 | < 0.01 | |
| POW | 15.91 | 3.108 | - | - | 0.97 | 902.6 | < 0.01 | |
| EXP | 5528 | 0.159 | - | - | 0.928 | 361.7 | < 0.01 | |
| D2 | LIN | -75972 | 739.7 | - | - | 0.983 | 1660.3 | < 0.01 |
| LOG | -1E+06 | 280937 | - | - | 0.869 | 186.3 | < 0.01 | |
| QUA | -13315 | 317.6 | 0.3825 | - | 0.996 | 3517 | < 0.01 | |
| CUB | -31764 | 487.7 | 0.0288 | 0.0002 | 0.996 | 2462.9 | < 0.01 | |
| POW | 15.91 | 1.554 | - | - | 0.97 | 902.6 | < 0.01 | |
| EXP | 23664 | 0.0036 | - | - | 0.867 | 182.3 | < 0.01 | |
| D0.1 | LIN | -390344 | 33385.1 | - | - | 0.925 | 343 | < 0.01 |
| LOG | -2E+06 | 611406 | - | - | 0.86 | 172.4 | < 0.01 | |
| QUA | 275457 | -42005 | 1844.01 | - | 0.981 | 696.3 | < 0.01 | |
| CUB | -445256 | 80012.7 | -4601.5 | 106.354 | 0.989 | 782.3 | < 0.01 | |
| POW | 7.04 | 3.385 | - | - | 0.961 | 695.9 | < 0.01 | |
| EXP | 4172 | 0.1752 | - | - | 0.928 | 362.9 | < 0.01 | |
| D0.12 | LIN | -99651 | 828.7 | - | - | 0.964 | 742.6 | < 0.01 |
| LOG | -2E+06 | 305703 | - | - | 0.86 | 172.4 | < 0.01 | |
| QUA | 7859 | 104.7 | 0.7173 | - | 0.987 | 1043.7 | < 0.01 | |
| CUB | -30223 | 453.3 | -0.0564 | 0.0005 | 0.988 | 721.3 | < 0.01 | |
| POW | 7.04 | 1.693 | - | - | 0.961 | 695.9 | < 0.01 | |
| EXP | 20529 | 0.0042 | - | - | 0.881 | 207.6 | < 0.01 | |
| D2H | LIN | -5209 | 34.9 | - | - | 0.995 | 5738.1 | < 0.01 |
| LOG | -1E+06 | 205386 | - | - | 0.877 | 199 | < 0.01 | |
| QUA | -15721 | 40.2 | -0.0002 | - | 0.997 | 4000.6 | < 0.01 | |
| CUB | -17734 | 41.7 | -0.0004 | 4.90E-09 | 0.997 | 2584.4 | < 0.01 | |
| POW | 11 | 1.125 | - | - | 0.959 | 656.2 | < 0.01 | |
| EXP | 35224 | 0.0002 | - | - | 0.785 | 102.3 | < 0.01 | |
| D0.12 H | LIN | -18747 | 39.3 | - | - | 0.995 | 5791.8 | < 0.01 |
| LOG | -2E+06 | 219854 | - | - | 0.877 | 199.2 | < 0.01 | |
| QUA | -20488 | 40.2 | -5.00E-05 | - | 0.995 | 2811.9 | < 0.01 | |
| CUB | -10661 | 33 | 0.0008 | -3.00E-08 | 0.996 | 1959.7 | < 0.01 | |
| POW | 5.65 | 1.204 | - | - | 0.959 | 654.2 | < 0.01 | |
| EXP | 32624 | 0.0002 | - | - | 0.808 | 118.1 | < 0.01 |
Fig. 3 illustrates the allometric relationships of stem volume to D0.1 and D0.12. As observed with the variable D, the use of D0.1 alsoshowed strong data fitting (R2 = 0.925) in the allometry (Tab. 2). This relationship is further improved (R2 = 0.964) when the D0.1 value is squared. The power equation for both the variables D0.1 and D0.12 showed the same coefficient of determination (R2 = 0.961). For both the variables D0.1 and D0.12 the polynomial cubic and quadratic equations showed a slight stronger fitting (Tab. 2) in comparison with other equations.
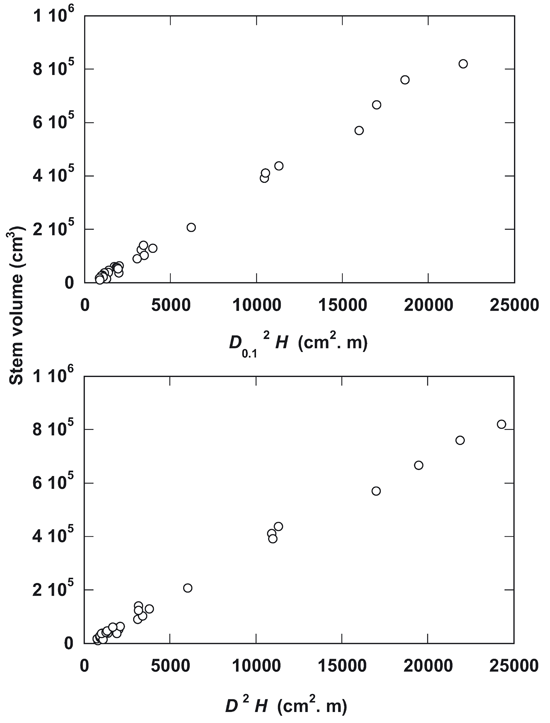
As illustrated in Fig. 4, the incorporation of tree height H in the allometric equation gives a better fitting in the linear equation, specially for both D2H (R2 = 0.995) and D0.12H (R2 = 0.995). The polynomial cubic along with the quadratic equation showed a very close fit in comparison with the linear equation for both variables D2H and D0.12H (Tab. 2).
Discussion
Although the allometric equations were highly significant (P < 0.01) there was considerable variation among them as indicated by the coefficient of determination R2 values (Tab. 2). The scatter plotting (Fig. 2) shows a non-linear trend for D as independent variable, which becomes linear when plotted against D2. This indicates that tree volume is more correlated with basal area than with simple dbh ([8]). Using the simple D as independent variable in the allometric equation, the cubic equation showed the best fit (R2 = 0.997) with a very close estimate by the quadratic equation (R2 = 0.993). However, there were low differences in the goodness-of-fit among the polynomial, power and linear equations. As the quadratic and cubic equations consist of several coefficients, for practical applications in stand volume estimation, because of simplicity, the linear or power equations the use of D2 as an independent variable should be preferred ([17]).
Like the commonly known variable D, the use of D0.1 also showed strong linear data fitting (R2 = 0.925) in the allometry (Tab. 2). This degree of linearity was further improved (R2 = 0.964) when D0.12 value is used instead of D0.1 ([14], [17]). Here, the cubic equation showed the best fit for both D0.1 (R2 = 0.989) and D0.12 (R2 = 0.988). The next strong fit is also from the quadratic equation for D0.1 (R2 = 0.981) and D0.12 (R2 = 0.987). Overall, it may be remarked that the allometric relationships of stem volume to the tree diameter at 10% of tree height (D0.1) did not improve the allometric strength in D. sissoo in comparison with simple D, as reported in case of some tree species ([14], [17]).
The multiplication of tree height H with diameter or basal area in the allometric equation gives high degree of linearity for both the variables D2 H (R2 = 0.995) and D0.12H (R2 = 0.995) in the allometric estimation. This suggests that biologically tree diameter and height change proportionality with the change of tree size ([17]). Hence, H is incorporated in the allometric equations, the polynomial cubic and quadratic equations showed a similar degree of fitting in comparison with linear equation for both the variables D2H and D0.12H, because of simplicity, the linear equation would be preferred for indirect estimation in the field with a good level of accuracy (R2 = 0.995).
For predicting timber yield ([21]) foresters often combine trunk diameter and height measurements ([21], [4]) as the independent variables in allometric relationships. However, for the D. sissoo plantations studied the stem dbh alone showed a very strong accuracy of estimation (R2 = 0.983 to 0.997) especially when used as D2. Thus, it is concluded that the use of tree height in the allometric equation ([32], [18], [28], [17]) can be neglected for D. sissoo, as far as the present study area is concerned. Therefore, for estimating the stem volume of sissoo, the use of D2 as an independent variable in the allometric equation with a linear or quadratic equation is recommended.
The findings of this study indicate that there is a variation in the use of independent variables in allometric equations for estimating the stem volume of the species. The allometric relationships described in this paper may not be appropriate in mixed or open forest stands, because the present study was carried out under monospecific and closed canopy conditions. For estimation stem volume of trees outside the size range of this investigation, care should be taken in extrapolating the present allometric relationships. Therefore, users of these allometric equations are recommended to check some individual trees outside the present size class.
Acknowledgements
We are grateful to Forestry and Wood Technology Discipline, Khulna University, Bangladesh for providing logistic support for the field data collection. The data analysis and manuscript preparation were performed in the Institute of Forest Growth and Forest Computer Sciences, Technische Universität Dresden, Germany, which was supported by the Alexander von Humboldt Stiftung / Foundation, Germany.
References
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Department Forest Biometry and Systems Analysis, Institute of Forest Growth and Forest Computer Sciences, TU Dresden, P.O. Box 1117, D-01735 Tharandt (Germany)
Corresponding author
Paper Info
Citation
Khan NI, Faruque O (2010). Allometric relationships for predicting the stem volume in a Dalbergia sissoo Roxb. plantation in Bangladesh. iForest 3: 153-158. - doi: 10.3832/ifor0554-003
Paper history
Received: Mar 04, 2010
Accepted: Oct 01, 2010
First online: Nov 15, 2010
Publication Date: Nov 15, 2010
Publication Time: 1.50 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2010
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 60205
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 49481
Abstract Page Views: 3728
PDF Downloads: 5439
Citation/Reference Downloads: 32
XML Downloads: 1525
Web Metrics
Days since publication: 5528
Overall contacts: 60205
Avg. contacts per week: 76.24
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2010): 11
Average cites per year: 0.69
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Tree volume modeling for forest types in the Atlantic Forest: generic and specific models
vol. 13, pp. 417-425 (online: 16 September 2020)
Research Articles
On the geometry and allometry of big-buttressed trees - a challenge for forest monitoring: new insights from 3D-modeling with terrestrial laser scanning
vol. 8, pp. 574-581 (online: 02 March 2015)
Research Articles
A rapid method for estimating the median diameter of the stem profile of Norway spruce (Picea abies Karst) trees
vol. 10, pp. 328-333 (online: 11 February 2017)
Research Articles
Integrating area-based and individual tree detection approaches for estimating tree volume in plantation inventory using aerial image and airborne laser scanning data
vol. 10, pp. 296-302 (online: 15 December 2016)
Research Articles
Modeling compatible taper and stem volume of pure Scots pine stands in Northeastern Turkey
vol. 16, pp. 38-46 (online: 22 January 2023)
Research Articles
The use of tree crown variables in over-bark diameter and volume prediction models
vol. 7, pp. 132-139 (online: 13 January 2014)
Technical Reports
Biomass equations for European beech growing on dry sites
vol. 9, pp. 751-757 (online: 17 June 2016)
Research Articles
Nonlinear mixed model approaches to estimating merchantable bole volume for Pinus occidentalis
vol. 5, pp. 247-254 (online: 24 October 2012)
Research Articles
Stem profile of red oaks in a bottomland hardwood restoration plantation forest in the Arkansas Delta (USA)
vol. 15, pp. 179-186 (online: 19 May 2022)
Research Articles
Simplified methods to inventory the current annual increment of forest standing volume
vol. 5, pp. 276-282 (online: 17 December 2012)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword