Tree volume modeling for forest types in the Atlantic Forest: generic and specific models
iForest - Biogeosciences and Forestry, Volume 13, Issue 5, Pages 417-425 (2020)
doi: https://doi.org/10.3832/ifor3495-013
Published: Sep 16, 2020 - Copyright © 2020 SISEF
Research Articles
Abstract
National Forest Inventories are important primary data sources for large-scale forest resource surveys, in which volume estimates of sampled trees are essential for quantitative analysis. Volume prediction models in natural forests are scarce in Brazil due to legal restrictions for cutting trees, especially in the Atlantic Forest. This study aimed to fit volume models for the main forest types and timber species of the Atlantic Forest in Rio de Janeiro state, considering two hypotheses: (I) generic volume models provide greater generalizability of estimates; however, (II) they may reduce the accuracy of forest type- and species-specific predictions. Four linear models with logarithmic transformation of variables were evaluated to fit volume models for generic and specific datasets, which correspond to the main forest types and timber species. Goodness-of-fit statistics were calculated to compare the accuracy and efficiency of the models, and selected models were validated through leave-one-out cross-validation procedures. The estimates obtained by generic and specific models were compared by non-parametric hypothesis tests. Generic models showed similar predictions to the specific models for forest types and timber species, with similar potential for stem and total volume predictions. Therefore, generic models can be used for Atlantic Forests in Rio de Janeiro state, while specific models are recommended to obtain more detailed local estimates.
Keywords
Allometric Models, National Forest Inventory, Non-destructive Methods, Goodness-of-fit, Stem and Total Volume
Introduction
Several international agreements on climate, biodiversity and sustainable use of forests require countries to continually report the condition of their forest resources ([26], [48]). In this context, National Forest Inventories are important primary data sources for national assessments and international reports ([26]), in which tree volume predictions are required for forest stock estimates ([18]). The predictions obtained by individual tree models are aggregated at plot level, providing estimates for large areas ([27]). However, few studies in Brazil have investigated tree volume models at geographic scales ([47]).
Due to the destructive peculiarity of data collection ([16], [32]), volume prediction models are rare for the Atlantic Forest, where there are legal restrictions to cutting down trees. As the reliability of these estimates depends on the extent and range of available data ([1]), the need to develop new local volume models is evident ([47]). However, for threatened ecosystems such as the Atlantic Forest, only highly fragmented remnants remain due to anthropogenic changes ([35]). In this context, precise assessments of allometric variables are required for adequate conservation and management planning of forest resources on a large-scale.
In addition, most allometric models developed for tropical and subtropical forests have been fitted to estimate only stem volume and do not consider tree crown volume ([41], [32]). These models exclude an important tree woody component and underestimate wood stocks present in natural forests. Another criticism is related to the model’s selection procedures, which are one of the most important sources of uncertainty in quantifying forest stocks ([43]). The volume models developed for Brazilian forests have commonly ignored linear regression assumptions, the bias in logarithmic back-transformation, and selection statistical parameters in variable original scales ([47]). Therefore, the lack of tree volume models for native forest, associated with statistical fragility of the available models, represents a gap in knowledge about stocks in Brazilian natural forests.
This paper aims to: (1) fit models for stem and total volumes for forest types of the Atlantic Forest: (2) fit models for stem volume for main timber species; and (3) compare the efficiency and accuracy of generic and specific models. For this, two hypotheses were considered: (I) generic volume models can provide a greater ability to generalize estimates, since they cover a larger variability of the allometric relationships; however, (II) due to increased data variability, generic models may result in lower accuracy for estimates by forest type and species.
Material and methods
Study area and data collection
The study area covers the three main forest types of the Brazilian Atlantic Forest in Rio de Janeiro state, namely Dense Ombrophilous Forest (DOF), Semi-deciduous Seasonal Forest (SSF), and Restinga Forest (RES). These forest types cover 98% of state territory ([42]) at altitudes ranging from 5 to 900 m a.s.l. Even with geographical proximity, these forest types display floristic and structural differences ([30], [7]) due to the climatic and edaphic gradients that characterize the landscapes ([36], [44]). The climate ranges from tropical to humid subtropical, according to the Köppen classification, with Aw-Tropical Dry Winter and Cwa-Subtropical Hot Summer climates predominating. The average annual temperature ranges from 12 °C to 24 °C, with total annual precipitation between 1000 to 2200 mm ([2]).
For tree measurements, 28 forest remnants (Fig. 1) were selected based on the sample allocated in the National Forest Inventory (NFI-RJ), including 18 Conservation Units and 10 private areas. Three-level samples were used for selecting the trees. The first level included the main forest types of the state territory (SSF, DOF, and RES). The second level regards the main species in abundance, based on the forest structure analysis of the state (NFI-RJ). The third level followed the diameter distribution in forest types.
Fig. 1 - Location of NFI-RJ sample plots (black points) and study area for tree measurements (white trees) in Rio de Janeiro State, Southeast of Brazil.
At these locations, a total of 583 tree stems and 172 tree crowns were used for sampling. The sample included 85 species of 29 botanical families (Tab. S1 in Supplementary material) that were classified according to APG IV ([46]). Botanical material was collected from all sample units for taxonomical identification, according to Jara et al. ([20]). Botanical vouchers were deposited in the RBR herbarium of the Department of Botany of the Federal Rural University of Rio de Janeiro. Species were identified using RBR herbarium reference collections and also by consulting with specialists. Spellings, synonyms, and taxonomic issues were checked and standardized using the Tropicos database ([8]).
A non-destructive method was used to climb trees and obtain their volume without cutting them down. In this method, diameter measurements along stem and crown were performed on standing trees with climbing techniques and equipment (Fig. S1 in Supplementary material), which do not cause physical damage to the trees ([23]). This method is an alternative for obtaining tree volume data ([16]), especially in the Atlantic Forest, where there are legal restrictions for cutting down trees. Remote Sensing Tools as Terrestrial Laser Scanning (TLS) are other alternatives to destructive techniques for assessing single-tree properties ([45]). However, the TLS use at a large scale was unfeasible due to the highly sloping landscapes in study area.
For stem volume data (vstem), 583 trees were measured: 264 in DOF, 209 in SSF, and 110 in RES (Tab. 1). The diameter at breast height (dbh), stem height (hstem), and diameters (di) at heights of 0.3, 0.5, 1, 1.3, and 2 m as well as each one meter until the crown base were measured. The stem height was assigned as the last measurement at the crown base, according to Vibrans et al. ([47]). Section volumes were calculated by the Smalian’s method ([5]), in which the sum of all sections correspond to the stem volume.
Tab. 1 - Descriptive statistics and sample sufficiency of the dataset by forest types. (DOF): Dense Ombrophilous Forest; (RES): Restinga Forest; (SSF): Semi-deciduous Seasonal Forest; (dev): deviations; (n): minimum sample size determined considering error of 10% and probability level of 95%.
| Data | Types | dbh (cm) | h (m) | v (m³) | Sampling sufficiency | ||||
|---|---|---|---|---|---|---|---|---|---|
| mean | dev | mean | dev | mean | dev | n | sampled trees |
||
| Stem | Generic | 25.04 | 7.16 | 9.68 | 2.56 | 0.41 | 0.27 | 45 | 583 |
| DOF | 26.18 | 8.17 | 10.11 | 2.44 | 0.46 | 0.31 | 46 | 254 | |
| RES | 21.3 | 4.89 | 7.23 | 1.61 | 0.23 | 0.12 | 18 | 110 | |
| SSF | 25.55 | 6.59 | 10.41 | 2.63 | 0.45 | 0.28 | 49 | 209 | |
| Total | Generic | 23.78 | 5.2 | 16.62 | 3.44 | 0.48 | 0.27 | 41 | 172 |
| DOF | 25.04 | 5.5 | 17.99 | 3.54 | 0.54 | 0.28 | 43 | 78 | |
| RES | 19.47 | 3.13 | 13.1 | 2.1 | 0.26 | 0.12 | 17 | 37 | |
| SSF | 24.86 | 4.93 | 17.03 | 3 | 0.55 | 0.29 | 44 | 57 | |
Tree total volume (vtotal) was obtained with the sum of stem and crown volumes (vcrown). For this, 172 crowns of the sampled trees were measured: 78 in DOF, 57 in SSF, and 37 in RES. Branches were sectioned at 1 m or in irregular sections (length < 1 m) and individually measured to the threshold diameter of 5 cm. Branch volume was calculated by the Smalian’s method, in which the sum of all branches’ volume corresponds to the crown volume. Total height (htotal) was measured with a ECII-R® precision clinometer (Haglöf, Sweden).
Exploratory data analysis was carried out to identify the dispersion and distribution of the variables used for modeling. Scatterplots of tree volume vs. dbh were used to explore the data trends, and box plots was applied to verified the data distributions. This analysis was performed for all data sets that corresponded to generic data and each subset by forest type and timber species. Different trends and patterns were evidenced for the datasets, as the heteroscedasticity and outliers presence.
Data analysis
Based on exploratory analysis, four traditional volume models (Tab. 2) were fitted in their linear form by logarithmic transformation to predict stem and total volumes. These models were fitted for generic and specific datasets, corresponding to the three main forest types (SSF, DOF, and RES) and four timber species with management potential in the Atlantic Forest, according to Nascimento et al. ([29]) and Oliveira et al. ([32]): Apuleia leiocarpa (Vogel) J. F. Macbr., Astronium graveolens Jacq., Miconia cinnamomifolia (DC.) Naudin, and Pseudopiptadenia contorta (DC.) G. P. Lewis & M. P. Lima. Only models to predicted stem volume were fitted due to the limited number of sample units for these species (Tab. S1 in Supplementary material).
Tab. 2 - Models for tree volume predictions in the Atlantic Forest of Rio de Janeiro state, Brazil. (v): tree volume (m³); (dbh): diameter measured at breast height (cm); (h): height (m); (εi): random error.
| Model | Author | Volume model | Independent variables |
|---|---|---|---|
| 1 | Kopezky-Gehrhardt | ln(v) = β0 + β1* ln(dbh²) + εi | Single-predictor |
| 2 | Brenac | ln(v) = β0 + β1·ln(dbh) + β2·(1/dbh) + εi | |
| 3 | Modified Spurr | ln(v) = β0 + β1·ln(dbh²·h) + εi | Two-predictors |
| 4 | Schumacher-Hall | ln(v) = β0 + β1·ln(dbh) + β2·ln(h) + εi |
Considering that back-transformation of logarithmic predictions to the original scale produces a bias, a correction term must be added to compensate for the scale change ([47]). This correction term is expressed by the exponential of residual variance divided by two. According to these authors, low values of the correction term provide low influence on the final result. Since all terms were < 0.05, they can be considered negligible. Therefore, the correction term was not applied in the present study.
Lower root mean square error (RMSE%), higher values of adjusted coefficient of determination (adj-R2) and Akaike information criterion (AIC) were the statistical criteria used to select the best models, by means of the formulation presented by Bennett et al. ([6]). These statistics were recalculated at their original scales due to the logarithmic transformation of the variables. The F test for lack of fit was conducted to verify that linear models present a good fit for the databases. This hypothesis test considered α = 0.05.
Residual analysis was considered decisive for selecting the best models ([6]), especially to verify the linear regression assumptions. The normality of residuals was verified by the Kolmogorov-Smirnov’s (KS) test ([34]) using the package “nortest” in R ([17]), while the Breusch-Pagan’s (BP) test was used for homoscedasticity assessment ([9]). All these hypothesis tests considered α = 0.01. Scatterplots of studentized residuals by estimated values and quantile-quantile plots at 95% probability were evaluated for the selected models.
The variance inflation factor (VIF) was calculated for two-predictor models, aiming to identify possible multicollinearities of predictor variables ([43]). Collinear variables were removed considering a VIF threshold value equal to 5. The significance of regression coefficients (βi) was evaluated by the t-test (α = 0.01). The influence of outliers was analyzed in the selected models through graphical analysis, considering the studentized residuals, leverage values, and Cooks’ Distance weights for each observation using the “car” R package ([15]).
Leave-one-out cross-validation was applied to validate the selected models ([25], [32]) using the “caret” R package ([22]). In this process, one observation (n) at a time was removed from the database, and the model was refitted n times. The root mean square error (RMSE%) and adjusted coefficient of determination (adj-R2) obtained from cross-validation were used to validate the models ([43]). The predicted volumes were graphically represented in relation to the observed volumes on the original scale ([20]), aiming to identify possible bias in predictions.
Model comparisons
For testing the hypotheses about predictions obtained by generic and specific models, the selected models were compared in two situations: (i) generic vs. specific models by forest type to estimate the stem and total volumes; and (ii) generic vs. specific models by timber species to estimate stem volume. The non-parametric chi-squared test (χ²) and the Wilcoxon test for paired data (V) were applied to verify significant similarity among the generic and specific predictions. Kruskal-Wallis’ non-parametric test (H) was used to compare simultaneously the predictions of generic and specific models with observed values. All these hypothesis tests used α = 0.01. Willmott’s Agreement Index (dw) was calculated ([49]) to verify agreement among the values estimated by the models, with the use of “hydroGOF” R package ([50]). The dw index ranges from 0 to 1, where the maximum value indicates perfect agreement between pairs of values. Additionally, variations in RMSE% and adj-R2 were calculated for models accuracy comparison.
Results
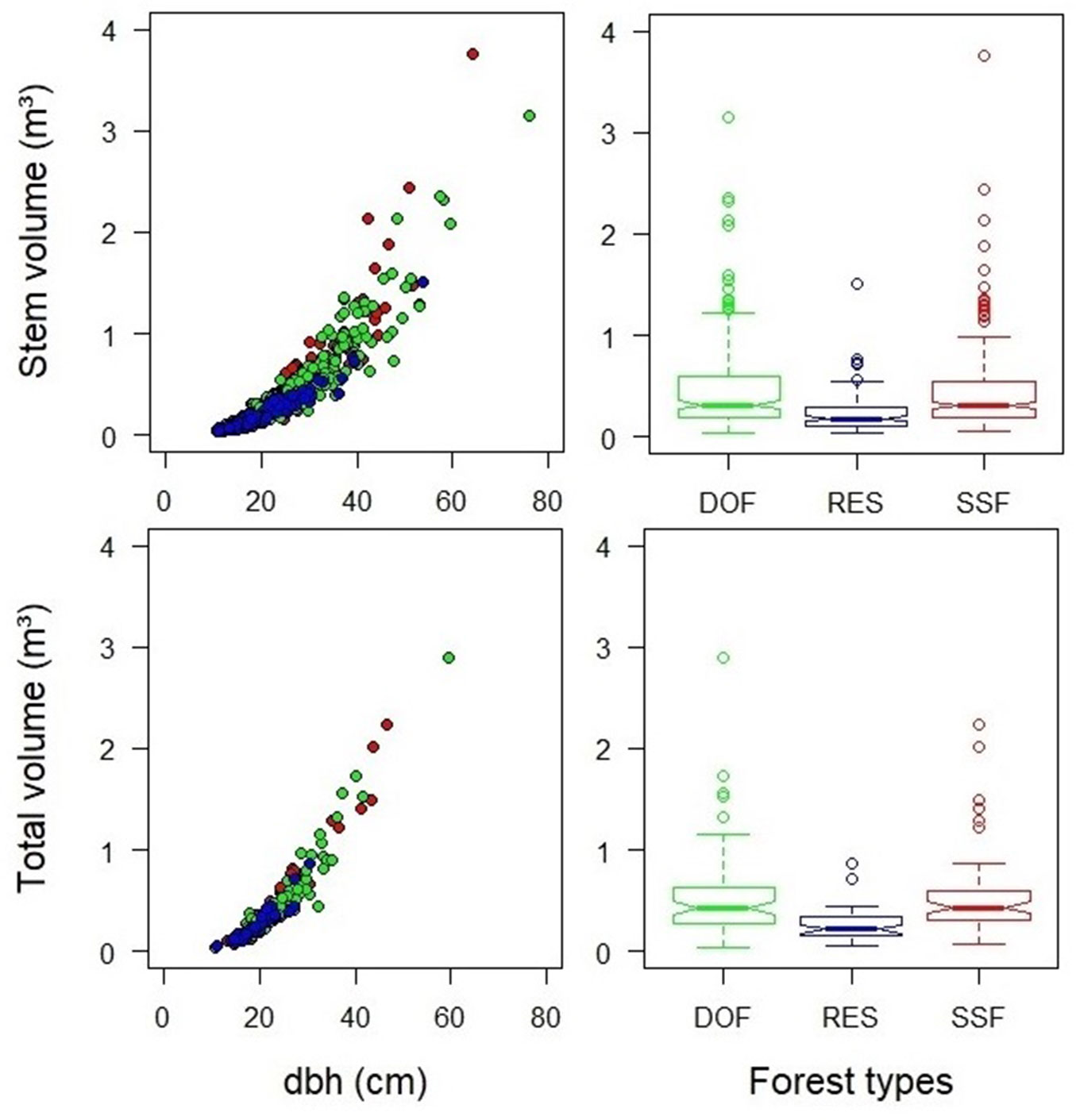
While allometric relationships showed similarity between SSF and DOF forest types (Fig. 2), a distinct pattern was observed in RES. In this forest type, the volumes are concentrated in the smallest diameter classes, and the allometric relationship was more uniform and possessed less variability. The correlation with predictor variables for total volume was higher (dbh = 0.92-0.96; htotal = 0.68-0.82) than that for stem volume (dbh = 0.88-0.93; hstem = 0.33-0.50). After logarithmic transformation, the correlation between predictor and response variables increased by 7% for stem volume and by 8% for total volume. In this sense, the distribution of allometric variables had become linear, and the presence of outliers was reduced. These results supported the decision to use linear models with logarithmic variables for all volume predictions.
Fig. 2 - Tree volume-diameter relationships in forest types of the Brazilian Atlantic Forest, showing Dense Ombrophilous Forest (DOF, green), Restinga Forest (RES, blue), and Semi-deciduous Seasonal Forest (SSF, red).
For timber species (Fig. S2 in Supplementary material), stem volume showed similarity between Apuleia leiocarpa and Miconia cinnamomifolia; while Astronium graveolens was more similar to Pseudopiptadenia contorta. Predictor variables showed moderate to high correlation in natural scale (dbh = 0.83-0.93; hstem = 0.16-0.69) with the response variable (vstem). In relation to allometric relationships, heteroscedasticity was detected for P. contorta due to high variability of the largest trees.
Tab. 3shows the fitting results and statistical criteria used to select the best models. The residuals of selected models presented normality (KS test) and homoscedasticity (BP test). The tests indicated that linear regression assumptions were satisfied, not rejecting any of the null hypotheses (p > 0.01). The selected models did not show lack of fit according to the F test. Model 4 presented the best fit (lowest AIC) for stem volume prediction, while model 3 showed the best performance for total volume. These models allowed more accurate predictions (lower RMSE) and high explications of observed data (higher adj-R2), with significant regression coefficients (p ≤ 0.01).
Tab. 3 - Statistical parameters of fitted models to estimate stem and total volumes in the Brazilian Atlantic Forest. The p-value corresponds to lack-of-fit test performed only on the best model selected for each dataset. (SE): standard error of estimated parameters; (*): p<0.05; (**): p<0.01; (ns): non-significant.
| Volume | Data | Model | β0 | SEβ0 | β1 | SEβ1 | β2 | SEβ2 | RMSE% | adj-R² | AIC | p |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stem | Generic | 1 | -8.375** | 0.098 | 1.131** | 0.015 | - | - | 36.39 | 0.865 | -550 | - |
| 2 | -7.198** | 0.601 | 1.982** | 0.144 | -6.568* | 3.308 | 35.32 | 0.872 | -583 | - | ||
| 3 | -9.359** | 0.052 | 0.952** | 0.006 | - | - | 17.05 | 0.971 | -1433 | - | ||
| 4 | -9.341** | 0.041 | 2.053** | 0.012 | 0.734** | 0.012 | 14.77 | 0.978 | -1599 | 0.25 | ||
| DOF | 1 | -8.070** | 0.139 | 1.087** | 0.022 | - | - | 32.84 | 0.876 | -238 | - | |
| 2 | -5.934** | 0.841 | 1.672** | 0.202 | -12.06* | 4.684 | 30.54 | 0.893 | -275 | - | ||
| 3 | -9.458** | 0.078 | 0.963** | 0.009 | - | - | 15.99 | 0.971 | -618 | - | ||
| 4 | -9.329** | 0.067 | 2.033** | 0.018 | 0.756** | 0.021 | 14.37 | 0.976 | -673 | 0.43 | ||
| RES | 1 | -8.360** | 0.217 | 1.101** | 0.036 | - | - | 21.29 | 0.934 | -348 | - | |
| 2 | -7.824** | 1.413 | 2.071** | 0.35 | -2.726ns | 7.105 | 20.85 | 0.937 | -350 | - | ||
| 3 | -9.454** | 0.113 | 0.971** | 0.014 | - | - | 10.67 | 0.984 | -500 | - | ||
| 4 | -9.414** | 0.082 | 2.077** | 0.024 | 0.739** | 0.025 | 9.24 | 0.988 | -529 | 0.87 | ||
| SSF | 1 | -8.416** | 0.168 | 1.144** | 0.026 | - | - | 34.42 | 0.873 | -184 | - | |
| 2 | -8.326** | 1.053 | 2.267** | 0.251 | -0.514ns | 5.928 | 34.48 | 0.872 | -182 | - | ||
| 3 | -9.418** | 0.095 | 0.957** | 0.011 | - | - | 18.39 | 0.964 | -446 | - | ||
| 4 | -9.402** | 0.073 | 2.082** | 0.022 | 0.718** | 0.021 | 14.06 | 0.979 | -557 | 0.16 | ||
| Total | Generic | 1 | -8.988** | 0.179 | 1.277** | 0.028 | - | - | 31.29 | 0.860 | -155 | - |
| 2 | -6.074** | 1.11 | 1.856** | 0.268 | -16.013** | 6.024 | 22.57 | 0.927 | -266 | - | ||
| 3 | -9.381** | 0.149 | 0.928** | 0.016 | - | - | 20.18 | 0.942 | -306 | 0.82 | ||
| 4 | -9.370** | 0.146 | 2.038** | 0.067 | 0.720** | 0.069 | 21.54 | 0.933 | -282 | - | ||
| DOF | 1 | -8.490** | 0.278 | 1.200* | 0.043 | - | - | 28.29 | 0.872 | -66 | - | |
| 2 | -5.968** | 1.618 | 1.799* | 0.389 | -14.163ns | 8.955 | 22.18 | 0.921 | -102 | - | ||
| 3 | -9.228** | 0.233 | 0.908* | 0.025 | - | - | 18.53 | 0.945 | -132 | 0.63 | ||
| 4 | -9.159** | 0.229 | 1.979* | 0.086 | 0.703* | 0.093 | 19.39 | 0.939 | -123 | - | ||
| RES | 1 | -9.493** | 0.426 | 1.354** | 0.072 | - | - | 20.95 | 0.887 | -104 | - | |
| 2 | -11.23** | 3.643 | 3.149** | 0.929 | 8.184ns | 17.03 | 21.04 | 0.882 | -102 | - | ||
| 3 | -9.848** | 0.344 | 0.987** | 0.041 | - | - | 16.97 | 0.926 | -119 | 0.59 | ||
| 4 | -9.849** | 0.346 | 2.089** | 0.175 | 0.853** | 0.183 | 16.99 | 0.924 | -118 | - | ||
| SSF | 1 | -9.130** | 0.329 | 1.304** | 0.052 | - | - | 22.98 | 0.911 | -68 | - | |
| 2 | -3.956ns | 2.186 | 1.387* | 0.521 | -30.05* | 12.57 | 17.87 | 0.945 | -95 | - | ||
| 3 | -9.671** | 0.291 | 0.963** | 0.032 | - | - | 19.17 | 0.938 | -89 | 0.31 | ||
| 4 | -9.621** | 0.294 | 2.073** | 0.139 | 0.780** | 0.158 | 19.75 | 0.933 | -83 | - |
In general, the two-predictor models (3 and 4) presented the best fit compared to the single predictor models (1 and 2). In this sense, the models calibrated for stem volume had the best predictions (higher adj-R2, lower AIC and RMSE) than the ones adjusted for total volume. Although model 1 presented higher prediction errors, it showed significant regression coefficients and satisfied the regression assumptions. Model 2 was the only one that presented regression coefficients with low significance or non-significance as well as multicollinearity, with variance inflation values (VIF) greater than 5. Based on these criteria, model 2 was excluded from the analysis.
Tab. 4shows the fitting results and respective statistical criteria used to select the best volume models for specific timber species. Model 3 was the best fitting for A. leiocarpa and M. cinnamomifolia; while model 4 was the most suitable for A. graveolens and P. contorta predictions. Residual analysis indicated that the residual normality (KS test) and homoscedasticity (BP test) were not rejected (p > 0.01). As observed for forest types, two-predictor models 3 and 4 provided more accurate estimates than single predictor models. The inclusion of height resulted in a four times lower error (RMSE%) for A. graveolens and an increase of 24% in the explanation of its volume variability (adj-R2).
Tab. 4 - Statistical parameters of fitted models to estimate stem volume of timber species in the Brazilian Atlantic Forest. The p-value corresponds to lack-of-fit test performed only on the best model selected for each timber species. (SE): standard error of estimated parameters; (*): p<0.05; (**): p<0.01; (ns): non-significant.
| Species | Model | β0 | SEβ0 | β1 | SEβ1 | β2 | SEβ2 | RMSE% | adj-R² | AIC | p |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Apuleia leiocarpa | 1 | -7.661** | 0.278 | 1.032** | 0.042 | - | - | 28.52 | 0.909 | -45 | - |
| 2 | -4.642** | 1.519 | 1.363** | 0.356 | -18.053* | 8.938 | 25.91 | 0.923 | -53 | - | |
| 3 | -9.551** | 0.192 | 0.976** | 0.022 | - | - | 9.25 | 0.990 | -160 | 0.92 | |
| 4 | -9.231** | 0.173 | 2.026** | 0.039 | 0.732** | 0.054 | 12.16 | 0.983 | -130 | - | |
| Astronium graveolens | 1 | -8.452** | 0.444 | 1.137** | 0.072 | - | - | 38.51 | 0.758 | -76 | - |
| 2 | -8.332** | 3.507 | 2.244** | 0.862 | -0.623ns | 18.06 | 38.49 | 0.753 | -74 | - | |
| 3 | -9.255** | 0.206 | 0.931** | 0.025 | - | - | 15.62 | 0.960 | -172 | - | |
| 4 | -9.529** | 0.125 | 2.115** | 0.038 | 0.706** | 0.027 | 7.89 | 0.990 | -242 | 0.63 | |
| Miconia cinnamomifolia | 1 | -8.002** | 0.306 | 1.094** | 0.047 | - | - | 33.45 | 0.777 | -36 | - |
| 2 | -6.524** | 2.040 | 1.833** | 0.494 | -7.962ns | 10.86 | 34.14 | 0.763 | -32 | - | |
| 3 | -9.322** | 0.161 | 0.951** | 0.018 | - | - | 10.08 | 0.980 | -156 | 0.49 | |
| 4 | -9.201** | 0.147 | 1.993** | 0.041 | 0.776** | 0.050 | 10.76 | 0.976 | -147 | - | |
| Pseudopitadenia contorta | 1 | -8.374** | 0.270 | 1.131** | 0.043 | - | - | 35.74 | 0.888 | -39 | - |
| 2 | -9.280** | 1.795 | 2.475** | 0.425 | 5.126ns | 10.05 | 36.29 | 0.882 | -36 | - | |
| 3 | -9.124** | 0.135 | 0.928** | 0.016 | - | - | 18.05 | 0.971 | -113 | - | |
| 4 | -9.096** | 0.099 | 2.004** | 0.032 | 0.703** | 0.035 | 12.70 | 0.986 | -149 | 0.37 |
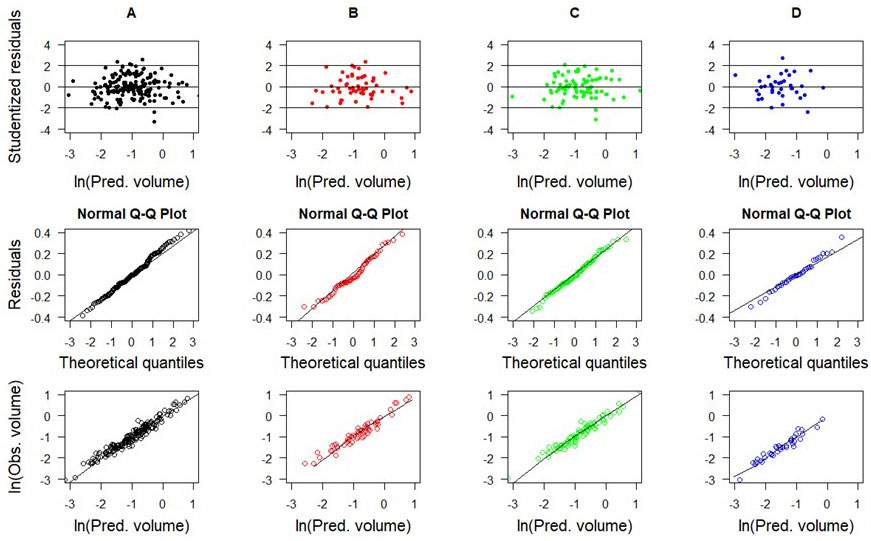
The selected models for forest types showed uniform residual distributions over the estimated volume range and absence of heteroscedasticity for stem (Fig. 3) and total (Fig. 4) volumes. These residuals were adequate for theoretical normal distribution, satisfying this condition for linear regression use. However, some models showed small residual deviations in the extreme tails of distribution (Fig. 3A, Fig. 3B and Fig. 4A, Fig. 4D).
Fig. 3 - Scatterplots of studentized residuals and observed vs. predicted tree volumes (using cross-validation) for best-fitted stem volume models in the forest types (model 4): (A) generic data, (B) SSF, (C) DOF, and (D) RES.
Fig. 4 - Scatterplots of studentized residuals and observed vs. predicted tree volumes (using cross-validation) for best-fitted total volume models in the forest types (model 3): (A) generic data; (B) SSF; (C) DOF; and (D) RES.
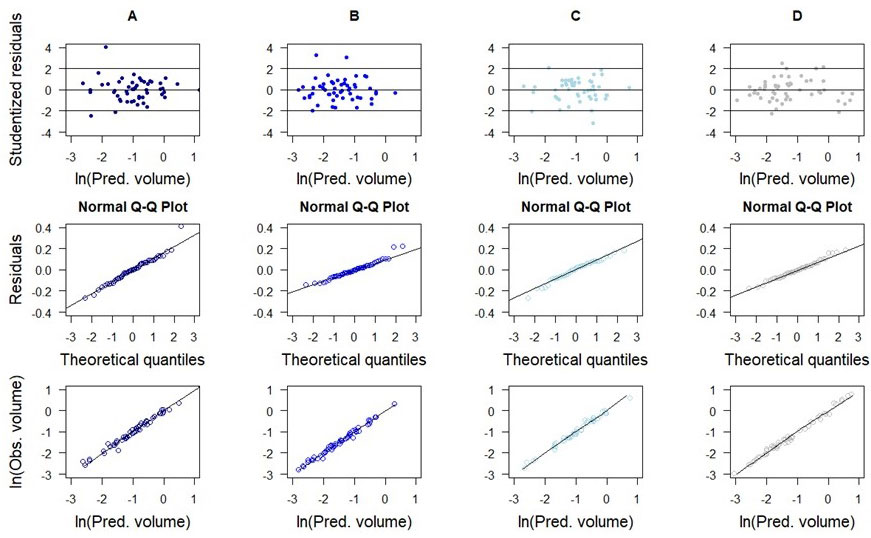
The residuals of selected models for species presented a uniform distribution over the range of predicted values (Fig. 5). The residuals’ distribution was adequate to the theoretical normal distribution, satisfying the condition for linear regression. Slight heteroscedasticity was observed for A. leiocarpa (Fig. 5A). Outliers were observed for A. leiocarpa (Fig. 5A) and A. graveolens (Fig. 5B) at the upper extremes of their distributions.
Fig. 5 - Scatterplots of studentized residuals and observed vs. predicted tree volumes (using cross-validation) of best-fitted stem volume models for timber species. (A): model 3 for Apuleia leiocarpa; (B): model 4 for Astronium graveolens; (C): model 3 for Miconia cinnamomifolia; (D): model 4 for Pseudopiptadenia contorta.
All selected models were submitted to the outlier detection test, which indicated the presence of discrepant observations with studentized residual values higher than -2 and 2. However, these have a small contribution to the estimates due to the low leverage values. Moreover, the exclusion of these observations resulted in negligible improvement in RMSE% and adj-R2. Therefore, we decided to keep these observations in the database, as they represent real values of the sampled populations. The selected models presented satisfactory statistical results through leave-one-out cross-validation (Tab. S2 in Supplementary material), such as high efficiency and reduced prediction errors, ensuring stability in the estimates.
Generic models presented similar fitting results to the specific models for forest types and timber species (Tab. 3, Tab. 4). The fitting and accuracy statistics were similar, even with using these models for other datasets (Tab. 5), in which the variation in efficiency (adj-R2) and accuracy (RMSE%) was minimal. The hypothesis tests (χ², V, and H) did not reject the null hypotheses (p>0.01), showing evidence of significant similarity between generic and specific predictions. Similarly, Willmott’s Agreement Index (dw) showed high agreement among predictions. Therefore, generic and specific models resulted in similar estimates (p>0.01). Finally, hypothesis I was accepted and hypothesis II was rejected, since non-significant loss of accuracy could be evidenced using generic models.
Tab. 5 - Chi-squared (χ²), Wilcoxon (V), Kruskal-Wallis (H), and Willmott’s Agreement Index (dw) statistics and differences between root mean square error in percentage (ΔRMSE%) and adjusted determination coefficient (Δadj-R2) by generic and specific models to estimate stem and total volumes in the Brazilian Atlantic Forest. (ns): non-significant.
| Volume | Test | χ² | V | H | dw | ΔRMSE% | Δadj-R² |
|---|---|---|---|---|---|---|---|
| Stem | GEN × DOF | 0.0048ns | 34846ns | 0.0123ns | 0.9999 | 0.560 | 0.0001 |
| GEN × RES | 0.0009ns | 5955ns | 0.0455ns | 0.9997 | -1.044 | 0.0001 | |
| GEN × SSF | 0.0043ns | 21945ns | 0.0085ns | 0.9999 | 0.401 | 0.0001 | |
| Total | GEN × DOF | 0.0054ns | 3168ns | 0.1687ns | 0.9978 | 2.443 | -0.0004 |
| GEN × RES | 0.0053ns | 661ns | 0.0598ns | 0.9953 | 1.786 | -0.0009 | |
| GEN × SSF | 0.0111ns | 1562ns | 0.2506ns | 0.9968 | -1.452 | 0.0003 | |
| Stem | GEN × APU | 0.0693ns | 1270ns | 0.0517ns | 0.9969 | 3.378 | -0.0007 |
| GEN × AST | 0.0028ns | 1486ns | 0.3380ns | 0.9984 | 2.967 | -0.0005 | |
| GEN × MIC | 0.0438ns | 1193ns | 0.2289ns | 0.9946 | 2.878 | -0.0013 | |
| GEN × PSE | 0.0087ns | 1415ns | 0.0888ns | 0.9997 | 2.877 | -0.0007 |
Discussion
The volume models of this study are new for the Brazilian Atlantic Forest. Volume prediction models for forest types and species on a regional scale were only developed for some Brazilian States ([40], [47]). Additionally, total volume models that consider crown volume are rare for Atlantic Forests ([32]), in which this study is also a pioneer. These models can provide estimates of forest growth in the National Forest Inventory ([18]) to support the management of secondary forests ([32], [13]).
Environmental heterogeneity may explain the variation in allometric relationships between forest types (Fig. 2). The wide environmental variability present in the Southeast of Brazil provides the formation of several vegetation types characterized by typical flora ([39], [30]). These environmental conditions determine the diversity and structural complexity among plant communities ([39]). In this sense, the similarities that were observed for allometric relationships among forest types (Fig. 2) are related to the affinity of their species composition and structure ([47]). Even with evident environmental variation, the Ombrophilous (DOF) and Seasonal (SSF) forests have greater floristic similarity to each other than to the other Atlantic Forest formations ([33]). In the study area, the similarity between these forest types is corroborated by the phytogeographic patterns found for the flora ([30]).
Environmental restrictions explain the lowest volume and difference of allometric relationship in the Restinga forests (RES - Fig. 2). This forest type covers the coastal sandy plains, where shrub vegetation predominates ([39]). Such soil conditions (low fertility and frequent flooding) provide more restrictive environments for establishing tree species ([4]) that restrict the tree size and density ([24]). Thus, this forest type has an evident floristic and structural difference in relation to the others, marked by the presence of typical and smaller species adapted to edaphic characteristics ([4], [24]).
The Schumacher-Hall’s model (4) selected as the most appropriate for estimating stem volume of forest types (Tab. 3) is widely used to predict tree volume in tropical and subtropical regions ([1], [47]). Spurr’s model (3), selected in this study for total volume, was also cited as the most accurate for tree total volume predictions in Tanzania, considering local specific models for four geographic regions ([25]).
The better prediction of stem volume in comparision to total volume (Tab. 3) may be related to the sample size ([41]). We highlight that the optimal sampling for all databases was achieved (Tab. 1). On the other hand, the high variability of tropical tree crown patterns can affect the fit of total volume models ([25]). In general, the stem volume is more homogeneous than total volume, and its allometric attributes are more easily described by tree diameter and height ([32]).
In this study, tree crown represented, on average, 30.1% of the total volume, varying according to forest type (DOF = 30.7%; RES = 34.2%; SSF = 28.0%). Crown volume in subtropical regions of the Atlantic Forest can represent up to 34.5% of total tree volume ([32]). However, most allometric models developed in tropical forests only estimate the stem volume and do not consider the volume of thick branches ([41]). Crown volume is an important component of timber stocks in natural forests, so it should not be ignored in management systems ([32]) or in forest biomass and carbon predictions ([31]).
Inserting height as a predictor variable increased the accuracy of the stem volume prediction by up to 10% and the total volume by 7% (Tab. 3). The use of height to estimate volume and biomass in tropical forests is controversial ([19]), especially due to measurement difficulties in dense forests ([41], [32]). However, height as a predictor of tree biomass, for example, significantly increases the accuracy of estimates in tropical forests ([10], [14], [19]). Tree height measurement can be improved by training the forest operators ([21]) and with the use of LIDAR sensor fine-scale data ([11]).
At regional scales, where environmental heterogeneity may increase the variability of allometric relationships ([25], [47]), using tree height is recommended for predictions ([14]). Height use is emphasized in situations where there is a wide range of heights for the same diameter range ([28]), as in natural rainforests. Tree height is still recommended for predicting the volume of large trees since it complements the effect of diameter in volume models ([37], [25]). As height measurements are time-consuming, it is recommended that sampling be optimized to produce an adequate local allometric relationship ([19]) and improve volume estimates in dense forests.
We highlight that Kopezky-Gehrhardt’s single-predictor model 1 provides estimates with valid confidence intervals and can be used for volume predictions (Tab. 3). Due to measurement difficulties and the increased cost of data collection, the use of single-predictor models with only diameter is an alternative for management operations in Brazilian dense forests ([16], [32]). Diameter is a variable easily measured in forest inventories ([41]) that expand the applicability of single-predictor models.
Similar to the models fitted for forest types, two-predictor models presented a superior performance for timber species (Tab. 4). For A. graveolens, the accuracy gain in the models was more evident with height inclusion due to the wide variation in height for the same diameter. Height explains the variation of tree biomass for a given value of diameter ([28]), increasing the predictive potential of models. The largest errors with specific models were obtained for P. contorta. This species produces the biggest trees in the Ombrophilous Forest in the Rio de Janeiro state ([12]). Morphological variability is more evident in large trees ([3]), for which the highest errors in volume predictions are justified ([25]).
Deviation from normality observed at the extreme of residual distributions (Fig. 4, Fig. 5) may indicate population mixing or the existence of subpopulations in the generic and specific databases. Local climate and soil conditions affect allometric relationships in tropical forests ([25]), conditioning the existence of different subpopulations within the same forest type. The effect of altitude on height/diameter relationships in the Atlantic Forest is known ([38]). This evidence emphasizes the influence of the local environment in tree allometric relationships and explains the presence of subpopulations on databases.
The assessment of volume models conducted by Vibrans et al. ([47]) in the Atlantic Forest indicated the need for specific models for each forest type. Their result was different from that of this study, in which generic models provided accurate estimates with valid confidence intervals (Tab. 3, Tab. 4, Tab. 5). The recommendation of specific models for forest types is related to the floristic and structural differences between these forests ([47]). Even though there are floristic differences in the forests of the Brazilian Southeast ([30]), generic and specific volume models did not present significant differences for the estimates (Tab. 5). The larger number of species in the generic models increases data variability and reduces the accuracy of estimates in relation to specific models ([25], [47]). Therefore, in this study, the accuracy and efficiency of generic models were not compromised. Thus, these models allow for improvement in the generalizability of the estimates for larger areas.
Generic volume models provide wider uses ([47]), as they cover a range of geographical and biophysical conditions ([25]). Moreover, it is evident that additional effort to collect data for species-specific models does not lead to a relevant gain in accuracy in comparison to generic models ([32]). In the context of NFIs, fieldwork should focus on allometric models that reduce population variability through larger and consistent samples ([27]), such as the selected generic models. Therefore, the generic models efficiently described the variability of tree volume between forest types. These models can be used for tree volume predictions in the Atlantic Forest in Rio de Janeiro state, while specific models are recommended for more detailed local estimates. Additionally, the selected specific models can be applied for forest types present in other regions of Atlantic Forest with lack of local models.
Conclusions
Two main conclusions were obtained in this study: (1) generic models allowed estimates with acceptable confidence intervals and can be used in all forest types in the studied area; and (2) contrary to expectations, estimates by generic models did not show a decrease in accuracy in relationship to the specific models by forest type and species.
Acknowledgements
VCC collected data, conducted data analyses and wrote the manuscript; TDG participated on data collection and conducted data analyses; ALP conducted data analyses and contributed to the text; TAM participated on data collection and graphic analyses; DCC, TBSF, HBA, SAM supervised data analyses and contributed to the text. The authors thank all members of the National Forest Inventory of Rio de Janeiro State and the Brazilian Council for Scientific and Technological Development (CNPq) for granting the scholarship to the first author (Process: 140594/2017-5). This study was sponsored by the Fundação Flora de Apoio a Botânica, through a partnership with the State Secretariat of the Environment (SEA-RJ) and State Institute of Environment (INEA-RJ), by Agreement no. 01/2017, for development and implementation of the Carbon Climate Rio Program. The authors grateful to anonymous reviewers for the valuable review and comments.
References
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Allan Libanio Pelissari 0000-0002-0915-0238
Sebastião do Amaral Machado 0000-0003-1010-4623
Universidade Federal do Paraná - UFPR, Av. Prof. Lothario Meissner 632, Jardim Botânico, CEP 80.210-170, Curitiba, PR (Brazil)
Instituto Nacional de Pesquisas da Amazônia - INPA, Av. André Araújo 2936, Petrópolis, CEP 69.067-375, Manaus, AM (Brazil)
Daniel Costa De Carvalho
Universidade de Brasília - UnB, Asa Norte, CEP 70.910-900, Brasília, DF (Brazil)
Tom Adnet Moura 0000-0002-5600-3281
Hugo Barbosa Amorim
Universidade Federal Rural do Rio de Janeiro - UFRRJ, Rodovia BR 465, Km 7, Seropédica, CEP 23.890-000, Rio de Janeiro, RJ (Brazil)
Corresponding author
Paper Info
Citation
Cysneiros VC, Gaui TD, Silveira Filho TB, Pelissari AL, Machado SA, De Carvalho DC, Moura TA, Amorim HB (2020). Tree volume modeling for forest types in the Atlantic Forest: generic and specific models. iForest 13: 417-425. - doi: 10.3832/ifor3495-013
Academic Editor
Nicola Puletti
Paper history
Received: May 05, 2020
Accepted: Jul 08, 2020
First online: Sep 16, 2020
Publication Date: Oct 31, 2020
Publication Time: 2.33 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2020
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 41431
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 34785
Abstract Page Views: 3160
PDF Downloads: 2771
Citation/Reference Downloads: 4
XML Downloads: 711
Web Metrics
Days since publication: 1937
Overall contacts: 41431
Avg. contacts per week: 149.72
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2020): 9
Average cites per year: 1.50
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Allometric relationships for predicting the stem volume in a Dalbergia sissoo Roxb. plantation in Bangladesh
vol. 3, pp. 153-158 (online: 15 November 2010)
Research Articles
Allometric models for estimating biomass, carbon and nutrient stock in the Sal zone of Bangladesh
vol. 12, pp. 69-75 (online: 24 January 2019)
Research Articles
Allometric models for the estimation of foliage area and biomass from stem metrics in black locust
vol. 15, pp. 281-288 (online: 27 July 2022)
Research Articles
Comparative analysis of taper models for Pinus nigra Arn. using terrestrial laser scanner acquired data
vol. 17, pp. 203-212 (online: 22 July 2024)
Research Articles
Simplified methods to inventory the current annual increment of forest standing volume
vol. 5, pp. 276-282 (online: 17 December 2012)
Research Articles
Alternative methods of scaling Eucalyptus urophylla trees in forest stands: compatibility and accuracy of volume equations
vol. 11, pp. 275-283 (online: 29 March 2018)
Research Articles
Compatible taper-volume models of Quercus variabilis Blume forests in north China
vol. 10, pp. 567-575 (online: 08 May 2017)
Review Papers
Integration of forest mapping and inventory to support forest management
vol. 3, pp. 59-64 (online: 17 May 2010)
Research Articles
Effects of planting density on the distribution of biomass in a douglas-fir plantation in southern Italy
vol. 8, pp. 368-376 (online: 09 September 2014)
Research Articles
Allometric relationships for volume and biomass for stone pine (Pinus pinea L.) in Italian coastal stands
vol. 6, pp. 331-335 (online: 29 August 2013)
iForest Database Search
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords