Evaluation of estimation methods for fitting the three-parameter Weibull distribution to European beech forests

doi:10.3832/ifor4145-015

Evaluation of estimation methods for fitting the three-parameter Weibull distribution to European beech forests

Ziva Bončina^(1-2), Vasilije Trifković⁽¹⁾, Christian Rosset⁽³⁾, Matija Klopčič⁽¹⁾

iForest - Biogeosciences and Forestry, Volume 15, Issue 6, Pages 484-490 (2022)
doi: https://doi.org/10.3832/ifor4145-015
Published: Dec 01, 2022 - Copyright © 2022 SISEF

Research Articles

PDF Version

Full Text

Citation

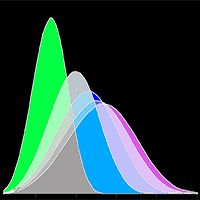
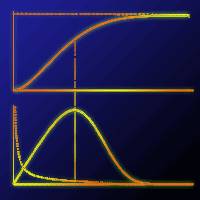
We evaluated three estimation methods for fitting the three-parameter Weibull distribution to even-aged European beech (Fagus sylvatica) forests by using experimental tree diameter data collected in 3709 sample plots (500 m² each). The maximum likelihood estimation method (MLE), the method of moments (MOM) and the method of modified moments type 1 (MM1) were applied for fitting the Weibull function. The goodness-of-fit of stand parameters (total tree number, stand basal area, dominant stand diameter and mean quadratic diameter) was tested by MAE and RMSE, and the probability and cumulative density functions of trees per 5 cm diameter classes were additionally tested by the Kolmogorov-Smirnov test and compared with Kolmogorov-Smirnov’s D statistic. All three methods are suitable for estimating stand parameters based on the fitted Weibull function. Fitting the diameter distribution per 5 cm diameter classes at the plot level was less accurate due to the low number of trees or irregular diameter distribution of trees. The MM1 method was found to be the most suitable for fitting the three-parameter Weibull distribution to beech forests represented by data derived from small plots.

Keywords

Diameter Distribution Fitting, Weibull Function, Parameter Estimation, Inventory Data, Circular Sample Plots, Near-natural Forests, Fagus Sylvatica, Slovenia

Authors’ address

(1)

0000-0002-7533-5708
0000-0003-2619-9073
Department of Forestry and Renewable Forest Resources, Biotechnical Faculty, University of Ljubljana, Večna pot 83, 1000 Ljubljana (Slovenia)

(2)

Slovenia Forest Service, Večna pot 2, 1000 Ljubljana (Slovenia)

(3)

Forest Ecosystem and Management, School of Agricultural, Forest and Food Sciences, HAFL, Bern University of Applied Sciences, Länggasse 85, 3052 Zollikofen (Switzerland)

Corresponding author

Matija Klopčič
matija.klopcic@bf.uni-lj.si

Citation

Bončina Z, Trifković V, Rosset C, Klopčič M (2022). Evaluation of estimation methods for fitting the three-parameter Weibull distribution to European beech forests. iForest 15: 484-490. - doi: 10.3832/ifor4145-015

Academic Editor

Andrea Cutini

Paper history

Received: May 30, 2022
Accepted: Sep 27, 2022

First online: Dec 01, 2022
Publication Date: Dec 31, 2022
Publication Time: 2.17 months

Open Access

This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Breakdown by View Type

(Waiting for server response...)

Article Usage

Total Article Views: 21123
(from publication date up to now)

Breakdown by View Type
HTML Page Views: 18491
Abstract Page Views: 1458
PDF Downloads: 979
Citation/Reference Downloads: 0
XML Downloads: 195

Web Metrics
Days since publication: 721
Overall contacts: 21123
Avg. contacts per week: 205.08

Article Citations

Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Feb 2023)

(No citations were found up to date. Please come back later)

(no Plumx Metrics available for this paper)

Publication Metrics

by Dimensions ^©

Articles citing this article

List of the papers citing this article based on CrossRef Cited-by.

(1)

Akram M, Hayat A (2014)
Comparison of estimators of the Weibull distribution. Journal of Statistical Theory and Practice 8: 238-259.
CrossRef | Gscholar

(2)

Bailey RL, Dell TR (1973)
Quantifying diameter distributions with Weibull function. Forest Sciences 19: 97-10.
Online | Gscholar

(3)

Bassil S, Nyland RD, Kern CC, Kenefic LS (2019)
Dynamics of the diameter distribution after selection cutting in uneven- and even-aged northern hardwood stands: a long-term evaluation. Canadian Journal of Forest Research 49 (12): 1525-1539.
CrossRef | Gscholar

(4)

Bohn U, Neuhäusl R, Gollub G, Hettwer C, Neuhäuslová Z, Raus T, Schlüter H, Weber H (2000)
Buchenwälder [Beech forests]. In: “Karte der natürlichen Vegetation Europas (Maßstab 1: 2.500.000)” [Map of the Natural Vegetation of Europe (scale 1:2.500.000)]. Landwirtschaftsverlag, Münster, Germany, pp. 523. [in German]
Gscholar

(5)

Bončina A, Rozman A, Dakskobler I, Klopčič M, Babij V, Poljanec A (2021)
Gozdni rastiščni tipi Slovenije: vegetacijske, sestojne in upravljavske značilnosti [Forest vegetation types in Slovenia: vegetation, stand, and management characteristics]. Biotechnical Faculty, Department of Forestry and Renewable Forest Resources and Slovenia Forest Service, Ljubljana, Slovenia, pp. 575. [in Slovenian]
Gscholar

(6)

Burkhart HE, Tomé M (2012)
Modeling forest trees and stands. Springer, Dordrecht, Netherlands, pp. 457.
Online | Gscholar

(7)

Cao QV (2004)
Predicting parameters of a Weibull function for modeling diameter distribution. Forest Science 50 (5): 682-685.
Online | Gscholar

(8)

Chu YK, Ke JC (2012)
Computation approaches for parameter estimation of Weibull distribution. Mathematical and Computational Applications 17 (1): 39-47.
CrossRef | Gscholar

(9)

Dubey SD (1967)
Some percentile estimators for Weibull parameters. Technometrics 9 (1): 119-129.
CrossRef | Gscholar

(10)

Duduman G (2011)
A forest management planning tool to create highly diverse uneven-aged stands. Forestry 84 (3): 301-314.
CrossRef | Gscholar

(11)

Gorgoso-Varela JJ, Rojo-Alboreca A, Camara-Obregon A, Dieguez-Aranda U (2012)
A comparison of estimation methods for fitting Weibull, Johnson’s SB and beta functions to Pinus pinaster, Pinus radiata and Pinus sylvestris stands in northwest Spain. Forest Systems 21 (3): 446-459.
CrossRef | Gscholar

(12)

Gove JH, Patil GP, Swindel DF, Taillie C (1994)
Ecological diversity and forest management. In: “Handbook of Statistics 12. Environmental Statistics” (Patil GP, Rao CR eds). Elsevier, Amsterdam, Netherlands, pp. 409-462.
CrossRef | Gscholar

(13)

Hasenauer H, Kindermann G, Steinmetz P (2006)
The tree growth model MOSES 3.0. In: “Sustainable Forest Management” (Hasenauer H ed). Springer, Berlin, Heidelberg, Germany, pp. 64-70.
CrossRef | Gscholar

(14)

Hossain A, Zimmer W (2003)
Comparison of estimation methods for Weibull parameters: complete and censored samples. Journal of Statistical Computation and Simulation 73 (2): 145-153.
CrossRef | Gscholar

(15)

Kangas A, Maltamo M (2000)
Performance of percentile-based diameter distribution prediction and Weibull method in independent data sets. Silva Fennica 24 (4): 381-398.
CrossRef | Gscholar

(16)

Kangas A, Maltamo M (2006)
Forest inventory. Methodology and applications. Springer, Dordrecht, Netherlands, pp. 362.
CrossRef | Gscholar

(17)

Klopčič M, Bončina A (2011)
Stand dynamics of silver fir (Abies alba Mill.)-European beech (Fagus sylvatica L.) forests during the past century: a decline of silver fir? Forestry 84 (3): 259-271.
CrossRef | Gscholar

(18)

Klopčič M, Bončina A (2012)
Recruitment of tree species in mixed selection and irregular shelterwood forest stands. Annals of Forest Science 69 (8): 915-925.
CrossRef | Gscholar

(19)

Lei Y (2008)
Evaluation of three methods for estimating the Weibull distribution parameters of Chinese pine (Pinus tabulaeformis). Journal of Forest Science 54 (12): 566-571.
CrossRef | Gscholar

(20)

Merganič J, Sterba H (2006)
Characterisation of diameter distribution using the Weibull function: method of moments. European Journal of Forest Research 125: 427-439.
CrossRef | Gscholar

(21)

Nanos N, Sjöstedt De Luna S (2017)
Fitting diameter distribution models to data from forest inventories with concentric plot design. Forest Systems 26 (2): 13.
CrossRef | Gscholar

(22)

Nord-Larsen T, Cao VQ (2006)
A diameter distiribution for even-aged beech in Denmark. Forest Ecology and Management 231 (1-3): 218-225.
CrossRef | Gscholar

(23)

O’Hara KL, Hasenauer H, Kindermann G (2007)
Sustainability in multi-aged stands: an analysis of long-term plenter systems. Forestry 80: 163-181.
CrossRef | Gscholar

(24)

Palahi M, Pukkala T, Trasobares A (2006)
Modelling the diameter distribution of Pinus sylvestris, Pinus nigra and Pinus halepensis forest stands in Catalonia using the truncated Weibull function. Forestry 79 (5): 553-562.
CrossRef | Gscholar

(25)

Palahi M, Pukkala T, Blasco E, Trasobares A (2007)
A comparison of beta, Johnson’s SB, Weibull and truncated Weibull functions for modelling diameter distribution of forest stands in Catalonia (north-east of Spain). European Journal of Forest Research 126 (4): 563-571.
CrossRef | Gscholar

(26)

Perperoglou A, Sauerbrei W, Abrahamowicz M, Schmid M (2019)
A review of spline function procedures in R. BMC Medical Research Methodology 19: 46.
CrossRef | Gscholar

(27)

Pobočíková I, Sedliačková Z (2014)
Comparison of four methods for estimating the Weibull distribution parameters. Applied Mathematical Sciences 8 (83): 4137-4149.
CrossRef | Gscholar

(28)

Poudel KP, Cao QV (2013)
Evaluation of methods to predict Weibull parameters for characterizing diameter distributions. Forest Science 59 (2): 243-252.
CrossRef | Gscholar

(29)

Pretzsch H, Biber P, Dursky J (2002)
The single tree-based stand simulator SILVA: construction, application and evaluation. Forest Ecology and Management 162 (1): 3-21.
CrossRef | Gscholar

(30)

Pretzsch H (2009)
Forest dynamics, growth and yield. From measurement to model. Springer, Berlin, Heidelberg, Gemany, pp. 664.
CrossRef | Gscholar

(31)

Rosset C, Dumollard G, Endtner J, Gollut C, Martin V, Sala Weber V D, Wyss F, Schütz JP (2018)
SiWaWa 2.0 et Placettes Permanentes de Suivi Sylvicole (PPSS). Rapport Final, SiWaWa, un modèle d’inventaire et de croissance à l’échelle du peuplement 2018 [SiWaWa 2.0 and Permanent Silvicultural Monitoring Plots (PPSS). Final Report, SiWaWa, a stand-scale inventory and growth model 2018]. Office fédéral de l’environnement - OFEV, Division Forêts, Berne, Switzerland, pp. 127. [in French]
Gscholar

(32)

Schmidt LN, Sanquetta MNI, McTague JP, Silva GF, Fraga Filho CV, Sanquetta CR, Soares Scolforo JR (2020)
On the use of the Weibull distribution in modeling and describing diameter distributions of clonal eucalypt stands. Canadian Journal of Forest Research 50 (10): 1050-1063.
CrossRef | Gscholar

(33)

Schütz JP, Rosset C (2020)
Performances of different methods of estimating the diameter distribution based on simple stand structure variables in monospecific regular temperate European forests. Annals of Forest Science 77, 47.
CrossRef | Gscholar

(34)

Senthamarai Kannan K, Manoj K, Arumugam S (2015)
Senthamarai Kannan K, Manoj K, Arumugam S (2015) Labeling Methods for Identifying Outliers. International Journal of Statistics and Systems 10 (2): 231-238.
Online | Gscholar

(35)

SFS (2021)
Letno poročilo o gozdovih za leto 2020 [Annual report on forests for 2020]. Slovenia Forest Service, Ljubljana, Slovenia, pp. 125. [in Slovenian]
Gscholar

(36)

Sghaier T, Cañellas I, Calama Sánchez-González M (2016)
Modelling diameter distribution of Tetraclinis articulata in Tunisia using normal and Weibull distributions with parameters depending on stand variables. iForest 9: 702-709.
CrossRef | Gscholar

(37)

Siipilehto J (1999)
Improving the accuracy of predicted basal-area diameter distribution in advanced stands by determining stem number. Silva Fennica 33 (4): 281-301.
CrossRef | Gscholar

(38)

Sterba H, Moser M, Hasenauer H, Monserud RA (1995)
PROGNAUS ein abstandsunabhangiger Wachstumssimulator fur ungleichaltrige Mischbestande [PROGNAUS a distance-independent growth simulator for mixed stands of the same age]. Deutscher Verband Forstlicher Forschungsanstalten, Sektion Ertragskunde, Eberswald, Berlin, Germany, pp. 173-183. [in German]
Gscholar

(39)

Teimouri M, Seyed M, Hoseini SM, Nadarajah S (2013)
Comparison of estimation methods for the Weibull distribution statistics. Journal of Theoretical and Applied Statistics 47 (1): 93-109.
CrossRef | Gscholar

(40)

Teimouri M (2020)
ForestFit: statistical modelling for plant size distributions. R package version 1.2.3, web site.
Online | Gscholar

(41)

Teimouri M, Podlaski R (2022)
Bayesian Inference for Johnson’s SB and Weibull distributions. Scandinavian Journal of Forest Research 37 (1): 74-82.
CrossRef | Gscholar

(42)

Tomppo E, Haakana M, Katila M, Peräsaari J (2008)
Multi-source national forest inventory - Methods and applications. Springer, Dordrecht, Netherlands, pp. 373.
CrossRef | Gscholar

(43)

Weibull W (1939)
A statistical theory of the strength of material. Ingeniors Vetenskapa Acadamiens Handligar 151: 1-45.
Gscholar

(44)

Zanakis SH (1979)
A simulation study of some simple estimators for the three-parameter Weibull distribution. Journal of Statistical Computation and Simulation 9: 101-116.
CrossRef | Gscholar

(45)

Zasada M, Cieszewski CJ (2005)
A finite mixture distribution approach for characterizing tree diameter distributions by natural social class in pure even-aged Scots pine stands in Poland. Forest Ecology and Management 204 (2-3): 145-158.
CrossRef | Gscholar

(46)

Zhang L, Packard KC, Liu C (2003)
A comparison of estimation methods for fitting Weibull and Johnson’s SB distributions to mixed spruce-fir stands in northeastern North America. Canadian Journal of Forest Research 33: 1340-1347.
CrossRef | Gscholar

(47)

Zutter BR, Oderwald RG, Murphy PA, Farrar RM (1986)
Characterizing diameter distributions with modified data types and forms of the Weibull distribution. Forest Science 32 (1): 37-48.
Online | Gscholar

(48)

Zuur AF, Ieno EN, Smith GM (2007)
Analysing ecological data. Springer, New York, USA, pp. 672.
CrossRef | Gscholar

iForest - Biogeosciences and Forestry

Contents

Search

Journal Info

Journal Subjects and Fields

For Authors

For Reviewers

For Readers

SISEF Publishing

Search iForest Contents