Properties and prediction accuracy of a sigmoid function of time-determinate growth

doi:10.3832/ifor1243-007

Properties and prediction accuracy of a sigmoid function of time-determinate growth

iForest - Biogeosciences and Forestry, Volume 8, Issue 5, Pages 631-637 (2015)
doi: https://doi.org/10.3832/ifor1243-007
Published: Jan 13, 2015 - Copyright © 2015 SISEF

Research Articles

PDF Version

Full Text

Citation

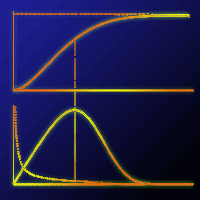
The properties and short-term prediction accuracy of mathematical model of sigmoid time-determinate growth, denoted as “KM-function”, are presented. Comparative mathematical analysis of the function revealed that it is a model of asymmetrical sigmoid growth, which starts at zero size of an organism and terminates when it reaches its final size. The function assumes a finite length of the growth period and includes a parameter interpretable as the expected lifespan of the organism. Moreover, the possibility for growth curve inflexion at any age is possible, so the function can be used for modelling of S-shaped growth trajectories with various degree of asymmetry. These good theoretical predispositions for realistic growth predictions were empirically evaluated. The KM-function used in three and four-parameter forms was compared with three classical (Richards, Korf and Weibull) growth functions employing two parameterisation methods - nonlinear least squares (NLS) and Bayesian method. The evaluation was conducted on the basis of the tree diameter series obtained from stem analyses. The main empirical findings are: (i) if the minimisation of the prediction bias is required, the KM-function in three-parameter form in connection with Bayes parameterisation can be recommended; (ii) if the minimisation of root square error (RMSE) is required, the best short-term prediction results for a particular dataset were obtained with four-parameter Weibull function employing NLS parameterisation; (iii) moreover, three-parameter functions parameterised by Bayesian methods show a considerably smaller RMSE by 15-25% as well as smaller biases by 40-60% than four-parameter functions employing NLS. Overall, all analyses confirmed relative usefulness of the KM-function in comparison with classical growth functions, especially in connection with Bayesian parameterisation.

Keywords

Growth Function, Determinate Growth, Nonlinear Least Squares, Bayes, Prediction

Authors’ address

(1)

Faculty of Forestry, Technical University in Zvolen, T.G. Masaryka 24, 960 53 Zvolen (Slovak Republic)

(2)

Faculty of Forestry and Wood Sciences, Czech University of Life Sciences Prague, Kamýcká 1176, 165 21 Praha 6 - Suchdol (Czech Republic)

Corresponding author

Lubomír Scheer
scheer@tuzvo.sk

Citation

Sedmák R, Scheer L (2015). Properties and prediction accuracy of a sigmoid function of time-determinate growth. iForest 8: 631-637. - doi: 10.3832/ifor1243-007

Academic Editor

Renzo Motta

Paper history

Received: Jan 15, 2014
Accepted: Oct 17, 2014

First online: Jan 13, 2015
Publication Date: Oct 01, 2015
Publication Time: 2.93 months

Open Access

This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Breakdown by View Type

(Waiting for server response...)

Article Usage

Total Article Views: 50607
(from publication date up to now)

Breakdown by View Type
HTML Page Views: 41992
Abstract Page Views: 2144
PDF Downloads: 5124
Citation/Reference Downloads: 42
XML Downloads: 1305

Web Metrics
Days since publication: 3600
Overall contacts: 50607
Avg. contacts per week: 98.40

Article Citations

Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Feb 2023)

Total number of cites (since 2015): 2
Average cites per year: 0.22

(no Plumx Metrics available for this paper)

Publication Metrics

by Dimensions ^©

Articles citing this article

List of the papers citing this article based on CrossRef Cited-by.

(1)

Bertalanffy L (1957)
Quantitative laws in metabolism and growth. Quarterly Review of Biology 32: 217-231.
CrossRef | Gscholar

(2)

Burkhart HE, Tomé M (2012)
Modelling forest trees and stands. Springer Science + Business Media BV, Dordrecht, The Netherlands, pp. 471.
Online | Gscholar

(3)

Birch CP (1999)
A new generalized logistic sigmoid growth equation compared with the Richards growth equation. Annals of Botany 83: 713-723.
CrossRef | Gscholar

(4)

Bock RD, du Toit SHC (2004)
Parameter estimation in the context of nonlinear longitudinal growth models. In: “Methods in Human Growth Research” (Hauspie RC, Cameron N, Molinari L eds). Series Cambridge Studies in Biological and Evolutionary Anthropology, vol. 39, Cambridge University Press, Cambridge, UK, pp. 198-220.
Gscholar

(5)

Carlin BP, Louis TA (2000)
Bayes and empirical Bayes methods for data analysis. Texts in Statistical Science, Chapman & Hall/CRC, Boca Raton, FL, USA, pp. 440.
Gscholar

(6)

D’Agostini G (2003)
Bayesian inference in processing experimental data: principles and basic applications. Reports on Progress in Physics 66 (9): 1383-1383.
CrossRef | Gscholar

(7)

Ek AR, Monserud RA (1979)
Performance and comparison of stand growth models based on individual tree diameter. Canadian Journal of Forest Research 9: 231-244.
CrossRef | Gscholar

(8)

Fekedulegn D, Mac Siurtain MP, Colbert JJ (1999)
Parameter estimation of nonlinear growth models in forestry. Silva Fennica 33 (4): 327-336.
CrossRef | Gscholar

(9)

Fitzhugh HA (1976)
Analysis of growth curves and strategies for altering their shape. Journal of Animal Science 42 (4): 1036-1051.
Online | Gscholar

(10)

Gompertz B (1825)
On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philosophical Transactions of the Royal Society 115: 513-585.
CrossRef | Gscholar

(11)

Halaj J, Petráš R (1998)
A growth and yield tables of main tree species in Slovakia. Slovak Academic Press, Bratislava, SK, pp. 325. [in Slovak]
Gscholar

(12)

Halaj J (1957)
Mathematical and statistical research of diameter structures of Slovak stands. Lesnícky časopis 3 (1): 39-74. [in Slovak]
Gscholar

(13)

Karkach AS (2006)
Trajectories and models of individual growth. Demographic Research 15: 347-400.
CrossRef | Gscholar

(14)

Kiviste AK (1988)
Mathematical functions of forest growth. Estonian Agriculture Academy, Tartu, Estonia, pp.108.
Gscholar

(15)

Korf V (1939)
Contribution to mathematical definition of the law of stand volume growth. Manuscript, Lesnická práce, Slovakia, pp. 339-379.
Gscholar

(16)

Kumaraswamy P (1980)
A generalized probability density function for double-bounded random processes. Journal of Hydrology 46: 79-88.
CrossRef | Gscholar

(17)

Li FG, Zhao BD, Su GL (2000)
A derivation of the generalized Korf growth equation and its application. Journal of Forestry Research 11 (2): 81-88.
CrossRef | Gscholar

(18)

Lunn DJ, Thomas A, Best N, Spiegelhalter D (2000)
WinBUGS - a Bayesian modeling framework: concepts, structure, and extensibility. Statistics and Computing 10: 325-337.
CrossRef | Gscholar

(19)

Mitscherlich EA (1919)
Problems of plant growth. Landwirtschaftliche Jahrbücher 53: 167-182. [in German]
Gscholar

(20)

Pagan J (1992)
Forestry dendrology. Technical University in Zvolen, Zvolen, Slovakia, pp. 347. [in Slovak]
Gscholar

(21)

Pretzsch H (2009)
Forest dynamics, growth and yield. From measurement to model. Springer-Verlag, Berlin, Germany, pp. 617.
CrossRef | Gscholar

(22)

Ratkowsky DA (1983)
Nonlinear regression modelling. Marcel Dekker, New York, USA, pp. 276.
Gscholar

(23)

Richards FJ (1959)
A flexible growth function for empirical use. Journal of Experimental Botany 10: 290-300.
CrossRef | Gscholar

(24)

Seber GAF, Wild CJ (2003)
Nonlinear regression. Wiley series in probability and statistics, John Wiley & Sons, Inc., New Jersey, USA, pp. 792.
Gscholar

(25)

Sedmák R (2009)
Growth and yield modelling of beech trees and stands. Msc Thesis, Technical University in Zvolen, Zvolen, Slovakia, pp. 181.
Gscholar

(26)

Sedmák R, Scheer L (2012)
Modelling of tree diameter growth using growth functions parameterised by least squares and Bayesian methods. Journal of Forest Science 58 (6): 245-252.
Online | Gscholar

(27)

Shvets V, Zeide B (1996)
Investigating parameters of growth equations. Canadian Journal of Forest Research 26: 1980-1990.
CrossRef | Gscholar

(28)

Sloboda B (1971)
Investigation of growth processes using first order differential equations. Mitteilungen der Baden-Württembergischen Forstlichen Versuchs und Forschungsanstalt 32: 1-109. [in German]
Gscholar

(29)

Schnute J (1981)
A versatile growth model with statistically stable parameters. Canadian Journal of Fisheries and Aquatic Sciences 38: 1128-1140.
CrossRef | Gscholar

(30)

StatSoft Inc (2010)
Electronic statistics textbook. Tulsa, OK, USA.
Online | Gscholar

(31)

Tsoularis A, Wallace J (2002)
Analysis of logistic growth models. Mathematical Biosciences 179: 21-25.
CrossRef | Gscholar

(32)

Vanclay JK (1994)
Modelling forest growth and yield: application to mixed tropical forests. CAB International, Wallingford, UK, pp. 312.
Online | Gscholar

(33)

Verhulst B (1838)
A note on population growth. Correspondence Mathematiques et Physiques 10: 113-121. [in French]
Gscholar

(34)

Weibull W (1951)
A statistical distribution of wide applicability. Journal of Applied Mechanics 18: 293-297.
Gscholar

(35)

Weiskittel AR, Hann DW, Kershaw JA, Vanclay JK (2011)
Forest growth and yield modelling (1st edn). John Wiley & Sons Ltd, Chichester, UK, pp.344.
Online | Gscholar

(36)

Yin X, Goudriaan J, Lantinga EA, Vos J, Spiertz HJ (2003)
A flexible sigmoid function of determinate growth. Annals of Botany 91 (3): 361-371.
CrossRef | Gscholar

(37)

Zeide B (1989)
Accuracy of equations describing diameter growth. Canadian Journal of Forest Research 19 (10): 1283-1286.
CrossRef | Gscholar

(38)

Zeide B (1993)
Analysis of growth equations. Forest Science 39 (3): 594-616.
Online | Gscholar

(39)

Zeide B (2003)
The U-approach to forest modelling. Canadian Journal of Forest Research 33 (3): 480-489.
CrossRef | Gscholar

(40)

Zeide B (2004)
Intrinsic units in growth modelling. Ecological Modelling 175 (3): 249-259.
CrossRef | Gscholar

(41)

Zhang L (1997)
Cross-validation of non-linear growth functions for modelling tree height-diameter relationships. Annals of Botany 79 (3): 251-257.
CrossRef | Gscholar

iForest - Biogeosciences and Forestry

Contents

Search

Journal Info

Journal Subjects and Fields

For Authors

For Reviewers

For Readers

SISEF Publishing

Search iForest Contents