Modeling of time consumption for selective and situational precommercial thinning in mountain beech forest stands
iForest - Biogeosciences and Forestry, Volume 14, Issue 2, Pages 137-143 (2021)
doi: https://doi.org/10.3832/ifor3556-014
Published: Mar 16, 2021 - Copyright © 2021 SISEF
Research Articles
Abstract
Rationalization and optimization of work is becoming increasingly important in the European forestry sector. In this study a tool for modeling three different precommercial thinning approaches in young beech mountain stands was developed based on several field studies. The simulation examines three primary types of precommercial thinning: selective thinning and two types of situational thinning. We studied the impact of the number of candidates/crop trees and the impact of harvesting intensity on the structure and consumption of productive time. We found that in terms of costs situational precommercial thinning is more rational than selective precommercial thinning, that harvesting intensity has a significant impact on time consumption and that the number of candidates or crop trees has a significant impact on time consumption as well as on the relationships between main and auxiliary productive time. The modeling has shown that situational thinning is an alternative to selective thinning and that, in addition to requiring smaller and more efficient harvesting machines, it offers a cost-effective and ergonomic option (more walking, less chainsaw operation) for the pre-commercial thinning of young forest.
Keywords
Precommercial Thinning, Selective Thinning, Situational Thinning, Modeling, Crop Tree
Introduction
Although the forest industry often focuses on economic results, the market is directly tied to the sustainable long-term management of forest ecosystems ([27]). The precommercial thinning of young forest stands is beneficial for the quality of selected trees, species mixture, forest stability and biodiversity ([12], [21], [23]). However, these benefits only become noticeable after a delay ([28]), and the effects of thinnings are difficult to evaluate directly due to long production cycles. Thinnings of the earlier developmental stages of the forest play an essential role in the development of mature forest stands ([21]). From an economic point of view, however, precommercial thinning today may represent a relatively uncertain investment in the future forest due to the increasing risk of natural disturbances related to climate change ([17], [30]).
In Central Europe (e.g., Switzerland, Slovenia, Italy) selective thinning begins in pole-stage stands and continues to mature stands, when it is replaced by increment or crown thinning ([33], [31]). The first entries are in mixed stands of light-demanding species after the thicket phase, which means a relatively large number of candidates (for future crop trees) per unit area (1500-2000 per ha). As a result, many trees favored as candidates in earlier thinnings become competitors or indifferent trees in subsequent thinning interventions, which renders previous interventions somewhat ecologically and economically unjustified ([3]). Comparative studies of untreated and thinned stands have also shown the negative impact of selective thinning on the course of self-differentiation and collective stand stability of forest stands ([4]). Due to the frequent interventions throughout the stand as a result of selective thinning, self-differentiation is impeded when compared to less intensive thinning approaches or stands with no intervention ([4]).
During the last three decades, negative economic results have triggered criticism of selective thinning in young stands due to (i) rising labor costs in relation to the declining market price of timber, (ii) the social and economic situation of forest owners (e.g., employment outside forestry, declining forestry skills), (iii) increased investment risks due to frequent natural disturbances (e.g., concerns about the decline of collective stability) and (iv) difficulty in justifying four to six precommercial tending interventions ([16], [33]).
In some respects, the practice of choosing a large number of candidates for selective thinning at younger developmental stages of a forest is seen as controversial. First, in theory the distance between crop trees cannot increase continuously as predicted by selective thinning; rather, it is more likely a multiple of the initial distance. Second, the collective stability of stands is often neglected for the sake of the stability of individual trees. Collective stability is significantly reduced because of the more frequent, all-encompassing and intensive interventions specific to selective thinning in Central Europe ([40]).
In the face of difficult environmental and economic conditions, tending models are in need of improvement. They must take into account the economic viability of interventions and the consequences of skipping some interventions for long-term stand development. The overarching goal should be to reduce labor costs and improve revenue for the forest owner without jeopardizing the functioning of the forest at the ecosystem level.
In the second half of the last century, situational tending emerged as an alternative model of tending young forest stands in Central Europe ([36]). It was developed under the influence of rationalization of selective thinning ([3]) by concentrating from the onset of interventions on a small number of future crop trees which are strictly favored until the regeneration (German “Z-Baum’’ - [2], [4]). Their number depends on the tree species, the thinning method (thinning at half-final or final distance between crop trees - [4]) and the target diameter of the forest stand ([18]).
This paper focuses on precommercial situational thinning, which is primarily intended for the tending of monodominant and mixed even-aged stands. These types of managed forest stands are globally dominant and will continue to be important due to the increasing frequency and intensity of natural disturbances.
The fields of traditional and fully mechanized harvesting for commercial thinning appear to be well researched from the standpoint of time studies ([14]). On the other hand, precommercial thinning and tending has been somewhat neglected from the standpoint of forestry operation research and productivity, although it accounts for 12-15% of costs within the forest rotation period ([16]). Despite several decades of development and testing of situational precommercial thinning, no detailed studies have been conducted on reducing workload in relation to the smaller number of selected future crop trees; there are only some estimates ([3]). While some literature already exists pertaining to the use of mechanized harvesting during precommercial thinning ([20], [8], [9]), there is a lack of knowledge regarding the optimization of motor-manual thinning during precommercial forest operations.
In order to evaluate the differences between situational and selective precommercial thinning, we developed a computer program for thinning simulation based on three previously conducted studies dealing with precommercial thinning of beech stands in Slovenia ([19], [26], [6]). The program is designed to model candidates or future crop tree position networks and remove competitors using three different thinning intensities for selective precommercial thinning and two alternatives of situational precommercial thinning. The research sought to determine: (i) how working time structure and productivity change with the number of selected candidates/future crop trees; (ii) how working time structure and productivity change with increasing thinning intensity; and (iii) differences in the costs of performing different types of precommercial thinning, based on the principle of concentration.
Materials and methods
We developed a program to simulate three different alternatives for the precommercial thinning of young beech stands in mountain forests using MS Visual Basic for Applications ([1]). In the simulation process, we included three different thinning systems: (i) selective precommercial thinning (ST1800), which in this case refers to the precommercial thinning of a stand in the sapling development stage with approximately 1800 selected candidates per ha; (ii) situational thinning at half-final distances (ST400) with approximately 400 selected candidates for crop trees per hectare; (iii) and situational thinning at final distances (ST100) with 100 selected crop trees per ha.
Thinning simulation algorithm
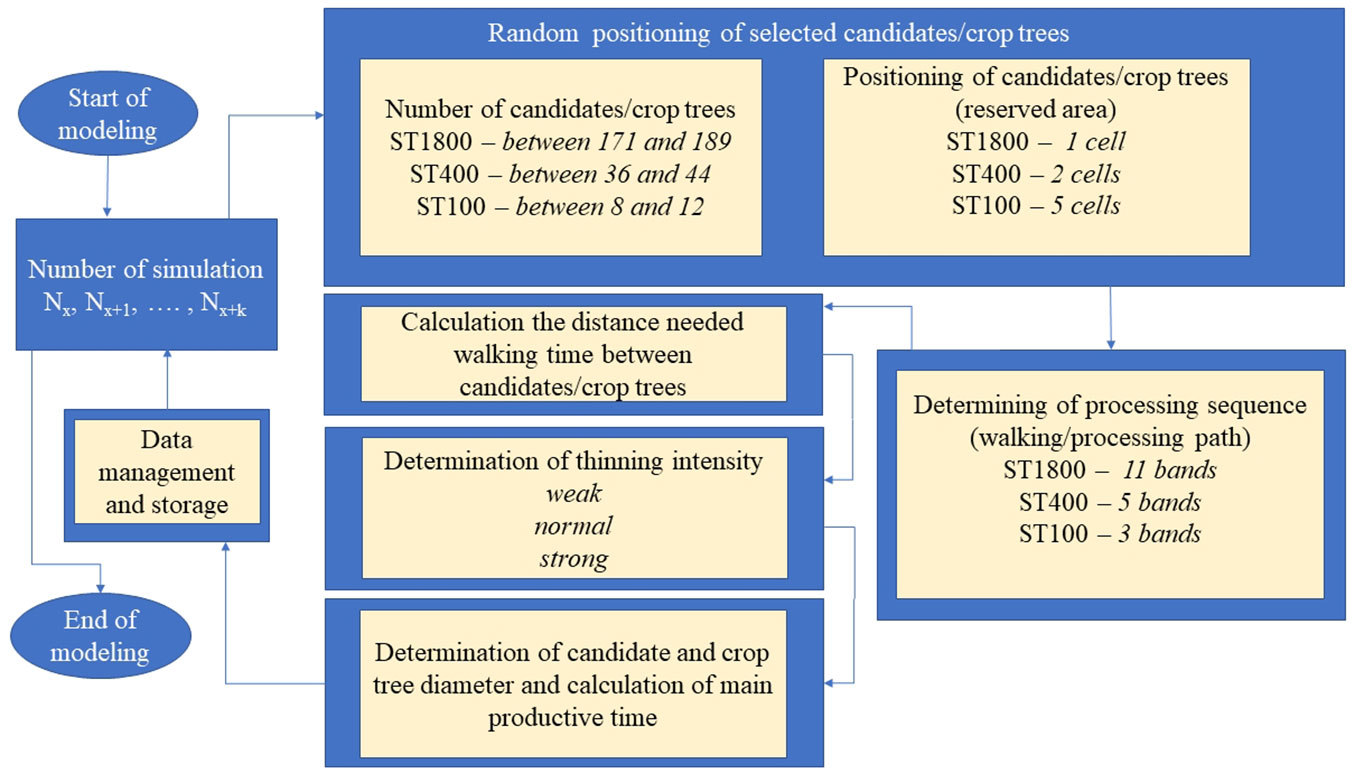
The thinning simulation algorithm is divided into seven procedures: (1) setting the number of simulations; (2) randomly selecting candidate/crop tree positions; (3) determining the processing sequence (walking/processing path); (4) calculating the distance between candidates/crop trees; (5) determining thinning intensity; (6) simulating DBH and productivity; and (7) data management and storage of the individual simulation (Fig. 1).
Number of simulations
At the beginning of the modeling process, the user first sets the number of thinning simulation repetitions. We generated 1000 simulations for each combination of precommercial thinning approach and thinning intensity ([13]).
Random positioning of selected candidates/crop trees
The virtual plot represents a 1000 m2 rectangular forest area with 1056 cells, each with a unique location identification number (ID) starting at 1 in the upper left corner and ending with ID 1056 in the lower right corner (32 columns and 33 rows). The cell ID is intended to identify the positions of the candidate trees within the virtual plot. The program selects a random number between 1 and 1056 when choosing the positions of crop trees based on the minimum distance between neighboring crop trees, which depends on the thinning system (ST1800 - 1; ST400 - 2; ST100 - 5 free cells). The number of crop trees in the virtual plot varies randomly for each simulation and depends on the thinning system (ST1800: between 171 and 189 candidates; ST400: between 36 and 44 crop trees; SR100: between 8 and 12 crop trees).
Determination of processing sequence
The tending operation sequence (virtual worker walking path) between selected crop trees depends on the division of the virtual plot into bands. The bands assist in determining the direction of the harvesting movement during the tending operation. Walking paths are established on the virtual plots systematically in right-to-left or opposite bands, and the band width depends on the thinning system (ST1800: 3 rows; ST400: 7 rows [last 5]; ST100: 11 rows - see Fig. S1 in Supplementary material).
The thinning intervention begins in the upper left corner of the virtual plot in each of the thinning systems and repetitions. The sequence of crop tree processing depends on the direction of virtual worker movement in a band (left or right) and on the column ID of a crop tree (cell location) in the virtual plot. If the direction of processing is to the right (left), the crop trees process in ascending order (descending) according to the column ID. In the case where two cells with crop trees in one band are distributed with the same column, the one whose row label ID is lower takes priority (the upper one).
Calculation of walking time between candidates/crop trees
The simulation calculates the mutual distances between subsequently processed candidates/crop trees. The calculation of mutual distances (R) simply uses Pythagoras’ theorem (eqn. 1), where x represents the absolute distance between columns of neighboring candidate/crop trees in a virtual plot (Idi and Idi+1 - eqn. 2) and y represents the absolute distance between rows of neighboring candidate trees in a virtual plot (Idz and Idz+1, - eqn. 3).
To convert our model distances to actual distances, the simulation program multiplied x by 0.99 (31.62 m in nature/32 columns) and y by 0.96 (31.62 m in nature/33 rows). The walking speed in the virtual plot was taken from previous research conducted in Slovenia ([5], [6]). At an average density of 43.950 trees per ha, with an average DBH of 4.8 cm and terrain slope of 70%, the average walking speed was 5.7 seconds per meter of horizontal distance. To account for the heterogeneity of stand density (43.950 ± 4.000 trees per ha), we calculated the following auxiliary productive time (time spent walking between subsequently selected crop trees - AT). The walking speed (H) for each movement between neighboring candidates or crop trees was randomly determined in the range of 5.7 ± 0.5 seconds per meter and multiplied by the distances between neighboring crop trees (eqn. 4). The variability of the walking speed was assumed based on the heterogeneity of stand density in which the previous study was carried out ([5]).
Determination of thinning intensity
Thinning intensity was determined by the number of competitors per candidate/crop tree. An algorithm for each of the individual candidates or crop trees selects a specific number of competitors from a pre-specified range of possible numbers for each of the three types of thinning intensity. In order to determine the impact of thinning intensity on the performance of tending operations, we ran 1000 thinning simulations and the associated thinning operation for weak (1.5 - competitors per selected crop tree), normal (2) and high thinning intensity (2.5) for each thinning system (Tab. S1 in Supplementary material). The thinning intensities used mimic methods for selection of competitors carried out by the public forestry service in Slovenia. For the first pre-commercial entry, due to the small size of the trees, densities are used to indicate the thinning intensity and not the basal area of the stand as in the following entries. The development of the model was based on data from studies on the first thinning entries ([5]).
Determination of candidate and crop tree diameter and calculation of main productive time
The model stand DBH of the candidates and crop trees was generated using data previously collected in Slovenia. The average DBH of candidates was 4.8 cm, the standard deviation was 1.13 cm, the minimum DBH was 3.5 cm and the maximum DBH was 8.1 cm ([5]).
Due to the lack of competitor DBH data in previous studies, we used the DBH of candidates (x) and its dispersion to derive a productive time equation ([19], [26], [5]). The main productive time (y) was calculated using an exponential equation ([22], [7] - eqn. 5) and according to the number of competitors assigned to each selected candidate/crop tree within an individual precommercial thinning simulation. The input data of previous studies are also briefly presented in the supplementary material (Tab. S2 in Supplementary material).
Data management and storage of individual simulations
For each thinning simulation, the results were recorded and stored in a database in three levels. At the first level, results were recorded for each selected candidate/crop tree in the individual simulations (ID, diameter, walking distance, number of competitors, main productive time, auxiliary productive time and the walking speed between the previous and subsequent candidate/crop tree). At the second level, summaries at the simulation level included data on the average diameter, average distance between candidate/crop trees, total number of competitors, total main productive time, auxiliary productive time and average walking speed. The results in the third and final level were summarized in a one-hectare virtual plot.
Information about the simulation model
The thinning simulation model presented in this work is based on time studies and data from the precommercial thinning of a young mountain beech forest with an average terrain slope of between 50-70%, an average tree DBH of 4.8 ± 1.1 cm, a stand density of 43.950 ± 4.000 trees per hectare, limestone bedrock and 100% vegetation coverage ([6] - see Tab. S3 in Supplementary material). The simulation model is applicable to all other terrain situations and tree species with previously conducted detailed time studies of thinning to enable the reconstruction of factors needed for the simulation model.
Statistical analysis
Due to a large difference in the number of candidates and also in time consumption among the three tested thinning systems (ST1800, ST400 and ST100 - Tab. 1), we only statistically tested the impact of thinning intensity. Due to the none-normally distributed data, statistical tests were performed using the Kruskal-Wallis test, which is a non-parametric ANOVA test.
Tab. 1 - Labor costs per hectare for the precommercial thinning of a young beech stand using different thinning approaches and different thinning intensities (TI). (ST1800): selective thinning; (ST400); situational thinning at half-final distances; (ST100): situational thinning at final distances. A coefficient of unproductive time for calculating working time and labor cost per working hour data was taken from previous research in Slovenia ([5]). (*): reduction of cost regarding to selective thinning - Normal TI.
| Thinning approach |
TI | Productive time (h ha-1) |
Working time (h ha-1) |
Labor costs (€ ha-1) |
Influence of TI (share of normal TI) |
Reduction of cost * |
|---|---|---|---|---|---|---|
| ST1800 | Weak | 27.1 ± 0.9 | 42.8 ± 1.4 | 1052 ± 34 | 80 ± 2 | - |
| Normal | 33.7 ± 1.2 | 53.3 ± 1.9 | 1311 ± 47 | 100 | ||
| High | 40.4 ± 1.5 | 63.9 ± 2.5 | 1572 ± 60 | 120 ± 4 | ||
| ST400 | Weak | 7.6 ± 0.5 | 12.0 ± 0.8 | 296 ± 19 | 83 ± 4 | 73 ± 4 % |
| Normal | 9.2 ± 0.6 | 14.5 ± 1.0 | 356 ± 25 | 100 | ||
| High | 10.7 ± 0.8 | 16.8 ± 1.2 | 414± 30 | 116 ± 7 | ||
| ST100 | Weak | 2.8 ± 0.3 | 4.5 ± 0.5 | 110 ± 12 | 88 ± 6 | 90 ± 1 % |
| Normal | 3.2 ± 0.4 | 5.1 ± 0.6 | 125 ± 15 | 100 | ||
| High | 3.6 ± 0.5 | 5.7 ± 0.7 | 140 ± 18 | 112 ± 10 |
The relationship between time consumption (TC) and the number of candidate/crop trees per hectare (NCT) for each category of thinning intensity was a result of the none-normally distributed and heteroscedastic data predicted by a general linear model (eqn. 6):
where k represents the slope and ε is the interception of the general linear model.
Logarithmic regression models were used to predict the relationships between elements of time structure (ETS) and the number of candidate trees per hectare (NCT) for each of the thinning intensities (eqn. 7):
where k represents the slope and ε is the interception of of the lin-log model.
Cost analysis
In order to compare thinning systems in terms of costs, productive time was first converted into working time using the coefficient of unproductive time from the national standard times for forest operation. The labor costs (€ 24.6 per working hour) were based on a previous survey in which a cost calculation was done for a chainsaw worker ([5]).
Results
Productive time
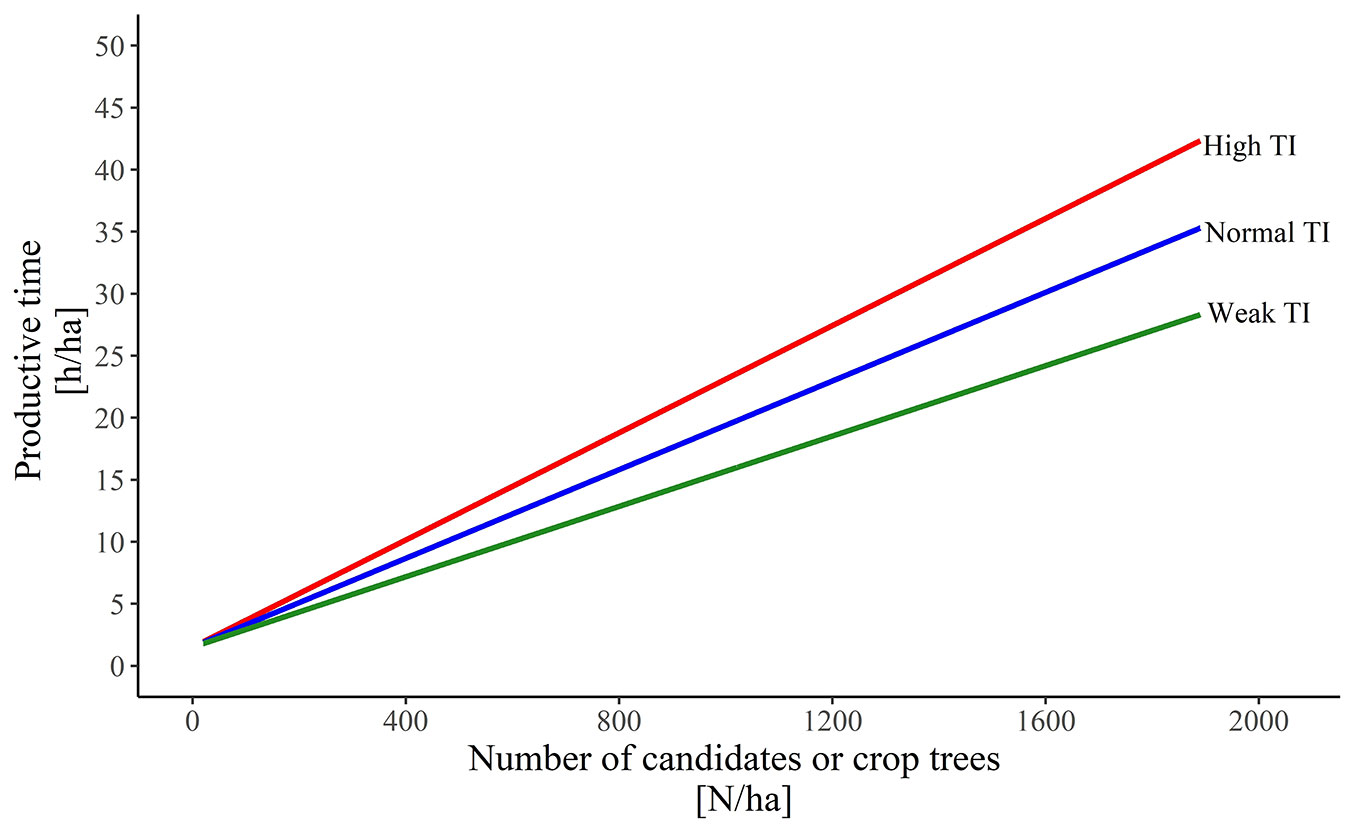
The productive time during precommercial thinning operations in young mountain beech stands increases linearly with the number of candidates/crop trees per ha (Fig. 2). The time consumption was 3.2 h ha-1 for situational precommercial thinning at a normal thinning intensity with final distances (ST100), 9.2 h ha-1 for situational precommercial thinning with half-final distances (ST400) and 33.7 h ha-1 for selective precommercial thinning (ST1800).
Fig. 2 - Productive time in hours per hectare, depending on the number of candidates/crop trees per hectare with high (red), normal (blue) and weak (green) thinning of a young beech mountain stand.
Thinning intensity also has a significant influence on time consumption (Kruskal-Wallis test; ST1800: χ2 = 26.569, p <0.001; ST400: χ2 = 2573, p <0.001; ST100: χ2 = 1920, p <0.001). The average consumption of productive time varied from normal thinning intensity by ± 6.5 h ha-1 for selective precommercial thinning (ST1800) depending on the variation in thinning intensity from weak to strong, by ± 1.5 h ha-1 for situational precommercial thinning at half-final distances (ST400) and by ± 0.4 h ha-1 for situational precommercial thinning at final distances.
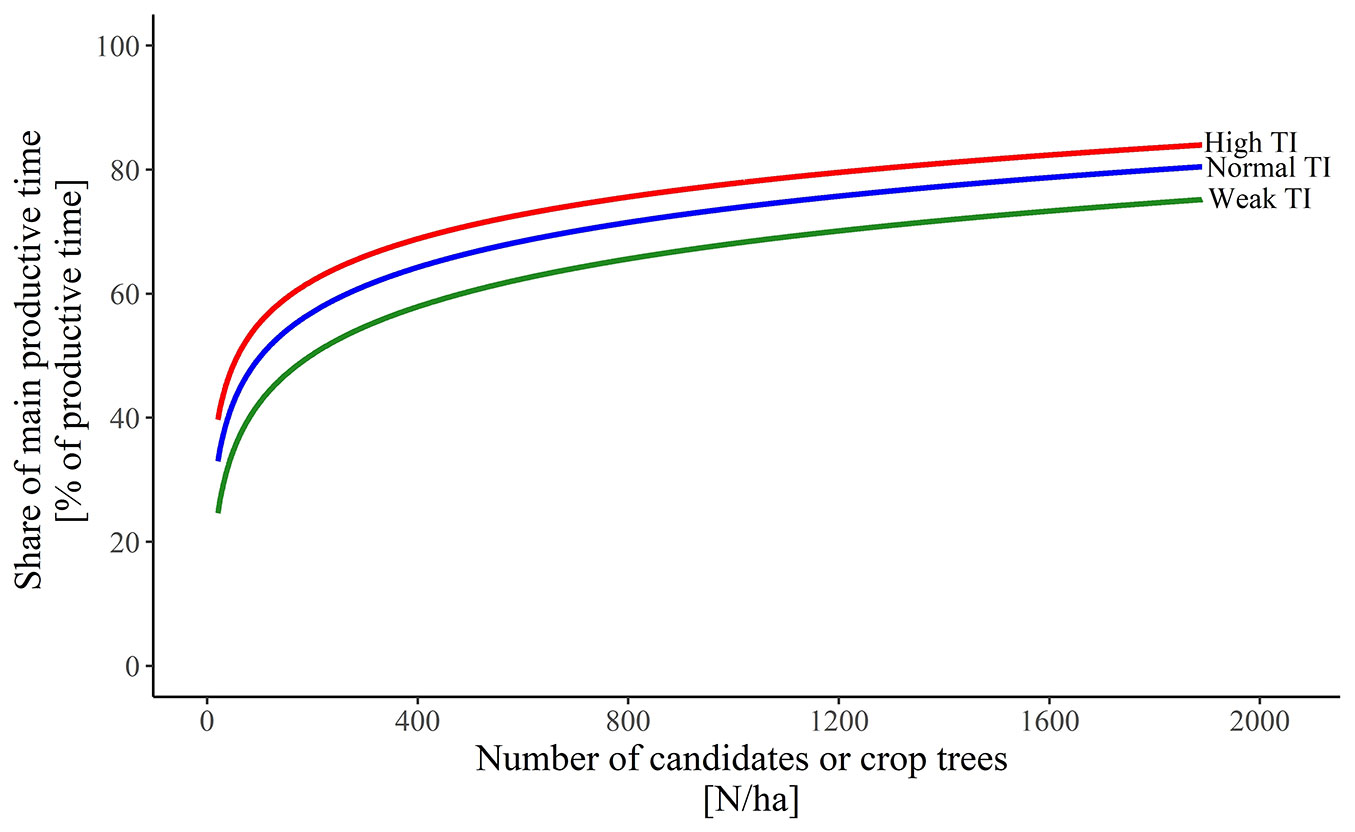
Main productive time
Analysis of the relationship between the proportion of main productive time and the number of candidates/crop trees in the precommercial thinning of young beech mountain stands showed that the data are distributed in the form of an increasing logarithmic curve (high thinning intensity: p <0.001, R2 = 0.936; normal thinning intensity: p <0.001, R2 = 0.947; weak thinning intensity: p <0.001, R2 = 0.966 - Fig. 3). In addition to the influence of the number of candidates or crop trees per hectare, a significant effect of thinning intensity was also observed (Kruskal-Wallis test; ST1800: χ2 = 2968.8, p <0.001; ST400: χ2 = 2891.6, p <0.001; ST100: χ2 = 2597.2, p <0.001).
Fig. 3 - Impact of the number of candidates/crop trees on the proportion of main productive time in high (red), normal (blue) and weak (green) thinning intensity of a young beech stand.
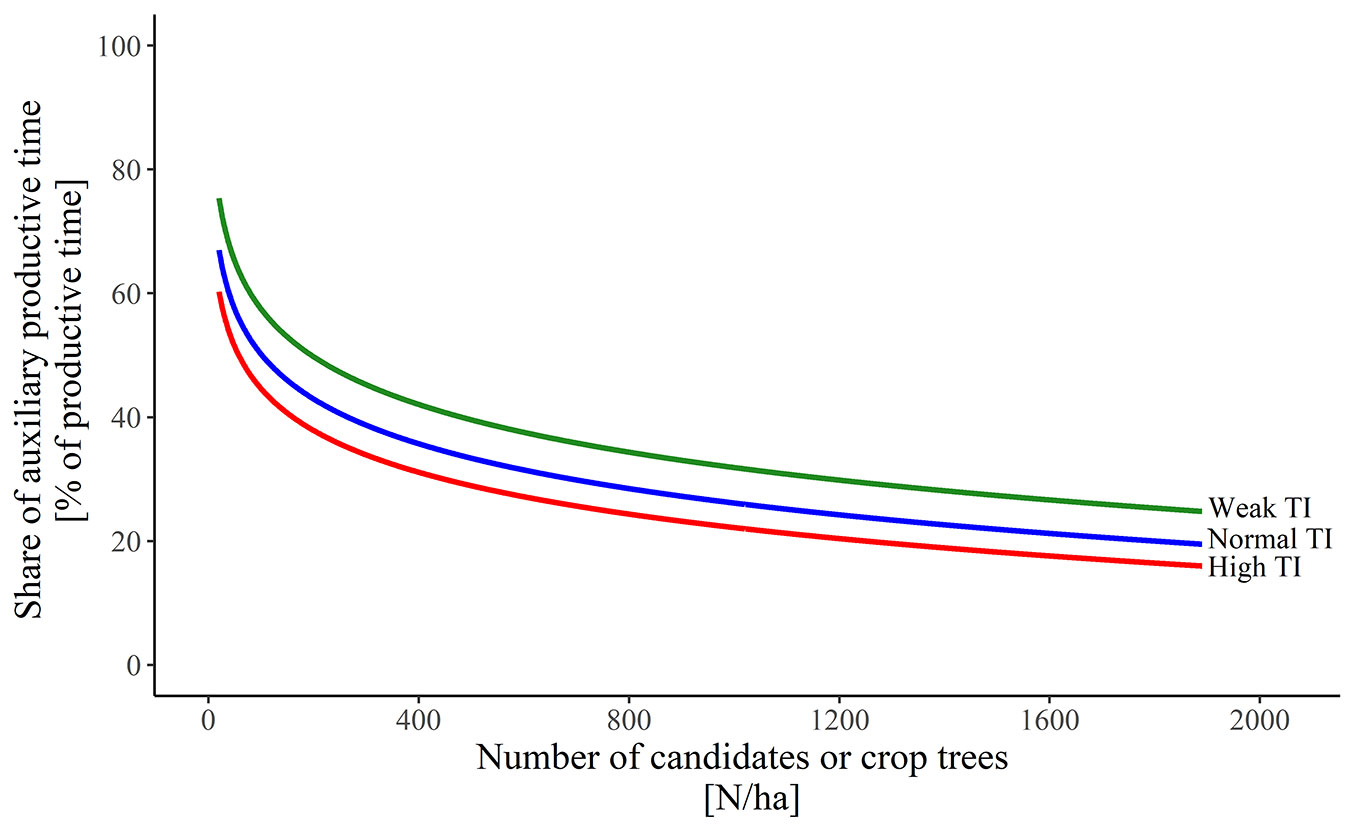
Auxiliary productive time
An analysis of the relationship between the share of auxiliary productive time (movements) within productive time and the number of candidate/crop trees showed that, irrespective of thinning intensity, auxiliary productive time depends on the number of candidates or crop trees. The data are distributed in the form of a descending logarithmic curve (high thinning intensity: p <0.001, R2 = 0.936; normal thinning intensity: p <0.001, R2 = 0.947; weak thinning intensity: p <0.001, R2 = 0.966 - Fig. 4). In addition to the number of candidates or crop trees, thinning intensity is also significantly affected by the auxiliary productive timeshare (Kruskal-Wallis test; ST1800: χ2 = 2968.8, p <0.001; ST400: χ2 = 2891.6, p <0.001; ST100: χ2 = 2597.2, p <0.001).
Fig. 4 - Impact of the number of candidates/crop trees on the share of auxiliary productive time in high (red), normal (blue) and weak (green) thinning intensity of a young beech mountain stand.
Cost analysis
Working time consumption was dependent on the precommercial thinning approach and thinning intensity. For selective precommercial thinning, working time varied between 42.8 and 63.9 h ha-1. For situational thinning at half-final distances, time consumption varied between 12 and 16.8 h ha-1, and for situational thinning at final distances, time consumption of varied between 4.5 and 5.7 h ha-1.
The resulting cost of tending young beech stands was between € 1052 and € 1572 for selective thinning, between € 296 and € 411 for situational thinning at half-final distances and between € 110 and € 140 per hectare for situational thinning at final distances. The influence of thinning intensity on labor costs, relative to the deviation from costs at normal thinning strength, decreased between thinning approaches (ST1800: ± 20%; ST400: ± 17%; ST100: ± 12% - Tab. S2 in Supplementary material).
Discussion
The relatively high cost of selective precommercial thinning, which is widespread in Southeast and Central Europe has triggered the development of less expensive alternative approaches for precommercial silvicultural operations ([36], [18], [4]). Situational precommercial thinning has become a rational alternative to selective precommercial thinning in Switzerland’s young forests ([2], [3]), and a similar form has also developed in Germany ([32]). The primary reasons for this include the poor economic performance of selective thinning ([36]), concerns about collective stability ([4]) and the emergence of even-aged young stands following large-scale disturbances ([25]). Therefore, when compared to selective thinning, situational thinning maintains collective stand stability through the processes of biological automation and concentration of silvicultural interventions ([3], [40]).
Due to a lower number of crop trees per hectare, the use of situational thinning leads to more effective rationalization of productive time consumption compared to selective thinning. Situational thinning at half-final distances between crop trees and normal thinning intensity reduced productive time by 67%, and situational precommercial thinning at final distances reduced it by 90%. Stirnweiß ([39]) reported an absolute time consumption of between 3-5 hours per hectare, which is similar to the results of our simulation for situational thinning at final distances. Similar time consumption for selective precommercial thinning at half-final distances was also reported in previous field experiments in Slovenia ([6]).
The structure of simulated productive time significantly differed across the analyzed precommercial thinning approaches with the reduction of candidates/crop trees per hectare. The relationship between main and auxiliary productive time was inverted with a reduced number of candidates/crop trees per hectare. Comparing selective precommercial thinning to situational precommercial thinning at final distances, the share of main productive time decreased from 79% to 49%. Therefore, auxiliary productive time increased between thinning approaches, and in the case of precommercial thinning at final distances and normal intensity, it accounted for 51% of total time. In addition, heart rate readings in the auxiliary productive time compared to main productive time in motor-manual forest work were 10% lower during situational precommercial thinning ([15]). Therefore, due to the lower time consumption, fuel consumption ([3]), heart rate and exposure to external factors (e.g., wood dust - [24]), situational thinning also appears to be ergonomically better than selective precommercial thinning.
Main productive time significantly increased with thinning intensity due to the higher number of felled competitors. Therefore, the greater number of competitors per hectare resulting from high thinning intensity negatively affected the share of auxiliary productive time in the productive time structure. In the case of weak thinning intensity, the relationship was reversed. An increase in thinning intensity from moderate to weak or high resulted in a ± 20% (± 6.1 h ha-1), ± 16% (± 1.5 h ha-1) and ± 12% (± 0.4 h ha-1) change in the share of the productive time consumption for selective thinning, situational thinning at half-final distances and situational thinning at final distances, respectively. Due to the lack of research in the field of thinning intensity in young stands, such findings related to its influence on time consumption are vital for the fields of silviculture, ecology and wood quality. Experience and preliminary research suggest that frequent interventions across the entire stand area with selective thinning decrease collective stand stability, which is problematic in an era of increasing natural disturbance intensity and frequency ([4], [35], [40]). Collective stability has a particularly important role in young forest stands where there is a strong relationship between tree diameter and tree height ([4]). Early onset and high thinning intensities may also restrict natural self-pruning processes and thus negatively affect future wood quality ([34]). In this respect, situational precommercial thinning based on the principle of concentration is more appropriate for preserving collective stability and positively influences the quality of crop trees ([2], [4]).
The simulation of situational precommercial thinning at half-final distances suggested a 73 ± 4% reduction in costs, and at final distances, 90 ± 1% lower costs can be expected when compared to selective thinning (Tab. 1). Similar economic savings of situational thinning have been reported for Switzerland ([3]) and Germany ([39]). Situational precommercial thinning was also experimentally used in the thinning of young forests within secondary succession on abandoned agricultural lands where the treatment time consumption was similar to situational thinning at half-final distances in this study. Labor costs of the whole operation in a pole stand were € 336 ([11]), which is similar to our results considering lower stand densities on abandoned agricultural lands.
In forest operations the application of situational precommercial thinning is still rare due to its relatively short history and current experimental status. This slow progress may be attributed to: (i) the long-term use of selective thinning which has yielded beneficial results in past economic and climatic conditions; (ii) lack of knowledge on the development and social differentiation of natural stands; (iii) distrust of early final selection of crop trees, which may prevent subsequent corrections; and (iv) a lack of knowledge on the development of crop trees during the process of situational thinning ([39]). All of these represent important areas for future research work.
Although the computer simulation showed similar results to those obtained in previous studies on thinning of beech and mixed forests, the results reflect only an approximation of real forest operation work. The most important constructing factors within the simulation model are detailed work time and field studies from which the formulas used for calculating main and auxiliary productive time are constructed. The presented model is transferable to other terrain and species mixtures for which the biggest deficit is the lack of time studies. Therefore, for further validation of the model, it is important to provide additional time studies of thinning forest operations within young forest stands in contrasting situations (e.g., species mixtures, slope conditions, DBH).
Silvicultural treatment of young forests will be an important challenge for the forestry sector in the coming decades. In temperate forests worldwide, the incidence of large-scale natural disturbances such as windthrows and bark beetle outbreaks has significantly increased in the last decades ([37]). This resulted in large areas covered with young, mostly even-aged forest stands. Interesting new mixtures are emerging, with many options for light-demanding species, many of which are economically interesting. In order to maintain attractive mixtures, the crop tree quality, stand stability and growth potential of these forest areas will need to be properly tended ([23]). This emphasizes the need for an improved model for the implementation of young forest tending. Mechanized harvest is not feasible in stands following disturbances were intervention is infrequent due to low densities of crop trees. In addition, identification of tree species is required, which can be carried out by a well-trained forest worker. Such operations remain interesting in private forests, where owners carry out logging by themselves.
Looking ahead, it appears that the technological development of pre-commercial thinning will continue to advance. One possibility is the increased use of small harvesting machines ([9], [38]). However, experience from young successional stands suggests that heavy thinning can trigger a reduction in the collective stability of stands ([11]). In addition, mechanized harvesting leads to greater damage to the forest soil and - in the case of inexperienced machine operators - to the remaining stand ([10]). There are no such problems in the further optimization of moto-manual pre-commercial thinning approaches based on the principle of concertation (such as situational thinning). The third option is based on biological automation, e.g., the preference for small-scale, uneven-aged stands with continuous cover as the primary silvicultural approach ([4]). Such models, as presented above, enable the optimization and quick assessment of work costs and investments. Thus, further development with objective field evaluations could increase the importance of computer simulations and support decision-making process in young forest tending ([29]).
Conclusions
Modelling time consumption for selective and situational precommercial thinning in mountain beech forest stands enables quantitative evaluation of the differences in time consumption (absolute and according to the time element structure) and thus a more accurate prediction of the resources required for alternative silvicultural approaches (material, costs, human work load). Quantifying differences in the resources required enables better planning, implementation and control of silvicultural treatments, which in the same cases is supported by society through fiscal policy measures (subsidies) to ensure sustainable forest management. The main findings are (i) that situational thinning approaches are less time consuming and significantly less expensive than selective thinning, and (ii) due to a larger share of auxiliary productive time (walking operation) and less chain-saw operation, situational thinning approaches also seem to be more ergonomically beneficial for silviculture workers.
Acknowledgments
All the authors contributed equally to this manuscript. The first author kindly acknowledges the Pahernik Foundation for a scholarship during the second year of his master’s studies. This research was funded by the Pahernik Foundation.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Slovenian Forestry Institute, Department of Forest Technique and Economics, Večna pot 2, SI-1000 Ljubljana (Slovenia)
Jurij Diaci 0000-0002-0991-5309
Department of Forestry and Renewable Forest Resources, Biotechnical Faculty, University of Ljubljana. Večna pot 83, Ljubljana 1000 (Slovenia)
Corresponding author
Paper Info
Citation
Arnič D, Krč J, Diaci J (2021). Modeling of time consumption for selective and situational precommercial thinning in mountain beech forest stands. iForest 14: 137-143. - doi: 10.3832/ifor3556-014
Academic Editor
Andrea Cutini
Paper history
Received: Jun 18, 2020
Accepted: Jan 16, 2021
First online: Mar 16, 2021
Publication Date: Apr 30, 2021
Publication Time: 1.97 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2021
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 36349
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 30435
Abstract Page Views: 2828
PDF Downloads: 2436
Citation/Reference Downloads: 9
XML Downloads: 641
Web Metrics
Days since publication: 1803
Overall contacts: 36349
Avg. contacts per week: 141.12
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2021): 2
Average cites per year: 0.40
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Long-term outcome of precommercial thinning on floristic diversity in north western New Brunswick, Canada
vol. 1, pp. 145-156 (online: 25 November 2008)
Research Articles
Interactions between thinning and bear damage complicate restoration in coast redwood forests
vol. 13, pp. 1-8 (online: 08 January 2020)
Research Articles
Comparison of alternative harvesting systems for selective thinning in a Mediterranean pine afforestation (Pinus halepensis Mill.) for bioenergy use
vol. 14, pp. 465-472 (online: 16 October 2021)
Research Articles
The conversion into high forest of Turkey oak coppice stands: methods, silviculture and perspectives
vol. 13, pp. 309-317 (online: 10 July 2020)
Research Articles
Acoustic evaluation of wood quality with a non-destructive method in standing trees: a first survey in Italy
vol. 10, pp. 700-706 (online: 17 July 2017)
Research Articles
Impact of thinning on carbon storage of dead organic matter across larch and oak stands in South Korea
vol. 9, pp. 593-598 (online: 01 March 2016)
Research Articles
Deriving tree growth models from stand models based on the self-thinning rule of Chinese fir plantations
vol. 15, pp. 1-7 (online: 13 January 2022)
Research Articles
Effects of thinning and pruning on stem and crown characteristics of radiata pine (Pinus radiata D. Don)
vol. 10, pp. 383-390 (online: 16 March 2017)
Research Articles
Long-term effects of thinning and mixing on stand spatial structure: a case study of Chinese fir plantations
vol. 14, pp. 113-121 (online: 08 March 2021)
Research Articles
Carbon emission reduction potentials through thinned wood in Japan
vol. 4, pp. 107-112 (online: 01 June 2011)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword