Allometric models for estimating biomass, carbon and nutrient stock in the Sal zone of Bangladesh
iForest - Biogeosciences and Forestry, Volume 12, Issue 1, Pages 69-75 (2019)
doi: https://doi.org/10.3832/ifor2758-011
Published: Jan 24, 2019 - Copyright © 2019 SISEF
Research Articles
Abstract
Allometric models are commonly used to estimate biomass, nutrients and carbon stocks in trees, and contribute to an understanding of forest status and resource dynamics. The selection of appropriate and robust models, therefore, have considerable influence on the accuracy of estimates obtained. Allometric models can be developed for individual species or to represent a community or bioregion. In Bangladesh, the nation forest inventory classifies tree and forest resources into five zones (Sal, Hill, Coastal, Sundarbans and Village), based on their floristic composition and soil type. This study has developed allometric biomass models for multi-species of the Sal zone. The forest of Sal zone is dominated by Shorea robusta Roth. The study also investigates the concentrations of Nitrogen, Phosphorus, Potassium and Carbon in different tree components. A total of 161 individual trees from 20 different species were harvested across a range of tree size classes. Diameter at breast height (DBH), total height (H) and wood density (WD) were considered as predictor variables, while total above-ground biomass (TAGB), stem, bark, branch and leaf biomass were the output variables of the allometric models. The best fit allometric biomass model for TAGB, stem, bark, branch and leaf were: ln (TAGB) = -2.460 + 2.171 ln (DBH) + 0.367 ln (H) + 0.161 ln (WD); ln (Stem) = -3.373 + 1.934 ln (DBH) + 0.833 ln (H) + 0.452 ln (WD); ln (Bark) = -5.87 + 2.103 ln (DBH) + 0.926 ln (H) + 0.587 ln (WD); ln (Branch) = -3.154 + 2.798 ln (DBH) - 0.729 ln (H) - 0.355 ln (WD); and ln (Leaf) = -4.713 + 2.066 ln (DBH), respectively. Nutrients and carbon concentration in tree components varied according to tree species and component. A comparison to frequently used regional and pan-tropical biomass models showed a wide range of model prediction error (35.48 to 85.51%) when the observed TAGB of sampled trees were compared with the estimated TAGB of the models developed in this study. The improved accuracy of the best fit model obtained in this study can therefore be used for more accurate estimation of TAGB and carbon and nutrients in TAGB for the Sal zone of Bangladesh.
Keywords
Introduction
Allometric models are commonly used for estimating forest biomass ([40]). The models use mathematical functions that relate tree biomass with easily measurable tree variables such as diameter at breast height (DBH), total height (H) and wood density (WD - [45]). Allometric equations can be developed for individual species or multiple species covering local, regional or pan-tropical scale. Species specific allometric models should logically provide a greater level of accuracy at a given location ([21]) to assist the assessment of biomass dynamics, net primary productivity, nutrient cycling and budgeting for research purpose ([28], [25]). However, equations developed from small sample sizes may misrepresent the broader population and reduce the accuracy of results ([45]). Regional and pan-tropical allometric models consider multiple species collectively defined by a climatic or geophysical association. Capturing species variability within such models has been overlooked in some notable examples ([10], [11]), while other models have addressed species variability with an additional variable such as wood density ([38], [12]). At local or sub-regional scale, the use of allometric biomass models for multiple species within a particular forest types can provide robust results while avoiding the frequently used pan-tropical or regional biomass models which are likely to be based on broader, more generalized suite of sample species ([8], [9], [10], [11], [12], [34], [37]).
Forests in Bangladesh have been actively managed for over 100 years ([18]). Indeed, sixteen inventories have been carried out in different forests types at different scales since 1960. Over this period, the objectives of forest monitoring have evolved from a focus on volume for timber resources to biomass for carbon related values. The National Forest and Tree Resources Assessment (NFA) in 2007 was the first country-wide inventory to measure tree biomass ([15]). In this assessment, biomass was calculated according to the Brown & Lugo ([9]) method using a generalized volume model, wood density and a biomass expansion factor (AGB = volume over bark × wood density × biomass expansion factor), with an average wood density of 0.57 t m-3 and a biomass expansion factor of 6 to represent the tropical Asia ([14]).
Similarly, carbon stock in the Sundarbans mangrove forest was estimated using the pan-tropical allometric biomass models of Chave et al. ([11]) and Komiyama et al. ([23]) during 2009 to 2010 ([43]). Tree species and their DBH, height and wood density ranges of pan-tropical models are not similar to the species available in different zones of Bangladesh. These generalized models sometimes fail to capture both variations in forest type ([11], [25]) and diversity of the natural vegetation communities, which range from mangrove forest in south-west, to tall tropical forests in the hilly areas in the east, and Sal (Shorea robusta Roth) dominated areas on inland terraced soils ([15]). Relying on pan-tropical models across such distinct structural forest types may distort estimates of biomass and carbon in the tropical forests ([47], [32]). For these reasons, initiatives to develop local allometirc models in Bangladesh have been undertaken ([31]).
The Bangladesh Forest Department has formalized the stratification of its forest areas into to five distinct zones: Sal, Hill, Sundarbans, Coastal and Village to represent different forest types ([6]). The zones are defined by their relative climatic and geophysical properties as described by Akhter et al. ([1]). This process allows the development of a localized, multiple species allometric models to represent a specific vegetation community within a narrower suite of plant functional types. The aims of this study were: (1) to derive total and component wise (leaf, branch, stem and bark) allometric biomass models for the Sal zone of Bangladesh; (2) to measure nutrients (N, P and K) and carbon concentration in leaf, branch, stem and bark of the studied tree species; and (3) to compare the model efficiency of frequently used regional and pan-tropical biomass model.
Materials and methods
Description of the study area
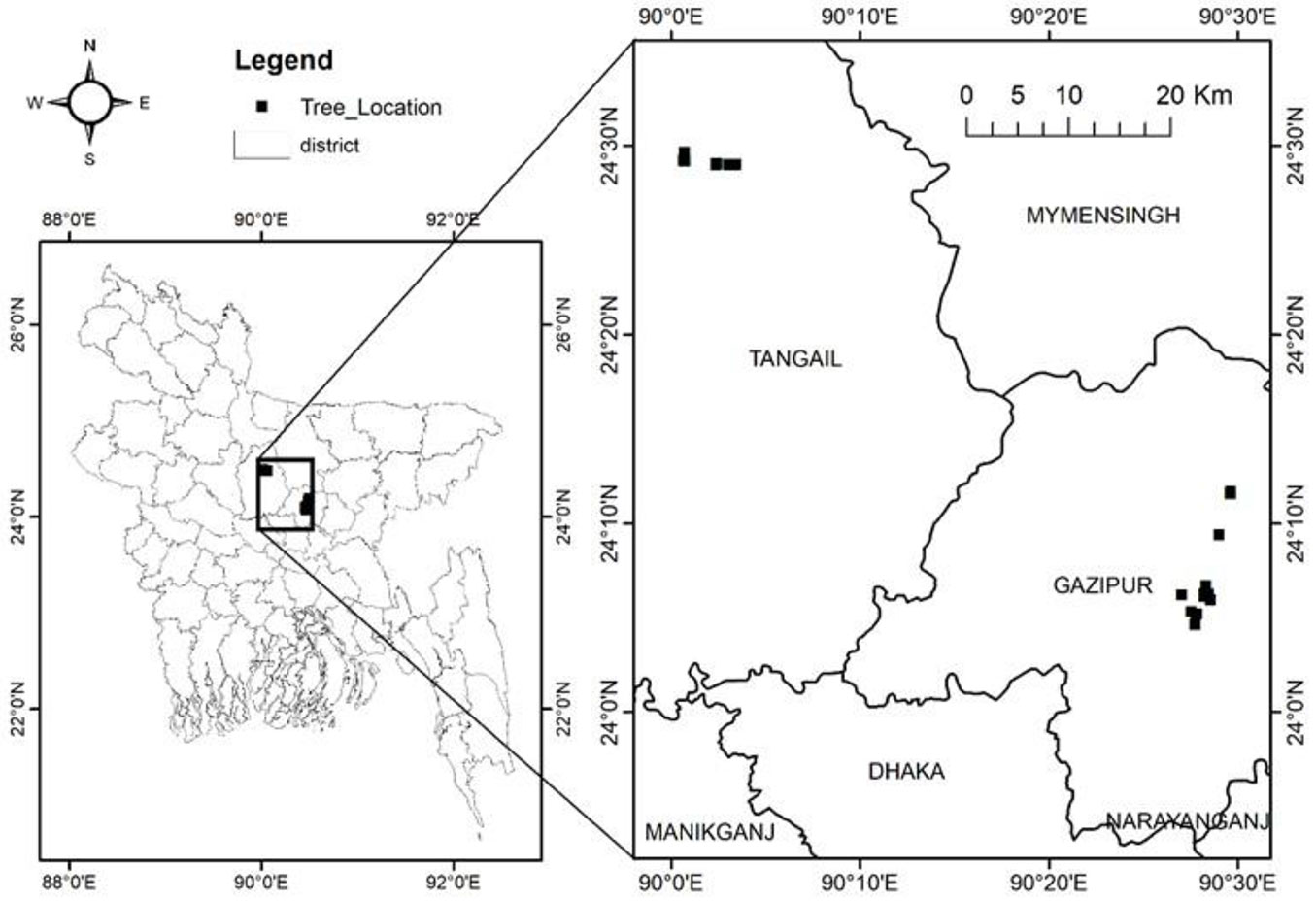
This study was conducted in the Sal zone of Bangladesh (Fig. 1). This zone comprises 121,000 ha of non-contiguous land scattered across the central and northern part of the country in the Districts of Gazipur, Tangail, Mymensingh, Jamalpur, Comilla, Dinajpur, Thakurgaon, Rangpur and Rajshahi. Soils of this zone are heterogeneous, well drained, acidic and have clayey to fine loamy texture ([17]). Shorea robusta, locally known as Sal, is the dominant species within the zone in association with Albizia spp., Swietenia spp., Terminalia spp., Azadirachta indica A. Juss. and Adina cordifolia (Roxb.). However, most of the area is heavily degraded due to intense population pressure, resulting in agricultural, industrial developments encroaching into forest areas and a legacy of unregulated or illicit timber extraction ([19]). In many areas the dominant Sal trees have been replaced with fast growing timber species (such as Acacia auriculiformis A.Cunn. ex Benth., A. mangium Willd. and Eucalyptus camaldulensis Dehnh.) and horticultural trees ([42]).
Measurement of biomass
Sample collection
Sample trees were harvested from areas of natural Sal forest, woodlots of fast growing species, and wooded homestead areas within the Sal zone. A total of 161 sample trees from 20 species (belonging to 14 families - Tab. 1) were selected in the districts of Tangail and Gazipur during 2016 and 2017. Sample trees were selected purposively, avoiding suppressed or diseases trees or those with broken tops, hollows, or other damages. All sampled trees were within a diameter at breast height (DBH) range of 6 to 38 cm, and total height (H) range of 4 to 29 m, respectively (see Tab. S1 in Supplementary material).
Tab. 1 - Species and families of the sampled individuals in this study.
| Family | Species |
|---|---|
| Anacardiaceae | Mangifera indica |
| Combretaceae | Terminalia arjuna |
| Terminalia bellerica | |
| Dipterocarpaceae | Shorea robusta |
| Elaeocarpaceae | Elaeocarpus serratus |
| Fabaceae | Acacia auriculiformis |
| Acacia mangium | |
| Albizia procera | |
| Lamiaceae | Tectona grandis |
| Malvaceae | Grewia microcosm |
| Moraceae | Artocarpus heterophyllus |
| Myrtaceae | Psidium guajava |
| Syzygium cumini | |
| Oxalidaceae | Averrhoa carambola |
| Phyllanthaceae | Phyllanthus emblica |
| Rhamnaceae | Ziziphus mauritiana |
| Rutaceae | Aegle marmelos |
| Citrus grandis | |
| Zanthoxylum rhetsa | |
| Sapindaceae | Litchi chinensis |
Biomass measurement
DBH of the selected trees were measured before felling. The trees were felled as close to ground level as possible and total tree length was measured using a linear tape to representing total height. The felled trees were separated into leaves, small branches (diameter < 7 cm), bigger branches (diameter > 7 cm) and stem, based on the method described by Picard et al. ([40]). The fresh weight of leaves and branches were weighed in the field using a portable digital hanging balance of 100 kg capacity. The stem was sectioned into suitable size for easy handling and their biomass was measured using a hanging digital balance of 400 kg capacity. Stem sections (1 m long) from different positions (base, middle and top) were debarked in the field to get fresh weight proportions of stem and bark to estimate bark and stem wood biomass of the individual sampled trees ([27], [30]). Ten sub-samples (0.25 kg) of each part (leaf, smaller branch, bark, disk of bigger branches and stem) of individual species were taken randomly from the felled trees and transported to laboratory for further analysis. These sub-samples were oven-dried at 105 °C until a constant weight was achieved to estimate the fresh to oven-dry weight conversion factor. The respective conversion factors were used to estimate the oven-dry weight of individual trees.
Carbon and nutrients (N, P and K) in total above-ground biomass (TAGB)
The oven-dried sub-samples of each part of individual species were grounded and sieved through a 2-mm mesh ([2]). The processed samples were acid digested using Kjeldhal digestion method and the sample extract was analyzed according to Beathgen & Alley ([5]) to determine Nitrogen in plant samples. Tri-acid (HNO3, H2SO4 and HClO3 in 10:1:3 ratio) digestion was adopted to determine phosphorus and potassium in sample extracts ([2]). Phosphorus concentration in sample extracts was measured according to Murphy & Riley ([36]), while a flame photometer (PFP7, Jenway Ltd., UK) was used to measure potassium concentration in sample extracts. Carbon content was measured by the loss of ignition method ([2]). Average and standard error of nutrients (N, P and K) and carbon concentration in leaf, branch, stem and bark of sampled tree species were also estimated.
Data analysis
Allometric equations
Descriptive statistics of predictors (DBH, H and WD) and output variables (TAGB, stem, branch and leaf biomass) were calculated. The wood density values of the sampled tree species were collected from Sattar ([44]). These variables were transformed to natural logarithm (ln) to improve the linearity and homoscedasticity. The eight most frequently used pan-tropical or regional biomass allometric equations were tested for the prediction of TAGB (Tab. 2) using R statistical software. Studentized residual analysis was performed to detect the outlier data. Natural logarithm transformation introduced a systematic bias during biomass estimation. Therefore, a correction factor (CF) was calculated for each equation to minimize the systematic bias introduced during the back transformation to biomass value. This correction factor (CF) was multiplied with the exponential factor of Ln biomass value to minimize the inherent systematic bias during biomass estimation ([46]).
Tab. 2 - Frequently used pan-tropical and regional allometric equations.
| Model no. |
Model | Source | Type |
|---|---|---|---|
| 1 | ln (B) = a + b ln (DBH) | Brown ([10]) | Pan-tropical |
| 2 | ln (B) = a + b ln (DBH) + c ln (H) | Nelson et al. ([38]) | Central Amazon |
| 3 | ln (B) = a + b ln (DBH) + c ln (H) + d ln (WD) |
Nelson et al. ([38]), Chave et al. ([11]) | Central Amazon; Pan-tropical |
| 4 | ln (B) = a + b ln (DBH) + c (ln (DBH))2 + d (ln (DBH))3 + e ln (WD) | Chave et al. ([11]) | Pan-tropical |
| 5 | ln (B) = a + b ln (DBH2 × H × WD) | Brown et al. ([8]), Chave et al. ([11]), Chave et al. ([12]) | Pan-tropical |
| 6 | ln (B) = a + b ln (DBH) + c ln (WD) | Djomo et al. ([13]) | Tropical Africa |
| 7 | ln (B) = a + b ln (DBH2 × H) + c ln (WD) |
Djomo et al. ([13]) | Tropical Africa |
| 8 | ln (B) = a + b ln (DBH2 × H) | Brown et al. ([8]), Djomo et al. ([13]) | Pan-tropical; Tropical Africa |
Model selection
The best fit allometric model was selected based on goodness-of-fit statistics. The model having the lowest Akaike Information Criterion (AIC) and Residual Standard Error (RSE), and the highest Akaike Information Criterion weight (AICw) and coefficient of determination (R2) values was selected as best fit model ([45], [40]). However, very small difference among the AIC values of models may lead to a false sense of confidence during model selection process. Therefore, AICw was calculated to overcome this confusion and to describe the relative performance of the models ([48]). AICw was calculated from the following equation (eqn. 1):
where Δi(AIC) is the difference between the model having minimum AIC value and AIC of the individual model.
Test of multicollinearity is important for the models containing identical multiple predictors ([45]). Therefore, multicollineary among the predictors of model 2, 3, 4, 6 and 7 were tested using Variance Influential Factor (VIF). Models having VIF>5 indicate the existence of multicollinearity among the predictors ([45]). VIF was calculated using the following formula (eqn. 2):
where SD is the standard deviation of individual predictor, SE is the standard error of each predictor, (n-1) is the total degree of freedom for the model, and MSR is the mean square residual.
Regional and pan-tropical model evaluation
Frequently used regional and pan-tropical biomass models were compared with the measured biomass data of the sampled trees of Sal zone in terms of model prediction error (MPE), model efficiency (ME) and root mean square error (RMSE - [35]), which were calculated using the following equations (eqn. 3, eqn. 4, eqn. 5);
where n is the number of trees, Yp is the predicted biomass from model, Yo is the observed biomass in field measurement and (hat)Y is the mean of the observed biomass.
Regression between Yp (in the X-axis) and Yo (in the Y-axis) was derived for the listed pan-tropical and regional models for TAGB estimation (Tab. 2) and significance of slope (b = 1) and intercept (a = 1) were also tested in accordance with Piñeiro et al. ([41]). This analysis helped to understand graphically the overestimation or underestimation of the predicted biomass value using each model from 1:1 line ([45]).
Results
Model selection
The mean DBH, H, and WD of the sample trees were 16.078 cm, 13.498 m and 0.669 g cm-3, respectively. A total of 1.242% data was observed as outlier for TAGB. Model 3 [ln (B) = ln (a) + b ln (DBH) + c ln (H) + d ln (WD)] of TAGB, stem, bark and branch had lowest AIC (-177.416, -128.402, -18.043 and 247.098) and RSE (0.136, 0.158, 0.223 and 0.508); and highest adjusted R2 (0.977, 0.973, 0.955 and 0.756) and AICw (0.918, 0.907, 0.614 and 0.550) values compared to other models. Model 4 of TAGB, stem, bark, branch and leaf has shown VIF>5 for its predictors compared to other models, which indicated multicollinearity among the identical independent variable (Tab. 3). Therefore, model 3 has appeared as best fit for estimating TAGB, stem, bark and branch biomass for the Sal zone and indicates that inclusion of wood density as predictor has improved the model accuracy. For leaf estimates, model 1 [ln (B) = ln (a) + b ln (DBH)] is the best model considering the AIC, AICw and adjusted R2 values (Tab. 3).
Tab. 3 - Parameter estimates (a-e) and comparison among the allometric models for different components of trees of Sal zone. Models labelled with an asterisk (*) are the best-fit models.
| Component | No. | a | b | c | d | e | Adj-R2 | RSE | AIC | AICw | CF | VIF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total above-ground biomass |
1 | -2.212 | 2.397 | - | - | - | 0.959 | 0.183 | -86.341 | 0.000 | 1.017 | - |
| 2 | -2.527 | 2.188 | 0.349 | - | - | 0.976 | 0.139 | -172.596 | 0.082 | 1.01 | b=1.428, c=1.428 | |
| 3* | -2.46 | 2.171 | 0.367 | 0.161 | - | 0.977 | 0.136 | -177.416 | 0.918 | 1.009 | b=1.214, c=1.497, d=1.055 | |
| 4 | 3.477 | -3.805 | 2.22 | -0.261 | 0.03 | 0.959 | 0.181 | -83.751 | 0.000 | 1.017 | b=10560, c=43036, d=11181, e=1.016 | |
| 5 | -2.071 | 0.844 | - | - | - | 0.932 | 0.236 | -4.028 | 0.000 | 1.028 | - | |
| 6 | -2.204 | 2.397 | 0.016 | - | - | 0.959 | 0.183 | -84.38 | 0.000 | 1.017 | b=1.006, c=1.006 | |
| 7 | -2.381 | 0.859 | 0.38 | - | - | 0.941 | 0.22 | -24.429 | 0.000 | 1.025 | b=1.00, c=1.00 | |
| 8 | -2.54 | 0.859 | - | - | - | 0.935 | 0.231 | -11.576 | 0.000 | 1.027 | - | |
| Stem without bark | 1 | -2.856 | 2.449 | - | - | - | 0.889 | 0.32 | 93.878 | 0.000 | 1.052 | - |
| 2 | -3.562 | 1.98 | 0.783 | - | - | 0.966 | 0.177 | -94.318 | 0.000 | 1.016 | b=1.428, c=1.428 | |
| 3* | -3.373 | 1.934 | 0.833 | 0.452 | - | 0.973 | 0.158 | -128.402 | 0.907 | 1.013 | b=1.367, c=1.497, d=1.055 | |
| 4 | 1.749 | -2.748 | 1.949 | -0.24 | 0.131 | 0.888 | 0.319 | 98.545 | 0.000 | 1.053 | b=10560, c=43036, d=11181, e=1.016 | |
| 5 | -3.079 | 0.911 | - | - | - | 0.965 | 0.179 | -93.176 | 0.000 | 1.016 | - | |
| 6 | -2.793 | 2.445 | 0.122 | - | - | 0.889 | 0.319 | 95.118 | 0.000 | 1.053 | b=1.006, c=1.006 | |
| 7 | -3.359 | 0.925 | 0.492 | - | - | 0.972 | 0.162 | -123.849 | 0.093 | 1.013 | b=1.00, c=1.00 | |
| 8 | -3.565 | 0.925 | - | - | - | 0.963 | 0.184 | -83.41 | 0.000 | 1.017 | - | |
| Bark | 1 | -5.339 | 2.679 | - | - | - | 0.871 | 0.382 | 151.379 | 0.000 | 1.076 | - |
| 2 | -6.115 | 2.164 | 0.861 | - | - | 0.946 | 0.246 | 11.134 | 0.000 | 1.031 | b=1.428, c=1.428 | |
| 3* | -5.87 | 2.103 | 0.926 | 0.587 | - | 0.955 | 0.223 | -18.043 | 0.614 | 1.026 | b=1.671, c=1.497, d=1.055 | |
| 4 | -5.815 | 3.156 | -0.112 | 0.005 | 0.217 | 0.87 | 0.38 | 155.503 | 0.000 | 1.076 | b=10560, c=43036, d=11181, e=1.016 | |
| 5 | -5.606 | 1 | - | - | - | 0.951 | 0.235 | -4.806 | 0.001 | 1.028 | - | |
| 6 | -5.225 | 2.671 | 0.22 | - | - | 0.871 | 0.38 | 151.64 | 0.000 | 1.076 | b=1.006, c=1.006 | |
| 7 | -5.856 | 1.012 | 0.625 | - | - | 0.955 | 0.225 | -17.113 | 0.386 | 1.026 | b=1.00, c=1.00 | |
| 8 | -6.119 | 1.012 | - | - | - | 0.944 | 0.252 | 16.859 | 0.000 | 1.032 | - | |
| Branch | 1 | -3.628 | 2.348 | - | - | - | 0.704 | 0.563 | 276.164 | 0.000 | 1.172 | - |
| 2 | -3.007 | 2.761 | -0.69 | - | - | 0.754 | 0.512 | 247.499 | 0.450 | 1.141 | b=1.428, c=1.428 | |
| 3* | -3.154 | 2.798 | -0.729 | -0.355 | - | 0.756 | 0.508 | 247.098 | 0.550 | 1.14 | b=1.478, c=1.497, d=1.055 | |
| 4 | 2.383 | -2.992 | 1.431 | -0.107 | -0.038 | 0.706 | 0.556 | 277.791 | 0.000 | 1.171 | b=10560, c=43036, d=11181, e=1.016 | |
| 5 | -2.64 | 0.714 | - | - | - | 0.509 | 0.726 | 357.744 | 0.000 | 1.301 | - | |
| 6 | -3.662 | 2.351 | -0.066 | - | - | 0.702 | 0.563 | 278.092 | 0.000 | 1.173 | b=1.006, c=1.006 | |
| 7 | -2.921 | 0.727 | 0.292 | - | - | 0.511 | 0.722 | 357.913 | 0.000 | 1.3 | b=1.00, c=1.00 | |
| 8 | -3.044 | 0.728 | - | - | - | 0.511 | 0.724 | 356.77 | 0.000 | 1.299 | - | |
| Leaf | 1* | -4.713 | 2.066 | - | - | - | 0.533 | 0.713 | 304.322 | 0.402 | 1.289 | - |
| 2 | -4.927 | 1.968 | 0.187 | - | - | 0.533 | 0.71 | 305.295 | 0.247 | 1.289 | b=1.35, c=1.35 | |
| 3 | -4.826 | 1.936 | 0.226 | 0.278 | - | 0.532 | 0.708 | 306.601 | 0.129 | 1.29 | b=1.412, c=1.448, d=1.076 | |
| 4 | -2.24 | -0.072 | 0.583 | -0.046 | 0.185 | 0.525 | 0.711 | 309.671 | 0.028 | 1.295 | b=9797, c=39949, d=10394, e=1.015 | |
| 5 | -4.737 | 0.743 | - | - | - | 0.509 | 0.731 | 311.299 | 0.012 | 1.306 | - | |
| 6 | -4.618 | 2.058 | 0.179 | - | - | 0.531 | 0.712 | 306.017 | 0.172 | 1.291 | b=1.07, c=1.07 | |
| 7 | -4.883 | 0.75 | 0.531 | - | - | 0.507 | 0.73 | 312.876 | 0.006 | 1.308 | b=1.00, c=1.00 | |
| 8 | -5.098 | 0.749 | - | - | - | 0.502 | 0.736 | 313.419 | 0.004 | 1.312 | - |
Nutrients (N, P and K) and carbon in tree components
Nutrients (N, P, and K) concentration were found to vary among the tree components and species. However, comparatively higher concentration of nitrogen (1.76 to 4.06%), phosphorus (0.02 to 0.54%) and potassium (0.28 to 3.10) were observed in leaves, while the lowest concentration was observed in woody components, especially the stem (Tab. S2 in Supplementary material). Conversely, comparatively higher concentration of carbon was observed in woody components of tree-like stems and larger branches. The ranges of carbon concentration in stems and bigger branches of the represented species was 48.86 to 56.61% and 49.75 to 59.23%, respectively. Moreover, species-specific variation in carbon concentration was also observed among individual species (Tab. 4).
Tab. 4 - Carbon concentration (%) in different parts of sampled species in the Sal zone of Bangladesh.
| Species | Leaf | Smaller branch | Bigger branch | Bark | Stem |
|---|---|---|---|---|---|
| Acacia auriculiformis | 46.87 ± 0.03 | 48.77 ± 0.18 | 49.73 ± 0.04 | 44.93 ± 0.03 | 49.75 ± 0.05 |
| Aegle marmelos | 50.20 ± 1.70 | 56.90 ± 3.01 | - | 51.05 ± 2.58 | 59.50 ± 3.99 |
| Albizia procera | 45.45 ± 0.65 | 49.22 ± 1.08 | 50.63 ± 1.50 | 45.52 ± 1.30 | 52.43 ± 1.58 |
| Artocarpus heterophyllus | 46.24 ± 2.28 | 46.88 ± 0.78 | 53.77 ± 0.81 | 43.93 ± 1.56 | 54.78 ± 1.59 |
| Averrhoa carambola | 49.26 ± 1.36 | 49.11 ± 1.51 | - | 47.48 ± 0.17 | 59.23 ± 1.91 |
| Citrus grandis | 43.89 ± 0.37 | 49.04 ± 0.25 | - | 43.22 ± 1.77 | 52.79 ± 1.80 |
| Elaeocarpus serratus | 57.34 ± 4.20 | 54.35 ± 1.64 | 54.45 ± 0.33 | 60.21 ± 2.64 | 56.66 ± 0.41 |
| Grewia microcosm | 45.04 ± 0.53 | 52.75 ± 0.55 | 54.25 ± 1.11 | 53.59 ± 1.69 | 52.86 ± 1.04 |
| Litchi chinensis | 44.33 ± 0.87 | 55.44 ± 0.97 | 53.65 ± 2.36 | 44.34 ± 2.34 | 53.50 ± 1.32 |
| Mangifera indica | 57.96 ± 2.89 | 51.74 ± 1.86 | 56.13 ± 1.78 | 48.88 ± 1.00 | 55.86 ± 0.29 |
| Phyllanthus emblica | 55.95 ± 2.23 | 49.66 ± 1.64 | 53.51 ± 0.17 | 66.31 ± 2.51 | 53.67 ± 1.54 |
| Psidium guajava | 50.59 ± 1.87 | 48.02 ± 1.29 | - | 48.88 ± 0.70 | 51.00 ± 0.40 |
| Shorea robusta | 49.74 ± 0.97 | 43.89 ± 6.68 | 50.94 ± 0.61 | 52.85 ± 2.16 | 56.24 ± 2.21 |
| Spondias pinnata | - | 44.71 ± 0.68 | 48.86 ± 0.90 | 50.17 ± 2.18 | 53.53 ± 1.48 |
| Syzygium cumini | 50.15 ± 0.39 | 46.86 ± 0.93 | 55.37 ± 1.40 | 50.59 ± 0.73 | 52.72 ± 0.08 |
| Tectona grandis | 41.80 ± 0.92 | 49.07 ± 0.44 | - | 46.82 ± 1.44 | 57.77 ± 1.30 |
| Terminalia arjuna | 47.88 ± 1.03 | 56.89 ± 3.25 | 56.61 ± 0.32 | 48.16 ± 0.98 | 52.41 ± 1.64 |
| Terminalia bellirica | 59.25 ± 1.67 | 55.26 ± 1.88 | 55.24 ± 3.63 | 44.73 ± 1.09 | 58.23 ± 3.38 |
| Zanthoxylum rhetsa | - | 50.22 ± 2.66 | 53.40 ± 1.05 | 55.21 ± 2.68 | 53.55 ± 1.05 |
| Ziziphus mauritiana | 47.50 ± 4.01 | 52.52 ± 0.39 | 52.31 ± 1.96 | 50.47 ± 4.03 | 54.73 ± 2.02 |
TAGB model evaluation
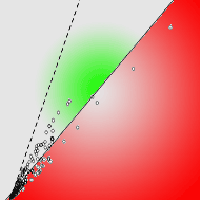
The comparison among the eight regional and pan-tropical biomass models has demonstrated that model 3 of Chave et al. ([11]) contained first lowest MPE (35.480%) and RMSE (7877.611) followed by model 8 (moist) of Brown et al. ([8] - Tab. 5). Visualization of the observed and predicted biomass has demonstrated deviation in biomass estimation from the line of significance of slope (b = 1) and intercept (a = 1), which indicates that all the regional and pan-tropical biomass models overestimated the biomass of the sampled trees of the Sal zone (Fig. 2).
Tab. 5 - Comparison of the frequently used regional and pan-tropical biomass models.
| No | Source | Equation | Type | n | R2 | MPE (%) | ME | RMSE |
|---|---|---|---|---|---|---|---|---|
| 1 | [10] (Moist) | B = exp (-2.134 + 2.5430 ln (DBH)) | Pan-tropical | 170 | - | 63.556 | -0.093 | 10666.328 |
| 3 | [38] | ln (B) = -1.8985 + 2.1569 ln (DBH) + 0.3888 ln (H) + 0.7218 ln (WD) | Central amazon | 132 | 0.991 | 42.958 | 0.636 | 6159.087 |
| 4 | [11] | B = WD × exp (-1.499 + 2.148 ln (DBH) + 0.207 (ln (DBH))2 - 0.0281 (ln (DBH))3) | Pan-tropical | 1808 | - | 85.508 | -1.878 | 17312.340 |
| 5 | [8] (Moist) | B = exp (-2.4090 + 0.9522 In (DBH2 ×H × WD)) | Pan-tropical | 94 | 0.99 | 65.820 | -0.164 | 11009.597 |
| [11] | B = exp (-2.977 + ln (DBH2 × H × WD)) | Pan-tropical | 1505 | - | 35.480 | 0.404 | 7877.611 | |
| [12] | B = exp (-2.6986 + 0.976 ln (DBH2 × H × WD)) | Pan-tropical | 4004 | - | 48.892 | 0.184 | 9217.913 | |
| 8 | [8] (Moist) | B = exp (-3.1141 + 0.9719 In (DBH2 × H)) | Pan-tropical | 168 | 0.97 | 42.676 | 0.376 | 8057.775 |
| [13] | ln (B) = -3.2249 + 0.9885 ln (DBH2 × H) | Tropical Africa | 274 | 0.971 | 46.016 | 0.228 | 8964.925 |
Fig. 2 - Regression between observed and predicted values of frequently used regional and pan-tropical biomass models. Solid line is the regression line and broken line is the significance of slope (b = 1) and intercept (a = 1). (a): Model 1 ([10]); (b): Model 3 ([38]); (c): Model 4 ([11]); (d): Model 5 ([8]); (e): Model 5 ([11]); (f): Model 5 ([12]); (g): Model 8 ([8]); (h): Model 8 ([13]).
Discussion
The use of allometric models presents a source of uncertainty in biomass estimation ([37]), which can be minimized through a process of selection and critical analysis of the parameters used ([31]). Model accuracy and the inclusion of predictor(s) are important considerations when selecting the best fit model ([45]). In our study, we have included 20 species with wood density ranging from 0.492 to 0.854 g cm-3 and a model with DBH, H and WD as identical predictors appeared as the best fit compared to other models, except leaf (Tab. 3). Several other studies have also demonstrated that multi-species allometric biomass models using DBH, H and WD as identical predictors resulted in accurate biomass estimation ([38], [11], [12], [13]).
Estimates of nutrient and carbon stock in trees is crucial to understand nutrient cycling and budgeting, which is important to maintain forest productivity ([7], [29]). This study has shown that differences are evident in nutrient and carbon concentration across tree components and species, and this is related to the characteristics of nutrients, stage of growth (sapling and tree) and availability to plants under various environmental conditions ([7], [33], [26]). Nitrogen is the major component of amino acid, enzymes, nucleic acid, chlorophyll and alkaloid and consequently a higher content is observed in photosynthetic tissue. Phosphorus is most abundant in meristematic tissue ([35]). While potassium is highly mobile and found to accumulate in physiologically active tissue, carbon is found to accumulate in the structural components of plants ([33]). The above physiological function and mobility nature of N, P, K and C may lead to a higher concentration of nutrients in leaves and higher carbon concentration in branch and stem ([26]).
The observed TAGB of sampled trees were compared with estimated TAGB from the frequently used regional and pan-tropical models. Model 4 by Chave et al. ([11]) and model 5 by Brown et al. ([8]) showed the higher prediction error (65.82% to 85.508) and resulted in a higher overestimation. Similarly, the pan-tropical model 5 of Chave et al. ([11]) with second higher model efficiency (0.404) also showed the lowest model prediction error (35.48%) in predicting the TAGB for the studies samples. This has implications for the estimation of forest biomass across broad-scales as these models are a commonly used option, particularly in developing countries for which they are relevant, where they may be applied under programmes such as REDD+ ([16], [22]). As this process is fundamentally based on estimation, allometric models will always present some level of error. The quantum of that error will determine the extent to which our understanding of the truth is distorted and subsequently influence how we understand the impacts of deforestation and environmental degradation resulting from forest disturbance potentially driven by climate change ([24]). Therefore, the development of improved allometric models, their validation and comparison with the existing pantropical and regional models to assess their uncertainty and suitability at local scale is a prudent step in forest biomass estimation ([45], [37]). Indeed, there remains numerous examples where biomass estimation using pan-tropical and regional models produce a higher bias compared to those from locally developed models, for instance the biomass study of Kalimantan ([4]), Sarawak ([20]), Columbia ([3], [39]), Indonesia ([32], [34]), and Vietnam ([37]). The context provided by these studies and the results presented herein demonstrate that at present, our derived model will more accurately estimate the TAGB and biomass of other components (stem, bark, branch and leaf) for the Sal zone of Bangladesh.
Conclusion
Regional and pan-tropical allometric models offer methodological efficiencies for biomass estimation compared to those developed for individual species at specific locations. However, they have the potential to misrepresent local, species- or community-specific variations and anomalies, and therefore can lead to increased error. The use of pan-tropical and regional models should therefore be scrutinized with respect to the source of sampling used to develop the model against local forest variation, before they are widely applied. The results of this study demonstrate that the development of local models derived from an appropriate sample of representative species can greatly improve the estimation of TAGB, as well as Carbon, Nitrogen, Phosphorus, and Potassium in TAGB. In summary, the best fit models presented in this study can provide greater confidence when estimating biomass in the Sal zone of Bangladesh.
Acknowledgements
We greatly acknowledge the financial support of Food and Agriculture Organization of the United Nations (FAO) through GCP/BGD/058/USA (LOA Code: FAOBGDLO A 2017-008) to accomplish the field and laboratory work. We would like to thank Tangail Forest Division and Dhaka Forest Division and Forestry and Wood Technology Discipline, Khulna University (Bangladesh) for their logistic supports during the field and laboratory analysis.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Authors’ Info
Authors’ Affiliation
Mohammad RH Siddique
SM Rubaiot Abdullah
Forestry and Wood Technology Discipline, Khulna University, Khulna (Bangladesh)
School of Ecosystem and Forest Sciences, The University of Melbourne, Victoria 3010 (Australia)
Tariq Aziz
Sayed Ali
Abdullah Al Mamun
Mariam Akhter
Zaheer Iqbal
Bangladesh Forest Department, Dhaka (Bangladesh)
Bangladesh Forest Research Institute, Chittagong (Bangladesh)
Corresponding author
Paper Info
Citation
Mahmood H, Siddique MRH, Costello L, Birigazzi L, Abdullah SMR, Henry M, Siddiqui BN, Aziz T, Ali S, Al Mamun A, Forhad MIK, Akhter M, Iqbal Z, Mondol FK (2019). Allometric models for estimating biomass, carbon and nutrient stock in the Sal zone of Bangladesh. iForest 12: 69-75. - doi: 10.3832/ifor2758-011
Academic Editor
Tomás Vrska
Paper history
Received: Feb 10, 2018
Accepted: Nov 10, 2018
First online: Jan 24, 2019
Publication Date: Feb 28, 2019
Publication Time: 2.50 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2019
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 56390
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 45958
Abstract Page Views: 5249
PDF Downloads: 4260
Citation/Reference Downloads: 14
XML Downloads: 909
Web Metrics
Days since publication: 2523
Overall contacts: 56390
Avg. contacts per week: 156.45
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2019): 18
Average cites per year: 2.57
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Review Papers
Integration of forest mapping and inventory to support forest management
vol. 3, pp. 59-64 (online: 17 May 2010)
Commentaries & Perspectives
Benefits of a strategic national forest inventory to science and society: the USDA Forest Service Forest Inventory and Analysis program
vol. 1, pp. 81-85 (online: 28 February 2008)
Research Articles
Comparing land use registry and sample based inventory to estimate forest area in Podlaskie, Poland
vol. 10, pp. 315-321 (online: 23 February 2017)
Research Articles
Simplified methods to inventory the current annual increment of forest standing volume
vol. 5, pp. 276-282 (online: 17 December 2012)
Research Articles
Using self-organizing maps in the visualization and analysis of forest inventory
vol. 5, pp. 216-223 (online: 02 October 2012)
Technical Advances
Improved estimates of per-plot basal area from angle count inventories
vol. 7, pp. 178-185 (online: 17 February 2014)
Research Articles
Spatial distribution of aboveground biomass stock in tropical dry forest in Brazil
vol. 16, pp. 116-126 (online: 17 April 2023)
Research Articles
Incorporating management history into forest growth modelling
vol. 4, pp. 212-217 (online: 03 November 2011)
Research Articles
Estimation of stand crown cover using a generalized crown diameter model: application for the analysis of Portuguese cork oak stands stocking evolution
vol. 9, pp. 437-444 (online: 02 December 2015)
Research Articles
Methods to inventory and strip thin in dense stands of aspen root suckers
vol. 8, pp. 590-595 (online: 22 April 2015)
iForest Database Search
Search By Author
- H Mahmood
- MRH Siddique
- L Costello
- L Birigazzi
- SMR Abdullah
- M Henry
- BN Siddiqui
- T Aziz
- S Ali
- A Al Mamun
- MIK Forhad
- M Akhter
- Z Iqbal
- FK Mondol
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
- H Mahmood
- MRH Siddique
- L Costello
- L Birigazzi
- SMR Abdullah
- M Henry
- BN Siddiqui
- T Aziz
- S Ali
- A Al Mamun
- MIK Forhad
- M Akhter
- Z Iqbal
- FK Mondol
Search By Keywords
PubMed Search
Search By Author
- H Mahmood
- MRH Siddique
- L Costello
- L Birigazzi
- SMR Abdullah
- M Henry
- BN Siddiqui
- T Aziz
- S Ali
- A Al Mamun
- MIK Forhad
- M Akhter
- Z Iqbal
- FK Mondol
Search By Keyword