Bayesian geographically weighted regression and its application for local modeling of relationships between tree variables

doi:10.3832/ifor2574-011

Bayesian geographically weighted regression and its application for local modeling of relationships between tree variables

Nirmal Subedi⁽¹⁾, Lianjun Zhang⁽¹⁾, Zhen Zhen⁽²⁾

iForest - Biogeosciences and Forestry, Volume 11, Issue 5, Pages 542-552 (2018)
doi: https://doi.org/10.3832/ifor2574-011
Published: Sep 01, 2018 - Copyright © 2018 SISEF

Research Articles

PDF Version

Full Text

Citation

Geo-mapping

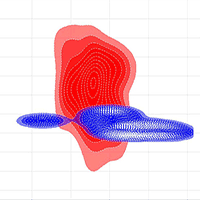
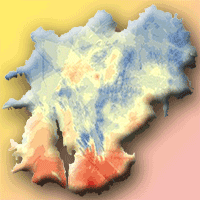
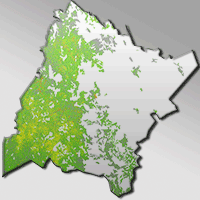
Geographically weighted regression (GWR) has become popular in recent years to deal with spatial autocorrelation and heterogeneity in forestry and ecological data. However, researchers have realized that GWR has some limitations, such as correlated model coefficients across study areas, strong influence of outliers, weak data problem, etc. In this study, we applied Bayesian geographically weighted regression (BGWR) and a robust BGWR (rBGWR) to model the relationship between tree crown and diameter using observed tree data and simulated data to investigate model fitting and performance in order to overcome some limitations of GWR. Our results indicated that, for observed tree data, the rBGWR estimated tree crown more accurate than both BGWR and GWR. For the simulated data, 74.1% of the estimated slope coefficients by rBGWR and 73.4% of the estimated slope coefficients by BGWR were not significantly different (α = 0.05) from the corresponding simulated slope coefficients. The estimation of model coefficients by rBGWR was not sensitive to outliers, but the coefficient estimation by GWR was strongly affected by those outliers. The majority of the coefficient estimates by rBGWR and BGWR for weak observations were not significantly (α = 0.05) different from the simulated coefficients. Therefore, BGWR (including rBGWR) may be a better alternative to overcome some limitations of GWR. In addition, both BGWR and rBGWR were more powerful than GWR to detect the spatial areas with non-constant variance or spatial outliers.

Keywords

Spatial Autocorrelation, Spatial Heterogeneity, Robust Regression, Spatially Varying Coefficients Models

Authors’ address

(1)

Department of Forest and Natural Resources Management, State University of New York College of Environmental Science and Forestry, One Forestry Drive, Syracuse, NY 13210 (USA)

(2)

School of Forestry, Northeast Forestry University, Harbin (China)

Corresponding author

Zhen Zhen
zhzhen@syr.edu

Citation

Subedi N, Zhang L, Zhen Z (2018). Bayesian geographically weighted regression and its application for local modeling of relationships between tree variables. iForest 11: 542-552. - doi: 10.3832/ifor2574-011

Academic Editor

Luca Salvati

Paper history

Received: Jul 30, 2017
Accepted: Jun 11, 2018

First online: Sep 01, 2018
Publication Date: Oct 31, 2018
Publication Time: 2.73 months

Open Access

This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Breakdown by View Type

(Waiting for server response...)

Article Usage

Total Article Views: 36604
(from publication date up to now)

Breakdown by View Type
HTML Page Views: 30859
Abstract Page Views: 1631
PDF Downloads: 3390
Citation/Reference Downloads: 9
XML Downloads: 715

Web Metrics
Days since publication: 2063
Overall contacts: 36604
Avg. contacts per week: 124.20

Article Citations

Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Feb 2023)

Total number of cites (since 2018): 6
Average cites per year: 1.00

(no Plumx Metrics available for this paper)

Publication Metrics

by Dimensions ^©

Articles citing this article

List of the papers citing this article based on CrossRef Cited-by.

(1)

Bailey TC, Gatrell AC (1995)
Interactive spatial data analysis. Longman, Essex, UK, pp. 413.
Online | Gscholar

(2)

Banerjee S, Carlin BP, Gelfand AE (2004)
Hierarchical modeling and analysis for spatial data. Chapman and Hall/CRC, Boca Raton, FL, USA, pp. 584.
Gscholar

(3)

Brunsdon C, Fotheringham AS, Charlton ME (1996)
Geographically weighted regression: a method for exploring spatial nonstationarity. Geographical Analysis 28: 281-298.
CrossRef | Gscholar

(4)

Carlin BP, Louis TA (2000)
Bayes and empirical Bayes methods for data analysis. Chapman and Hall/CRC, Boca Raton, FL, USA, pp. 440.
Gscholar

(5)

Casella G, George EI (1992)
Explaining the Gibbs sampler. The American Statistician 46: 167-174.
CrossRef | Gscholar

(6)

Clifton EV, Romero-Barrutieta A (2006)
Institutions versus geography: subnational evidence from the United States. IMF Working Papers WP/06/169, pp. 1-26.
Online | Gscholar

(7)

Congdon P (2006)
Bayesian statistical modelling. John Wiley and Sons, New York, USA, pp. 581.
Gscholar

(8)

Cressie N (1993)
Statistics for spatial data. John Wiley and Sons, Toronto, Canada, pp. 461.
Gscholar

(9)

Ek AR (1969)
Stem map data for three forest stands in northern Ontario. Information Report no. OX-113, Canadian Forest Service Publications, Marie, Canada, pp. 23.
Gscholar

(10)

Farber S, Páez A (2007)
A systematic investigation of cross-validation in GWR model estimation: empirical analysis and Monte Carlo simulations. Journal of Geographical Systems 9: 371-396.
CrossRef | Gscholar

(11)

Foody GM (2004)
Spatial nonstationarity and scale-dependency in the relationship between species richness and environmental determinants for the sub-Saharan endemic avifauna. Global Ecology and Biogeography 13: 315-320.
CrossRef | Gscholar

(12)

Fortin MJ, Dale MRT (2005)
Spatial analysis: a guide to ecologists. Cambridge University Press, Cambridge, UK, pp. 365.
Gscholar

(13)

Fotheringham AS, Brunsdon C, Charlton M (2002)
Geographically weighted regression: the analysis of spatially varying relationships. John Wiley and Sons, West Sussex, UK, pp. 284.
Gscholar

(14)

Fox JC, Ades PK, Bi H (2001)
Stochastic structure and individual-tree growth models. Forest Ecology and Management 154: 261-276.
CrossRef | Gscholar

(15)

Furutani T (2004)
Bayesian geographically weighted regression model and its application for land price model estimation. Journal of City Planning Institute of Japan 39: 787-792.
Gscholar

(16)

Garrigues S, Allard D, Baret F, Weiss M (2006)
Quantifying spatial heterogeneity at the landscape scale using variogram models. Remote Sensing of Environment 103 (1): 81-96.
CrossRef | Gscholar

(17)

Gelfand AE (2000)
Gibbs sampling. Journal of the American Statistical Association 95: 1300-1304.
CrossRef | Gscholar

(18)

Gelfand AE, Smith AFM (1990)
Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association 85: 398-409.
CrossRef | Gscholar

(19)

Geweke J (1993)
Bayesian treatment of the independent student-t linear model. Journal of Applied Econometrics 8 (S1): S19-S40.
CrossRef | Gscholar

(20)

Gotway CA, Young J (2002)
Combining incompatible spatial data. Journal of the American Statistical Association 97: 632-648.
CrossRef | Gscholar

(21)

Green JL, Hastings A, Arzberger P, Ayala FJ, Cottingham KL, Cuddington K, Davis F, Dunne JA, Fortin M-J, Gerber L, Neubert M (2005)
Complexity in ecology and conservation: mathematical, statistical, and computational challenges. Bioscience 55: 501-510.
CrossRef | Gscholar

(22)

Guo L, Ma Z, Zhang L (2008)
Comparison of bandwidth selection in application in geographically weighted regression: a case study. Canadian Journal of Forest Research 38: 2526-2534.
CrossRef | Gscholar

(23)

Haining R (2004)
Spatial data analysis: theory and practice. Cambridge University Press, Cambridge, UK, pp. 432.
Gscholar

(24)

Legendre P, Fortin MJ (1989)
Spatial pattern and ecological analysis. Plant Ecology 80: 107-138.
CrossRef | Gscholar

(25)

Legendre P (1993)
Spatial autocorrelation: trouble or new paradigm? Ecology 76: 1659-1673.
CrossRef | Gscholar

(26)

LeSage JP (1997)
Bayesian estimation of spatial autoregressive models. International Regional Science Review 20: 113-129.
CrossRef | Gscholar

(27)

LeSage JP (2004)
A family of geographically weighted regression models. In: “Advances in Spatial Econometrics” (Anselin LR, Florax JGM, Rey SJ eds). Springer-Verlag, Berlin, Germany, pp. 240-264.
CrossRef | Gscholar

(28)

Levin SA (1992)
The problem of pattern and scale in ecology. Ecology 73: 1943-1967.
CrossRef | Gscholar

(29)

Li H, Reynolds JF (1995)
On definition and quantification of heterogeneity. Oikos 73: 280-284.
CrossRef | Gscholar

(30)

Lin CH, Wen TH (2011)
Using geographically weighted regression (GWR) to explore spatial varying relationships of immature mosquitoes and human densities with the incidence of dengue. International Journal of Environmental Research and Public Health 8: 2798-2815.
CrossRef | Gscholar

(31)

Lindley DV (1971)
The estimation of many parameters. In: “Foundation of Statistical Inference” (Godambe VP, Sprott DA eds). Holt, Rinehart and Winston, New York, USA, pp. 435-455.
CrossRef | Gscholar

(32)

Lloyd CD (2006)
Local models for spatial analysis. CRC Press, Boca Raton, FL, USA, pp. 244.
Gscholar

(33)

Lovett GM, Jones CG, Turner MG, Weathers KC (2005)
Ecosystem function in heterogeneous landscapes. Springer, New York, USA, pp. 489.
Online | Gscholar

(34)

Lu J, Zhang L (2010)
Evaluation of parameter estimation methods for fitting spatial regression models. Forest Science 56: 505-514.
CrossRef | Gscholar

(35)

Lu J, Zhang L (2012)
Geographically local linear mixed models for tree height-diameter relationship. Forest Science 58: 75-84.
CrossRef | Gscholar

(36)

Lu J, Zhang L (2013)
Evaluation of structure specification in linear mixed models for modeling the spatial effects in tree height-diameter relationships. Annals of Forest Research 56: 137-148.
Gscholar

(37)

Ma Z, Zuckerberg B, Porter WF, Zhang L (2012)
Use of localized descriptive statistics for exploring the spatial pattern changes of bird species richness at multiple scales. Applied Geography 32 (2): 185-194.
CrossRef | Gscholar

(38)

Ma Z, Zhang L (2015)
Modeling bird species richness at multiple spatial scales using 2D wavelets analysis. Forest Science 61: 1-16.
CrossRef | Gscholar

(39)

McMillen DP (2003)
Neighbourhood house price indexes in Chicago: a Fourier repeat sales approach. Journal of Economic Geography 3: 57-73.
CrossRef | Gscholar

(40)

Meng Q, Cieszewski CJ, Strub MR, Borders BE (2009)
Spatial regression modeling of tree height-diameter relationships. Canadian Journal of Forest Research 39 (12): 2283-2293.
CrossRef | Gscholar

(41)

Nelsen RB (1999)
An introduction to copulas. Springer, New York, USA, pp. 315.
Gscholar

(42)

Raftery A, Lewis S (1992)
How may sampler in the Gibbs sampler? Bayesian Statistics 4: 763-774.
Gscholar

(43)

Reed DD, Burkhart HE (1985)
Spatial autocorrelation of individual tree characteristics in loblolly pine stands. Forest Science 31: 575-587.
Online | Gscholar

(44)

Schabenberger O, Gotway CA (2005)
Statistical methods for spatial data analysis. Chapman and Hall/CRC Press, Boca Raton, FL, USA, pp. 488.
Gscholar

(45)

Spiegelhalter DJ, Best NG, Carlin Pet B (2002)
Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society 64: 583-639.
CrossRef | Gscholar

(46)

Valentine HT, Herman DA, Gove JH, Hollinger DY, Solomon DS (2000)
Initializing a model stand for process-based projection. Tree Physiology 20 (5-6): 393-398.
CrossRef | Gscholar

(47)

Wagner HH, Fortin MJ (2005)
Spatial analysis of landscapes: concepts and statistics. Ecology 86: 1975-1987.
CrossRef | Gscholar

(48)

Waller LA, Zhu L, Gotway CA, Gorman DM, Gruenewald PJ (2007)
Quantifying geographic variations in associations between alcohol distribution and violence: a comparison of geographically weighted regression and spatially varying coefficient models. Stochastic Environmental Research and Risk Assessment 21 (5): 573-588.
CrossRef | Gscholar

(49)

Wang M, Upadhyay A, Zhang L (2010)
Trivariate distribution modeling of tree diameter, height, and volume. Forest Science 56: 290-300.
Online | Gscholar

(50)

Wheeler DC, Páez A (2010)
Geographically weighted regression. In: “Handbook of Applied Spatial Analysis: Software Tools, Methods and Applications” (Fisher MM, Getis A eds). Springer, Heidelberg, Germany, pp. 461-486.
CrossRef | Gscholar

(51)

Wiens JA (1989)
Spatial scaling in ecology. Functional Ecology 3: 385-397.
CrossRef | Gscholar

(52)

Zhang L, Gove JH (2005)
Spatial assessment of model errors from four regression techniques. Forest Science 51: 334-346.
Gscholar

(53)

Zhang L, Shi H (2004)
Local modeling of tree growth by geographically weighted regression. Forest Science 50: 225-244.
Gscholar

(54)

Zhang L, Ma Z, Guo L (2008)
Spatially assessing model errors of four regression techniques for three types of forest stands. Forestry 81: 209-225.
CrossRef | Gscholar

(55)

Zhang L, Ma Z, Guo L (2009)
Spatial autocorrelation and heterogeneity in the relationships between tree variables. Forest Science 55: 533-548.
Gscholar

iForest - Biogeosciences and Forestry

Contents

Search

Journal Info

Journal Subjects and Fields

For Authors

For Reviewers

For Readers

SISEF Publishing

Search iForest Contents