Changes in tree layer and altitudinal distribution of herbaceous species in temperate old-growth forests over 30 years
iForest - Biogeosciences and Forestry, Volume 15, Issue 3, Pages 206-212 (2022)
doi: https://doi.org/10.3832/ifor3749-015
Published: Jun 11, 2022 - Copyright © 2022 SISEF
Research Articles
Abstract
Temperate forest ecosystems, including old-growth fragments, are subject to increasing pressures, both from biotic and abiotic factors. Frequent disturbance events, rising mean annual temperatures and longer-lasting droughts are causing changes in tree species composition, probably shifting the altitudinal distribution of herbaceous species as well. Our goal was to examine whether such shifts can be observed even in old-growth temperate forests, and if the changes in the species composition and spatial distribution of trees is reflected in the herbaceous layer. Our study was based on a survey of several old-growth forests from the 1970s that was repeated after 30 years. Using spatial point pattern methods and generalized linear mixed effect models, repeated measurements of mapped phytosociological relevés and detailed maps of tree positions from two survey periods allowed us to examine how the species composition of the herb layer and the spatial distribution of trees ≥ 10 cm DBH (diameter at breast height) changed over 30 years. On most of the studied sites, the total number of trees declined and the proportion of broadleaves increased between the two surveys. Analyses of tree spatial distribution showed a general shift from a regular spatial distribution in the 1970s to a clustered spatial distribution of trees in the 2000s. In the 2000s, herbaceous species showed an upwards shift in their distribution compared to the 1970s, even after accounting for the effect of changing tree spatial distributions in both survey periods. These effects could be an outcome of warmer and drier weather conditions during the past decades. Further investigation is needed to examine whether this trend is related to changes in climatic conditions.
Keywords
Herb Layer, Species Presence, Forest Structure, Altitude, Climate Conditions
Introduction
In the past decades, forests in Central Europe have come under increasing pressure, for example from repeated outbreaks of insect pests ([30]), fungal pathogens ([24]), rising mean annual temperatures and longer-lasting drought periods ([8]). Forest structure is more and more being changed by disturbances, which, among other things, change tree species composition ([37]). Moreover, the effects of climate change on the mortality and growth of trees has gradually led to shifts in tree species dominance ([2]). This is exemplified by the trend of beech expansion in central European old-growth forests during the past decades ([20]). Its share is growing both at the expense of long-term receding fir and at the expense of bark beetle-weakened spruce ([10]).
Changes in the species composition and spatial distribution of trees are reflected in the cover and species composition of the herb layer ([18], [33]). In old-growth forests, higher light availability in canopy gaps is often a key driver of changes in the herb layer ([12]). The diversity of the herb layer usually increases after canopy gaps are formed, but is gradually reduced with an increasing cover of woody regeneration ([31]). However, the structure and species composition of the herb layer can also reflect the legacy effects of long-term tree canopy dynamics ([15]). Rising mean annual temperatures and more common drought periods observed during recent decades could also have impacted the herb layer in old-growth forests. Further research focused on changes in the species composition and distribution of herbaceous species would help clarify the effect of both forest dynamics and climate.
Shifts in the distribution of herbaceous species along altitudinal or latitudinal gradients ([48], [28]) are usually interpreted as an outcome of rising temperatures ([18]). Many studies reporting shifts in the distribution of herbaceous species have focused on alpine vegetation ([38]), but the consequences of rising temperatures can also be noticed in forest ecosystems at lower altitudes. In relation to rising temperatures, changes in tree recruitment, decreasing relative cover of herbaceous species, and also increasing compositional similarity to communities in warmer regions have been observed ([17]). Nevertheless, the question of whether there is a shift in the distribution of forest herbaceous species along the altitudinal gradient with respect to the spatial distribution of trees has not yet been sufficiently answered. We examined changes in the composition and spatial distribution of species in Central European old-growth forests over the past 30 years. The research questions were as follows: (i) did the composition and spatial distribution of trees change over the period of 30 years? (ii) Did herbaceous species shift upwards along the altitudinal gradient during the studied period? (iii) Could an upward shift in altitude be observed for herbaceous species, after controlling for co-occurring changes in the spatial distribution of the tree layer?
Methods
Data collection
We used data from five natural forest sites in the Czech Republic belonging to the Hercynian and Bohemian-Moravian mountain region. Specifically, these included Boubín, Milešice, and Stožec in the Šumava mountains, Zofín in the Novohradské hory mountains and Zákova hora in the Ceskomoravská vrchovina highlands (Tab. 1).
Tab. 1 - Studied sites. (N): number of relevés.
| Locality | Area (ha) |
Latitude N |
Longitude E |
Altitude (m a.s.l.) |
N | First survey |
Repeated survey |
|---|---|---|---|---|---|---|---|
| Boubín | 46.6 | 48°58′ 43″ | 13°48′ 43″ | 925-1107 | 23 | 1972 | 2006 |
| Milešice | 8.9 | 48°59′ 05″ | 13°50′ 21″ | 1070-1125 | 2 | 1972 | 2011 |
| Stožec | 16.2 | 48°52′ 50″ | 13°50′ 06″ | 750-900 | 16 | 1974 | 2013 |
| Zákova hora | 17.5 | 49°39′ 20″ | 15°59′ 39″ | 752-800 | 22 | 1974 | 2011 |
| Zofín | 74.2 | 48°39′ 58″ | 14°42′ 28″ | 730-837 | 42 | 1975 | 2008 |
All the studied sites have been unmanaged for decades. Cambisols are the predominant soils at these sites, with fragments of hydromorphic soils in Boubín and Zofín. Boubín, Stožec, Milešice, and Zofín are mostly north-east to north-west oriented with slopes of 5-25°. Zákova hora is south-west oriented with slopes up to 15°. Except for Milešice, beech dominates the studied sites with occurrences of either spruce or fir. Milešice represents a mountain spruce forest with rare occurrences of fir in the main canopy layer and beech in the upper understorey. The sites are fenced, except for Stožec and Zákova hora. The mean annual precipitation is 740 mm and the mean annual temperature 6.1 °C in Zákova hora ([45]). At the other sites, mean annual precipitation is about 800 mm and the mean annual temperature about 4-5 °C ([47]). Mean annual temperature and precipitation in decades during the period of the survey, processed on the basis of data from Czech Hydrometeorological Institute (⇒ https://www.chmi.cz/), are shown in Tab. 2.
Tab. 2 - Mean annual temperature and precipitation in decades during the period of survey. Mean values for whole Czech Republic (CZ) and for regions where surveyed forests are located (South Bohemia, Czech-Moravian highlands) are shown. Processed on the basis of data from the Czech Hydrometeorological Institute (⇒ https://www.chmi.cz/).
| Parameter | Locality | Period | ||||
|---|---|---|---|---|---|---|
| 1970-1979 | 1980-1989 | 1990-1999 | 2000-2009 | 2010-2019 | ||
| Mean temperature (°C) |
CZ | 7.36 | 7.33 | 7.97 | 8.39 | 8.71 |
| South Bohemia | 6.84 | 6.91 | 7.39 | 7.88 | 8.26 | |
| Highlands | 6.94 | 6.87 | 7.46 | 7.97 | 8.53 | |
| Annual precipitation (mm) |
CZ | 655.8 | 668.9 | 659.6 | 703.9 | 657.5 |
| South Bohemia | 655.8 | 653.6 | 644.4 | 743.2 | 672.3 | |
| Highlands | 677.5 | 650.7 | 623.3 | 702.6 | 633.6 | |
All standing and lying tree stems ≥ 10 cm DBH were repeatedly mapped and identified to species level (Tab. 3 and Tab. S1-S5 in Supplementary material). The spatial distribution of trees in 50 × 50 m plots was used for spatial point pattern analyses, with each plot concentric with a phytosociological relevé. The first large-scale measurements, including the establishment of phytosociological relevés, date back to the 1970s ([34]). The distribution of relevés respected the site-specific level of habitat heterogeneity. The relevés were circular with a diameter of 25 m. Detailed maps of standing and lying trees and phytosociological relevés were updated at the turn of the millennium ([47], [21], [22]). The centres of phytosociological relevés were relocated in stem position maps. Based on the position of standing and lying tree stems, we could repeatedly localise the centres of phytosociological relevés with a precision of 1-2 m and thus minimize relocation error ([44]). In total, we used 105 plots, of which 42 were in Zofín, 23 in Boubín, 16 in Stožec, 22 in Zákova hora, and two in Milešice.
Tab. 3 - Number and volume of living trees and volume of deadwood in studied localities, average cover of herb layer and number of species of herb layer recorded in relevés in the survey periods. More detail information about number and volume of living trees is provided in Supplementary material (Tab. S1-S5).
| Layer | DBH Class |
Parameter | Boubín | Milešice | Stožec | Zofín | Zákova hora | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1972 | 2000 | 1972 | 2011 | 1974 | 2013 | 1975 | 2008 | 1974 | 2011 | |||
| Living trees |
≥ 10 cm | No. all living trees ha-1 | 314.7 | 209.9 | 257.0 | 333.1 | 160.0 | 149.7 | 233.2 | 218.5 | 254.4 | 308.1 |
| No. deciduous trees ha-1 | 121.0 | 107.6 | 85.9 | 72.1 | 96.7 | 80.1 | 146.5 | 156.8 | 222.9 | 286.9 | ||
| No. coniferous trees ha-1 | 193.6 | 102.3 | 171.1 | 260.9 | 63.3 | 69.6 | 86.7 | 61.7 | 31.6 | 21.2 | ||
| Total volume (m3 ha-1) | 547.0 | 674.1 | 330.3 | 632.8 | 671.6 | 648.1 | 622.6 | 539.6 | 375.5 | 666.6 | ||
| 10-39 cm | No. all living trees ha-1 | 236.0 | 107.6 | 205.3 | 214.7 | 58.1 | 72.5 | 145.6 | 152.1 | 200.6 | 208.6 | |
| No. deciduous trees ha-1 | 96.8 | 60.3 | 72.7 | 30.5 | 26.0 | 29.5 | 110.5 | 117.6 | 186.4 | 202.4 | ||
| No. coniferous trees ha-1 | 139.2 | 47.3 | 132.6 | 184.2 | 32.1 | 43.1 | 35.1 | 34.5 | 14.1 | 6.2 | ||
| Total volume (m3 ha-1) | 134.5 | 72.4 | 132.9 | 123.5 | 56.0 | 33.2 | 89.0 | 76.4 | 106.1 | 121.6 | ||
| 40-79 cm | No. all living trees ha-1 | 72.0 | 89.4 | 50.0 | 111.3 | 92.7 | 56.0 | 77.2 | 53.3 | 50.3 | 89.9 | |
| No. deciduous trees ha-1 | 24.0 | 45.9 | 13.2 | 41.1 | 65.9 | 35.6 | 32.7 | 33.0 | 34.1 | 78.2 | ||
| No. coniferous trees ha-1 | 47.9 | 43.5 | 36.8 | 70.2 | 26.8 | 20.4 | 44.4 | 20.3 | 16.2 | 11.6 | ||
| Total volume (m3 ha-1) | 333.8 | 456.1 | 183.4 | 447.7 | 496.2 | 327.0 | 400.1 | 294.9 | 227.2 | 430.3 | ||
| ≥ 80 cm | No. all living trees ha-1 | 6.6 | 12.8 | 1.7 | 7.1 | 9.3 | 21.2 | 10.4 | 13.1 | 3.6 | 9.6 | |
| No. deciduous trees ha-1 | 0.2 | 1.4 | 0.0 | 0.6 | 4.8 | 15.1 | 3.3 | 6.2 | 2.3 | 6.2 | ||
| No. coniferous trees ha-1 | 6.5 | 11.5 | 1.7 | 6.5 | 4.4 | 6.1 | 7.1 | 6.9 | 1.2 | 3.4 | ||
| Total volume (m3 ha-1) | 78.7 | 145.5 | 13.9 | 61.6 | 119.3 | 287.9 | 133.4 | 168.4 | 86.4 | 192.0 | ||
| Deadwood | - | No. of deadwood (pcs ha-1) | 111.6 | 153.9 | 40.5 | 126.9 | 14.7 | 86.0 | 32.2 | 122.4 | 42.0 | 68.2 |
| Volume of deadwood (m3 ha-1) | 147.8 | 364.6 | 75.9 | 171.7 | 51.0 | 183.3 | 111.9 | 355.1 | 101.2 | 149.6 | ||
| Herb layer | - | Average cover (%) | 66 | 53 | 70 | 10 | 77 | 65 | 76 | 51 | 66 | 28 |
| No. of recorded species | 48 | 64 | 20 | 15 | 34 | 70 | 70 | 97 | 42 | 47 | ||
Data analysis
Tab. 4 - Changes in tree layer between surveyed periods. The total number of trees ≥ 10 cm DBH in 50 × 50 m plots recorded at all sites in two survey periods. The proportion of coniferous (con70, con00) and broadleaved (leaf70, leaf00) trees and the results of Fisher’s exact test comparing the proportion of coniferous and broadleaved between the first and repeated surveys are given.
| Parameter | Boubín | Milešice | Stožec | Zákova hora |
Zofín |
|---|---|---|---|---|---|
| No. of trees 1970 | 1237 | 229 | 637 | 1462 | 1758 |
| No. of trees 2000 | 785 | 238 | 548 | 1458 | 1529 |
| con70 (%) | 62 | 61 | 41 | 10 | 23 |
| con00 (%) | 48 | 69 | 41 | 6 | 9 |
| leaf70 (%) | 38 | 39 | 59 | 90 | 77 |
| leaf00 (%) | 52 | 31 | 59 | 94 | 91 |
| Fisher’s P value | <0.0002 | ns | ns | < 0.001 | <0.0001 |
A nonparametric Wilcoxon paired test for dependent samples was used to compare the number of coniferous and broadleaved trees in the 50 × 50 m plots between the initial and repeated surveys. The difference in the proportion of coniferous and broadleaved trees between surveys was assessed with Fisher’s exact test (Tab. 4). We used the pair correlation function to describe the changes in spatial patterns of trees over 30 years ([39]). We compared the results of spatial analyses from the first 1970s and repeated 2000s surveys to examine whether the spatial distribution of trees had the potential to drive a possible shift in the distribution of herbaceous species along the altitudinal gradient. This function is defined by Stoyan & Penttinen ([40]) as follows: “consider two infinitesimally small discs of areas dx and dy at distance r. Let p(r) denote the probability that each disc contains a point of the process”. Then (eqn. 1):
where λ is the density of trees. According to Law et al. ([26]), the function g(r) is a normalised measure of how, on average, a plant perceives the density of other plants as it “looks out” over increasing distances r into the community in which it lives. The pair correlation function has a non-cumulative character; it uses annuli as distance classes. Under the assumption of a homogenous Poisson process, g(r) = 1. Values of g(r) larger than one indicate clustering, while values smaller than one indicate regularity ([19]). The pair correlation function g(r) was estimated for each plot (n = 105) within the interval 0.5-4.0 m in steps of 0.5 m. The nonparametric bias-corrected and accelerated (BCa) confidence intervals (95%) based on 1000 bootstrap replications ([13]) were constructed for these mean g(r) values. The BCa limits were given by the percentiles of the bootstrap distribution, which were related to acceleration and bias correction ([13]). To perform spatial analysis, the minimum tree density was 10 individuals per plot ([1]). Spatial analyses were conducted in R ([35]), using the library “spatstat” ([3]). The library “bootstrap” ([13]) was used for the construction of BCa confidence intervals.
We applied two generalized linear mixed models with a binomial error distribution and logit link function ([7]) to investigate the effects of altitude, survey period, spatial distribution of trees and the interaction of altitude and survey period on the probability of species presence. In the case of the herb layer, presence-absence data were used for analyses. Our main focus was on the interaction of altitude and survey period, because its positive/negative effect indicates that species tend to occur at a higher/lower altitude in the 2000s compared to the 1970s. In the first model, phytosociological relevé, site and species were used as random intercepts to account for variation in the baseline probability of species presence among relevés, sites and species (random intercepts model). We did not include the Milešice site in these analyses due to the low number of plots found at this site. The probability of presence pjks of species j in relevé k and site s was modelled as follows (eqn. 2):
where β0 is the global intercept, β1, β2, β3 and β4 the effect of altitude (A), survey period (P), the interaction of altitude and survey period (A×P), and spatial distribution of trees (T), respectively. Parameters µj, µk and µs represent the random intercepts of species, relevé, and site, respectively. Because the effects of altitude, survey period and their interaction were not allowed to vary among species, this model was used to examine the mean response of any species in the community to these variables (community-wide response). The model represented a baseline against which we compared the second more complex model.
In the second model, we added species-specific random slopes to β1, β2 and β3, which, in contrast to the previous model, allowed each species to vary in its response to altitude, survey period, and their interaction (random slopes model). It was specified as follows (eqn. 3):
where β1- β3 were allowed to vary among species.
The performance of these two model types (random intercepts vs. random slopes models) was compared with a likelihood ratio test ([7]). If the p-value of the likelihood ratio test was less than 0.05, we considered species to vary significantly in response to altitude, survey period, and their interaction. With a special focus on the interaction, we evaluated the average species-specific response to the interaction (average β3j) and species-specific random slopes associated with the interaction (individual β3j). Coefficients above/below zero indicate that species tended to occur at higher/lower altitudes in the 2000s compared to the 1970s.
In both models, we included 28 herbaceous species which were common to all sites: Actaea spicata, Athyrium filix-femina, Avenella flexuosa, Calamagrostis villosa, Circaea alpina, Deschampsia cespitosa, Dryopteris carthusiana, Dryopteris filix-mas, Equisetum sylvaticum, Galeobdolon montanum, Galium odoratum, Geranium robertianum, Gymnocarpium dryopteris, Homogyne alpina, Impatiens noli-tangere, Milium effusum, Oxalis acetosella, Paris quadrifolia, Petasites albus, Phegopteris connectilis, Prenanthes purpurea, Rubus idaeus, Sanicula europaea, Senecio ovatus, Stellaria nemorum, Urtica dioica, Vaccinium myrtillus, Viola reichenbachiana. Owing to variation in altitude among sites, we standardized this variable within sites by subtracting the site-specific mean and dividing by one standard deviation. The spatial distribution of trees on the 50 × 50 m plots associated with each relevé was represented by the value of the pair correlation function ([4]). It can be considered a proxy for the relative level of tree clustering in our models, with lower and higher values indicating relatively weaker and stronger tree clustering, respectively. Because the pair correlation functions indicated non-random spatial distribution of trees up to a distance of 1 m in survey periods, we separately used the values of the pair correlation function estimated at distances of 0.5 and 1 m in preliminary models with random intercepts. We compared the models with different distances and selected a distance of 0.5 m showing the lowest Akaike’s Information Criterion for the final models ([9]). Generalized linear mixed models were fitted in R v. 4.0.2 ([35]) using the library “lme4” v. 1.1-23 ([5]).
Results
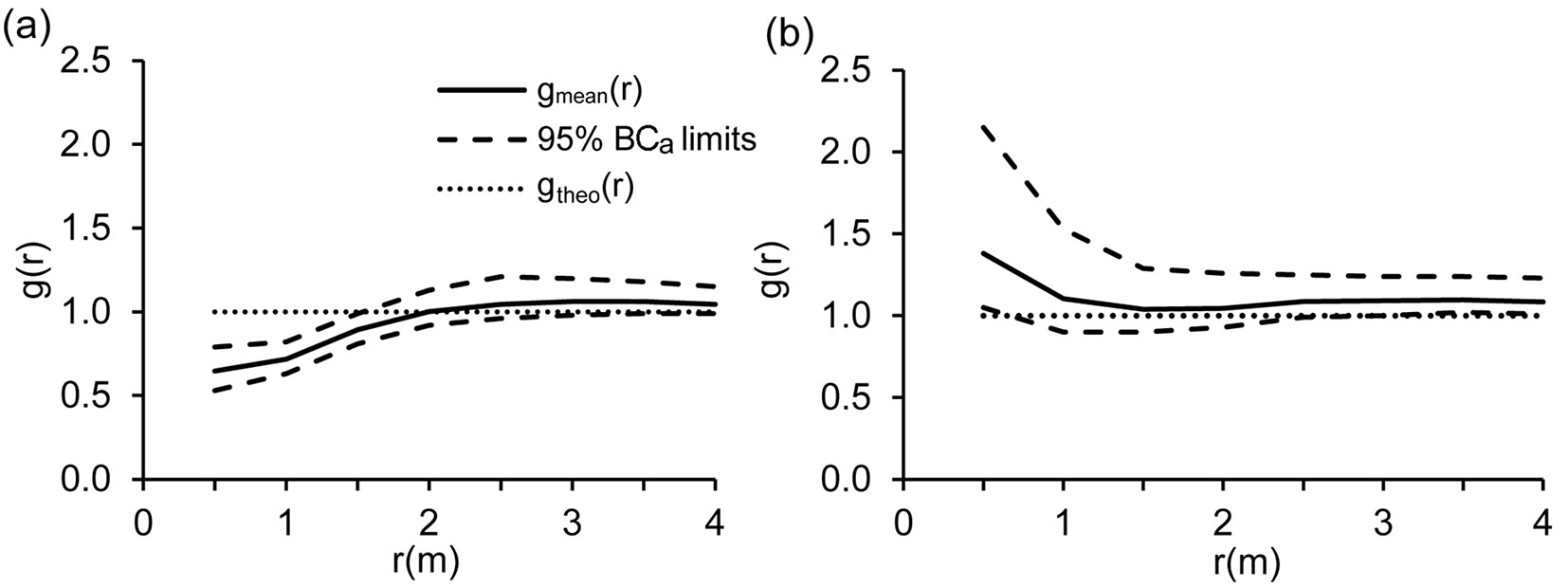
The total number of trees ≥ 10 cm DBH per plot was significantly higher in the 1970s than the 2000s, based on the results of the Wilcoxon paired test for dependent samples (P = 0.00002). This was because the total number of coniferous trees per plot was significantly lower in the 2000s than 30 years before (Wilcoxon paired test: P < 0.0001). In contrast, the total number of broadleaved trees did not vary between the survey periods. As shown by the results of the Fisher’s exact test, the proportion of broadleaved and coniferous trees significantly differed in Zofín, Boubín and Zákova hora (Tab. 4). Analyses of tree spatial patterns on 105 plots showed a general shift to more clustered patterns from the 1970s to the 2000s (Fig. 1). In the 1970s, the trees largely showed a regular distribution up to a distance of 1 m and then a clustered distribution. In the 2000s, tree spatial patterns were clustered up to distances of 0.5 m. Signs of regularity completely disappeared.
Fig. 1 - Comparison of tree spatial patterns based on the pair correlation function g(r) in the 1970s (a) and the 2000s (b). Solid lines [gmean(r)] show the mean values from 105 plots. Dashed lines (95% BCa limits) show the 95% nonparametric bias-corrected and accelerated confidence intervals based on 1000 bootstrap replications for the mean values of gmean(r). Dotted lines [gtheo(r)] show the theoretical value of complete spatial randomness. If the value of the lower 95% BCa limit is larger than gtheo(r) then the trees show clustering at the respective distances. If the value of the upper 95% BCa limit is smaller than gtheo(r) then the trees show a regular distribution at the respective distances. The variable “r(m)” refers to distance.
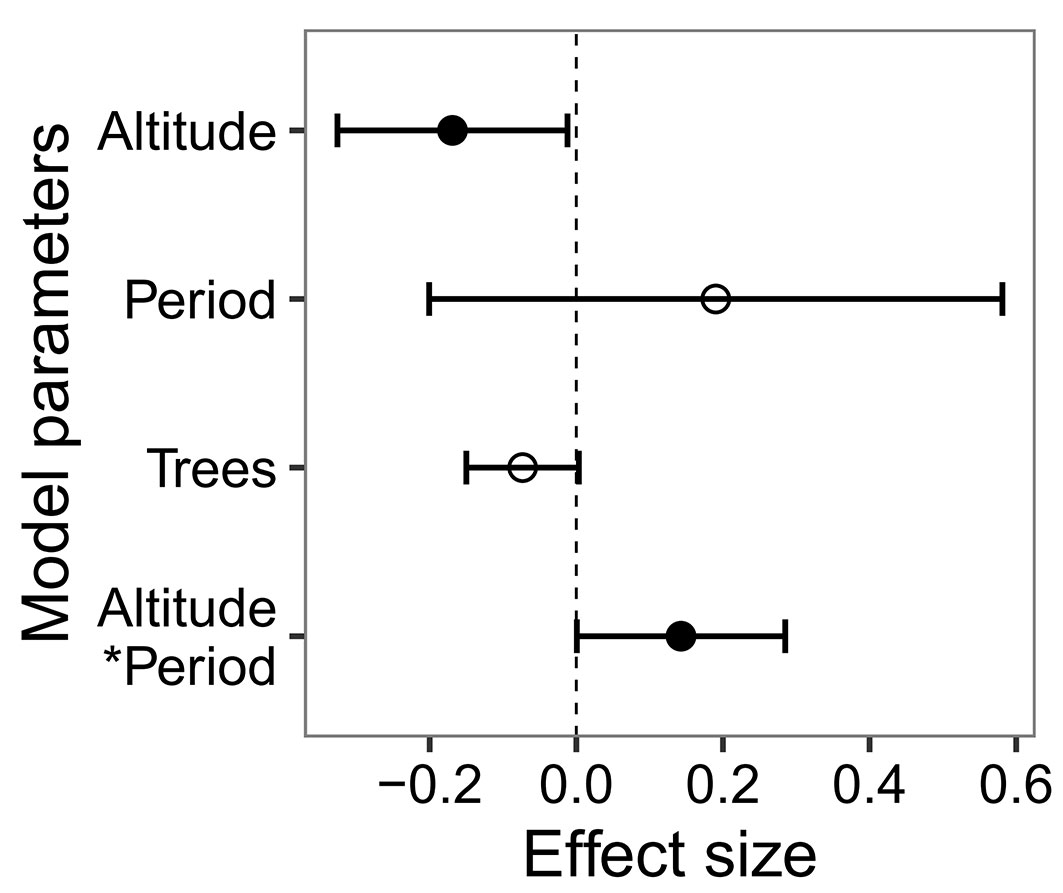
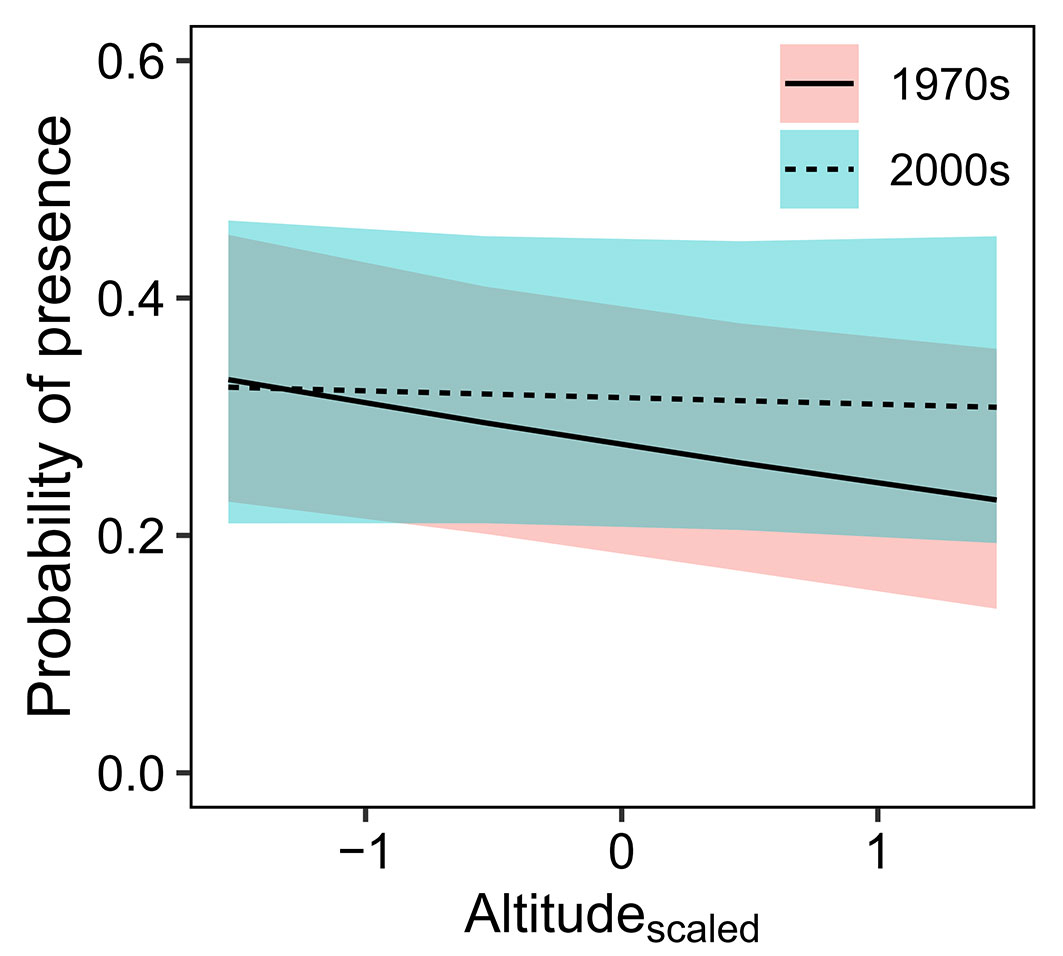
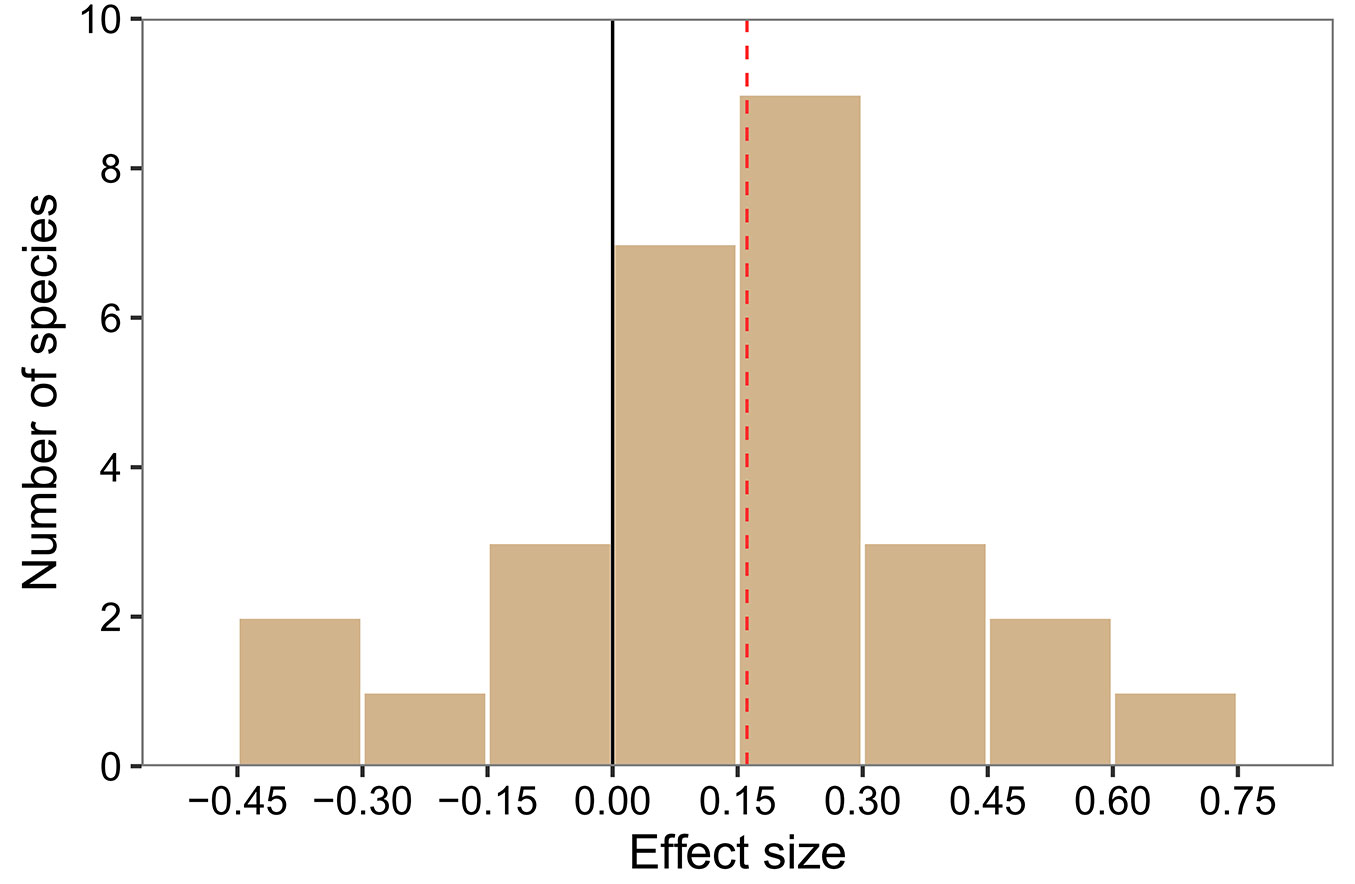
By comparing the random intercepts and random slopes models with a likelihood ratio test, the random slopes model showed better fit (df = 9, χ2 = 363.01, p < 0.001), demonstrating that species significantly varied in response to altitude, survey period and their interaction. Based on the results of this random slopes model, the probability of species presence was on average negatively related to altitude and positively related to the interaction between altitude and survey period (Fig. 2). Although non-significant, the probability of species presence was also reduced by the effect of tree clustering (Fig. 2). On average, the effect of altitude increased the probability of species presence in the 2000s compared to the 1970s (Fig. 3). This interactive effect varied among species, with almost 80% of species showing that the probability of their presence decreased more strongly with altitude in the 1970s than in the 2000s (Fig. 4).
Fig. 2 - The effects of altitude, survey period (Period, P), spatial distribution of trees (Trees, T) and the interaction of altitude and survey period (Altitude × Period, A × P) on the probability of species presence based on the results of the random slopes model. Altitude was standardised within sites by subtracting the site-specific mean altitude and dividing by one site-specific standard deviation. The spatial distribution of trees is represented by relevé-specific values of the pair correlation function estimated at a distance of 0.5 m. Solid symbols denote statistically significant effects with p < 0.05.
Fig. 3 - The interactive effects of altitude and survey period on the probability of species presence based on the results of the random slopes model. The predicted probabilities with 95% confidence intervals are displayed. Altitude (Altitudescaled) was standardised within sites by subtracting the site-specific mean altitude and dividing by one site-specific standard deviation.
Fig. 4 - Distribution of interactive effects of altitude and survey period on the probability of species presence based on the results of the random slopes model. Histogram bars are based on species-specific regression coefficients (random slopes) for 28 herbaceous species. Bars to the right of the solid zero line indicate species that occur at higher altitude in the 2000s compared to the 1970s. The average species-specific response (coefficient) to the interactive effect of altitude and survey period is indicated by the red dashed line.
Discussion
It is clear that the number of trees on studied plots was lower at the beginning of the new millennium than in the 1970s (Tab. 4). This could be explained by the decline of conifers owing to bark beetle outbreaks, natural forest dynamics ([25]), or natural gap dynamics driven by the mortality and falls of individual trees or small tree groups ([23]). Possibly the intermediate-scale windstorm events of Kyrill (2007) and Emma (2008) also played a crucial role. The recruitment of tree seedlings will likely increase the number of trees with DBH ≥ 10 cm in the future, as was the case with declines of silver fir being gradually replaced by European beech in Western Carpathian natural forests ([46]).
In line with our findings, the proportion of European beech has rapidly increased over approximately the same time span in many Central European old-growth forests ([46], [21], [22]). The long-term replacement of silver fir by expanding beech has been explained by changes in forest management practices ([46]), pressure from insect pests ([36]), or fungal pathogens ([41]), and by the sensitivity of fir to changes in abiotic factors ([27]). Greater pressure on Abies alba from forest game can also play a role here, even though most of the studied localities are fenced. Moreover, juvenile beech trees naturally form the understory in many spruce stands ([22]), which are often exposed to repeated outbreaks of bark beetles. With the exception of wet sites, the new tree generation is mostly dominated by beech in these post-disturbance areas. The replacement of tree species is thus considerably accelerated by the effects of disturbances, thereby allowing for faster adaptation of forests to changing conditions ([42]). Ongoing changes in the tree layer are also in line with our findings on tree spatial distributions in both survey periods. The regular spatial distribution of trees in the 1970s indicates that density-dependent processes, such as long-term competitive interactions, were important for the formation of tree spatial distributions. Conversely, we found a clustered spatial distribution of trees 30 years after the first survey in the 1970s, which can be attributed to the recruitment of new trees released by the fall of individual trees and/or groups of trees from the aging tree generation ([14], [29]).
Thinning of the tree canopy layer indicated by clustered tree distribution ([43]) mostly gives rise to conditions that are favourable for herbaceous species with requirements for higher light availability in the understorey. Gap dynamics and related changes in light availability are often mentioned as key drivers of changes in the understorey ([6], [32]). On the other hand, some changes of the herb layer can be independent of changes in forest structure ([18]). An example could be an upward shift of herbaceous species along the altitudinal gradient as one of the outcomes of rising temperatures and lower precipitation ([28]). However, it may be difficult to detect in temperate forests. The effect of changing climatic conditions can be reduced depending on the presence/absence of an upper understorey ([49]) and thermophilous plants can be dramatically suppressed due to shading by the tree canopy ([11]). Our findings show an increase in the probability of species presence at higher altitudes in the 2000s compared to the 1970s, which could indicate a shift in species distribution along the altitudinal gradient. From this perspective, it is interesting that the number of herbaceous species showing this relationship was almost 80%. Because we accounted for the effect of tree spatial distribution on species presence/absence in both survey periods, we suspect that the observed shift in the distribution of herbaceous species along the altitudinal gradient is not directly related to temporal changes in forest structure and light conditions in the understorey ([16]). Other biotic and environmental conditions such as light availability, precipitation and the density of juvenile woody individuals deserve further attention in future studies for the evaluation of temporal changes in the altitudinal distribution of herbaceous species.
A changing distribution of plant species along the altitudinal gradient has been associated with climate change at both regional and global scales ([48]). Although this cannot be directly concluded based on our findings, we demonstrate that the tree and herb layers have changed in a way that may be indicative of ongoing climate-related changes. We also show that the drivers of the distribution of herbaceous species may not be directly related to the spatial distribution of trees, and that the shifts in the distribution of herbaceous species along the altitudinal gradient can also be observed in temperate forests. Whether this is only a temporary phenomenon or rather a long-term trend needs to be examined in future studies
Conclusion
We have shown that changes in the tree layer over the 30 year period indicate a shift towards a more complex forest structure and the gradual replacement of conifers by broadleaved tree species, especially beech. We also show that herbaceous species tended, on average, to occur at higher altitudes 30 years after the initial survey in the 1970s. This relationship was observed for almost 80 % of the studied herbaceous species, even when accounting for the spatial distribution of trees in both survey periods. This was mainly related to shade-tolerant species, which are usually independent of the distribution, size of canopy openings and of early-succession stages of forest communities following disturbance events.
Acknowledgements
This research was supported by the Czech Science Foundation, project 20-17282S and by the institutional subsidy of Ministry of Education, Youth and Sports of the Czech Republic.
References
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Authors’ Info
Authors’ Affiliation
David Janík 0000-0002-8271-7456
Dušan Adam
Jan Holík 0000-0002-7949-9689
The Silva Tarouca Research Institute for Landscape and Ornamental Gardening, Department of Forest Ecology, Lidická 25/27, Brno (Czech Republic)
Corresponding author
Paper Info
Citation
Unar P, Janík D, Adam D, Holík J (2022). Changes in tree layer and altitudinal distribution of herbaceous species in temperate old-growth forests over 30 years. iForest 15: 206-212. - doi: 10.3832/ifor3749-015
Academic Editor
Paola Mairota
Paper history
Received: Jan 11, 2021
Accepted: Apr 17, 2022
First online: Jun 11, 2022
Publication Date: Jun 30, 2022
Publication Time: 1.83 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2022
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 29475
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 25173
Abstract Page Views: 2535
PDF Downloads: 1331
Citation/Reference Downloads: 0
XML Downloads: 436
Web Metrics
Days since publication: 1298
Overall contacts: 29475
Avg. contacts per week: 158.96
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
(No citations were found up to date. Please come back later)
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Towards a functional phytosociology: the functional ecology of woody diagnostic species and their vegetation classes in Northern Italy
vol. 14, pp. 522-530 (online: 22 November 2021)
Technical Reports
Diversity pattern of vegetation in and around proposed Kotlibhel hydroelectric project along the Alaknanda River in Garhwal Himalaya (India)
vol. 4, pp. 38-43 (online: 27 January 2011)
Research Articles
Influences of mature Pinus nigra plantations on the floristic-vegetational composition along an altitudinal gradient in the central Apennines, Italy
vol. 13, pp. 279-285 (online: 03 July 2020)
Research Articles
Growing at the forest edges: how natural regeneration develops under fragmentation
vol. 15, pp. 248-255 (online: 19 July 2022)
Research Articles
Typology and synecology of aspen woodlands in the central-southern Apennines (Italy): new findings and synthesis
vol. 13, pp. 202-208 (online: 19 May 2020)
Research Articles
The cork oak in the Mountains of Palermo (Italy): ecological insights from the south-eastern edge of its distribution range
vol. 13, pp. 336-344 (online: 07 August 2020)
Short Communications
Biodiversity inventory of trees in a neotropical secondary forest after abandonment of shaded coffee plantation
vol. 10, pp. 303-308 (online: 23 February 2017)
Research Articles
Disassociating tree species associations in the eastern United States
vol. 7, pp. 248-254 (online: 13 March 2014)
Research Articles
A state-and-transition approach to alpine grasslands under abandonment
vol. 3, pp. 44-51 (online: 02 March 2010)
Research Articles
Drought effects on the floristic differentiation of Greek fir forests in the mountains of central Greece
vol. 8, pp. 786-797 (online: 08 April 2015)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword