Allometric equations to estimate above-ground biomass of small-diameter mixed tree species in secondary tropical forests
iForest - Biogeosciences and Forestry, Volume 13, Issue 3, Pages 165-174 (2020)
doi: https://doi.org/10.3832/ifor3167-013
Published: May 02, 2020 - Copyright © 2020 SISEF
Research Articles
Abstract
Accounting for small-size tree biomass is critical to improve total stand biomass estimates of secondary tropical forests, and is essential to quantify their vital role in mitigating climate change. However, owing to the scarcity of equations available for small-size trees, their contribution to total biomass is unknown. The objective of this study was to generate allometric equations to estimate total biomass of 22 tree species ≤ 10 cm in diameter at breast height (DBH), in the Yucatan peninsula, Mexico, by using two methods. First, the additive approach involved the development of biomass equations by tree component (stem, branch and foliage) with simultaneous fit. In the tree-level approach, total tree biomass equations were fit for multi-species and wood density groups. Further, we compared the performance of total tree biomass equations that we generated with multi-species equations of previous studies. Data of total and by tree component biomass were fitted from eight non-linear models as a function of DBH, total height (H) and wood density (ρ). Results showed that two models, identified as model I and II, best fitted our data. Model I has the form AGB = β0 (ρ·DBH2·H)β1 + ε and model II: AGB = exp(-β0)(DBH2·H)β1 + ε, where AGB is biomass (kg). Both models explained between 53% and 95% of the total observed variance in biomass, by tree-structural component and total tree biomass. The variance of total tree biomass explained by fit models related to wood density group was 96%-97%. Compared foreign equations showed between 30% and 45% mean error in total biomass estimation compared to 0.05%-0.36% error showed by equations developed in this study. At the local level, the biomass contribution of small trees based on foreign models was between 24.38 and 29.51 Mg ha-1, and model I was 35.97 Mg ha-1. Thus, from 6.5 up to 11.59 Mg ha-1 could be excluded when using foreign equations, which account for about 21.8% of the total stand biomass. Local equations provided more accurate biomass estimates with the inclusion of ρ and H as predictors variables and proved to be better than foreign equations. Therefore, our equations are suitable to improve the accuracy estimates of carbon forest stocks in the secondary forests of the Yucatan peninsula.
Keywords
Species Diversity, Biomass-carbon Stocks, Additive Equations, Simultaneous Fit, Wood Density Groups
Introduction
The importance of tropical secondary forests for biodiversity conservation, provision of ecosystem services and climate change mitigation is globally recognized ([52], [18], [46]). These forests have expanded partly due to abandonment of agricultural land, increasing of extensive grazing, and deforestation and degradation of old-growth forests ([43], [22], [46]). Secondary forests hold a relative high abundance of small-diameter trees ([18], [36]). In this study, small trees are defined as trees smaller or equal than 10 cm diameter at breast height (DBH, 1.30 m above the ground). Small-diameter trees are an important component of woody plants diversity, show positive growth rates, and are key to study changes in demographic features of tropical species ([54], [36]). The high density and diversity of small trees give forests high levels of relative resilience against anthropogenic and natural disturbances ([2], [36]).
Small-diameter trees are an important component of total tree density and biomass in tropical forests in the Yucatan peninsula, Mexico. This component represents between 2.4% to 60% of the total tree density in forests of the state of Campeche, Mexico ([55], [25]). In other young secondary neotropical forests, small trees might represent from 65% to 93.6% of the total tree density ([5], [36]). Small trees might also contribute from 3.4% to 41.3% of the total biomass, depending on the forest successional stage ([34], [36]). For example, in secondary tropical forests of Mexico, Brazil, Nicaragua and Central Africa, abandoned since 0, 17, 25, 37 and more than 48 years, the contribution of small trees to total biomass was ~ 43.35 Mg ha-1 (41.3%), 51.27 (27.5%) Mg ha-1, and 15 to 29.75 (5.7 to 14.45%) Mg ha-1, respectively ([35], [34], [36]).
Tree biomass is commonly estimated with allometric models that use easily measured tree variables as predictors, namely DBH, total height and wood density ([10], [17]). Most allometric biomass equations are developed with trees > 10 cm in DBH and at large scales ([6], [10]). Notwithstanding the structural and ecological importance that trees ≤ 10 cm in DBH represent in secondary tropical forests, they are not typically incorporated into biomass models ([8], [36]). Hence, the actual biomass locally stored in secondary tropical forests is likely underestimated.
Biomass equations generated at the local scale might become a reliable tool to reduce uncertainty of carbon stock estimates. For instance, biomass errors ranging from 10% to 40%, and in extreme cases up to 70% have been reported for neotropical regions ([52], [34], [24]). The inclusion of tree height and wood density into the fitting process could also help to reduce uncertainty and improve the accuracy of biomass estimations. For example, Baker et al. ([3]) and Lima et al. ([34]) reported an inter-regional variation in tree wood density close to 16% in four regions of the Amazonia. As a result, there was a high variability among regions in biomass stocks estimated with the same generic allometric equations, likely due to a variation of DBH to total height ratio, which is also influenced by species wood density ([3]). In the Republic of Congo forests, Bastin et al. ([4]) found large bias in biomass estimations which were based on models that used wood density obtained at a global scale. In this case, the overestimation in biomass ranged from 20% to 40% in species with wood densities from 0.52 to 0.68 g cm-3. Thus, wood density, which can vary among tree species of the same region and even more among those of different geographical regions, is a tree characteristic with considerable influence in determining total biomass variability ([11]).
In Mexican tropical forests, the study and analysis of the biomass of small-size trees and their contribution to the ecosystem is limited, though many non-linear and exponential type biomass equations have been developed. Indeed, most equations have been generated for temperate forests, especially for valuable timber species of the Pinaceae and Fagaceae families ([48]). Furthermore, equations for tropical forests and particularly for small-size trees are fairly uncommon. Hughes et al. ([26]) developed a general equation for tropical trees ≤ 10 cm in DBH in central-east Mexico, which was further re-parametrized by Chave et al. ([9]) to estimate biomass of small-size trees in Panama’s forests. In the southern Yucatan peninsula, Cairns et al. ([7]) developed nine species-specific equations for trees ≤ 10 cm in DBH and a general equation for large-diameter trees. However, the applicability of these species-specific equations is limited for secondary forests because they were developed using old-growth stands data sets. Many of the biomass estimations for small-size trees in tropical secondary forests in Mexico are based on the general equations by Hughes et al. ([26]) and Chave et al. ([9]). However, so far there has been no evaluation of these equations when comparing with local equations generated for small-size trees in the Yucatan peninsula; such assessment would be useful to detect the variability of biomass across forest stands with high-density of small-size trees obtained from forest inventories. Also, local biomass equations could become valuable tools to evaluate the contribution of secondary forests to the global carbon cycle through improved estimations of carbon stocks.
In this study, we developed allometric equations to estimate the biomass of small diameter trees (DBH ≤ 10 cm) for 22 tree species that are structurally important in secondary tropical forests of the southern Yucatan peninsula, Mexico. The main objectives were to: (i) generate biomass equations by tree structural components (i.e., stem, branches and foliage); (ii) develop multi-species equations and by wood density groups (i.e., high, intermediate and low density) to estimate total tree biomass; (iii) compare the estimation error of the multi-species and wood density group equations against generalized biomass equations developed for other tropical regions; and (iv) examine the ability to accurately estimate biomass at the stand level of the Hughes et al. ([26]) and Chave et al. ([9]) equations compared with the best equation generated in this study using data from young secondary forest. The hypotheses were: (I) equations that include total height and wood density as independent variables, besides DBH, fit the data better than simple equations (i.e., based on one or two predictors), since they include the wood properties that determine the species growth form; and (II) the equations developed in this study are more accurate for total tree biomass estimation at local level than those generated in other tropical regions, because the former incorporate the effects of growth and allometric characteristics of the species in the model.
Materials and methods
Study site
This study was performed in secondary tropical forests ranging from nine to 35 years-old and in an old-growth stands. The stand age corresponds to the time (years) elapsed after the last application of slash and burn agriculture system (maize, beans and squash as main products). Stands were located in the southeast region of the Yucatan peninsula, Mexico, between the Sian Ka’an Biosphere Reserve in Quintana Roo (19° 05′ and 20° 06′ N, 87° 30’ and 87° 58’ W) and Calakmul Reserve in Campeche (19° 15′ and 17° 45′ N, 90° 10′ and 89° 15’ W - Fig. 1). The Calakmul Biosphere Reserve is the largest continuous conservation area of tropical rainforest in Mexico (7.231.85 km2). The Sian Ka’an and Calakmul Biosphere Reserves are part of the Mesoamerican Biological Corridor, which serves to conserve the habitat of different species of flora and fauna, and also to promote a sustainable social and economic development of the region ([37]).
The dominant vegetation type is mid-stature, semi evergreen tropical forest ([42]). The region is characterized by large areas of secondary vegetation growing in different successional stages, due to shifting cultivation and other types of land use. The climate is tropical sub-humid with mean annual rainfall ranging from 948 to 1500 mm, most of which falls in summer, while the driest months (March and April) have less than 600 mm of rainfall ([33]). Mean annual temperature is about 26 °C ([23]). Topography is mostly flat with slight undulations. Soil types correspond to gleysols, vertic cambisols and vertic luvisols, which are thin and shallow with a slow water drainage, and surface flooding occurs in the rainy season or during storms or hurricanes ([19]).
Biomass data collection
We performed a pre-assessment on each stand to collect information to estimate the Structural Importance Index (IVI) of each tree species ([14]). The IVI was calculated as the sum of the relative abundance, frequency and dominance of each species within a given stand or forest. The tree species were ranked according to the index IVI. A total of 22 species ranging from 1 to 10 cm DBH (denoted as small-size trees) were selected.
We selected and harvested between 12 and 18 trees by species (311 trees in total - Tab. S1 in Supplementary material) for biomass calculations. The fresh weight of each structural component of the selected trees (i.e., stem, branches, and foliage) was recorded with an electronic scale TORREY CRS-HD® of 500 kg capacity and ± 100 g accuracy. Three random samples of 100 ± 10 g were obtained from branches and foliage to determine the dry weight/fresh weight ratio of both structural components. Further, three sections (disks) 5 to 7 cm thick per tree were obtained from the base, middle and upper tree stem and weighed with an electronic scale OHAUS Pioneer® of 5 kg (accuracy ± 0.1 g). In the case of trees ≤ 2.5 cm in DBH, the total structural components were sent to the laboratory. All samples were oven-dried at 70 °C until they reached constant dry mass. The dry weight /fresh weight ratio was used to obtain the tree dry weight of stem, branches, and foliage. The total above-ground tree biomass of sampled trees was calculated by adding up the total dry weight of each of the three structural components ([39]).
Wood density
Wood samples (cubes) were taken from each tree at 1.30 m from the base of the stem to determine wood basic density (g cm-3). Each sample included the pith, heartwood, sapwood and cambium because the distribution of these elements influences the wood density along the stem ([11]). We used the water displacement method to obtain the green volume of each cube ([11]). Subsequently, the cubes were oven-dried at 105 °C to constant dry mass. Basic density of each wood sample was estimated using the dry mass/green volume ratio. The species were classified in three wood density groups (Tab. S1 in Supplementary material): low (≤ 0.40 g cm-3), intermediate (0.41-0.60 g cm-3) and high (≥ 0.61 g cm-3). Basic density is considered an economic indicator for the industry, and a good wood descriptor for the study of trees and their ecological behavior ([11]).
Model fitting and statistical analysis
Scatter plots of total biomass against DBH by species were used to explore data trends, and decide whether a linear or a non-linear model would be more suitable to fit the data. Based on scatter plots, we tested eight allometric regression model types that were previously reported in other studies to estimate total tree biomass (Tab. S2 in Supplementary material).
We performed independent fitting for each model to estimate their parameters by structural component and for total tree biomass. Model fitting was performed by applying the Newton’s iterative method with Ordinary Least Squares (OLS) using the PROC MODEL in SAS ([50]). Weighted functions were applied to the regression models to improve the homogeneity of variances and goodness-of-fit statistics ([1]). The models’ goodness of fit was assessed with the following statistics: (i) root mean square error of the estimate (RMSE); (ii) proportion of variance explained by the model corrected by the number of parameters estimated (adjusted R2); and (iii) the Akaike’s Information Criterion (AIC - [28]). The AIC measures the goodness of fit of a regression model for a set of species ([10]). The best model minimizes the values of RMSE and AIC, and maximizes the adjusted R2.
After we selected the models following the independent fitting, they were fitted by tree structural components (i.e., stem, branch, and foliage) using a simultaneous equation system. The systems were integrated with the biomass equations (functions) for stem (eqn. 1), branches (eqn. 2) and foliage (eqn. 3) to account for total tree biomass by adding to the three structural components a property known as “model additivity” ([49]). Total tree biomass (eqn. 4) is a function of the independent variables in the equations for structural components, including constraints on the model parameters and is expressed as:
where AGB is above-ground biomass (kg), β is the vector of regression parameters to be estimated, DBH is diameter at breast height (cm), H is total tree height (m), ρ is wood density (g cm-3) by species. We assumed that the error terms are independent and identically distributed as ε~ N(0,σ2e).
The simultaneous fit, without analytical relations among equations, was solved with the NSUR technique (nonlinear seemingly unrelated regressions) and iteratively applying the ITSUR option of PROC MODEL in SAS using Newton Algorithm ([49] - Tab. S3). It is very common to detect heteroscedasticity once the models are fitted and the residuals obtained, and to correct this problem, we fit models using weighted regression (weighting functions) to improve homogeneity of variances and guarantee model additivity, as recommended by Alvarez-González et al. ([1]) and Sanquetta et al. ([49]).
Multi-species (i.e., mixture of species) equations were fitted using models previously selected after independent fitting (Tab. S4 in Supplementary material). Biomass equations by species and wood density groups (i.e., high and intermediate) were developed with a nonlinear model (eqn. 5), whereas equations for species with low wood density a linearized model was used (eqn. 6), assuming that errors are positive and multiplicative; because biomass data showed a more linear trend than the remaining species, we also used a correction factor (eqn. 7) for correcting bias introduced by the logarithmic transformation:
where AGB is the above-ground biomass (kg), β0 and β1 are regression coefficients of the parameters to be estimated, ρ is the wood density (g cm-3) by species, DBH is the diameter at breast height (cm), H = total tree height (m), ln is the natural logarithm function, CF is the correction factor, σ is the residual standard error, and β′0 is the regression coefficient estimated in model fitted. We assumed that the error terms are independent and identically distributed as ε~N(0,σ2e).
We used the independent model approach with weighted regression to fit multi-species and wood density group models to improve homogeneity of variance and goodness of fit. Model’s predictive ability was assessed with the “k-fold cross-validation” method ([51], [53]). The original dataset was split into k = 10 disjoint subsets of similar sample size, where elements of each subset were chosen at random. We used each subset as a validation dataset, and the remaining k-1 subset was integrated to the training set. The “10-fold cross-validation” provides a good balance between both bias and variance, and is an indicator of models’ performance with independent datasets since it uses all the observations available for model fitting ([53]). To evaluate the accuracy and compare the performance of the equations to estimate the biomass by structural component and total tree biomass, we calculated the relative mean error (RME% - eqn. 8) and mean absolute percentage error or bias (MAPE% -eqn. 9) for the selected models ([15], [13], [51]) as follows:
where RME% and MAPE% are the relative mean error and absolute bias, respectively, AGBest and AGBobs are predicted (or estimated) and observed biomass, respectively, and n is the sample size (tree numbers).
We compared the RME% and MAPE% of biomass estimated with equations used in this study against equations generated for other tropical regions to assess uncertainty and select a final model. For example, multi-species equations were compared with Hughes et al. ([26]) and Chave et al. ([9]) equations (eqn. 10, eqn. 11):
where AGBpred is the predicted above-ground biomass (kg), DBH is the diameter at breast height (cm), ρ is the wood density (g cm-3) by species, and ρav is the mean wood density (0.54 g cm-3) of the plot and ln is the natural logarithm function.
We selected eqn. 10 and eqn. 11 because they were developed for a mixture of tree species with DBH ≤ 10 cm, which is the same size range of the trees used in this study. Hughes et al. ([26]) generated their equation for a tropical forest in central-east Mexico, and its application is based only on DBH as the predictor of biomass. Chave et al. ([9]) equation was generated for tropical forests located in Panama, and it is a re-parametrization of Hughes et al. ([26]) model; it incorporates wood density as a second independent variable, in addition to DBH. We hypothesized that the inclusion of wood density would be beneficial for models’ performance and accuracy.
The RME% and MAPE% of equations fitted by wood density groups was compared to Djomo et al. ([15]) and Van Breugel et al. ([52]) equations (eqn. 12, eqn. 13):
where AGBpred is the predicted above-ground biomass (kg), DBH is the diameter at breast height (cm), H is the total tree height, ln is the natural logarithm function, and ρ is the wood density (g cm-3) by species.
Our main interest was to assess the performance of eqn. 12 and eqn. 13 since they were also developed for mixed tropical forests with trees ranging from 1 to 138 cm DBH, and included wood density and DBH as predictors. Djomo et al. ([15]) developed their equation using data collected in mature forests from different countries and continents, and included total height, wood density and DBH as predictors. The Van Breugel et al. ([52]) equation was generated using data from secondary forests from one to 25 years-old and from mature stands > 40 years-old, and using wood density and DBH as predictors.
The RME% and MAPE% of equations generated in other tropical regions was calculated from “K-fold-cross-validation” tests ([44], [29]). Negative and positive values of RME% indicate underestimation and overestimation, respectively, of the total biomass of a set of trees. Statistical differences in RME% and MAPE% values among equations were analyzed with the Kruskal-Wallis tests at 95% confidence intervals by the “kruskal.test” function in R version 3.5.1 ([47]). We performed a Duncan multiple range test, by using the “dunn.test” function implemented in the PMCMR package in R, to determine among which equations the mean RME and MAPE were statistically different ([45]). We analyzed the accuracy of models estimation using a linear regression between the predicted and observed values (without intercept) of the biomass obtained, as well as the “lm” function in R. If the models fit the data correctly, the slope of the estimated coefficient should be around one, whereas values that are not around one indicate an inadequate fit ([51]).
Lastly, we evaluated the accuracy of estimations of total biomass stored in small-size trees (≤ 10 in DBH) with the equations of Hughes et al. ([26]) and Chave et al. ([9]) against the best equation of this study. Large-trees (DBH >10 cm) biomass was estimated with the equation of Cairns et al. ([7]). The data were collected in 18 plots of 500 m2 size (10 × 50 m) distributed across tropical secondary forests ranging from nine to 80 years-old of abandonment after traditional slash-and-burn agriculture (maize, beans and squash).
Results
We tested eight regression models to predict above-ground biomass (Tab. S2 in Supplementary material). The adjusted R2 values for these models ranged from 80% to 94%. Model I (named as Model 7 in Tab. S2) and model II (named as Model 8 in Tab. S2) showed the highest adjusted R2 and the smallest RMSE and AIC (Tab. S5). We selected these models based on their best goodness-of-fit statistics.
Equation by structural component
Equations fitted with models I and II accounted for 53% to 95% of the biomass variance observed by structural components, and from 92% to 95% of the total tree biomass (Tab. 1). The smaller explained variances of 71% and 53% were observed for branch biomass estimation. When considering the RMSE values, model I showed greater accuracy for stem, branches and total tree biomass. The weighting function, i.e., 1/DBH2H, was adequate to improve the homogeneity of variances and goodness-of-fit statistics by tree structural component and for total tree biomass.
Tab. 1 - Allometric equations for biomass estimation by tree structural component and total tree biomass derived with simultaneous fit and multi-species equations. (Model I): AGB = β0(ρ·DBH2·H)β1; (Model II): AGB = exp(-β0)(DBH2H)β1. (AGB): stem, branches, foliage or total tree estimated above-ground biomass (kg); (ρ): wood density (g cm-3); (DBH): diameter at breast height (cm); (H): total tree height (m); (β0, β1): regression coefficients of the models to be estimated; (RMSE): root mean square error of the estimate; (adj-R2 ): proportion of variance explained by the model. We assumed that the error terms are independent and identically distributed: ε~N(0,σ2e).
| Model | No. | Allometric model | RMSE | adj-R2 |
|---|---|---|---|---|
| Model I | 1 | AGBstem=0.057541(ρ·DBH2·H)0.916963 | 1.6538 | 0.95 |
| 2 | AGBbranches=0.019758(ρ·DBH2·H)0.980837 | 1.6293 | 0.73 | |
| 3 | AGBfoliage=0.022462(ρ·DBH2·H)0.724191 | 0.4491 | 0.71 | |
| 4 | AGBtotal-tree=AGBstem+AGBbranches+ AGBfoliage | 2.6009 | 0.95 | |
| 5 | AGBtotal-tree multi-species=0.078479(ρ·DBH2·H)0.945339 | 0.1389 | 0.96 | |
| Model II | 6 | AGBstem= exp(-3.471635)(DBH2·H)0.956893 | 2.1974 | 0.93 |
| 7 | AGBbranches=exp(-4.047339)(DBH2·H)0.954151 | 2.4432 | 0.76 | |
| 8 | AGBfoliage=exp(-3.838296)(DBH2·H)0.712222 | 0.8329 | 0.53 | |
| 9 | AGBtotal-tree=AGBstem+AGBbranches+ AGBfoliage | 3.7892 | 0.92 | |
| 10 | AGBtotal-tree multi-species= exp(-2.97501)(DBH2·H)0.957051 | 0.1552 | 0.95 |
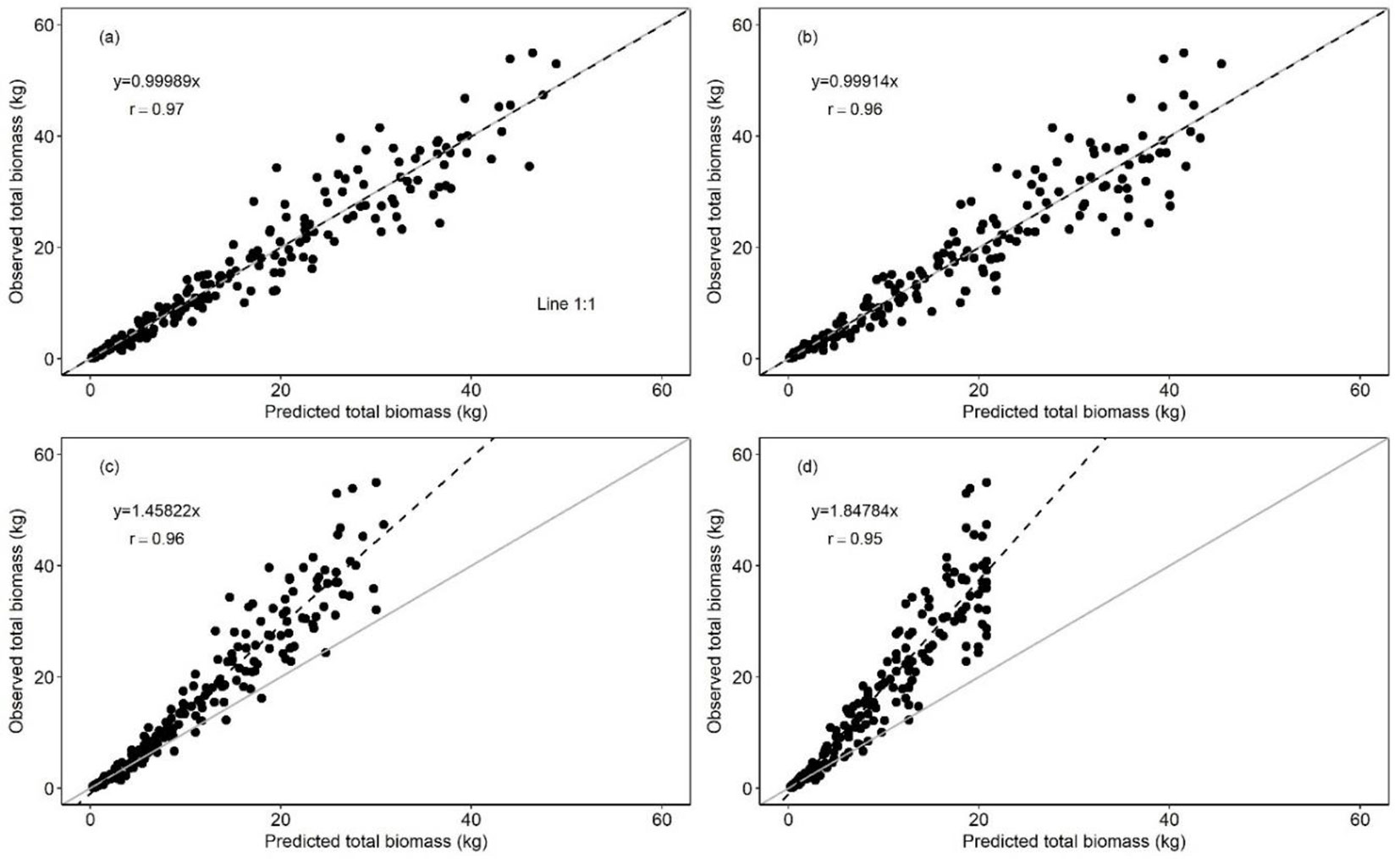
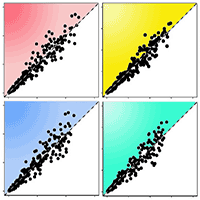
The biomass of structural components and total tree for multi-species calculated with models I and II of Tab. 1 showed good fit when compared to the biomass observed, since slope values (y) and correlation coefficient (r) being close to one (Fig. 2).
Fig. 2 - Relationship between observed and predicted biomass. Model I: total biomass (a), stem biomass (b), branch biomass (c), and foliage biomass (d). Model II: total biomass (e), stem biomass (f), branch biomass (g), and foliage biomass (h). The gray solid line represents the 1:1 ratio between the biomass values. The black dotted line represents the linear regression between observed and predicted biomass.
Both the RME% and bias (MAPE%) for estimating the biomass by structural component (i.e. stem, branches and foliage) was conservative between model I and II (Tab. 2). However, there were statistical differences in branch (p ≤ 0.01) and foliage biomass (p ≤ 0.01) obtained with the two models (Tab. 2).
Tab. 2 - Comparison of the relative mean error (RME, %) and bias (MAPE, %) of biomass estimations by structural component and total tree among multi-species equations (derived from models I and model II), Hughes et al. ([26]) and Chave et al. ([9]) equations. Different letters indicate significant statistical differences (p < 0.05) between structural components after Duncan’s multiple range test (± standard error).
| Parms | Structural component |
Model I | Model II | Hughes et al. | Chave et al. |
|---|---|---|---|---|---|
| RME | Stem | -0.20 ± 1.57 a | -0.02 ± 1.65 a | - | - |
| Branch | -0.41 ± 2.56 a | 0.14 ± 2.78 b | - | - | |
| Foliage | 0.93 ± 4.86 a | 2.41 ± 6.18 b | - | - | |
| Total-tree | -0.36 ± 2.08 a | 0.05 ± 1.92 a | -44.51 ± 0.92 b | -30.36 ± 1.21 c | |
| MAPE | Stem | 0.08 ± 0.06 a | 0.008 ± 0.05 a | - | - |
| Branch | 0.15 ± 0.10 a | 0.05 ± 0.09 a | - | - | |
| Foliage | 0.32 ± 0.18 a | 0.84 ± 0.17 a | - | - | |
| Total-tree | 0.13 ± 0.07 a | 0.01 ± 0.07 a | 15.57 ± 0.04 b | 10.63 ± 0.05 c |
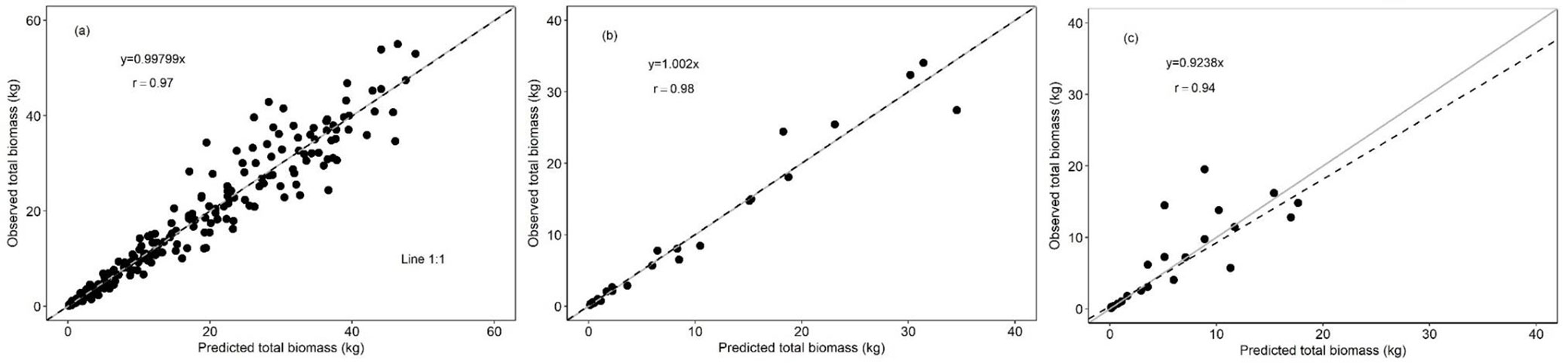
Total tree biomass estimated with multi-species equations of Tab. 1 showed high correlation with the biomass observed, as indicated by the slope of the linear regression (Fig. 3a, Fig. 3b). When comparing the performance of these equations with those developed by Hughes et al. ([26]) in central-east Mexico and Chave et al. ([9]), biomass appears to be consistently underestimated by these older equations (Fig. 3c, Fig. 3d). Furthermore, these older equations cannot accurately estimate the biomass of trees > 5 cm DBH or greater than 20 and 30 kg of dry weight (Fig. 3c, Fig. 3d).
Fig. 3 - Comparison between observed total tree and predicted total tree biomass. (a): Model I; (b): model II; (c): Chave et al. ([9]); (d): Hughes et al. ([26]). The gray solid line represents the 1:1 ratio between biomass values. The black dotted line represents the linear regression between observed and predicted biomass.
Model I and II showed less error and bias in the estimation of total tree biomass compared to the Hughes et al. ([26]) and Chave et al. ([9]) equations (Tab. 2). Particularly, the equations developed by Hughes et al. ([26]) and Chave et al. ([9]) underestimated total tree biomass by 44.51% and 30.36%, respectively, on average (Tab. 2). Also, the values of the estimation error of multi-species equations in this study with respect to Hughes et al. ([26]) and Chave et al. ([9]) equations showed significant statistical differences (p ≤ 0.0001 - Tab. 2).
Equation by wood density groups
The distribution of residuals and models goodness-of-fit statistics for species with high and intermediate wood density improved with the weighting factor 1/DBH2H. The equations fit by wood density groups (Tab. 3) accounted for 96% to 97% of the total variance in total tree biomass. The effect of estimated coefficient β1, representing the influence of the three variables ρ, DBH and H on total biomass, was highly significant (p < 0.0001). As a result, the exponential and linear relationships of the combined variable ρDBHH proved to be good predictors of total tree biomass for species with high, intermediate and low wood density.
Tab. 3 - Allometric equations for total tree biomass estimation for tree species with high, intermediate and low wood density. (n): sample size (number of trees); (AGB): total tree estimated above-ground biomass (kg); (ρ): wood density (g cm-3); (DBH): diameter at breast height (cm); (H): total tree height (m); (RMSE): root mean square error of the estimate; (adj-R2): proportion of variance explained by the model. A correction factor (CF) of 1.05 was used to reduce the bias of log-transformation for the biomass equation for low wood density species.
| No | Wood density group |
n | Equation | RMSE | adj-R2 |
|---|---|---|---|---|---|
| 1 | High | 234 | AGBtotal-tree=0.077022(ρ·DBH2·H)0.947669 | 0.1421 | 0.96 |
| 2 | Intermediate | 21 | AGBtotal-tree=0.079603(ρ·DBH2·H)0.962061 | 1.0873 | 0.97 |
| 3 | Low | 20 | AGBtotal-tree=0.0814549(ρ·DBH2·H)0.971735 | 0.3083 | 0.97 |
Results of the linear regression analysis also showed the existence of a stronger association between the biomass estimated for species with high and intermediate wood density than for species with low wood density (Fig. 4a, Fig. 4c).
Fig. 4 - Comparison between observed versus estimated total tree biomass by wood density groups. High (a) intermediate (b) and low (c). The gray solid line represents the 1:1 ratio between the biomass values. The black dotted line represents the linear regression between observed and predicted biomass.
Furthermore, the equations fit by wood density group estimated total tree biomass with a smaller error and bias (Tab. 4) than the equations obtained by Van Breugel et al. ([52]) for tropical forests of Panama, and by Djomo et al. ([15]). Significant statistical differences were obtained for the error and bias between model I and Djomo et al. ([15]) for estimating biomass by wood density group: high, p ≤ 0.0001; intermediate, p ≤ 0.01; low, p ≤ 0.003.
Tab. 4 - Comparison of the relative mean error (EMR, %) and bias (MAPE, %) of total tree biomass estimated with equations fit by wood density groups (this study) and foreign equations. Different letters indicate significant statistical differences (p < 0.05) between structural components, result of Duncan’s multiple range test (± standard error).
| Parms | Model | High | Intermediate | Low |
|---|---|---|---|---|
| EMR | This study | -0.34 ± 0.99 a | -0.65 ± 4.74 a | 2.66 ± 15.97 a |
| Djomo et al. ([15]) | -98.70 ± 0.05 c | -98.31 ± 0.14 c | -97.45 ± 0.05 b | |
| Van Breugel et al. ([52]) | -1.23 ± 1.34 a | -10.15 ± 3.19 ad | -14.38 ± 5.23 ac | |
| MAPE | This study | 0.03 ± 0.02 a | 9.50 ± 0.01 b | 0.11 ± 0.03 a |
| Djomo et al. ([15]) | 0.31 ± 0.42 a | 34.14 ± 0.34 b | 3.53 ± 0.28 a | |
| Van Breugel et al. ([52]) | 0.14 ± 1.98 a | 35.58 ± 1.03 b | 5.57 ± 0.83 a |
Comparing predicting ability of equations
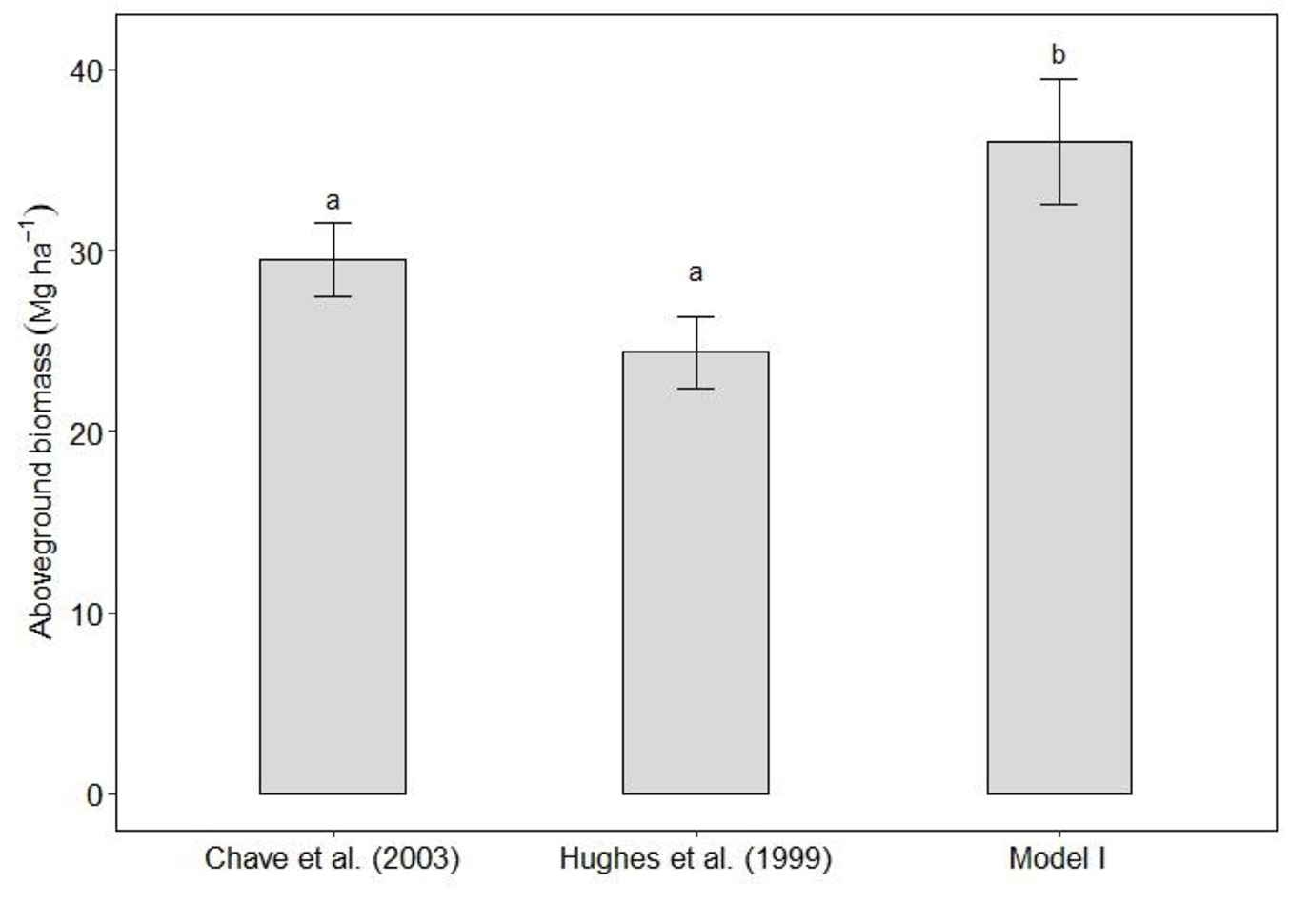
Based on inventory data, the biomass average of trees with DBH >10 cm was 128.97 ± 14.46 Mg ha-1. Small trees (2.5-10 cm in DBH) biomass estimated with Model I was greater (p < 0.05) than the biomass estimated with Hughes et al. ([26]) and Chave et al. ([9]) equations (Fig. 5). Particularly, using Model I the small trees averaged 35.97 ± 3.47 Mg ha-1 biomass and accounted for 21.8% of total stand biomass. Hughes et al. ([26]) equation estimated 24.38 ± 2.07 Mg ha-1 biomass, and this value represented 15.9% of the total biomass. Chave et al. ([9]) equation showed that biomass accumulated in small trees was 29.51 Mg ha-1, which accounted for 18.62% of the total biomass. The biomass estimates using the equations by Hughes et al. ([26]) and Chave et al. ([9]) were similar.
Discussion
We developed allometric equations to estimate total above-ground biomass of small trees in tropical forests of the Yucatan peninsula, by structural components (i.e., stem, branches, foliage), and for groups of species with differences in wood density (i.e., high, intermediate and low). Models that only considered DBH had the largest estimation errors, while equations that included total height and wood density, in addition to DBH, significantly improved goodness of fit and reduced the estimation error (Tab. S5 in Supplementray material), which supports our hypothesis I. This is consistent with other studies of tropical forests in Asia, Africa and at global scale, which documented a better fit for models including such variables when compared with models that did not ([15], [39]). Total height and wood density influence the variability of tree biomass because of their close correlation with structural tree characteristics and physiological and mechanical properties of woody species ([12]). According to Kenzo et al. ([30]), a careful selection of predictors of biomass is required for tropical forests to improve model accuracy and goodness of fit. However, many statistical models use DBH as the only independent variable as biomass predictor, whereas other models use only DBH and wood density ([39]) and exclude total height because it is difficult to be measured in the field ([15], [27]). Nevertheless, it is highly recommended to include both total height and wood density in allometric equations because they might help lower errors in model fitting ([10], [21]), as observed in this study.
Estimation of biomass by structural components
The use of NSUR to fit models by tree structural component (i.e., stem, branches, and foliage - Tab. 1) improved model accuracy for small trees as the method guarantees that total tree biomass is the result of summing up the biomass of each component. Besides, the simultaneous estimation method produced a better fit when considering the total variability of the biomass of the three structural components. A number of authors have also reported similar results for tropical and temperate forests, since the method helps to minimize the sum of residuals and generates more consistent coefficients of biomass components and total biomass, guaranteeing additivity ([49], [56]). In this study, the simultaneous fit method produced a better fit when considering the total variability of the biomass of the three structural components, which concurred with similar studies using the additivity method to fit biomass equations simultaneously ([41], [49]).
Model I showed a lower relative mean error for stem (-0.03%), branch (-2.5%) and foliage (-0.17%) biomass than model II (Tab. 2). Previous studies in forests of Africa, Asia and Mexico reported bigger errors in biomass estimation for tree structural components (stem: ~ 4.06%; branches: 1.5% up to 58.2%; foliage: 8.6% to 15.8%) when wood density was not included as predictor ([15], [32], [16]). Since tree crown architecture differs among tropical species ([31], [20]), we assumed that the sample size (i.e., trees harvested) was large enough to obtain a good model fit, thereby these models better explain the variability of the branches and foliage biomass. In addition, the inclusion of total height and wood density in the models improved biomass estimations, because they better reflect the allometry (i.e., growth) and crown architecture of tree species ([3], [40]). Thus, there is a strong relationship between total height and wood density with the biomass of branch and foliage. Many studies indicate that species, forest structure and site quality can also affect the variation in biomass of tree components ([38], [53]). We did not include these factors in our models, thus their effect could not be tested in this study. However, we emphasize that the models obtained in this study are efficient and statistically reliable to estimate the biomass of small trees.
Sources of error in total biomass estimation with multi-species equations
The inclusion of wood density in addition to DBH and total height in the multi-species models I and II improved total tree biomass predictions as showed by their lowest biomass estimation error (Tab. 2). In contrast, eqn. 10, which uses DBH as the only predictor of biomass, had on average 45% mean error in the total biomass estimation. The eqn. 11 improved the estimation of total tree biomass with the inclusion of wood density, though still showing a 30% relative mean error (Tab. 2).
The large error in the biomass estimated with eqn. 10 might be associated to the use of DBH as the only predictor, and to the sample size used (66 trees). Other studies, similar to the one presented here, showed that allometric models using DBH as the only predictor can underestimate total biomass by 4.6% or overestimate it by 4.0%, 5.9%, or up to 52% error on average ([15], [8], [13]). This can be explained mainly because DBH is insufficient to describe biomass relationships that are also determined by total height, wood density, crown diameter, or architectural type ([40], [17]).
Regarding the sample size, Van Breugel et al. ([52]) fitted two generic local models with 244 trees of 26 species in secondary forests, using only DBH in one model and DBH and wood density in the second model as predictors. When these authors used 80% (195 trees) and 20% (49 trees) of the total sampled trees, the relative mean error increased from 4% to 21%. In our study, we did not split the sample to evaluate models’ performance, but about 0.5% error was obtained when using 311 trees. Therefore, the development of models for multi-species using only DBH as the main predictor - such as those by Hughes et al. ([26]), and Chave et al. ([9]) equations - requires a larger sample size than a model including both DBH and wood density, since model parameters are systematically sensitive to small sample sizes ([52], [17]).
The eqn. 11 ([9]) was developed to analyze moist tropical forests in Panama, using DBH and wood density as predictors of biomass. However, the wood density used in the above model was the average value calculated over 123 species, corresponding to 0.54 g cm-3. In contrast, we used wood density values for each species obtained from samples measured in the field. We considered that environmental conditions, sample size and the predictors used in eqn. 10 and eqn. 11 might be the main factors leading to the larger error observed when the above models were tested on our datasets.
In general, generic equations developed for a different region and applied at the local level, give results similar to those obtained in this study. For example, Ketterings et al. ([31]) generated equations for specific sites with trees 5 to 50 cm in DBH (overall 29 trees) in secondary forests of Sumatra. Further, they contrasted the performance of their equations (which included wood density and DBH as predictors) with those developed at global scale using data collected in a wide range of tropical conditions and neotropical vegetation types, resulting in a reduction by 35%-51% of the error for total biomass estimates. Likewise, when the model fitted by Brown ([6]) was used for Sumatra’s tree data, biomass estimations were higher than the total biomass observed. In Brazilian forests, 10.6% and 14.8% mean estimation errors were obtained with the pan-tropical equations by Brown ([6]) and Chave et al. ([10]), whereas the local models showed a 5.63% mean estimation error ([34]). In southeast Asian forests, a mean error of 19.8% was obtained locally, but when regional and global scale equations were used the average error increased from 29.2% up to 38.4%, respectively ([39]). These findings support the hypothesis that local equations can estimate biomass more precisely than foreign equations, as the latters hardly reflect the allometric relationships of local species.
Ketterings et al. ([31]) and Mugasha et al. ([38]) pointed out that large errors in biomass estimations are mainly due to: (i) the relatively small sample size used to fit the equations, which implies that equation parameters are not adequate for other sites with high tree densities and variety of species different to the range of tree diameters used in the fitting process; (ii) the predictors are not adequate and sufficient to explain the relationship with total biomass (in this case, only DBH); (iii) wood density can affect the equation coefficients since it is influenced by site characteristics (i.e., soil, precipitation, species mixture, among other factors), i.e., parameter values could not be appropriate for sites where no estimations are available.
Equations by wood density groups
Biomass models for wood density groups are not common for tropical regions and particularly for the Yucatan peninsula. In this study, we developed three biomass equations for species with high (0.61-0.80 g cm-3), intermediate (0.42-0.52 g cm-3) and low (0.25-0.29 g cm-3) wood density (Tab. 3). The exponential and linear models provided the best fit and performance in estimating total tree biomass of species grouped by wood density. RMSE values obtained using the above models ranged from 0.0873 to 0.3083, which are similar to the RMSE (0.287 to 0.548) reported for Vietnam forests and for a global scale using exponential and linear models on species with wood density ranging from 0.50 to 0.83 g cm-3 ([13], [39]). In this study, the higher model accuracy was obtained for species showing high wood density, followed by species with intermediate wood density, whereas larger errors were observed for low wood density species. In this last group, we believe that the small sample size (only two species with a total of 25 trees) was not sufficient to obtain reliable equations. Nam et al. ([39]) suggested that it is important to sample tree species covering the whole range of wood densities where different species coexist, in order to develop reliable allometric equations. In this study, greater accuracy in biomass predictions was observed for species with high wood density, due perhaps to the large sample size (18 of the 22 species analyzed were included in this group). Indeed, it is likely that the 18 species fully reflected the large variability of species with high wood density in the studied secondary forest.
The pan-tropical model by Djomo et al. ([15] - eqn. 12) underestimated the total biomass for species with high, intermediate and low wood density 98% of the time (Tab. 4) and no significant differences in biomass estimation among wood density groups were observed. Such model was developed with trees ranging from 1 to 138 cm in DBH and 0.25-0.57 g cm-3 in wood density, collected from different tropical regions of the world. Therefore, this model was not appropriate to accurately estimate the biomass of small trees (≤ 10 cm DBH) in this study.
The model by Van Breugel et al. ([52] - eqn. 13) was developed for 26 species and 244 trees from 3 to 29 cm in DBH; trees were harvested in secondary forests of 1 to 25 years-old, and in stands younger than 40 years-old, within forests located between agricultural fields and grasslands; wood density of the species included in the present study averaged 0.49 g cm-3. This model was mostly generated for soft and intermediate wood density tree species (almost 80% of the species harvested). In contrast, we harvested more trees from species with high wood density (mean wood density was 0.64 g cm-3) mainly located in secondary forests with a relative good conservation status and a history of moderate land use (between one and two years of agricultural use). Differences in environmental patterns, forest type, species biometric characteristics and wood density values of species evaluated by Van Breugel et al. ([52]) and those obtained in this study likely had a large influence on models’ performance. The large bias in biomass estimations observed in this study using models generated for other regions, confirmed that the use of such models intended to be applied in those areas, is actually a significant source of uncertainty in estimating local biomass and carbon stocks.
Comparing the predictive ability of equations
We observed that model I had the best accuracy in estimating the contribution of small trees to total biomass (Fig. 5). In contrast, eqn. 10 (which is widely used to estimate small tree biomass in the Yucatan peninsula) gave lower biomass estimates compared with eqn. 11. We observed that between 6.5 and 11.59 Mg ha-1 biomass could be excluded when eqn. 10 and 11 are used, respectively. The lower performance of the former equation can be attributed to the fact that total height and wood density values are not included as predictors in the model. Also, we noticed that eqn. 10 underestimated (around 45%) the total biomass of trees higher than 20 kg (trees > 5 cm in DBH). Therefore, we assumed that the number of trees of 5 to 10 cm DBH that were harvested for this study was not representative, which could have also contributed to the low model performance. Our results demonstrated that using eqn. 10 an important bias is introduced in biomass estimations for the Yucatan peninsula forests, which supports our second hypothesis. Furthermore, this model may underestimate the variability of carbon stocks at landscape level, in particular for young secondary forests where small trees dominate.
Conclusions
We developed allometric equations to estimate biomass by tree component (stem, branch, and foliage), and total tree biomass for 22 small-size (≤ 10 cm DBH) tree species in secondary forests of the Yucatan peninsula, Mexico. We confirmed the hypothesis that the inclusion of total height and wood density in allometric models improve equations fit and biomass estimation compared with models including a single predictor variable such as DBH.
The equations used in this study yielded more accurate biomass estimations than those developed for other tropical regions. These results support the hypothesis that local equations can better explain the biomass variability in a region when both total height and wood density are included in the fitting process, since these parameters are highly correlated with growth type and wood physical properties of trees.
The equations developed in this study can be conveniently used to reduce uncertainty in biomass and carbon stocks estimations in secondary forests of the Yucatan peninsula, where a large proportion of the community is composed by small-size trees and the sites are constantly affected by natural and anthropogenic disturbances. Managing tropical secondary forests for climate change mitigation requires the estimation of biomass/carbon stocks with a low level of uncertainty; therefore, these equations can be a useful tool in the context of climate change within the projects implemented by REDD+ in Mexico, and similar regions in developing countries.
Acknowledgements
This study was financially supported by the Sustainable Landscapes Program of the Agency for International Development of the United States of America, through the USDA Forest Service International Programs Office and the Northern Research Station (Agreement No. 12-IJ-11242306-033).
References
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Gregorio Ángeles-Pérez 0000-0002-9550-2825
José René Valdéz-Lazalde 0000-0003-1888-6914
Valentín José Reyes-Hernández 0000-0002-1804-412X
Paulino Pérez-Rodríguez 0000-0002-3202-1784
Colegio de Postgraduados, Km. 36.5 Carr. Mexico-Texcoco, Montecillo, Texcoco, C.P. 56230 (México)
Recursos Naturales, Centro de Investigación Científica de Yucatán (CICY), Calle 43 No. 130, Colonia Chuburná de Hidalgo, C.P. 97200, Mérida, Yucatán (México)
Department of Geography, Rutgers University, 54 Joyce Kilmer Avenue, Piscataway, NJ 08854 (USA)
Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias, Campo Experimental Chetumal, Km. 25, Carretera Chetumal-Bacalar, C.P. 77930, Xul-ha, Quintana Roo (México)
Corresponding author
Paper Info
Citation
Puc-Kauil R, Ángeles-Pérez G, Valdéz-Lazalde JR, Reyes-Hernández VJ, Dupuy-Rada JM, Schneider L, Pérez-Rodríguez P, García-Cuevas X (2020). Allometric equations to estimate above-ground biomass of small-diameter mixed tree species in secondary tropical forests. iForest 13: 165-174. - doi: 10.3832/ifor3167-013
Academic Editor
Rodolfo Picchio
Paper history
Received: Jun 12, 2019
Accepted: Feb 13, 2020
First online: May 02, 2020
Publication Date: Jun 30, 2020
Publication Time: 2.63 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2020
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 56202
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 45568
Abstract Page Views: 6472
PDF Downloads: 3454
Citation/Reference Downloads: 17
XML Downloads: 691
Web Metrics
Days since publication: 2049
Overall contacts: 56202
Avg. contacts per week: 192.00
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2020): 4
Average cites per year: 0.67
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Allometric equations to assess biomass, carbon and nitrogen content of black pine and red pine trees in southern Korea
vol. 10, pp. 483-490 (online: 12 April 2017)
Research Articles
Allometric relationships for volume and biomass for stone pine (Pinus pinea L.) in Italian coastal stands
vol. 6, pp. 331-335 (online: 29 August 2013)
Research Articles
Effects of planting density on the distribution of biomass in a douglas-fir plantation in southern Italy
vol. 8, pp. 368-376 (online: 09 September 2014)
Research Articles
Tree growth, wood and bark water content of 28 Amazonian tree species in response to variations in rainfall and wood density
vol. 9, pp. 445-451 (online: 16 January 2016)
Research Articles
Estimation of fuel loads and carbon stocks of forest floor in endemic Dalmatian black pine forests
vol. 13, pp. 382-388 (online: 01 September 2020)
Research Articles
Tree biomass and carbon density estimation in the tropical dry forest of Southern Western Ghats, India
vol. 11, pp. 534-541 (online: 01 August 2018)
Technical Reports
Biomass equations for European beech growing on dry sites
vol. 9, pp. 751-757 (online: 17 June 2016)
Research Articles
Aboveground tree biomass of Araucaria araucana in southern Chile: measurements and multi-objective optimization of biomass models
vol. 14, pp. 61-70 (online: 09 February 2021)
Research Articles
Equations for estimating belowground biomass of Silver Birch, Oak and Scots Pine in Germany
vol. 12, pp. 166-172 (online: 15 March 2019)
Research Articles
Allometric models for estimating biomass, carbon and nutrient stock in the Sal zone of Bangladesh
vol. 12, pp. 69-75 (online: 24 January 2019)
iForest Database Search
Google Scholar Search
Citing Articles
Search By Author
- R Puc-Kauil
- G Ángeles-Pérez
- JR Valdéz-Lazalde
- VJ Reyes-Hernández
- JM Dupuy-Rada
- L Schneider
- P Pérez-Rodríguez
- X García-Cuevas
Search By Keywords