The influence of age and crown position on growth efficiency along a Scots pine chronosequence
iForest - Biogeosciences and Forestry, Volume 12, Issue 5, Pages 474-479 (2019)
doi: https://doi.org/10.3832/ifor2953-012
Published: Oct 14, 2019 - Copyright © 2019 SISEF
Research Articles
Abstract
The study deals with the effects of age and crown position (either dominant or intermediate, as determined by Kraft’s social class) on stemwood growth efficiency (GE), which is viewed as the ratio of annual stemwood volume increment of the previous five years to needle volume of the entire tree, in eight even-aged pure stands of Scots pine (Pinus sylvestris L.). The highest GE was observed in the youngest stands, and the lowest in the oldest ones. There was no clear interdependence of GE on the age of intermediate stands. GE was most variable in the youngest, the 25-year-old stand, and was the least variable in the 74-year-old stand. GE in dominant trees was lower in 25- 74- and 85-year-old stands and higher in 33-, 44-, 56-, 64- and 93-year-old stands. The GE ratios of dominant trees to intermediate trees in 25-, 33-, 44-, 56-, 64-, 74-, 85- and 93-year-old stands were 0.47:1, 1:0.93, 1:0.87, 1:0.81, 1:0.86, 0.88:1, 0.90:1 and 1:0.61, respectively. Tree age had a statistically significant effect on GE; however, the contribution of the age factor to GE was assessed as weak. Generally, the position of trees (whether dominant or intermediate) had no effect on GE, while age × position of trees had a statistically significant effect on GE, which means that the two factors interacted. The correlation between GE and tree height, diameter at breast height (DBH), and the needle volume of the entire empirical material was statistically significant with a negative sign; however, the situation varied among the particular stands.
Keywords
Pine, Needle Volume, Growth Efficiency, Dominant Trees, Intermediate Trees
Introduction
The growth of forests is a function of resource supply, the proportion of resources used by trees, and the efficiency with which the resources are used for carbon dioxide fixation. Growth efficiency (GE) estimated as the ratio between biomass production and resource supply is an indicator of forest productivity. It can be determined as either gross or net primary production. Gross primary production refers to the total biomass produced at a certain time and area. Net primary production is defined as the biomass that remains after the elimination of respiration losses. Light, water or nutrient supply can be used as a denominator. Light (or proxies for light) was found to be most closely related to wood production, as it is the main driver for photosynthesis ([24]). The production of wood depends on the absorption of light, and the efficiency with which it is used. Larger trees absorb more light and use it more efficiently ([4]). Their greater growth results from a combination of increased light absorption and increased efficiency.
The GE index may be determined in various ways depending on the available volume increments and the measured elements of the crown. Dengler ([10]) defined it as the ratio of increment in stem volume to dry needle mass. Schmidt ([33]) defined it as the mass of annual increment in the absolute dry matter of wood per unit of dry needle mass. Mayer ([22]) introduced the concept of assimilation intensity or assimilation energy, defined on the basis of annual increment in tree volume per unit area of crown projection or crown mantle. A similar approach was adopted by Borowski ([5]). Lemke ([16]) proposed determining the GE in Scots pine (Pinus sylvestis L.) as the ratio of increment in stem volume to volume of leafy twigs. Waring et al. ([42]) calculated GE from the ratio of stemwood volume increment (vi, dm3) to projected leaf area. The index proposed by Waring et al. ([42]) is the one most commonly used nowadays.
There are three relationship patterns between growth efficiency (GE) and projected leaf area (LA): monotonic increasing, peaking, or monotonic decreasing. All of them arise from a strong relationship between the increment of stemwood volume and the area of projected leaves. The graphs display concave, sigmoid or convex shapes ([35]). Interestingly, the monotonically decreasing GE pattern appears to gather strong empirical support ([30], [13], [19]).
The variation in GE is relatively well scrutinized among the even-aged stands of a single species. However, it is less evident in cases of varied structural characteristics, i.e., a history of past suppression ([19]) or specific forest management ([41], [40]), site quality, stand structure, canopy strata, age and tree size or crown class ([25], [26], [18], [29], [13], [38], [35], [7], [27], [2]), as well as shade tolerance ([30], [12]).
The aim of this study was to investigate the effects of age and different positions of the crown (dominant or intermediate, as determined by Kraft’s social class) on growth efficiency in eight even-aged and pure stands of Scots pine (P. sylvestis) which grew in one location in western Poland. The study evaluates differences in productivity potential in the naturally variable P. sylvestris chronosequence.
Owing to concerns expressed by Waring et al. ([42]) about their own GE index, which proved to be inconsistent with suppressed trees and may be sensitive to environment and the influence of competition, GE in this study was calculated following the model of Lemke ([16]) with modification introduced by the authors. The GE used in the study is viewed as a ratio of annual increment in stemwood volume of the last five years to volume of twigs with needles which come from the entire tree. A similar approach has recently been proposed by Burkes et al. ([7]), who calculated growth efficiency as an annual increment in stemwood volume to needle biomass. Therefore, the following two hypotheses were considered: (i) both tree age and biosocial position are factors which influence growth efficiency; and what is more (ii) growth efficiency depends on the size of the tree (breast height and height) and the volume of needles.
Material and methods
The empirical material was comprised of measurements taken from 200 sample trees, which were selected from among eight Scots pine stands, according to the Draudt scheme.
Study site
The sampling process was carried out in eight pure stands of the Scots pine (P. sylvestis) growing in a fresh mixed forest, close to Murowana Goslina (52° 34′ N, 17° 00′ E) in western Poland. The stands were even-aged (25-, 33-, 44-, 56-, 64- 74-, 85- and 93-years-old) and were characterized by irregular canopies. In each stand one plot with 200-350 trees was chosen. The reasoning behind choosing the particular plot locations in each stand was in order to minimize the non-age-related differences between the trees. All plots created a trajectory of changes resulting from the chronosequence. The volume-based stand density was 0.81-1.23 and the number of trees per hectare was 402-2927 (Tab. 1). The average temperature in the five years prior to the study was 8.02 °C, with average annual rainfall at 544.2 mm.
Tab. 1 - Structural characteristics of stands and sample trees. (Dg): mean diameter at breast height; (H): mean stand height; (d1.3): diameter at breast height; (h): tree height; (vn): needle volume of the whole tree; (iv1): mean annual stemwood volume increment in the previous 5 years; (CV): coefficient of variation.
| Stand | Sample trees | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age (yrs) |
Density | Trees ha-1 |
Dg (cm) |
H (m) |
d1.3 (cm) | h (m) | vn (m3) | iv1 (m3) | Number of sample trees | |||||
| Mean | CV (%) |
Mean | CV (%) |
Mean | CV (%) |
Mean | CV (%) |
Dominant trees |
Intermediate trees |
|||||
| 25 | 1.17 | 2590 | 13.4 | 15.49 | 12.9 | 24.4 | 13.4 | 9 | 0.0094 | 100.1 | 0.0067 | 71.8 | 19 | 6 |
| 33 | 1.2 | 2927 | 13.7 | 16 | 12.2 | 29.5 | 14.6 | 7.9 | 0.0082 | 77.5 | 0.0055 | 83.3 | 17 | 8 |
| 44 | 1.23 | 1225 | 20.4 | 21.23 | 19 | 22.4 | 20.4 | 7.1 | 0.0151 | 69.8 | 0.0138 | 64.1 | 18 | 7 |
| 56 | 1.1 | 1160 | 20 | 21.65 | 17.8 | 25.7 | 20 | 8.9 | 0.0139 | 73.7 | 0.0119 | 73 | 17 | 8 |
| 64 | 0.94 | 766 | 23.7 | 24.74 | 21.9 | 21.7 | 23.2 | 8 | 0.0204 | 62 | 0.0155 | 66.9 | 17 | 8 |
| 74 | 0.81 | 537 | 25.5 | 24.46 | 24.8 | 21.3 | 23.4 | 7 | 0.0197 | 64.2 | 0.0156 | 57.2 | 19 | 6 |
| 85 | 0.88 | 419 | 30.8 | 28.32 | 30.2 | 17.9 | 26.8 | 6.3 | 0.0293 | 54.9 | 0.0234 | 51.3 | 20 | 5 |
| 93 | 0.91 | 402 | 31.4 | 26.12 | 29.4 | 17.6 | 25.6 | 5.9 | 0.0334 | 53.5 | 0.0162 | 59.2 | 19 | 6 |
Sample tree selection
All trees in each plot were numbered. The height (h, m) and diameter at breast height (d1.3, cm) of each of the standing trees was determined. The mean stand height (H, m) was calculated following Lorey’s model. The mean diameter at breast height (Dg, cm) of the stand was calculated as DBH of the tree with mean basal area. In each plot, 25 sample trees (200 in total, from all of the eight stands) were selected according to the Draudt method.
Measurements on the sample trees
The social position of each tree within the stand was assessed according to Kraft’s classification. The sample trees were felled and divided into one-meter-long sections. Stemwood discs which were 5-cm thick were cut at the heights of 0.0, 0.5, 1.3 (breast height), 1.5, 2.5 m, and upwards to the top. All twigs with needles were trimmed from the crown of each tree, and their mass (M, kg) was determined immediately afterwards. The samples of fresh twigs with needles were collected for laboratory analyses; 20% of twigs were collected for laboratory analyses from the trees aged between 25 and 56 years, whereas in the group aged 64-93 years only 10% of twigs were collected. The sample mass of twigs with needles (Ms, kg) was not lower than 2 kg and its weight depended on the stand’s age.
Laboratory procedure
Stemwood discs were used to estimate the stemwood volume and to calculate the mean annual stemwood volume increment in the previous five years (iv1, m3). The twig samples with needles were used to estimate the volume of needles from one tree (vi, m3). Next, the needles were separated from the twigs and then the total volume of needles in each sample was measured by means of xylometry, and this was used to determine the volume of needles of the entire tree (vn, m3) according to the formula (eqn. 1):
GE was estimated from the ratio of annual stemwood volume increment in the previous five years (iv1) to needle volume of the entire tree (vn). GE indicates the volume of stemwood produced within one year per needle volume of the entire tree.
Statistical analysis
The GE of each of 200 sampled trees allowed the calculation of the arithmetic means and coefficients of variation (CV) for each of the eight examined stands. Both measures were calculated for dominant (Kraft’s classes 1, 2, 3) and intermediate trees (Kraft’s classes 4, 5). The assumptions of normality and the equal variance of GE were assessed using the Shapiro-Wilk test in order to adopt the appropriate tests and procedures necessary for further analysis. The relationship between GE and height (h), diameter at breast height (d), and needle volume of the trees (vn) in each stand was assessed using the Pearson’s correlation coefficient. The differences in GE between the eight stands and the contribution of the independent variables (age, dominant or intermediate trees, age × dominant or intermediate trees) to GE were analyzed using a two-way ANOVA. The significance of the difference between GE in the eight stands was calculated using the non-parametric Kruskal-Wallis test. The computed probability level for this test was <0.0001. The extent of the influence of age and position on growth efficiency was analyzed with coefficients η2 and ω2 ([36]). η2 is the proportion of variance associated with one or more main effects, errors or interactions in ANOVA, while ω2 is a measure of effect size, or the degree of association for a population.
Results
The structural characteristics of each stand (density, number of trees per hectare, average diameter at breast height and mean stand height) and of the sample trees are presented in Tab. 1. In the sample trees: (i) diameter at breast height (d1.3) and the tree height (h) were smallest in, respectively, the 33- and 25-year-old stands (12.2 cm and 13.4 m) and they increased with age (30.2 cm and 26.8 m in the 85-year-old stand); (ii) needle volume (vn) and annual stemwood volume increment (iv1) were lowest in the 33-year-old stand (0.0082 m3 and 0.0055 m3, respectively) and highest in the 85- and 93-year-old stands (0.0293 m3 and 0.0334 m3, and 0.0162 m3 and 0.0234 m3); (iii) trees with a dominant crown position accounted for 68% in the 33-, 56- and 64-year-old stands and up to 80% in the 85-year-old stand. The smallest variation was observed in the tree diameter at breast height (17.6-29.5%) and the tree height (5.9-9.0%). A much greater variation occurred in the needle volume (53.5-100.1%) and the annual stemwood volume increment (51.3-83.3%). The variability of the individual characteristics was most noticeable in the two youngest stands, and smallest in the two oldest stands.
In the sample trees, GE was: (i) highest in the youngest, 25-year-old stand (0.9515) and smallest in the oldest, 93-year-old stand (0.4789 - Tab. 2); (ii) similar in the 56-, 74- and 85-year-old stands (0.8317-0.8478); (iii) variable between 33- and 85-year-old-stands; (iv) most variable (5.4-fold, CV = 57.6%) and least variable (1.8-fold, CV = 17.1%) in, respectively, the 25- and 74-year-old stands; (v) higher in dominant trees than in the intermediate trees of the 33-, 44-, 56-, 64- and 93-year-old stands (from 7.5 to 63%); (vi) lower in the dominant trees than in the intermediate trees of the 25-, 74- and 85-year-old stands (over twofold in the youngest stand). In the dominant trees, GE varied most in the 85-year-old stand (CV = 31.1%) and least in the 64-year-old stand (CV = 14.6%). In intermediate trees, GE was most variable in the 25-year-old stand (CV = 50.1%).
Tab. 2 - Growth efficiency (GE) of all sample trees and of dominant and intermediate trees.
| Age of stand (yrs) |
All sample trees | Dominant trees | Intermediate trees | Contribution of dominant trees (%) |
|||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Min | Max | CV (%) | Mean | CV (%) | Mean | CV (%) | ||
| 25 | 0.9515 | 0.4854 | 2.6286 | 57.6 | 0.7493 | 27.8 | 1.5919 | 50.1 | -53 |
| 33 | 0.6713 | 0.4912 | 0.888 | 19 | 0.6867 | 16.5 | 0.6386 | 24.8 | +7.5 |
| 44 | 0.9116 | 0.3292 | 1.3099 | 24.1 | 0.9444 | 18.4 | 0.8271 | 37.5 | +14 |
| 56 | 0.8478 | 0.4883 | 1.2347 | 21.2 | 0.9028 | 18.6 | 0.7308 | 21 | +23.5 |
| 64 | 0.7299 | 0.4432 | 0.952 | 17.9 | 0.7628 | 14.6 | 0.6599 | 22.6 | +15.5 |
| 74 | 0.8317 | 0.5473 | 1.06 | 17.1 | 0.8047 | 18.3 | 0.9174 | 9.4 | -12 |
| 85 | 0.8377 | 0.3508 | 1.3421 | 29 | 0.8193 | 31.1 | 0.9113 | 20.9 | -10 |
| 93 | 0.4789 | 0.2086 | 0.8701 | 33.7 | 0.5279 | 27.8 | 0.3239 | 29.5 | +63 |
The age of trees had a statistically significant effect on GE (FAge = MSAge / MSError = 18.024 (Tab. 3). The contribution of age to GE was 40.68% (see η2Age in Tab. 4). The sum of the partial variance ω2 was 49.17%.
Tab. 3 - Results of ANOVA tests for the effect of age and position on growth efficiency (GE). (df): degrees of freedom.
| Effect | SS | df | MS | F | p |
|---|---|---|---|---|---|
| Intercept | 98.81039 | 1 | 98.81039 | 2103.699 | <0.0001 |
| Age | 5.92625 | 7 | 0.84661 | 18.024 | <0.0001 |
| Dominant and intermediate trees | 0.09795 | 1 | 0.09795 | 2.085 | 0.1504 |
| Age × dominant and intermediate trees | 3.76578 | 7 | 0.53797 | 11.453 | <0.0001 |
| Error | 8.64245 | 184 | 0.04697 | - | - |
Tab. 4 - Contribution of age and position to growth efficiency (GE, %).
| Independent variable | η 2 | ω 2 |
|---|---|---|
| Age | 40.68 | 30.29 |
| Dominant and intermediate trees | 1.12 | 0.28 |
| Age × dominant and intermediate trees | 30.35 | 18.60 |
In comparison to the intermediate trees, GE in the dominant trees was lower in 25- 74- and 85-old stands (10-53%) and greater in 33- 44-, 56- 64- and 93-old-stands (7.5-63% - Tab. 2). The ratios of the GE of dominant trees to the GE of intermediate trees in 25-, 33-, 44-, 56-,64-, 74-, 85- and 93-year-old stands were 0.47:1, 1:0.93, 1:0.87, 1:0.81, 1:0.86, 0.88:1, 0.90:1, and 1:0.61. Generally, however, the position of trees (whether dominant or intermediate) had no significant effect on GE (p =0.1504, η2Dominant and intermediate trees = 1.12 - Tab. 3, Tab. 4).
Age × position of trees had a statistically significant effect on GE, which means that the two factors interacted (η2Age × dominant and intermediate trees = 30.35 - Tab. 4). The contribution of other factors (including any that were not part of this study) was 50.83% (Tab. 4).
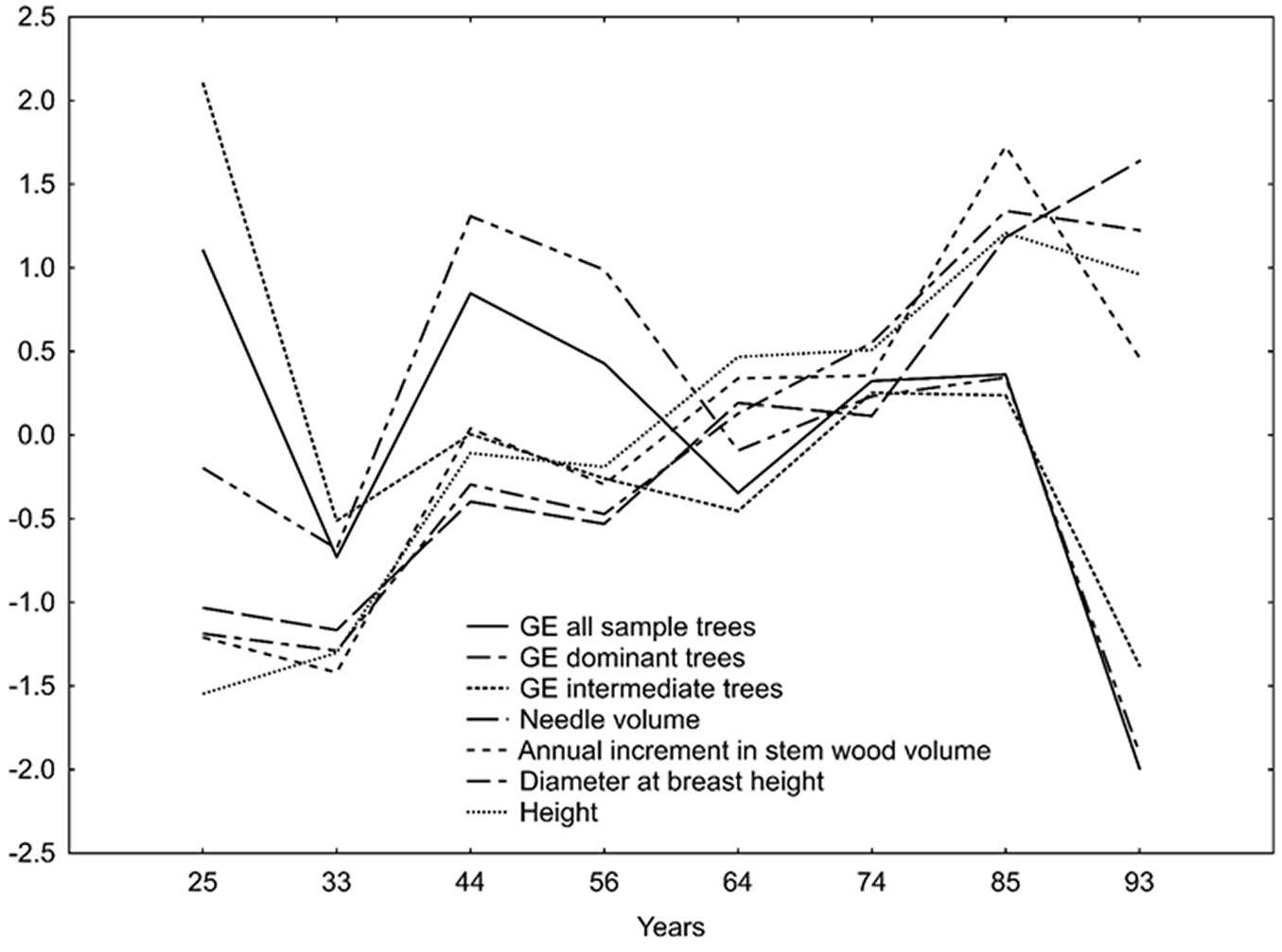
GE was negatively correlated with tree height, diameter at breast height, and needle volume at the ages of 25 and 74 (partly), and positively correlated at the ages of 44, 64, and 93 years (partly - Tab. 5). A long-lasting GE decline was, however, associated with the independent, possibly confounding, effects of a moderate but continuous increase in mean tree height, mean diameter at breast height, annual stemwood volume increment, and needle volume (Fig. 1).
Tab. 5 - Pearson’s correlation coefficients between growth efficiency (GE) and diameter at breast height (d1.3), tree height (h) and needle volume (vn). (*): p<0.05.
| Age of stand (years) | d 1.3 | h | v n |
|---|---|---|---|
| 25 | -0.528* | -0.505* | -0.460* |
| 33 | 0.180 | 0.234 | -0.023 |
| 44 | 0.283 | 0.526* | 0.014 |
| 56 | 0.350 | 0.388 | 0.064 |
| 64 | 0.451* | 0.477* | 0.401* |
| 74 | -0.295 | -0.166 | -0.484* |
| 85 | -0.131 | 0.005 | -0.321 |
| 93 | 0.430* | 0.548* | 0.095 |
| 25-93 (all sample trees) | -0.144* | -0.155* | -0.195* |
Fig. 1 - Growth efficiency (GE) in sample trees in association with mean height, mean diameter at breast height, annual stemwood volume increment and needle volume (standardized values - Statistica® ver. 13.1, Tulsa, OK, USA).
The Shapiro-Wilk test indicated that the GE of 25-year-old trees was not normally distributed. Thus, the non-parametric Kruskal-Walis test was used to compare the mean GE of the sample trees from the eight stands. The results showed that the GE of trees was not significantly different among the majority of stands. Multiple comparison analyses showed that the GE of trees in the 93-year-old stand differs significantly from all the others, except the 33-year-old one. Another significant difference occurs between 33- and 44-year-old trees; the differences in GE among trees of other ages were statistically insignificant (Tab. 6, Tab. 7).
Tab. 6 - Assessment of normality of distribution of growth efficiency using the Shapiro-Wilk test.
| Shapiro-Wilk test |
Stand (years) | |||||||
|---|---|---|---|---|---|---|---|---|
| 25 | 33 | 44 | 56 | 64 | 74 | 85 | 93 | |
| W | 0.70328 | 0.92582 | 0.97733 | 0.95761 | 0.96254 | 0.96259 | 0.97887 | 0.95334 |
| p-value | 0.00001 | 0.06964 | 0.82769 | 0.36887 | 0.46727 | 0.46838 | 0.86172 | 0.29774 |
Tab. 7 - Significance of differences in growth efficiency (GE) among the eight studied stands. Multiple comparisons p-values (Kruskal-Wallis test, 2-tailed) are shown. Independent (grouping) variable: Age (years); Kruskal-Wallis H[7, 200] = 63.82966, p <0.0001. (R): mean rank value.
| Stand Age (years) |
Stand Age (years) | |||||||
|---|---|---|---|---|---|---|---|---|
| 25 | 33 | 44 | 56 | 64 | 74 | 85 | 93 | |
| (R=108.76) | (R=71.920) | (R=138.04) | (R=122.00) | (R=91.520) | (R=122.76) | (R=118.48) | (R=30.520) | |
| 25 | - | 0.683929 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 0.000049 |
| 33 | 0.683929 | - | 0.001504 | 0.062156 | 1.000000 | 0.053180 | 0.124702 | 0.320371 |
| 44 | 1.000000 | 0.001504 | - | 1.000000 | 0.125662 | 1.000000 | 1.000000 | <0.000001 |
| 56 | 1.000000 | 0.062156 | 1.000000 | - | 1.000000 | 1.000000 | 1.000000 | 0.000001 |
| 64 | 1.000000 | 1.000000 | 0.125662 | 1.000000 | - | 1.000000 | 1.000000 | 0.005444 |
| 74 | 1.000000 | 0.053180 | 1.000000 | 1.000000 | 1.000000 | - | 1.000000 | <0.000001 |
| 85 | 1.000000 | 0.124702 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | - | 0.000002 |
| 93 | 0.000049 | 0.320371 | <0.000001 | 0.000001 | 0.005444 | <0.000001 | 0.000002 | - |
Discussion
The growth of individual forest trees declines with age and, furthermore, the decline stems from their reduced resource-use efficiency ([31]).
We observed that the GE of a P. sylvestris forest in even-aged plantations varied with age. Generally, in the long term, between the ages 25-93, there was a slow but continuous decline, with temporary fluctuations observed as the stand was aging. The highest GE value was observed relatively early, in the 25-year-olds. This was followed by a substantial aberration between 30- and 85-year-olds and a sudden decline afterwards (GE = 0.4789 at 93 years). The high GE in the youngest plantation resulted largely from the contribution of the intermediate trees.
Such or similar age-related GE patterns have also occurred in other coniferous and deciduous forests ([18], [14], [15], [31], [32]). P. sylvestris is the most widely distributed pine species in the world, found in many, ecologically diverse habitats, and has become very important commercially, socially and culturally. Only recently its growth has been studied by numerous authors ([39], [21], [28]).
Although the growth efficiency was calculated as a ratio of annual increment in the stemwood volume to the volume of needles, and not to the projected leaf area as proposed by Seymour & Kenefic ([35]), we still observed the monotonically decreasing pattern, which is the most common one. In Poland similar monotonically decreasing patterns of GE in P. sylvestris were earlier observed by Lemke ([17]). A similar pattern among Abies balsamea (L.) Mill., Picea rubens Sarg., Pinus contorta Dougl. ex Loud, and Pinus strobus L. was observed in Europe and the USA by Roberts et al. ([30]), Maguire et al. ([19]), and DeRose & Seymour ([11]).
We also analyzed fluctuations in GE in dominant vs. intermediate trees and the results were connected with age. A higher GE of dominant trees was observed in most stands and ages; however, it declined with age. The ratio of the GE of dominant trees to the GE of intermediate trees was only partly in agreement with Lemke’s estimates ([16]), who observed that in a 35-year-old stand of P. sylvestris the ratios of the GE of class 1 trees to the GE of class 2, 3, 4 and 5 trees were 1:1.18, 1:1.13, 1:0.94 and 1:0.67, and in a 50-year-old stand the ratios were 1:1.10, 1:1.02, 1:0.77 (with no class 5).
The fluctuations in age-related GE agree with the hypothesis put forward by Binkley ([3]), who observed regular and continuous changes in contribution of dominant and non-dominant trees to productivity of forest. In younger stands, prior to canopy closure, the dominance is usually low, and resource-use efficiency for all trees is high. In older stands near canopy closure, however, the increasing dominance reduced resource-use efficiency by non-dominant trees, which decreased forest productivity. Furthermore, in older stands the resource-use efficiency continuously declined in the largest trees and reduced the level of dominance. The growth dominance pattern has been observed in stands of native forest co-dominated by Pseudotsuga menziesii Carriere, Tsuga heterophylla (Raf.) Sarg. and Picea sitchensis (Bong.) Carr. ([3]), Pinus elliottii Engelm. and Pinus taeda L. ([20]), and Pinus resinosa Sol. ex Aiton ([6]).
An increasing GE in trees with more dominant crown classes of the same species has been observed by Waring et al. ([42]), O’Hara ([25]), and Sterba ([37]). However, Reid et al. ([27]) found an opposed pattern. The differences resulted from stand structure, ecological conditions, species-specific effects, methods used to evaluate tree increment and crown projection area, and variations in assimilation efficiency. The history of past suppression, planting density, canopy/strata class, age, size, availability of light, and tolerance to shade have significant effects on the crown leaf area, contributing to growth efficiency ([1], [34], [8], [26], [25], [19], [38], [35], [7], [27], [12]). It is vital to observe that (i) greater past suppression diminished growth efficiency in Picea rubens; (ii) shade significantly decreased (50%) growth efficiency in intermediate trees of Betula and Picea, compared to dominant trees growing under advantageous light conditions; (iii) low density of planting decreased growth efficiency in Pinus taeda and Pinus elliottii .
This study was conducted on sites which were considered as having a high productivity potential. A better site quality usually positively influences GE. The effect may, however, be species-specific; GE increased significantly in shade-intolerant Abies balsamea, moderately in shade-tolerant Abies lasiocarpa (Hook.) Nutt. and Picea engelmannii Parry ex Engelm., and was stable in shade-tolerant Picea rubens and shade-intolerant Pinus contorta ([23], [27], [35]). It is possible that the GE response depends on site quality. However, the reaction depends also on the species. DeRose & Seymour ([11]) observed that a higher site index caused an increase in growth efficiency in Abies balsamea, but not in Picea rubens.
Conclusion
The long-term productivity of P. sylvestris forest declines with age. The greatest mean growth efficiency in the Scots pine was found in the youngest trees, while it was lowest for the oldest trees. This may result from the fact that the analyses did not include increment in the biomass of branches or roots, increasing with age.
The mean growth efficiency of the youngest intermediate trees was over 2-fold greater than for the dominant trees. An opposite situation was found in the oldest trees, in which mean growth efficiency for dominant trees was over 1.6-fold greater than for intermediate trees.
The greatest variation in growth efficiency was observed for the youngest trees. Regarding tree social position, variation in the growth efficiency of intermediate trees is greater than that of dominant trees in six out of eight analyzed stands.
Only in the youngest stand and in the 64-year-old stand we found a significant dependence of growth efficiency (GE) on diameter at breast height (d1.3), tree height (h), and needle volume (vn) observed. An increase in each of the three traits in the case of the youngest trees resulted in a reduction of growth efficiency, while for 64-year-old trees it led to its increase. The two-way analysis of variance indicated a significant effect of the tree age on growth efficiency. However, the affiliation of trees to the group either as dominant or intermediate trees caused no such effect.
According to the arbitrary scale of effects of the analysis of variance given by Cohen ([9]), the effect of the age on the growth efficiency needs to be considered as weak (30.29%), that of the social class of tree position (dominant vs. intermediate trees) very small (0.28%), while that of the interaction of factors dominant or intermediate trees as small (18.60%).
Acknowledgements
This works was co-financed within the framework of Ministry of Science and Higher Education programme as “Regional Initiative Excellence” in years 2019-2022, project number 005/RID/2018/19.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Authors’ Info
Authors’ Affiliation
Hanna Kwasna 0000-0001-6135-4126
Cezary Beker 0000-0002-7929-2477
Roman Jaszczak 0000-0003-2517-5766
Katarzyna Kazmierczak 0000-0003-0201-7917
Tomasz Najgrakowski 0000-0003-2913-0434
Wojciech Borzyszkowski
Department of Forest Management, Faculty of Forestry, Poznan University of Life Sciences, Poznan (Poland)
Corresponding author
Paper Info
Citation
Turski M, Kwasna H, Beker C, Jaszczak R, Kazmierczak K, Najgrakowski T, Borzyszkowski W (2019). The influence of age and crown position on growth efficiency along a Scots pine chronosequence. iForest 12: 474-479. - doi: 10.3832/ifor2953-012
Academic Editor
Angelo Nolè
Paper history
Received: Aug 27, 2018
Accepted: Aug 02, 2019
First online: Oct 14, 2019
Publication Date: Oct 31, 2019
Publication Time: 2.43 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2019
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 40938
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 34901
Abstract Page Views: 2370
PDF Downloads: 2872
Citation/Reference Downloads: 1
XML Downloads: 794
Web Metrics
Days since publication: 2291
Overall contacts: 40938
Avg. contacts per week: 125.08
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2019): 1
Average cites per year: 0.14
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Growth patterns of Scots pine (Pinus sylvestris L.) under the current regional pollution load in Lithuania
vol. 8, pp. 509-516 (online: 12 November 2014)
Research Articles
Role of photosynthesis and stomatal conductance on the long-term rising of intrinsic water use efficiency in dominant trees in three old-growth forests in Bosnia-Herzegovina and Montenegro
vol. 14, pp. 53-60 (online: 28 January 2021)
Research Articles
Effects of mild drought on the morphology of sun and shade needles in 20-year-old Norway spruce trees
vol. 12, pp. 27-34 (online: 10 January 2019)
Research Articles
Amount and distribution of coarse woody debris in pine ecosystems of north-western Spain, Russia and the United States
vol. 7, pp. 53-60 (online: 28 October 2013)
Research Articles
Effect of family, crown position, number of winter buds, fresh weight and the length of needle on rooting ability of Pinus thunbergii Parl. cuttings
vol. 9, pp. 370-374 (online: 11 January 2016)
Research Articles
Allometric equations to assess biomass, carbon and nitrogen content of black pine and red pine trees in southern Korea
vol. 10, pp. 483-490 (online: 12 April 2017)
Research Articles
Needle traits of understory Silver fir, Norway spruce, and Scots pine in response to increased canopy openness in a birch-dominated stand
vol. 18, pp. 273-282 (online: 14 October 2025)
Research Articles
Analyzing regression models and multi-layer artificial neural network models for estimating taper and tree volume in Crimean pine forests
vol. 17, pp. 36-44 (online: 28 February 2024)
Research Articles
The growth dynamics of East European Scots pine (Pinus sylvestris L.) populations - a Lithuanian field trial
vol. 17, pp. 59-68 (online: 06 March 2024)
Research Articles
Evaluation of methods to improve the direct estimation of standing trees volume
vol. 18, pp. 87-92 (online: 17 April 2025)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword