A model of shrub biomass accumulation as a tool to support management of Portuguese forests
iForest - Biogeosciences and Forestry, Volume 8, Issue 2, Pages 114-125 (2015)
doi: https://doi.org/10.3832/ifor0931-008
Published: Jul 27, 2014 - Copyright © 2015 SISEF
Research Articles
Abstract
The evaluation of forest fuel loading is required by most fire management activities. However, the consideration of shrub biomass for forest planning purposes has been limited by the inability to predict its growth and accumulation. The main objective of this study was to model shrub biomass over time under a tree canopy to be able to include shrub management in fire risk mitigation plans. Data for this purpose was obtained from the 4th and 5th Portuguese National Forest Inventories. Five biologically realistic models were built to describe shrub biomass accumulation in Portuguese forests. The selected model indicates that maximum biomass is affected by stand basal area and the percentage of resprouting shrub species in the stand. Biomass growth rate was clearly affected by the regeneration strategies of shrubs in combination with climatic conditions (mean annual temperature). The model can be used in the accumulation form for initialization purposes or in one of the two alternative difference forms to project observed shrub biomass. The acquired ability to estimate shrub biomass facilitates its inclusion in forest growth models and simulators and will contribute to more accurate estimates of fire behaviour characteristics and stored carbon. This is instrumental to improve decision-making in forest management plans that integrate fire risk, namely to schedule understory fuel treatments.
Keywords
Shrub Growth, Understory Vegetation, Wildfire Risk, Fire Management, Forest Planning, Decision Making
Introduction
During the last decades, significant land use change took place in Portugal and elsewhere in the Mediterranean region. Many marginal agricultural or grazing lands were either abandoned or afforested. Natural succession led to changes in vegetation structure and composition where agricultural activities ceased, thus contributing to the expansion of shrubland, woodland and forests with a well-developed shrub understory ([30]). These changes resulted in higher carbon stocks as well as in more flammable ecosystems prone to large and high-severity fires ([60], [15]).
Fuel dynamics refers to the structural and temporal modifications undergone by a fuel layer or fuel complex. Shrub accumulation models could assist in forecasting the dynamics of biomass and carbon storage. Many modeling of fuel dynamics follows the simple model by Olson ([54]) that describes the relationship between production and decomposition as a modified exponential function that flattens out to a plateau. Other studies describe fuel and shrub dynamics by time-dependent models of forest fire hazard ([37]). However, shrub biomass accumulation information for Mediterranean areas is very limited. Few studies addressed the temporal dynamics of shrub structure and/or biomass in shrublands ([3]), which are expected to be different under a forest canopy, due to competition for resources (i.e., light, water). Hence, little attention has been given to understory vegetation, likely due to its limited economic importance. Nonetheless, the ecological significance of the understory is high, since it plays an important role on nutrient cycles, carbon storage and fire hazard.
Currently available carbon models still lack details on biomass dynamics, which in turn affect the calculation of these processes. A recent study by Rosa et al. ([67]) to estimate pyrogenic emissions of greenhouse gases, aerosols and other trace gases from wildfires in Portugal identified shrub biomass as the variable with the greatest impact on the uncertainty inherent in such estimates. Therefore, it is essential to improve the assessment of forest biomass, including its spatial and temporal variation.
In the Mediterranean region, fire is one of the most important factors affecting forest ecosystems, both ecologically and economically ([63]). Higher shrub loading implies higher flammability, likelihood of crowning fire, and difficulty in fire control ([69], [28]). Fernandes et al. ([26]) observed differences in fire behavior and severity among maritime pine (Pinus pinaster) plots depending on fuel age (i.e., time since last treatment) and the presence or absence of surface fuel treatments. Furthermore, recent research aimed at developing wildfire occurrence models in Portugal included the understory shrubs biomass as a significant variable. Indeed, shrubs have a large impact on fire risk with obvious implications to forest planning ([33], [34], [48], [8]).
The integration of wildfire risk in forest management planning depends on the continuously changing variables related with fuel dynamics (e.g., tree and shrub growth) and stand management ([36], [35]). Therefore, it is very important to obtain information as much accurate as possible on all key variables (e.g., shrub growth) affecting the likelihood and severity of fire over time. The lack of tools to project shrub growth over time has hindered its inclusion in the forest management planning ([35]).
A broad range of growth modeling techniques applied to forest ecosystems has been reported in the scientific literature. However, biomass growth and yield information of understory is scarce. The usefulness of shrub biomass models in forest planning depends on the input information they need and whether the future values of predictors can be estimated with reasonable accuracy. Moreover, an increasing amount of information is being collected in forest inventories focused on sustainability and biodiversity. For example, the Portuguese National Forest Inventory (NFI) systematically collects plot-level information on the shrubs type (i.e., species and regeneration mechanism), their ground cover and mean height. This information may be used to develop a shrub biomass build-up model, which would contribute to more accurate estimates of fire behavior and may quantify the impact of silvicultural treatments on the probability of wildfire occurrence. It can also improve decision-making in forest management, especially taking into account the risk of forest fires ([31], [32]).
The aim of this study is to develop a model to describe the temporal dynamics of shrub biomass in the forest understory of Portuguese forests. One hypothesis is that maximum potential biomass, defined by the model asymptote, is affected by stand variables (e.g., basal area) and shrub regeneration types (resprouter vs. non-resprouter). Considering the biomass growth rate, our hypothesis is that it is affected by stand and shrub characteristics, as well as by site conditions and climate. This model may then be used to predict fuel accumulation as well as to update carbon stock inventories and may also be instrumental to include that information in forest management systems aiming at reducing the risk of fire.
Material and Methods
Study area
Mainland Portugal (Fig. 1) is located in southwester Europe at latitudes of 37° N to 42° N and longitudes of 6° W to 10° W. Climate is warm and dry during summer, and cool and wet in winter ([40]). Mean annual temperature and precipitation follow a gradient of increasing temperature and decreasing rainfall from northwest to southeast. Topography is rugged, especially in the northern half of the country, and most wild-land vegetation is evergreen, drought resistant and highly flammable. Forests and woodlands are a key element in the Portuguese landscape, covering more than one third of the country ([24]).
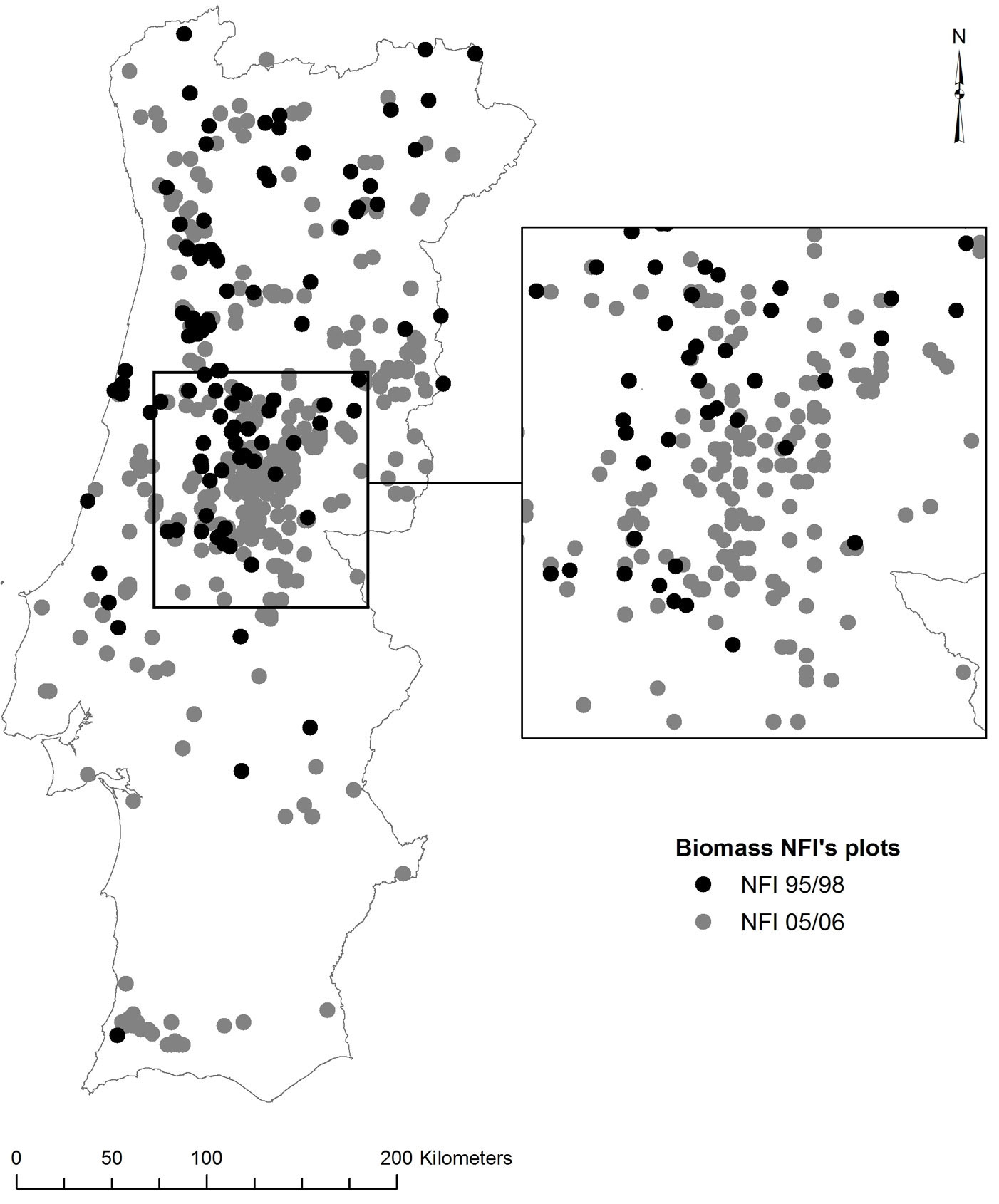
Fig. 1 - National Forest Inventory (NFI) plots used in the study. NFI 1995-1998 (n=102): black circles; NFI 2005-2006 (n=318): grey circles.
The variables considered for the development of a shrub build-up model were divided into three main groups: (i) variables related to shrub properties, (ii) stand characteristics, and (iii) environmental factors, i.e., stand location and climate (Tab. 1). Most data were obtained from the Portuguese National Forest Inventories (NFI) carried out over the whole country within two different and discontinuous periods (1995-1998 and 2005-2006), corresponding to the 4th and 5th NFIs, respectively. The NFI measurements were based on two different square grids of a systematic sample of temporary circular plots (measured only once). The number of measured plots varies across inventories, totaling 2336 plots for the 4th NFI and 12258 plots (with 5267 plots of forest stands) for the 5th NFI.
Tab. 1 - Description of the continuous (Type: cont) and categorical (Type: cat) variables and mean, standard deviation (SD), and range of continuous variables considered for shrub biomass modeling. (Psoft): softwoods; (Phard): hardwoods excluding oaks and eucalypt; (Peuc): eucalypt; (Poak): oak trees.
| Group | Variable | Description | Type | Units | Mean | SD | Max | Min |
|---|---|---|---|---|---|---|---|---|
| Stand variables |
N | Stand density | cont | trees/ha | 739 | 607 | 1800 | 5 |
| G | Basal area | cont | m2/ha | 5.65 | 7.48 | 55 | 0.04 | |
| dg | Quadratic mean diameter | cont | cm | 11.9 | 9.7 | 67.7 | 2.5 | |
| Composition | Pure/mixed forests | cat | - | - | - | - | - | |
| Structure | Even/uneven stand | cat | - | - | - | - | - | |
| Age | Young: dbh<5cm Adult: dbh>5cm |
cat | - | - | - | - | - | |
| Forest type | Species composition (Phard, Psoft, Peuc, Poak) | cat | - | - | - | - | - | |
| Shrub variables | t | Shrub age (time since disturbance) |
cont | years | 7.30 | 4.59 | 15 | 1 |
| Resp (R) | % of resprouters in the stand | cont | % | 39 | 40 | 100 | 0 | |
| SpDom | Dominant shrub species | cat | - | - | - | - | - | |
| SpDens | Shrub species by density (<1.5 kg m-3 ,1.5-3 kg m-3 , >3 kg m-3) | cat | - | - | - | - | - | |
| Location variables | Precipitation (P) | Number of rain days ≥ 1.0 mm | cont | days year-1 | 103 | 20 | 155 | 35 |
| Temperature (T) | Mean annual temperature | cont | °C | 13.3 | 2.4 | 21.3 | 8.8 | |
| Slope | Terrain slope | cont | % | 14.6 | 10.3 | 65 | 0 | |
| Altitude | Terrain altitude | cont | m | 419 | 239 | 1145 | 5 | |
| Aspect | North, south, west, east | cat | - | - | - | - | - |
The variable shrub age equals the elapsed time (years) since the last fire (TSF) or since the stand establishment on the inventory date. To this purpose, the NFI plots and the Forest Service digital fire atlas (burned areas ≥ 5 ha) obtained by semi-automated classification of high-resolution remote sensing data were compared using the software package ArcGIS®. A total of 722 burnt plots were identified, ranging in TSF from 1 to 31 years. However, not all plots were included in the analysis. Shrub age could not exceed stand age since tree planting implies shrub clearing. Therefore, plots corresponding to shrub ages above 15 years were discarded, to decrease the uncertainty on the timing of silvicultural and fuel treatments that disturb the shrub layer. Indeed, it is difficult to find forest plots with shrubs formations older than 15 years with good accuracy. Overall, a total of 420 plots were finally selected for further modeling purposes (Fig. 1).
The main criteria used for plot selection were the availability of tree biometric measurements and understory biomass data, including information on the date of the most recent disturbance (clear, planting, fire or harvesting). Direct biomass measurement is laborious and time-consuming, thus shrub biomass is usually estimated non-destructively from the respective phytovolume and bulk density. Both NFI’s field plots provide data on understory shrub species composition, percent cover, and mean height, which were used to estimate shrub biomass. Shrub phytovolume (m3 ha-1) per species was calculated as the product of shrub height (h, m) and ground cover (m2 ha-1), and combined with species-specific bulk density to obtain the biomass yield of the understory shrub fuel loading (Mg ha-1). Bulk density (kg m-3) is defined as the fuel load (dry weight) per unit volume of vegetation ([4]) and was obtained from a literature review (Appendix 1).
A total of 23 shrub types (defined at the species or genus level) were detected in the NFI plots. The most abundant understory shrub species in the selected plots were Erica spp. (26%), Ulex spp. (17%), Cytisus spp. (16%), and Cistus ladanifer (15% - Tab. 2). Since the resprouting ability is a relevant trait affecting the rate of biomass re-accumulation in fire-prone environments ([41], [61]), the abundance of resprouting shrubs in the stand (Resp, %) was considered as an independent variable (Appendix 1). Resprouter cover percentage was calculated for each plot, equaling “100” when shrub resprouters coverage was total, and “0” when there was no presence of resprouters. Note however that many resprouter species can also regenerate by seed ([62]). Additionally, to assess the impact of other shrub characteristics, the relative richness of shrub species belonging to each NFI plot was included as a predictor. Dominant shrub species were assessed by computing the cover proportion of each species in the studied plot. Further, a dummy variable regarding the class bulk densities was tested as predictor, i.e., we assigned all shrub species identified in the plot to their specific bulk density (see Appendix 1 for more details - [61]). Thus, three major groups of shrub species could be observed: (i) < 1.5 kg m-3, the smallest bulk density; (ii) an intermediate bulk density between 1.5 and 3 kg m-3; and (iii) > 3 kg m-3, the highest bulk density, corresponding to 22%, 52% and 26%, respectively.
Tab. 2 - The most abundant shrub species found in the forest understory of the 4th and 5th NFI plots (n= 102 and n= 318, respectively).
| Shrub species | 4th NFI (%) | 5th NFI (%) |
|---|---|---|
| Arbutus unedo | 2 | 4.4 |
| Cistus ladanifer | 4.9 | 18.2 |
| Cistus salvifolius | 3.9 | 7.2 |
| Cytisus spp. | 15.7 | 16 |
| Dittrichia viscosa | - | 0.3 |
| Erica spp. | 26.5 | 21.4 |
| Lavandula spp. | 1.9 | 0.9 |
| Pistacia lentiscus | - | 0.3 |
| Pterospartum tridentatum | 9.8 | 9.1 |
| Pyrus spp. | - | 0.3 |
| Rubus spp. | 2 | 4.7 |
| Ulex spp. | 22.5 | 15 |
| Others | 10.8 | 2.2 |
As for stand variables, information was obtained for each plot regarding the number of trees per hectare (N), basal area (G), quadratic mean diameter (dg), stand age (adult or young), stand structure (even or uneven), stand composition (pure or mixed) and forest type (main species in the plot - Tab. 1). Forest stands were initially classified into 12 composition classes (Tab. 3), but for modeling purposes plots were reclassified in four forest cover types (Tab. 1 and Tab. 3) according to similar tree characteristics and to proportion of the dominant tree species in the plot:
Tab. 3 - Descriptive statistics for the estimates of understory shrub biomass (Mg ha-1) for the NFI plots (n=420) and per forest type.
| Forest type | Code | Median | Mean | Range | Inter quartile Range |
N |
|---|---|---|---|---|---|---|
| Eucalyptus globulus | Eg | 5.15 | 6.91 | 0.05 - 35.44 | 7.75 | 149 |
| E .globulus + other (Hw and/or Sw) |
EgO | 4.15 | 5.41 | 0.28 - 21.3 | 6.14 | 13 |
| E. globulus + P. pinaster | EgPp | 4.24 | 5.80 | 0.15 - 19.94 | 4.98 | 17 |
| other hardwoods | Hw | 3.12 | 4.66 | 0.86 - 14.53 | 4.65 | 19 |
| Pinus pinaster | Pp | 5.425 | 8.48 | 0.24 - 41.67 | 8.59 | 122 |
| P. pinaster + E. globulus | PpEg | 2.465 | 2.54 | 0.56 - 4.4 | 1.18 | 6 |
| P. pinaster + other (Hw and/or Sw) |
PpO | 5.38 | 10.83 | 0.14 - 45.46 | 13.87 | 18 |
| others oak species | Q | 5.22 | 9.88 | 0.3 - 30.56 | 12.02 | 11 |
| Q. Pyrenaica | Qp | 6.75 | 8.11 | 0.12 - 28.36 | 8.57 | 26 |
| Q. rotundifolia | Qr | 1.77 | 3.49 | 0.24 - 9.44 | 4.36 | 9 |
| Quercus suber | Qs | 5.84 | 7.64 | 0.39 - 37.56 | 7.67 | 27 |
| other softwoods | Sw | 3.17 | 8.45 | 1.74 - 20.45 | 9.36 | 3 |
- “Phard” - hardwoods including deciduous and evergreen species, but excluding oaks and eucalypt (n = 19);
- “Poak” - oaks including Quercus suber, Q. rotundifolia and Q. pyrenaica (n = 73);
- “Psoft” - softwoods including Pinus pinaster, P. pinea and short-needled conifers such as P. sylvestris (n = 149);
- “Peuc” - eucalypt (n = 179).
Stand location, slope, aspect and elevation of the plots were obtained from the NFI database and the country’s Digital Terrain Model (DTM). Climate variables were collected from the database by Tomé et al. ([71]). A GIS layer with climate information was overlaid with the 420 plots layer, i.e., a map was created using a spatial interpolation technique (Thiessen polygon method) to associate climate data to each plot, i.e., the number of days with rain exceeding 1.0 mm and yearly average temperature.
Model fitting and selection
Few studies exist on the development and modeling of shrub growth, and in general concern shrubland, i.e., tree cover is absent ([25], [53], [15]). Shrubland biomass accumulation in Portugal has been previously described by Rosa et al. ([67]), by fitting the model by Olson ([54]) as a function of the time since wildfire occurrence. However, shrub growth and accumulation are also affected by other factors. Would other combinations of variables improve the success of biomass accumulation prediction?
In the present study, biomass accumulation was modeled using potential independent variables as predictors, including: (1) all possible linear combinations of stand variables (e.g., basal area) and shrub regeneration types (resprouter vs. non-resprouter) as factors affecting the model asymptote; and (2) shrub characteristics, site conditions and climate as factors affecting biomass accumulation. Existing growth equations, including the most commonly used ([70], [66], [54]) were considered. After testing several possible candidate equations with explicit consideration of forest stand variables, the deterministic approach for biomass accumulation represented by the single exponential function of Olson ([54]) was selected (eqn. 1):
where a is the asymptote representing the maximum (steady-state) shrub biomass (Mg ha-1), b is a parameter related to growth rate and t is the shrub age (years). The above model assumes constant rates of biomass accumulation and decomposition: this simplification makes it suitable to fit measured values of fuel load with time ([64]). While Olson’s model begins to accumulate at time zero (t0), the Schumacher’s model does not accumulate immediately. This difference can be especially important when the understory is dominated by seed-regenerating species, which implies an initially lower rate of biomass accumulation. The Olson’s function has been used in similar studies ([49]) due to its simplicity and straightforward biological interpretation.
Previous studies indicate that both stand’s biometric factors and climate affect the shrub growth rate ([11], [15]). Hence, all available variables (i.e., shrub, stand and location variables) were tested as possible effects on growth rate (parameter b). In total, 16 independent variables (9 continuous and 7 categorical) were analyzed (Tab. 1). Similarly, our hypothesis was that the biomass asymptote would vary depending on the competition with overstory and/or shrub composition, thus stand and shrub variables were tested for their influence on parameter a. Possible combinations of these variables were tested and only models biologically consistent with all statistically significant variables (p<0.05) were further analyzed and compared. The selection was done according to literature and to common ecological knowledge of biomass growing under tree canopy cover in Mediterranean region. We checked if the estimated signs of the parameters were ecologically meaningful: for example, with higher stand density or basal area, shrub biomass should decrease because of competition.
Estimation of the model parameters was based on the least squares method ([68]). Collinearity among variables was assessed through the variance inflation factors (VIF), accepting values up to 10 ([52]). Normality of regression residuals was inferred by quantile-quantile plots of the studentized residuals. When departure from normality was detected, an iteratively reweighed least square regression using the Huber’s function was applied to reduce the influence of observations containing large fit errors ([52]). Heteroscedasticity associated with the error term of the models was examined graphically by plotting the studentized residuals against the predicted values and corrected when necessary. Weighted regression was used to account for heterocedasticity. Weights were obtained according to the methods proposed by Parresol ([57]) where residuals or the logarithm of squared residuals are expressed as a function of several variables. The most parsimonious model with good fit and all variables significant (p<0.05) were used as a weight function.
Model evaluation and validation
Model selection was based on the fitting and prediction ability of the candidate models. The residual mean square error (MSE - eqn. 2) was used as a measure of goodness-of-fit. Some authors use model efficiency, a measure similar to the coefficient of determination for linear models, assessing model performances on a relative scale ranging from 1 (perfect fit) to 0 (the model is not better than a simple average - [74]). We used a similar measure but adjusted for the degrees of freedom (R2adj - eqn. 3).
Due to the limited amount of shrub biomass data on a chronosequence, we did not split our dataset in two for model fitting and validation purposes. Instead, all data were used to fit the models, and the PRESS statistic (Prediction Sum of Squares - eqn. 4) was used to validate the model ([52]). Calculation of the PRESS statistic is equivalent to deleting the i-th observation and fitting the model to the remaining observations. Each of the regression equations (i.e. one equation per observation) is used to calculate single predicted values, which are then used to obtain the PRESS residuals ([52]). The PRESS residuals are true prediction errors with the predicted value being independent of the observed value. Each candidate model has n PRESS residuals associated with it, and their sum gives the PRESS statistics.
In summary, the following statistics were calculated for model evaluation (eqn. 2, eqn. 3, eqn. 4):
where n is the number of observations, p the number of parameters in the model, yi is the i-th measured value, (hat) y is the i-th predicted value and (hat) yi* is the predicted value by omitting the i-th observation in the PRESS procedure. Accuracy of the selected models, in terms of bias and precision, was obtained by computing the PRESS residuals, the mean PRESS residuals (bias, MPRESS) and the mean of the absolute PRESS residuals.
Plots of predicted vs. observed shrub biomass and plots of residuals against predicted values were also used to identify possible bias. In any case, models showing good fit but biologically unrealistic meaning were discarded ([38]).
Model verification
Independent data from a 2 ha area within an even-aged maritime pine stand in the northeast of Portugal at latitude 41° 27’ N and longitude 07° 30’ W was used to verify the estimates generated by the selected final model. Site elevation, aspect, slope and mean annual temperature were 910 m a.s.l., SE, 10% and 11°C, respectively. Shrub biomass was estimated by either destructive sampling or double sampling based on site-specific equations ([26], [29]). The dataset included five different moments in time in the undisturbed stand (shrub age ≥ 15 years, control), plus data reflecting shrub growth (t = 2, 3, 10, 13) after experimental surface fires ([26], [29]). Resprouting ability of the understory shrub community ranged from R = 13% to R= 100%. Details of the independent data source are reported in Tab. 4.
Tab. 4 - Stand characteristics and measured biomass in a Pinus pinaster stand in northeast Portugal in control (shrub age ≥15 years) and prescribed burnt (shrub age < 15 years) plots. Data are listed according to the understory age at the time of sampling.
| Year of sampling |
Stand age (years) |
Shrub age (years) |
Shrub load (Mg ha-1) |
Basal area (m2 ha-1) |
Resprouters (%) |
|---|---|---|---|---|---|
| 2002 | 28 | 2 | 0.96 | 24.9 | 95.16 |
| 1992 | 18 | 3 | 2.78 | 12.8 | 81.4 |
| 2002 | 28 | 3 | 1.23 | 28.9 | 100 |
| 1999 | 25 | 10 | 6.74 | 32.1 | 79 |
| 2002 | 28 | 13 | 7.88 | 19.7 | 53.04 |
| 1989 | 15 | 15 | 10.48 | 6.9 | 15.4 |
| 1992 | 18 | 18 | 10.32 | 15 | 15.4 |
| 1995 | 21 | 21 | 7.9 | 22.6 | 13.15 |
| 1999 | 25 | 25 | 8.44 | 32.7 | 13 |
| 2002 | 28 | 28 | 7.49 | 28.3 | 10.95 |
Defining two alternative difference equation forms
A difference equation represents a family of growth functions with all the parameters common except one, the “free” parameter ([72]). Growth functions expressed as difference equations are used by many authors as a very powerful way of modeling tree and stand growth ([1], [19], [55]).
Once the best biological and statistical model was chosen, a difference equation was derived through the guide curve method ([20]). This method is used to generate anamorphic equations, which are commonly used with temporary plot data. It consists on the transformation of a single equation for specific conditions to be rearranged to a difference equation where the biomass at the initial measurement age (t1) is taken as the basis to predict biomass at time t2. The difference equation originates a family of curves differing by the value of one of the parameters which depends on the initial value (y1, t1 - [10]).
Suppose a function yt = ƒ(t, β1, β2). In order to express such function as a difference equation, the expression for one of the parameters, say β1, may be obtained as (eqn. 5):
The expression for yt+i can then be derived as follows (eqn. 6):
In this way, yt+i can be estimated from an initial value yt. Thus the above equation may be used to predict the unknown future biomass based on an initial known biomass quantity. The use of the difference equation is illustrated by using a small independent data set (Tab. 4).
Moreover, a second differential equation form was obtained from the selected final model. This difference equation form was developed following the methodology proposed by Tomé et al. ([72]) to formulate growth functions as an age-independent difference equation. This conceptual approach can be used when age data (t1) is not available. Suppose a function yt = ƒ(t, β1, β2). In order to express this function without age being explicit, we start by transforming it as follows (eqn. 7):
Then, yt+i may be derived as (eqn. 8):
The proposed equations have the advantage of allowing direct modeling of yield (instead of growth) by using data not evenly spaced across time, as it is the case for most data sets ([72]), and therefore it may be usefully applied for modeling shrub biomass accumulation in uneven-aged stands of unknown age.
Results
Model fitting and selection
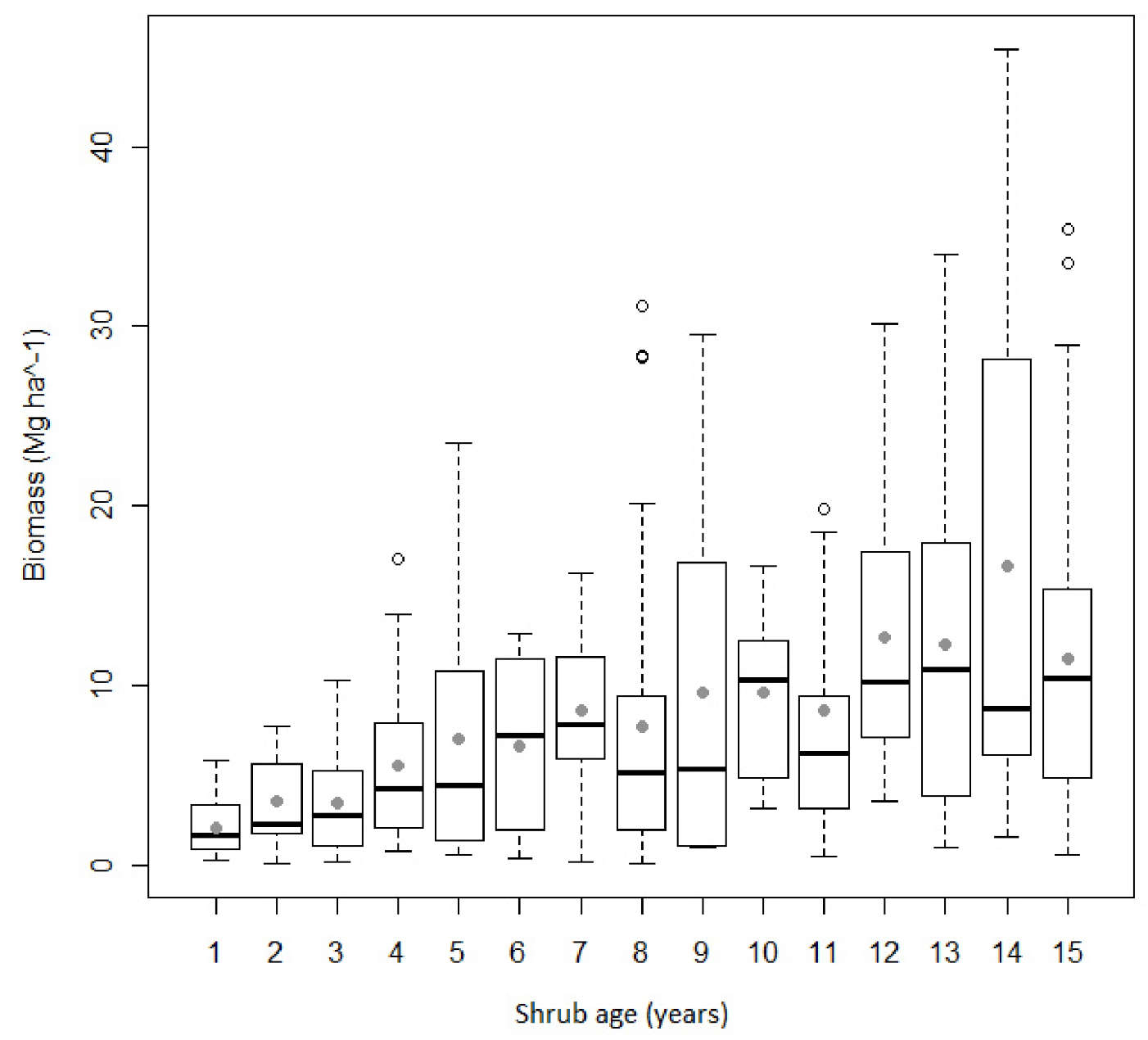
The wide range in biomass values observed for each shrub age reflects the high variability of the dataset used for modeling purposes, which encompass 420 forest plots (Fig. 2). Eucalyptus understory is dominated by Ulex spp., Erica spp. and Cistus ladanifer. In softwood stands the understory is characterized by the presence of Erica spp., Pterospartum tridentatum and Cistus ladanifer. In oaks plots, species of the genus Citysus are the most abundant. As for regeneration strategies, resprouter species were not present in 41% of the observations. A box-plot analysis revealed a lack of symmetry around the median (Fig. 2).
Fig. 2 - Comparative box-plots of shrub biomass (Mg ha-1) as a function of age (n=420). Grey circles and horizontal lines inside the box represent the mean and median, respectively. The upper and lower box limits represent the distance between the 25th and 75th percentiles and the whiskers extend to 10th and 90th percentile.
The general equation form selected for modeling the shrub biomass accumulation was as follows (eqn. 9):
where Biomi, is the shrub biomass (Mg ha-1), resp is the resprouting percentage (R, %), G is stand basal area (m2 ha-1), P is precipitation (rain days year-1), slope is in %, T is the mean annual temperature (°C), t is shrub age (years), and ai and bi are regression coefficients.
The five best-fitted equations are displayed in Tab. 5. All regression coefficients of the shrub biomass equations (a1, a2, a3, b1, b2, b3, b4) were significant (p<0.05) and biologically meaningful. Model Biom1 had the best fit (model efficiency) and the smaller MSE, whereas models Biom4 and Biom5 showed the lowest R2adj as well as the highest residual values (Tab. 5).
Tab. 5 - Adjusted coefficient of determination (R2 adj), mean square error (MSE) and parameter estimates (standard error in parentheses) of the regression coefficients (an, bn) for the selected shrub biomass models (see eqn. 9). All the coefficients were significant at the 0.05 level.
| Model | R 2 adj | MSE | Asymptote | Growth rate | |||||
|---|---|---|---|---|---|---|---|---|---|
| a 1 | a 2 | a 3 | b 1 | b 2 | b 3 | b 4 | |||
| Biom 1 | 0.255 | 27.7 | 32.72 (6.47) |
-0.239 (0.054) |
-0.1528 (0.084) |
- | 0.00108 (0.00035) |
0 | 0.00249 (0.00069) |
| Biom 2 | 0.252 | 28.74 | 36.55 (7.97) |
-0.268 (0.066) |
-0.1998 (0.0974) |
0.00021 (0.00006) |
0.00089 (0.00030) |
0.00061 (0.00025) |
0 |
| Biom 3 | 0.227 | 29.72 | 31.77 (6.37) |
-0.2286 (0.0639) |
-0.159 (0.0897) |
0.0003 (0.00008) |
0.00109 (0.00036) |
0 | 0 |
| Biom 4 | 0.181 | 32.23 | 16.33 (2.41) |
-0.0454 (0.0151) |
-0.1582 (0.0666) |
0.00107 (0.00023) |
0 | 0 | 0 |
| Biom 5 | 0.165 | 31.5 | 12.47 (1.42) |
0 | -0.115 (0.0635) |
0.00133 (0.00025) |
0 | 0 | 0 |
The maximum biomass accumulation, defined by the model asymptote (ai parameters), is depending on stand variables, shrub regeneration strategies and the tree cover. No equation with a fixed asymptote was found for which model efficiency was acceptable. For all the five best-fitting equations, stand basal area (G, m2 ha-1) and/or the shrub biological traits affected the asymptote, i.e. the amount of shrub biomass decreased as G and the percentage of resprouters increased. Excluding G as a predictor and refitting the five models, the corresponding R2adj and MSE for the different models were 0.24 and 31.0 (Biom1), 0.23 and 32.0 (Biom2), 0.21 and 32.4 (Biom3), 0.17 and 35.4 (Biom4) and 0.16 and 35.0 (Biom5), respectively. Thus, the exclusion of G from the models decreased the prediction accuracy (R2adj) and increased the errors (MSE).
Biomass growth rate (bi parameters in eqn. 9) is affected by stand and shrub characteristics, as well as by topography and climate. Four out of the five selected equations included the precipitation, while the fifth included the temperature. As expected, higher precipitation and/or temperature increase the shrub growth rate, hence reaching the steady-state biomass faster. Prediction ability of the equations was considerably improved by including the resprouting-related variable. Only model Biom2 included a topographic descriptor (the slope - Tab. 5). Elevation, aspect and the forest composition were not statistically significant in any of the model tested (p>0.05).
Model validation and biological evaluation
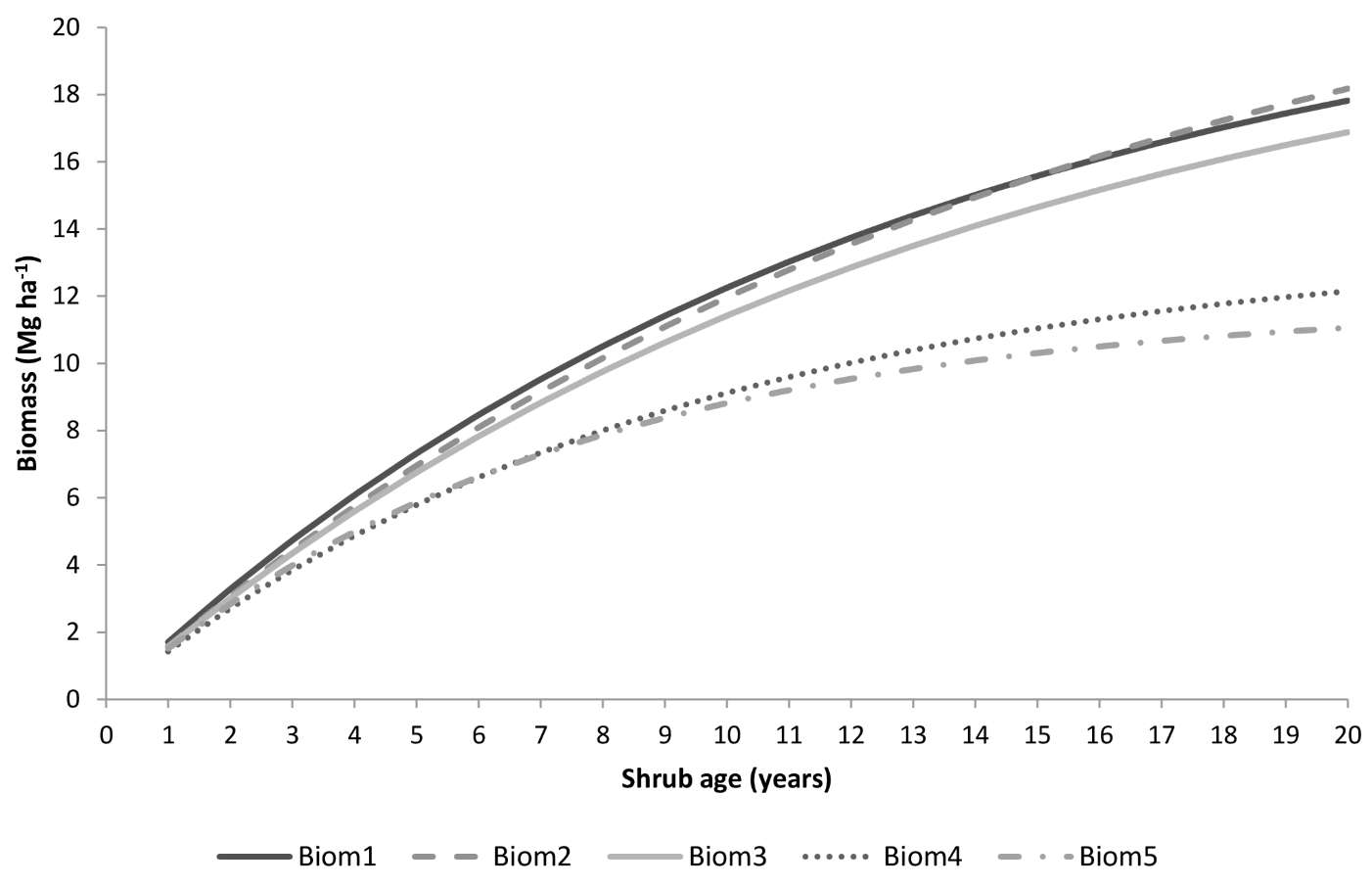
All the five models described are ecologically meaningful, showing higher asymptotic values associated with lower canopy covers (as assessed by G) and quicker accumulation of shrubs when resprouters are present in the understory and for higher values of temperatures and/or precipitation. However, models Biom4 and Biom5 have a rather low asymptote and growth rate (Fig. 3). It is reasonable to expect slightly lower maximum biomass accumulation of shrubs in forest than in shrubland, but the two equations would considerably underestimate total biomass. They also present the lowest model efficiency and the least accurate estimates (i.e., high MSE). On the other hand, models Biom1, Biom2 and Biom3 showed higher accuracy (highest R2adj, lowest MSE - Tab. 5) and provided estimates of the maximum biomass accumulation in agreement with those reported in the literature (Fig. 3). Moreover, equations Biom1 and Biom4 had the lowest bias as revealed by the PRESS residuals (Tab. 6).
Fig. 3 - Shrub biomass predicted by the selected models as a function of shrub age using the following parameter values: precipitation = 103 days, temperature = 14.6 °C, resprouting =39.3%, basal area=5.65 m2 ha-1 and slope=14.6%.
Tab. 6 - Prediction Sum of Squares (PRESS), mean PRESS (MPRESS) and mean absolute PRESS residuals (MAPRESS) for the shrub biomass equations considered for the evaluation and validation.
| Model | PRESS | MPRESS | MAPRESS |
|---|---|---|---|
Biom 1 |
306.6 | 0.73 | 4.38 |
Biom 2 |
343 | 0.82 | 4.49 |
Biom 3 |
353.9 | 0.84 | 4.52 |
Biom 4 |
335.8 | 0.8 | 4.67 |
Biom 5 |
343.7 | 0.82 | 4.71 |
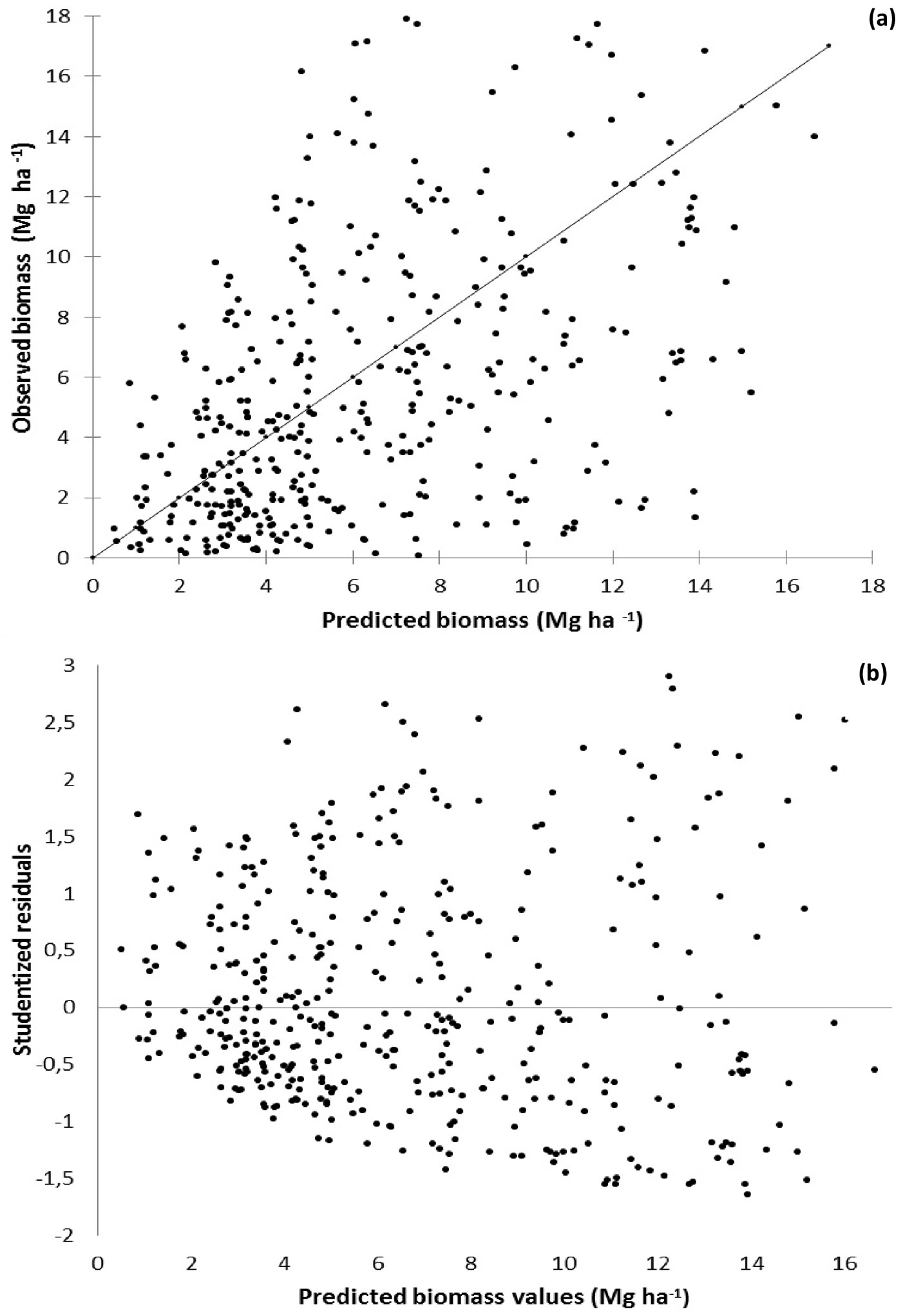
Model Biom1 (which included resprouting percentage, basal area and temperature as independent variables) proved to be the most accurate model, while Biom4 (one of the less biased models) was the less precise in terms of predictions (Tab. 6). To further characterize the selected Biom1 model, graphs of predicted shrub biomass vs. observed biomass values (Fig. 4a) and vs. studentized residuals (Fig. 4b) were also plotted.
Fig. 4 - Predicted shrub biomass accumulation vs. observed biomass (a) and studentized residuals (b) in Portuguese forests using the model Biom1.
Model verification
The equation obtained for model Biom1 closely describes the observed shrub accumulation pattern as a function of age (years), basal area and resprouter percentage (Tab. 4, Fig. 5). Despite the substantial variation in fuel accumulation, such equation may accurately predict the fuel build-up in various forest types. However, it should be noticed that the model was developed from data up to 15 years and its use for extrapolation on longer periods could be inappropriate, as suggested by the poor performances of the model at older ages. For extrapolation over periods longer than 15 years, the use of one of the difference equation forms seems more suitable (see below).
Fig. 5 - Comparative patterns of shrub biomass accumulation with stand age (after 15 years) and prescribed fire in a northeastern Portugal Pinus pinaster stands. Black symbols depict the measured shrub biomass and grey symbols represent the corresponding shrub biomass estimated by the model Biom1. Actual shrub biomass (Bio1 = 6.78 Mg ha-1, t1 = 10 years and Bio1 =10.48 Mg ha-1, t1 = 15 years) are connected by a dotted line to the value estimated by the difference eqn. 10 (Bio2). The solid biomass lines display the predicted (model Biom1) shrub biomass in Portuguese forests, the fixed values are the whole dataset means (resprouting = 15.4%, temperature= 11 °C).
Difference equation forms
Equation Biom1 was used to obtain the difference equation form when age at time t1 is known (eqn. 10):
where Bio1 and Bio2 are the biomass values (Mg ha-1) at times t1 and t2, respectively; a1 = 32.72; a2 = 0.239; a3 = 0.1528; b2 = 0.00108; b4 = 0.00249; G1 and G2 are the stand basal area (m2 ha-1) at t1 and t2, respectively; resp is the percentage (%) of resprouters, assumed as fixed over time (15.4%), and T is the mean annual temperature (11 °C).
In addition, rearranging eqn. 9 the above model can also be used when age (t1) is not known, making it more useful for practical applications. Solving the equation Biom1 for t, and substituting this expression into eqn. 11, the correspondent difference equation form is derived as (eqn. 11):
where Biot and Biot+í are the biomass (Mg ha-1) at ages t and t+i, respectively; a = 32.72 - 0.239 resp - 0.1528 G; b2 = 0.00108; b4 = 0.00249; i is the projection length; G is the stand basal area (m2 ha-1) at t; resp is the percentage (%) of resprouters assumed as invariable over time, and T is the mean annual temperature.
Biomass accumulation may vary for several reasons (e.g., differences in site productivity, fire severity, climate, and competition) and part of the relevant factors may be unknown. The difference equation (eqn. 10) allows the estimation of future biomass at time t2 when biomass at time t1 is known (i.e., information on the age and the shrub biomass at t1). For demonstration purposes, based on the information displayed in Fig. 5, the actual shrub load from the maritime pine stand chronosequence was used to estimate the biomass Bio2 at time t2, i.e., the initial shrub load (Bio1 =6.74 Mg ha-1 and 10.48 Mg ha-1) at time t1 (10 and 15 years) was taken as the basis to predict biomass Bio2 at time t2 (13 and 18 years), with a stand basal area G1 (32.1 and 6.9 m2 ha-1) and G2 (19.7 and 15 m2 ha-1), respectively. For more details, the values of parameters describing the Fig. 5 are listed in Tab. 4. The applicability of the eqn. 10 is clearly depicted in Fig. 5 (black dotted lines for the range t1 = 10 years to t2 = 13 years and grey dotted lines for the range t1 = 15 years to t2 = 18 years). Indeed, the estimated values Bio2 (8.86 Mg ha-1 and 11.34 Mg ha-1, eqn. 10) are similar to the measured biomass (black symbol in Fig. 5). For shrub ages below 15 years the predictions of Biom1 model (grey symbol in Fig. 5) closely match the observed shrub accumulation. Therefore, eqn. 10 predicts quite well future biomass for accumulation periods above 15 years.
If information about initial shrub age (t1) is missing, the difference equation form (eqn. 11) should be used to project the future shrub biomass, for it does not use age as an explicit variable. In these cases we do not assume that the shrubs follow strictly the curves of biomass accumulation prediction (model Biom1) as it may start from a different level of biomass.
Thereby, the use of the difference equations forms implies one of the following situations: (i) when only one measurement is available and age is known at t1, biomass can be obtained from eqn. 10; (ii) when only one measurement is available and age is unknown, with no other additional information, the biomass may be estimated by eqn. 11. If no information on shrub load for a specific age is available, the model Biom1 should be used for initialization and prediction of forest shrub accumulation.
Implications for forest management - application examples
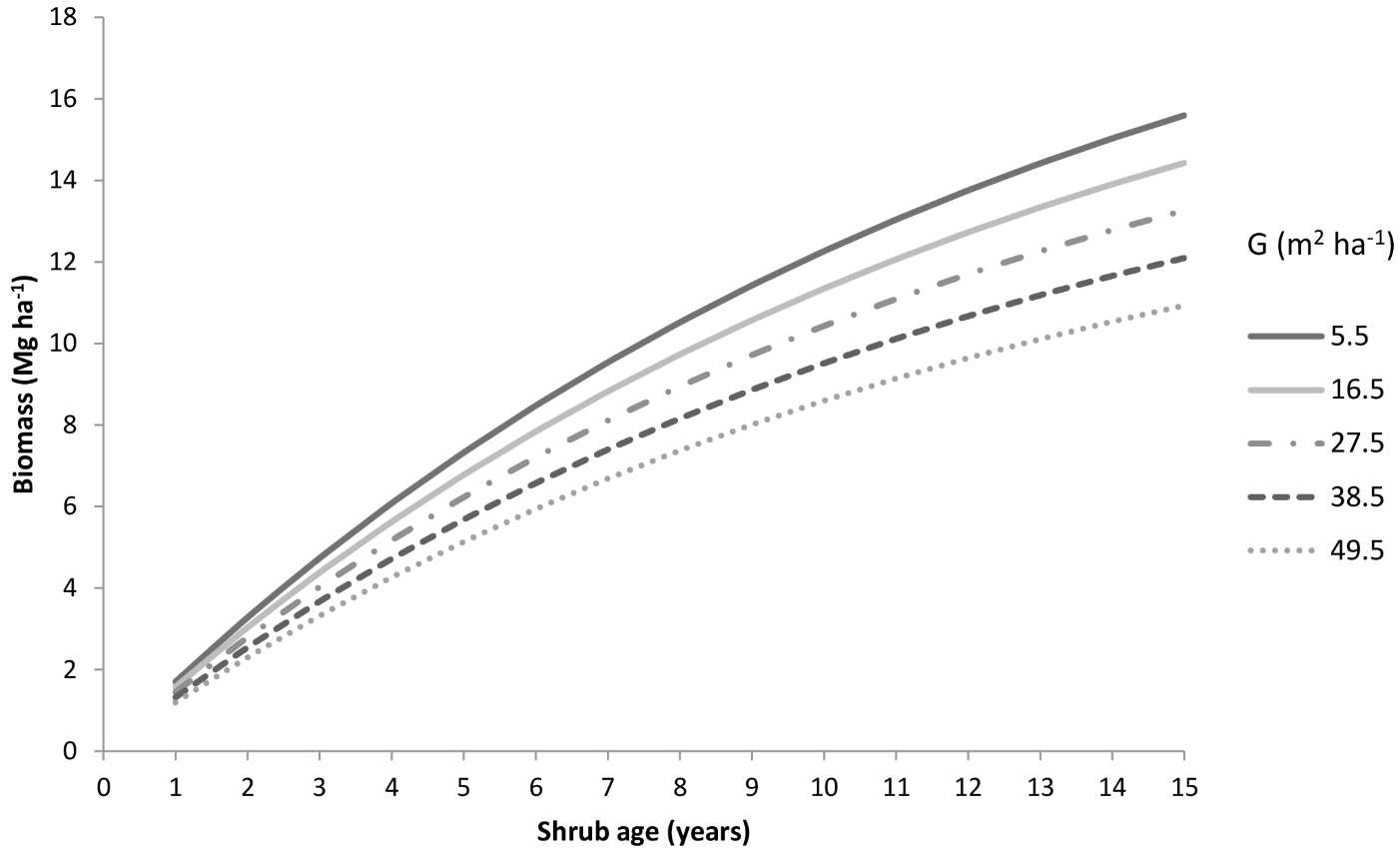
For forest management purposes, the model Biom1 was used to compute the shrub biomass in a hypothetical stand using the mean values of the independent variables considered (Fig. 6). Basal area, used as an indicator of stand-level competition, ranged from 5.5 m2 ha-1 to 49.5 m2 ha-1. In general, an increase in the basal area implies a higher canopy cover, reducing light and water availability for the shrub layer. Thus, increasing competition for resources reduces shrub growth over time (Fig. 6). Setting t = 15, a difference in fuel load of about 5 Mg ha-1 was observed for extreme basal area values.
Fig. 6 - Shrub biomass predicted over time as a function of the basal area using the model Biom1 for a stand characterized by mean conditions (temperature = 14.6 °C, resprouting = 39.3%).
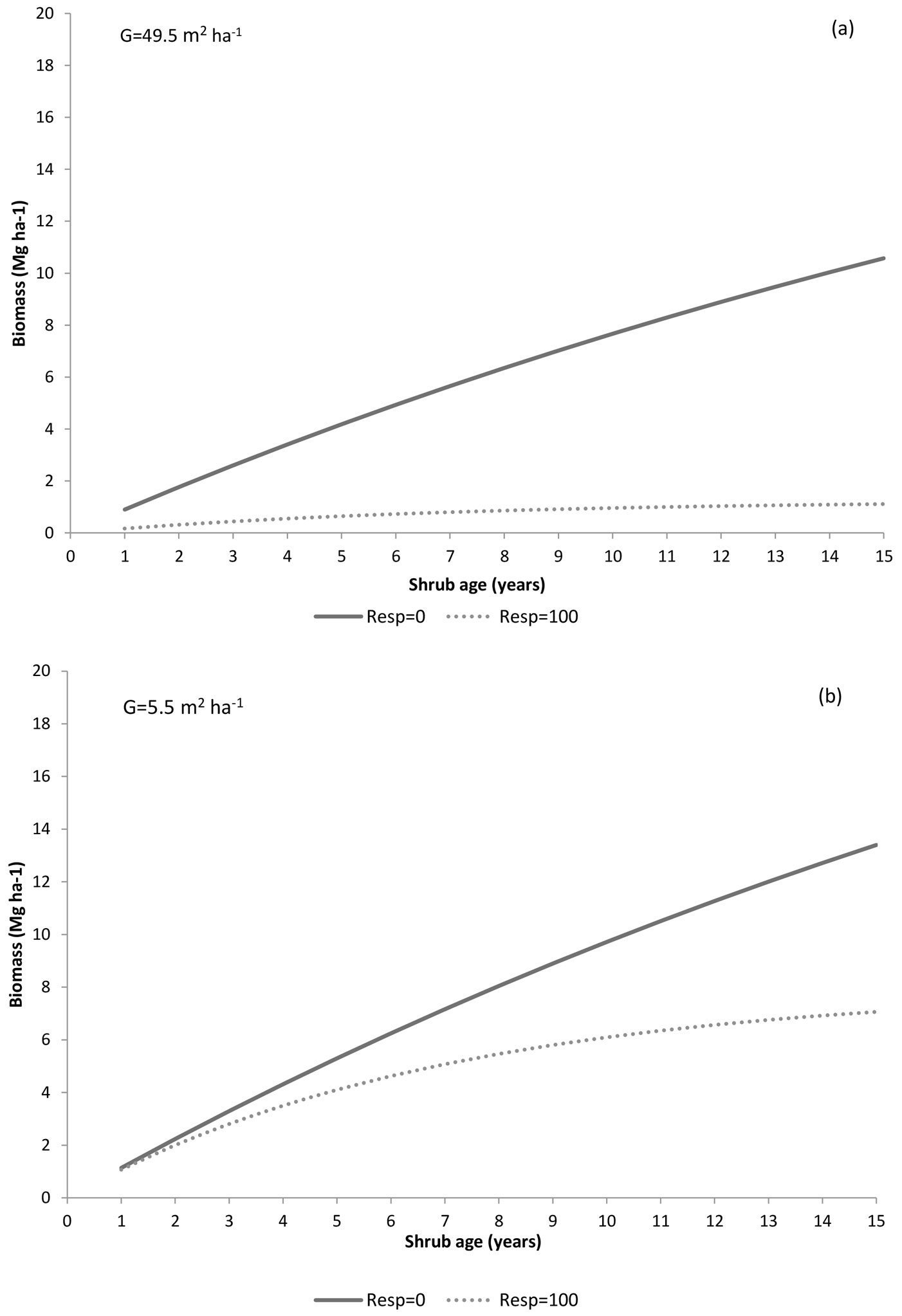
Fig. 7 displays how shrub biomass is impacted by shrub regeneration strategy (two levels of resprouter abundance) and by basal area (two extreme values of basal area) using model Biom1. The lowest biomass usually appears in the resprouters’ community (R = 100%), particularly in the highest basal area stands (Fig. 7a). In contrast, biomass recovery is faster and reaches higher levels when the understory is comprised exclusively of seeders (i.e., R = 0%), particularly at the lowest basal area level, where 13-15 Mg ha-1 is reached after 15 years (Fig. 7b).
Fig. 7 - Shrub biomass over time predicted by the model Biom1 using two levels of resprouter abundance (0 and 100%) and two levels of stand basal area (49.5 and 5.5 m2 ha-1).
Discussion and Conclusions
Mediterranean-type shrublands and forests are highly variable in aboveground biomass ([40]). Biomass estimation in different forest stands is a difficult task due to structural heterogeneity and the dynamic nature of vegetation. Given current knowledge gaps in this topic, the main objective of the present study was to model shrub accumulation over time in the presence of a tree overstorey. Our starting hypothesis was that shrub growth under a tree canopy should depend on both stand variables and climate, reflecting their importance to biomass growth. Prediction models were developed based on NFI data of diverse geographical origin and various floristic compositions, in order to extend their applicability to most Portuguese forests with an abundant understory vegetation, especially those dominated by Erica spp., Ulex spp., Cytisus spp. or Cistus ladanifer. The strategy adopted can be viewed as an advantage over site-specific models ([18]).
Dynamics of shrub biomass under tree cover in the Mediterranean climate, and its relation to stand variables had been poorly studied. This study extends previous investigations by introducing measurable stand variables and shrub regenerating strategy in a time-dependent shrub biomass model, using a non-linear regression technique based on Olson’s model. Moreover, two alternative difference equation forms obtained directly from the selected model could be used to project the observed shrub biomass: difference eqn. 10 when age is known and difference eqn. 11 when age is not available. This will increase the quality of the shrub build-up models when shrub age is not readily available. Moreover, to provide information on biomass trends over time, the proportion of resprouters in the understorey is the sole shrub information required by our model. Indeed, field assessment of shrub regeneration strategy has the advantage of being relatively straightforward.
Among the studied models, Biom1 provided the best performances for shrub biomass estimation under forest canopies in Portugal. Also models Biom4 and Biom5 provided biologically meaningful predictions, but their asymptote and growth rate parameters are low and inconsistent with the range of values reported in the literature ([65]). On one hand, the function Biom1 depends on a shrub trait (regeneration mode), affecting both growth rate and maximum biomass, and on a descriptor of the tree overstorey (stand basal area), an indicator of stand-level competition. On the other hand, climatic conditions such as temperature influence vegetative growth rate. As expected, forest shrub biomass estimated with our models is lower than that reported for shrublands in the Mediterranean (e.g., [75]). Furthermore, our estimates of shrub biomass grown under tree canopy are in line with values reported by previous studies in Portugal, which do not exceed 24 Mg ha-1 ([27]).
Rosa et al. ([67]) indicates that shrublands in Portugal require 15 years to reach a steady-state aboveground biomass. Our results indicate that longer periods are needed when tree cover is present. Obviously, such slower build-up of shrub biomass may be explained by the competition for available resources between the understory and the overstory ([43]). Similarly, Castedo-Dorado et al. ([14]) showed that selected overstory variables could be suitable indicators of the relative availability of light, nutrients, water or growing space in modeling the maximum shrub development. Nevertheless, several authors reported that the amount of understory vegetation in maritime pine and eucalyptus stands is practically the same 10 and 30 years after fire. Indeed, after an initial period of relatively vigorous growth, understory biomass tends to stabilize when shrubs reach their adult size ([73]).
Shrub biomass tends to increase with time since disturbance, with variations depending on the shrub type. However, the highest accumulation usually occurs in seeders communities, particularly when basal area is low (Fig. 7). This agrees with the general knowledge on different growth patterns between resprouters and non-resprouters. Non-resprouters begin flowering earlier and more abundantly after disturbance ([58], [5]), allowing a faster colonization of suitable microhabitats as compared to resprouting species, whose regrowth from established root systems is restricted to microsites previously occupied ([41], [11]). Moreover, resprouters need more energy and time to regenerate after disturbance, due to their resource allocation to the replacement of damage tissues ([5], [2]). According to our results, several authors (e.g. [5], [51]) reported that many resprouting species have lower growth rates than non-resprouters of comparable age (Fig. 7). In Mediterranean-type ecosystems, frequent fires decrease the abundance of seeders, while at intermediate fire-return intervals, they are favored in comparison to resprouters ([76], [59], [45]).
Overstory basal area in the proposed models is a proxy for competition, decreasing shrub biomass with higher tree stocking. This general trend is consistent with other studies, reporting that the maximum shrub development was also limited by overstory variables such as basal area (G - [21], [14]). Thus G serves as an indicator of stand competition, and has the advantage of being relatively simple to obtain in the field or to be inferred from growth and yield models ([14]).
In a Mediterranean-type climate, the regional patterns of vegetation structure and composition are mainly dependent on temperature and water availability ([44], [40]). Hence it was not surprising to find temperature as a significant predictor in proposed model. Most phenological models include temperature as a proxy for developmental rates ([16]). For instance, higher air temperature values in spring strongly induces an earlier start of plant development ([22], [46], [17]). Moreover, temperature directly affects soil moisture, which is the main source of water for plant growth ([44]).
Forest composition did not contribute to explain variation in shrub biomass. However, post fire composition, structure and richness of the whole plant community are directly related to the re-establishment of the dominant species in the canopy ([45], [9]). Differences in shrub biomass accumulation among the different forest types considered in this study were generally poor; Maritime pine plots attained higher values and maximum biomass was qualitatively similar to other species. It is important to remark that forest composition in Portugal is strongly determined by human action and it is often decoupled from the potential vegetation type. The dominant shrub communities generally occur independently of overstorey composition. Consequently, variation in basal area and site quality are likely to overwhelm the influence of forest composition on shrub biomass.
Several limitations of the proposed models have also to be highlighted here. The variability of the initial dataset was considerably high, lowering the model efficiency. Variation in shrub species composition, the use of generic bulk densities to estimate biomass, and site-specific factors are certainly involved in the modeling performance. Similarly, several models with low R2 values (indicating that some variation remains unexplained) were considered useful to support optimal forest management decisions, for instance, mushrooms yields in pine forest planning ([6], [56]). In any case, we consider this study to be an important step forward, since similar models have seldom been developed for Europe.
Future research would greatly benefit from the existence of information from permanent shrub/biomass plots measured over time, in order to better understand biomass dynamics (e.g., shrub senescence) and carbon sequestration rates at different spatial scales. Additionally, variables such as soil type and summer water deficit may contribute to improve the model performances.
The successful management of fuel load in fire-prone regions is a challenging task that calls for the integration of forest and fire management activities in order to decrease fire hazard. Several studies indicate that fuel treatments (i.e., reduction of fuels in forests) change wildfire behavior and severity and enhance the effectiveness of fire suppression operations ([50]). Models such those developed in this study have practical applications in the assessment of fire hazard and in the definition of general prescriptions to plan fuel treatments. In fact, such models allow to quantify the impact of silviculture operations and help to define management options that may decrease wildfire occurrence. For instance, a preliminary shrub build-up model ([7]) was integrated with a growth and yield model to accomplish maritime pine stand-level optimizations and determine optimal stand-level treatments (e.g., thinning, fuel treatment), so as to reduce the hazard of fire ([32]). This information is very valuable as it may effectively support the development of adaptive management strategies ([31], [32]).
Investigations on carbon flux implications of fuels reduction treatments are of increasing interest ([39]). Fire-related climate change mitigation options include decreasing emissions through fuel reduction treatments and using the removed biomass to replace fossil fuels for energy production ([13], [47]). The shrub build-up model can be used by forest managers to predict fuel loads in the frame of understory removal to decrease fire hazard. It may also have practical application for ecologists, allowing the estimation of carbon storage in the understory and the assessment of how future wildfire emissions will change in response to fuel treatments, helping to reduce the uncertainty in emission estimates. This analysis may be done in two steps. If no information on shrub biomass is available the proposed model would be used for initialization (i.e. estimate initial shrub biomass) and to predict curves of forest shrub accumulation without previous information on shrub load over a specific time span; otherwise one of the difference equation forms are recommended to estimate future biomass from the initial biomass.
Despite disregarding site-specific conditions in relation to shrub composition and some simplifications in regards to the whole fuel complex, it is reasonable to conclude that the combination of the proposed model and the difference equation forms is able to adequately describe the typical shrub biomass accumulation in Portuguese forests (Fig. 5). Additionally, our biomass models provide sound estimates of biomass growth on the short term. For longer periods (more than 15 years), information on regeneration, mortality, thinning and succession has to be taken into consideration in order to increase the accuracy of biomass estimates. These general equations are expected to help forest management decision-making as a tool to support decisions on where and when fuel treatments are required.
Acknowledgments
This research was conducted in the frame of the project PTDC/AGR-CFL/64146/2006 “Decision Support Tools for Integrating Fire and Forest Management Planning” and project FIRE-ENGINE “Flexible Design of Forest Fire Management Systems” (MIT/ FSE/ 0064/2009), funded by the Portuguese Science Foundation (FCT), and and partly funded by the project ForEAdapt “Knowledge exchange between Europe and America on forest growth models and optimization for adaptive forestry”, under grant agreement no. PIRSES-GA-2010-269257 and INTEGRAL “Future Oriented Integrated Management of European Forest Lands, both funded by the European Union Seventh Framework Programme (FP7-PEOPLE-2010 -IRSES). The FCT support for funding the doctoral program plan of Brigite Roxo Botequim (SFRH-BD-44830-2008) and Susete Marques (SFRH/BD/62847/2009) is also acknowledged. JGG participated in this research under the framework of the Project PTDC/AGR-FOR/4526/2012 “Models and Decision Support Systems for Addressing Risk and Uncertainty in Forest Planning” (SADRI).
Authors would also like to thank the financial support for a post-fellowship by the FCT (SFRH/BPD/63979/ 2009) and by the University of Eastern Finland. Finally, the Portuguese Forest Service (ICNF) is acknowledged for supplying the NFI databases.
References
Gscholar
CrossRef | Gscholar
Online | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Ane Zubizarreta-Gerendiain
Jordi Garcia-Gonzalo
Andreia Silva
Susete Marques
José MC Pereira
Margarida Tomé
Universidade de Lisboa, Instituto Superior de Agronomia, Centro de Estudos Florestais, Tapada da Ajuda, 1349-017 Lisboa (Portugal)
University of Eastern Finland, School of Forest Sciences, Faculty of Science and Forestry, Joensuu (Finland)
Centre for the Research and Technology of Agro-Environmental and Biological Sciences (CITAB), University of Trás-os-Montes e Alto Douro, Quinta de Prados, 5001-801 Vila Real (Portugal)
Corresponding author
Paper Info
Citation
Botequim B, Zubizarreta-Gerendiain A, Garcia-Gonzalo J, Silva A, Marques S, Fernandes PM, Pereira JMC, Tomé M (2015). A model of shrub biomass accumulation as a tool to support management of Portuguese forests. iForest 8: 114-125. - doi: 10.3832/ifor0931-008
Academic Editor
Giorgio Matteucci
Paper history
Received: Dec 14, 2012
Accepted: Apr 15, 2014
First online: Jul 27, 2014
Publication Date: Apr 01, 2015
Publication Time: 3.43 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2015
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 57671
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 47017
Abstract Page Views: 4268
PDF Downloads: 4917
Citation/Reference Downloads: 50
XML Downloads: 1419
Web Metrics
Days since publication: 4180
Overall contacts: 57671
Avg. contacts per week: 96.58
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2015): 37
Average cites per year: 3.36
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Wildfire risk and its perception in Kabylia (Algeria)
vol. 11, pp. 367-373 (online: 04 May 2018)
Research Articles
Developing wildfire risk probability models for Eucalyptus globulus stands in Portugal
vol. 6, pp. 217-227 (online: 27 May 2013)
Editorials
Spatial information and participation in socio-ecological systems: experiences, tools and lessons learned for land-use planning
vol. 7, pp. 349-352 (online: 19 May 2014)
Research Articles
Public participation GIS to support a bottom-up approach in forest landscape planning
vol. 6, pp. 347-352 (online: 29 August 2013)
Research Articles
Assessing the performance of fire danger indexes in a Mediterranean area
vol. 11, pp. 563-571 (online: 01 September 2018)
Research Articles
Shifting to a holistic approach in national wildfire management policies: the Italian case
vol. 18, pp. 163-175 (online: 01 July 2025)
Research Articles
Harmonized dataset of surface fuels under Alpine, temperate and Mediterranean conditions in Italy. A synthesis supporting fire management
vol. 13, pp. 513-522 (online: 13 November 2020)
Review Papers
Public participation: a need of forest planning
vol. 7, pp. 216-226 (online: 27 February 2014)
Research Articles
Forest fire occurrence modeling in Southwest Turkey using MaxEnt machine learning technique
vol. 17, pp. 10-18 (online: 02 February 2024)
Research Articles
Usefulness and perceived usefulness of Decision Support Systems (DSSs) in participatory forest planning: the final users’ point of view
vol. 9, pp. 422-429 (online: 02 January 2016)
iForest Database Search
Google Scholar Search
Citing Articles
Search By Author
- B Botequim
- A Zubizarreta-Gerendiain
- J Garcia-Gonzalo
- A Silva
- S Marques
- PM Fernandes
- JMC Pereira
- M Tomé
Search By Keywords
PubMed Search
Search By Author
- B Botequim
- A Zubizarreta-Gerendiain
- J Garcia-Gonzalo
- A Silva
- S Marques
- PM Fernandes
- JMC Pereira
- M Tomé
Search By Keyword