Developing wildfire risk probability models for Eucalyptus globulus stands in Portugal
iForest - Biogeosciences and Forestry, Volume 6, Issue 4, Pages 217-227 (2013)
doi: https://doi.org/10.3832/ifor0821-006
Published: May 27, 2013 - Copyright © 2013 SISEF
Research Articles
Abstract
This paper presents a model to predict annual wildfire risk in pure and even-aged eucalypt stands in Portugal. Emphasis was in developing a management-oriented model, i.e., a model that might both: (a) help assess wildfire occurrence probability as a function of readily available forest inventory data; and (b) help predict the effects of management options (e.g., silvicultural treatments) on the risk of fire in eucalypt stands. Data from both the 1995/1998 and the 2005/2006 Portuguese National Forest Inventories as well as wildfire perimeters’ data were used for modeling purposes. Specifically, this research considered 1122 inventory plots with approximately 1.2 million trees and 85 wildfire perimeters. The model to predict the probability of wildfire occurrence is a logistic function of measurable and controllable biometric and environmental variables. Results showed that wildfire occurrence probability in a stand increases with the ratio basal area/quadratic mean diameter and with the shrubs biomass load, while it decreases with stand dominant height. They further showed that the probability of wildfire occurrence is higher in stands that are over 1 Km distant from roads. These results are instrumental for assessing the impact of forest management options on wildfire risk levels thus helping forest managers develop plans that may mitigate wildfire impacts.
Keywords
Forest Fires, Forest Management, Eucalyptus globulus Labill, Annual Wildfire Risk Model
Introduction
Fire is a major disturbance impacting the Mediterranean landscape ([81]). In recent decades its incidence has increased dramatically in southern Europe ([77], [66], [74], [70]). The Portuguese territory is characterized by a Mediterranean climate and a rugged topography. Moreover, the Portuguese vegetation cover is mostly evergreen and drought resistant. The country is thus prone to vegetation fires. Recent demographic, socio-economic and climatic trends (e.g., [57], [75]) have further contributed to the country’s vulnerability to wildfires. In Portugal, wildfire is the most important agent of land cover change ([73]). In fact, in the period extending from 1975 to 2007 the total burned area approximated 3.8 · 106 hectares, representing 40% of the country’s area ([54]).
In Portugal, around 90% of the total forest land is managed by private landowners ([20]) and most stands are monospecific or dominated by one species. Eucalypt is the most important forest species in terms of area as it extends over 8.12 · 103 ha, corresponding to 26% of the country’s forestland ([48]). Further, it provides key raw material to the export driven pulp and paper industry (about 5.75 million m3 of pulpwood per year - [21]). Wildfires constrain the economic viability of eucalypt in commercial forestry and the competitiveness of this industry ([67], [64]). The development of forest plans that may mitigate wildfire impacts on the profitability of eucalypt management scheduling is thus a key factor to the sustainability of this forestry sub-sector. This prompted the research of models to assess wildfire occurrence probability in eucalypt plantations as a function of variables that may be controlled by forest managers.
The forestry literature has associated the term risk with the probability of occurrence of a natural hazard ([41], [49], [56]). In this research, we will refer to risk as the probability of a stand to be affected by a wildfire (i.e., probability of burning) if an ignition exists ([56]). Thus, rather than modeling fire ignition probability, the focus of this research is on modeling at stand level the probability of wildfire occurrence at stand level. This is understood as a spatial process related to forest structure as potential fire spread is impacted by fuel presence/composition ([24]).
In Portugal, former studies have focused on the characterization of wildfire ignition or of wildfire risk as a function of environmental or socioeconomic variables ([92], [73], [68], [10], [12], [13], [54]). It was demonstrated that in general wildfire impacts depend on the forest cover types where they occur ([64], [38], [68], [65], [87], [35]). The characterization of these impacts on eucalypt plantations was addressed recently by Fernandes et al. ([29]) and Marques et al. ([55]). Nevertheless, no models to assess the impact of changes in controllable biometric variables on fire occurrence in eucalypt plantations were available in Portugal. This lack of information was a major obstacle to effective eucalypt forest management planning in Portuguese fire-prone regions.
The forest cover type and the understory fuel load have a substantial impact on the probability of wildfire occurrence ([18], [14], [11], [87], [54], [56]) and may be manipulated by management planning to minimize risk. Some authors have analyzed the impact of tree species composition and of fuel reduction activities on wildfire occurrence ([1], [26], [25]). Fire hazard and spread do depend on both the tree species composition and the understory fuel structure (e.g., [79], [44], [76], [28], [87]). They thus depend too on forest and fuel management regimes ([43], [69], [49], [16]). In fact, the relationship between fuel load, rate of spread, and fire intensity has provided a simple but powerful argument to support fuel reduction in eucalypt forests ([58], [59], [72]). The effectiveness of forest management under wildfire risk depends on the availability of information about the impact of management-controllable variables, i.e., understory fuel load and stand biometric characteristics on wildfire occurrence probability ([18], [33], [41]).
The modeling approach to wildfire occurrence in eucalypt stands presented in this paper builds from research targeting the development of wildfire occurrence models in other forest cover types that might take into account the impact of changes in controllable biometric variables (e.g., [41], [56], [37]). These models quantify the impact of silvicultural treatments and management options on wildfire occurrence probability in the corresponding forest cover type. Their usefulness has been further demonstrated in the framework of the development of optimal management plans under wildfire risk ([42], [35], [30], [31]).
The objective of this research was thus to develop a management-oriented model to predict annual wildfire risk in pure and even-aged eucalypt stands in Portugal, i.e., a model that might both: (a) help assess wildfire occurrence probability as a function of readily available forest inventory data; and (b) help predict the effects of management options (e.g., silvicultural treatments) on the risk of fire in eucalypt stands. After describing the modeling approach, results are discussed to highlight the contribution of this research to address eucalypt wildfire and forest management concerns and help mitigate catastrophic damage to eucalypt plantations.
Materials and methods
Materials
Wildfire perimeters and inventory plots
The assessment of wildfire risk probability in eucalypt stands was based on historical fire information from 1998 to 2007. The fire data consisted of all perimeters of wildfires larger than 5 hectares. Burned area maps were produced at the Remote Sensing Laboratory of Instituto Superior de Agronomia by semi-automated classification of medium-resolution remote sensing data (i.e., Landsat Multi-Spectral Scanner - MSS, Landsat Thematic Mapper -TM, and Landsat Enhanced - TM+). In this period, wildfires burned over 1.5 · 105 hectares distributed over 12 273 perimeters larger than 5 hectares.
This research was further based on data from the 4th and 5th Portuguese National Inventories (NFIs) carried out in two different and discontinuous periods (1995-1998 and 2005-2006, respectively). Each NFI used its own grid to layout the plots. Therefore no permanents plots were available. Additionally, the number of measured plots has not been constant across NFI. In total, 615 and 1 351 pure and even-aged eucalypt plots were inventoried out of the 2 336 and 12 258 total plots measured in the 4th and the 5th NFI, respectively. This research considered plots that were classified by the NFI as productive even-aged pure eucalypt forest and that included the measurement of biometric variables as well as information about the fuel load understory (very young plots where trees are no measured were not included). Thus all plots considered for modeling purposes did include biometric and environmental data relevant for management planning purposes such as tree height, tree diameter at breast height (d) - for trees holding a d greater or equal to 7.5 cm -, stand age, stump diameter (e.g., the mean stump diameter of trees that died as a consequence of a wildfire), condition of the tree (dead, alive, cut), number of trees, shrubs species, mean shrubs height, aspect and slope.
An altitude map obtained from the Country’s Digital Terrain Model (DTM) with a 30 m pixel accuracy was overlaid with the NFI plots layers to get the altitude of each plot. The latter were further overlaid with a GIS layer that classifies the territory into two road proximity classes (the threshold being 1 kilometer - [54]) to classify each plot according to its distance to the closest road. A similar procedure was used to classify each plot according to the population density (number of inhabitants living in each parish - [54]), precipitation (average of number of days per year with precipitation ≥ 1.0 mm) and temperature (yearly average air temperature). The historical weather records used were developed by Tomé et al. ([89]), based on the climatological normal of reference (period 1931-1960 in 334 different places in Portugal) from the Atlas do Ambiente.
Analyzing the status of eucalypt plots
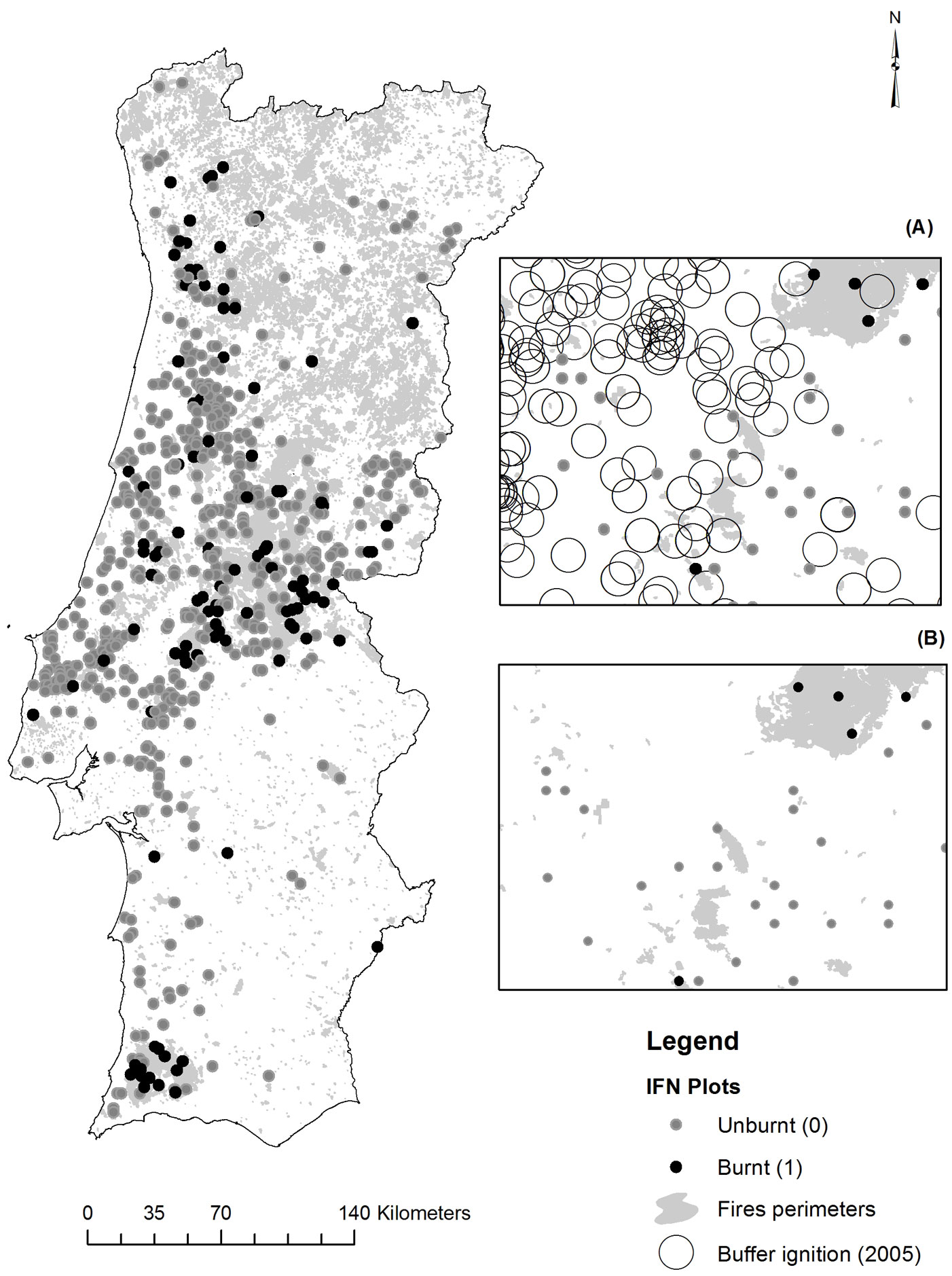
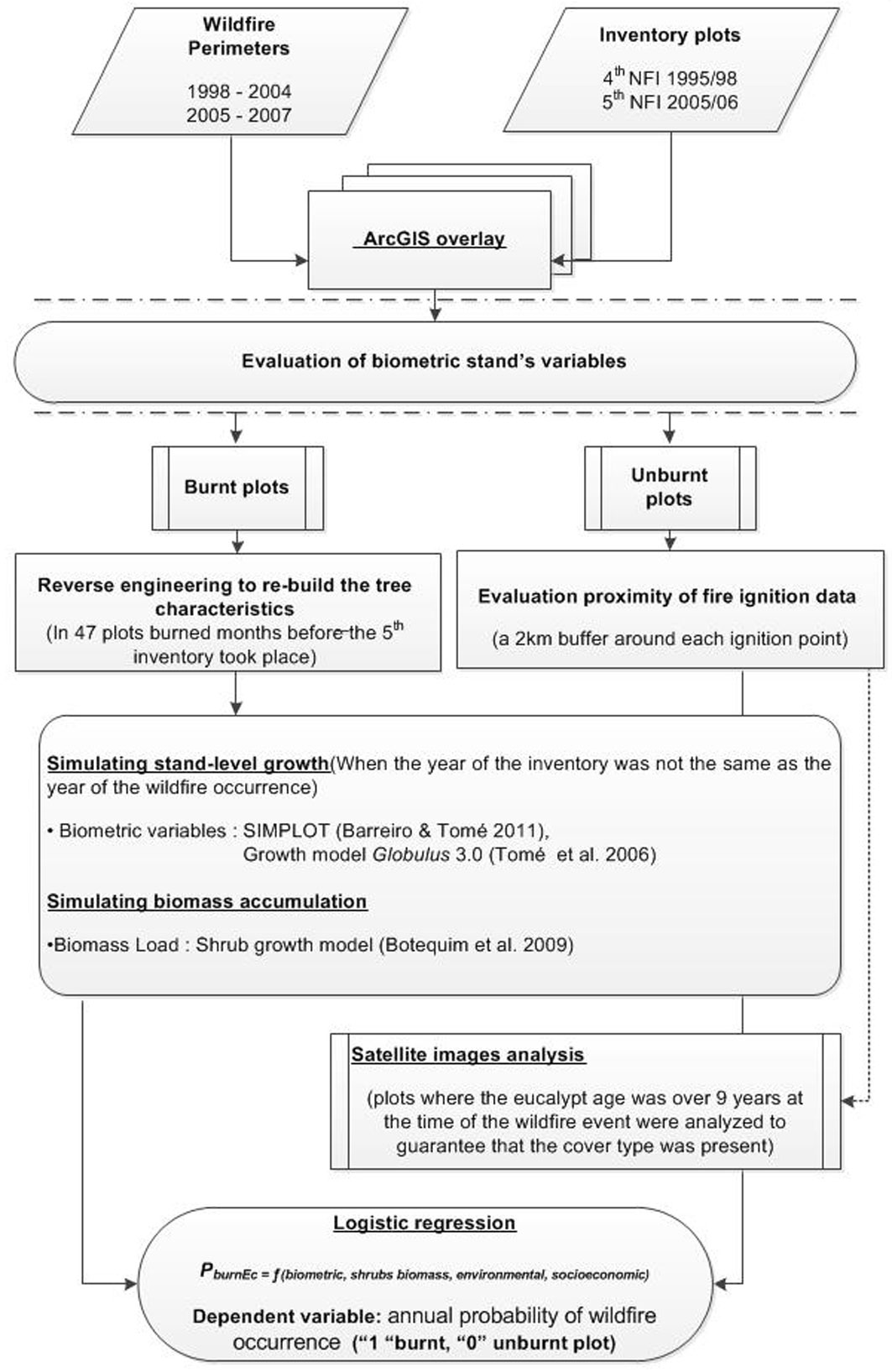
Wildfire perimeters and NFI maps were overlaid using ArcGIS® 9.2 to check whether the eucalypt plots were burned or not within sub-periods extending up to six years (1998-2004) after the first inventory and up to two years (2005-2007) after the second one (data from 2008 were not available). This provided the status (burnt/unburnt) of each eucalypt plot. The definition of these time frames balanced the benefits of having a larger sample size and the costs associated with potential land cover changes in the period ranging from the inventory and the wildfire occurrence. Over the two sub-periods, 109 (59 plots from 4th NFI and 50 from 5th NFI) pure and even-aged eucalypt plots were burned at least one time, while 446 were left unburned (117 plots from 4th NFI and 329 plots from the 5th NFI, respectively - Fig. 1).
Fig. 1 - Distribution of forest fires occurred in Portugal during the period 1998-2007, overlaid with the pure/even-aged eucalyptus plots. Boxes on the right represent: (A) selection of unburned plots (example for the year 2005) based on their distance from ignition points; (B) a part of the National Forest Inventory plots used in the study.
Reverse engineering to rebuild the tree characteristics
The sample size was constrained by the low number of even-aged and pure eucalypt stands and by the fact that most of the 5th NFI plots had been burned before the inventory in 2005. In fact, 47 out of the 50 plots selected by the 5th NFI, burned months before the inventory took place. In order to overcome this problem and take advantage of available inventory data, a reverse engineering methodology ([60], [8], [22], [36]) was used to re-build the forest plot before the wildfire occurrence (Fig. 2). Firstly, these plots were further inventoried to get the diameter of stumps from trees that burned and had been harvested. Secondly, this diameter was input to an equation developed by Marques et al. ([55]) to estimate the pre-fire tree diameter at breast height. Thirdly, the latter was input to an equation developed for eucalypt by Tomé et al. ([90]) to estimate the tree height (eqn. 1):
where h is the tree height (m), d is the diameter of the breast height (cm), β0 = 0.6733 and β1 = 0.0130.
In the case of plots with standing burned trees, pre-fire diameter at breast height was assumed to be unaffected by fire and tree height was estimated by eqn. 1.
Simulating vegetation growth
The development of a model to estimate the annual probability of wildfire occurrence as a function of biometric variables required the simulation of vegetation growth. Both a stand-level growth and yield model ([4]) and a shrub growth model ([5]) - previously used by Marques et al. ([56]) to estimate understory growth in Portuguese forests - were used to estimate the annual values of biometric variables of each plot in the period ranging from the inventory date to either the fire event date or the date of the next inventory. The simulation thus provided n temporal snapshots of each plot, where n is the number of years of this projection period. For modeling purposes, a dichotomous variable was assigned to each snapshot of each plot. This categorical variable takes the value “1” if a wildfire occurred in that year or the value “0” if the plot did not burn in that year. The former thus corresponded to the first simulation stopping criteria. If no fire events occurred, projections in the case of 4th NFI plots stopped in year 2004 as another inventory was available for year 2005, thus meeting the second simulation stopping criteria.
In order to strengthen to snapshot assumption by the simulation, satellite images were processed using IDRISI 3.2 to check whether there had been any harvest and forest cover change both in plots where the eucalypt age was over 9 years at the time of the wildfire event and in plots where the forest growth was projected over more than 6 years (Fig. 2). Specifically, Landsat 5TM images were used to check the cover type in 76 4th NFI unburned plots in each year in the period from 1998 to the year of wildfire occurrence or to 2004. MOS - Modular Optoelectronic Scanner and SPOT Satellite imagery were used to check the cover type in 101 5th NFI unburned plots in each year of the period from 2005 to the year of wildfire occurrence or to 2007. This check provided a list of 103 plots where no harvests and no cover type changes did occur (38 plots from the 4th NFI and 65 from 5th NFI).
Selecting unburned plots: proximity of fire ignition data
The official database from the Portuguese Forest Service (AFN) that stores the starting coordinates (ignition) of wildfires was used to further select plots to be considered for modeling purposes. For each year, a 2 kilometers buffer around each ignition was created to cover all burned plots in that year. This procedure eliminated from the analysis unburned plots that were not affected by a wildfire because there was no ignition point nearby rather than because of its biometric and environmental characteristics (Fig. 1, Fig. 2). In total, 319 unburned observations (plot yearly simulation snapshots) from 1998 to 2004 and 694 unburned observations (plot yearly simulation snapshots) from 2005 to 2007 were used to fit the model (Tab. 1). Thus the model was fit considering a total of 1 122 observations (1 013 unburned observations and 109 burned observations).
Fig. 2 - Methodology applied to develop an annual wildfire risk probability model for eucalypt stands in Portugal.
Tab. 1 - Number of observations recorded as burnt and unburnt areas in the studied period (1998-2007).
| Year | Unburnt | Burnt | Total |
|---|---|---|---|
| 1998 | 14 | 1 | 15 |
| 1999 | 6 | 2 | 8 |
| 2000 | 45 | 2 | 47 |
| 2001 | 67 | 3 | 70 |
| 2002 | 74 | 2 | 76 |
| 2003 | 62 | 46 | 108 |
| 2004 | 51 | 3 | 54 |
| 2005 | 266 | 46 | 312 |
| 2006 | 222 | 1 | 223 |
| 2007 | 206 | 3 | 209 |
| Total | 1013 | 109 | 1122 |
Methods
Annual wildfire occurrence probability model
The occurrence of wildfire in a stand is a binomial outcome that may be modeled by logistic regression. Actually, this is one of the most popular mathematical modeling approaches to describe the relationships of a set of variables with a dichotomous dependent variable ([47]). The logistic function in eqn. 2 is mathematically flexible, easy to use, and has a meaningful interpretation ([47]). The logistic regression model can be presented as (eqn. 2):
where Y is the dependent variable, i.e., the annual probability of wildfire occurrence in a pure even-aged eucalypt stand, x1 to xp are independent variables and β0 to βp, are parameters to be estimated.
For modeling purposes, this research considered the plot-level dichotomous categorical variable that takes the value “1” if a wildfire did occur (burnt plot) and “0” otherwise (unburnt plot). It further considered a large set of explanatory variables including biometric (e.g., stand basal area, age, quadratic mean diameter of trees in the stand), environmental (e.g., altitude, aspect, number of precipitation days) and socioeconomic variables (e.g., distance to roads, population). In total, 14 independent variables, 12 of which are continuous (Tab. 2) and two are categorical (Tab. 3) were considered. In the case of the variable distance to the closest road a dummy variable was created indicating the plot accessibility. This variable was assigned the value “1” when the distance from the road network was more than 1 kilometer (Road distance > 1km) and “0” if the distance was less than 1 kilometer (Road distance < 1km).
Tab. 2 - Statistics for the fitting dataset. (U): Unburnt; (B): Burnt.
| Variables | Description | Min | Mean | Max | |||
|---|---|---|---|---|---|---|---|
| U | B | U | B | U | B | ||
| Age (years) | Stand age | 1 | 2 | 10.09 | 11.42 | 27 | 30 |
| Altitude (m) | Terrain altitude | 15 | 48 | 217.43 | 257.88 | 1015 | 688 |
| Bshrubs (Mg ha-1) |
Shrubs biomass load | 0 | 0.44 | 5.81 | 11.3 | 15.2 | 15 |
| dg (cm) | Quadratic mean diameter |
0.8 | 2.52 | 12.32 | 13.2 | 31.39 | 23.69 |
| hdom (m) | Stand dominant height | 1.58 | 4.35 | 17.66 | 17.93 | 33.89 | 33.65 |
| G (m2 ha-1) | Stand basal area | 0.1 | 0.09 | 12.5 | 12.09 | 52.64 | 36.16 |
| G/dg | Stand structure | 0.01 | 0.01 | 1 | 1.03 | 3.73 | 13.19 |
| Ntrees (N/ha) |
Stand density | 20 | 20 | 1113.88 | 980.44 | 5334 | 5007 |
| Precipita (days/year) | Precipitation days in the area | 55.8 | 55.2 | 105.1 | 100.64 | 145 | 145 |
| Pop (hab/m2) |
Population per parish | 8.22 | 0.68 | 151.27 | 142.91 | 2325.43 | 1239.6 |
| Slope (º) | Terrain slope | 0 | 0 | 11.5 | 12.47 | 45 | 35 |
| Temp (ºC) | Yearly main temperature in the area |
8.75 | 8.75 | 14.39 | 14.44 | 21.3 | 16.75 |
Tab. 3 - Statistics for the categorical fitting dataset. (U): Unburnt; (B): Burnt.
| Variables | Description | U | B |
|---|---|---|---|
| Sunny aspect |
East (E) | 146 | 13 |
| Flat (F) | 49 | 3 | |
| North (N) | 148 | 14 | |
| Northeast (NE) | 181 | 25 | |
| Northwest (NW) | 111 | 8 | |
| Shady aspect |
South (S) | 92 | 18 |
| Southeast (SE) | 66 | 5 | |
| Southwest (SW) | 96 | 4 | |
| West (W) | 124 | 19 | |
| Road Distance |
< 1km | 464 | 42 |
| > 1km | 549 | 67 |
The annual wildfire occurrence probability model was developed using maximum likelihood methods ([63]) as implemented in the PROC LOGISTIC routine of the SAS 9.1 package ([84]). The selection of predictors out of the proposed set of explanatory variables was based on the test of the models corresponding to all possible combinations of variables x1 to xp ([34]). Model building further took advantage of an understanding of the process of wildfire occurrence. All predictors had to be logical and significant (α=0.05, as from Wald χ2 statistics). The presence of collinearity was assessed by adding new variables to the model and observing its impact on the slope coefficients and the estimated standard errors ([47]). Alternative models were compared using the Akaike Information Criterion (AIC - [7], [87]) and further considering the ecological consistency of predictors (i.e., signs of coefficients that are biologically reasonable) as well as management relevance (i.e., the model includes variables easy to obtain by a forest inventory). Model goodness-of-fit was assessed using Hosmer-Lemeshow goodness-of-fit statistics.
The validation of the models encompassed the analysis of the functional relations. No specific validation data sets were set aside and later used for that purpose. Two main reasons justify this decision. Firstly, the relatively small number of observations in the dataset used. Secondly, the emphasis of this research was in obtaining the best possible parameter estimates. The authors are aware of the advantages and disadvantages of splitting the data set for model validation purposes (well discussed for instance in [62] and [53]). However, they concluded that cross validation by data splitting and double cross validation would provide little, if any, additional information to the evaluation of the regression models.
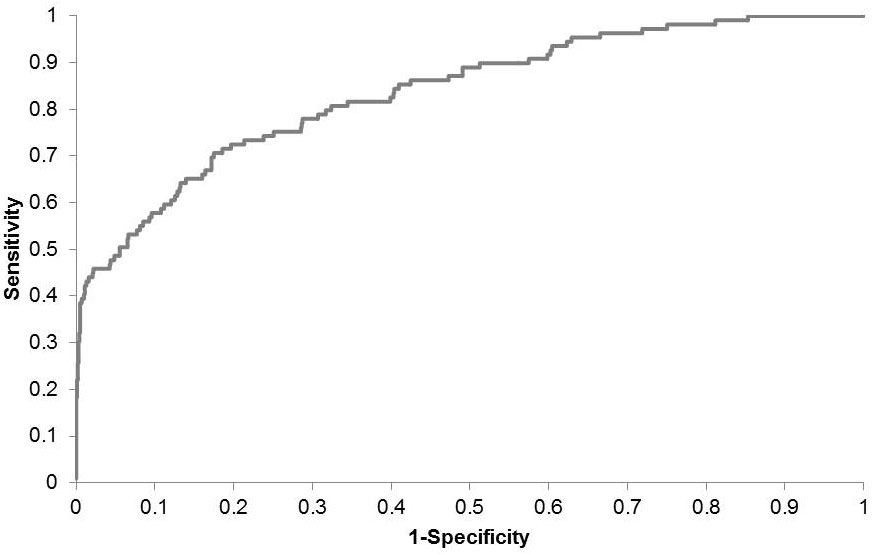
The Receiver Operating Characteristic (ROC) curve (SAS Institute, Cary, NC) was used to assess the functional relations in the wildfire occurrence model ([86], [47]). The ROC curve relies on the false/true - positive/negative proportion, where sensitivity is the proportion of wildfire occurrence responses that are correctly predicted and specificity is the proportion of no wildfire occurrence - responses that are also correctly predicted. A model with a ROC curve of 0.5 suggests no discrimination, 0.7-0.8 suggests having an acceptable discrimination, and 0.8-0.9 provides an excellent discrimination ([47]). The concordance analysis procedure was further used to support the interpretation of model outcomes ([52], [47]).
The odds ratio was further used to help interpret the role of each independent variable in explaining the probability of wildfire occurrence, as it estimated the net increase in the event probability caused by a unit change in the independent variable ([52], [47]). However, the change in the odds ratio resulting from non-marginal changes in the independent variable is often of greater interest and was further considered. Exponentiation of the parameter estimate for the independent variables in the model by the number “c” yields the odds ratio, where “c” is the increase in the corresponding independent variable.
The logistic model predicts the probability of an occurrence ranging continuously between 0 and 1. In order to convert an event probability (wildfire risk) to a dichotomous (e.g., burnt/unburnt) data an optimal cut-point must be defined and compared to each estimated probability ([47]). Different methods have been proposed to select the cut-point/threshold ([63], [16]). The optimal cut-point value can be defined according to data specificities or risk perception/needs of the users, and sometimes classification between burnt/unburnt stands is not even necessary in forest planning. Although we do not need this cut-point, we calculated it as an indicative value for users who just want to use the model to predict if a stand may burn or not. For this purpose, three different methods were used to define the cut-point: (1) the value that maximizes the index of concordance and correct classification rate (CCR - e.g., [82]); (2) the value where the sensitivity curve and the specificity curve cross each other ([47]); (3) the average observed percentage of event occurrence in the original data ([63]). In order to select optimal values, tables with classification error rates associated with the different methods were constructed.
Eucalypt coppice stand management scheduling
The annual wildfire risk model was used to help assess the impact of potential management actions in a typical eucalypt stand. In Portugal, a typical eucalypt prescription encompasses a plantation of about 1 250 seedlings ha-1. A full rotation may include up to 2 or 3 coppice cuts, each cut being followed by a stool thinning that may leave an average number of shoots per stool ranging from 1 to 2. Harvest ages typically range from 10 to 12 ([88]). Prescriptions further include several shrub cleanings over a rotation (i.e., 1 to 3 fuel treatments per cycle - [23]).
For demonstration purposes, it was assumed that the eucalypt stand was located at more than 1 kilometer from the road network. It was further assumed that the terrain altitude was 217 meters, the slope was 11.5º, the mean annual precipitation was 650 mm and that the understory shrub vegetative community had a re-sprouting ability of 50%. The prescription included a cutting cycle of 10 years, 3 coppice cuts and 1 or more shrub cleanings per cycle. It was also assumed that the stand was within the range of ignition points every year of the planning horizon. Stand and understory growth were estimated using the simulators developed by Barreiro & Tomé ([4]) and Botequim et al. ([5]), respectively.
Results
Annual wildfire occurrence probability model
The logistic model selected to predict the annual wildfire occurrence in a pure and even-aged eucalypt stand is as follows (eqn. 3):
where Bshrubs is the total biomass of shrubs (Mg ha-1), hdom is the stand dominant height (m), G /dg is a predictor combining information about density and tree sizes where G is the basal area (m2 ha-1) and dg is the quadratic mean diameter of trees in the stand (cm) and RoadDist is a dummy variable indicating the proximity to the road network. Specifically, if the distance to the network is less than 1 kilometer, RoadDist takes the value “0” otherwise it takes the value “1”.
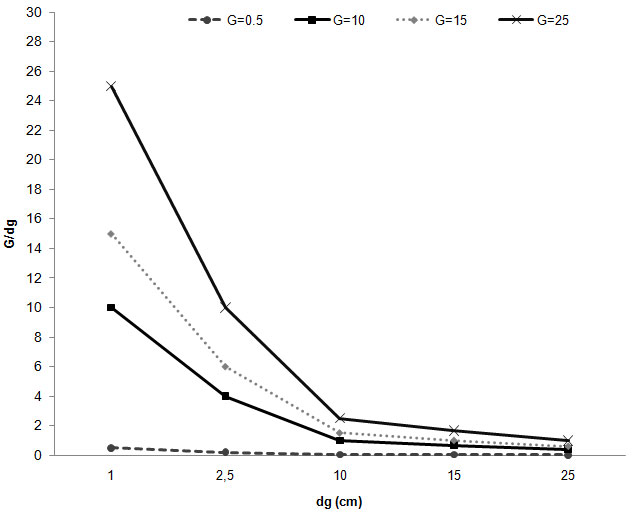
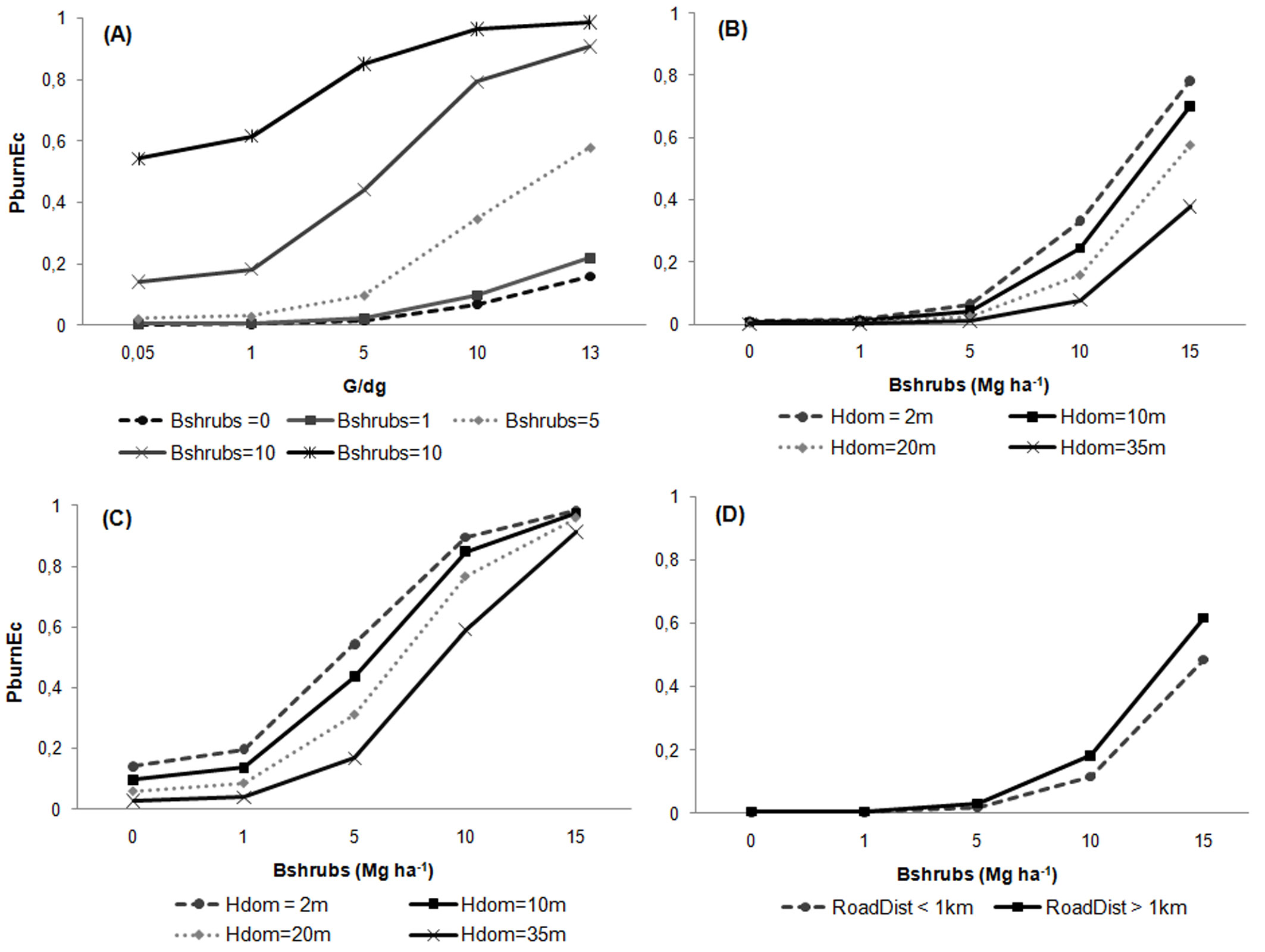
According to the model, stands with higher density are in general more prone to burn (Fig. 3). Yet this further depends on the tree sizes. For the same basal area, the value of predictor G/dg decreases with the quadratic mean diameter, thus highlighting that the wildfire occurrence probability is higher in stands with prevailing smaller trees (Fig. 3, Fig. 4a). As expected from biological reasons, the model indicates that shrub biomass was the most important variable affecting the probability of wildfire occurrence (p<0.0001 - Tab. 4). Further, higher shrub biomass increases the probability of a stand to burn (Fig. 4b e Fig. 4c). On the contrary, the increase of stand dominant height (hdom) decreases this probability. Finally, the model indicates that larger distances to the road network lead to an increase of the probability of fire occurrence (Fig. 4d).
Fig. 3 - Values of the variable G/dg for different combinations of basal area (G) and quadratic mean diameter (dg).
Fig. 4 - Effects of independent variables on the annual wildfire probability (PburnEc) obtained using eqn. 3 for an example eucalypt stand. (A) Effect of shrubs (Bshrubs, Mg ha-1) and G/dg (basal area over quadratic mean diameter); (B) effect of shrub biomass and stand dominant height (with G/dg = 1 m2 ha-1 cm-1); (C) effect of shrub biomass and stand dominant height (with G/dg = 10 m2 ha-1 cm-1); (D) effect of road distance and shrub biomass. Fixed values are the mean values of the whole dataset (Bshrubs =5 Mg ha-1, hdom = 17 m, RoadDist > 1km).
Tab. 4 - Logistic regression parameter estimates and fit statistics for the model predicting the annual wildfire occurrence probability (eqn. 3).
| Variable | Parameter | Estimate | SE | Wald > χ2 | Pr > χ2 |
|---|---|---|---|---|---|
| Intercept | β 0 | -5.4005 | 0.5561 | 94.3193 | <0.0001 |
| hdom | β 1 | -0.054 | 0.0232 | 5.4292 | 0.0198 |
| G/dg | β 2 | 0.3166 | 0.1319 | 5.7635 | 0.0164 |
| Bshrubs | β 3 | 0.3959 | 0.0375 | 111.1485 | <0.0001 |
| RoadDist > 1km | β 4 | 0.5372 | 0.232 | 5.3601 | 0.0206 |
All parameters estimates in eqn. 3 were found significantly different from zero at the 0.05 level as from the Wald χ2 statistics ([47] - Tab. 4). The model was successful in predicting whether fire did occur in 83.5% of stands (i.e., percentage of concordant pairs). The adequacy of the model was further assessed by the analysis of the ROC curve from the logistic model. The area under the ROC curve (0.838 - Fig. 5) indicates an excellent discrimination ([47]), thus showing that the selected model performs adequately. Collinearity assessment showed no collinearity among variables included in the model.
The odds ratio further helped the interpretation of results as it provides an intuitive and easily understood assessment of the contribution of an independent variable to the occurrence of an event ([52], [47]). The odds ratio analysis highlighted that the chance of a stand to burn increases 1.486 times if the total biomass of shrubs (Bshrubs) increases one Mg per ha. Similarly, an eucalypt stand that is more than 1 km distant from the road network is 1.711 times more prone to burn than a stand that is closer to this network. On the other hand, an increase in 1 meter of eucalypt stand dominant height (hdom) would decrease 0.947 times the fire occurrence probability, whereas an increase in 5 meters would decrease that probability by 0.763 times.
The most appropriate cut-point for the model was 0.11 as both sensitivity and specificity reach the same proportion is recommended this, enabling a better match between the stands where higher wildfire occurrence probability is predicted and the stands where a wildfire did actually occur. Using this value led to a CCR of 73.7% (Tab. 5).
Tab. 5 - Overall prediction rates for the annual wildfire occurrence probability model (eqn. 3). The observed burnt plots percentage was 9.71%. (a): the sensitivity and specificity curves cross ([47]); (b): average observed survival rate ([63]); (c) value that maximizes the CCR ([82]).
| Approach (cut-point) |
CCR (%) |
Sensitivity (%) |
Specificity (%) |
False burnt (%) |
Predicted as burnt (%) |
|---|---|---|---|---|---|
| 0.11a | 73.7 | 73.7 | 73.4 | 76.9 | 30.87 |
| 0.28b | 89.9 | 47.7 | 94.5 | 51.9 | 10.52 |
| 0.42c | 93.4 | 38.5 | 99.3 | 14.3 | 6.59 |
Eucalypt coppice stand management scheduling- application example
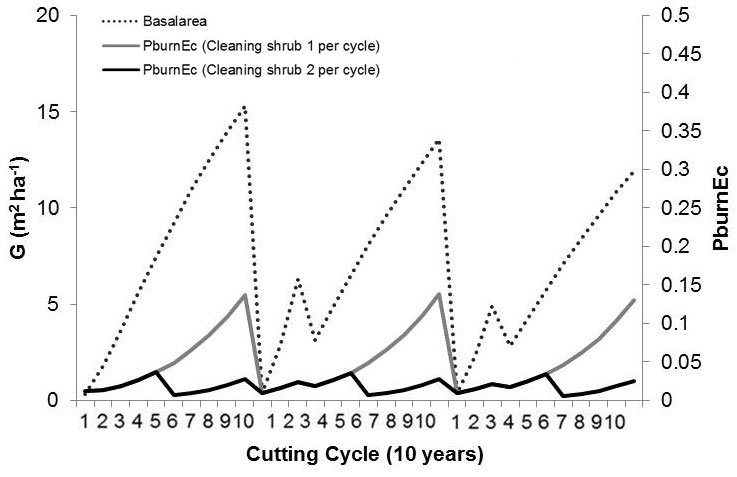
The model highlighted that coppice cuts and periodic removal of the fuel load do contribute to decrease fire occurrence probability. The annual fire occurrence probability ranged from 0 to 0.2% in a pure even-aged eucalypt stand if cleaned once in every cutting cycle, and from 0 to 0.04% if fuel treatments are prescribed to occur twice every cutting cycle (Fig. 6).
Fig. 6 - Eucalypt coppice stand management scheduling followed by 2 coppiced stands, with an average cutting cycle of 10 years and 1 or 2 shrub cleanings during each cutting cycle.
Discussion and conclusions
The development of a forest management plan should not ignore the probability of a wildfire occurrence as this may lead to poor decisions and gross miscalculations of output flows. Wildfire occurrence models are needed to help foresters assess the impact of forest management options on wildfire risk levels and thus design plans that may target effectively production, conservation and protection objectives. Traditional approaches to fire behavior simulation taking into account the fuel type (e.g., amount, size, and humidity of dead fuels - [33]), the value of environmental variables (e.g., topography and climate), as well as the ignition occurrence, can hardly be used in a typical forest management planning context. They rely on very specific data (e.g., ignition occurrence 20 years from now in the planning horizon, prevailing weather conditions before and during a wildfire occurrence 10 years from now in the planning horizon) that cannot be predicted to support the development of a forest management plan. Fire behavior simulation is a very important tool to enhance policy-making and management planning processes as well as to support strategic zoning and regeneration decisions. Yet forest management planning requires further information to address effectively wildfire risk.
Forest managers need information about the impact of controllable variables (e.g., understory fuel availability, tree species composition, structure and stand density) on the probability of wildfire occurrence ([18], [33], [61]). This information is influential to design and plan management options aimed to reduce wildfire risk (e.g., [41], [35], [31]). Nevertheless, such information was not available to support eucalypt forest management planning.
Several authors have addressed the effects of fire on eucalypt stands ([19], [45], [55]). Fire modeling indicated that wildfire control operations in eucalypt plantations are effective even under extreme weather conditions ([29]). Frequent fuel treatments have been demonstrated to reduce fire risk in these ecosystems ([2], [15]), thus suggesting the importance of a proactive stand and fuel management strategy ([24]). Nevertheless, no quantitative information was available to support the development of an eucalypt forest management plan under wildfire risk.
A logistic modeling approach using simple input variables that are measurable and/or predictable, as well as controllable by forest managers (e.g., shrub fuel load, basal area, dominant height and quadratic mean diameter) was developed to address this shortcoming. Contrarily to former approaches ([41]), this research took into account vegetation growth dynamics. Our research further confirmed the potential of the logistic model to assess the annual fire occurrence probability in pure and even-aged eucalypt stands in Portugal. In our model, all parameters were significant based on the Wald χ2 statistic test. The area under the ROC curve (0.838) indicated excellent discrimination between wildfire occurrence and non-occurrence ([47]).
According to the proposed model, wildfire risk (i.e., annual burn probability) strongly increases with the shrubs’ biomass load. This is in concordance with findings from previous investigations (e.g., [40], [38]). Castro et al. ([11]) showed that the amount of forest fuels, namely shrubs biomass, may further increase fire severity. Higher amount of shrubs dry biomass determines higher flammability and lower capability to prevent the advance of fire ([85], [11]). Generally, the fuel load generated by eucalypts increases with stand basal area ([40]). The impact of fuel management on wildfire occurrence has been underlined by the relation between fire risk and shrubs’ age ([83], [40], [50]). The rate of fuel accumulation after a wildfire in a eucalypt forest is relatively high, declining progressively after 5-8 years and stabilizing at a level that depends on the prevailing environmental conditions ([40]). Moreover, the abundance of shrubs contributes to an easier spread of surface fires and facilitate the starting of crown fires because of the vertical fuel continuity ([80], [32], [17]). From a fire suppression viewpoint, the effectiveness of silvicultural treatments can be gauged by their ability to prevent crown fires ([51]). In a study carried out in Australia by Bradstock & Williams ([6]) crown fires are unlikely in 1 to 5-year old fuels in eucalypt forest even under extreme weather.
Wildfire occurrence in eucalypt stands is also impacted by both tree size indicators (i.e., quadratic mean diameter and stand dominant height) and density indicators (basal area) that may be controlled by management planning. Wildfire occurrence probability increases with higher densities especially in stands with low quadratic mean diameter (i.e., higher G/dg). This is in concordance with other studies, where similar predicting variables have also been used as an indicator of stand-level competition and have been shown to influence fire risk probability ([41]). Denser stands comprised of smaller trees are more prone to high-intensity crown fire due to high vertical and horizontal continuity ([91], [17]). Wildfire occurrence probability also decreases with stand dominant height (hdom). The literature also provides evidence that such stands are less vulnerable to fire ([24], [27], [29]).
According to the proposed model, eucalypt stands located less than 1 km from the road network are less prone to burn. This is in concordance with other studies reporting that the proportion of burned areas increases with the distance from roads as a consequence of the lower accessibility by fire fighters ([9], [92], [3]). Other studies in Portugal demonstrated that larger distances impacted the proportion of area burned ([54]) or that ignitions that resulted in large fires occur further away from roads ([78]).
In this research, the climate variables used (i.e., number of days of precipitation equal or greater than 1.0 mm per year and yearly average temperature) express the long-term weather conditions that influence the stand vegetation features (e.g., fuel types). Therefore they characterize the site rather than the weather during a specific fire event. The weather before and/or during a specific wildfire can hardly be predicted within a long-term forest management planning context. According to other studies (e.g., [41], [56]), we used climate variables to model wildfire occurrence over long timespans rather than to characterize weather conditions for specific wildfire occurrences.
Our results underlined the importance of fuel treatments to decrease burn probability, and provide indications on which stands are more vulnerable or resistant to fire. Typically, eucalypt stands in Portugal are even-aged plantations with high densities and flammability ([55]). This research highlighted that emphasis has to be placed on managing the forest structure (i.e., stand density and height) and the fuel loads. This is in concordance with findings by Fernandes et al. ([28]) and Fernandes ([24]) who showed that stand structure is a major determinant of fire vulnerability.
The modeling approach adopted in this study provide valuable information to integrate risk considerations in both operational and strategic eucalypt forest management planning. It helps quantify the impact of silviculture treatments (e.g., coppice cuts and fuel treatments) on wildfire risk and provides an important tool to define management options aimed to reduce wildfire occurrence and develop effective fires prevention strategies.
The proposed model may be integrated with a growth and yield model (following the approach suggested by [46]) to predict the probability of a wildfire to occur upon ignition. To this purpose, it may take advantage of wildfire ignition models, such as the ones developed by Vasconcelos et al. ([92]) or Catry et al. ([12], [13]), or else consider a stochastic ignition ([41]). Additionally, the proposed wildfire occurrence probability model can easily be implemented in decision support systems to address wildfire risk in developing management plans either at stand level (e.g., [42], [71], [35], [30], [31]) or at landscape level ([39]).
The presented model may be applied in different contexts thus contributing to integrate effectively fire risk into forest management planning, and supporting forest managers in the design of prescriptions to manipulate stand endogenous variables that impact the probability of wildfire occurrence. Further research may extend current model with the aim of including landscape structure variables (e.g., neighboring stands biometric variables).
Acknowledgements
This research was supported by project “Decision support tools for integrating fire and forest management planning” (PTDC/ AGR-CFL/64146/2006) funded by the Portuguese Science Foundation; project FIRE-ENGINE: “Design Flexível de Sistemas de Gestão de Incêndios Florestais” (MIT/FSE/ 0064/2009); project MOTIVE: “Models for Adaptive Forest Management”, funded by 7th EU Framework Programme; and project ForEAdapt, funded by the EU 7th Framework Programme (FP7-PEOPLE-2010-IRSES) under grant agreement no. PIRSES-GA-2010-269257. The authors would like to thank the Portuguese Science Foundation for funding the PhD of Brigite Botequim (SFRH/BD/44830/2008) and Susete Marques (SFRH/BD/62847/2009). The authors wish also to acknowledge the Portuguese Forest Service for providing the perimeters of wildfires and NFI Databases. The authors want to thank Dr. Paulo Fernandes and Dr. Ane Zubizarreta-Gerendiain for the relevant remarks and suggestions and Dr. João Freire for his advice using the statistical software. The authors are also grateful to Susana Barreiro for the use of the software SIMPLOT to model the growth of the inventory plots.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
J Garcia-Gonzalo
S Marques
A Ricardo
JG Borges
M Tomé
Forest Research Centre, School of Agriculture, Departamento de Recursos Naturais, Ambiente e Território, Technical University of Lisbon, tapada da Ajuda, P-1349-017 Lisboa (Portugal)
Research Centre in Mathematics and Applications, Colégio Luís Verney, University of Évora, rua Romão Ramanho 59, P-7000-671 Évora (Portugal)
Corresponding author
Paper Info
Citation
Botequim B, Garcia-Gonzalo J, Marques S, Ricardo A, Borges JG, Tomé M, Oliveira MM (2013). Developing wildfire risk probability models for Eucalyptus globulus stands in Portugal. iForest 6: 217-227. - doi: 10.3832/ifor0821-006
Academic Editor
Marco Borghetti
Paper history
Received: Oct 12, 2012
Accepted: Mar 18, 2013
First online: May 27, 2013
Publication Date: Aug 01, 2013
Publication Time: 2.33 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2013
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 59759
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 48659
Abstract Page Views: 4137
PDF Downloads: 5373
Citation/Reference Downloads: 36
XML Downloads: 1554
Web Metrics
Days since publication: 4602
Overall contacts: 59759
Avg. contacts per week: 90.90
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2013): 29
Average cites per year: 2.23
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Wildfire risk and its perception in Kabylia (Algeria)
vol. 11, pp. 367-373 (online: 04 May 2018)
Research Articles
Impact of rotation length of Eucalyptus globulus Labill. on wood production, kraft pulping, and forest value
vol. 15, pp. 433-443 (online: 20 October 2022)
Research Articles
Variation of wood and bark density and production in coppiced Eucalyptus globulus trees in a second rotation
vol. 9, pp. 270-275 (online: 08 September 2015)
Research Articles
Wildfire cause analysis: four case-studies in southern Italy
vol. 3, pp. 8-15 (online: 22 January 2010)
Research Articles
Wildfires in Algeria: problems and challenges
vol. 8, pp. 818-826 (online: 25 March 2015)
Research Articles
Analysis of forest fires causes and their motivations in northern Algeria: the Delphi method
vol. 6, pp. 247-254 (online: 13 June 2013)
Research Articles
Moderate wildfire severity favors seed removal by granivores in a Mexican pine forest
vol. 18, pp. 121-127 (online: 24 May 2025)
Research Articles
Post-fire effects and short-term regeneration dynamics following high-severity crown fires in a Mediterranean forest
vol. 5, pp. 93-100 (online: 30 May 2012)
Research Articles
Harmonized dataset of surface fuels under Alpine, temperate and Mediterranean conditions in Italy. A synthesis supporting fire management
vol. 13, pp. 513-522 (online: 13 November 2020)
Research Articles
A model of shrub biomass accumulation as a tool to support management of Portuguese forests
vol. 8, pp. 114-125 (online: 27 July 2014)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword