Predictive capacity of nine algorithms and an ensemble model to determine the geographic distribution of tree species
iForest - Biogeosciences and Forestry, Volume 15, Issue 5, Pages 363-371 (2022)
doi: https://doi.org/10.3832/ifor4084-015
Published: Sep 20, 2022 - Copyright © 2022 SISEF
Research Articles
Abstract
The different models that predict the distribution of species are a useful tool for the evaluation and monitoring of forest resources as they facilitate the planning of their management in a changing climate environment. Recently, a significant number of algorithms have been proposed for this purpose, making it difficult to select the most appropriate to use. The evaluation of performance and predictive stability of these models can elucidate this problem. Distribution data of 17 pine species with high economic importance for Mexico were collected and distribution models were carried out. We carried out a pre-modeling design to select the prediction variables (climatic, edaphic and topographic), after which nine algorithms and an ensemble model were contrasted against one another. The true skill statistic (TSS) and the area under the curve (AUC) were used to evaluate the predictive performance of the models, and the coefficient of variation of the predictions was used to evaluate their stability. The number of predictive variables in the final models fluctuated from 6 to 12; the mean diurnal range and the maximum temperature of warmest month were included in the models for most species. Random forests, the ensemble model, generalized additive models and MaxEnt were the ones that best described the distribution of the species (AUC >0.92 and TSS >0.72); the opposite was found in Bioclim and Domain (AUC<0.75 and <0.82; and TSS<0.5 and <0.55). Support vector machine, Mahalanobis distance, generalized linear models and boosted regression trees obtained intermediate settings. The coefficient of variation indicated that Bioclim, Domain and Support vector machine have low predictive stability (CV>0.055); on the contrary, Maxent and the ensemble model attained high predictive stability (CV<0.015). The ensemble model obtained greater performance and predictive stability in the predictions of the distribution of the 17 species of pines. The differences found in performance and predictive stability of the algorithms suggest that the ensemble model has the potential to model the distribution of tree species.
Keywords
TSS, AUC, BRT, SVM, MaxEnt, Random Forests, GAM, Ensemble Model
Introduction
Species distribution models (SDM) are statistical methods or machine learning algorithms used to model and map past, present or future species distributions ([11], [37]). These tasks are relevant for forest resources management ([36]) and for forest conservation planning ([43]).
The SDM are performed by three different approaches: correlative, mechanistic, and process-oriented or hybrid ([39]). The correlative approach is the most widely used due to the availability of databases of the presence records of a species, climatic and meteorological data, and computerized algorithms that facilitate the modeling process ([24]). Additionally, the models with a correlative approach are the simplest to apply, since they rely on the statistical relationship that exists between the presence records of the species and the data that describes the environment they inhabit ([39]). Recent studies showed that the choice of the algorithm used for SDM is a source of variation in the process of the spatial prediction of the species, which can significantly affect the performance of the model ([28], [36]). This is the reason why the current trend is to examine multiple algorithms and select the most appropriate for their application, in accordance with the objective of each research ([44], [46]).
The algorithms available to implement SDM under the correlative approach are diverse (Tab. 1), all of which present advantages and disadvantages in its application, performance and predictive stability ([39]). In SDM, an algorithm is rarely identified as the best one in a consistent manner ([44]), since they are sensitive to the data and mathematical functions used to describe the distribution of the species based on environmental variables. In order to reduce this variation, it has been suggested to combine the predictions of different algorithms in a composite called ensemble model ([2]). The way to build the ensemble model can be through the median, the mean, and the weighted mean based on the predictive performance of the individual algorithms, measuring the performance based on statistics such as the area under the curve (AUC) and the true skill statistic (TSS - [2], [20]). Recent studies report that evaluating ensemble models from two or more algorithms is a viable alternative to improve prediction and consequently reduce uncertainty ([36]).
Tab. 1 - Evaluated algorithms to build the spatial distribution models of 17 species of pines. *For these analyzes, for each evaluated species we selected 20.000 pseudo-absences at random.
| Statistical approach - General description |
Data | Algorithm | Reference |
|---|---|---|---|
| Distance - they are considered climate envelope algorithms and calculate the similarity that exists between candidate pixels with respect to the selected presence records. | Presence | Bioclim (BIO) | Nix ([34]) |
| Domain (DOM) | Carpenter et al. ([5]) | ||
| Mahalanobis distance (MD) | Etherington ([13]) | ||
| Regression - they are algorithms that model the median of a response variable regarding prediction variables; they use the Logit Link Function to relate the expected value of the response variable with included predictors. | Presence/ absence* | Generalized linear model (GLM) | Guisan et al. ([18]) |
| General additive models (GAM) | |||
| Machine Learning - within SDM they are algorithms that focus on classification. Their main objective is to automatically improve the classification of training data until finally obtaining a better model. | Presence/ absence* | Sector-vector machine (SVM) | Betancourt ([3]) |
| Boosted regression trees (BRT) | Hijmans & Elith ([24]) | ||
| Random forests (RF) | Mi et al. ([32]) | ||
| Presence/ Background* | MaxEnt (MAX) | Phillips et al. ([40]) |
The genus Pinus has a notable importance in the Mexican economy by contributing around 6.3 million cubic meters of wood per year ([9]). According to the Biometric System for Planning Sustainable Forest Management (SIBIFOR), 17 pine species contribute with about 70% of the timber production in the country ([48]); these 17 species were incorporated to our SDM modelling analysis.
Recently, efforts have been made in Mexico to model the distribution areas of some pine species by means of the MaxEnt algorithm ([1], [16], [45], [29]). However, it has not been considered to evaluate the performance and predictive stability of other algorithms, which could mean that the most robust and reliable models designed to carry out this task are not being used. Consequently, forest resource managers would be dispensing with the best information in their process of decision-making. Therefore, the objective of this study was to evaluate the performance and predictive stability of nine algorithms and an ensemble model in defining the geographic distribution area of 17 coniferous species with high economic importance in Mexico.
Materials and methods
Species and presence records
The seventeen pine species that most contribute to timber production in Mexico (up to 70 %) were considered in the study: Pinus arizonica (P.ar), P. ayacahuite (P.ay), P. cembroides (P.ce), P. devoniana (P.de), P. douglasiana (P.do), P. durangensis (P.du), P. hartwegii (P.ha), P. herrerae (P.he), P. leiophylla (P.le), P. maximinoi (P.ma), P. montezumae (P.mo), P. oocarpa (P.oo), P. patula (P.pa), P. pseudostrobus (P.ps), P. strobiformis (P.st), P. strobus var. chiapensis (P.sc), and P. teocote (P.te). A database containing 17.908 presence records for the 17 species (Tab. 2) was assembled with information from the National Forest and Soil Inventory of Mexico (INFyS 2009-2014), the Global Biodiversity Information Facility ([17]), the National Commission for the Knowledge and Use of the Biodiversity ([8]). We used two land use and vegetation type maps scale 1:250.000 corresponding to years 1985 and 2014 (INEGI’s series 1 and 6 respectively -[26], [27]) to eliminate repeated, incomplete and poorly georeferenced data. For species distributed beyond the limits of Mexico, we use of a global land cover map ([19]). For coarse scale presence record validation, we used the Atlas of the World’s Conifers ([14]), but the available scientific literature ([43], [1], [16], [45], [29]) was used for finer scale validation of the records collected for each species so that they coincided with their reported natural distribution.
Tab. 2 - Number of occurrences by species used to estimate the distribution area of 17 species of pines. (NP): Number of presences.
| Species | NP | Species | NP |
|---|---|---|---|
| Pinus arizonica (P.ar) | 1165 | Pinus maximinoi (P.ma) | 370 |
| Pinus ayacahuite (P.ay) | 234 | Pinus montezumae (P.mo) | 560 |
| Pinus cembroides (P.ce) | 1846 | Pinus oocarpa (P.ooc) | 2182 |
| Pinus devoniana (P.de) | 540 | Pinus patula (P.pa) | 479 |
| Pinus douglasiana (P.do) | 394 | Pinus pseudostrobus (P.ps) | 1667 |
| Pinus durangensis (P.du) | 1426 | Pinus strobiformis (P.st) | 1430 |
| Pinus hartwegii (P.ha) | 448 | Pinus strobus var. chiapensis (P.sc) | 117 |
| Pinus herrerae (P.he) | 803 | Pinus teocote (P.te) | 1786 |
| Pinus leiophylla (P.le) | 2461 | - | - |
The databases for each species were entered into the Diva-GIS program ver. 7.5 ([23]). Through jacknife resampling ([6]) atypical climatic values were excluded, all of which might be related to poor georeferencing or to problems in the taxonomic identification of the species. For all species, records that contained three or more atypical climate conditions were excluded from the analysis ([6]). Finally, the density of the presence records was reduced to one record per km2 to reduce the effects of sampling bias and thus avoid over-fitting the models due to redundant environmental information ([24]).
Selection of environmental variables and calibration area
The environmental variables that characterize the areas where the species presence were recorded were obtained from the WorldClim version 2 repository, with an approximate resolution of 1 km2 ([15]). From 19 available variables, isothermality (Bio3), temperature seasonality (Bio4), temperature annual range (Bio7) and precipitation seasonality (Bio15) were eliminated, since biologically they are difficult to interpret. Escobar et al. ([12]) reported that the mean temperature of wettest quarter (Bio8), mean temperature of driest quarter (Bio9), precipitation of warmest quarter (Bio 18) and precipitation of coldest quarter (Bio19) show discontinuities between neighboring pixels, and therefore these variables were also excluded (Tab. 3). We incorporated to the analysis edaphic variables available in the SoilGrids database ([22]), since it has been shown that the combined use of edaphic and climatic variables improve the precision of predictions, compared to those constructed only with climatic variables ([49]). We also considered topographic variables in the modeling process (altitude, slope, diurnal anisotropic heat, Convergence index, Terrain ruggedness index, Topographic wetness index) derived from the digital elevation model available at the WorldClim website in SAGA-GIS v. 7.5.0 ([10]), as they were formerly identified important for modeling the spatial distribution of some pine species analyzed in our study ([43]).
Tab. 3 - Description of climatic, edaphic and topographic variables employed to build the spatial distribution models of 17 species of pines.
| Category | Variable | Key |
|---|---|---|
| Climatic | Annual mean temperature (°C) | bio1 |
| Mean diurnal range (°C) | bio 2 | |
| Maximum temperature of warmest month (°C) | bio 5 | |
| Minimum temperature of coldest month (°C) | bio 6 | |
| Mean temperature of warmest quarter (°C) | bio10 | |
| Mean temperature of coldest quarter (°C) | bio11 | |
| Annual precipitation (mm) | bio12 | |
| Precipitation of wettest month (mm) | bio13 | |
| Precipitation of driest month (mm) | bio14 | |
| Precipitation of wettest quarter (mm) | bio16 | |
| Precipitation of driest quarter (mm) | bio17 | |
| Soil proprieties | Sand (g kg-1) | sa |
| Cation exchange capacity (mmol(c) kg-1) | cec | |
| Clay content (g kg-1) | clc | |
| Organic carbon soil (dg kg-1) | ocs | |
| Bulk density (cg cm-3) | bd | |
| Organic carbon density (g dm-3) | ocd | |
| Silt (g kg-1) | sil | |
| Nitrogen (cg kg-1) | nit | |
| pH water (pH·100) | pH | |
| Soil organic carbon stock (t ha-1) | socs | |
| Topographic | Altitude (m a.s.l.) | alt |
| Slope (°) | slo | |
| Diurnal anisotropic heat | dah | |
| Convergence index | ci | |
| Terrain ruggedness index (m) | tri | |
| Topographic wetness index | twi |
The selection of the environmental variables to be used in SDM is an important aspect in the modeling process, since they have a significant effect on the predictive performance of the models ([7]). In this study, for each species a pre-modeling exercise was initially performed to identify the five most important predictor variables according to each tested algorithm. We fitted models iteratively (including or excluding each variable) and monitored the area under the curve (AUC) statistic value obtained to identify the five variables with the greatest contribution to predict the potential distribution area of the species. Variables that were identified in the top five by more than one algorithm were added only once to conform a set of likely predictor variables for a given pine species. We ended up with preliminary sets of 12-19 predictor variables depending on the pine species analyzed. We also implemented a variance inflation factor analysis (VIF <5 - [7]) to identify and minimize the presence of multicollinearity in the subset of relevant predictor variables. The final number of uncorrelated predictive variables was different for each species (Tab. S2 in Supplementary material).
In the process of building species distribution models, the definition of the accessible area for the species is a critical factor for the result of the calibration, evaluation and comparison of the model ([39]). In this study, the accessible area for each species was made from the terrestrial ecoregions of the world that delimit the distribution of each of the species, since they are zones with common physiographic, biological and historical characteristics. In this sense, climatological, geological and edaphological conditions are similar, and they are of great importance in the distribution of species and communities ([14]).
Spatial modeling process: algorithms and predictions
The modeling process for each species was carried out with the following configuration: 20.000 randomly pseudo-absences were generated and the evaluation of the models was executed with the bootstrap resampling method with 10 repetitions ([33]), since using 70% and 30% of the presence data for the calibration and evaluation of the model respectively can overestimate the evaluation parameters of the models ([42]). The SDM was performed for each of the species of interest using nine algorithms (Tab. 1) and an ensemble model, which was built from the weighted arithmetic mean of the true skill statistic (TSS) values obtained for the three algorithms with the highest predictive performance ([31]).
The performance of the algorithms was evaluated through the TSS ([21]) and the AUC ([36]). In order to calculate the TSS, binary predictions (presence/absence) are required, which is the reason we applied the cut-off threshold criterion to generate continuous predictions; this maximizes the sum of sensitivity and specificity, since it has been shown to be useful in modeling methods that employ only presence data ([29]). To denote differences between algorithms we performed the non-parametric Kruskall-Wallis test on the AUC values. Then we grouped the algorithms using the Fisher’s least significant difference criterion after correcting the p-value through the Bonferroni method. To compare the predictive stability of the algorithms including the ensemble model, we followed the methodology reported by Ren-Yan et al. ([44]). For each species and each algorithm, we calculated the coefficient of variation (CV = σx/xmean) for the TSS statistic values obtained from the modeling process through bootstrap resampling with 10 repetitions. A scatter plot was generated to show the results, including the mean and the standard error of the CV (y-axis) and TSS (x-axis) of the 17 species. The predictions of the best algorithm found for each species were applied to the cutoff threshold that maximizes the sum of sensitivity and specificity, and were projected on binary maps (suitable-not suitable).
Software
The pre-modeling and modeling processes were carried out using the “sdm” package ([33]), whereas for secondary information processes we used “raster” packages ([25]), “ntbox” ([35]), “rgdal” ([4]), all of which were implemented in the R software ([41]).
Results
Presence records and relevant environmental variables
The models were fitted with different number of presence records. In this regard, P.sc and P.le were the species with the lowest (117) and highest (2461) number of records; the models for the rest of the species were adjusted with a number of records that ranged between 234 and 2182 (Tab. 2). The premodeling and VIF analyses identified the important variables (Tab. S1 in Supplementary material) and with low collinearity (Tab. S2) to fit the models of the 17 species of pines. The number of variables used for the final models fluctuated between 6 variables for P.ar and up to 12 variables for P.de. Variables bio2 and bio5 were included as predictors in a large number of the SDM (Tab. 4). In contrast, variables bio6, bio12, bio16 and socs were included in very few of the generated models.
Tab. 4 - Important and uncorrelated variables used in the spatial distribution models of 17 pine species in Mexico. (bio1): annual mean temperature (°C); (bio2): mean diurnal range (°C); (bio5): maximun temperature of warmest month (°C); (bio6): minimun temperature of coldest month (°C); (bio10): mean temperature of warmest quarter (°C); (bio11): mean temperature of coldest quarter (°C); (bio12): annual precipitation (mm); (bio13): precipitation of wettest month (mm); (bio14): precipitation of driest month (mm); (bio16): precipitation of wettest quarter (mm); (bio17): precipitation of driest quarter (mm); (sa): sand (g kg-1); (cec): cation exchange capacity (mmol (c) kg-1); (clc): clay content (g kg-1); (ocs): organic carbon soil (dg kg-1); (bd): bulk density (cg cm-3); (ocd): organic carbon density (g dm-3); (sil): silt (g kg-1); (nit): nitrogen (cg kg-1); (pH): pH water (pH·100); (socs): soil organic carbon stock (t ha-1); (alt): altitude (m); (slo): slope (°); (dah): diurnal anisotropic heat; (ci): convergence index; (tri): terrain ruggedness index (m); (twi): topographic wetness index.
| Variable | P. arizonica | P. ayacahuite | P. cembroides | P. devoniana | P. douglasiana | P. durangensis | P. hartwegii | P. herrerae | P. leiophylla | P. maximinio | P. montezumae | P. oocarpa | P. patula | P. pseudostrobus | P. strobiformis | P. strobus chiapensis | P. teocate |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bio1 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| bio2 | - | x | x | x | x | x | x | x | - | x | x | - | x | x | x | x | x |
| bio5 | - | x | x | x | - | x | x | x | - | x | x | x | x | x | - | x | x |
| bio6 | - | - | x | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| bio10 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| bio11 | - | - | - | - | - | - | - | - | x | - | - | - | - | - | - | - | x |
| bio12 | - | - | x | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| bio13 | x | x | - | x | x | x | - | x | - | x | - | x | x | - | x | - | x |
| bio14 | x | x | x | - | - | x | x | - | - | x | - | x | x | x | - | - | - |
| bio16 | - | - | - | - | - | - | - | - | - | - | x | - | - | - | - | x | - |
| bio17 | - | - | - | x | x | - | - | x | - | - | - | - | - | - | x | - | - |
| sa | - | x | - | x | - | - | - | - | - | - | - | x | - | - | - | x | - |
| cec | - | - | x | x | - | - | x | - | x | - | x | x | - | x | - | x | x |
| clc | - | x | x | - | - | - | - | - | - | - | - | x | - | - | - | x | - |
| ocs | - | - | - | - | - | x | - | x | - | - | - | - | - | x | - | - | x |
| bd | x | x | - | x | - | - | x | - | - | x | x | - | x | x | x | x | - |
| ocd | - | - | - | - | - | - | - | - | x | - | - | - | - | - | - | - | - |
| sil | - | - | - | x | - | - | x | - | - | x | x | x | x | - | - | x | - |
| nit | - | - | - | x | x | - | - | x | - | x | - | - | - | - | - | x | x |
| pH | - | - | x | x | x | x | x | x | x | - | - | - | - | - | - | - | x |
| socs | x | x | - | - | - | - | x | - | - | - | x | - | x | - | x | x | - |
| alt | x | - | - | - | x | - | - | - | x | - | - | - | - | - | x | - | - |
| slo | x | x | - | x | - | - | x | - | - | - | - | - | - | - | x | - | - |
| dah | - | - | - | x | x | - | - | - | - | x | x | x | - | - | - | - | - |
| ci | - | - | - | - | - | - | - | - | - | - | - | - | x | - | - | - | - |
| tri | - | - | x | - | - | - | - | - | - | - | - | x | x | x | - | - | x |
| twi | - | - | - | - | x | - | x | x | x | - | - | - | - | x | - | - | - |
Predictive performance of the algorithms
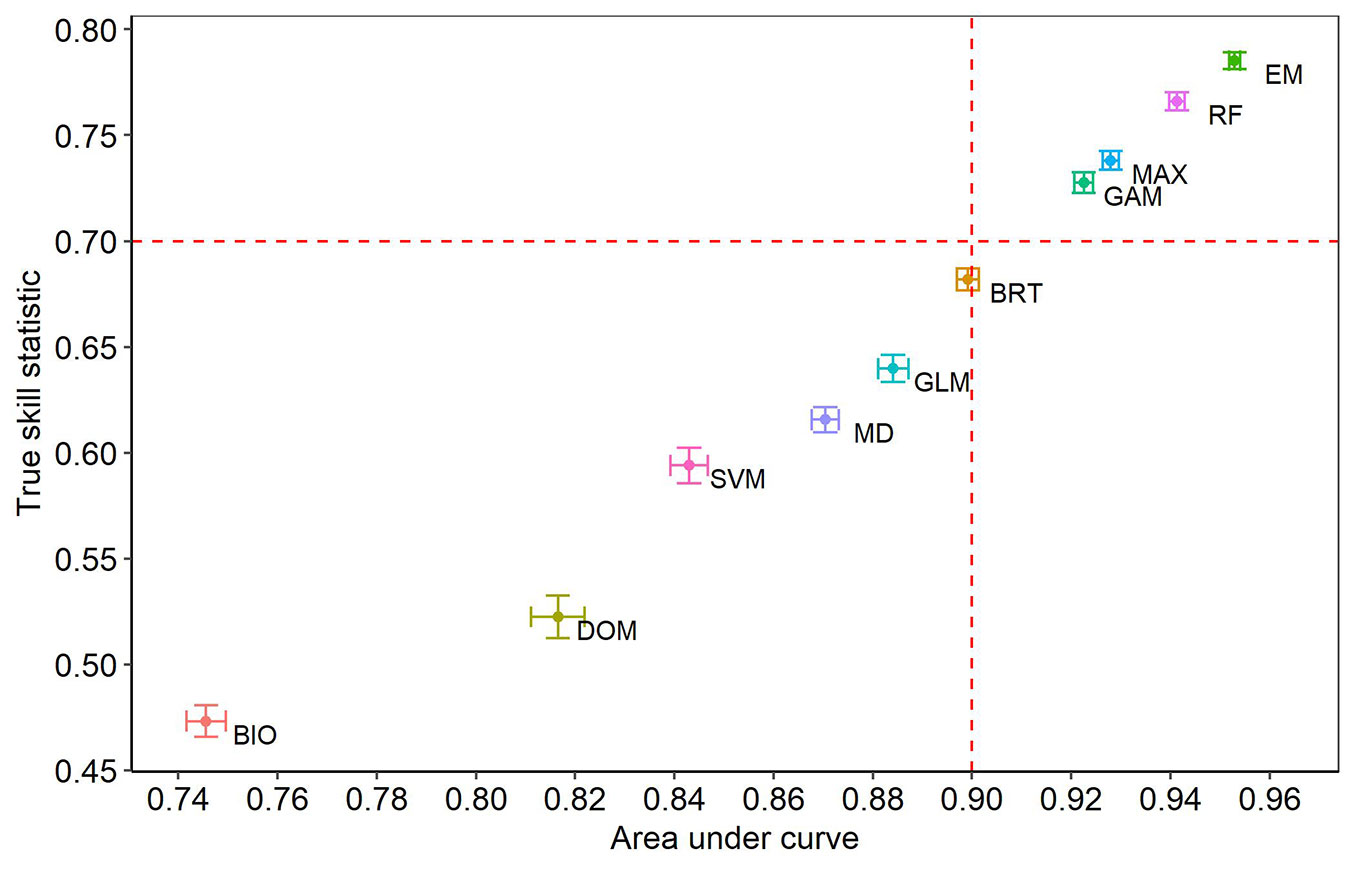
The evaluating statistics of the predictive performance of the algorithms as well as the ensemble model obtained different values. Six of the analyzed algorithms generated low values in the AUC (<0.90) and TSS (<0.70) statistics with respect to the rest of the algorithms (Fig. 1). GAM, MAX, RF and the ensemble model attained the highest values in AUC and TSS (>0.90 and >0.70, respectively). The algorithms with the lowest predictive performance were BIO and DOM, which obtained low values in AUC (<0.75 and <0.82) and TSS (<0.5 and <0.55). The SVM, DMAH, GLM and BRT algorithms obtained intermediate values for both statistics. The non-parametric Kruskall-Wallis test denoted that the performance between the algorithms was statistically different; the post-hoc test allowed us to rank the performance of the algorithms in descending order, and the assembled model obtained the best performance (Fig. S3a in Supplementary material). In contrast, BIO obtained the lowest performance (Fig. S3h), while MAX and GAM obtained a similar performance (Fig. S3c).
Fig. 1 - True skill statistic (TSS) and area under the curve (AUC) of nine algorithms and ensemble model for predicting the geographic range of 17 pine species. (BIO): Bioclim; (DOM): Domain; (SVM): Support Vector Machine; (MD): Mahalanobis distance; (GLM): Generalized linear models; (BRT): Boosted regression trees; (GAM): Generalized additive models; (MAX): MaxEnt; (RF): Random forests; (EM): Ensemble model.
Predictions and stability of the algorithms
The nine algorithms and the ensemble model differed in predicting spatial ranges for all species. For most species DOM predicted a larger distribution area (Fig. 2). Conversely, BIO and SVM predicted lesser areas of distribution for all species. The rest of the algorithms projected surfaces of different magnitude with a relatively lower difference than the previously mentioned algorithms. The algorithms with the highest performance (GAM, MAX, RF and the ensemble model) predicted similar areas (Fig. 2). According to the performance, the ensemble model better described the distribution of the pine species (Fig. S1 in Supplementary material).
Fig. 2 - Distribution area predicted by nine algorithms and ensemble model for the modeling of 17 pine species in Mexico. (Bio): Bioclim; (BRT): Boosted regression trees; (EM): Ensemble model; (MD): Mahalanobis distance; (DOM): Domain; (GAM): Generalized additive models; (GLM): Generalized linear models; (MAX): MaxEnt; (RF): Random forests; (SVM): support vector machine.
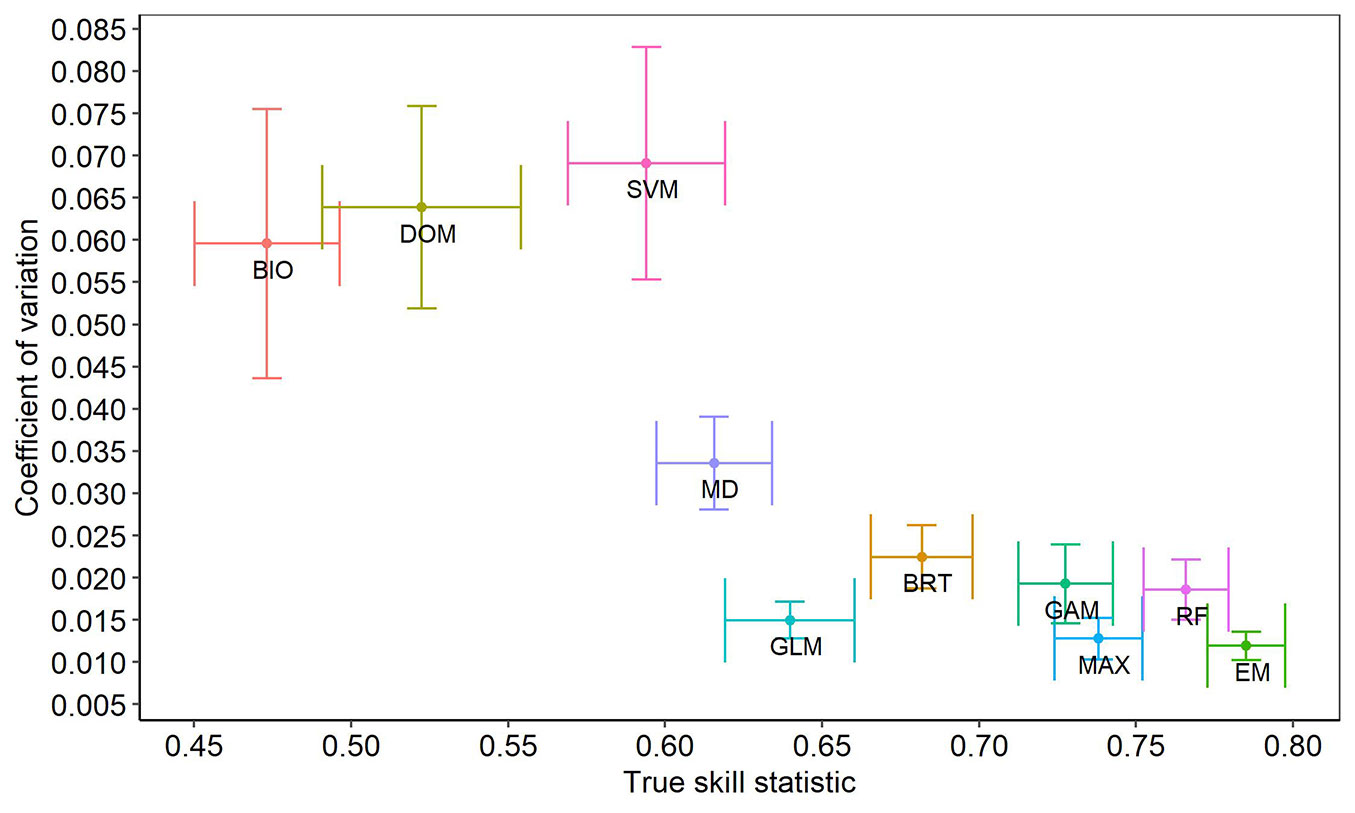
The coefficient of variation indicated that BIO, DOM and SVM have the lower stability in predictions (CV >0.055); also, their error bars are large, indicating that CV values differ widely between species (Fig. 3). EM and MAX obtained smaller variation (CV <0.015) and the standard error was low. MD, GLM, BRT, GAM, and RF were the algorithms that obtained a mean coefficient of variation in the TSS statistic (CV ≥0.015 and CV <0.040 - Fig. 3).
Fig. 3 - Coefficient of variation and TSS of nine algorithms and ensemble model for the modeling of the geographic distribution of 17 pine species in Mexico. (Bio): Bioclim; (DOM): Domain; (SVM): support vector machine; (MD): Mahalanobis distance; (GLM): Generalized linear models; (BRT): Boosted regression trees; (GAM): Generalized additive models; (MAX): MaxEnt; (RF): Random forests; (EM): Ensemble model.
Discussion
Environmental variables and final models
The SDMs with their correlative algorithms are the result of the projection of an ecological niche model created in the environmental space with different variables ([47]). It is clear that the selection of variables is an important factor in SDM and a set of important and uncorrelated variables can increase the predictive power and reduce the complexity of the model ([7]). Watling et al. ([50]) found that selecting uncorrelated variables with biological significance did not affect the predictive performance between the models; however, they did not find the same in spatial predictions, as using the RF algorithm with uncorrelated predictors, more stable predictions were obtained. In the same study, GLM provided more unstable predictions, which indicates that the algorithms are sensitive to the selection of environmental variables that affect the stability.
In our study, final models for all species used different combinations of variables, although it was observed that bio2 and bio5 were important variables for many species. This suggests that the distribution of the pine species considered in the present study is explained by variables related to temperature, which coincides with Ramos-Dorantes et al. ([43]), who reported temperature as one of the most important variables for the distribution of seven pine species in Mexico. In another study by Aceves-Rangel et al. ([1]), altitude was the most important variable in the models of 11 species of the same genus in Mexico. Due to the fact that altitude has a high degree of correlation (r=0.9) with temperature in an indirect manner, it can be inferred that it is a key variable in the distribution of pine species. The two formerly cited studies and our research obtained similar results due to the fact that the pine species of Mexico are distributed in temperate habitats where temperature is an important ecological factor ([14]). In this context, Perry ([38]) indicated that the pine species distributed in Mexico and part of Central America were strongly influenced by climatic fluctuations during the Paleogene period. This historical fact indicates that temperature and precipitation are key factors in the current distribution of pine trees and that the variables selected in our models were adequate. It is also worthwhile noting that for all the species analyzed, variables bio1, bio10 and bio15 were not considered in the model because they have a high collinearity with other variables.
Predictive performance of algorithms
Testing several algorithms to perform SDM helps to have a broader view of the advantages and disadvantages of the use of each single algorithm ([28]). Numerous studies on SDM of Mexican pines ([1], [16], [45], [29]) only used the MaxEnt algorithm, though the prediction of the distribution areas can be improved by employing an ensemble or an RF model. In this study, we found that all the analyzed algorithms obtained better predictions than those obtained by chance (Fig. 1). Nevertheless, it was observed that RF and the ensemble model were superior than the rest of the algorithms. In other studies ([31], [44], [36]), RF presented a superior predictive performance with respect to other algorithms, which is consistent with our results. However, it is important to mention that RF does not always attains the best prediction performance ([46], [30]). Discrepancies found between these studies can be explained by the different configurations of the algorithm ([32]). On the other hand, the ensemble model achieved the highest predictive performance (TSS >0.78 and AUC >0.95), although for P. ooc and P. ps it obtained a lower predictive performance than RF (Fig. S2 in Supplementary material). These findings are consistent with Hao et al. ([21]), who found that the ensemble model did not always obtain a higher predictive performance than the individual models.
Regarding the remaining evaluated algorithms, it was observed that SVM, MD, GLM and BRT obtained a medium predictive performance. BIO and DOM were the algorithms with the lowest predictive performance. These results are similar to those of Ren-Yan et al. ([44]) and Pecchi et al. ([36]), who classified algorithms according to their predictive performance (high and low). Nonetheless, we consider that this may be ambiguous as those findings could not represent the potential of the algorithms, since under certain conditions (predictors, size and sample quality) a method may or may not be effective ([39], [24]). As explained by Jarnevich & Young ([28]), the evaluation of algorithms is a practice that should be done in each case study and, depending on the obtained results and the objectives of the research, the most appropriate one should be selected in order to make the necessary inferences, since under certain conditions one of them can be better or worse than the others.
Prediction and variability of the algorithms
The predicted distribution areas for each of the 17 analyzed pine species (Fig. S1 in Supplementary material) coincided with the distribution reported by Farjon & Filer ([14]). Nonetheless, they differed for P.ce, P.do, P.du, P.ha and P.st with respect to the distribution described by Perry ([38]), since he identified more restricted distributions than those mentioned by Farjon & Filer ([14]). The distribution of the remaining species (P.ar, P.ay, P.de, P.he, P.le, P.ma, P.mo, P.ooc, P.pa, P.ps, P.sc and P.te) was similar.
The different algorithms showed significant differences in the predicted spatial distribution areas (Fig. 2). These results are due to the fact that the correlative models depend to a great extent on the chosen modeling algorithms ([2]), since each one starts from different assumptions for its construction. Therefore, it can be said that the prediction differences are inherent to the models ([39], [24]). Because of the above, it will always be difficult to choose a priori the best algorithm to model the distribution of species. However, the results of this study can be helpful when deciding which is the best algorithm to use ([28]).
The results indicated that three of the tested algorithms have a high prediction variability, except for EM and MAX (Fig. 3). The ensemble model had a low variation and high performance compared to the other algorithms, which provides an advantage in the prediction of the distribution of species. If species conservation problems or predictions are to be addressed under climate change scenarios, it is important to have a smaller variation caused by the modeling algorithms, since more robust inferences can be made with less variation ([21]). In several studies, ensemble models have been used as an alternative to reduce variability between the different algorithms, and they have even been proposed as promising techniques for species distribution modeling ([2], [31], [20]). Yet another way to minimize variability problems between algorithms is to repeatedly evaluate and compare multiple algorithms and, based on the obtained results, select the most adequate for modeling ([28]).
Conclusions
The ensemble model showed the highest predictive performance in modeling the spatial distribution of 17 pine species in Mexico, although RF, MAX and GAM also provided good predictions. The rest of the applied algorithms (BRT, GLM, MD, SVM, DOM and BIO) presented a lower accuracy; BIO, DOM and SVM were the algorithms with the greatest variability in predictions and, on the other hand, MAX and EM obtained the smallest variation. The rest of the algorithms attained a medium variability in the prediction of the distribution areas. For most of the species (16), the ensemble model showed the best predictive performance, although for P. ooc the most accurate predictions were obtained using RF.
The assessment of algorithms’ performance for predicting the spatial species distribution is an important step in the modeling process and must be carried out carefully, since the selection of one algorithm over another could lead to different results and therefore to different conclusions. Because the predictive differences between the algorithms are relatively large, the choice of one over the other should be based on the study objectives. The results derived from this research suggest that it is not convenient to choose an algorithm a priori, but rather to carry out tests among the available algorithms in order to increase the confidence in the prediction performance and stability of SDM.
Acknowledgements
The first author thanks CONACYT (Consejo Nacional de Ciencia y Tecnología, México, México) for the scholarship granted to carry out a doctorate in forest sciences. We also thank CONAFOR (Comisión Nacional Forestal) for providing data from the National Forest and Soil Inventory.
References
Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Authors’ Info
Authors’ Affiliation
José René Valdez-Lazalde 0000-0003-1888-6914
Gregorio Ángeles-Perez 0000-0002-9550-2825
Héctor Manuel De Los Santos-Posadas 0000-0003-4076-5043
Postgrado en Ciencias Forestales. Colegio de Postgraduados. Campus Montecillo (México)
Instituto Politécnico Nacional, CIIDIR-IPN-Michoacán, COFAA, Justo Sierra 28, 59510 Jiquilpan, Michoacán (México)
Corresponding author
Paper Info
Citation
Montoya-Jiménez JC, Valdez-Lazalde JR, Ángeles-Perez G, De Los Santos-Posadas HM, Cruz-Cárdenas G (2022). Predictive capacity of nine algorithms and an ensemble model to determine the geographic distribution of tree species. iForest 15: 363-371. - doi: 10.3832/ifor4084-015
Academic Editor
Maurizio Marchi
Paper history
Received: Feb 22, 2022
Accepted: Jul 12, 2022
First online: Sep 20, 2022
Publication Date: Oct 31, 2022
Publication Time: 2.33 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2022
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 32212
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 27093
Abstract Page Views: 2811
PDF Downloads: 1838
Citation/Reference Downloads: 17
XML Downloads: 453
Web Metrics
Days since publication: 1215
Overall contacts: 32212
Avg. contacts per week: 185.58
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2022): 12
Average cites per year: 3.00
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Climate change may threaten the southernmost Pinus nigra subsp. salzmannii (Dunal) Franco populations: an ensemble niche-based approach
vol. 11, pp. 396-405 (online: 15 May 2018)
Research Articles
Local ecological niche modelling to provide suitability maps for 27 forest tree species in edge conditions
vol. 13, pp. 230-237 (online: 19 June 2020)
Research Articles
Predicting the impacts of climate change on the distribution of Juniperus excelsa M. Bieb. in the central and eastern Alborz Mountains, Iran
vol. 11, pp. 643-650 (online: 04 October 2018)
Research Articles
Distribution factors of the epiphytic lichen Lobaria pulmonaria (L.) Hoffm. at local and regional spatial scales in the Caucasus: combining species distribution modelling and ecological niche theory
vol. 17, pp. 120-131 (online: 30 April 2024)
Research Articles
Potential natural vegetation pattern based on major tree distribution modeling in the western Rif of Morocco
vol. 17, pp. 405-416 (online: 22 December 2024)
Research Articles
Hemlock woolly adelgid niche models from the invasive eastern North American range with projections to native ranges and future climates
vol. 12, pp. 149-159 (online: 04 March 2019)
Research Articles
Forest fire occurrence modeling in Southwest Turkey using MaxEnt machine learning technique
vol. 17, pp. 10-18 (online: 02 February 2024)
Research Articles
Spatial modeling of the ecological niche of Pinus greggii Engelm. (Pinaceae): a species conservation proposal in Mexico under climatic change scenarios
vol. 13, pp. 426-434 (online: 16 September 2020)
Research Articles
Modeling compatible taper and stem volume of pure Scots pine stands in Northeastern Turkey
vol. 16, pp. 38-46 (online: 22 January 2023)
Research Articles
Modelling the carbon budget of intensive forest monitoring sites in Germany using the simulation model BIOME-BGC
vol. 2, pp. 7-10 (online: 21 January 2009)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword