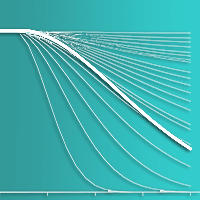
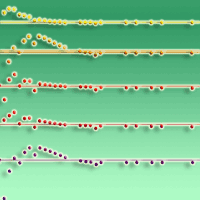
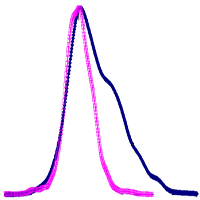
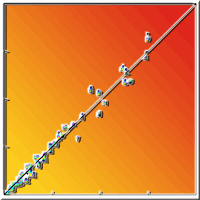
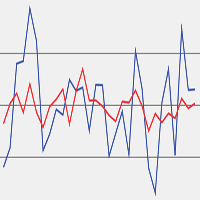
Self-thinning due to density-dependent mortality usually occurs during the forest development. To improve predictions of such processes during forest successions under climate change, reliable stand-level models are needed. In this study, we developed an integrated system of tree- and stand-level models by deriving tree diameter and survival models from stand growth and survival models based on climate-sensitive self-thinning rule of Chinese fir plantations in subtropical China. The resulting integrated system, having a unified mathematical structure, should provide consistent estimates at both tree and stand levels. Predictions were reasonable at both stand and tree levels. Because stand-level values aggregated from the tree model outputs are different from those predicted directly from the stand models, the disaggregation approach was applied to provide numerical consistency between models of different resolutions. Compared to the unadjusted approach, predictions from the disaggregation approach were slightly worse for tree survival but slightly better for tree diameter. Because the stand models were developed under the climate-sensitive self-thinning trajectory, the integrated system could offer reasonable predictions that could aid in managing Chinese fir plantations under climate change.
Keywords
, , , ,
Citation
Zhang X, Cao QV, Qu Y, Zhang J (2022). Deriving tree growth models from stand models based on the self-thinning rule of Chinese fir plantations. iForest 15: 1-7. - doi: 10.3832/ifor3792-014
Academic Editor
Alessio Collalti
Paper history
Received: Feb 24, 2021
Accepted: Nov 17, 2021
First online: Jan 13, 2022
Publication Date: Feb 28, 2022
Publication Time: 1.90 months
© SISEF - The Italian Society of Silviculture and Forest Ecology 2022
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Breakdown by View Type
(Waiting for server response...)
Article Usage
Total Article Views: 10314
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 4358
Abstract Page Views: 3387
PDF Downloads: 2026
Citation/Reference Downloads: 1
XML Downloads: 542
Web Metrics
Days since publication: 1520
Overall contacts: 10314
Avg. contacts per week: 47.50
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2022): 7
Average cites per year: 1.75
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
(1)
Allen MGII, Coble DW, Cao QV, Yeiser J, Hung I (2011)A modified stand table projection growth model for unmanaged loblolly and slash pine plantations in east Texas. Southern Journal of Applied Forestry 35: 115-122.
CrossRef |
Gscholar
(2)
Bailey RL, Clutter JL (1974)Base-age invariant polymorphic site curves. Forest Science 20: 155-159.
Online |
Gscholar
(3)
Berger U, Hildenbrandt H, Grimm V (2002)Towards a standard for the individual-based modeling of plant populations: self-thinning and the field-of-neighborhood approach. Natural Resource Modelling 15: 39-54.
CrossRef |
Gscholar
(4)
Berger U, Hildenbrandt H, Grimm V (2004)Age-related decline in forest production: modelling the effects of growth limitation, neighbourhood competition and self-thinning. Journal of Ecology 92 (5): 846-853.
CrossRef |
Gscholar
(5)
Bi H (2001)The self-thinning surface. Forest Science 47: 361-370.
Online |
Gscholar
(6)
Bi H (2004)Stochastic frontier analysis of a classic self-thinning experiment. Austral Ecology 29: 408-417.
CrossRef |
Gscholar
(7)
Burkhart HE (2013)Comparison of maximum size-density relationships based on alternate stand attributes for predicting tree numbers and stand growth. Forest Ecology and Management 289: 404-408.
CrossRef |
Gscholar
(8)
Burkhart HE, Tomé M (2012)Modeling forest trees and stands. Springer Science and Business Media, Dordrecht, The Netherlands, pp. 458.
Online |
Gscholar
(9)
Cao QV (2017)An integrated system for modeling tree and stand survival. Canadian Journal of Forest Research 47: 1405-1409.
CrossRef |
Gscholar
(10)
Cao QV (2019)A method to derive a tree survival model from any existing stand survival model. Canadian Journal of Forest Research 49: 1598-1603.
CrossRef |
Gscholar
(11)
Carretero AC, Alvarez ET (2013)Modelling diameter distributions of
Quercus suber L. stands in “Los Alcornocales” Natural Park (Cádiz-Málaga, Spain) by using the two-parameter Weibull functions. Forest Systems 22: 15-24.
CrossRef |
Gscholar
(12)
Charru M, Seynave I, Morneau F, Rivoire M, Bontemps JD (2012)Significant differences and curvilinearity in the self-thinning relationships of 11 temperate tree species assessed from forest inventory data. Annals of Forest Science 69 (2): 195-205.
CrossRef |
Gscholar
(13)
Daniels RF, Burkhart HE (1988)An integrated system of forest stand models. Forest Ecology and Management 23 (2): 159-177.
CrossRef |
Gscholar
(14)
DeSiervo MH, Jules ES, Bost DS, De Stigter EL, Butz RJ (2018)Patterns and drivers of recent tree mortality in diverse conifer forests of the Klamath Mountains, California. Forest Science 64 (4): 371-382.
CrossRef |
Gscholar
(15)
Eid T, Tuhus E (2001)Models for individual tree mortality in Norway. Forest Ecology and Management 154: 69-84.
CrossRef |
Gscholar
(16)
García O (2001)On bridging the gap between tree-level and stand-level models. In: Proceedings of IUFRO 4.11 Conference “Forest Biometry, Modelling and Information Science” (Renols K ed). University of Greenwich, London, UK, pp. 311-323.
Gscholar
(17)
Ge F, Zeng W, Ma W, Meng J (2017)Does the slope of the self-thinning line remain a constant value across different site qualities? An implication for plantation density management. Forests 8 (10): 355.
CrossRef |
Gscholar
(18)
Hann DW, Wang CH (1990)Mortality equations for individual trees in the mixed-conifer zone of southwest Oregon. Bulletin no. 76, Forest Research Laboratory, Oregon State University, Corvallis, OR, USA, pp. 17.
Online |
Gscholar
(19)
Hevia A, Cao QV, Alvarez-González JG, Ruiz-González AD, Von Gadow K (2015)Compatibility of whole-stand and individual-tree models using composite estimators and disaggregation. Forest Ecology and Management 348: 46-56.
CrossRef |
Gscholar
(20)
Huuskonen S, Miina J (2007)Stand-level growth models for young scots pine stands in Finland. Forest Ecology and Management 241: 49-61.
CrossRef |
Gscholar
(21)
Lam TY, Guan BT (2020)Modeling stand basal area growth of
Cryptomeria japonica D. Don under different planting densities in Taiwan. Journal of Forest Research 25: 174-182.
CrossRef |
Gscholar
(22)
Lei JF (2005)Forest resources in China. China Forestry Publish House. Beijing, China, pp. 172. [in Chinese]
Gscholar
(23)
Mabvurira D, Miina J (2002)Individual-tree growth and mortality models for
Eucalyptus grandis (Hill) Maiden plantations in Zimbabwe. Forest Ecology and Management 161: 231-245.
CrossRef |
Gscholar
(24)
Monserud RA, Sterba H (1999)Modeling individual tree mortality for Austrian forest 465 species. Forest Ecology and Management 113: 109-123.
CrossRef |
Gscholar
(25)
Monserud RA, Ledermann T, Sterba H (2004)Are self-thinning constraints needed in a tree-specific mortality model? Forest Science 50 (6): 848-858.
Online |
Gscholar
(26)
Nepal SK, Somers GL (1992)A generalized approach to stand table projection. Forest Science 38: 120-133.
Online |
Gscholar
(27)
Ogawa K (2018)Mathematical consideration of the age-related decline in leaf biomass in forest stands under the self-thinning law. Ecological Modelling 372: 64-69.
CrossRef |
Gscholar
(28)
Ogawa K, Adu-Bredu S, Yokota T, Hagihara A (2010)Leaf biomass changes with stand development of Hinoki cypress (
Chamaecyparis obtusa [Sieb. et Zucc.] Endl.). Plant Ecology 211: 79-88.
CrossRef |
Gscholar
(29)
Puettmann KJ, Hann DW, Hibbs DE (1993)Evaluation of the size-density relationships for pure red alder and Douglas-fir stands. Forest Science 39: 7-27.
Online |
Gscholar
(30)
Qin J, Cao QV (2006)Using disaggregation to link individual-tree and whole-stand growth models. Canadian Journal of Forest Research 36: 953-960.
CrossRef |
Gscholar
(31)
Reineke LH (1933)Perfecting a stand-density index for even-age forests. Journal of Agricultural Research 46: 627-638.
Gscholar
(32)
Ritchie MW, Hann DW (1997)Implications of disaggregation in forest growth and yield modeling. Forest Science 43 (2): 223-233.
Online |
Gscholar
(33)
SAS Institute (2011)SAS/STAT 9.3 user’s guide. SAS Institute, Cary, NC, USA, pp. 3316.
Gscholar
(34)
Scolforo HF, Mctague JP, Burkhart H, Roise J, Alvares CA, Stape JL (2019)Modeling whole-stand survival in clonal eucalypt stands in Brazil as a function of water availability. Forest Ecology and Management 432: 1002-1012.
CrossRef |
Gscholar
(35)
Stankova TV, Diéguez-Aranda U (2020)Dynamic structural stand density management diagrams for even-aged natural stands and plantations. Forest Ecology and Management 458 (2): 117733.
CrossRef |
Gscholar
(36)
Subedi N, Sharma M (2011)Individual-tree diameter growth models for black jack pine plantations in northern Ontario. Forest Ecology and Management 261: 2140-2148.
CrossRef |
Gscholar
(37)
Tang S, Meng CH, Meng FR, Wang YH (1994)A growth and self-thinning model for pure even-age stands: Theory and applications. Forest Ecology and Management 70: 67-73.
CrossRef |
Gscholar
(38)
VanderSchaaf CL, Burkhart HE (2012)Development of planting density-specific density management diagrams for loblolly pine. Southern Journal of Applied Forestry 36: 126-129.
CrossRef |
Gscholar
(39)
Woodall CW, Miles PD, Vissage JS (2005)Determining maximum stand density index in mixed species stands for strategic-scale stocking assessments. Forest Ecology and Management 216: 367-377.
CrossRef |
Gscholar
(40)
Wyckoff PH, Clark JS (2002)The relationship between growth and mortality for seven co-occurring tree species in the southern Appalachian Mountains. Journal of Ecology 90: 604-615.
CrossRef |
Gscholar
(41)
Yang Y, Titus SJ, Huang S (2003)Modeling individual tree mortality for white spruce in Alberta. Ecological Modelling 163 (3): 209-222.
CrossRef |
Gscholar
(42)
Yoda K (1963)Self-thinning in overcrowded pure stands under cultivated and natural conditions (intraspecific competition among higher plants XI). Journal of Biology, Osaka City University 14: 107-129.
Gscholar
(43)
Zhang X, Lei Y, Cao QV (2010)Compatibility of stand basal area predictions based on forecast combination. Forest Science 56 (6): 552-557.
Online |
Gscholar
(44)
Zhang X, Lei Y, Cao QV, Chen X, Liu X (2011)Improving tree survival prediction with forecast combination and disaggregation. Canadian Journal of Forest Research 41: 1928-1935.
CrossRef |
Gscholar
(45)
Zhang X, Cao QV, Duan A, Zhang J (2016)Self-thinning trajectories of Chinese fir plantations in Southern China. Forest Science 62 (6): 594-599.
CrossRef |
Gscholar
(46)
Zhang X, Lu L, Cao QV, Duan A, Zhang J (2018)Climate-sensitive self-thinning trajectories of Chinese fir plantations in south China. Canadian Journal of Forest Research 48 (11): 1388-1397.
CrossRef |
Gscholar
(47)
Zhang X, Cao QV, Wang H, Duan A, Zhang J (2020)Projecting stand survival and basal area based on a self-thinning model for Chinese fir plantations. Forest Science 66: 361-370.
CrossRef |
Gscholar