On the geometry and allometry of big-buttressed trees - a challenge for forest monitoring: new insights from 3D-modeling with terrestrial laser scanning
iForest - Biogeosciences and Forestry, Volume 8, Issue 5, Pages 574-581 (2015)
doi: https://doi.org/10.3832/ifor1449-007
Published: Mar 02, 2015 - Copyright © 2015 SISEF
Research Articles
Abstract
In many old-growth natural and close-to-natural forest types, notably in humid tropical forests, a relatively small number of very tall trees contribute considerably to stand basal area and biomass. Such trees often show distinct buttress roots with irregular non-convex shapes. Buttresses are complex structures in the lowest stem section, where most tree biomass is located. The methods used to assess the diameter of buttressed trees have a large impact on the determination of volume and biomass, as well as on the resulting estimates of the aboveground carbon stock in tropical forests. As the measurement of diameter at breast height (DBH at 1.3 m) is not feasible in such conditions, the diameter above buttress (DAB), where the cylindrical bole of the tree begins, is usually measured and included as an independent variable in biomass models. We conducted a methodological study aimed at determining the volume and biomass of individual buttressed trees belonging to several tropical species by the application of terrestrial laser scanning (TLS). The geometry and allometry of the buttresses, as well as the change with height along the stem in buttress volume and cross-sectional area were analyzed. Our results suggest that the relationship between cross-sectional areas at DAB height (ADAB) and the actual tree basal area measured at 1.3 m height is relatively strong (R² = 0.87) across a range of different species, buttress morphologies and tree dimensions. Furthermore, the change in stem cross-sectional area with tree height was surprisingly similar and smooth. Despite the small number of trees sampled, the methodological approach used in this study provided new insights on the very irregular geometry of buttressed trees. Our results may help improving the volume and biomass models for buttressed trees, that are crucial contributors to carbon stocks in tropical forests.
Keywords
Introduction
One of the most meaningful attributes used to describe forests both as a resource and as an ecosystem is biomass density per unit area. Nondestructive measurements of tree biomass are not possible - at least if the term “measurement” is used in its generic sense. Therefore, models are established based on destructively sampled trees to estimate total biomass. Tree variables commonly used for such models are the diameter at breast height (DBH, measured at 1.3 m height) or DBH in combination with total tree height. These allometric relationships (from the ancient Greek word “αλλος” = “other”) are commonly modeled as power functions ([25], [41], [43], [32], [14]) of the form M = aDb, where M is the mass of dry matter, D is the diameter, b is the allometric scaling factor and a is a coefficient determining the allometric intercept ([29]). The general model formulation also complies with assumptions of process models in plant allometry that are based on considerations on the hydraulic architecture and structural design of vascular plants and derive a particular scaling exponent of 8/3 ([40], [41], [42], [13], [26], [27]). Total tree biomass is expected to scale proportionally to the conducting tissue that determines the metabolic rate.
The predicted biomass value, however, is not to be understood as a “measurement”, but rather as “model-based estimation”, carrying not only measurement errors (introduced by the measurement of the input variables to the model used) but also model errors ([7]). In many old-growth natural and close-to-natural forest types, in particular tropical forests, the relatively few very large trees fix a large amount of carbon ([39]) and contribute a considerable share to the stand basal area and total biomass: “Large trees drive forest aboveground biomass variation in moist lowland forests across the tropics” ([37]).
In tropical forests the largest proportion of buttressed trees is usually among the emergent trees in the upper crown layer. These huge trees frequently show very irregular non-convex shapes ([3], [20], [9]). Clark ([6]) reports for a Costarican lowland rain forest that about 52% of the stands’ above ground woody biomass was constituted by trees whose diameter needed to be measured above stem irregularities. A study in southwest China shows that the percentage of buttressed trees is highest in the larger diameter classes ([16]). Buttresses are complex features that are regarded as an adaptation to poor tropical soils, enabling trees to form a flat root system in the upper, nutrient richer soil layers while maintaining their mechanical stability and anchorage ([34], [35], [12], [8], [23], [27]). Usually Dipterocarpaceae, Ligumninosae and Sterculiaceae show a greater tendency to produce buttresses than other tree species. Physiologically, buttress roots are the result of secondary xylem formed on the upper side of lateral roots. In very large trees the buttresses may extend to heights of more than 9 m. Early studies have already shown that the size and profile of buttresses vary considerably between species, while within species the development and morphology of buttressing often appears to follow a fairly fixed character ([34], [38], [16]).
The methods used to measure the diameter of buttressed trees have a large impact on the determination of the volume and biomass, and consequently on the resulting estimates on aboveground carbon stocks in tropical forests ([5]). Measuring the DBH of these trees is practically impossible and actually counterproductive, because a proper interpretation of such a measurement is not possible as of yet ([24]). Commonly, a diameter above buttress (DAB) is measured where the cylindrical bole of the tree starts ([5], [6], [1], [21]). However, ignoring the buttressed part of the stem when determining total tree biomass and carbon stocks (e.g., by applying biomass models that are calibrated based on DBH measurements) will lead to a considerable under-estimation ([28], [9]). This is a dilemma as there are no operational allometric models for buttressed trees, even though they are known to be one of the most important contributors to total biomass in many forests ([30], [17]). Even if buttressed trees are included in some general allometries (like e.g., [4]), unbiased predictions could only be expected if the model is applied to a forest that has a similar proportion of buttressed trees as the calibration dataset.
Hence the challenging shape of buttressed trees has long attracted the attention of forest researchers and ecologists and their morphology has been investigated by different techniques. The measurement of the cross-sectional area for buttressed parts of the trunk with conventional techniques is difficult ([24]) and precise volume estimates of the buttressed stem section for larger trees are rare and often based on destructive techniques ([28]).
Terrestrial laser scanning (TLS), on the other hand, offers new possibilities to tackle the issue of buttress shape by providing a contactless and non-destructive approach to derive 3-dimensional point clouds of the stem surface that can be used as a basis to establish operational allometric models for buttressed trees. The application of terrestrial “close-range remote sensing” is not entirely new. For example, Dean ([10]) presented a study where terrestrial photography was applied to assess the stem taper of buttressed trees. Moreover, a study on modeling irregularly shaped trees with TLS and photogrammetry was recently conducted in Central Africa ([2]).
The overall goal of this study is to contribute to improving buttressed tree mensuration, in particular in the context of determining individual tree volume and biomass. We were interested in tree geometry and allometry of buttress variables and how buttress volume can be determined from variables that can realistically be measured in the field during standard forest monitoring projects. If multiplied with mean wood density the buttress volume can also be used to predict the biomass of respective stem sections. Further, in order to apply existing allometric biomass models that are based on DBH or tree basal area at 1.3 m above the ground, our study evaluates whether these input variables could be modeled from DAB measurements. For this study we scanned 12 huge buttressed trees of different species in the Botanical Garden of Bogor, Indonesia and analyzed the geometry of the buttresses, specifically investigating the change of the stem cross-sectional area and compactness over tree height for individual trees, as well as the common allometry of the buttresses over different species. Despite the relatively small number of sample trees does not allow general conclusions about buttress morphology in different species, our study does give valuable indications about the suitability of the methodological approach.
Material and methods
Study site
Data were collected in the Bogor Botanical Garden (Kebun Raya Bogor) located in the city of Bogor, 60 km south of Jakarta, Indonesia (WGS 84: 6° 35′ 51″ S, 106° 47′ 54″ E). The Botanical Garden, founded in 1817, has a total area of 87 hectares and contains a wide diversity of flora and fauna, approximately 15 000 plant and tree species including huge buttressed trees. Due to the great variety of buttressed trees and the good visibility of their stems, the study site offers ideal conditions for prelimininary methodological studies.
We selected 12 different isolated buttressed trees spanning a variety of species, buttress heights and buttress geometric complexity (Tab. 1) and that were well visible by the terrestrial laser scans, since buttresses were not covered by climbers or other vegetation.
Tab. 1 - List of the tree species sampled in this study.
| Tree (#) | Species | Family | Height (m) |
|---|---|---|---|
| 1 | Koompassia excelsa | Fabaceae | 43.3 |
| 2 | Ficus robusta | Moraceae | 39.9 |
| 3 | Celtis rigescens | Cannabaceae | 48.3 |
| 4 | Ficus albipila | Moraceae | 53.7 |
| 5 | Shorea leprosula | Dipterocarpaceae | 51.7 |
| 6 | Sterculia urceolata | Sterculiaceae | 34.0 |
| 7 | Sterculia urceolata | Sterculiaceae | 39.1 |
| 8 | Sterculia foetida | Sterculiaceae | 39.1 |
| 9 | Ceiba pentandra | Bombacaceae | 32.6 |
| 10 | Bombax ceiba | Bombacaceae | 34.1 |
| 11 | Bombax valetonii | Bombacaceae | 30.3 |
| 12 | Bombax valetonii | Bombacaceae | 30.1 |
Terrestrial laser scanning
A phase-based terrestrial laser scanner (Zoller and Fröhlich Imager 5010c, Zoller and Fröhlich GmbH, Wangen i.A., Germany) was used to obtain three-dimensional point clouds. The single-scan resolution is defined by an angular step width of 0.036° and a field-of-view of 360° horizontally and 320° vertically, resulting in up to 44 million measurements per scan. The wavelength of the emitted light beam is 1500 nm. Scan settings were selected to provide a good balance of scan time and resolution; the time-consuming HDR image capture option was not used. A multiscan method was applied to retrieve a complete high-density point cloud of the bole and buttresses. In order to eliminate scan shadows up to 8 single scans from different positions were merged by placing artificial targets around the tree to co-register the single point clouds using ZF Laser Control 8.2 (Zoller and Fröhlich GmbH, Wangen i.A. Germany) with a maximum registration error of less than 6 mm. The laser returns of single trees were extracted manually using Cyclone (Vers. 6, Leica Geosytems, Heerbrugg, Switzerland) and exported as .xyz file for further processing in R ([33]).
Point cloud processing
We used the Poisson Surface Reconstruction method ([18]) for solid modeling based on the algorithm provided by the software MeshLAB (Version 1.3.2). The meshes were applied to the whole trunk, but visual quality checks reveal that the resulting surface models do not describe the actual stem form very well, especially for very irregular trees. For an automated polygonal outline delineation of cross sections in different tree heights we applied the basic alpha shapes ([11]) based on the Delaunay triangulation to each polygon. However, this approach failed, especially in cases of high complex tree geometries, due to variation in point density.
In order to determine accurate outlines of the non-convex cross sections at different heights for those trees that show more complex buttress morphology, we separated the point clouds in continuous thin layers (“discs”) of 5 cm height, according to z values to the upper end of buttresses. Above buttresses the distance between layers was increased to 50 cm up to the first strong branches. The lowermost disc was defined as the first cross-section that is free of ground elements (soil). The height of this disc was also used as reference for the determination of DBH height (1.3 m).
Each layer of the point cloud was projected to a plane by removing the height information and a non-convex polygonal outline was delineated manually in standard GIS software (ArcGIS 10). Area, perimeter and shape metrics were calculated for each height from the outline delineated polygon. Further, we computed the convex hull and calculated its perimeter (Fig. 1). The latter is equal to a girth measured by tape around the buttresses at a specific height.
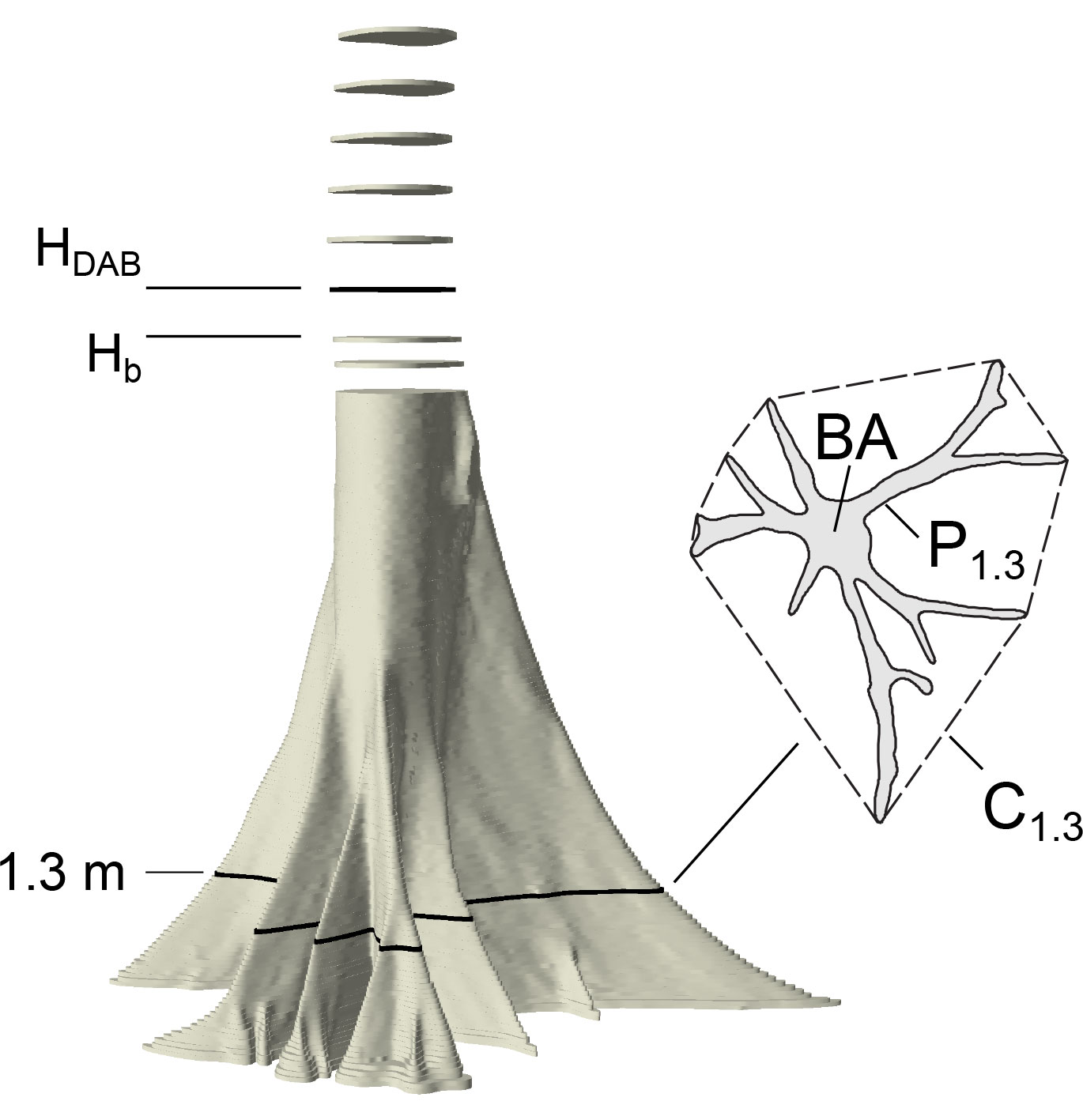
Fig. 1 - Graphical representation of the measurements taken on each sample tree analyzed. Hb is the maximum height of buttresses, HDAB is the height of the diameter above buttresses (Hb+50 cm), A is the actual cross-sectional area (here at breast height), P1.3 is the actual non-convex perimeter of the cross section at breast height and C1.3 is the perimeter of the convex hull (dashed line).
Estimation of buttress volume
From the delineated cross sections, the volume of each disc was calculated using the Smalian’s formula (eqn. 1):
where Al and Au are the cross-sectional areas at the lower and upper side of each disk and l is its height (5 cm or 50 cm, in our case). The single layer volumes were then accumulated over tree height, so that the actual volume up to each height interval is available.
Characterization of buttress shape
For each cross section we calculated the actual perimeter P of the polygon, the cross-sectional area A and their ratio (P/A). Moreover, we computed different metrics characterizing the shape of the cross sections. The isoperimetric quotient Q is a measure of compactness and describes the ratio of the actual cross-sectional area A and that of the circle of same perimeter P (eqn. 2):
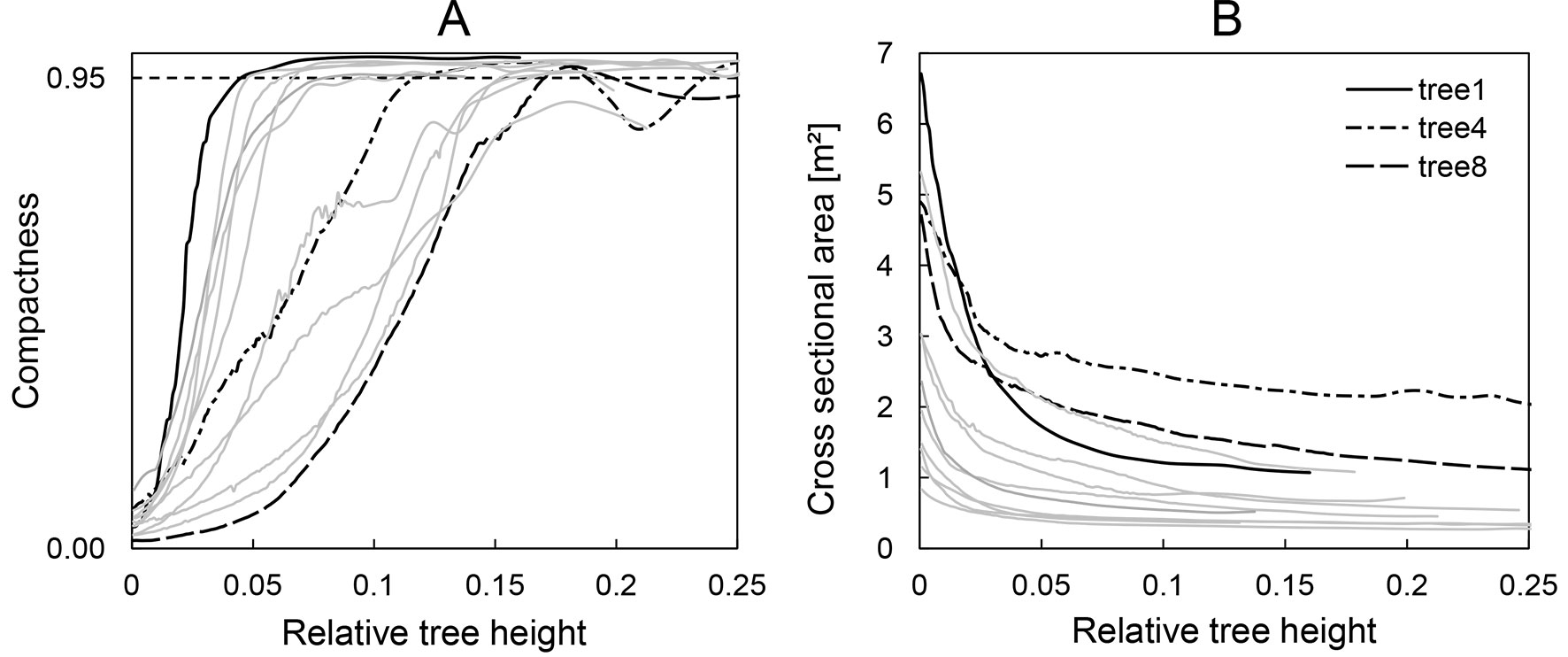
The end of buttresses refers to the height at which the isoperimetric index becomes ≥ 0.95, indicating that the shape of the cross section is close to a circle (Fig. 2A). DAB was derived as diameter of a coextensive circle at 50 cm distance above the last buttress, which differed little from the average of two perpendicular direct measurements in the point clouds. There is no consistent definition of the height at which DAB is measured (and neither a consistent definition of what is meant by the “top” of buttress); distances above the highest buttress of 0 cm ([24], [36]), 20 cm ([22]), 30 cm ([1] citing [15]), and 50 cm ([23]) appear to be most common. However, the differences in diameter between these positions at the stem are minimal in our data set. The perimeter of the convex hull in breast height C1.3 is the girth measured above the buttresses at 1.3 m above the ground. The cross-sectional area at breast height is the tree basal area (BA).
Fig. 2 - (A) Development of the isoperimetric quotient (Q) over the relative tree height. (B) Development of the cross-sectional area over the relative tree height.
Based on the DAB and its height we derived a buttress form factor fb that describes the relation between the actual buttress volume (Vb) and the volume of a cylinder with a diameter equal to DAB and a length equal to the DAB measurement height HDAB as follows (eqn. 3):
This form factor can be interpreted as an “indicator” for the potential under-estimation of the volume of the lower stem section in case that DAB is used in the context of volume modeling.
In order to search for any relations among buttress variables that are of practical relevance, we fitted functions to describe the relation between the actual tree basal area, the cross-sectional area in DAB height and the C1.3. Acknowledging the small sample size, we did not focus on the best fit to the twelve data points, but we chose functions that make sense on first principles and that could extend over the full possible range of data. Power functions were fitted by linear regression on log-transformed data.
Results
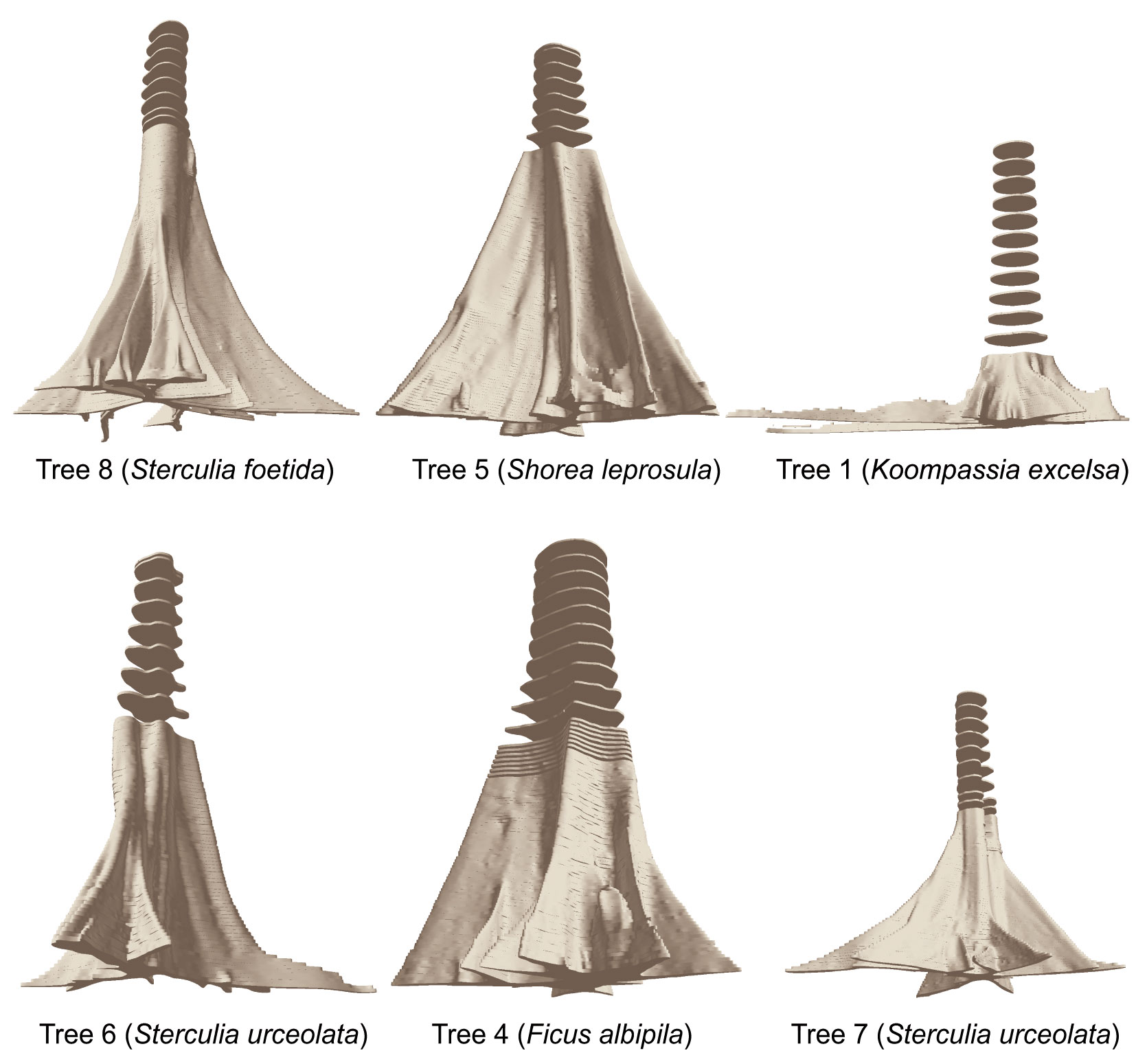
In this study, the selected trees had very different dimensions and buttress morphologies, which was also reflected in the variables extracted. Tab. 2 thus gives an overview of the main characteristics of the 12 sample trees. The highest volume of the buttressed stem section was found for tree #4 (Ficus albipila) with 20.2 m3 up to a height of 7.18 m (and 38.2 m3 up to 15.5 m height). The total height of buttresses showed large variations. Some of the species analyzed were characterized by very tall buttresses of more than 8 m (e.g., Sterculia urceolata or Ficus robusta), while others tend to develop long lateral buttresses though quite low upwards (e.g., Koompassia excelsa or Bombax valetonii). Fig. 3 shows a perspective view of the delineated cross sections. Here the polygons are extruded to their original height of 5 cm, giving an overview of the different buttress morphologies detected for the selected trees.
Tab. 2 - Buttress characteristics obtained for each sampled tree. (BA): basal area; (C1.3) girth at 1.3 m; (HDAB): height of DAB measurement; (DAB): diameter above buttress, (Vb): buttress volume; (fb): buttress form factor.
| Tree | BA (m²) |
C1.3 (m) |
HDAB (m) |
DAB (cm) | Vb (m3) |
f b |
|---|---|---|---|---|---|---|
| 1 | 2.41 | 5.84 | 2.43 | 1.40 | 7.45 | 1.99 |
| 2 | 1.49 | 8.78 | 7.07 | 0.88 | 7.97 | 1.85 |
| 3 | 0.52 | 3.40 | 5.08 | 0.72 | 2.67 | 1.29 |
| 4 | 3.15 | 10.18 | 7.18 | 1.66 | 20.50 | 1.32 |
| 5 | 2.73 | 12.68 | 9.08 | 1.18 | 17.41 | 1.75 |
| 6 | 0.88 | 6.17 | 7.23 | 0.81 | 5.10 | 1.37 |
| 7 | 1.27 | 8.06 | 6.78 | 0.95 | 6.97 | 1.45 |
| 8 | 2.35 | 13.38 | 7.03 | 1.32 | 13.67 | 1.42 |
| 9 | 0.77 | 3.53 | 2.98 | 0.85 | 2.65 | 1.57 |
| 10 | 0.43 | 3.27 | 2.63 | 0.67 | 1.24 | 1.34 |
| 11 | 0.46 | 2.50 | 1.98 | 0.72 | 1.33 | 1.65 |
| 12 | 0.52 | 2.83 | 2.98 | 0.73 | 1.72 | 1.38 |
Fig. 4 shows how the cross sections change along the lowest 5-m stem section for some sample trees: the geometries vary considerably, so that for many trees the stem could not be distinguished at the lowest cross sections.
Fig. 4 - Cross sections at different heights of tree #1 (Koompassia excels), tree #2 (Ficus robusta), tree #4 (Ficus albipila), tree #5 (Shorea leprosula), tree #7 (Sterculia urceolata) and tree #8 (Sterculia foetida). The dashed line at 1.3 m height represents the outline of the convex hull that could be tape-measured as girth “around” butressess.
Comparing the lower profiles of the depicted trees, the different morphology of lateral buttresses becomes obvious. While the horizontal projection of the laterals for tree #4 (Ficus albipila) was characterized by a trapezoid form that narrows with increasing distance, the buttresses of tree #8 (Sterculia foetida) were extremely thin.
In contrast to the different buttress morphologies of sample trees and their irregular cross sections, the development of the stem cross-sectional area over tree height was surprisingly similar and smooth. Fig. 2 shows the compactness (A, left) and the development of the cross-sectional area over the relative tree height (B, right).
Buttress allometry
Despite the different morphology of buttressing across the tree species analyzed, the buttress form factor we derived for every individual tree showed a surprisingly small variability (Tab. 2). The mean form factor derived from the sample trees was fb=1.53 with a standard deviation of 0.23. A simple generalized form factor may be applied to assess the volume of the buttressed lower stem section Vb. Such calculation is based on two measurements, the DAB and its height HDAB (eqn. 4):
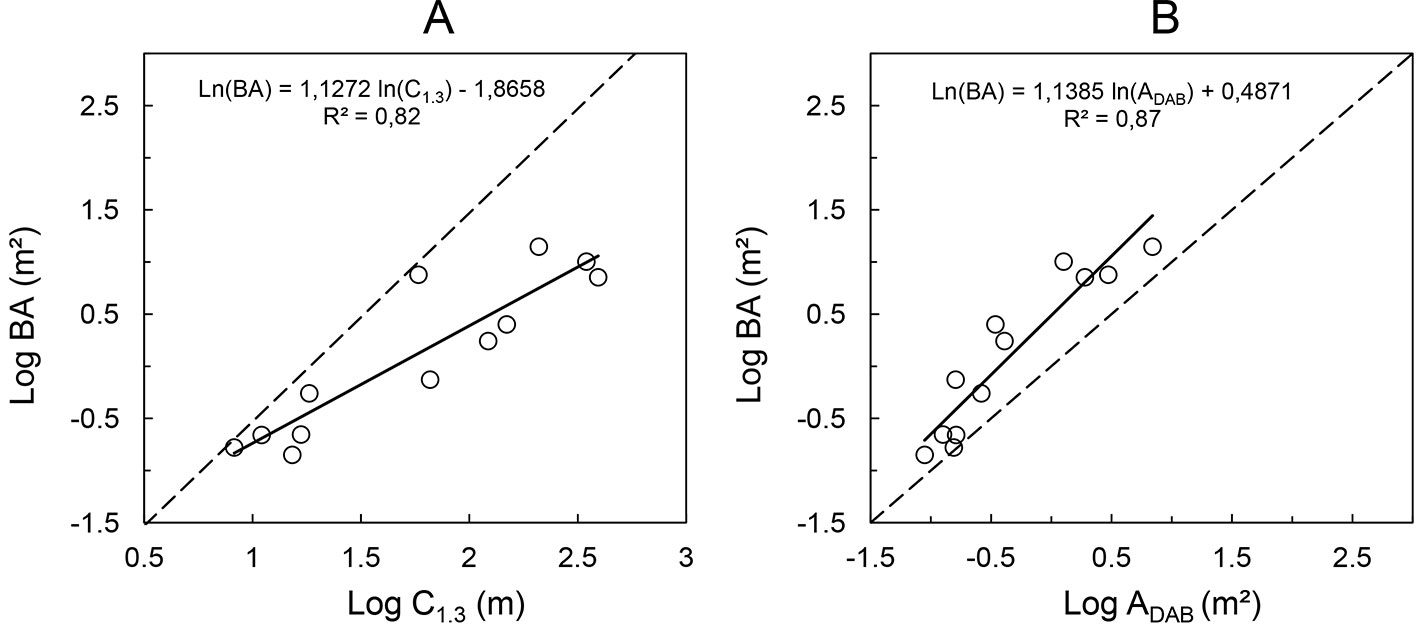
Another relation of practical relevance is that between the perimeter of the convex hull at 1.3 m height and the actual cross-sectional area. The former can be tape-measured as girth over the buttresses at breast height, while the latter is the actual basal area of the tree. The relationship between the cross-sectional area above the buttress and the basal area at 1.3 m height (BA) is crucial for practical applications, as it allows for the prediction of the stand basal area of buttressed trees. The relatively strong relationships found in this study between the above parameters are displayed in Fig. 5. These results are consistent with the findings by Ngomanda et al. ([24]), who measured the buttress perimeter with a wire. As there is visual evidence of heteroscedasticity, linear models were fit to the log-transformed variables. The plot of BA versus ADAB includes a 1:1 line, while the dashed line in the plot of BA versus C1.3 shows the relationship for a perfect circle.
Fig. 5 - (A) Relationship between the perimeters of the convex hull measured “around” buttresses at 1.3 m height (C1.3) and the actual basal area of the respective tree; (B) relationship between cross-sectional area at DAB height and basal area at 1.3 m height.
Discussion
The estimation of forest biomass has received much attention over the past years. In spite of the increasing number of global forest biomass maps available, many basic questions on the determination of single tree biomass, volume or carbon still remain to be solved.
Large trees carry the largest variability in volume and biomass - in particular in tropical lowland rain forests - and exhibit considerable stem irregularities, most notably buttresses. Measuring the volume, biomass or carbon for these trees is evidently difficult and constitutes a considerable source of error when estimating forest above ground biomass and carbon stocks. In this study, we used a terrestrial laser scanner to scan 12 buttressed trees of different species in the Botanical Garden of Bogor, Indonesia in order to analyze the geometry and allometry of these highly irregular stems. Although the 3D analyses carried out on buttresses revealed new insights into their very irregular geometry, our small sample size does not allow the derivation of generalized allometric relationships for different tree species or dimensions. However, the methodological approach described in our study may easily be extended to a more comprehensive data sample, including larger numbers of trees per species, covering a wider range of diameters, and including trees grown-up within forest stands.
The changes in actual cross sections along the buttressed part of sampled trees follow highly variable patterns. For trees characterized by very high but slim buttresses, the diameter of the central solid stem is decreasing with increasing the cross-sectional area of buttresses (see e.g., tree #2 and #8 in Fig. 4). For other trees analyzed, like tree #4 (Ficus albipila), #9 (Ceiba pentandra) or #1 (Koompassia excelsa), the solid stem (even if reduced in diameter) reaches down to the ground, contributing significantly to the lowest cross-sectional area.
We may conclude that the geometry of the buttress cross sections towards the tree base is much more complex than expected. To our knowledge, the geometric feature of cross sections of buttressed trees has not been described yet in this details. Indeed, our results contradict the assumption that a distinct stem becomes thinner towards the ground, laterally supported by buttresses ([19]). In some cases, the concept of a distinct stem appears to dissolve towards the ground. This also means that the measurement protocol described by Picard et al. ([31], p. 68 and Fig. 4.6) for the calculation of buttress volume is not generally applicable, but holds for “simply buttressed” trees only.
Despite the small sample size analyzed, our results suggest that the relation between the cross-sectional area in DAB height and the actual tree basal area measured at 1.3 m height is relatively strong (R² = 0.87) for a range of buttress morphologies and tree dimensions, regardless of the very different geometries observed in the cross-sectional areas. By means of relationships between DAB and basal area, it would be possible to model the actual basal area of tropical forests including the buttressed trees. As the basal area is one of the most important variables in forestry, being highly correlated to total stand volume and biomass, knowledge about this variable would allow deriving models for fast volume approximations. For the analysis of the buttress allometry, we chose a general allometric model that allows the interpretation based on first principles and that could extend over the full possible range of data. The fitted power of the relationships between C1.3, ADAB and tree basal area was close to one, suggesting a nearly isometric scaling. However, the relation between the log-transformed tree basal area and cross-sectional area at DAB height showed a slightly non-linear trend, thus better results were obtained using a logarithmic function (BA = 1.5545·ln(ADAB) + 1.9434, R² = 0.93).
The mean form factor of 1.53 we derived from the sampled trees gives an indication of the potential under-estimation of volume and biomass for the lower buttressed stem section. The buttressed lower stem section contains 153% of the volume of the cylindrical volume calculated based on the DAB.
The relation between C1.3 and basal area showed a nearly linear trend. Besides the actual tree size, it should be noted that the C1.3 is very much influenced by the number and direction of main buttresses that span the convex hull. In this study, trees having a low number of main buttresses tend to extend farther from the stem axis than those with more main buttresses.
Allometric relationships are commonly used for the biomass estimation of individual trees. According to Ngomanda et al. ([24]), we expect that such allometric relationships can be derived with reasonable model accuracy also for irregularly shaped large trees, either using a buttress form factor (as introduced here) or by using the diameter above buttress and/or the length of the convex hull at 1.3 m height as input variables. However, any measurement taken from such trees in the field is difficult to obtain. Therefore, it is certainly worthwhile to look into potential measurement errors when developing allometric functions based on variables that are difficult to be measured.
Even if multiple scanning positions were necessary to avoid scan shadows, the applied TLS approach was easy to implement under the given conditions in a botanical garden. A single tree could be scanned in less than 35 min, including the time for scanner repositioning. The duration of a single scan with normal quality and high-angle resolution is 3:22 min. Pre-processing, co-registration and cleaning of the laser point clouds is office work, taking about half a day for highly-complex tree geometries. The manual delineation of cross-sectional areas in 5 cm height intervals was the most time-expensive activity. However, considering that destructive sampling is not a viable alternative to research into the allometry of big-buttressed trees in a similar level of detail, the proposed method proves to be a useful and non-destructive approach that allows for a range of meaningful measurements.
In a dense tropical rain forest, however, the understory vegetation and lianas may hamper fast and easy scanning, especially if the multi-scan method is used. Under these conditions, data collection and pre-processing could be more complicated and time-consuming. Our approach of manual delineation of the cross sections turned out to be robust as compared with the existing algorithms for automated identification of non-convex shapes. The proposed method might help to convert diameters measured at different heights to a single standard reference height, not only in context of model application but also for model building. This allows estimating a stand basal area at a defined reference height for forest stands including buttressed trees.
Further research should be addressed to the relationships among variables that are relevant and feasible to measure in the field, e.g., the relation between DAB and the tree basal area. The patterns observed in this study suggest that general allometric relations may exist for buttressed trees, though a confirmation based on a larger sample size is required.
Acknowledgements
This study was made possible through financial support from the German Academic Exchange Service (DAAD) which has been granted through the Higher Education Program HEP between the Agricultural University of Bogor IPB and the Faculty of Forest Sciences and Forest Ecology and SETSAF at Georg-August-Universität Göttingen. The study contributes to project B05 of the DFG funded CRC990 “Efforts”. Data was collected in the context of a TLS course delivered at the Bogor Agricultural University IPB by Dominik Seidel and Nils Nölke. We thank our Bachelor students Michael Weber and Markus Klingemann for help in data collection and preparation. We are grateful to the Faculty of Forest Sciences and Forest Ecology in Göttingen for granting financial support. We thank PT. Datascrip and Zoller + Fröhlich GmbH in Jakarta for making available the laser scanner for our project. We are also grateful to Didik Widyatmoko of LIPI for granting the permission to implement our study in the Bogor Botanical Garden.
References
Online | Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Authors’ Info
Authors’ Affiliation
Lutz Fehrmann
Dominik Seidel
Christoph Kleinn
Chair of Forest Inventory and Remote Sensing, Universität Göttingen, Büsgenweg 5, D-37075 Göttingen (Germany)
Tatang Tiryana
Division of Forestry Planning, Department of Forest Management, Faculty of Forestry, Bogor Agricultural University (Indonesia)
Corresponding author
Paper Info
Citation
Nölke N, Fehrmann L, I Nengah SJ, Tiryana T, Seidel D, Kleinn C (2015). On the geometry and allometry of big-buttressed trees - a challenge for forest monitoring: new insights from 3D-modeling with terrestrial laser scanning. iForest 8: 574-581. - doi: 10.3832/ifor1449-007
Academic Editor
Matteo Garbarino
Paper history
Received: Sep 19, 2014
Accepted: Dec 22, 2014
First online: Mar 02, 2015
Publication Date: Oct 01, 2015
Publication Time: 2.33 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2015
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 64365
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 53357
Abstract Page Views: 4361
PDF Downloads: 4992
Citation/Reference Downloads: 58
XML Downloads: 1597
Web Metrics
Days since publication: 3913
Overall contacts: 64365
Avg. contacts per week: 115.14
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2015): 24
Average cites per year: 2.18
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Allometric relationships for volume and biomass for stone pine (Pinus pinea L.) in Italian coastal stands
vol. 6, pp. 331-335 (online: 29 August 2013)
Research Articles
Effects of planting density on the distribution of biomass in a douglas-fir plantation in southern Italy
vol. 8, pp. 368-376 (online: 09 September 2014)
Research Articles
Estimation of above-ground biomass and sequestered carbon of Taurus Cedar (Cedrus libani L.) in Antalya, Turkey
vol. 6, pp. 278-284 (online: 01 July 2013)
Review Papers
Integration of forest mapping and inventory to support forest management
vol. 3, pp. 59-64 (online: 17 May 2010)
Research Articles
Growth, morphology, and biomass allocation of recently planted seedlings of seven European tree species along a light gradient
vol. 13, pp. 261-269 (online: 03 July 2020)
Research Articles
Estimation of aboveground forest biomass in Galicia (NW Spain) by the combined use of LiDAR, LANDSAT ETM+ and National Forest Inventory data
vol. 10, pp. 590-596 (online: 15 May 2017)
Research Articles
Simplified methods to inventory the current annual increment of forest standing volume
vol. 5, pp. 276-282 (online: 17 December 2012)
Research Articles
Tree volume modeling for forest types in the Atlantic Forest: generic and specific models
vol. 13, pp. 417-425 (online: 16 September 2020)
Research Articles
Alternative methods of scaling Eucalyptus urophylla trees in forest stands: compatibility and accuracy of volume equations
vol. 11, pp. 275-283 (online: 29 March 2018)
Research Articles
Ozone fumigation effects on the morphology and biomass of Norway spruce (Picea abies L.) saplings
vol. 2, pp. 15-18 (online: 21 January 2009)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword