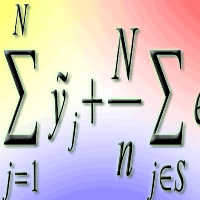
Integration of forest mapping and inventory to support forest management
iForest - Biogeosciences and Forestry, Volume 3, Issue 3, Pages 59-64 (2010)
doi: https://doi.org/10.3832/ifor0531-003
Published: May 17, 2010 - Copyright © 2010 SISEF
Review Papers
Abstract
Forest inventory and forest mapping can be considered as monitoring and assessment applications that respond to different demands. However, the integration of mapping and inventory provides an effective framework for the support of forest management from multiple perspectives: (i) use of thematic maps for stratifying the inventory sample for the purpose of improving the precision of inventory estimates; (ii) coupling remotely sensed and sample inventory data for the purpose of constructing maps of inventoried forest attributes; (iii) coupling remotely sensed data and sample inventory data for the purpose of improving the precision of the inventory estimates; (iv) using inventory data as prior information to support thematic mapping; and (v) using inventory data to correct map areal estimates. This paper aims to provide general considerations on this integration issue in the form of a scientific review and commentary discussion.
Keywords
Thematic mapping, Forest inventory, Monitoring and assessment programs, Remote sensing, Probability sampling
Introduction
Sound forest ecosystem management depends on accurate, complete, and concise information regarding the extent, condition and productivity of the natural resources. Estimation of these attributes is commonly an agreed objective of forest monitoring and assessment programs at a variety of spatial scales ([25], [10]). Each of such properties can also be investigated with regard to its change with time. Forest management information needs are focused and fostered by the global context, in relationship to biodiversity, soil and water conservation, timber provision, non-wood products, potential to sequester atmospheric carbon, etc. Distinctively, monitoring and assessment programs are valuable for providing broad overviews to help strategic and tactical planning development and allow to place forest managers into a perspective that facilitates the prioritization of limited financial resources usually available.
Technological advancements have led to sophisticated tools for the acquisition of current, meaningful, and accurate information, and methodological developments have contributed to greater efficiency in the processing and management of such information ([26]).
Forest inventory and forest mapping can be considered as monitoring and assessment applications that respond to different demands. For forest inventory, the demand is for information pertaining to the amount of forest resources and related attributes in a given region, and is satisfied by investigating a small part of the region in the form of a sample. For forest mapping, the demand is for a geographical depiction of the location of forest and related attributes within the region. These different objectives are targeted by different operational approaches which may vary considerably with the size of the surveyed region.
The integration of inventory and mapping data is emerging as a major issue for the development of programs that monitor and assess land and multiple environmental functions. Stehman ([54]) highlights this issue in the context of estimating the area of land cover and land cover change. From this perspective, the present paper aims to provide general considerations on the integration of forest inventory and mapping in the form of commentary discussion for the community of foresters with basic knowledge of geomatics and inventory.
Forest mapping
For purposes of supporting operational forest management, the cartographic representation of forest cover is generally based on a minimum mapping unit defined to be 0.5 ha ([61]). Thus, remotely sensed imagery with high and very high geometric resolution is required.
Remote sensing is defined as the acquisition of data from sensors on board aircraft or space-based platforms. There are two categories of sensors, passive and active: the first measures the reflectance of naturally occurring solar radiation (e.g., photography), and the second measures radiation that is transmitted from the sensor and reflected from the earth’s surface back to the sensor (e.g., radar). Aircraft sensors principally involve aerial photos linked to a geographical reference system or light detection and ranging (LiDAR) imagery, with image resolutions of 1 m or less. Satellite-based sensors acquire images covering large geographical areas and have variable geometric resolution, ranging from submetric to kilometers (for further background on remote sensing, see [5]; for forestry application, see [62]).
Until recently, aerial imagery has been the main source of remotely sensed data for operational purposes. However, in the last two decades new technologies have enabled a transition from data such as a mosaic of photos to digital imagery in form of a matrix of pixels and has produced many advantages for data acquisition, management and analysis. Meaningful examples of airborne digital imagery include the ADS40 ([50]) and the ASPIS ([46]) systems. An example of a typical airborne application is the assessment of forest burnt areas ([11]) in environments where most fires are small (e.g., less than 10-ha wide) as in Europe (⇒ http://effis.jrc.ec.europa.eu/about/technical-background/).
Airborne imagery is usually less efficient in terms of the ratio of quality to cost than satellite images for the multitemporal monitoring and assessment of forest resources for large areas. Satellite imagery with metric or submetric resolution in the panchromatic channel (e.g., Formosat, IKONOS, QuickBird, OrbView-3, WorldView-2, Pleiades) is suitable for mapping at scales of 1:5000-1:10000, while Landsat TM, Spot HRV, Spot5 and Aster data probably represent the current best trade-off in terms of the quality-cost ratio for mapping at scales of 1:25000-1:50000.
On-screen image interpretation is commonly adopted for forest mapping at a professional level: panchromatic and/or natural colors and/or false color (eventually fused with the panchromatic channel) images are the base for the manual delineation and thematic classification of the delineated vectorial objects (polygons). However, the quality of products obtained with this procedure is dependent to some degree on interpreter subjectivity.
Automatic (unsupervised) and semiautomatic (supervised) methods of multispectral image classification have been developed to produce cheaper and more objective products. Supervised methods are based on ground-truthing, a term used extensively to describe the best available determination of the true thematic class at a specified location. With supervised classification, ground-truth data is acquired for a specified number of training pixels for each thematic class as a means of determining the spectral signature (distribution of the digital numbers, DN, across the spectral channels) typical of the class. The multispectral reflectance of the target pixels (i.e., the pixels to be classified) is compared with the spectral signatures of the classes so that each target pixel can be assigned (e.g., by discriminant analysis) to the thematic class whose signature is most similar to the pixel’s multispectral reflectance. Unsupervised methods do not require the acquisition of training pixels. Instead, the classification is carried out by grouping (cluster analysis) the pixels on the basis of their similarity in terms of multispectral reflectance. The resulting groups are viewed as thematic classes and labelled a posteriori by the interpreter. If ground data have been acquired, labels could be assigned to groups on the basis of the most common class (or some other measure) of the ground data points included in the group (for further details, see e.g., [5]).
The previously described approaches are characterized as pixel-oriented because the classification is carried out on a per-pixel basis. In the last decade alternative techniques have been developed based on object-oriented classification ([3]) of polygons produced by image segmentation. Image segmentation refers to partitioning an image into meaningful regions based on either homogeneity or heterogeneity criteria (see [23]) and repre-sents the interface between image pre-processing and image interpretation (object recognition). The advantage of this approach is that greater information content can be associated with the polygons than with single pixels; such content includes the geometry and hierarchy of the polygons and the spectral heterogeneity of the pixels in each polygon. The segmentation of digital imagery can be carried out (semi)automatically faster and more objectively ([1]) than manual polygon delineation. Map products obtained using digital segmentation and object-oriented classification are more suitable to customer expectations and more similar to the conventional maps obtained by manual interpretation than those produced by the pixel-oriented approach.
LiDAR techniques, particularly aerial laser scanning, have tremendous potential for supporting operational forest management and represent the frontier of current research in this area. By measuring forest canopy height and eventually the width and depth of individual tree crowns, LiDAR data can be used effectively to represent the structure of forest stands and to estimate standing wood volume, biomass, etc. Considerable research is ongoing to establish reliable and feasible survey protocols for integrating LiDAR and forest inventory data (e.g., [47], [38], [41], [12]). This issue will not be directly addressed in this paper.
Forest inventory
A forest inventory is the statistical description of the quantitative and qualitative attributes of the forest resources in a given region. Forest inventory information is generally reported for management and/or administrative units (e.g., district, province, country) and/or for thematic or resource classes (e.g., forest type, age). Forest inventories are currently evolving towards multipurpose resources surveys ([28], [10]) and are broadening their scope in two major directions ([25]): (i) inclusion of additional variables that are not directly related to timber assessment and wood harvesting, such as biodiversity attributes; (ii) expansion of the target population to include non-traditional objects such as trees outside forests and urban forests.
Forest inventory could, in principle, be based on a complete census for which every tree in a given region is measured. However, this is usually impossible because of the time and/or costs associated with the large areas involved. Therefore, information is typically acquired using sampling methods for which only a proportion of the population (the sample) is inspected, and inferences regarding the whole population are based on this sample ([24]). Multiple sampling strategies (e.g., [22], [29]) are associated with the wide variety of types of forest inventories (for a typology of forest inventories, see [26]). However, all sample-based inventories over large areas share a common methodological feature: sample units are objectively selected by rigorous probabilistic rules as a means of guaranteeing the credibility of estimates ([44]).
Traditionally, forest inventory data are analysed in the framework of design-based inference for which population values are regarded as fixed constants and the randomization distribution resulting from the sampling design is the basis of inference. In this framework, the bias and variance of an estimator of a population parameter are determined from the set of all possible samples (the sample space) and from the probability associated with each sample. Särndal et al. ([51]), Gregoire ([21]) and Fattorini ([15]) provide extensive discussion of design-based inference and contrast it with model-based inference. Usually, forest inventories adopt sampling schemes in which a set of points is randomly selected from the study region in accordance with a spatial sampling design. Subsequently, plots of adequate radius are then established with centres at the selected points, and forest attributes are recorded for the plots (e.g., [13], [52], [17]). Ground data obtained from these plots are the type to which this paper refers.
Relationships between forest inventory and mapping
The potential to integrate multisource information is a key element of forest monitoring and assessment programs ([28], [26], [38]). Inter alia, the relationships between forest inventory and mapping can be framed in the perspective of:
- exploiting thematic maps for stratifying the inventory sample for purposes of improving the precision of inventory estimates;
- coupling the remotely sensed data for an entire region with sample inventory data to produce maps of the inventoried forest attributes;
- coupling the remotely sensed data with the sample inventory data to improve the precision of the inventory estimates;
- exploiting the inventory data as prior information to support thematic mapping;
- exploiting the inventory data for the correction of map areal estimates.
Exploiting thematic maps for stratifying the inventory sample
Stratified sampling consists of dividing the population into subpopulations, called strata, that are relatively homogeneous, and then sampling each stratum separately. In most situations, stratified probability sampling is likely to yield more precise population estimates (i.e., estimates with smaller standard errors) than non-stratified probability sampling with the same sample size.
The strata can be obtained directly as thematic classes or groups of classes from a thematic map; in this case, the map implicitly provides the complete coverage of auxiliary information to improve the precision of the inventory estimates. The operational procedure (map polygon stratification) includes five steps: (1) the proportion of the area of each stratum with respect to the area of the mapped region is calculated; (2) a specified number of sample units is allocated to each stratum, usually in proportion to the area of the stratum as determined from the map or possibly in proportional to stratum variances; (3) sample units are geolocated independently within each stratum according to a given probability sampling scheme; (4) statistical parameters (e.g., mean, total and their variances) are estimated for each stratum; and (5) stratum estimates are combined to obtain the overall estimates for the population. Practical examples can be found in Lund & Thomas ([27]) and Suárez et al. ([57]).
Post-stratification is often applied too: it is not used to select the sample, but is instead used to assign plots to strata after the sample has been selected. However, the same stratified estimators are used for the analysis. When an inventory uses permanent plots, there is no opportunity for stratified sampling; nevertheless, stratified estimation may still substantially improve the precision of estimates. The auxiliary information is the proportion of area in each of the post-strata constructed from the mapped classes. Examples of post-stratification can be found in McRoberts et al. ([36], [37]) and Nilsson et al. ([43]).
Note that application of both the above approaches usually ignores complications arising from map errors and spatial misregistration of inventory data locations to the map: of course, the amount by which the stratification improves precision diminishes to the degree that such shortcomings are present. The issue of the above complications affects almost all the applications discussed in this paper but it will not be further addressed.
Coupling remotely sensed data and inventory data to map forest attributes
Estimation of the relationship between remotely sensed data and the biophysical attributes of forest vegetation (standing wood volume, biomass increment, etc.) permits maps of the attributes observed at the sample inventory units to be constructed for the entire region of interest, i.e., the attributes can be predicted for all the pixels in the region thus producing maps. The exploited auxiliary variables are usually the DNs of the spectral channels (and/or their combination to produce vegetation indices, e.g., [30]) which are available for all the N pixels in the region, while the values of the Y-variable of interest (the forest attribute) are known only for the sample of n pixels corresponding to the inventory sample units, characterized as the reference set.
The mapping procedures can be based on either parametric or non-parametric approaches to predicting the values of Y for pixels that do not correspond to the inventory sample units, characterized as the target set. Non-parametric approaches are distribution-free in that they do not rely on any underlying probability distribution for estimation.
Nearest Neighbors (NN) techniques are well known non-parametric approaches whose operational application is increasing, even at the forest professional level. Other non-parametric approaches such as decision trees (classification and regression tree, Random Forest) and neural networks (multilayer perceptrons, self-organising maps, radial basis function networks, adaptive resonance theory networks, etc.) are promising, albeit usually less effective than NN techniques for mapping forest attributes (e.g., [31], [56]). NN techniques predict the unknown value of Y for the j-th target pixel as a weighted mean of the Y values for the k reference pixels nearest to the j-th target pixel in the multidimensional space defined by the auxiliary variables (eqn. 1):
where k (<n) denotes the number of neighbours adopted for the prediction and the wis are weights such that w1 +…+wi = 1. A straightforward and suitable choice for the weights is wi =1/k for any i=1,…,k ([39], [2]), but they are often selected to be inversely proportional to the multidimensional distance between the j-th target pixel and each of the k nearest neighbor reference pixels. Examples of NN applications are provided by Franco-Lopez et al. ([19]), Tomppo et al. ([58], [60]), Chirici et al. ([7]), McRoberts ([33]).
Among parametric approaches, the most commonly used is generalized regression (GREG) for which the prediction of Y for each target pixel is based on a regression (or ratio) established between Y and the auxiliary variables using data from the reference set. The adopted model is often linear, such as (eqn. 2):
where X1, …, Xq are the auxiliary variables. However, the GREG estimator may encompass a wide range of additional models. Examples of application of the GREG approach are provided by Moisen & Edwards ([40]), Puhr & Donoghue ([48]) and Opsomer et al. ([45]).
All other factors being equal, some Monte Carlo investigations empirically demonstrate that GREG is usually more effective than NN ([2]), but in some situations it may give rise to unlikely results (e.g., negative predictions). A major advantage of the NN approach is that it is multivariate in the sense that it can estimate multiple Y-variables simultaneously and still retain their complex variance-covariance structure and natural variation within the bounds of biological reality, at least as long as k =1 (see [34]). On the contrary, with regression approaches Y-variables are often estimated separately which may lead to estimates with unreasonable relationships and variance-covariance structures that differ greatly from the original field data ([14]). However, with respect to the above issues, NN tends to behave more like regression approaches as k increases.
Coupling remotely sensed data with the sample inventory data to improve the precision of the inventory estimates
This section is complementary to the preceding one in that the maps constructed using auxiliary remotely sensed information that is correlated with the Y-variables of interest may also be used to more efficiently estimate statistical parameters (e.g., [42]).
In the case of model-assisted estimation, if the locations of the reference set S (the inventory sample) are obtained using simple random or systematic sampling without replacement, then prediction approaches such as kNN and GREG can be used with the approximately unbiased estimator of the population total Y over the entire study region given by (eqn. 3):
where yj denotes the predicted value of Y for the j-th pixel and ej = yj - {tilde}yj denotes the prediction error. Moreover, an approximately conservative estimator of the sampling variance is given by (eqn. 4):
where (eqn. 5):
If only the sample inventory data from the reference set are used for estimation (i.e., the auxiliary information from remote sensing is not used), then the unbiased estimator of the total Y under simple random sampling without replacement is (eqn. 6):
while the unbiased estimator of the sampling variance is (eqn. 7):
where y = T / N.
If the relationship between Y and the auxiliary variables is sufficiently strong, the model-assisted estimator Tasst tends to be more precise thanformula. In relative terms, the relative advantage of Tasst over Twith respect to precision increases as the size of the reference set decreases. Note, however, that even the estimation error of Tasst may be large for small areas with few sampled pixels. This problem is well-recognized in the statistical literature as small area estimation and can be handled only by using model-based approaches (e.g., [49]).
Model-assisted estimators can be used with any probability sampling design (for general formulation of the estimators - see [2], chapt. 3.2) and allow great flexibility in modelling the relationship between the Y and the auxiliary variables. While the improvement in the precision of a model-assisted estimator is dependent on how well the specified model corresponds to the actual relationship between the Y and the auxiliary variables, the validity of the inference is not dependent on correct model specification but instead remains based on the randomization distribution associated with the sampling design. In particular, model-assisted estimators are approximately (asymptotically) design unbiased regardless of whether the working model is correct or not, and are particularly efficient if the working model is correct.
Inventory data as prior information to supportthematic mapping
The information from forest inventory data about the distribution of given thematic classes in relation to environmental characteristics can be exploited as a priori knowledge for the thematic classification of remotely sensed imagery.
Prior probability can be incorporated in classical discriminant analysis ([59]) and, more generally, with Bayesian classifiers. The radiometric information in the remote sensing data (i.e., the multispectral reflectance of each pixel/polygon) is combined with the additional, independently available forest inventory data (the prior information) to produce a full probability distribution (posterior distribution), so that the class with the highest posterior probability can be assigned to each pixel or polygon. This approach exploits the potential of forest inventory data for establishing quantitative relationships between the spatial distribution of the thematic classes (e.g., forest types) to be mapped and environmental factors such as altitude, exposure, soil type, etc. Examples of forest mapping applications are provided by [53] and Finley et al. ([18]).
Exploiting inventory data for the correction of map areal estimates
There are important risks in using thematic maps produced by interpretation of remotely sensed imagery as a direct tool to estimate spatial variables. When mapping, the interpretation errors tend to be systematic, and there is no compensation between commission and omission errors, i.e., areas of a land-use type A incorrectly mapped as land-use type B are not offset by areas of land-use type incorrectly mapped as A ([6], [8]).
Area estimation can be viewed as a value-added analysis appended to a forest inventory when the sample obtained from the inventory is used to estimate the area of each class from a given map, i.e., the confusion matrix obtained from the inventory sample is used to adjust the area of each thematic class (e.g., [54], [35]). Obviously this is feasible only when the inventory nomenclature is analogous to that of the map.
If points are selected completely at random over the study area (simple random sampling) or randomly within the polygons partitioning the study area (tessellation stratified sampling) the classical estimator for the size of the area of type m is (eqn. 8):
where p m is the proportion of inventory points classified as type m with respect to the total number of inventory points, say n, and A is the size of the study region. In this case the variance estimator (eqn. 9):
is unbiased under simple random sampling and conservative under tesselation stratified sampling ([16]). However, if a thematic map of the study area is previously available, and if A1 , …, Ac are the areas of the C thematic classes partitioning the map, an alternative estimator for the area of type m is given by (eqn. 10):
where {hat}phm represents the proportion of the inventory points mapped as forest type h but actually belonging to forest type m. In this case the variance estimator (eqn. 11):
is once again unbiased under simple random sampling and conservative under tesselation stratified sampling.
Gallego ([20]) provides a comprehensive review of area estimation methods, Stehman & Foody ([55]) review basic methods of accuracy assessment, and Stehman ([54]) uses model-assisted estimation as a unifying framework for estimating the area of land cover and land-cover change from remote sensing.
For the sake of completeness, it must be acknowledged that even model-based approaches are gaining importance for this topic area. The criteria underlying model-based inference differ considerably from those underlying the design-based inference for the above mentioned model-assisted estimation framework. The statistical properties of design-based estimators are derived with respect to all the possible samples arising from the adopted sampling scheme, considering the population values as a set of fixed constants. On the other hand, the properties of model-based estimators are obtained with respect to all the populations which may be generated from the assumed superpopulation model, considering the sample as fixed (i.e., purposively selected). The validity of a model-based inference is based on the validity of the model, not the probabilistic nature of the sample as is the case for design-based inference. In fact, purposive, non-probability samples may produce entirely valid model-based inferences. Model-based approaches are distinctively (but not only) suitable for small areas, as already stressed (see § 4.3). A model-based approach to estimating forest area is reported by McRoberts ([32]).
Final remark
The improvement of forest surveys through multi-purpose and multi-source networks is a topic of increasing interest and is usually regarded more positively by the stakeholders, governmental or not, than establishment of new monitoring and assessment programs. Support for forest management should therefore be framed according to a multi-faceted approach that integrates mapping and inventory as a means of providing comprehensive knowledge on the state and trends of forest resources as well as on the interactions and interdependencies with other land uses.
As remote sensing technology and associated analytical methods continue to improve rapidly with reasonable costs, they are likely to play an even more substantial role for forest monitoring and assessment in the future. In this light, it must be stressed that the conceptual and methodological differences between forest mapping and forest inventory are often unduly amplified by the lack of standardization / harmonization between their nomenclature systems. Instead, nomenclature systems may constitute fundamental bridges, and the value of shared and integrated typological frameworks, from continental (e.g., [4]) to local (e.g., [9]) scales, should be more readily acknowledged.
Acknowledgements
This paper was partially carried out under the project PRIN2007 “Innovative methods for the identification, characterization and management of old-growth forests in the Mediterranean environment” (research unit: DISAFRI, University of Tuscia; national coordinator: G. Chirici) funded by the Italian Ministry of University and Research. I would like acknowledging Fattorini L (University of Siena, Italy), McRoberts RE (Forest Service, USDA, USA) and Tabacchi G (Italy) for the helpful discussions and precious suggestions.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Dipartimento di Scienze dell’Ambiente Forestale e delle sue Risorse, Università della Tuscia, v. San Camillo de Lellis, I-01100 Viterbo (Italy)
Corresponding author
Paper Info
Citation
Corona P (2010). Integration of forest mapping and inventory to support forest management. iForest 3: 59-64. - doi: 10.3832/ifor0531-003
Paper history
Received: Dec 04, 2009
Accepted: Jan 23, 2010
First online: May 17, 2010
Publication Date: May 17, 2010
Publication Time: 3.80 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2010
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 61651
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 49389
Abstract Page Views: 5105
PDF Downloads: 5767
Citation/Reference Downloads: 73
XML Downloads: 1317
Web Metrics
Days since publication: 5639
Overall contacts: 61651
Avg. contacts per week: 76.53
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2010): 66
Average cites per year: 4.13
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Review Papers
Accuracy of determining specific parameters of the urban forest using remote sensing
vol. 12, pp. 498-510 (online: 02 December 2019)
Review Papers
Remote sensing of selective logging in tropical forests: current state and future directions
vol. 13, pp. 286-300 (online: 10 July 2020)
Review Papers
Remote sensing support for post fire forest management
vol. 1, pp. 6-12 (online: 28 February 2008)
Research Articles
Estimation of aboveground forest biomass in Galicia (NW Spain) by the combined use of LiDAR, LANDSAT ETM+ and National Forest Inventory data
vol. 10, pp. 590-596 (online: 15 May 2017)
Technical Advances
Improved estimates of per-plot basal area from angle count inventories
vol. 7, pp. 178-185 (online: 17 February 2014)
Research Articles
Afforestation monitoring through automatic analysis of 36-years Landsat Best Available Composites
vol. 15, pp. 220-228 (online: 12 July 2022)
Review Papers
Remote sensing-supported vegetation parameters for regional climate models: a brief review
vol. 3, pp. 98-101 (online: 15 July 2010)
Research Articles
Integrating area-based and individual tree detection approaches for estimating tree volume in plantation inventory using aerial image and airborne laser scanning data
vol. 10, pp. 296-302 (online: 15 December 2016)
Research Articles
Optimizing line-plot size for personal laser scanning: modeling distance-dependent tree detection probability along transects
vol. 17, pp. 269-276 (online: 07 September 2024)
Technical Reports
Detecting tree water deficit by very low altitude remote sensing
vol. 10, pp. 215-219 (online: 11 February 2017)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword








