Introduction 

Amazon forest has a fundamental role in the control of biogeochemical cycles of the planet, making important exchanges of energy, humidity and mass between the continental surface and the atmosphere ([12], [33]). it is thought that biodiversity of the Amazon forest represents about 50% of the whole biodiversity of the planet ([26], [7]). In recent years, countering the loss of biodiversity has become one of the major challenges for the scientific community. Deforestation and forest fragmentation caused by the expansion of agriculture and selective logging have generated irreparable losses and serious concerns about the ecological and genetic factors underlying the maintenance of biodiversity in the Amazon forest ([22], [5], [2]).

Mezilaurs itauba (Meins.) Taub. Ex Mez (Lauraceae - [1]) is an Amazon species distributed throughout South America, from the southern Amazon and northern Brazil to Colombia, Venezuela, Guyana, French Guiana and Ecuador. It is the fifth most exploited timber species in the region, due the excellent technical characteristics of the wood, and it is listed as threatened for extinction in the Amazon region by the International Union for Nature Conservation ([21]).

The shortage of studies on the structure and diversity of the Amazon forest represents a large deficiency in the ecological and management research ([16], [17]). In this context, the spatial distribution of tree species is a key issue for better understanding how a species uses the available resources, its successful establishment and reproduction ([8]). The horizontal distribution of a species in the forest is affected by the density of seed sources, seed dispersion and post-dispersion processes. In turn, seed source density is affected by the density of potentially reproductive individuals and by the reproductive system of the species ([4]), with important implications concerning its genetic diversity. Moreover, spatial distribution patterns are often related to interactions between biotic and abiotic factors that control the dynamics of the ecological processes within a population ([6]).

Timber exploitation can alter the spatial distribution of individuals scattered over a given area, affecting the reproduction, competition, survival ability and predation mechanisms of the populations. For example, reproductive processes such as pollen flow may be affected by significant alterations in the dynamics of clearings originated from harvesting ([10]). Furthermore, logging may significantly reduce tree density and consequently increase the distance between individual trees, leading to alterations in the pollen flow between individuals ([25], [13]).

Basically, the distribution of individual trees in the forest may show three theoretical patterns: uniform, random and aggregate ([3], [35]). Aggregated patterns are commonly observed when a positive or attractive association among individuals takes place, leading to the positive autocorrelation values at short distances ([30]). On the contrary, uniform or regular patterns are characterized by negative autocorrelation with repulsive relationships among individuals. In general, species present clustered patterns when considered at larger scales, mainly due to the contiguity of suitable habitats ([24], [14]). However, populations of species may show different combinations of spatial patterns, depending of the scale considered. Indeed, some populations present clustered patterns at large scales and random at small scales, which can be related to the aforementioned synecological aspects, such as pollination, seed and propagules dispersal, the reproductive systems, etc.

Ripley’s K function ([32]) is a descriptive statistics of spatial patterns widely used in the analysis of spatial patterns of forests. It is based on the computation of the expected number of points within a circle of radius (r) centered at an arbitrary reference point, divided by the intensity (λ) of the pattern ([6]). This method evaluates how the spatial patterns of any event at different scales simultaneously occupies a space ([6]), thus the degree of interaction between trees within a population or community can be evaluated ([28], [15], [35]).

The concept of Complete Spatial Randomness (CSR) is crucial for the quantitative description of any spatial pattern. An event X is a partial realization of a homogeneous Poisson process, which involves a single parameter, λ (intensity) or the average number of events per unit area. According to Durigan ([16]), the actual number of events (n) in X is an observation of a Poisson distribution with a mean intensity λ (X). Moreover, the same author reported that the hypothesis to be tested in the bivariate analysis is not CSR, but the Complete Spatial Independence (CSI) of processes, shifting the focus from “aggregate vs. regularity” to “attraction vs. repulsion” among processes.

The present study aimed at identifying the spatial patterns of tree distribution in a population of Mezilaurus itauba (Meins.) Taub. Ex mez. in a seasonal forest of the southern Amazon (Brazil). The main goal was to understand how the reproduction and establishment of such species can be influenced by timber exploitation under the current forest management regime in the southern Amazon region ([8], [11]), thus contributing to sustainable forest management and conservation of genetic diversity of the species ([6], [23]).

  Material and methods 

Study area

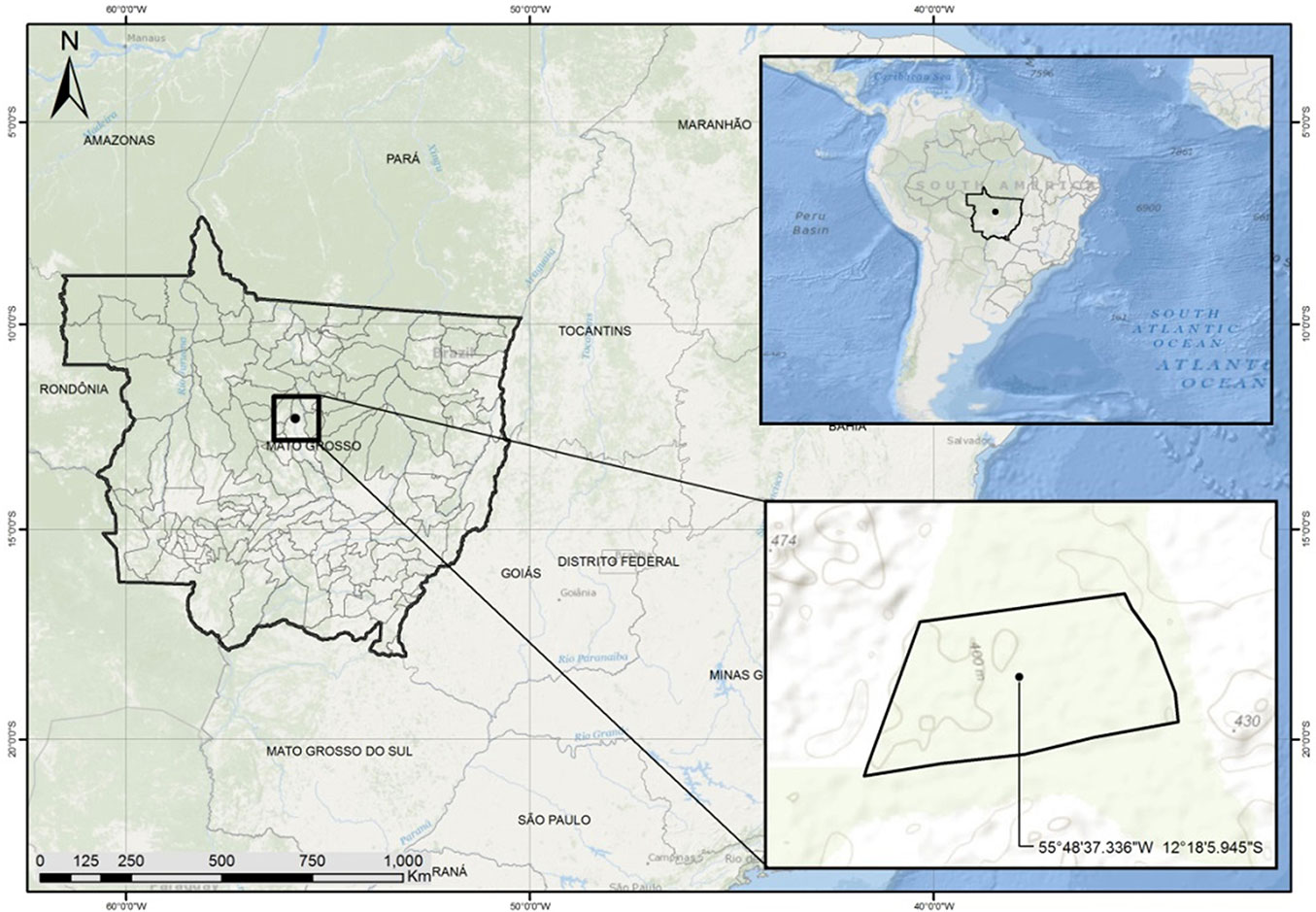
The study was carried out in an area of tropical rainforest located in the north of the Mato Grosso state, Brazil (12° 18′ S, 55° 48′ W - Fig. 1). A fragment of forest typologically classified as semi-deciduous seasonal forest was selected in the southern Amazon plane, predominantly composed by evergreen or semi-deciduous trees and influenced by both the super humid climate of the Amazon and the humid tropical central plateau ([20]). Soils were dystrophic red-yellow latosol, i.e., hydromorphic mineral soils with latossolic B horizon, characterized by red and red-yellow colors due to high levels of Fe₂O₃. The study area is set in a typical agricultural region, with scattered fragments of the Amazon forest included in reserves established by law in order to allow the dynamic conservation of the forest ecosystem resources.

Fig. 1 - Map of the study area.

  Enlarge/Shrink   Download   Full Width  Open in Viewer

A preliminary mapping of the study site was made using the software ArcGIS^® 10.0 based on orbital images obtained by remote sensing. A total area of 185 ha was delineated in the forest interior with a minimum distance of 100 m from stream margins, swampy and infrastructure areas, to avoid any edge effect or interference with the frequency and density of the studied species. Eighteen transects of 50 m were established over the area, and all the stems of Mezilaurus itauba with a minimum diameter at breast height (DBH) of 30 cm were identified along the transects. Tree positioning was taken using a hand-held GPS. For each tree the DBH was measured, total and commercial height estimated using an electronic clinometer, and the phytosanitary state of the stem recorded. All the data were collected simultaneously. Species identification was carried out in situ by comparing specimens collected in the field with the specimens deposited in the Central Herbarium of the Federal University of Mato Grosso (Brazil).

During tree inventory, individuals were classified into two groups according to their maturity stage: juvenile trees (< 50 cm DBH) and adult trees (> 50 cm DBH). Such threshold was chosen based on the current legislation of Brazil, which allows only trees with > 50 cm to be harvested.

Mathematical and statistical analyses were carried out using electronic worksheets and the statistical software package R version 3.0.1. The K function proposed by Ripley ([19]) was tested against the null hypothesis of complete spatial randomness (CSR) based on diagrams where the distances tested between events are represented in the abscissa, and the values of the K function in the ordinate. Such graphical representation facilitated the visualization of deviations from the null hypothesis. Data were processed both pooled together and independently for juveniles (DBH < 50 cm) and adult (DBH > 50 cm) trees. Circles with radius of 10, 20 and 30 m were used in the analyses.

Confidence envelopes for Ripley’s K values were constructed through Monte Carlo simulations, whose number varied according to the required precision. According to Cunha ([10]), 19 simulations are required to achieve 5% confidence envelopes, and 99 simulation for 1% confidence envelopes. When the number of trees was not too large, 1000 simulations were carried out to achieve an acceptable level of probability.

The complete spatial randomness (CSR) scenario was defined by performing 1000 Monte Carlo simulations with α = 0.01 using a Poisson homogeneous process. Envelopes with maximum and minimum values were then generated and confidence limits obtained. Values of the K function at different distances were plotted along with confidence intervals obtained under the null hypothesis of complete spatial randomness. Values falling within the envelope were not statistically different from their expectation based on CSR. Values above the superior line of the envelope indicated a grouped or aggregate spatial distribution of individuals, while values below the inferior line indicated a spatially uniform (regular) distribution of individuals.

  Results and discussion 

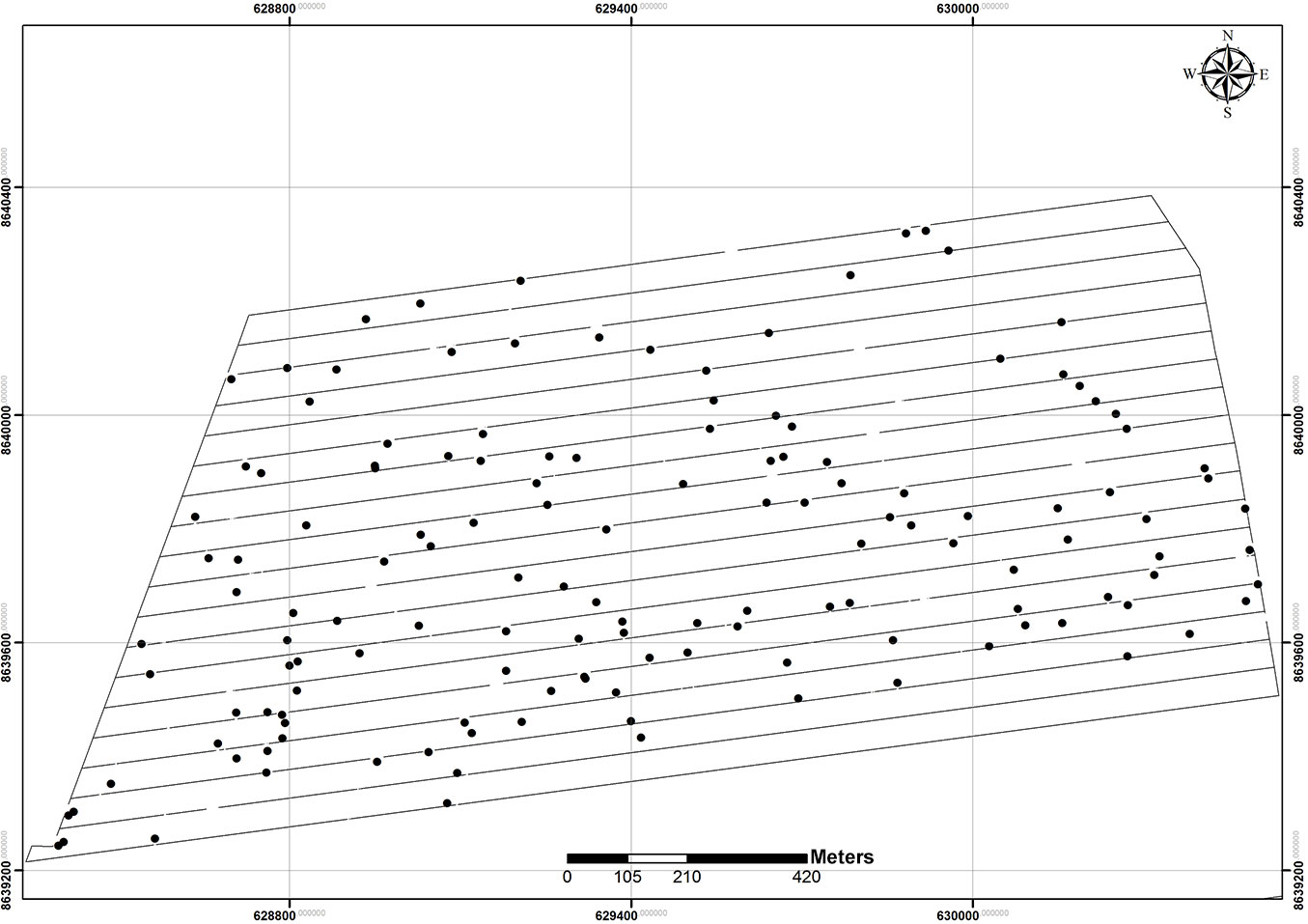
Overall, 229 individuals of Mezilaurus itauba were detected across the study area, resulting in an absolute density of 1.23 individuals ha^-1. At least one individual of the studied species was detected along each transect. The x and y coordinates were represented in a Cartesian orthogonal plane to display the spatial localization of trees (Fig. 2).

Fig. 2 - Pinpoint distribution map of Mezilaurus itauba trees sampled in the study area (reference: SIRGAS 2000 map datum).

  Enlarge/Shrink   Download   Full Width  Open in Viewer

The total abundance of individuals was 156 for adult trees (DBH > 50 cm) and 73 for juveniles (DBH < 50 cm). This distribution of individuals within diametric classes was atypical when compared to other tree species. Indeed, in tropical forests such distribution usually shows an “inverted J” shape, with a lower number of trees at intermediate DBH. Costa & Mantovani ([9]) described the frequency distribution of size classes to follow an inverted J curve in various species, reporting a large number of individuals in the lower classes gradually decreasing as size increased. Similar results were presented by Severiano et al. ([34]) and Dalmaso et al. ([11]). Péllico Neto et al. ([31]) reported that the diametric structure of Ocotea odorifera in fragmented forests also follows an inverted J curve, with a high frequency in the small-size classes gradually decreasing with increasing the tree size.

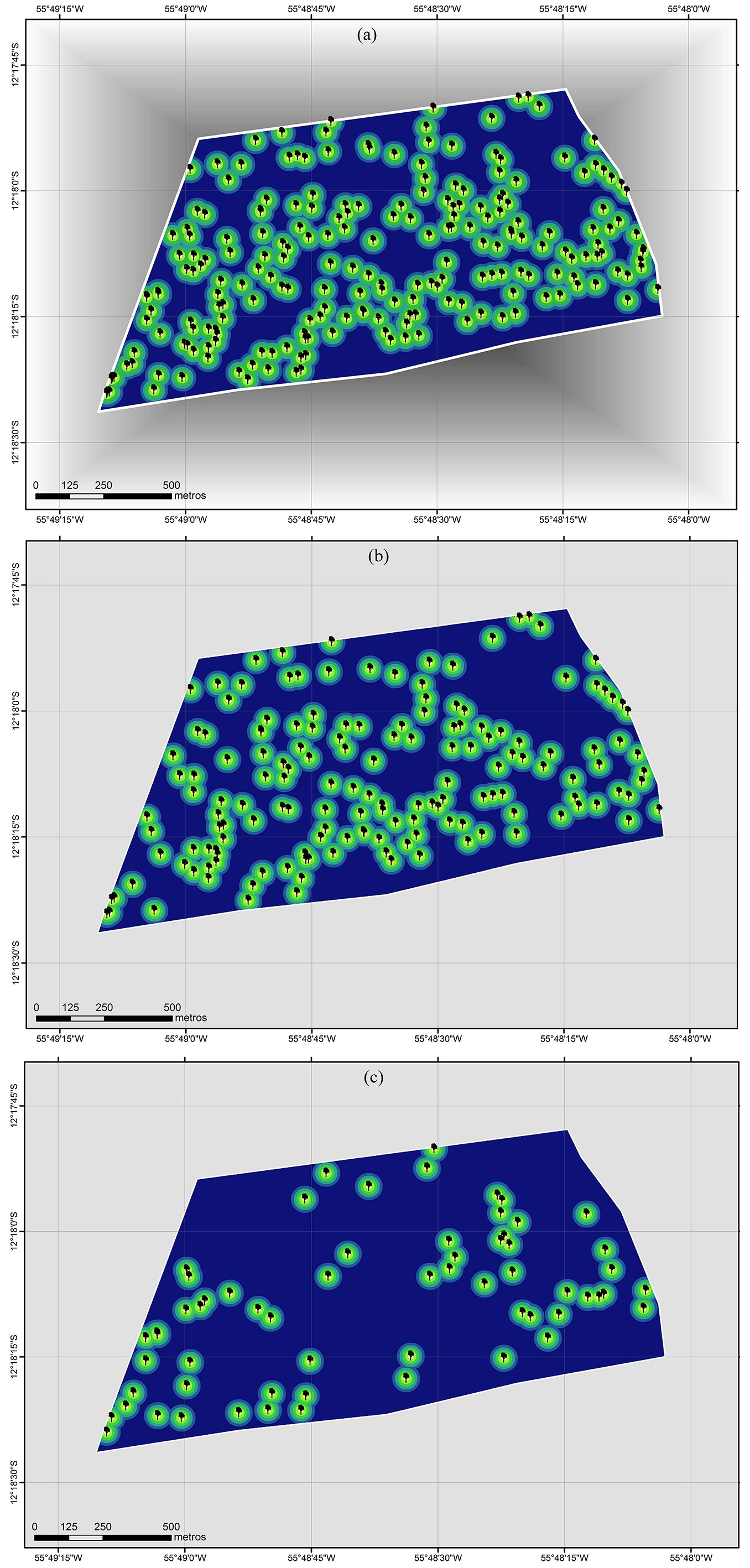
To verify the spatial distribution of adult trees in the study area, a map was generated including only individuals with DBH > 50 cm and using the same radius distance (Fig. 3a). Scattered groups of trees were detected over the whole area, though a grouping tendency was observed particularly in the lower section of the map, with 10 to 20 individuals per group. Due to their close distance, these individuals might be subject of preferential mating by biotic and abiotic pollination. In contrast, the upper part of Fig. 3a suggests spatial randomness of individuals with more scattered trees fewer groups. However, the fairly close distance among trees still allows potential genetic exchanges among these individuals.

Fig. 3 - Spatial point distribution of inventoried Mezilaurus itauba trees: (a) general with all adult and juvenile trees; (b) adult trees only; (c) juvenile trees only. A distance radius of 10, 20 and 30 m was used.

  Enlarge/Shrink   Download   Full Width  Open in Viewer

When the spatial distribution of juvenile trees was analyzed using the same distance radius, a reduction in the number of events was observed as well as a random distribution of individual trees (Fig. 3c). Even in this case, juvenile trees were observed in all transects.

Distribution pattern by Ripley’s K function

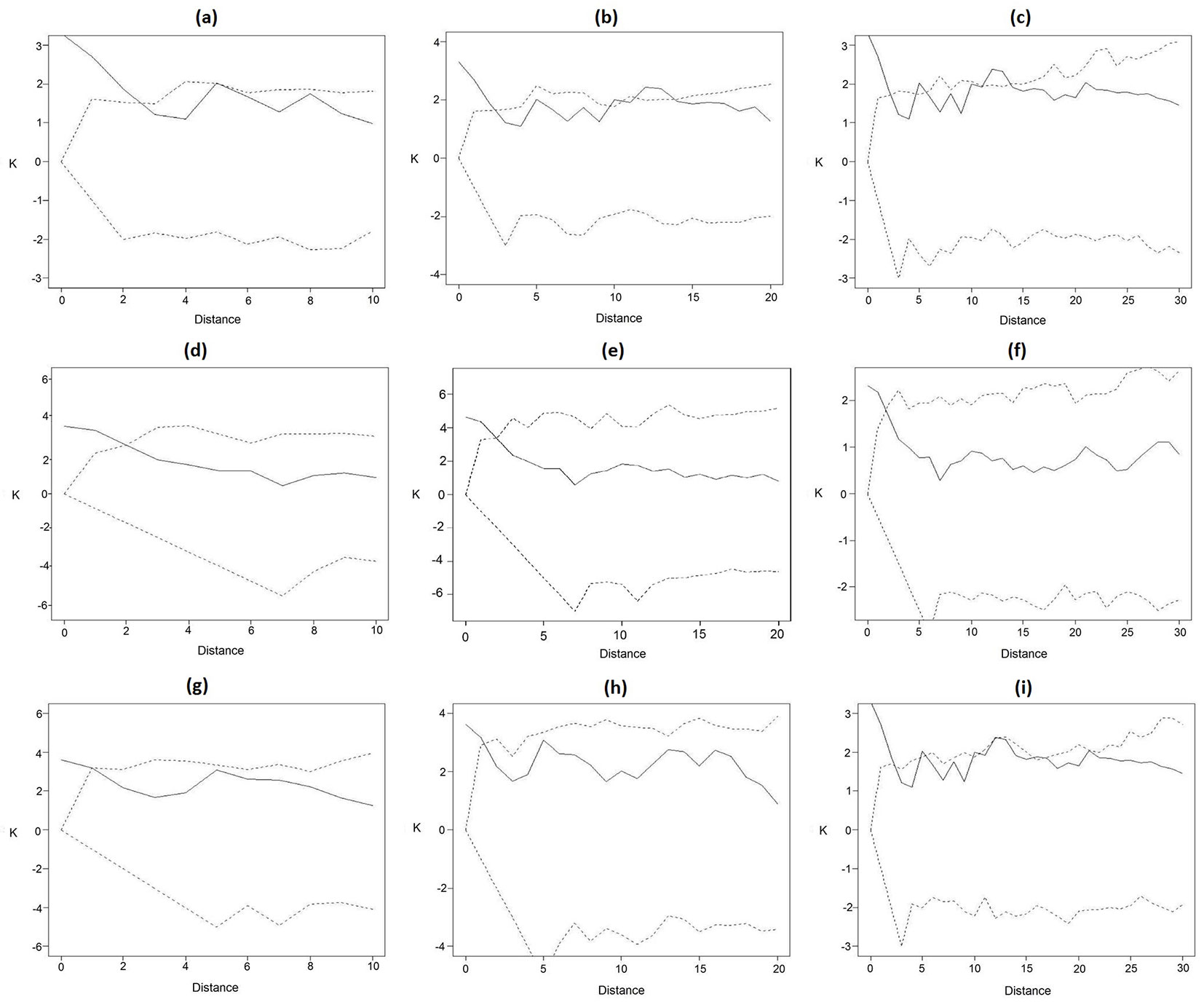
Overall, the starting hypothesis of complete spatial randomness of Mezilaurus itauba in the study area was confirmed based on our analysis. However, the Ripley’s K function at short distances showed values exceeding their expectations based on the random distribution, indicating a weak though significant aggregation of the sampled trees. Similar results were obtained when the analysis was carried out independently on adults and juvenile trees, with K values calculated for distances of 5-13 m were exceeding their random expectations. For larger distances, K values were always included within the envelopes based on the CSI hypothesis, indicating no significant differences from the random distribution of trees.

Using a 10 m-distance radius, a random distribution pattern was detected, with all points falling within the confidence envelope (Fig. 4a, Fig. 4d, Fig. 4g). However, a significant spatial clustering (as inferred from the K line above the upper 97.5% quantile) was detected for distances up to 3 meters (Fig. 4a), 2 meters (Fig. 4b) and 3 meters (Fig. 4g), indicating a tendency to aggregation. Similar patterns were observed when a radius of 20 or 30 m was set in the analysis, confirming the occurrence of small groups of 10 to 15 individuals of Mezilaurus itauba close to each other with a likely co-ancestral origin (Fig. 4).

Fig. 4 - Analysis of the spatial distribution pattern through the Ripley’s K function for different distances (L) of juvenile and adult Mezilaurus itauba individuals; (a, d, g): L = 10 m; (b, e, h): L = 20 m; (c, f, i): L = 30 m. (a, b, c): all inventoried individuals; (d, e, f): adult inventoried individuals; (g, h, I): the juvenile inventoried individuals. The dotted line represents the confidence envelope (%) for 1000 Monte Carlo simulations, whereas dashed lines are 0.025 and 0.0975 quantiles of K estimated from 1000 simulations.

  Enlarge/Shrink   Download   Full Width  Open in Viewer

In general, a random distribution of juvenile individuals was detected in this study (Fig. 4a, Fig. 4b, Fig. 4c), regardless the radius used in the analysis (10, 20 or 30 m). The density of juvenile individuals was lower then that of adult trees, which could be related to factors like pollination and/or seed dispersion. It could be hypothesized that CSR of juveniles might be due to inter- and intra-specific competition.

In the univariate analysis of adult trees a random spatial distribution was observed, but with a tendency to cluster at a distance up to 20 m (Fig. 4b). The density observed for adult trees was higher when compared to young individuals of Mezilaurus itauba. This behavior was observed in studies on nost tree species in the Amazon region. The lower density of young trees has been interpreted as due to intra- and interspecific competition, and the reproductive system of the species, as well as to soil and microclimatic conditions.

The spatial distribution of Mezilaurus itauba trees detected in this study may reflect both autoecological aspects (e.g., seed dispersal) and interaction with the environment (e.g., availability of resources such as light and essential nutrients). Odum ([27]) reported that, in general, regular or random distribution of individuals may be related to either competition on limited resources or direct antagonism (e.g., allelopathy). Gourlet-Fleury et al. ([18]) reported the effects of the removal of larger individuals in populations of timber trees, highlighting the importance of reproductive ecology in determining the distribution and dynamics of the populations.

  Conclusions 

In this study, the main spatial pattern of the population of Mezilaurus itauba in the southern Amazon was random, though a tendency to aggregation at very close distances was detected. Perry & Dixon ([29]) reported that biological factors such as vegetative growth, dispersal or inter- and intra-specific interactions, were responsible for the aggregate patterns found for some species. Indeed, the spatial arrangement reflects the structure of populations, which in turn affects their renewal by the adult reproductive trees.

Juvenile trees of Mezilaurus itauba in this study presented a pattern of complete spatial randomness. The observed distance between adult and juvenile trees within the analyzed population is consistent with a substantial pollen exchange, thereby allowing a considerable gene flow and a long-term maintenance of the observed genetic structure.

The distribution patterns analyzed by the Ripley’s K function may provide a baseline for the exploration of other native species in the southern Amazon, as well as for forest management programs aimed at determining the gene flow rates and the reproductive system of economically exploited species. Spatial distribution of harvested species provide the essential information needed in the development of sustainable management plans and conservation of natural ecosystems programs.

  Acknowledgements 

This study was financially and supported by “Coordenação de Aperfeiçoamento de Pessoal de Nível Superior” (CAPES) and “Conselho Nacional de Desenvolvimento Científico e Tecnológico” (CNPq), Brazil.

  References