Quantifying forest net primary production: combining eddy flux, inventory and metabolic theory

doi:10.3832/ifor2159-010

Quantifying forest net primary production: combining eddy flux, inventory and metabolic theory

iForest - Biogeosciences and Forestry, Volume 10, Issue 2, Pages 475-482 (2017)
doi: https://doi.org/10.3832/ifor2159-010
Published: Apr 12, 2017 - Copyright © 2017 SISEF

Research Articles

Abstract

Article

Authors’ Info

Info & Metrics

References

Images & Tables

Net primary production (N_PP) is a central and fundamental carbon-related term in global change studies. We proposed a top-down method to quantifying forest N_PP which overcomes the deficits of the traditional bottom-up method. The new top-down method combines eddy flux data, climate variables, tree inventory and metabolic theory. Our method was tested in six forests and provides reliable annual N_PP estimations which are consistent with bottom-up results. Carbon use efficiency also supports this new method. Taking advantage of fine temporal resolution of our top-down method, we examined whether and confirmed N_PP was well correlated with leaf area index at a seasonal scale, as suggested by past studies. The potential value of our new method as a standard N_PP method is high because of the world-wide network on eddy tower and inventory plot, however further data of performance of the new method is needed to fully evaluate its performance under different conditions.

Carbon Use Efficiency, Metabolic Theory of Ecology, Autotrophic Respiration, Biomass, Eddy Covariance

The earth’s surface environment changed dramatically between 1960s and 2010s, including changes in atmospheric gas concentrations, temperatures, and land-cover. Notably, the surface temperature increased by 0.9 °C and the atmospheric CO₂ levels increased by 23% (from 316 to 389 part per million - [3]). The surface warming was most likely caused by radiative forcing resulting from atmospheric CO₂ buildup. Consequently, understanding the carbon balance of ecosystems is a critical component in global change studies.

Net primary production (N_PP) is a central carbon-related term which integrates climatic, ecological, geochemical and human influences on the biosphere ([35]). N_PP is the rate of biomass change in plants, including woody, leaf and root tissues, but also root exudates and volatile organic carbon compounds.

N_PP is defined as the difference between gross primary production (G_PP) and total plant respiration (R_a) in an ecosystem ([41]). In the past, directly measuring both G_PP and R_a were impractical due to methodological constraints, especially for tall forest G_PP ([7]). Whole ecosystem R_a was not only difficult to estimate but also involved significant uncertainties ([26]). Due to methodological advances, it is now possible to obtain ecosystem G_PP by using eddy-covariance techniques ([2]). Furthermore, a potential way for reliable R_a estimation has been developed based upon metabolic theory ([34]).

The traditional method to quantify N_PP was developed during International Biosphere Program (IBP - [36]), which calculate N_PP by combining the organic tissue biomass growth of all quantifiable components within a plant or an area. Currently N_PP is normally calculated using the IBP-method with field-surveys ([8]).

Though widely-used, several intrinsic deficits exist in the IBP-method. First, not all N_PP components can be directly measured in the field due to environmental variations during the measuring interval ([7]). Second, it is difficult to obtain a fine temporal resolution N_PP (i.e., daily), and thus to explore the explicit links of N_PP to environmental conditions. Third, the IBP-Method is labor intensive and therefore difficult to implement automatically. Methodological constraints not only limit field-data availability, but also hinder the accuracy of N_PP estimation and prediction. Therefore, alternative new methods are urgently needed for forest N_PP studies.

We propose a new method to quantify N_PP, which more accurately quantifies its various components and explores how these components co-vary with climatic variation at a high temporal resolution. The new method was tested in six primary forests. To overcome major deficits of the traditional IBP-method, we directly address weaknesses within the IBP method and compare the results derived from both methods. Top-down design, high temporal resolution, and automatic monitoring represent a significant advance in forest N_PP estimation, and could provide a way of comparing N_PPof forests globally. It could also serve as an independent way to verify estimation derived from the current IBP-method.

The new top-down method for N_PP

The new method estimates N_PP via top-down analysis (eqn. 1):

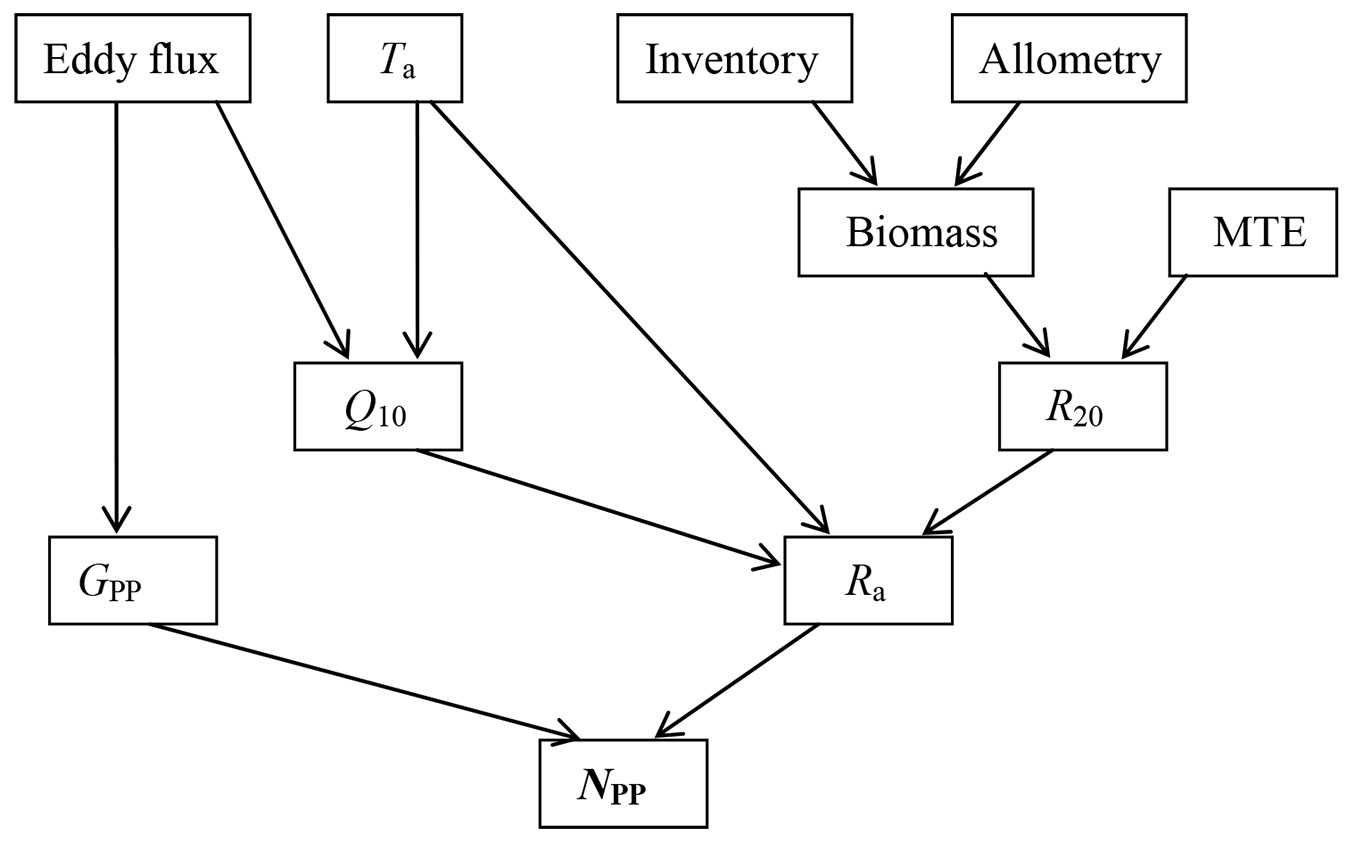
\begin{equation} N_{pp} = G_{pp} - R_{a} \end{equation}

Fig. 1 - Flow schema of top-down estimation of forest net primary production (N_PP). Eddy flux is carbon flux measured by eddy covariance technique; (T_a): temperature; (Q₁₀): respiration temperature sensitivity index; (G_PP): gross primary production; (R₂₀): tree autotrophic respiration at 20°C; (R_a): autotrophic respiration; (MTE): metabolic theory of ecology here specified to Mori et al. ([34])’s work. Tree census (Inventory) data and site-specific allometric equations were used in calculating tree biomass individually.

Enlarge/Shrink Download Full Width Open in Viewer

The general work flow is illustrated in Fig. 1. Most data required by this method are derived from eddy flux, air temperature, and tree size. Tree size is converted into biomass by using allometric equations. R_a of each tree at 20 °C (R₂₀) was estimated according to the common tree biomass-respiration relationship reported by Mori et al. ([34] - eqn. 2):

\begin{equation} {\frac{ 1} { R_{20}}} = {\frac{ 1} { 201.78 M^{1.408}}} + {\frac{ 1}{ 0.410 M^{0.805}}} \end{equation}

where M is the biomass of a tree. The coefficients were estimated from 271 naturally growing trees in tropical, temperate and boreal forests, with a regression correlation coefficient of 0.99 ([34]). R_a was constructed from the Q₁₀ model of Janssens & Pilegaard ([19] - eqn. 3):

\begin{equation} R_{a} = R_{ref} - Q_{10}^{\frac{(T -T_{ref})}{10}} \end{equation}

where R_ref is R_a at the reference temperature T_ref, here specified to R₂₀ at 20 °C. G_PP is obtained by partitioning eddy flux after necessary data treatment.

Forests for testing

Six forests were used to test the new method.

Forest 1: A temperate forest in Changbaishan (CBS), northeastern China. The geographic location is 128° 28′ E, 42° 24′ N. The CBS forest is primary and over 250 years old with a canopy height of 26 meters. The annual mean temperature was 4 °C and the annual rainfall was 700 mm. The dominant tree species are Pinus koraiensis, Tilia amurensis, Acer mono, Fraxinus mandshurica, and Quercus mongolica. Inventory data were collected from a 20 ha plot very close to the eddy flux site ([16]).

Forest 2: A tropical seasonal forest in Xishuangbanna (BNS), Southwest China. The geographic location is 101° 15′ E, 21° 55′ N. The annual mean temperature and rainfall were 21.7 °C and 1490 mm respectively. The mean canopy height was 30 m. Trees in the topmost layer primarily include Pometia tomentosa, Terminalia myriocarpa, Gironniera subaequalis, and Garuga floribunda. Inventory data were collected from a 1 ha plot beneath the eddy flux tower ([50]).

Forest 3: A tropical seasonal deciduous forest in Mae Klong (MKL), Thailand. The geographic location is 108° 53′ E, 18° 43′ N. The annual mean temperature and rainfall were 25 °C and 1500 mm respectively. The mean canopy height was 30 m. The stand age was around 30 years in 2008. Domestic species in overstory are Shorea siamensis, Vitex peduncularis, Xylia xylocarpa. Inventory data were collected from a 4 ha plot ([31]).

Forest 4: A tropical lowland rainforest in Pasoh (PSO), Malaysia. The geographic location of the forest is 102° 18′ E, 02° 58′ N. The annual mean temperature and rainfall were 25.3 °C and 1865 mm respectively. The mean canopy height was 35 m. The studied forest is primary. Domestic species in overstory predominantly belong to Dipterocarpaceae, Leguminosae, Burseraceae. A total of 814 species existed in the 50 ha plot. Inventory data were collected from a 6 ha plot beneath the eddy flux tower ([18], [23]).

Forest 5: A tropical secondary forest in Bukit Soeharto (BKS), Indonesia. The geographic location is 117° 02′ E, 0° 51′ S. The annual mean temperature and rainfall were 27 °C and 3300 mm respectively. The studied forest is a secondary forest. In 1998, the secondary-growth forest disappeared due to a forest fire facilitated by El Niño Southern Oscillation (ENSO) event. The mean canopy height was 12.4 m in year 2004. We used eddy flux data in 2001 and 2002 and tree census data in 2003. Dominant species in overstory were Macaranga gigantea. Inventory data were collected from three 1 ha plots which were not logged ([40]).

Forest 6: A logged tropical rainforest in Tapajos (K83), Brazil. The geographic location is 54° 31′ E, 03° 01′ S. The annual mean temperature and rainfall were 25 °C and 1911 mm respectively. The mean canopy height was 35 m. The inventory plot is 16 ha in the east of an eddy flux tower ([32]).

The eddy flux based G_PP

Eddy covariance based net ecosystem CO₂ exchange (N_EE) is estimated as ([33] - eqn. 4):

\begin{equation} N_{EE} = \rho\; \overline{w^{\prime} c^{\prime}} + \rho \int_{0}^{z} {\frac{dc } {dt }} dz \end{equation}

The overbar indicates averaging over time, primes represent fluctuations from the average, ρ is the molar density of dry air, w is vertical wind velocity, c is the mixing ratio of CO₂ measured by infrared gas analyzer, dc/dt is the change in CO₂ mixing ratio with time, and z_r is the measurement height.

The N_EE could be decomposed into G_PP and ecosystem respiration (R_e) as (eqn. 5):

\begin{equation} G_{PP} = -(N_{EE} -R_{e}) \end{equation}

The minus sign outside the parenthesis results from discipline convention. Total R_e is the sum of nighttime and daytime R_e, and conceptually nighttime N_EE is equivalent to nighttime R_e. However, nighttime N_EE is usually underestimated during periods of low turbulence. The common way to correct this underestimation is the so-called u* filtering method. In this method, the threshold u* was determined by finding a saturation point in u* and nighttime N_EE plot. All N_EE observations were filtered by removing all values below the u* threshold prior to analysis.

Inventory, tree biomass, R₂₀ and R_a estimation

Mori et al. ([34]) suggests a common tree biomass-respiration relationship. R₂₀was estimated from tree biomass obtained by Kato et al. ([21]) for BKS, MKL and PSO; by Chen & Guo ([5]) for CBS; by Chambers et al. ([4]) for K83; and by Lv et al. ([28]) for BNS.

A mixed-power scaling rather than the single-power scaling of eqn. 2 was recommended by Mori et al. ([34]). We compared R₂₀ estimated with both scaling. On the other hand, we used the Q₁₀ derived from flux tower R_e, which includes the temperature sensitivity of both heterotrophic (R_h) and autotrophic respiration (R_a), to obtain R_a with eqn. 3. In some cases, the Q₁₀ of R_h and R_a is different and this might lead to biased estimate for R_a. Furthermore, we cannot obtain Q₁₀ value for an equatorial tropical rainforest where temperature range was very narrow. Under such circumstance, we used a fixed Q₁₀ of 2 for the equatorial rainforest ([1], [42]). A sensitivity analysis was also used to investigate how Q₁₀ affect R_a.

The IBP based N_PP

The detail on estimating N_PP with IBP method has been extensively discussed in an IBP book ([36]) and a review by Clark et al. ([7]). In general, IBP based N_PP was estimated as the sum of biomass increment and biomass losses occurred during the investigation interval both above- and below-ground. We did not estimate IBP based N_PP for each site but rather collected the published values.

Other supporting measurements and calculations

Remote sensing-derived leaf area index was generally used to estimate N_PP at large scales ([13], [37]). We calculated leaf area index (L_AI) to examine whether it could explain the seasonal variation of evergreen tropical forest N_PP at daily resolution.

Following Jarvis & Leverenz ([20]), L_AI was estimated as (eqn. 6):

\begin{equation} L_{AI} = - \ln \left (\frac{Q_{T}}{Q_0} \right ) \kappa^{-1} \end{equation}

where κ is extinction coefficient which varied between 0.4 and 0.65. We used 0.55. Q_t is the transmitted photosynthetically active radiation (P_AR), and was monitored by a sensor (LI-190SB^®, LI-Cor, USA) placed at the height of 3.9m, and Q_o is the P_AR above the canopy measured by a sensor at the height of 36.2 m.

The R_a derived from metabolic theory and its uncertainties

The application of Mori et al. ([34])’s finding in estimating forest R_a is the key issue of this new method. Mori et al. ([34]) claimed that a mixed-power function rather than a single-power function is better in describing the biomass-respiration relationship. The mixed-power function implying a gradual ontogenetic transition in the scaling of metabolism is theoretically sound. We compared R₂₀ obtained with mixed-power function to that with single-power one (Tab. 1). The single-power based R₂₀ is 13% higher that of mixed-power. In the statistic perspective, both single-power and mixed-power functions have a good ability at simulating R₂₀ with correlation coefficient as high as 0.99 ([34]). The R₂₀, however, is very sensitive to the choice of single- or mixed-power function.

Tab. 1 - Estimated biomass and reference respiration rate at 20 °C (R₂₀). (MAT): mean annual temperature; (MAP): mean annual precipitation.

Forest	MAT [°C]	MAP [mm]	Biomass [t dry matter ha^-1]	R₂₀ [μmol m^-2 s^-1]
Forest	MAT [°C]	MAP [mm]	Biomass [t dry matter ha^-1]	Single power	Mixed power
Forest1: CBS	4	700	291	3.437	3.067
Forest2: BNS	21.7	1490	375	3.998	3.545
Forest3: MKL	25	1500	265	2.416	2.090
Forest4: PSO	25.3	1865	456	4.872	4.317
Forest5: BKS	27	3300	239	2.532	2.235
Forest6: K83	25	1911	348	4.091	3.660

Enlarge/Reduce Open in Viewer

Other than R₂₀, another important parameter which affects R_a estimation is the Q₁₀ value. Currently, data for Q₁₀ of R_a are scarce. As shown in the flow chart of this new method (Fig. 1), we used Q₁₀ of R_e derived from eddy flux observations. However, neither R_e nor soil respiration Q₁₀ of equatorial tropical forest is available partly due to narrow temperature ranges. Some studies even found a negative or quadratic relationship between soil respiration and temperature ([15]). Furthermore, R_e is the sum of autotrophic (R_a) and heterotrophic components (R_h). The Q₁₀ derived from flux tower R_e, which includes the temperature sensitivity of both R_a and R_h, might induce some bias when Q₁₀ of R_a and R_h is not the same.

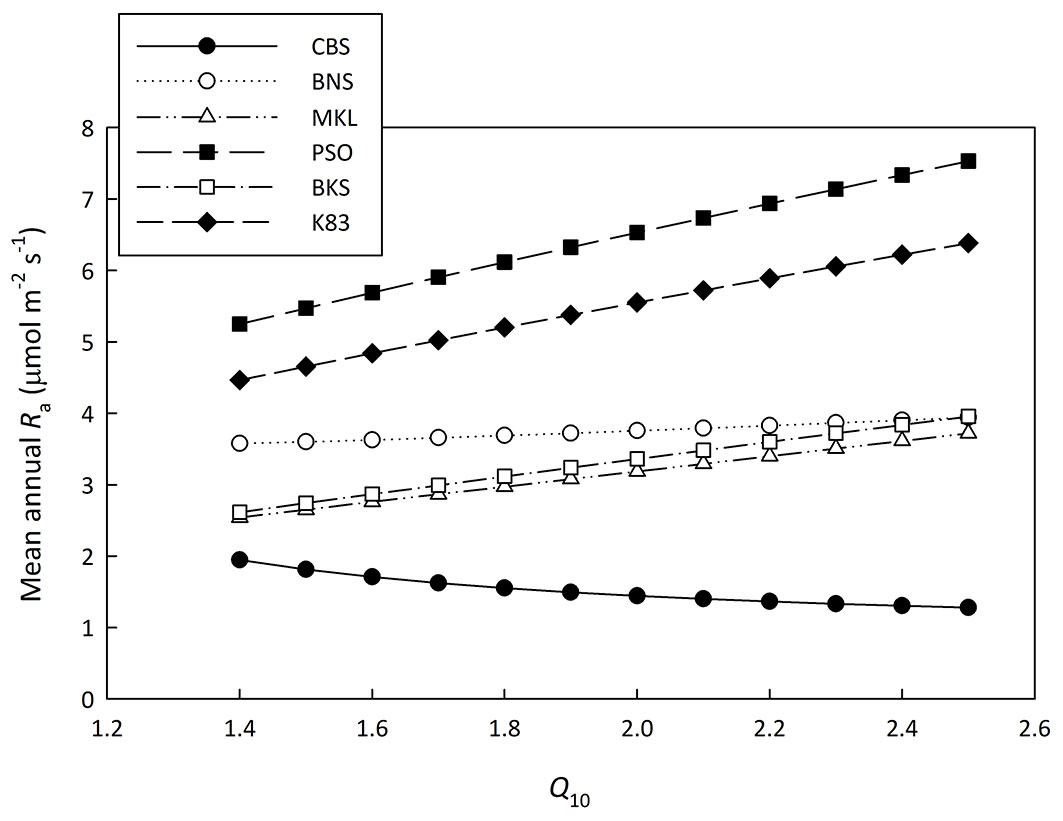
Concerning Q₁₀, we analyzed the sensitivity of Q₁₀ with R_a (Fig. 2). When the Q₁₀ value varied from 1.4 to 2.5, R_a changed slightly for sites which have mean annual temperatures near 20 °C, (i.e., BNS - Fig. 2). However, these changes could be up to around 40% for other sites (Fig. 2). This means the Q₁₀ sensitivity is a critical issue in the new method. The Q₁₀ value for R_e is available for CBS and BNS sites and it was used to drive the new method. For the other five tropical forests where Q₁₀ is not available, it was set as 2.0 ([1], [42]) and the corresponding R_a estimates are shown in Tab. 2.

Fig. 2 - Sensitivity analysis of R_a to temperature sensitivity index (Q₁₀). The mean annual autotrophic respiration rate (R_a) estimated with Q₁₀ varied from 1.4 to 2.5 for each site.

Enlarge/Shrink Download Full Width Open in Viewer

Tab. 2 - A summary table for eddy flux based gross primary production (G_PP), IBP based net primary production (IBP-N_PP), metabolic theory based autotrophic respiration (R_a) and the new top-down method based N_PP (New-N_PP). All values are in the unit of tC ha^-1 yr^-1. (‡): For CBS and BNS, Q₁₀ was derived from eddy flux based R_e, for other forests Q₁₀ was set at 2.0; (§): values in parentheses represent the range from estimates when Q₁₀=1.4 to Q₁₀=2.5; (£): values after “±” in this column are 20% uncertainties, as suggested by Desai et al. ([10]); other values after “±” in this table are standard deviations (STD); (1) Chen et al. ([6]); (2) Zhang et al. ([50]); (3) Dlioksumpun et al. ([11]); (4) Kosugi et al. ([23]); (5) Hirata et al. ([17]); (6) Malhi et al. ([30]); (7) Wang et al. ([44]); (8) Zhang et al. ([50]); (9) Kira ([22]); (10) Toma et al. ([43])

Forest	Eddy flux G_PP	IBP-N_PP	R _a ^‡	New-N_PP ^£
Forest1: CBS	13.38 ⁽¹⁾	7.69 ⁽⁷⁾	5.32 ± 0.31	8.06 ± 1.61
Forest2: BNS	23.42 ± 1.74 ⁽²⁾	8.80 ⁽⁸⁾	14.63 ± 0.86	8.79 ± 1.75
Forest3: MKL	23.98 ⁽³⁾	7.97 ⁽³⁾	12.06 (9.60~14.08)^§	11.92 ± 2.38
Forest4: PSO	32.16 ± 1.32 ⁽⁴⁾	12.85 ⁽⁹⁾	24.72 (19.87~28.50)	7.44 ± 1.48
Forest5: BKS	27.10 ⁽⁵⁾	14.70 ⁽¹⁰⁾	12.71 (9.87~14.97)	14.39 ± 2.87
Forest6: K83	31.40 ⁽⁶⁾	14.40 ± 1.30 ⁽⁶⁾	21.00 (16.90~24.15)	10.40 ± 2.08
Mean ± STD	25.24 ± 6.85	11.07 ± 3.27	15.07 ± 6.90	10.17 ± 2.64

Enlarge/Reduce Open in Viewer

The third relevant issue which may induce additional uncertainties is the use of temperature response function to evaluate R_a. Several alternative functions are available for this case ([12]). For example, the highly cited Lloyd & Taylor ([27])’s function as (eqn. 7):

\begin{equation} R_{a} = R_{ref} \cdot exp \left [E_0 \left ({\frac{1 } {T_{ref} - T_0}} - {\frac{1 } { T-T_0}} \right ) \right ] \end{equation}

where E₀ and T₀ are two parameters which could be related to Q₁₀ as (eqn. 8):

\begin{equation} Q_{10} = exp \left [{\frac{10 E_0 } { (T-T_0)(T+10-T_0)}} \right ] \end{equation}

Similar to this, the classic Arrhenius function could be related to Q₁₀ as (eqn. 9):

\begin{equation} Q_{10} = exp \left [{\frac{ 10E_{a}} { RT(T+10)}} \right ] \end{equation}

where E_a is the activation energy. We compared the application of Lloyd & Taylor ([27])’s function to the Q₁₀ function of eqn. 3 with the dataset in CBS site. The uncertainty caused by this difference is small. To simplify the methodology, we eventually used eqn. 3 for all cases in this study.

Eddy flux based G_PP and its uncertainties

One crucial component of the new top-down method is reliably calculating G_PP with eddy covariance based carbon fluxes (Fig. 1). The G_PP can be obtained by decomposing N_EE as shown in eqn. 5. Extrapolating the post u* filtering nighttime R_e to that of daytime is a common method within the flux community ([38]). It has successfully been used to reproduce global G_PP ([2]). Nevertheless, the Reichstein et al. ([38]) method was criticized for not providing a reliable G_PP value. Leaf respiration may be inhibited under light conditions. Using values extrapolated from nighttime, but rather that of daytime, overestimates R_e and subsequently the G_PP ([47], [46]).

As an alternative method, daytime respiration could be also obtained by extending daytime measurements to zero light, commonly termed as light response method ([48], [24]). Rather than an extensive discussion and comparison on decomposition techniques separating N_EE into G_PP and R_e, we used CBS site’s data as a case analysis. The light response regression was done with a window of 10 days by using the Michaelis-Menten function as (eqn. 10):

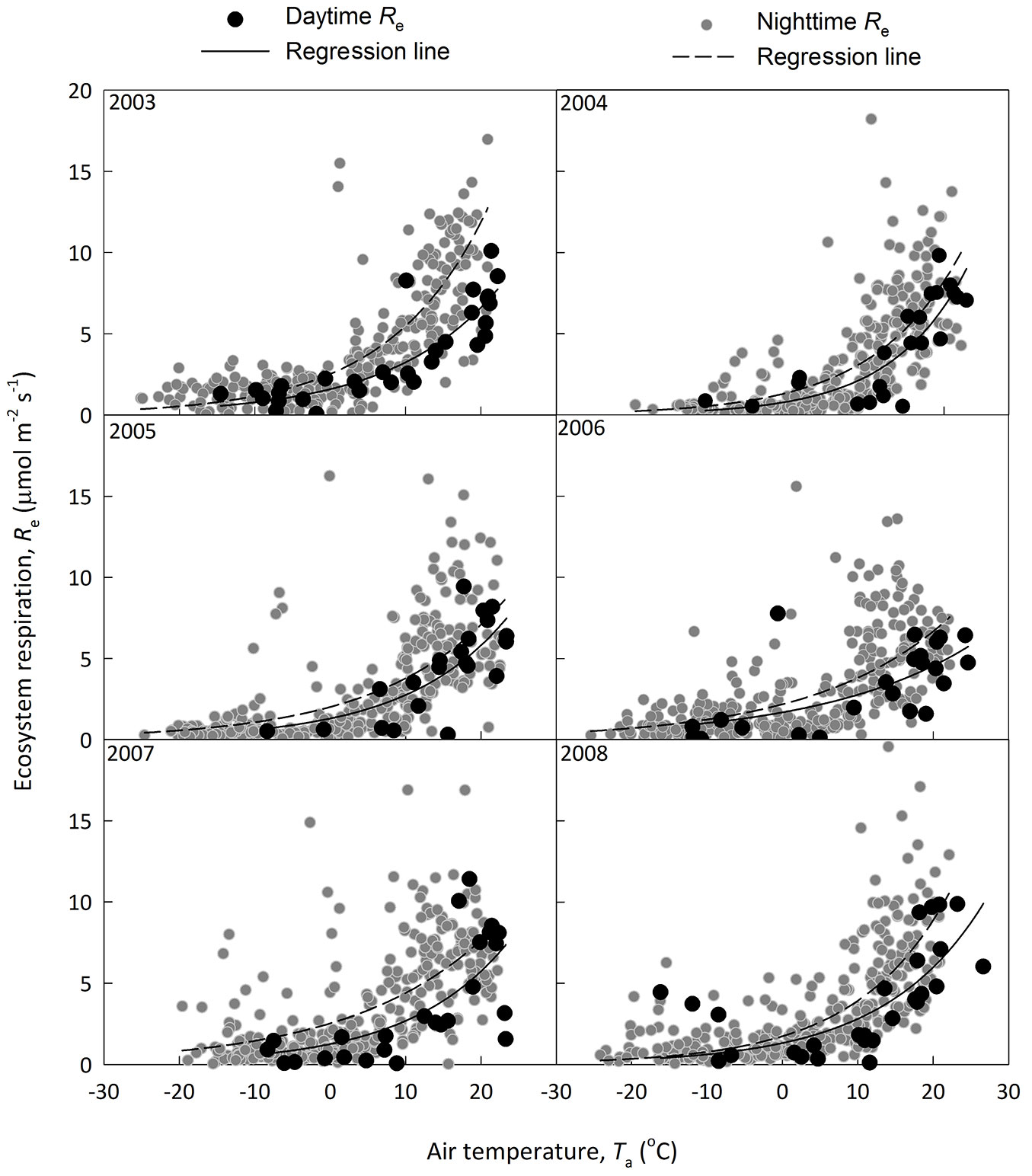
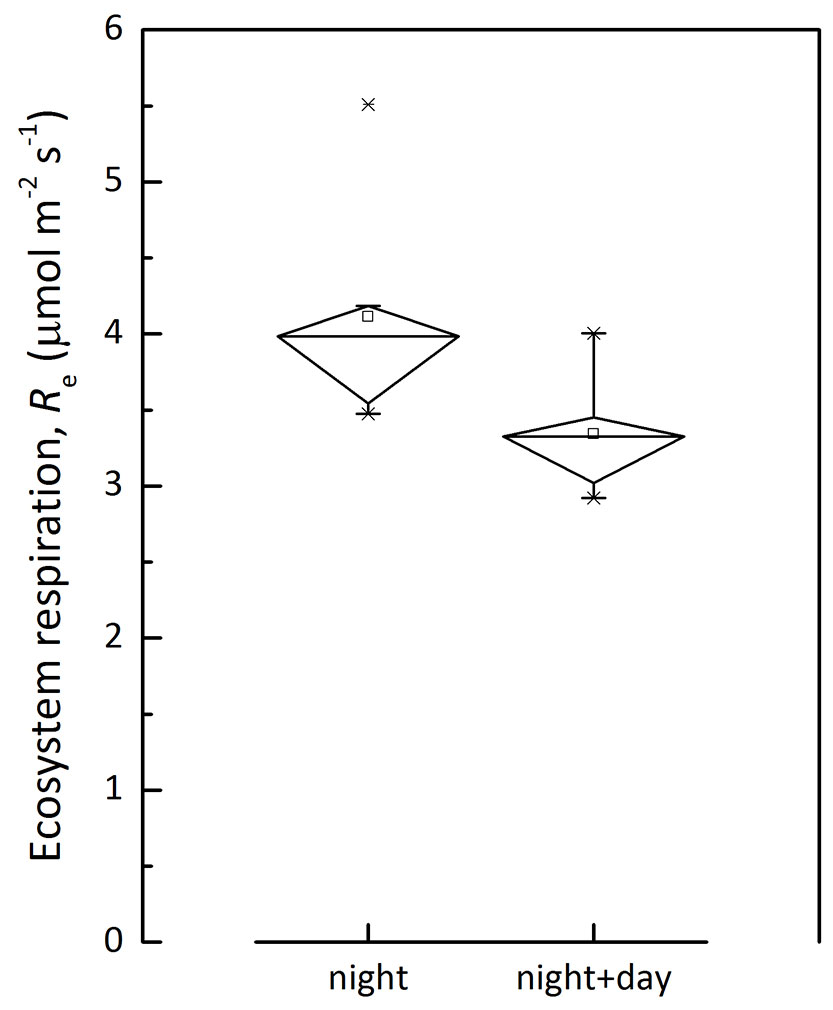
\begin{equation} N_{EE} = - \left ({\frac{ \alpha P_{m} I } { \alpha I +P_{m}}} -R_{d} \right ) \end{equation}

where I is the light intensity, α is the apparent quantum yield representing the slope under weak light, P_m is the light-saturated photosynthesis rate, R_d is the derived daytime ecosystem respiration. The temperature dependence of R_d and nighttime R_e of CBS site is shown in Fig. 3. Nighttime R_e was generally higher than that of daytime R_e derived from light response. The R_e estimation was compared between that derived from nighttime data only and that based on both day- and nighttime data (Fig. 4). This supports the claim that R_e with nighttime flux was overestimated ([46]), though the methods include some difficulties to quantify components.

Fig. 3 - A comparison on daytime ecosystem respiration (R_e, black circles and solid regression line) derived from light response and nighttime R_e (dark grey circles with dashed line). The Q₁₀ model (see text for detail) was used in fitting the dataset.

Enlarge/Shrink Download Full Width Open in Viewer

Fig. 4 - A comparison on mean ecosystem respiration rate estimated with nighttime data only (night) and a combining of both day- and night-time data (night+day).

Enlarge/Shrink Download Full Width Open in Viewer

(i) Can R_d accurately represent the daytime ecosystem respiration? R_d estimate is very sensitive to weak light observations. Weak light intensity usually occurs under transitional periods in the early morning, late afternoon or in periods of high cloud cover. Rapid and large changes in atmospheric stability will cause unnecessary uncertainties in this process, i.e., the flux burst effect in the morning ([14]).

(ii) Could R_d derived from the simple light response model represent the daytime ecosystem respiration in reality? A group of variables drive daytime fluxes including R_d. Lasslop et al. ([24]), for example, showed that a model water vapor pressure deficit (VPD) included could work better in obtaining R_eand G_PP than a model drive by temperature only.

Uncertainties along with decomposition techniques in deriving G_PP are substantial. Desai et al. ([10]) compared 23 decomposition methods and reported that most methods differed up to 20% in estimates of both G_PP and R_e (see also [38], [48], [10], [24], [39]).

In this study, we cite published G_PP values for each site (Tab. 2) as a defensible, persuasive and unified decomposition technique on eddy flux based G_PP is currently unavailable ([10], [46]). Eddy flux data processing usually needs further site-specific information. We also compare the reported G_PP to that obtained with an online processing procedure (⇒ http://www.bgc-jena.mpg.de/bgi/index.php/Services/REddyProcWeb) widely used in European Flux communities for CBS and BNS, both of which show high levels of agreement. Thus, the up-to-date G_PP reported by site’s investigators could be viewed as a good option.

The matching of inventory plot with eddy flux footprint

To apply the proposed method, we should ensure that the plot used for the inventory is comparable with the eddy covariance flux footprint for that site. Nevertheless, the scale of inventory plot and eddy flux footprint is usually not well matched both in space and time. While an inventory plot is usually set in a few hectares, an eddy flux footprint could be as large as ~1 km². In the current study, we selected six forests to validate the proposed method. The inventory plots of CBS, BNS, and PSO sites were just located within the eddy flux footprint. For the K83 site, inventory and eddy flux data have already been used in a matching method to address carbon balance ([32]). The forest type and disturbance history were the same in the inventory plot and eddy footprint for all six sites.

Another helpful experimental design is setting multiple small plots instead of a big one. Multiple small plots distributed in the footprint, when all footprint biomass estimation is not affordable, are definitely better in terms of representativeness than a single big one placed somewhere in the vicinity ([25]). This helpful design was not involved in the current study but was strongly recommended for future studies.

Comparison on the new top-down N_PP and IBP based N_PP

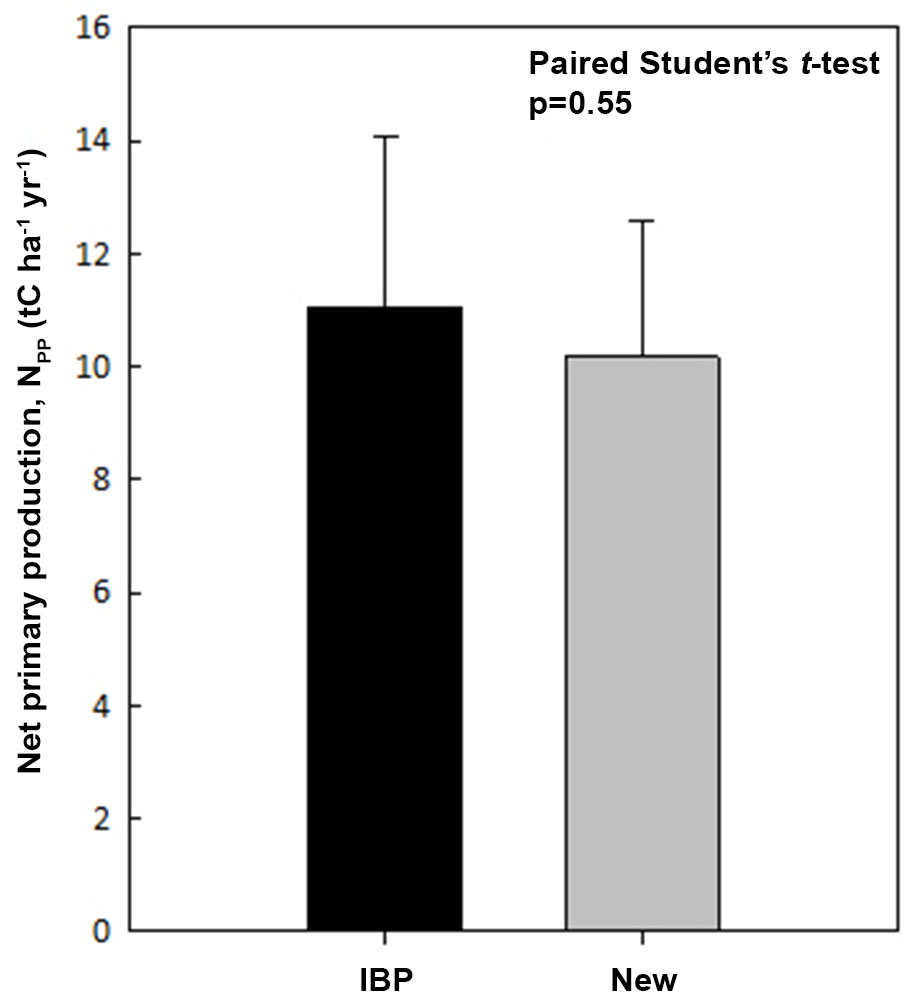
Both the new top-down N_PP and the IBP based N_PP estimates are listed in Tab. 2, and a paired Student t-test showed no significant difference (p=0.55 - Fig. 5). We also found N_PP estimates are nearly identical for the CBS and BNS sites where Q₁₀ is available, providing strong support for the new top-down method.

Fig. 5 - A comparison on net primary production (N_PP) estimated with IBP method (IBP-NPP) and the new top-down method (New-NPP).

Enlarge/Shrink Download Full Width Open in Viewer

Nevertheless, the new N_PP differed from the IBP N_PP in the MKL, PSO and K83 sites. For the PSO and K83 sites, the new N_PP seems to be underestimated whilst R_a overestimated. This underestimation may be related to the assumed fixed Q₁₀ value. Conversely the MKL site shows the opposite, and the biomass of the MKL site is as low as that of the temperate CBS forest. The MKL forest is under its secondary growth. The stand age of this secondary forest is only around 38 years and the inventory data used to calculate biomass and R_a was collected in year 1992, when the stand age was only 14. Since biomass is expected to increase during the early stages of secondary growth, the biomass and R_a derived with data collected in 1992 is likely to be underestimated, which may account for the overestimation of R_a with the new method in MKL.

Further support for the new top-down methods can be derived from the carbon use efficiency (C_UE), i.e., the ratio between N_PP and G_PP. C_UE was reported to be about 0.50 in temperate forests ([45], [9], [49]) and about 0.35 in tropical forests ([29]). C_UE derived from the new top-down method was 0.60 in temperate forest and around 0.3 for primary tropical forests (C_UE is 0.37, 0.23, 0.33 for BNS, PSO, K83, respectively), which agree well with the previous suggestions.

The seasonal variation of N_PP

Accurately quantifying the seasonal variation of forest N_PP by the IBP method is challenging. The tradition temporal resolution for IBP based N_PP is a year ([7]), which ignores temporal variability in climatically variable sites. Most of our knowledge of N_PP seasonality is indirectly obtained through remote sensing ([13], [37]). The remote sensing inversion of N_PP is based on the strong relationship between N_PP and the vegetation index. We utilized the finest temporal resolution available for the top-down N_PP to test the relationship between the N_PP and the vegetation index.

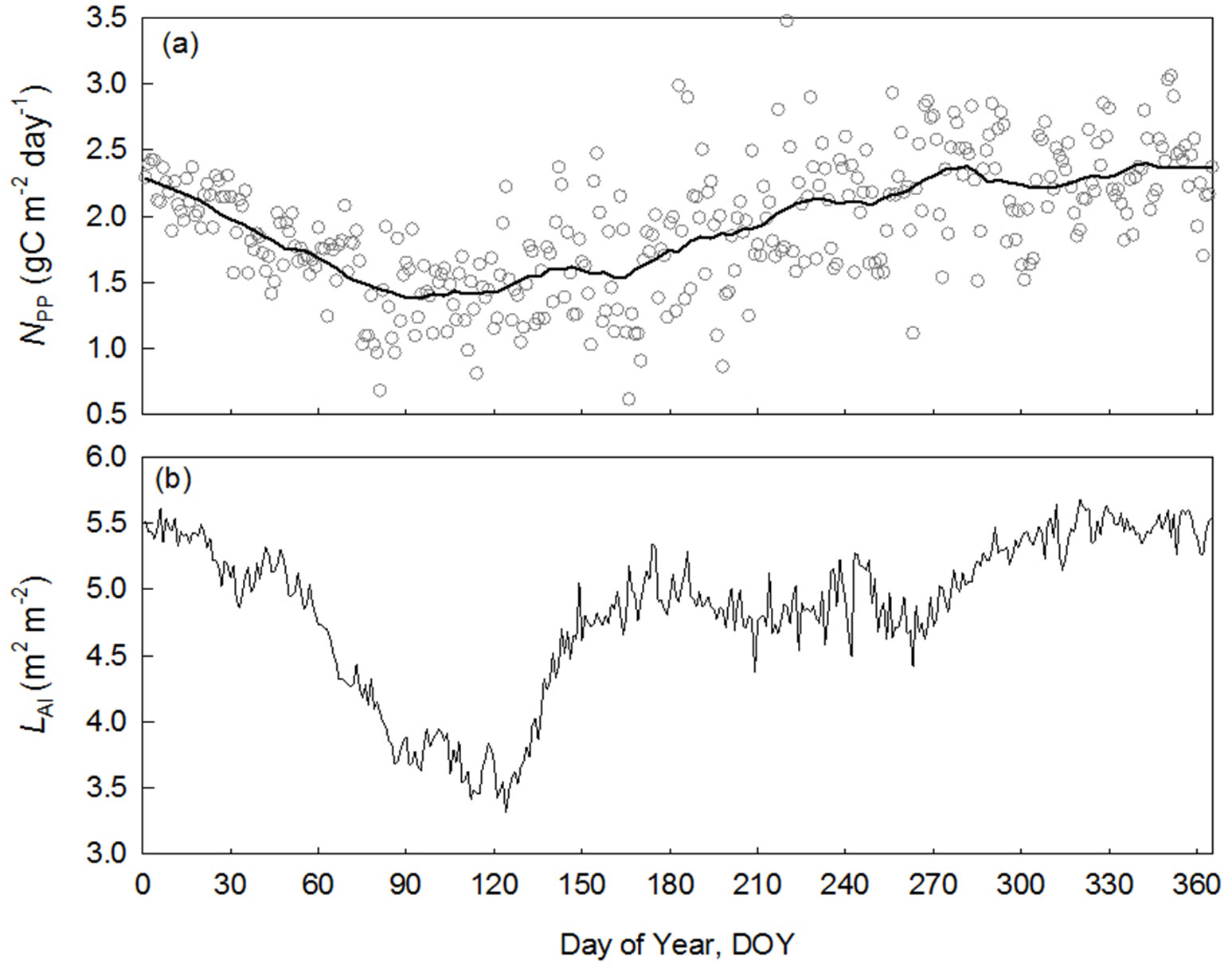
The seasonality in N_PP is clear in BNS (Fig. 6a), and is lowest during the late dry season when water vapor pressure deficit (V_PD) and soil water deficit peak (indicated by soil water content, S_WC). The leaf area index (L_AI) was also lowest in the period. A close relationship was found between L_AI and N_PP (Pearson’s r=0.56, n=365). This result confirmed the reliability of remote sensing derived N_PP and provides a direct estimate on seasonal N_PP.

Fig. 6 - Seasonal variation of net primary production (N_PP) calculated by the proposed new method and leaf area index in a tropical rainforest of Xishuangbanna (BNS), China. (a): daily N_PP in open circles in black grey, solid line show smoothing line; (b): daily leaf area index (L_AI) derived from light transmittance.

Enlarge/Shrink Download Full Width Open in Viewer

Currently, many forest sites have installed eddy covariance systems and established inventory plots. A world-wide test on this new top-down method will both advance our knowledge on N_PP and give a more solid terrestrial N_PP estimation. The limitations and uncertainties of the new top-down method are substantial. Incorporating other process based models into the top-down method would increase accuracy and may enhance its value as a standard method.

Forest N_PP is a fundamental parameter describing the ecosystem functioning. It is the change rate of biomass including woody, leaf and woody tissues, exudates and volatile organic carbon compounds. We proposed a novel method to quantify N_PP using measurements that are different from the traditional IBP method. We propose the use of eddy covariance together with the total biomass and the scaling factor proposed by Mori et al. ([34]) to estimate the autotrophic respiration (R_a). Then N_PP is simply obtained from the gross primary production (G_PP) derived from eddy covariance, with the simple equation N_PP= G_PP- R_a.

Six sites were used to validate the proposed new method. They were selected because of the good match between inventory plot and eddy flux footprint. The new method provides reliable annual N_PP estimations which are consistent with bottom-up results. This consistence was also supported by the past knowledge on carbon use efficiency. Taking the advantage of fine temporal resolution of the new top-down method, the seasonal changes of N_PP at daily interval was presented. A close relationship between N_PP and leaf area index was found at seasonal scale. This finding validated the new method on the one hand, and provided further support of using satellite vegetation index to address N_PP dynamics on the other. The potential of this new method as a standard N_PP method is high because of the world-wide network on eddy tower and inventory plot, however further work of using the method with cases under environmental stress is needed to fully evaluate its performance under variable conditions.

Eddy flux data sources include ChinaFLUX, AsiaFLUX, CForBio, website ⇒ http://www.ess.uci.edu/~lba/ and ⇒ http://www.ffpri.affrc.go.jp/labs/EA-FDPN/. We would like to express thanks to the projects of “Long-term monitoring of forest carbon dynamics in East Asia [EA-FDPN Phase II]”, ChinaFLUX, AsiaFLUX, CForBio and LBA for providing the data. The study was supported by National Natural Science Foundation of China (NSFC no. 31660142, 31200347), Youth Innovation Promotion Association of Chinese Academy of Sciences, and C-Project for talents of Hainan University.

(1)

Amthor JS (1984). The role of maintenance respiration in plant growth. Plant, Cell and Environment 7: 561-569.
CrossRef | Gscholar

(2)

Beer C, Reichstein M, Tomelleri E, Ciais P, Jung M, Carvalhais N, Rodenbeck C, Arain MA, Baldocchi DD, Bonan GB, Bondeau A, Cescatti A, Lasslop G, Lindroth A, Lomas M, Luyssaert S, Margolis H, Oleson KW, Roupsard O, Veenendaal E, Viovy N, Williams C, Woodward FI, Papale D (2010). Terrestrial gross carbon dioxide uptake: global distribution and covariation with climate. Science 329: 834-838.
CrossRef | Gscholar

(3)

Brohan P, Kennedy JJ, Haris I, Tett SFB, Jones PD (2006). Uncertainties estimates in regional and global observed temperature changes: a new dataset from 1850. Journal of Geophysical Research Atmosphere 111: D12106.
CrossRef | Gscholar

(4)

Chambers JQ, Santos JD, Ribeiro RJ, Higuchi N (2001). Tree damage, allometric relationships, and above-ground net primary production in central Amazon forest. Forest Ecology and Management 152: 73-84.
CrossRef | Gscholar

(5)

Chen CG, Guo XF (1984). Biomass of broadleaved red pine forest. Forest Investigation and Design 2: 10-19.
Gscholar

(6)

Chen Z, Yu G, Ge J, Sun X, Hirano T, Saigusa N, Wang Q, Zhu X, Zhang Y, Zhang J, Yan J, Wang H, Zhao L, Wen X, Shi P, Zhao F (2013). Temperature and precipitation control of the spatial variation of terrestrial ecosystem carbon exchange in the Asian region. Agricultural and Forest Meteorology 182-183: 266-276.
CrossRef | Gscholar

(7)

Clark DA, Brown S, Kichlighter DW, Chambers JQ, Thomlinson JR, Ni J (2001a). Measuring net primary production in forests: concepts and field methods. Ecological Applications 11: 356-370.
CrossRef | Gscholar

(8)

Clark DA, Brown S, Kichlighter DW, Chambers JQ, Thomlinson JR, Ni J, Holland EA (2001b). Net primary production in tropical forests: an evaluation and synthesis of existing field data. Ecological Applications 11: 371-384.
CrossRef | Gscholar

(9)

DeLucia E, Drake JE, Thomas RB, Melers MG (2007). Forest carbon use efficiency: is respiration a constant fraction of gross primary production? Global Change Biology 13: 1157-1167.
CrossRef | Gscholar

(10)

Desai AR, Richardson AD, Moffat AM, Kattge J, Hollinger DY, Barr A, Falge E, Noormets A, Papale D, Reichstein M, Stauch VJ (2008). Cross site evaluation of eddy covariance GPP and RE decomposition techniques. Agricultural and Forest Meteorology 148: 821-838.
CrossRef | Gscholar

(11)

Dlioksumpun S, Visaratana T, Panuthai S, Ladpala P, Janmahasatien S, Sumran S (2009). Carbon cycling in the Sakaerat dry evergreen and the Marklong mixed deciduous forests. Thailand Journal of Forestry 28: 67-81.
Gscholar

(12)

Gomez-Casanovas N, Anderson-Teixeira K, Zeri M, Bernacchi CJ, DeLucia EH (2013). Gap filling strategies and errors in estimating annual soil respiration. Global Change Biology 19: 1941-1952.
CrossRef | Gscholar

(13)

Gower ST, Kucharik CJ, Norman JM (1999). Direct and indirect estimation of leaf area index, fAPAR, and net primary production of terrestrial ecosystems. Remote Sensing of Environment 70: 29-51.
CrossRef | Gscholar

(14)

Grace J, Malhi Y, Lloyd J, McIntyre J, Miranda AC, Meir P, Miranda HS (1996). The use of eddy covariance to infer the net carbon dioxide uptake of Brazilian rain forest. Global Change Biology 2: 209-217.
CrossRef | Gscholar

(15)

Hanpattanakit P, Leclerc MY, Mcmillan AMS, Limtong P, Maeght JL, Panuthai S, Inubushi K, Chidthaisong A (2015). Multiple timescale variations and controls of soil respiration in tropical dry dipterocarp forest, western Thailand. Plant and Soil 390: 167-181.
CrossRef | Gscholar

(16)

Hao ZQ, Li BH, Zhang J, Wang XG, Ye J, Yao XL (2008). Broad-leaved Korean pine (Pinus koraiensis) mixed forest plot in Changbaishan (CBS) of China: community composition and structure. Acta Phytoecologica Sinica 32 (2): 238-250.
Gscholar

(17)

Hirata R, Saigusa N, Yamamoto S, Ohtani Y, Ide R, Asanuma J, Gamo M, Hirano T, Kondo H, Kosugi Y, Li SG, Nakai Y, Takagi K, Tani M, Wang H (2008). Spatial distribution of carbon balance in forest ecosystems across East Asia. Agricultural and Forest Meteorology 148: 761-775.
CrossRef | Gscholar

(18)

Hoshizaki K, Niiyama K, Kimura K, Yamashita T, Bekku Y, Okuda T, Quah ES, Noor NSM (2004). Temporal and spatial variation of forest biomass in relation to stand dynamics in a mature, lowland tropical rainforest, Malaysia. Ecological Research 19: 357-363.
CrossRef | Gscholar

(19)

Janssens IA, Pilegaard K (2003). Large seasonal changes in Q₁₀ of soil respiration in a beech forest. Global Change Biology 9: 911-918.
CrossRef | Gscholar

(20)

Jarvis PG, Leverenz JW (1983). Productivity of temperate, deciduous and evergreen forests. In: “Physiological Plant Ecology IV. Ecosystem processes: mineral cycling, productivity, and man’s influence” (Lange OL, Nobel PS, Osmond CB, Ziegler H eds). Encyclopedia of Plant Physiology, Springer-Verlag, New York, USA, vol. 12D, pp. 233-280.
CrossRef | Gscholar

(21)

Kato R, Tadaki Y, Ogawa H (1978). Plant biomass and growth increment studies in Pasoh Forest. Malaysian Nature Journal 30: 211-224.
Gscholar

(22)

Kira T (1978). Primary productivity of Pasoh forest - a synthesis. Malaysian Nature Journal 30: 291-297.
Gscholar

(23)

Kosugi Y, Takanashi S, Ohkubo S, Matsuo N, Tani M, Mitani T, Tsutsumi D, Abdul Rahim N (2008). CO2 exchange of a tropical rainforest at Pasoh in Peninsular Malaysia. Agricultural and Forest Meteorology 148: 439-452.
CrossRef | Gscholar

(24)

Lasslop G, Reichstein M, Papale D, Richardson AD, Arneth A, Barr A, Stoy P, Wohlfahrt G (2010). Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: critical issues and global evaluation. Global Change Biology 16: 187-208.
CrossRef | Gscholar

(25)

Law B, Arkebauer T, Campbell JL, Chen J, Sun O, Schwartz M, Van Ingen C, Verma SB (2008). Terrestrial carbon observations: protocol for vegetation sampling and data submission. TCO panel of the Global Terrestrial Observing System (GTOs-55), Global Terrestrial Observing System, Rome, Italy, pp. 4-8.
Online | Gscholar

(26)

Lavigne MB (1997). Comparing nocturnal eddy covariance measurements to estimates of ecosystem respiration made by scaling chamber measurements at six coniferous boreal sites. Journal of Geophysical Research Atmosphere 102: 28977-28985.
CrossRef | Gscholar

(27)

Lloyd J, Taylor J (1994). On the temperature dependence of soil respiration. Functional Ecology 8: 315-323.
CrossRef | Gscholar

(28)

Lv XT, Tang JW, He YC, Duan WG, Song JP, Xu HL, Zhu SZ (2007). Biomass and its allocation in tropical seasonal rain forest in Xishuangbanna, Southwest China. Journal of Plant Ecology 31: 11-22.
CrossRef | Gscholar

(29)

Malhi Y (2012). The productivity, metabolism and carbon cycle of tropical forest vegetation. Journal of Ecology 100: 65-75.
CrossRef | Gscholar

(30)

Malhi Y, Aragão LEOC, Metcalfe DB, Paiva R, Quesada CA, Almeida S, Anderson L, Brando P, Chambers JQ, Costa ACL, Hutyra LR, Oliveira P, Patino S, Pyle EH, Robertson AL, Teixeira LM (2009). Comprehensive assessment of carbon productivity, allocation and storage in three Amazonian forests. Global Change Biology 15: 1255-1274.
CrossRef | Gscholar

(31)

Marod D, Kutintara U, Yarwudhi C, Tanaka H, Nakashizuka T (1999). Structural dynamics of a natural mixed deciduous forest in Western Thailand. Journal of Vegetation Science 10: 777-786.
CrossRef | Gscholar

(32)

Miller SD, Goulden ML, Menton MC, Da Rocha HR, Freitas HC, Figueira AMS, Sousa CAD (2004). Biometric and micrometeorological measurements of tropical forest carbon balance. Ecological Applications 14 (sp4): 114-126.
CrossRef | Gscholar

(33)

Monson R, Baldocchi DD (2014). Terrestrial biosphere-atmosphere interactions. Cambridge University Press, Cambridge, UK, pp. 339.
Online | Gscholar

(34)

Mori S, Yamaji K, Ishida A, Prokushkin SG, Masyagina OV, Hagihara A, Hoque A, Suwa R, Osawa A, Nishizono T (2010). Mixed-power scaling of whole-plant respiration from seedlings to giant trees. Proceedings of the National Academy of Sciences USA 107: 1447-1451.
CrossRef | Gscholar

(35)

Nemani RR, Keeling CD, Hashimoto H, Jolly M, Running SW, Piper SC, Tucker CJ, Myneni R (2003). Climate driven increases in terrestrial net primary production from 1982 to 1999. Science 300: 1560-1563.
CrossRef | Gscholar

(36)

Newbould PJ (1967). Methods for estimating the primary production of forests. Blackwell Scientific Press, New York, USA, pp. 5-8. -
Online | Gscholar

(37)

Ollinger SV, Treuhaft RN, Braswell BH, Anderson JE, Martin ME, Smith ML (2007). The role of remote sensing in the study of terrestrial net primary production. In: “Principles and standards for measuring primary production” (Fahey TJ, Knapp AK eds). Oxford University Press, Oxford, UK, pp. 204-237.
CrossRef | Gscholar

(38)

Reichstein M, Falge E, Baldocchi D, Papale D, Aubinet M, Berbigier P, Bernhofer C, Buchmann N, Gilmanov T, Granier A, Grunwald T, Havrankova K, Ilvesniemi H, Janous D, Knohl A, Laurila T, Lohila A, Loustau D, Matteucci G, Meyers T, Miglietta F, Ourcival JM, Pumpanen J, Rambal S, Rotenberg E, Sanz M, Tenhunen J, Seufert G, Vaccari F, Vesala T, Yakir D, Valentini R (2005). On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm. Global Change Biology 11 (9): 1424-1439.
CrossRef | Gscholar

(39)

Reichstein M, Stoy PC, Desai AR, Lasslop D, Richardson AD (2012). Partioning of net fluxes. In: “Eddy covariance: a practical guide to measurement and data analysis” (Aubinet M, Vesala T, Papale D eds). Springer, New York, USA, pp. 263-289.
CrossRef | Gscholar

(40)

Ruslim Y, Matius P, Sutisna M (2000). A case study of second felling in a logged-over dipterocarp forest. In: “Rainforest Ecosystems of East Kalimantan” (Guhardja E, Fatawi M, Sutisna M, Mori T, Ohta S eds). Springer, Tokyo, Japan, pp. 219-227.
CrossRef | Gscholar

(41)

Schulze ED (2006). Biological control of the terrestrial carbon sink. Biogeosciences 3: 147-166.
CrossRef | Gscholar

(42)

Slot M, Rey-Sánchez C, Gerber S, Lichstein JW, Winter K, Kitajima K (2014). Thermal acclimation of leaf respiration to tropical trees and lianas: response to experimental canopy warming and consequences for tropical forest carbon balance. Global Change Biology 20: 2915-2926.
CrossRef | Gscholar

(43)

Toma T, Matius P, Hastaniah Kiyono Y, Watanabe R, Okimori Y (2000). Dynamics of burned lowland Dipterocarp forest stands in Bukit Soeharto, East Kalimantan. In: “Rainforest Ecosystems of East Kalimantan: El Nino, Dorught, Fire and Human Impacts” (Guhardja E, Fatawi M, Sutisna M, Mori T, Ohta S eds). Springer Press, Tokyo, Japan, pp. 107-120.
CrossRef | Gscholar

(44)

Wang M, Guan DX, Wang YS, Hao ZQ, Liu YQ (2006). Estimate of productivity in ecosystem of the broadleaved Korean pine mixed forest in Changbai Mountain. Science in China D 49: 74-88.
CrossRef | Gscholar

(45)

Waring RH, Landsberg JJ, Williams M (1998). Net primary production of forests: a constant fraction of gross primary production? Tree Physiology 18: 129-134.
CrossRef | Gscholar

(46)

Wehr R, Munger JW, McManus JB, Nelson DD, Zahniser MS, Davidson EA, Wofsy SC, Saleska SR (2016). Seasonality of temperate forest photosynthesis and daytime respiration. Nature 534: 680-683.
CrossRef | Gscholar

(47)

Wohlfahrt G, Bahn M, Haslwanter A, Newesely C, Cermusca A (2005a). Estimation of daytime ecosystem respiration to determine gross primary production of a mountain meadow. Agricultural and Forest Meteorology 130: 13-25.
CrossRef | Gscholar

(48)

Wohlfahrt G, Anfang C, Bahn M, Haslwanter A, Newesely C, Schmitt M, Drosler M, Pfadenhauer J, Cernusca A (2005b). Quantifying nighttime ecosystem respiration of a meadow using eddy covariance, chambers and modeling. Agricultural and Forest Meteorology 128: 141-162.
CrossRef | Gscholar

(49)

Zanotelli D, Montagnani L, Manca G, Tagliavini M (2013). Net primary productivity, allocation pattern and carbon use efficiency in an apple orchard assessed by integrating eddy covariance, biometric and continuous soil chamber measurements. Biogeosciences 10: 3089-3108.
CrossRef | Gscholar

(50)

Zhang Y, Tan Z, Song Q, Yu G, Sun X (2010). Respiration controls the unexpected seasonal pattern of carbon flux in an Asian tropical rain forest. Atmospheric Environment 44: 3886-3893.
CrossRef | Gscholar

Authors’ Affiliation

(1)

Ecology Program, Department of Environmental Science, Hainan University, Haikou 570228 (China)

(2)

Xishuangbanna Tropical Botanical Garden, Chinese Academy of Sciences, Kunming 650223 (China)

(3)

Department of Forest Vegetation, Forestry and Forest Products Research Institute, Tsukuba 305-8687 (Japan)

(4)

Institute of Applied Ecology, Chinese Academy of Sciences, Shenyang 110016 (China)

(5)

Forest Hydrology Lab, Graduate School of Agriculture, Kyoto University, Kyoto 606-8502 (Japan)

(6)

Department of Earth System Science, University of California, Irvine 92697 (USA)

(7)

Institute of Geographic Science and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101 (China)

(8)

Institute of Botany, Chinese Academy of Sciences, Beijing 100093 (China)

Corresponding author

Zheng-Hong Tan
tanzh@xtbg.ac.cn

Citation

Tan Z-H, Hughes A, Sato T, Zhang Y-P, Han S-J, Kosugi Y, Goulden M, Deng X-B, Cao M, Hao Z-Q, Hu Y-H, Yu G-R, Ma K-P (2017). Quantifying forest net primary production: combining eddy flux, inventory and metabolic theory. iForest 10: 475-482. - doi: 10.3832/ifor2159-010

Academic Editor

Silvano Fares

Paper history

Received: Jul 01, 2016
Accepted: Feb 13, 2017

First online: Apr 12, 2017
Publication Date: Apr 30, 2017
Publication Time: 1.93 months

Open Access

This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Breakdown by View Type

(Waiting for server response...)

Article Usage

Total Article Views: 47026
(from publication date up to now)

Breakdown by View Type
HTML Page Views: 39890
Abstract Page Views: 2408
PDF Downloads: 3733
Citation/Reference Downloads: 29
XML Downloads: 966

Web Metrics
Days since publication: 2780
Overall contacts: 47026
Avg. contacts per week: 118.41

Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Feb 2023)

Total number of cites (since 2017): 2
Average cites per year: 0.29

(no records found)

Publication Metrics

by Dimensions ^©

List of the papers citing this article based on CrossRef Cited-by.

iForest Similar Articles

Review Papers

Separating soil respiration components with stable isotopes: natural abundance and labelling approaches

Braig E, Tupek B

vol. 3, pp. 92-94 (online: 15 July 2010)

Research Articles

Do the rubber plantations in tropical China act as large carbon sinks?

Song Q-H, Tan Z-H, Zhang Y-P, Sha L-Q, Deng X-B, Deng Y, Zhou W-J, Zhao J-F, Zhao J-B, Zhang X, Zhao W, Yu G-R, Sun X-M, Liang N-S, Yang L-Y

vol. 7, pp. 42-47 (online: 21 October 2013)

Research Articles

Effect of different dolomitic limestone dosages on soil respiration in a mid-altitudinal Norway spruce stand

Rosíková J, Darenova E, Kučera A, Volarík D, Vranová V

vol. 12, pp. 357-365 (online: 05 July 2019)

Research Articles

Effects of altitudinal gradients on leaf area index, soil microbial biomass C and microbial activity in a temperate mixed forest ecosystem of Northwestern Turkey

Bolat I, Öztürk M

vol. 10, pp. 334-340 (online: 15 December 2016)

Research Articles

Carbon and water vapor balance in a subtropical pine plantation

Posse G, Lewczuk N, Richter K, Cristiano P

vol. 9, pp. 736-742 (online: 25 May 2016)

Research Articles

Distribution factors of the epiphytic lichen Lobaria pulmonaria (L.) Hoffm. at local and regional spatial scales in the Caucasus: combining species distribution modelling and ecological niche theory

Pshegusov R, Khanov Z, Chadaeva V

vol. 17, pp. 120-131 (online: 30 April 2024)

Short Communications

Respiratory costs of woody tissues in a Quercus pyrenaica coppice

Salomón RL, Rodríguez-Calcerrada J, Gil L, Valbuena-Carabaña M

vol. 11, pp. 437-441 (online: 18 June 2018)

Short Communications

Influences of Black Locust (Robinia pseudoacacia L.) afforestation on soil microbial biomass and activity

Bolat I, Kara O, Sensoy H, Yüksel K

vol. 9, pp. 171-177 (online: 16 February 2015)

Research Articles

Soil C:N stoichiometry controls carbon sink partitioning between above-ground tree biomass and soil organic matter in high fertility forests

Alberti G, Vicca S, Inglima I, Belelli-Marchesini L, Genesio L, Miglietta F, Marjanovic H, Martinez C, Matteucci G, D’Andrea E, Peressotti A, Petrella F, Rodeghiero M, Cotrufo MF

vol. 8, pp. 195-206 (online: 26 August 2014)

Research Articles

Soil respiration and carbon balance in a Moso bamboo (Phyllostachys heterocycla (Carr.) Mitford cv. Pubescens) forest in subtropical China

Tang X, Fan S, Qi L, Guan F, Cai C, Du M

vol. 8, pp. 606-614 (online: 02 February 2015)

iForest Database Search

Search By Author

Search By Keyword

Google Scholar Search

Citing Articles

GScholar

Search By Author

Search By Keywords

PubMed Search

Search By Author

Search By Keyword

iForest - Biogeosciences and Forestry

Contents

Search

Journal Info

Journal Subjects and Fields

For Authors

For Reviewers

For Readers

SISEF Publishing

Search iForest Contents