Standing tree assessment for the maintenance of historic wooden buildings: a case study of a World Heritage site in China
iForest - Biogeosciences and Forestry, Volume 6, Issue 4, Pages 169-174 (2013)
doi: https://doi.org/10.3832/ifor0753-006
Published: May 08, 2013 - Copyright © 2013 SISEF
Research Articles
Abstract
Historic wooden buildings are a symbol of China’s “culture of wood” and require extraction of forest resources for their renovation. In the 21st century, natural resources are limited globally, and sustainable solutions are needed. In this study, we established a new method to connect building and forest sites for efficient utilization of limited forest resources for the renovation of historic buildings. We obtained measurements of large wooden components from Shenyang Imperial Palace. We also performed morphometric analyses on 47 thinned, old-growth larch trees to determine the relative taper curve, and selected 108 standing trees for simulation of the tree-height curve in the Mt. Changbai area, Jinlin Province, Northeast China. On the basis of forest metrology, we established an upper tree prediction method. By measuring the diameter at breast height (DBH) alone, we could compare size information (e.g., diameter, length) for standing trees and wooden building components. This method was then applied to estimate the required DBH class of standing trees for the renovation of Shenyang Imperial Palace.
Keywords
Sustainable Renovation, Relative Taper Curve, Tree Height Curve, Standing Tree Assessment, Historic Wooden Buildings
Introduction
Environmental protection has become one of the most urgent contemporary issues. Understanding the relationship between humans and nature requires that the wooden heritage buildings, a global concern, be considered the most important wealth for individuals who constantly reflect on their roles in nature ([14]). Intact historic wooden buildings are evidence of the wisdom and craftsmanship of ancient people and are of practical significance for exploring the sustainable use and restoration of renewable forest resources.
As of 2010, 29 world cultural heritage sites have been approved in China, including 14 timber-frame buildings. China includes 1080 historic building complexes that are listed as protected sites, more than half of which are timber-frame buildings. The International Council on Monuments and Sites (ICOMOS) under the auspices of the United Nations Educational, Scientific and Cultural Organization (UNESCO) established the “principles for the preservation of historic timber structures” that include the preservation of the “same tree species”, “tree quality” and “building techniques” ([16]). Therefore, the maintenance of traditional Chinese wooden buildings requires that specific types and quantities of high-quality wood be available in the timber market.
Recently, there has been a precipitous decrease in the production of large-diameter, high-quality wood due to social and economic changes. In 1998, the Chinese government implemented the Natural Forest Conservation Projects (NFCP) policy in an effort to promote forest management activities that prevent further deterioration of these resources ([2]). This policy, which emphasizes the protection of existing natural forests from excessive cutting, has been implemented in 18 provinces and several autonomous regions ([8]). Although this policy has facilitated ecological preservation, it has affected domestic timber production. The challenge of promoting conservation while seeking to acquire large volumes of wood from natural forests for historic renovation is not unique to China but is also experienced in countries such as Japan and Sweden ([10]).
Efficient utilization of natural forest resources is the key issue in renovating historic wooden buildings, and the amount of wood required from standing trees needs to be accurately assessed. Methods for estimating the upper stem diameter have been used by many researchers ([7], [3], [12], [1]) and can be considered as a tool for improving the economic utilization of timber.
The objective of this research was to develop a method for the identification of standing tree branches using the forest measurement techniques to obtain the large wood components required for the renovation of the Shenyang Imperial Palace. By using this method and the data acquired from the measurements of the building sites, we could predict the required standing tree size for the renovation of the Shenyang Imperial Palace. Such prediction will facilitate compatibility between building conservation and forest management and help promote sustainable management of historic wooden buildings in China.
Materials and methods
Two steps were taken to ensure consistency between the types of wooden structures that comprised the Shenyang Imperial Palace and the tree species present in the Mt. Changbai forest site: (1) measurement of wood structures and data collection from Shenyang Imperial Palace (building site); and (2) field work in the natural forest in the Mt. Changbai area (forest site).
Building Site
The Shenyang Imperial Palace is located in northeast China. Built in 1624-1625 (Qing Dynasty), the palace was catalogued as the 28th cultural heritage site of the UNESCO World Heritage Committee’s Ming and Qing Imperial Palace expansion projects, comparable to the Forbidden City in Beijing. The total land area occupied by the palace is approximately 0.6 km2 and includes 67 buildings ([11]).
Three-dimensional information (length, width, height) of wooden components was measured to determine the size of timbers that would be necessary for the renovation of Shenyang Imperial Palace. According to different architectural types, 28 representative buildings, including 4 major categories (column, beam, purlin, and tie-beam) were selected in this research. The remaining buildings having the same architectural features and forms of the 28 representative buildings were not measured.
Morphometric measurements of each large wooden component were obtained on the basis of the following sources ([16]):
- The building plans, including the floor plan, building-section plan, and cross-section plan (scale: 1:30, 1:40, and 1:50, respectively), drawn by Tianjin University.
- On-site measurement of the bottom diameter of the eave column of each of the 28 buildings in the palace complex to verify the accuracy of the data measured on the plan ([16]). The statistical test of accuracy was derived using the method proposed by Wang et al. ([13]).
Assuming that each large wooden building component was constructed using a single raw wooden column, and that the cross-sections of some wood components were square or polygonal, the maximum diagonal cross-section was calculated for each wooden component to estimate the diameter of the raw timber required.
Forest Site
Tree species
Old-growth larch (Larix olgensis) forests are primarily distributed in northeast China, in Jilin Province. Excessive logging in recent decades has led to the gradual reduction and eventually uneven distribution of natural larch forest. In this study, L. olgensis was selected as experimental tree species for two reasons: (1) it was used for many of the large wooden components found in imperial palaces ([6]); and (2) it is the main species of several rare natural forest reserves.
Study site description and sampling
As per the UNESCO guidelines, sites at Huang Songpu Forest Farm in the Baihe Forest District of Jilin Province (lat. 42°08’21”N, long. 128°16’53”E) were selected for allometric measurement. These sites are located 10 km north of the Mt. Changbai Biosphere Reserve area ([15]) and have a mean annual temperature of 5.0 °C. The lowest and highest monthly mean temperatures are -17.1 °C in January and 17.1 °C in July, respectively; mean annual precipitation is 719 mm ([18]).
Two adjacent sub-compartments with a total area of 6.57 ha were selected due to the first thinning activities conducted by Huang Songpu Forest Farm. Both the sub-compartments were representatives of natural, old-growth, multi-storied coniferous forest in northeast China. These forested areas are dominated by Changbai larch (L. olgensis Henry), followed by spruce (Picea jezoensis var. microsperma), Korean pine (Pinus koraiensis Sieb. et Zucc.), and fir (Abies nephrolepis, Trautv, Maxim).
Forty-seven trees were felled, and the total height of each was measured to the nearest 0.03 m. Diameter outside bark (DOB) was measured at breast height (DBH, 1.3 m). DOB was also measured at intervals of 2 m along the length of the stem, beginning at 0.3 m. The DOB at 1/10 tree height was recorded to create a relative taper curve. The maximum tree height (34.7 m), maximum DBH (67.8 cm), and maximum diameter at 1/10 tree height (58.2 cm) of the 47 trees sampled were recorded. In addition to the 47 thinned trees, the DBH and height of 61 standing trees in the same field area were measured. In total, 108 standing old-growth larch trees were measured to calculate the tree height curve.
Establishing the size exchange method for building components and standing trees based on tree height curve and relative taper curve
The relationship between tree height and DBH is considered to define the tree height curve (H-D). The Henricksen equation was applied to simulate the tree height curve (eqn. 1):
where H is the tree height, D is the DBH, and a and b are model parameters to be estimated.
The tree-height curve of L. olgensis in plantation forests has been estimated by several researchers; however, the majority of plantation trees were <50 years old ([17], [9]). To our knowledge, there is no literature reporting on the tree-height curve of old-growth larch in natural forests of Mt. Changbai. Thus, we calculated the curve based on the 108 samples from our study area.
Relative taper curve is the mathematical expression of the change in stem diameter as a function of stem height, which is calculated on the basis of tree conditions ([5] - eqn. 2):
where Dr is the relative diameter, D is the diameter at a specified height, and D0.1h is the diameter at 1/10 tree height; and (eqn. 3):
where Hr is the relative tree height, H is the tree height at a specified point, and Ht is the total tree height.
Measured field data (e.g., diameter at different heights) were converted into relative height and relative diameter to generate the model. Sato and co-workers ([12]) utilized a third-order equation to create a relative taper curve across an entire range of tree-height data. However, the portions of standing trees that can be utilized as timber for historic renovation occur within specific height intervals. Therefore, a third-order equation would reduce the accuracy of the results for our purposes. In this research, third-, fourth-, fifth-, and sixth-order formulae were applied separately for comparing the accuracy for specific tree-height intervals (eqn. 4, eqn. 5, eqn. 6, eqn. 7):
where Dr is the relative diameter, H is the relative height, and a to t are model coefficients to be estimated.
Assuming that wooden tree parts are cylindrical, the length of a trunk can be considered to be equal to the height from the ground, and the diameter can be considered to be equal along the length of the tree. Tree mensuration data were converted into 2 variables of a standing tree. The variables DBH, Hi (any height above ground) and Di (upper diameter at Hi) could be used to estimate Di on the basis of the other 2 variables. Following eqn. 1-7, the derivation process was as follows:
- DBH and eqn. 1 were used to deduce the total tree height.
- Total tree height and eqn. 3 were used to deduce the relative tree height at 1.3 m.
- The relative tree height at 1.3 m and eqn. 4, eqn. 5, eqn. 6, or eqn. 7 were used to deduce the relative diameter at 1.3 m.
- DBH and relative diameter at breast height were used to deduce D0.1h.
Hi, total tree height, and eqn. 3 were used to deduce the relative tree height at thatHi.- Relative tree height at
Hi and eqn. 4, eqn. 5, eqn. 6, or eqn. 7 were used to deduce the relative diameter atHi. - Known D0.1h, relative diameter at
Hi, and eqn. 2 were used to deduceDi.
Estimating the sapwood with bark value of standing trees
The information on wooden components from the building site and trees from the forest site were well connected; however, for renovation purposes, sapwood with bark could not be included as their physical and chemical properties are not suitable for construction. Therefore, the values of sapwood and bark were recorded together. For each sample, two perpendicular lines intersecting at the centre were measured in order to derive four sapwood with bark values; corresponding stem diameter values were also recorded. In all, 52 sets of paired data were measured.
Model evaluation
The criteria for model evaluation in this research followed recommendations by Kozak & Smith ([7]). The statistics used for comparing the models were average bias (B), standard error of the estimate (SE), and a fit index (FI). These evaluation statistics were expressed as (eqn. 8, eqn. 9, eqn. 10):
where Yi is value for the i-th observation, Ŷi is the predicted value for the i-th observation, Y is the mean of Yi values, k is the number of estimated parameters, and n is the number of observations in the dataset.
Results
Size of wooden building components
Statistical results ([16]) showed that direct measurements of eave columns and data derived from building plans coincide well (R2 = 0.94, p < 0.01), suggesting that the use of building plans to measure eave columns and other components is accurate.
The basic criteria for the selection of large wooden components used for the statistical analyses in this study were length ≥ 4 m and diameter ≥ 50 cm. A total of 368 large wooden components were calculated from the study materials, and these data were segregated and tallied by length and diameter in 1-m and 2-cm intervals, respectively (Tab. 1). There was no significant bias between the diameter of the bottom and top of each wooden component; thus the diameter reported in Tab. 1 is the bottom diameter value. The building site data revealed the longest wooden component to be a hypostyle column with length of 13.7 m. Tab. 1 shows that large wooden components ranged in size from 4 to 14 m long and from 50 to 86 cm in diameter.
Tab. 1 - Number of large-sized wooden components from Shenyang Imperial Palace.
| Diameter class (cm) |
Length (m) | Total | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 | 10-11 | 11-12 | 12-13 | 13-14 | ||
| 50-52 | 12 | - | 4 | 10 | - | 8 | - | - | - | - | 34 |
| 52-54 | 32 | 8 | - | 2 | - | - | - | - | - | - | 42 |
| 54-56 | 20 | - | 8 | 4 | - | - | - | - | - | - | 32 |
| 56-58 | - | 6 | 4 | - | - | - | - | - | - | 12 | 22 |
| 58-60 | - | 12 | 32 | - | - | - | - | - | - | - | 44 |
| 60-62 | - | - | - | - | - | - | - | - | - | - | 0 |
| 62-64 | - | - | 12 | 14 | - | - | - | - | - | - | 26 |
| 64-66 | - | 16 | - | - | - | - | - | - | - | - | 16 |
| 66-68 | 6 | - | - | - | - | - | - | - | - | - | 6 |
| 68-70 | - | - | - | 26 | - | - | - | - | - | - | 26 |
| 70-72 | - | 6 | - | - | - | - | 12 | - | - | - | 18 |
| 72-74 | - | - | - | 8 | 6 | - | 2 | - | - | - | 16 |
| 74-76 | - | - | 6 | 12 | - | 16 | - | - | - | - | 34 |
| 76-78 | - | - | 8 | - | - | - | - | - | - | - | 8 |
| 78-80 | - | - | - | - | - | - | 18 | - | - | 6 | 24 |
| 80-82 | - | - | - | - | 18 | - | - | - | - | - | 18 |
| 82-84 | - | - | - | - | - | - | - | - | - | - | 0 |
| 84-86 | - | - | - | - | - | 2 | - | - | - | - | 2 |
| Total | 70 | 48 | 74 | 76 | 24 | 26 | 32 | 0 | 0 | 18 | 368 |
Measurement of sapwood with bark value
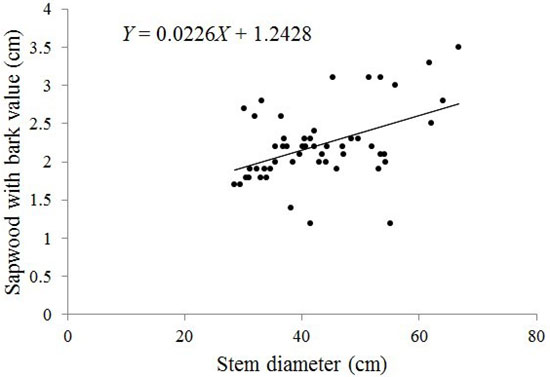
The relationship between stem diameter value and sapwood with bark value is shown in Fig. 1. The Kolmogorov-Smirnov test showed that the stem diameter value was significantly correlated with the sapwood with bark value (p = 0.001, correlation is significant at the 0.01 level). The correlation coefficient between stem diameter and the sapwood with bark value is 0.46. The linear regression model was calculated as (eqn. 11):
where Y is the sapwood with bark value (one side) and X is stem diameter.
Tree height curve
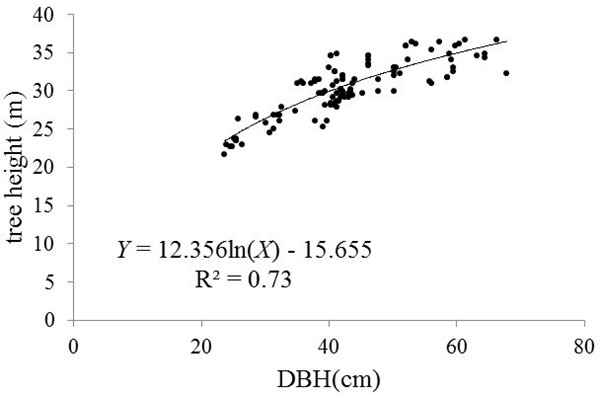
The range of sample DBH values varied from 23.6 to 67.8 cm, and tree height ranged from 21.7 to 36.8 m (Fig. 2). The relationship between DBH and tree height is evident from eqn. 12:
where Y is tree height and X is DBH.
Relative taper curve
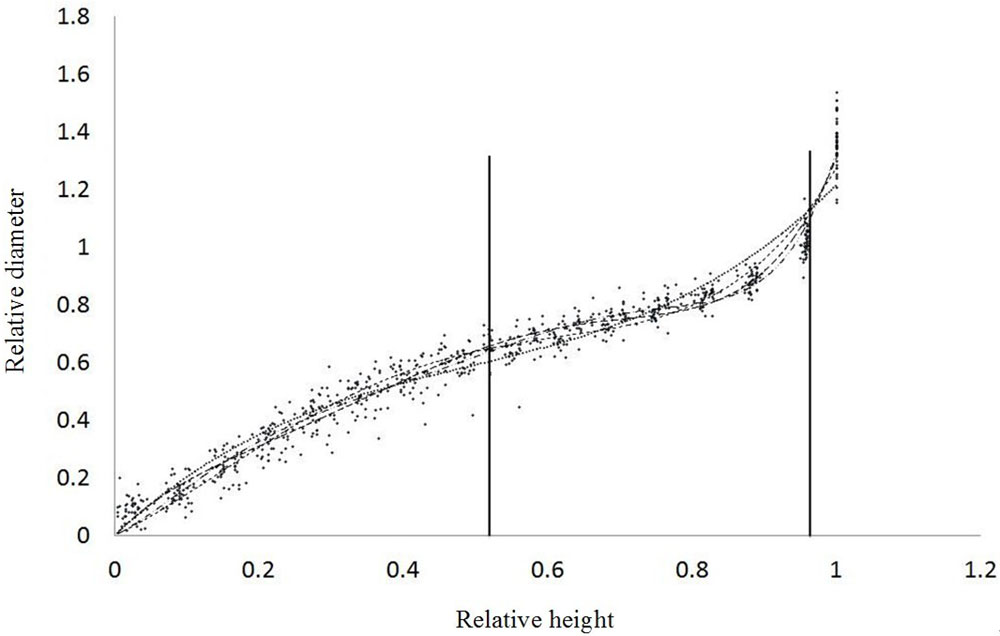
The third- through sixth-order equations were expressed as (eqn. 13 - 3rd order, eqn. 14 - 4th order, eqn. 15 - 5th order, eqn. 16 - 6th order, respectively):
Segmented polynomial models appear to be more accurate than other model formulations for estimating tree diameter ([4]). We compared eqn. 13 to 16 within a certain range for improving the overall statistical accuracy (Tab. 2). The longest wooden components from Shenyang Imperial Palace were up to 13.7 m. The portion of forest trees up to 1 m aboveground was not considered as useful timber material because of the trunk shape. Therefore, the useful range for supporting renovation of the historic palace was considered to be located between 1-14.7 m above ground. The average value of 47 samples used to generate the taper curve was 30.55 m in height; therefore, the segmented polynomial range was set on the scale between 0.52 and 0.97 (relative height - Fig. 3).
Tab. 2 - Segmented stem-fit statistics of for relative taper curve simulations.
| Equation | B | SEE | FI |
|---|---|---|---|
| Third-order | -0.019 | 0.0694 | 0.8271 |
| Fourth-order | -0.0071 | 0.0602 | 0.8441 |
| Fifth-order | -0.0081 | 0.0531 | 0.8411 |
| Sixth-order | -0.0046 | 0.0465 | 0.858 |
Overall statistics of fit (B, SEE, and FI) for the four segmented polynomial equations are presented in Tab. 2. The B value was negative for all equations, indicating that the predicted diameter was greater than the actual diameter. Size information derived from the model will thus be larger than the actual diameter in case the predicted value cannot satisfy the size of replacement wooden parts from the building site. The FI value indicates a trend of increasing fit with increasing equation order. When the estimated SEE values from eqn. 13 to eqn. 16 are transformed into actual diameter, the values are 2.87, 2.49, 2.19, and 1.93 cm, respectively. In this study, an acceptable error range for diameter is 2 cm, equal to the unit of measurement in the wood market. Therefore, the sixth-order equation was chosen for simulating the relative taper curve in this study.
The diameter of a tree’s upper section could be considered as a desirable size for wooden building components, because the upper diameter is considered to produce the maximum timber size. The derivation process presented in the methods (using eqn. 13 for relative taper curve) can be used to determine the diameter of a standing tree’s upper section by using the single measurement of DBH (Tab. 3). Furthermore, the estimation data must incorporate the two-sided value of sapwood with bark (calculated using eqn. 11). Finally, the suitability of standing trees for use in wooden components can be matched with the requirements of the building sites.
Tab. 3 - Upper diameter prediction for a given tree height.
| DBH (cm) |
Upper tree diameter prediction (m) | ||||||
|---|---|---|---|---|---|---|---|
| h = 3 | h = 4 | h = 5 | h = 6 | ... | h = 19 | h = 20 | |
| 40 | 33.4 | 31.6 | 30.6 | 30 | … | 18.8 | 17.6 |
| 42 | 35.1 | 33.2 | 32.1 | 31.4 | … | 20.1 | 18.9 |
| 44 | 36.8 | 34.7 | 33.5 | 32.9 | … | 21.4 | 20.2 |
| 46 | 38.5 | 36.3 | 35 | 34.3 | … | 22.7 | 21.5 |
| 48 | 40.2 | 37.9 | 36.5 | 35.8 | … | 24 | 22.7 |
| 50 | 41.9 | 39.5 | 38 | 37.2 | … | 25.3 | 24 |
| … | … | … | … | … | … | … | … |
| 70 | 59.1 | 55.5 | 53.2 | 51.8 | … | 38.4 | 36.8 |
| 80 | 67.8 | 63.6 | 60.8 | 59.1 | … | 45 | 43.3 |
| 90 | 76.5 | 71.7 | 68.5 | 66.5 | … | 51.7 | 49.9 |
| 100 | 85.2 | 79.8 | 76.2 | 73.8 | … | 58.4 | 56.4 |
For example, when the DBH of a standing tree is 50 cm (Tab. 3), the upper tree diameter at a tree height of 5 m is 38 cm. By applying eqn. 11, the two-sided sapwood with bark value at a tree height of 5 m can be calculated as (2.1 cm × 2 = 4.2 cm). Therefore, the maximum available diameter at a tree height of 5 m is: 38 cm - 4.2 cm = 33.8 cm. Furthermore, the lowest 1 m from ground of the trunk cannot be used as wooden parts for buildings since it has an irregular shape. In conclusion, standing trees that can produce timber having a diameter of 33.8 cm and a length of 4 m will have a minimum DBH of 50 cm. According to this method, the wooden parts’ information obtained from building sites is well associated with the DBH information obtained from the forest sites.
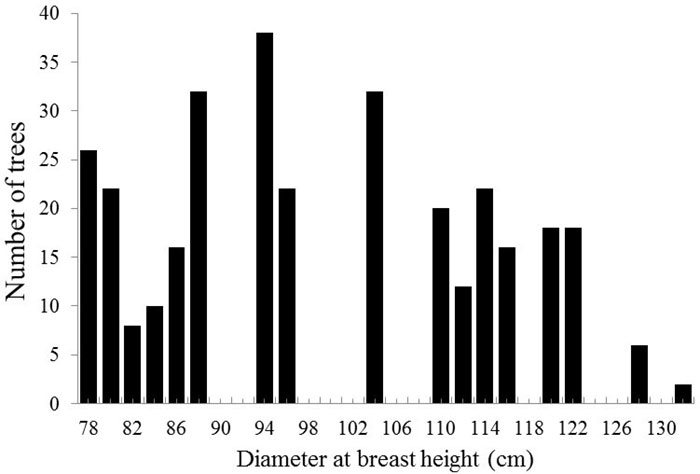
By using the information presented in Tab. 3 and the data on the requirements of the building site (Tab. 1), one can estimate the standing tree size requirements. Fig. 4 shows the number of Larix DBH size-classes required to support renovation of the Shenyang Imperial Palace.
Fig. 4 - Number of Larix trees by diameter class required to support the renovation of Shenyang Imperial Palace.
Discussion
Application of samples from forest sites
Tree samples collected from the forest had some limitations. For example, the largest tree had a length of 34.7 m and DBH of 67.8 cm. Thus, the diameter class under 67.8 cm can be estimated accurately, but estimation of larger trees may be of limited accuracy. We separated 47 tree samples into 2 groups based on D0.1h. Six samples were >45 cm at D0.1h (maximum D0.1h was 58.2 cm). For the remaining 41 samples, the maximum D0.1h was 44.6 cm. The SEE values of these 2 groups, simulated using sixth-order equations, were 0.01 and 0.04, respectively. Transferring the difference into real diameter (44.6 cm × 0.04 - 58.2 cm × 0.01), a value of 1.2 cm was obtained. Therefore, the size of the sample trees would not significantly affect the relative taper curve, and the method of estimating upper tree diameter can also be applied to larger samples. The method confirmed that the relative taper curve can be stabilized by dividing existing samples into 2 groups; nevertheless, there is still uncertainty for predicting the taper curve for some samples that have larger diameter beyond the sample’s size. The predicted values in Tab. 3 (e.g., DBH >70 cm) were obtained by extrapolating from the taper curve; accordingly, the results may be inaccurate. Therefore, future research should test the accuracy of the created relative taper curve.
Rethinking the outline of ICOMOS and the possibility of shifting NFCP policy
According to our experimental results, availability of large-size timber material in China is unlikely to be sufficient to meet the requirements of historic renovation. This problem is not exclusive to China; it is relevant in other countries where wooden buildings play an important historical role. In Japan, obtaining good-quality wood from natural forests is a serious problem. Former conservators used alternative tree species that could be obtained easily when the preferred tree was not available ([10]). In Norway, the Wood Bank Project was implemented in 1992 to supply lumber for the renovation of 300 middle-age wood buildings.
Our results (Fig. 4) suggest that the estimated required DBH value of standing trees ranges from 78 to 136 cm for the renovation of the Shenyang Imperial Palace. This range of DBH represents extremely high-quality forest resources, which we did not find based on our experimental forest work. The ICOMOS ideals are summarized with the phrase: “Same tree species, tree quality and building technique”. These ideals will be difficult to realize for the reasons discussed in this paper. Efforts should be made regarding both building and forest sites. In the case of building sites, it should be a priority to compile details on the volume of wooden components that comprise each site. With regard to forest sites, an alternative system of tree production should be devised to enable maintenance of renovation cycles for historic wooden buildings. Because the wood supply cannot be derived from natural forest resources alone, an effective combination that utilizes plantation and natural forest resources will be necessary.
Conclusions
This research developed an efficient method for identifying upper tree diameter based on natural forests in the Mt. Changbai area, northeast China. By applying this method, we transferred the information on wooden components from a historic building site into DBH information on standing trees and estimated available standing tree resources for the renovation of the Shenyang Imperial Palace. Nevertheless, further attempts to bridge the sometimes-contrasting interests of building renovation and forest management are required.
Acknowledgments
This study was funded by a Grant-in-Aid for Scientific Research, Scientific Research-A, No. 20240074 (2008-2010) and No. 23240113 (2011-2013) from the Japan Society for the Promotion of Science. We would like to thank Sun Chen, Marcin, and Yang Jian for their efforts on this paper; Sato Juri and Assist. Prof. Terada for their kind advices; and Prof. Yin Mingfang and their collegues for support in the field work.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
H Yamamoto
Graduate School of Frontier Science, the University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, 277-8563 Chiba (Japan)
Corresponding author
Paper Info
Citation
Yin W, Yamamoto H (2013). Standing tree assessment for the maintenance of historic wooden buildings: a case study of a World Heritage site in China. iForest 6: 169-174. - doi: 10.3832/ifor0753-006
Academic Editor
Marco Borghetti
Paper history
Received: Aug 29, 2012
Accepted: Mar 07, 2013
First online: May 08, 2013
Publication Date: Aug 01, 2013
Publication Time: 2.07 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2013
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 53541
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 45410
Abstract Page Views: 2837
PDF Downloads: 3826
Citation/Reference Downloads: 19
XML Downloads: 1449
Web Metrics
Days since publication: 4577
Overall contacts: 53541
Avg. contacts per week: 81.88
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2013): 6
Average cites per year: 0.46
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Simplified methods to inventory the current annual increment of forest standing volume
vol. 5, pp. 276-282 (online: 17 December 2012)
Research Articles
Comparative analysis of taper models for Pinus nigra Arn. using terrestrial laser scanner acquired data
vol. 17, pp. 203-212 (online: 22 July 2024)
Research Articles
Analyzing regression models and multi-layer artificial neural network models for estimating taper and tree volume in Crimean pine forests
vol. 17, pp. 36-44 (online: 28 February 2024)
Research Articles
Compatible taper-volume models of Quercus variabilis Blume forests in north China
vol. 10, pp. 567-575 (online: 08 May 2017)
Research Articles
Site quality assessment of degraded Quercus frainetto stands in central Greece
vol. 8, pp. 53-58 (online: 12 May 2014)
Research Articles
Modelling taper and stem volume considering stand density in Eucalyptus grandis and Eucalyptus dunnii
vol. 14, pp. 127-136 (online: 16 March 2021)
Research Articles
Environmental Kuznets curve for deforestation: evidence using GMM estimation for OECD and non-OECD regions
vol. 10, pp. 196-203 (online: 13 December 2016)
Research Articles
Climatic factors defining the height growth curve of forest species
vol. 10, pp. 547-553 (online: 05 May 2017)
Research Articles
Nonlinear mixed model approaches to estimating merchantable bole volume for Pinus occidentalis
vol. 5, pp. 247-254 (online: 24 October 2012)
Research Articles
Total tree height predictions via parametric and artificial neural network modeling approaches
vol. 15, pp. 95-105 (online: 21 March 2022)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword